Vibration Power Flow and Transfer Path Analysis of Two-Dimensional Truss Structure by Impedance Synthesis Method
Abstract
:1. Introduction
2. Dynamic Response of Truss Structure
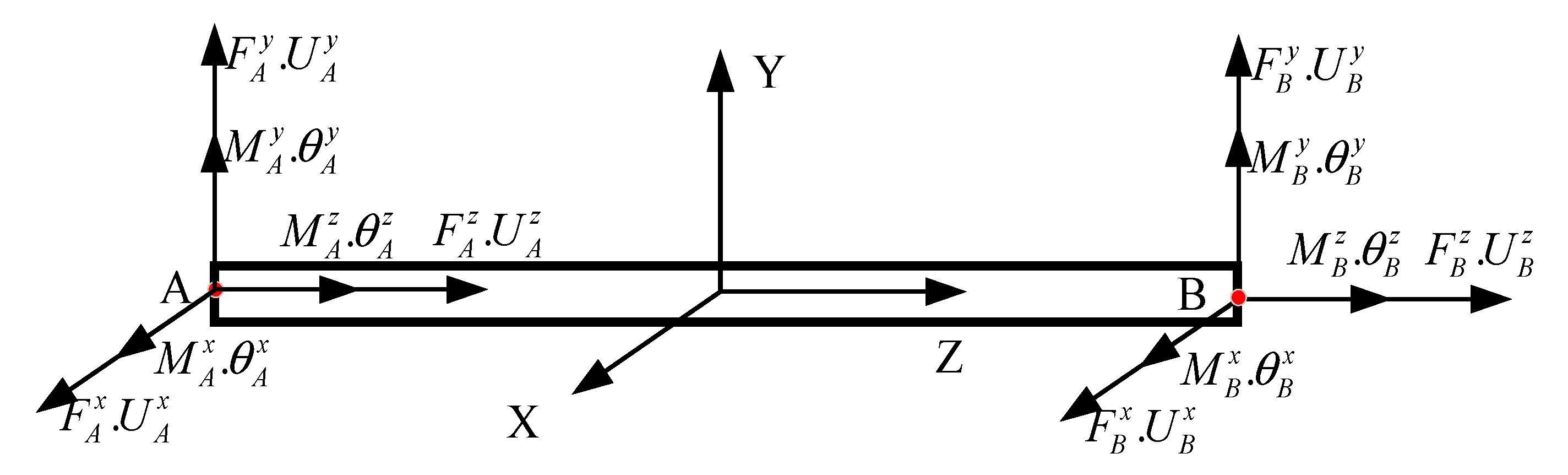
2.1. Impedance Matrix of Truss Beam
2.2. Locally and Global Coordinate Transfer and Assemble
3. Numerical Discussion
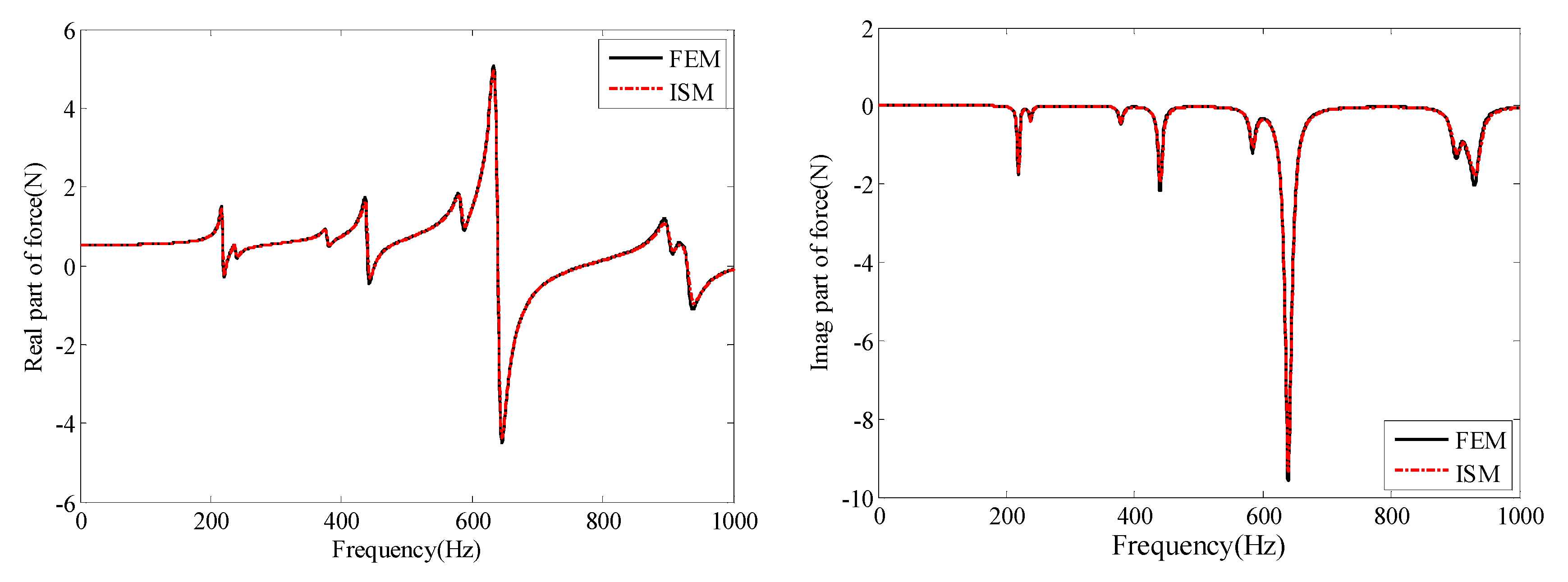
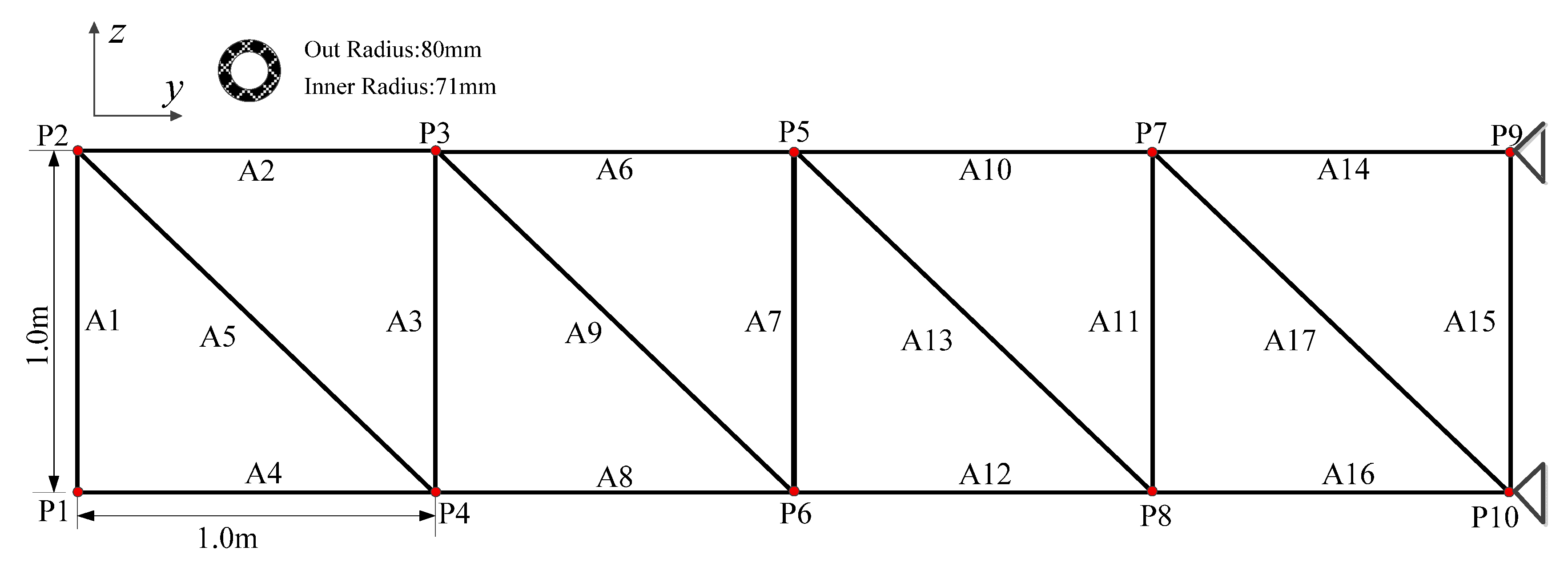
3.1. Simple Truss Structure
3.2. Periodic Frame Structure
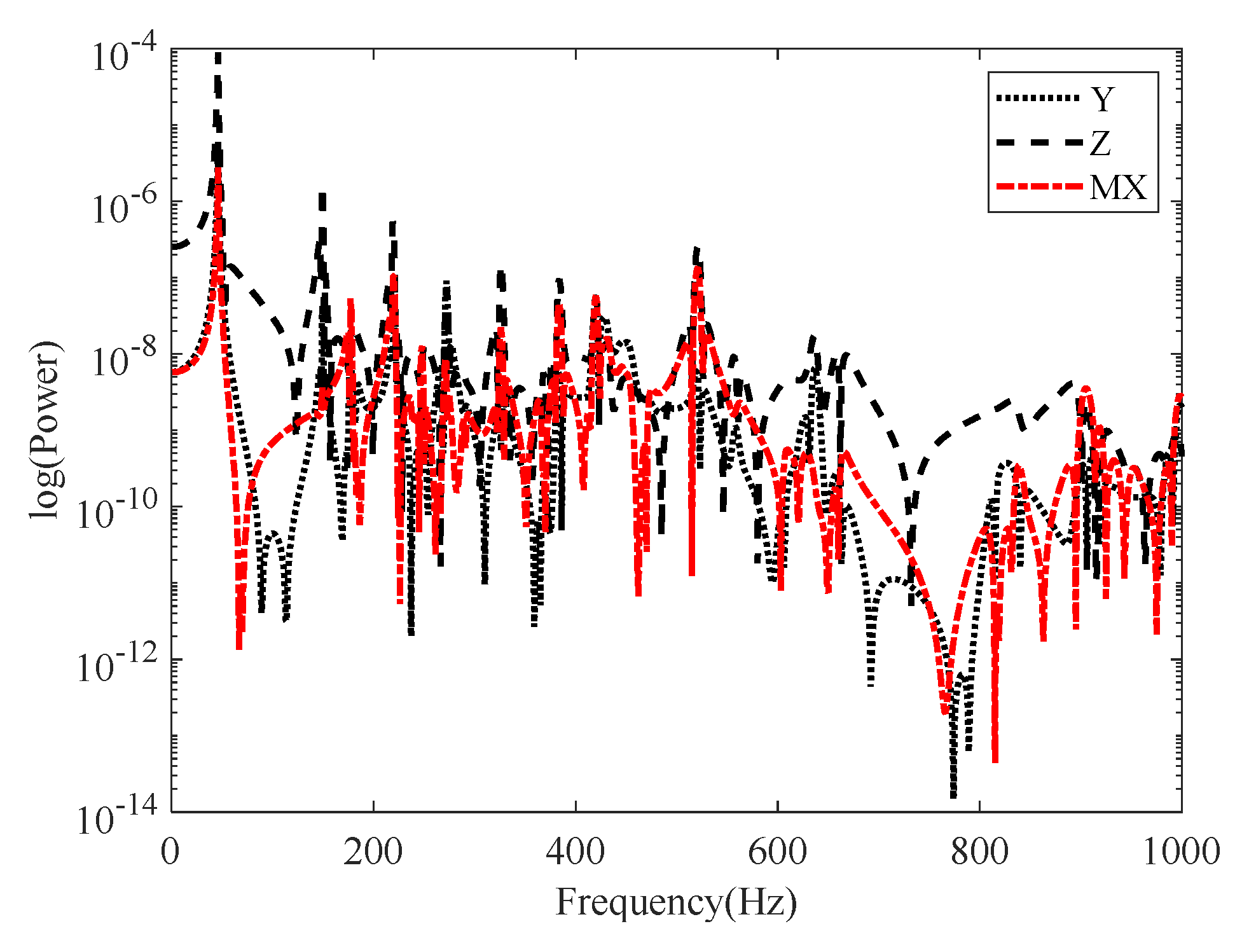
3.3. Analysis of Vibration Power Flow
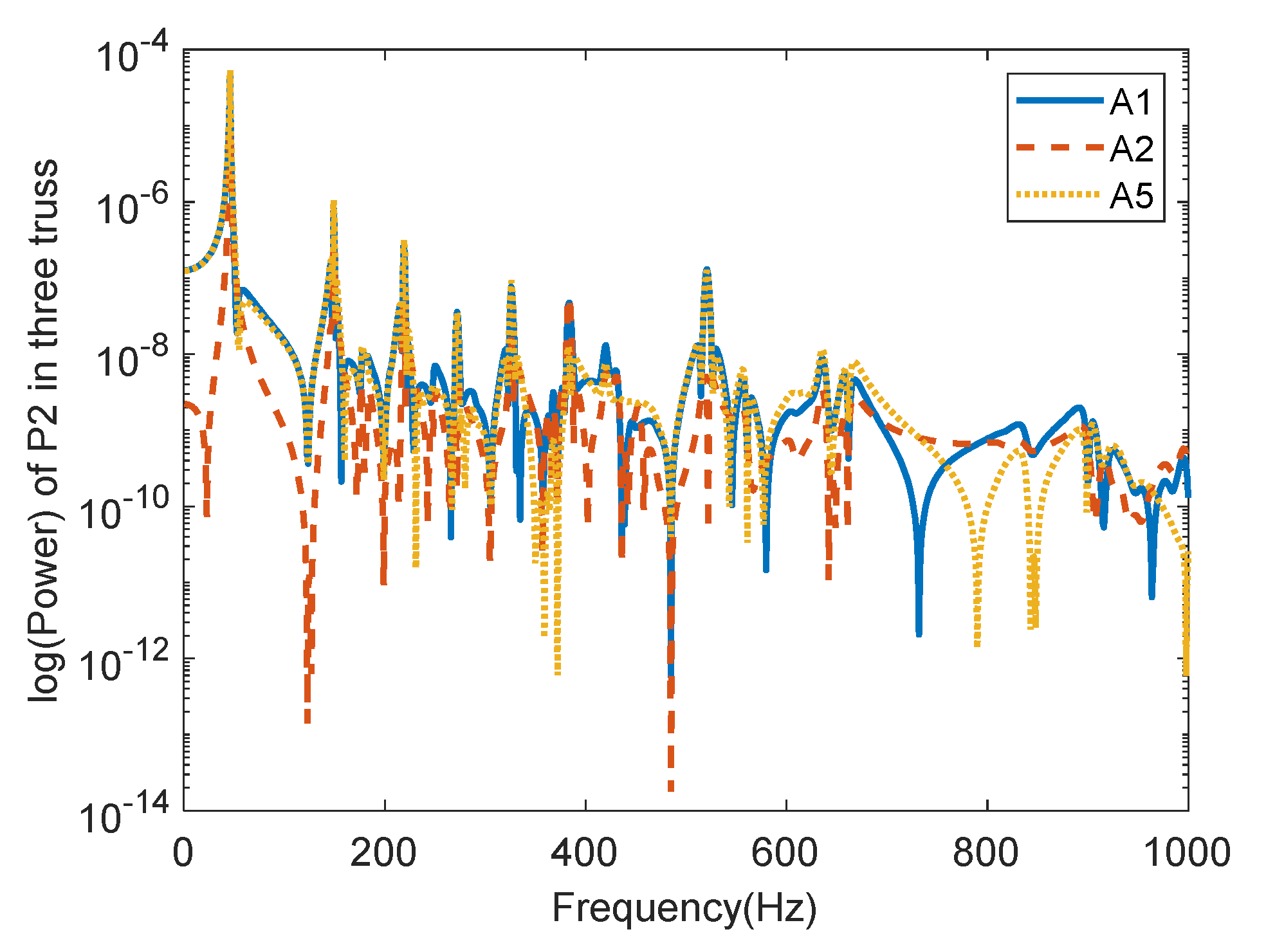
3.4. Transfer Path Analysis of Power Flow
4. Conclusions
- (1)
- The ISM can be effectively applied to investigate the dynamic responses and vibration power flow of truss-like structures, especially in mid- and high-frequency ranges;
- (2)
- Cross-section of the truss beam has a litter effect on the dynamic responses of the whole structure in the low-frequency domain, but can affect the dynamic responses in mid- and high-frequency ranges;
- (3)
- Transfer path analysis can find the main transfer path and line spectrum frequency of complex truss-like structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Shan, J.; Zhang, Y. Dynamics modeling and analysis of spacecraft with large deployable hoop-truss antenna. J. Spacecr. Rocket. 2016, 53, 471–479. [Google Scholar] [CrossRef]
- Bondaryk, J.E. Vibration of truss structures. J. Acoust. Soc. Am. 1997, 102, 2167–2175. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Khaji, N.; Moharrami, H.; Bahreininejad, A. Damage detection of truss bridge joints using artificial neural networks. Expert Syst. Appl. 2008, 35, 1122–1131. [Google Scholar] [CrossRef]
- Kaya, M.O.; Ozgumus, O.O. Flexural–torsional-coupled vibration analysis of axially loaded closed-section composite Timoshenko beam by using DTM. J. Sound Vib. 2007, 306, 495–506. [Google Scholar] [CrossRef]
- Aksencer, T.; Aydogdu, M. Vibration of a rotating composite beam with an attached point mass. Compos. Struct. 2018, 190, 1–9. [Google Scholar] [CrossRef]
- Zhou, D. Free vibration of multi-span Timoshenko beams using static Timoshenko beam functions. J. Sound Vib. 2001, 241, 725–734. [Google Scholar] [CrossRef]
- Lin, H.P.; Chang, S.C. Free vibration analysis of multi-span beams with intermediate flexible constraints. J. Sound Vib. 2005, 281, 155–169. [Google Scholar] [CrossRef]
- Wu, J.S.; Chen, C.T. A lumped-mass TMM for free vibration analysis of a multi-step Timoshenko beam carrying eccentric lumped masses with rotary inertias. J. Sound Vib. 2007, 301, 878–897. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.Y. Free vibration analysis using the transfer-matrix method on a tapered beam. Comput. Struct. 2016, 164, 75–82. [Google Scholar] [CrossRef]
- Jun, L.; Hongxing, H. Dynamic stiffness analysis of laminated composite beams using trigonometric shear deformation theory. Compos. Struct. 2009, 89, 433–442. [Google Scholar] [CrossRef]
- Zhu, H.Z.; Wang, W.B.; Yin, X.W.; Gao, C.F. Spectral element method for vibration analysis of three-dimensional pipes conveying fluid. Int. J. Mech. Mater. Des. 2019, 15, 345–360. [Google Scholar] [CrossRef]
- Tho, N.C.; Ta, N.T.; Thom, D.V. New numerical results from simulations of beams and space frame systems with a tuned mass damper. Materials 2019, 12, 1329. [Google Scholar] [CrossRef] [PubMed]
- Tho, N.C.; Thanh, N.T.; Tho, T.D.; Van Minh, P.; Hoa, L.K. Modelling of the flexoelectric effect on rotating nanobeams with geometrical imperfection. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 510. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Hong, T.T.; Vinh, P.V.; Thom, D.V. An efficient beam element based on Quasi-3D theory for static bending analysis of functionally graded beams. Materials 2019, 12, 2198. [Google Scholar] [CrossRef] [PubMed]
- Nguyen Thai, D.; Minh, P.V.; Phan Hoang, C.; Ta Duc, T.; Nguyen Thi Cam, N.; Nguyen Thi, D. Bending of symmetric sandwich FGM beams with shear connectors. Math. Probl. Eng. 2021, 2021, 7596300. [Google Scholar] [CrossRef]
- Abbas, I.A. Three-phase lag model on thermoelastic interaction in an unbounded fiber-reinforced anisotropic medium with a cylindrical cavity. J. Comput. Theor. Nanosci. 2014, 11, 987–992. [Google Scholar] [CrossRef]
- Abbas, I.A.; Abo-Dahab, S.M. On the numerical solution of thermal shock problem for generalized magneto-thermoelasticity for an infinitely long annular cylinder with variable thermal conductivity. J. Comput. Theor. Nanosci. 2014, 11, 607–618. [Google Scholar] [CrossRef]
- Vasilyeva, M.; Ammosov, D.; Vasil’ev, V. Finite element simulation of thermo-mechanical model with phase change. Computation 2021, 9, 5. [Google Scholar] [CrossRef]
- An, X.; Fan, H.; Zhang, C. Elastic wave and vibration bandgaps in planar square metamaterial-based lattice structures. J. Sound Vib. 2020, 475, 115292. [Google Scholar] [CrossRef]
- Liu, X.; Yan, S. Bandgap and wave propagation of spring-mass-truss elastic metamaterial with a scissor-like structure. J. Phys. D Appl. Phys. 2021, 55, 055303. [Google Scholar] [CrossRef]
- Martinsson, P.G.; Movchan, A.B. Vibrations of lattice structures and phononic band gaps. Q. J. Mech. Appl. Math. 2003, 56, 45–64. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, T.; Wang, Z.; Tang, Y. Band gap characteristics of flexural wave of two-dimensional periodic frame structure composed of locally resonant composite beam. Mech. Syst. Signal Process. 2019, 131, 364–380. [Google Scholar] [CrossRef]
- Zuo, S.L.; Li, F.M.; Zhang, C. Numerical and experimental investigations on the vibration band-gap properties of periodic rigid frame structures. Acta Mech. 2016, 227, 1653–1669. [Google Scholar] [CrossRef]
- Wu, Z.J.; Wang, Y.Z.; Li, F.M. Analysis on band gap properties of periodic structures of bar system using the spectral element method. Waves Random Complex Media 2013, 23, 349–372. [Google Scholar] [CrossRef]
- Wu, Z.J.; Li, F.M.; Zhang, C. Vibration band-gap properties of three-dimensional Kagome lattices using the spectral element method. J. Sound Vib. 2015, 341, 162–173. [Google Scholar] [CrossRef]
- Yong, X.; Mace, B.R.; Xisen, W. Wave propagation in periodic truss beams with members of different materials. In Proceedings of the 16th International Congress on Sound and Vibration: Recent Developments in Acoustics, Noise and Vibration, Krakow, Poland, 4–8 July 2009. [Google Scholar]
- Pan, J.; Hansen, C.H. Active control of total vibratory power flow in a beam. I: Physical system analysis. J. Acoust. Soc. Am. 1991, 89, 200–209. [Google Scholar] [CrossRef]
- Horner, J.L.; White, R.G. Prediction of vibrational power transmission through bends and joints in beam-like structures. J. Sound Vib. 1991, 147, 87–103. [Google Scholar] [CrossRef]
- Wang, Z.H.; Xing, J.T.; Price, W.G. Power flow analysis of indeterminate rod/beam systems using a substructure method. J. Sound Vib. 2002, 249, 3–22. [Google Scholar] [CrossRef]
- Signorelli, J.; Von Flotow, A.H. Wave propagation, power flow, and resonance in a truss beam. J. Sound Vib. 1988, 126, 127–144. [Google Scholar] [CrossRef]
- Beale, L.S.; Accorsi, M.L. Power flow in two-and three-dimensional frame structures. J. Sound Vib. 1995, 185, 685–702. [Google Scholar] [CrossRef]
- Rubin, S. Transmission matrices for vibration and their relation to admittance and impedance. J. Manuf. Sci. Eng. 1964, 86, 9–21. [Google Scholar] [CrossRef]
- Wu, J.H.; Tijsseling, A.S.; Sun, Y.D.; Yin, Z.Y. In-plane wave propagation analysis of fluid-filled L-shape pipe with multiple supports by using impedance synthesis method. Int. J. Press. Vessel. Pip. 2020, 188, 104234. [Google Scholar] [CrossRef]
- Wu, J.H.; Zhu, H.Z.; Sun, Y.D.; Yin, Z.Y.; Su, M.Z. Reduction of flexural vibration of a fluid-filled pipe with attached vibration absorbers. Int. J. Press. Vessel. Pip. 2021, 194, 104525. [Google Scholar] [CrossRef]
- Wu, J.H.; Zhu, H.Z.; Yin, Z.Y.; Sun, Y.D. Vibration wave propagation analysis of a liquid-filled pipe–plate coupled system with multiple supports. AIP Adv. 2021, 11, 025110. [Google Scholar] [CrossRef]
- Lesmez, M.W.; Wiggert, D.C.; Hatfield, F.J. Modal analysis of vibrations in liquid-filled piping systems. ASME J. Fluids Eng. 1990, 112, 311–318. [Google Scholar] [CrossRef]
- Casimir, J.B.; Nguyen, M.C.; Tawfiq, I. Thick shells of revolution: Derivation of the dynamic stiffness matrix of continuous elements and application to a tested cylinder. Comput. Struct. 2007, 85, 1845–1857. [Google Scholar] [CrossRef]
- Thinh, T.I.; Nguyen, M.C. Dynamic stiffness matrix of continuous element for vibration of thick cross-ply laminated composite cylindrical shells. Compos. Struct. 2013, 98, 93–102. [Google Scholar] [CrossRef]
- Goyder HG, D.; White, R.G. Vibrational power flow from machines into built-up structures, part I: Introduction and approximate analyses of beam and plate-like foundations. J. Sound Vib. 1980, 68, 59–75. [Google Scholar] [CrossRef]
- van der Seijs, M.V.; de Klerk, D.; Rixen, D.J. General framework for transfer path analysis: History, theory and classification of techniques. Mech. Syst. Signal Process. 2016, 68, 217–244. [Google Scholar] [CrossRef]
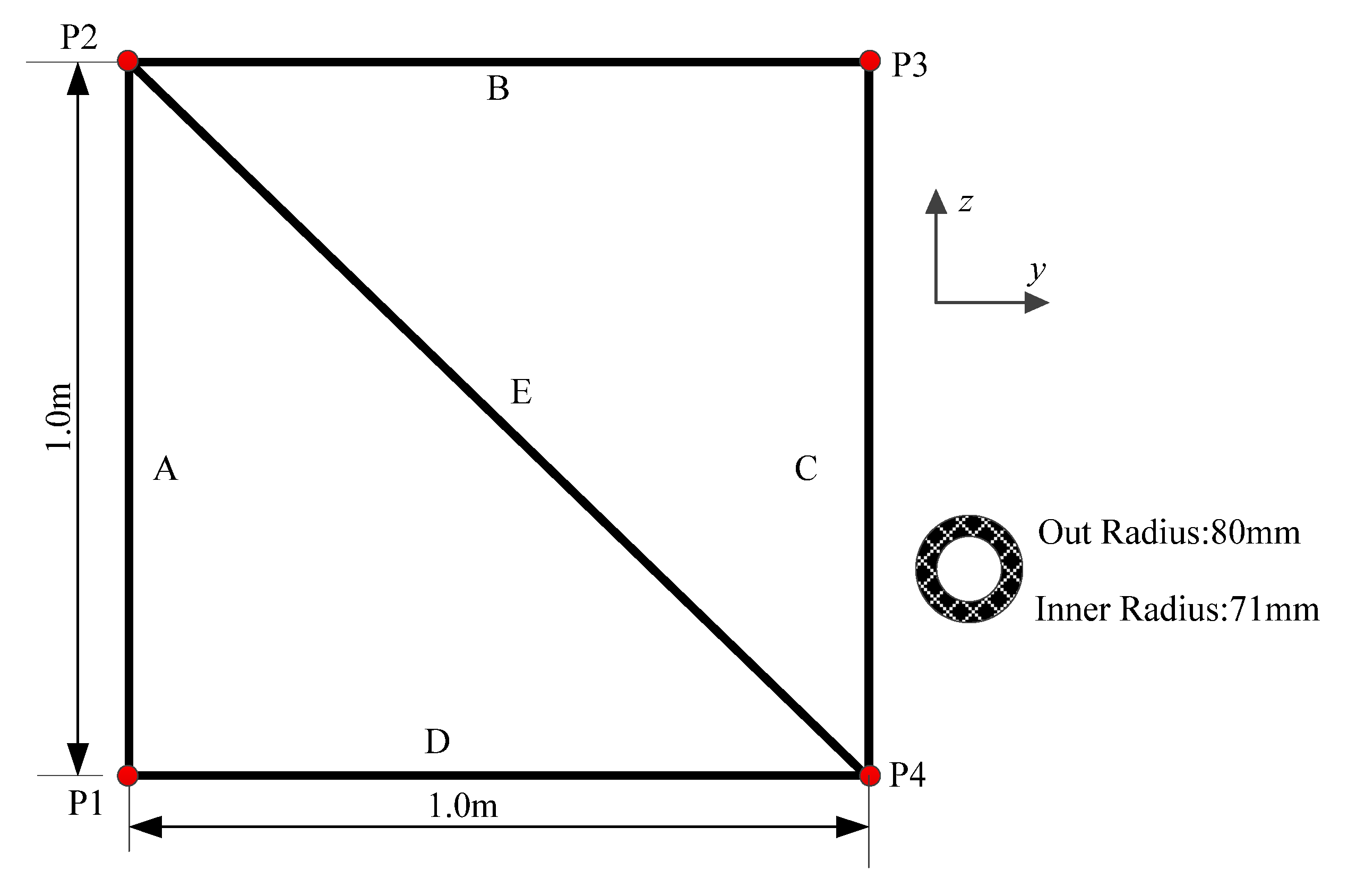
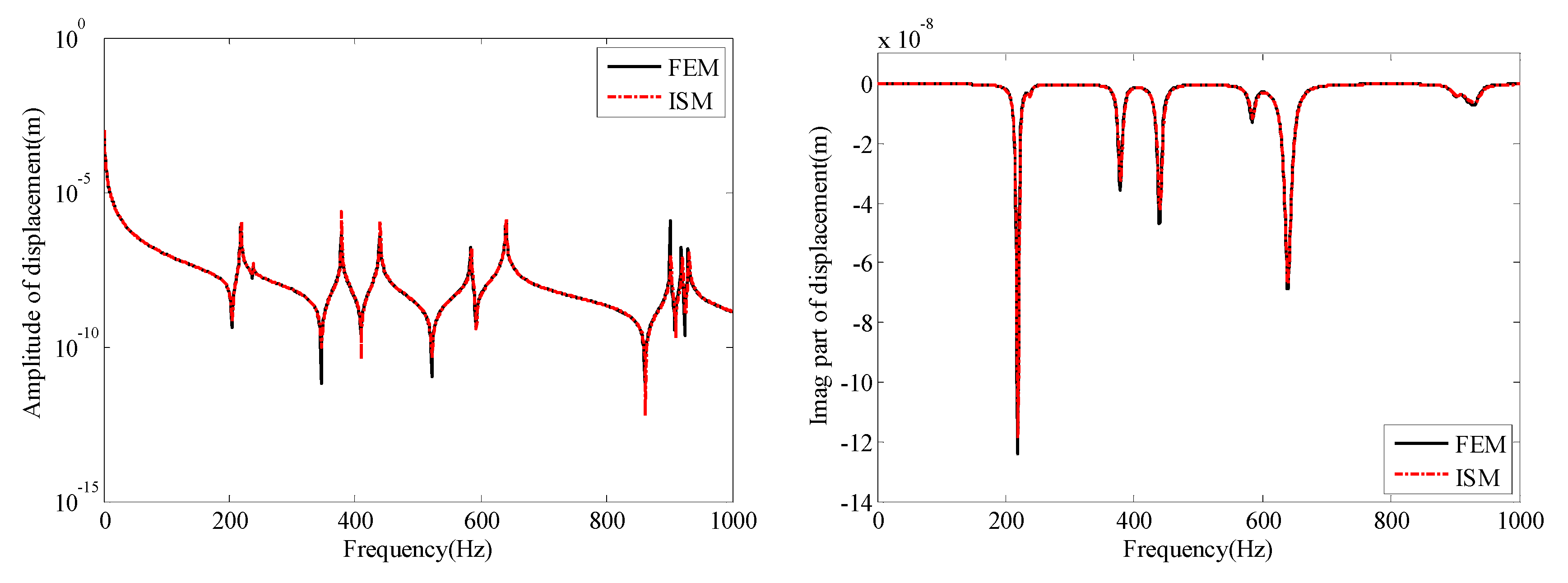
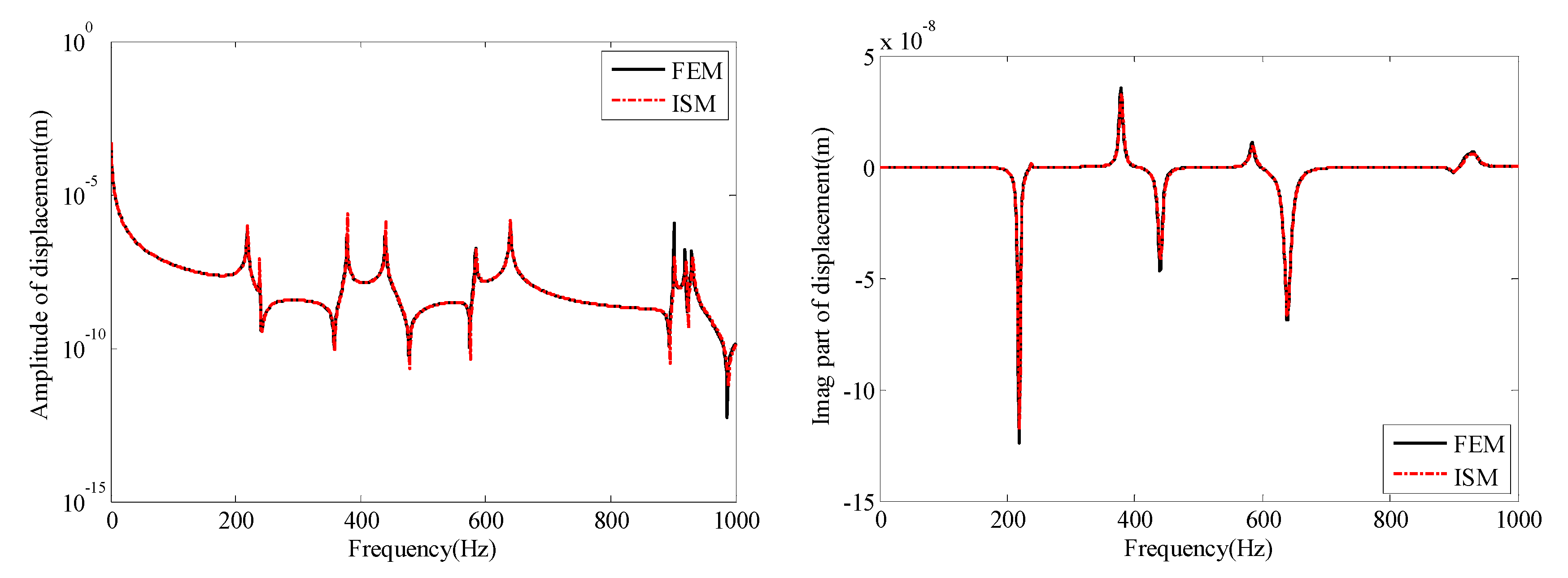


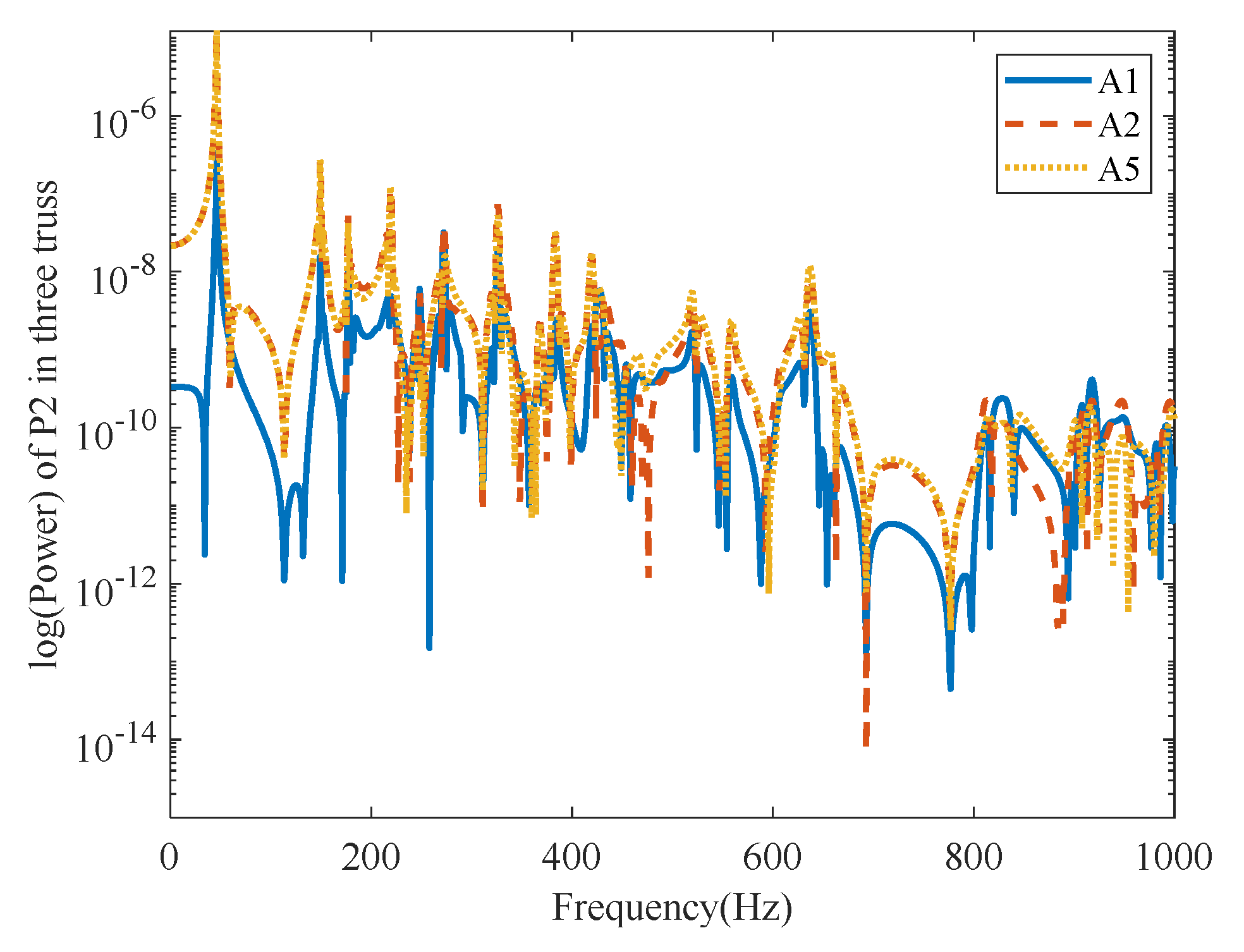

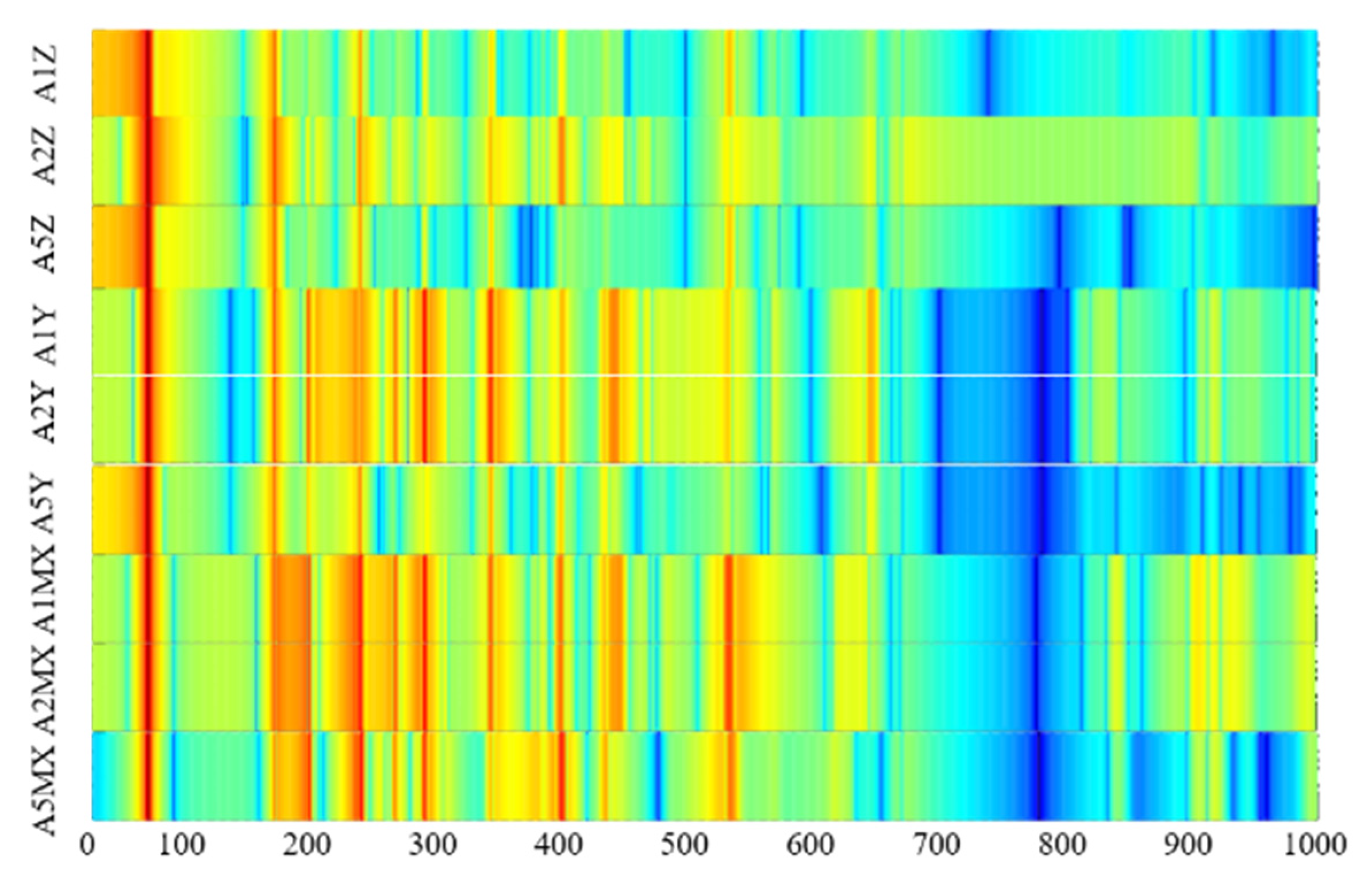
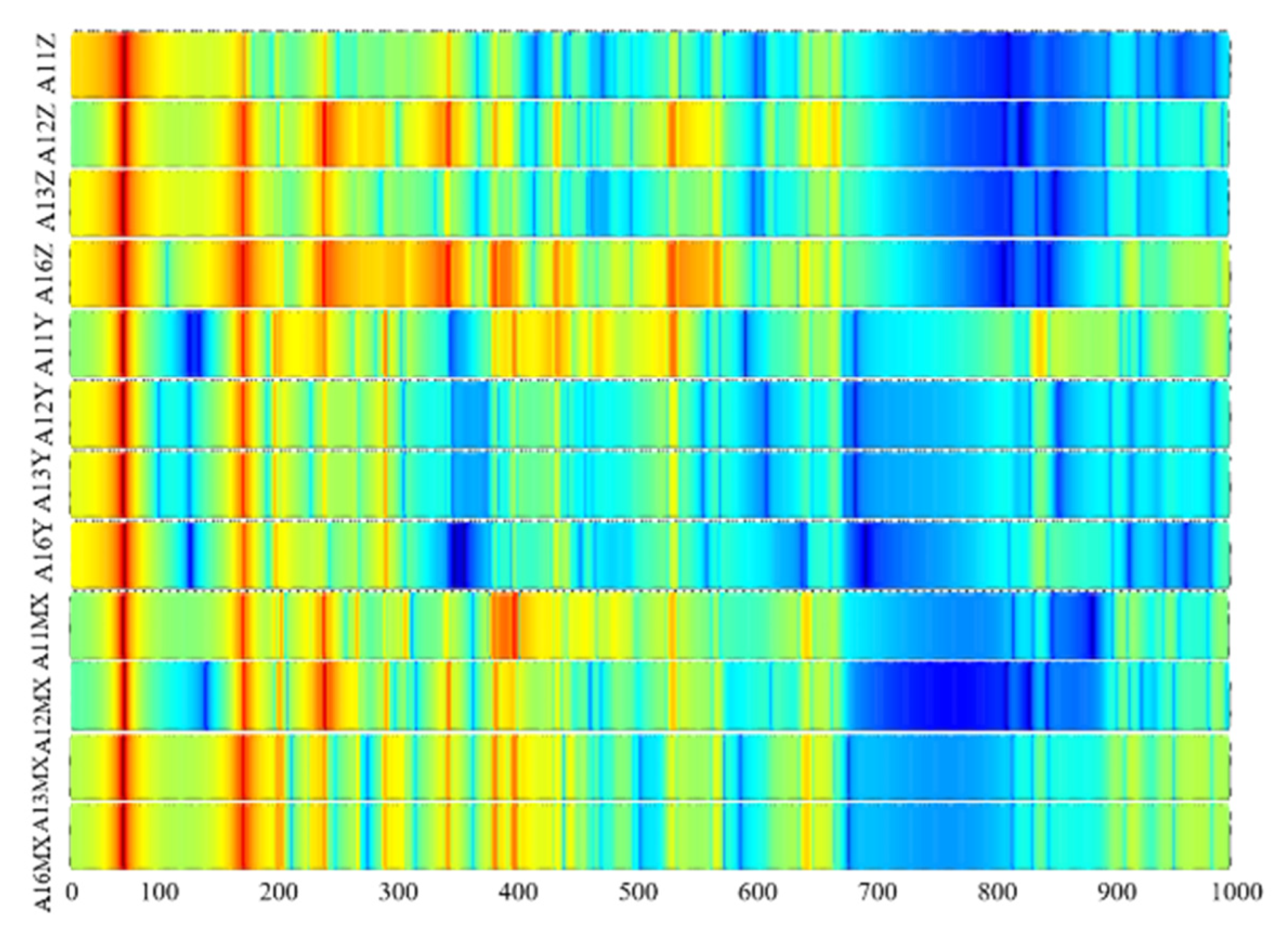
| Modes No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Zuo [23] | 4.71 | 27.58 | 70.09 | 85.58 | 122.55 | 176.45 | 224.25 | 232.45 |
| FEM (400 elements) | 4.71 | 27.58 | 70.16 | 85.68 | 122.94 | 177.81 | 228.60 | 236.88 |
| FEM (800 elements) | 4.71 | 27.58 | 70.11 | 85.60 | 122.65 | 176.73 | 225.24 | 233.45 |
| The present | 4.71 | 27.58 | 70.08 | 85.57 | 122.55 | 176.38 | 224.10 | 232.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.-Z.; Wu, J.-H.; Sun, Y.-D. Vibration Power Flow and Transfer Path Analysis of Two-Dimensional Truss Structure by Impedance Synthesis Method. Appl. Sci. 2022, 12, 8863. https://doi.org/10.3390/app12178863
Zhu H-Z, Wu J-H, Sun Y-D. Vibration Power Flow and Transfer Path Analysis of Two-Dimensional Truss Structure by Impedance Synthesis Method. Applied Sciences. 2022; 12(17):8863. https://doi.org/10.3390/app12178863
Chicago/Turabian StyleZhu, Hong-Zhen, Jiang-Hai Wu, and Yu-Dong Sun. 2022. "Vibration Power Flow and Transfer Path Analysis of Two-Dimensional Truss Structure by Impedance Synthesis Method" Applied Sciences 12, no. 17: 8863. https://doi.org/10.3390/app12178863
APA StyleZhu, H.-Z., Wu, J.-H., & Sun, Y.-D. (2022). Vibration Power Flow and Transfer Path Analysis of Two-Dimensional Truss Structure by Impedance Synthesis Method. Applied Sciences, 12(17), 8863. https://doi.org/10.3390/app12178863






