Machine Learning and Deep Learning Models Applied to Photovoltaic Production Forecasting
Abstract
:Featured Application
Abstract
1. Introduction
2. Application and Assessment of Models
2.1. Data Preparation
2.2. Modeling
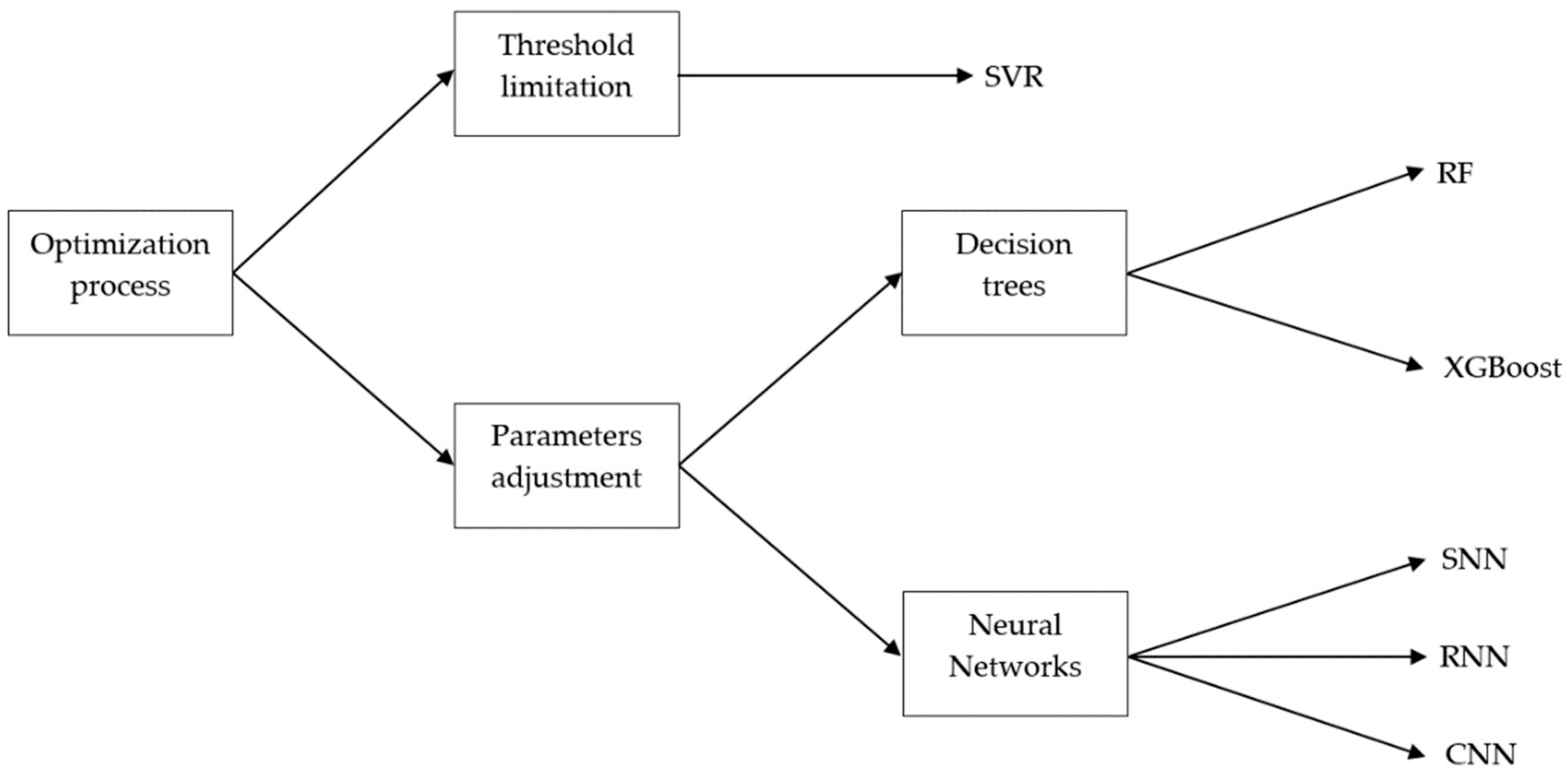
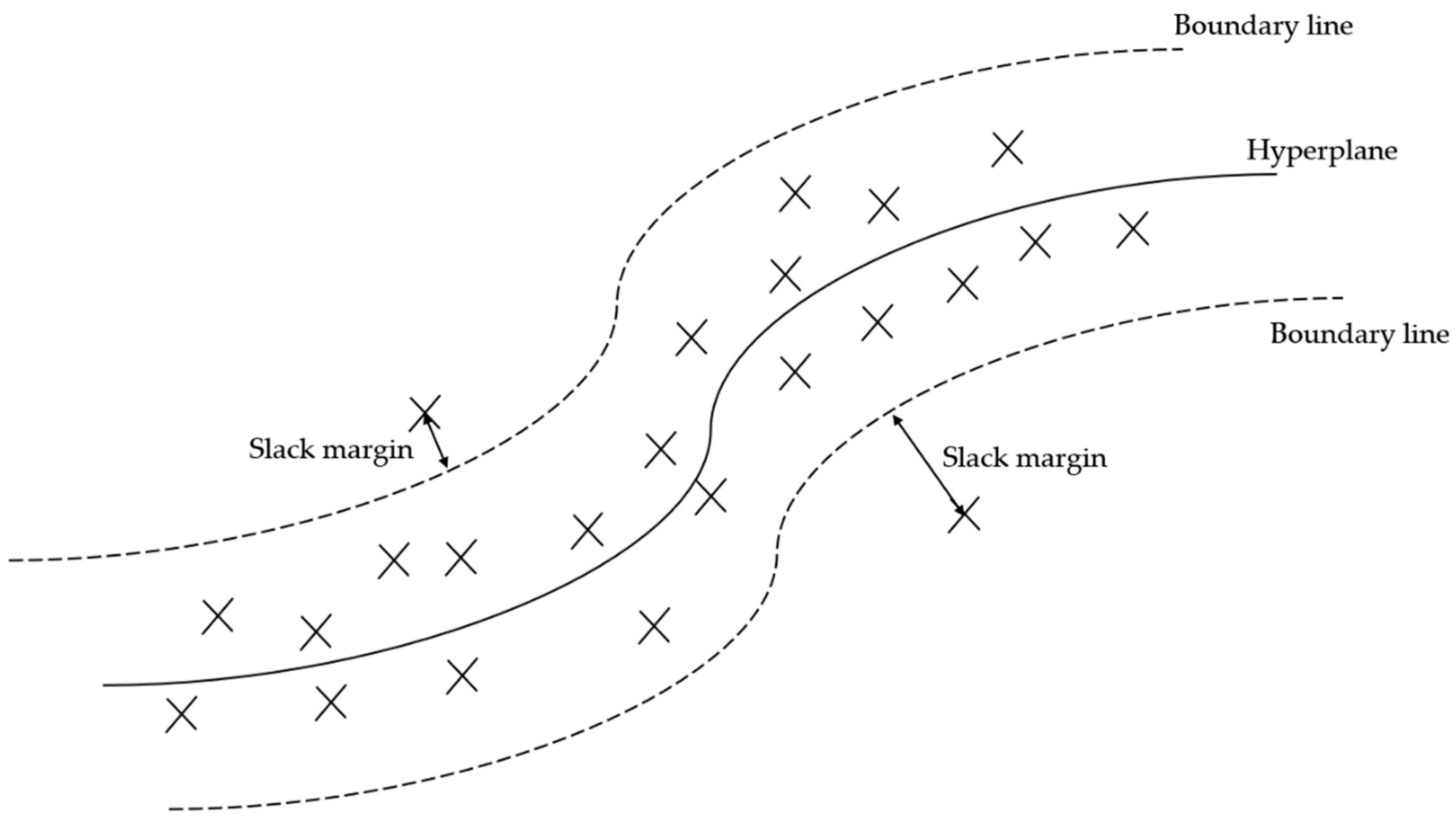
2.2.1. Optimization Carried out by Threshold Limitation
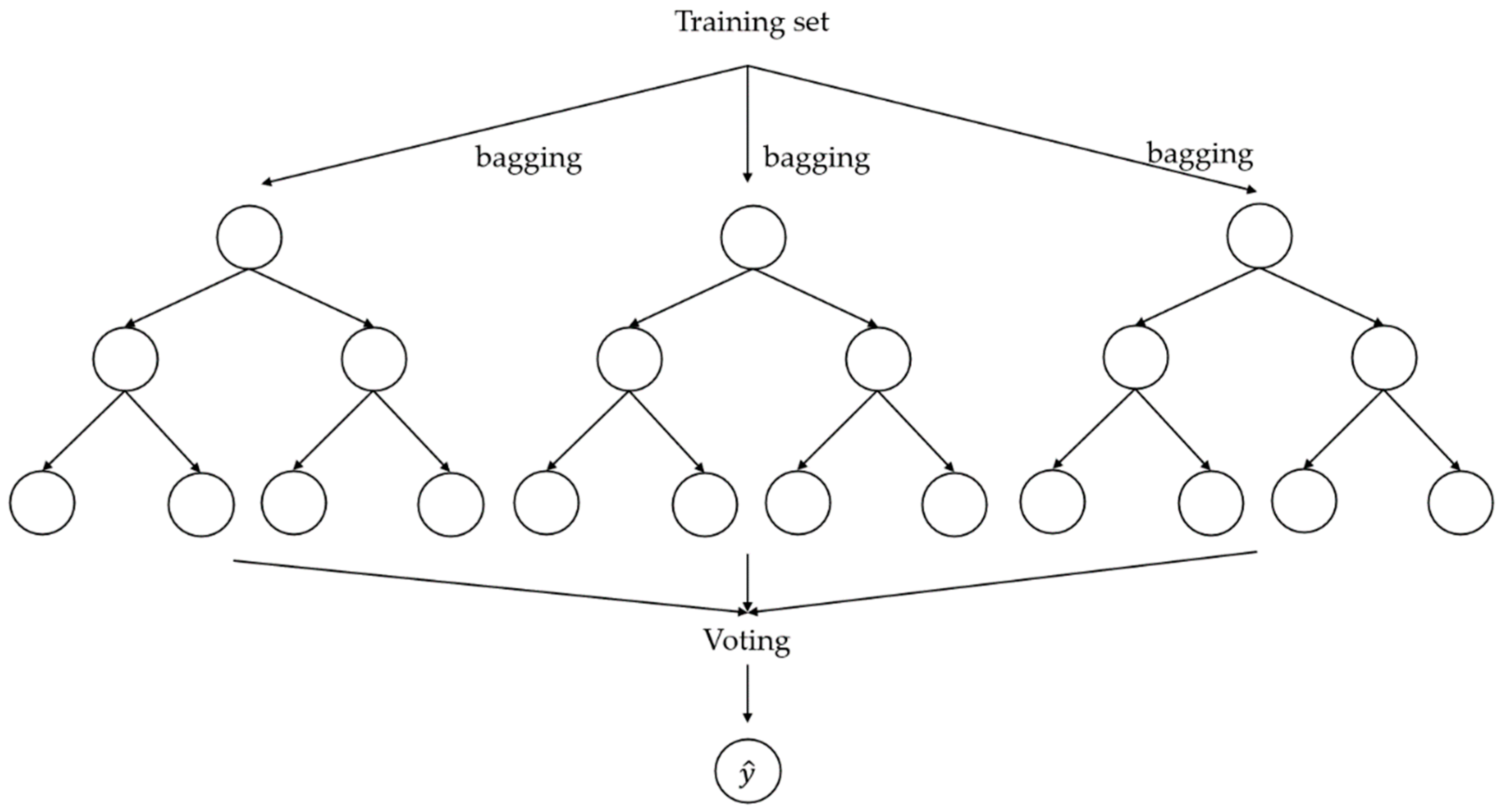
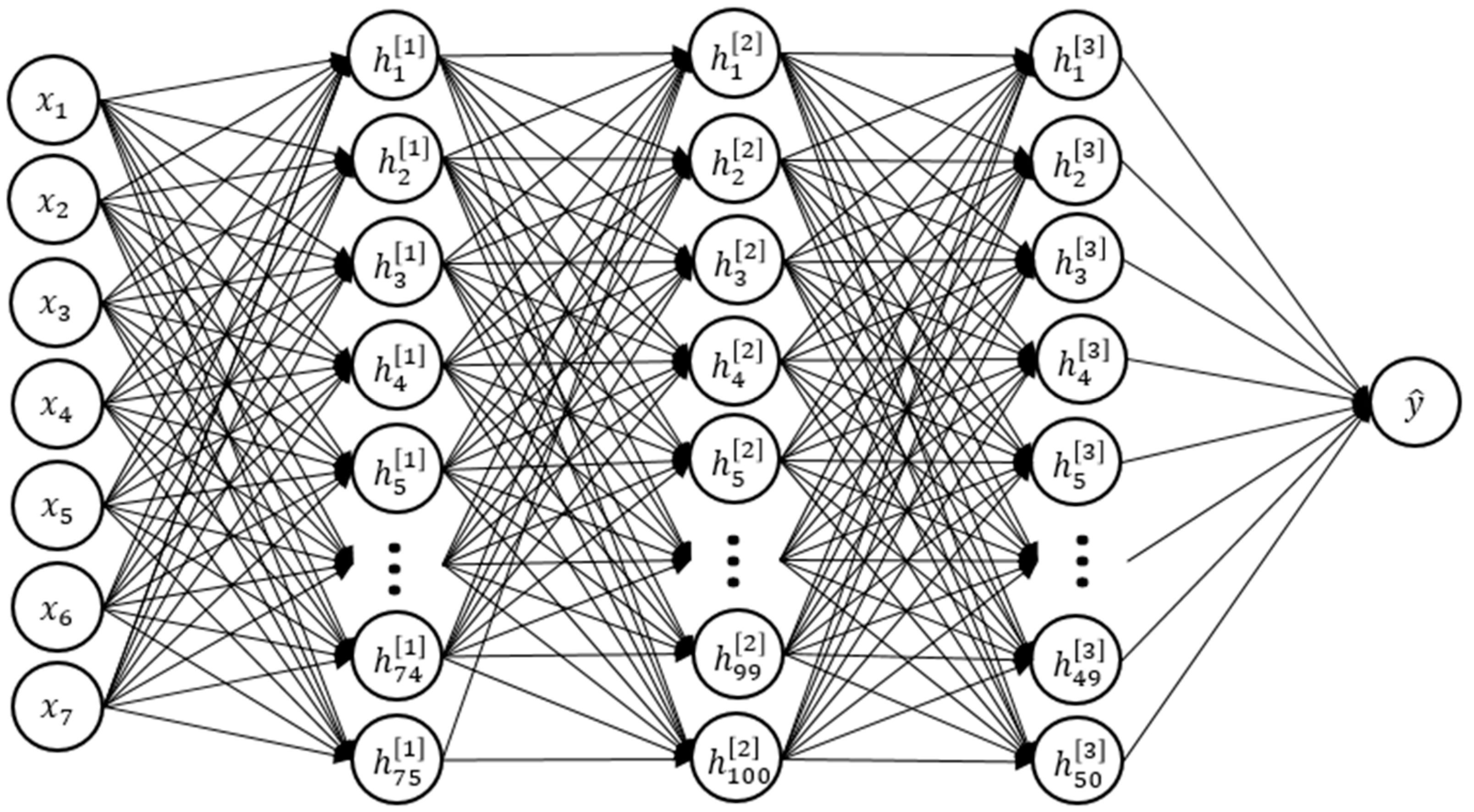
2.2.2. Optimization Carried out by Parameters Adjustment
- Decision trees
- Neural Networks
2.3. Error Assesment
3. Case Study
4. Results
5. Implication of the Study Associated with Practice and Theory
6. Conclusions
- The most suitable models for forecast photovoltaic production are SVR, SNN, and CNN.
- The RF, XGBoost, and RNN models are not recommended to be used in the photovoltaic production forecasting
- The SNN and CNN models can fit with or without night consideration, CNN model being the best option.
- In the case of avoiding nights, SVR model is a very good option. It is also possible to use the RNN or CNN models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Commission. Regulation 2018/84; European Union: Brussels, Belgium, 2018. [Google Scholar]
- Hussain, I.; Jalil, A.A.; Hassan, N.S.; Hamid, M.Y.S. Recent advances in catalytic systems for CO2 conversion to substitute natural gas (SNG): Perspective and challenges. J. Energy Chem. 2021, 62, 377–407. [Google Scholar] [CrossRef]
- Villanueva, D.; Cordeiro, M.; Feijoó, A.; Míguez, E.; Fernández, A. Effects of adding batteries in household installations: Savings, efficiency and emissions. Appl. Sci. 2020, 10, 5891. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Global Energy Review 2020; IEA: Paris, France, 2020. [Google Scholar]
- International Energy Agency (IEA). Electricity Market Report—July 2021; IEA: Paris, France, 2021. [Google Scholar]
- European Commission. 100 Climate-Neutral Cities by 2030—by and for the Citizens; European Union: Brussels, Belgium, 2020. [Google Scholar]
- European Commission. A European Long-Term Strategic Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy; Eurpean Union: Brussels, Belgium, 2018. [Google Scholar]
- Ballesteros-Gallardo, J.A.; Arcos-Vargas, A.; Núñez, F. Optimal Design Model for a Residential PV Storage System. An Application to the Spanish Case. Sustainability 2021, 13, 575. [Google Scholar] [CrossRef]
- Solar Power Europe. EU Market Outlook for Solar Power/2019–2023; Solar Power Europe: Brussels, Belgium, 2019. [Google Scholar]
- Belussi, L.; Barozzi, B.; Bellazzi, A.; Danza, L.; Devitofrancesco, A.; Fanciulli, C.; Ghellere, M.; Guazzi, G.; Meroni, I.; Salamone, F.; et al. A review of performance of zero energy buildings and energy efficiency solutions. J. Build. Eng. 2019, 25, 100772. [Google Scholar] [CrossRef]
- Brambilla, A.; Salvalai, G.; Imperadori, M.; Sesana, M.M. Nearly zero energy building renovation: From energy efficiency to environmental efficiency, a pilot case study. Energy Build. 2018, 166, 271–283. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Villanueva, D.; Cordeiro-Costas, M.; Feijoó-Lorenzo, A.E.; Fernández-Otero, A.; Míguez-García, E. Towards DC energy efficient homes. Appl. Sci. 2021, 11, 6005. [Google Scholar] [CrossRef]
- López-Gómez, J.; Ogando-Martínez, A.; Troncoso-Pastoriza, F.; Febrero-Garrido, L.; Granada-Álvarez, E.; Orosa-García, J.A. Photovoltaic Power Prediction Using Artificial Neural Networks and Numerical Weather Data. Sustainability 2020, 12, 10295. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.T.; Chen, Z.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
- Oh, S. Comparison of a Response Surface Method and Artificial Neural Network in Predicting the Aerodynamic Performance of a Wind Turbine Airfoil and Its Optimization. Appl. Sci. 2020, 10, 6277. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Portugal, I.; Alencar, P.; Cowan, D. The use of machine learning algorithms in recommender systems: A systematic review. Expert Syst. Appl. 2018, 97, 205–227. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Comesaña, M.; Ogando-Martínez, A.; Troncoso-Pastoriza, F.; López-Gómez, J.; Febrero-Garrido, L.; Granada-Álvarez, E. Use of optimised MLP neural networks for spatiotemporal estimation of indoor environmental conditions of existing buildings. Build. Environ. 2021, 205, 108243. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoundian, M.; Mekhilef, S.; Idris, M.Y.I.; van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- van der Meer, D.W.; Widén, J.; Munkhammar, J. Review on probabilistic forecasting of photovoltaic power production and electricity consumption. Renew. Sustain. Energy Rev. 2018, 81, 1484–1512. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization Methods for Large-Scale Machine Learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]
- Lu, C.; Shi, J. Relative density prediction of additively manufactured Inconel 718: A study on genetic algorithm optimized neural network models. Rapid Prototyp. J. 2022, 28, 1425–1436. [Google Scholar] [CrossRef]
- Khorasani, M.; Ghasemi, A.H.; Leary, M.; Sharabian, E.; Cordova, L.; Gibson, I.; Downing, D.; Bateman, S.; Brandt, M.; Rolfe, B. The effect of absorption ratio on meltpool features in laser-based powder bed fusion of IN718. Opt. Laser Technol. 2022, 153, 108263. [Google Scholar] [CrossRef]
- Rashed, K.; Kafi, A.; Simons, R.; Bateman, S. Fused filament fabrication of nylon 6/66 copolymer: Parametric study comparing full factorial and Tauguchi design of experiments. Rapid Prototyp. J. 2022, 28, 1111–1128. [Google Scholar] [CrossRef]
- Agrawal, R. Sustainable design guidelines for additive manufacturing applications. Rapid Prototyp. J. 2022, 28, 1221–1240. [Google Scholar] [CrossRef]
- Alshehri, M.; Kumar, M.; Bhardwaj, A.; Mishra, S.; Gyani, J. Deep Learning Based Approach to Classify Saline Particles in Sea Water. Water 2021, 13, 1251. [Google Scholar] [CrossRef]
- Anjos, O.; Iglesias, C.; Peres, F.; Martínez, J.; García, A.; Taboada, J. Neural networks applied to discriminate botanical origin of honeys. Food Chem. 2015, 175, 128–136. [Google Scholar] [CrossRef]
- Marichal-Plasencia, G.N.; Camacho-Espino, J.; Ávila Prats, D.; Peñate Suárez, B. Machine Learning Models Applied to Manage the Operation of a Simple SWRO Desalination Plant and Its Application in Marine Vessels. Water 2021, 13, 2547. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Region-based convolutional networks for accurate object detection and segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 7112511. [Google Scholar] [CrossRef]
- Jun, Y.; Leyuan, F.; Min, H. Spectral-Spatial Latent Reconstruction for Open-Set Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 5227–5241. [Google Scholar] [CrossRef]
- Li, D.; Dawei, L.; Qifan, T.; Jun, W. Yarn Density Measurement for 3-D Braided Composite Preforms Based on Rotation Object Detection. IEEE Trans. Instrum. Meas. 2022, 71, 5016711. [Google Scholar] [CrossRef]
- Chen, L.; Hu, X.; Xu, T.; Kuang, H.; Li, Q. Turn Signal Detection During Nighttime by CNN Detector and Perceptual Hashing Tracking. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3303–3314. [Google Scholar] [CrossRef]
- Xuemin, H.; Bo, T.; Long, C.; Sheng, S.; Xiuchi, T. Learning a Deep Cascaded Neural Network for Multiple Motion Commands Prediction in Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7585–7596. [Google Scholar] [CrossRef]
- Hui, Z.; Liuchen, W.; Yurong, C.; Ruibo, C.; Senlin, K.; Yaonan, W.; Jianwen, H.; Jonathan, W. Attention-Guided Multitask Convolutional Neural Network for Power Line Parts Detection. IEEE Trans. Instrum. Meas. 2022, 71, 5008213. [Google Scholar] [CrossRef]
- Shi, J.; Lee, W.-J.; Liu, Y.; Yang, Y.; Wang, P. Forecasting Power Output of Photovoltaic Systems Based on Weather Classification and Support Vector Machines. IEEE Trans. Ind. Appl. 2012, 48, 1064–1069. [Google Scholar] [CrossRef]
- De Paiva, G.M.; Pimentel, S.P.; Alvarenga, B.P.; Marra, E.G.; Mussetta, M.; Leva, S. Multiple Site Intraday Solar Irradiance Forecasting by Machine Learning Algorithms: MGGP and MLP Neural Networks. Energies 2020, 13, 3005. [Google Scholar] [CrossRef]
- Mehrkanoon, S. Deep shared representation learning for weather elements forecasting. Knowl. Based Syst. 2019, 179, 120–128. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-Khah, M.; Catalao, J.P.S. Improved EMD-Based Complex Prediction Model for Wind Power Forecasting. IEEE Trans. Sustain. Energy 2020, 11, 2790–2802. [Google Scholar] [CrossRef]
- Ridzuan, F.; Zainon, W.M.N.W. A Review on Data Cleansing Methods for Big Data. Procedia Comput. Sci. 2019, 161, 731–738. [Google Scholar] [CrossRef]
- Munappy, A.R.; Bosch, J.; Olsson, H.H.; Arpteg, A.; Brinne, B. Data management for production quality deep learning models: Challenges and solutions. J. Syst. Softw. 2022, 191, 111359. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Saleh, R.; Fleyeh, H. Using Supervised Machine Learning to Predict the Status of Road Signs. Transp. Res. Procedia 2022, 62, 221–228. [Google Scholar] [CrossRef]
- Heaton, J. An empirical analysis of feature engineering for predictive modeling. In Proceedings of the IEEE SOUTHEASTCON, Norfolk, VA, USA, 30 March–3 April 2016; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Verdonck, T.; Baesens, B.; Óskarsdóttir, M.; vanden Broucke, S. Special issue on feature engineering editorial. Mach. Learn. 2021, 1–12. [Google Scholar] [CrossRef]
- Feng, Y.; Tu, Y. Phases of learning dynamics in artificial neural networks: In the absence or presence of mislabeled data. Mach. Learn. Sci. Technol. 2021, 2, 043001. [Google Scholar] [CrossRef]
- Vrablecová, P.; Ezzeddine, A.B.; Rozinajová, V.; Šárik, S.; Sangaiah, A.K. Smart grid load forecasting using online support vector regression. Comput. Electr. Eng. 2018, 65, 102–117. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, J.; Jia, H.; Mu, Y.; Lv, S. Vector field-based support vector regression for building energy consumption prediction. Appl. Energy 2019, 242, 403–414. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine Learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Booth, A.; Gerding, E.; McGroarty, F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014, 41, 3651–3661. [Google Scholar] [CrossRef]
- Touzani, S.; Granderson, J.; Fernandes, S. Gradient boosting machine for modeling the energy consumption of commercial buildings. Energy Build. 2018, 158, 1533–1543. [Google Scholar] [CrossRef]
- Martínez-Comesaña, M.; Febrero-Garrido, M.; Granada-Álvarez, E.; Martínez-Torres, J.; Martínez-Mariño, S. Heat Loss Coefficient Estimation Applied to Existing Buildings through Machine Learning Models. Appl. Sci. 2020, 10, 8968. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Chang, G.W.; Lu, H.J.; Chang, Y.R.; Lee, Y.D. An improved neural network-based approach for short-term wind speed and power forecast. Renew. Energy 2017, 105, 301–311. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, S.; Jin, B. Sequential Fault Diagnosis Based on LSTM Neural Network. IEEE Access 2018, 6, 12929–12939. [Google Scholar] [CrossRef]
- Ju, Y.; Sun, G.; Chen, Q.; Zhang, M.; Zhu, H.; Rehman, M.U. A Model Combining Convolutional Neural Network and LightGBM Algorithm for Ultra-Short-Term Wind Power Forecasting. IEEE Access 2019, 7, 28309–28318. [Google Scholar] [CrossRef]
- Pereira, S.; Pinto, A.; Alves, V.; Silva, C.A. Brain Tumor Segmentation Using Convolutional Neural Networks in MRI Images. IEEE Trans. Med. Imaging 2016, 35, 1240–1251. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Lu, C.; Li, X.; Kim, H.J.; Wang, J. A full convolutional network based on DenseNet for remote sensing scene classification. Math. Biosci. Eng. 2019, 16, 3345–3367. [Google Scholar] [CrossRef]
- William, H.; Fanney, A.H.; Dougherty, B.; Payne, W.V.; Ullah, T.; Ng, L.; Omar, F. Net Zero Energy Residential Test Facility Instrumented Data; Year 2; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016. [CrossRef]
- William, H.; Chen, T.H.; Dougherty, B.; Fanney, A.H.; Ullah, T.; Payne, W.V.; Ng, L.; Omar, F. Net Zero Energy Residential Test Facility Instrumented Data; Year 1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [CrossRef]

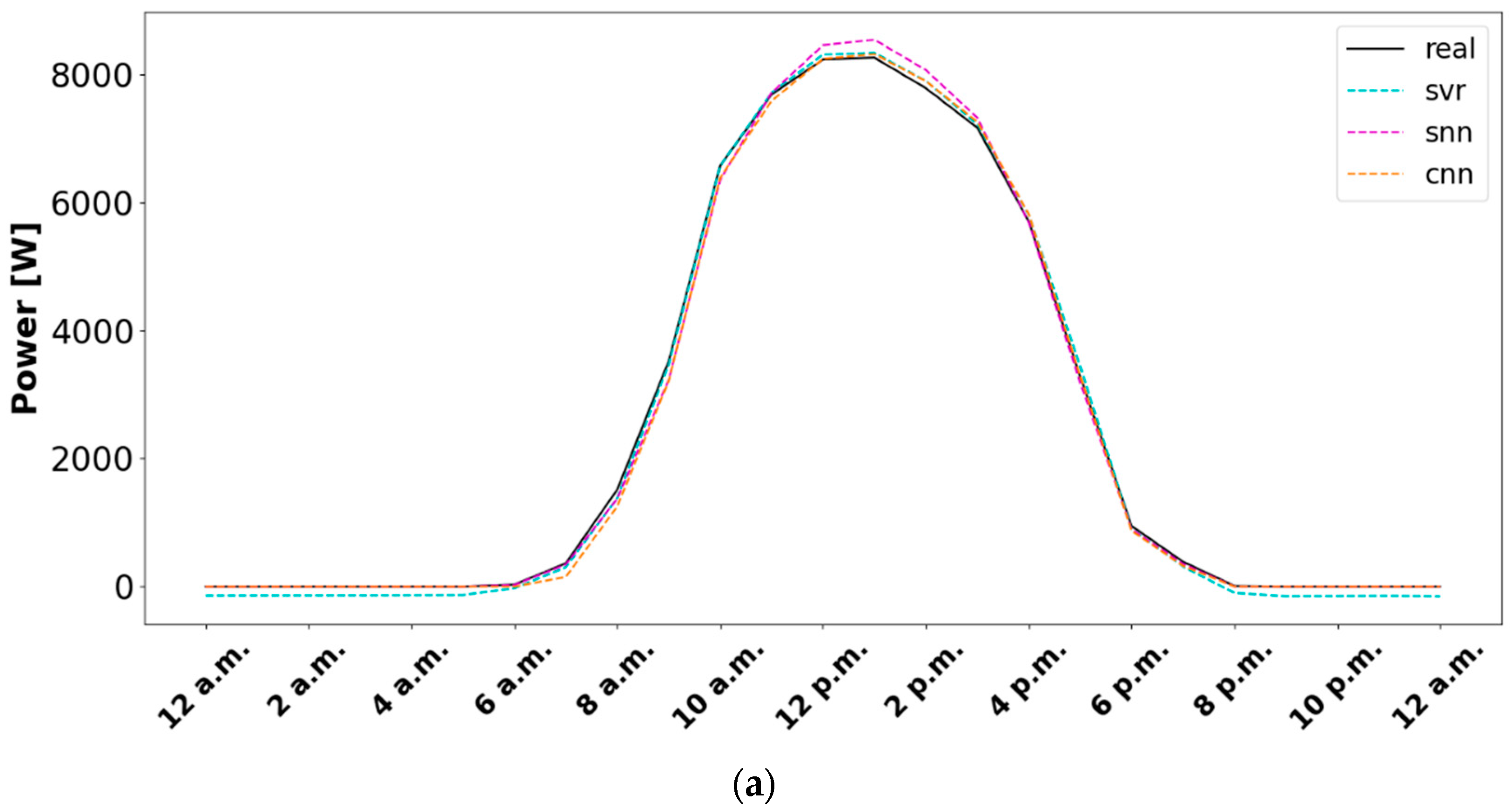
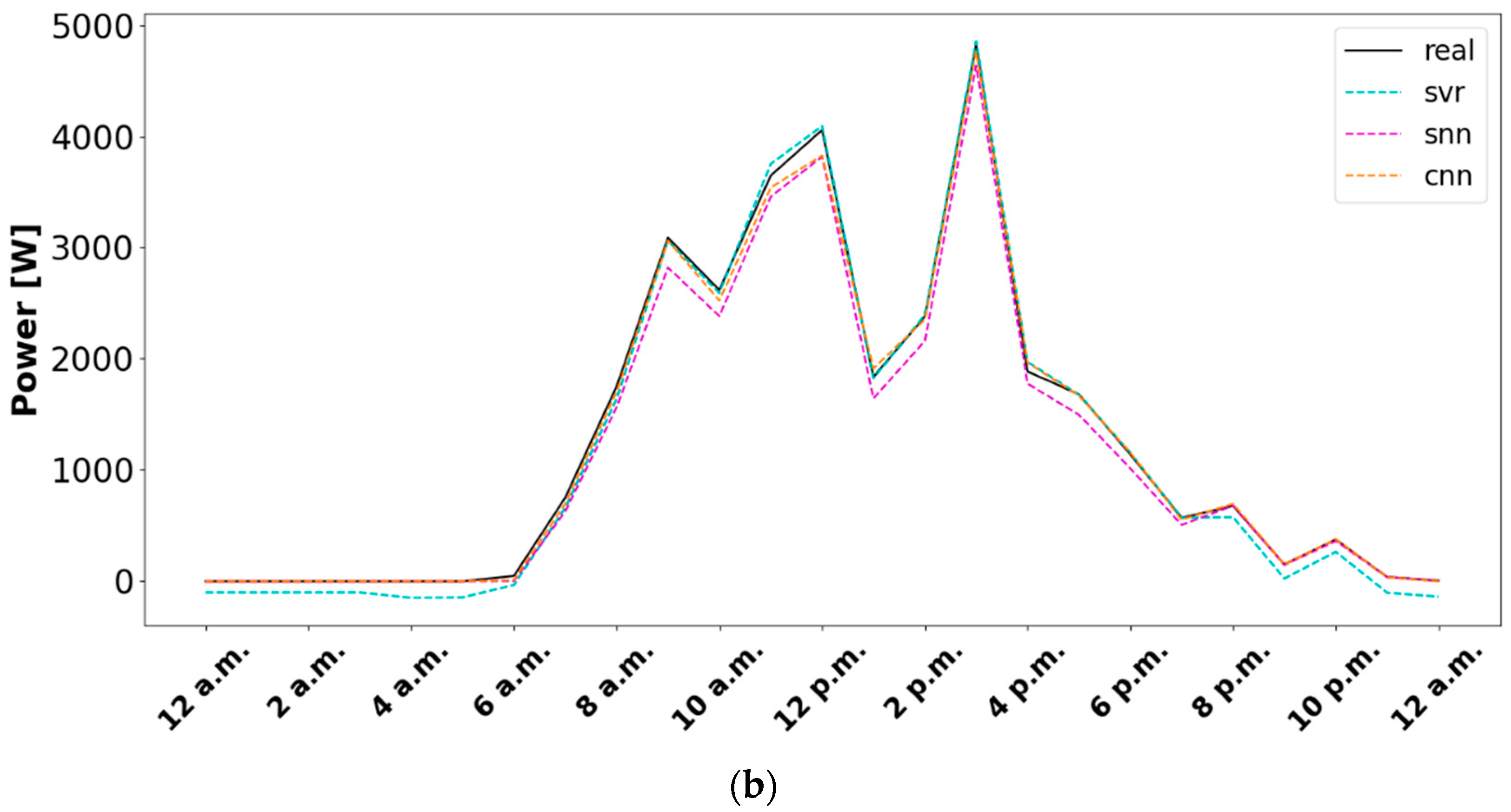
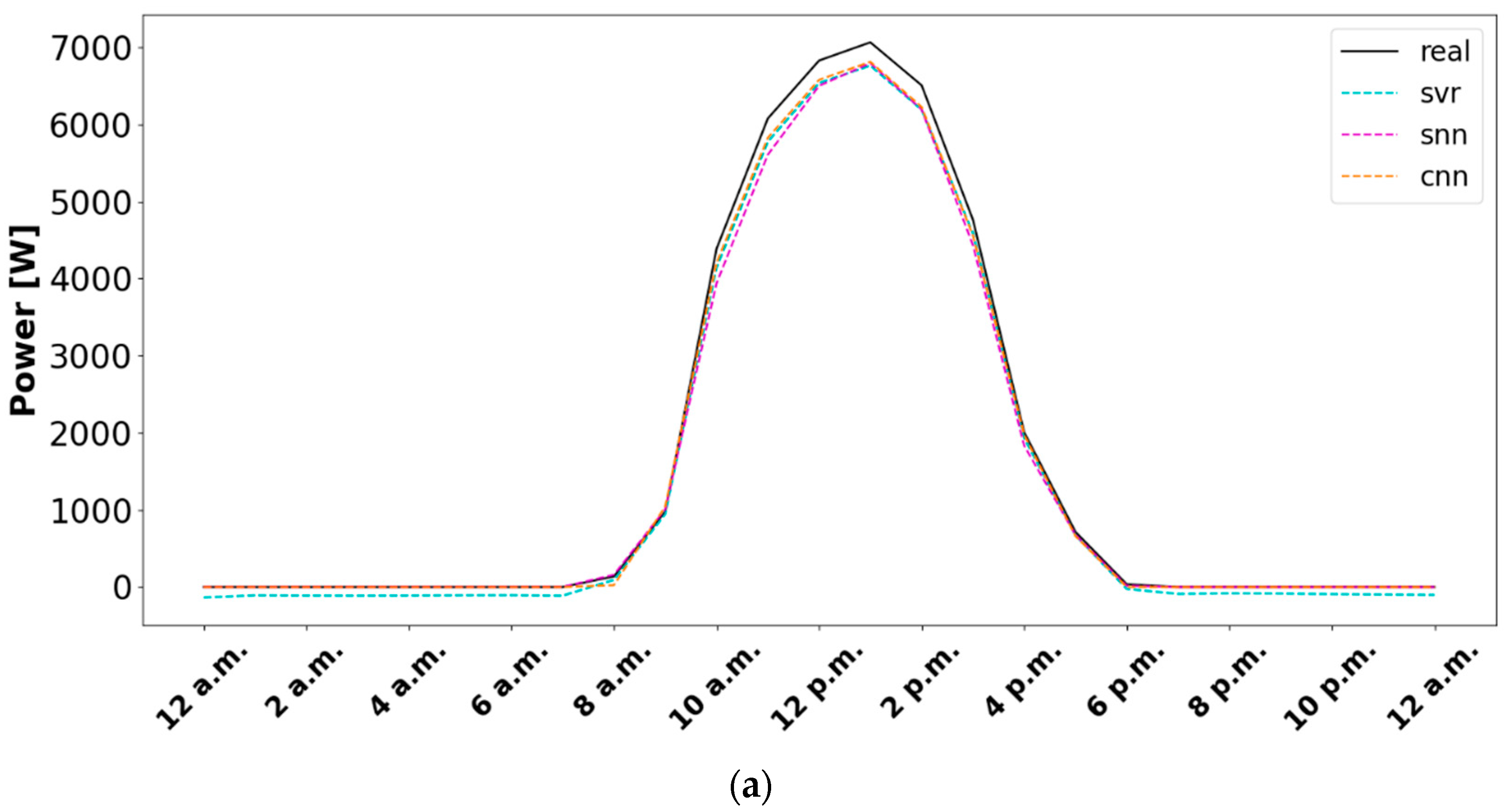
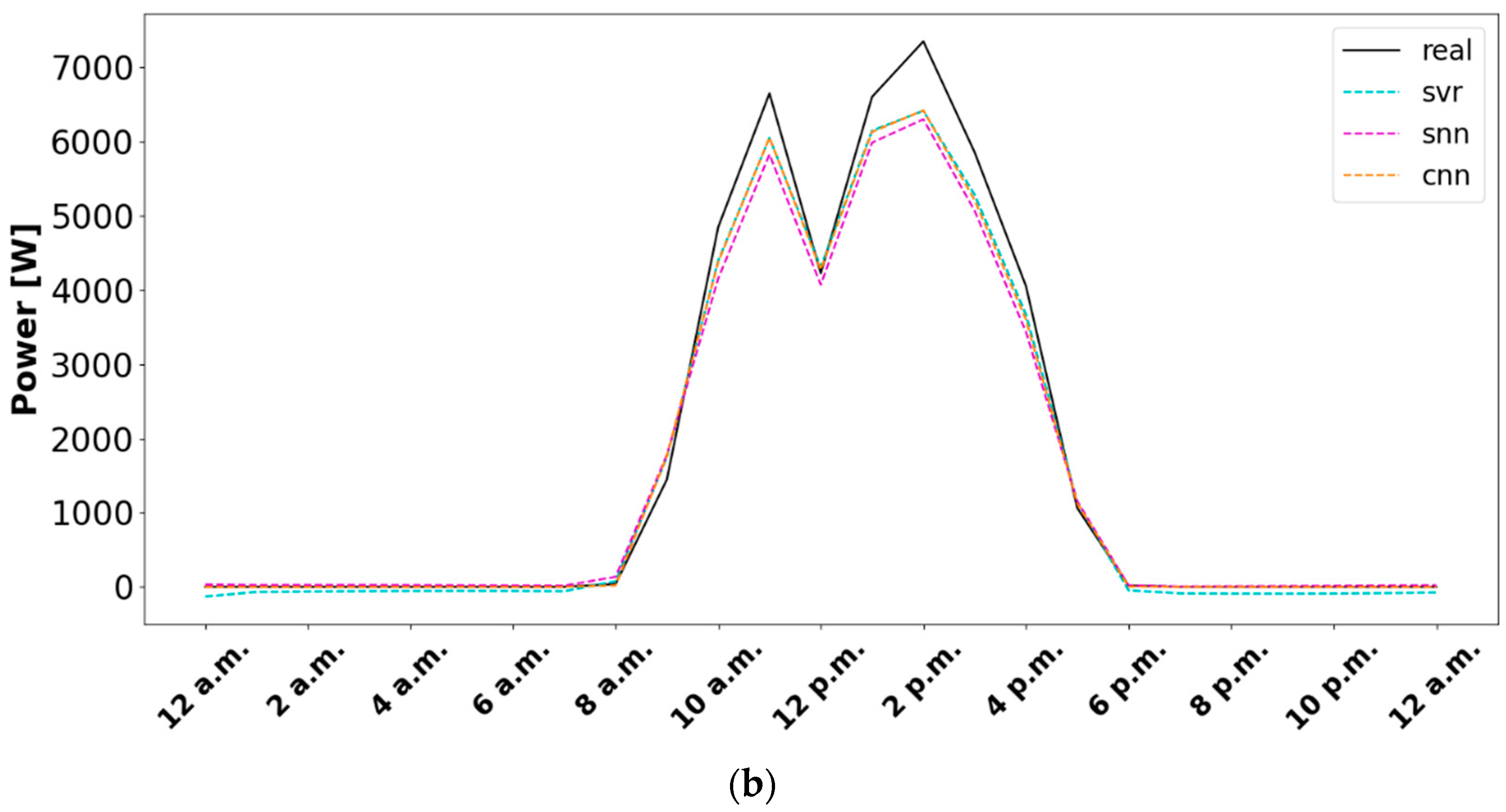
| Split | Metric | RF | XGBoost | SVR | SNN | RNN | CNN |
|---|---|---|---|---|---|---|---|
| Train | nMBE | 0.41% | 0.45% | 0.81% | 0.45% | −0.07% | 0.39% |
| sd nMBE | 0.02 | 0.02 | 0.04 | 0.04 | 0.06 | 0.04 | |
| nRMSE | 1.88% | 2.51% | 4.01% | 3.99% | 6.51% | 3.85% | |
| sd nRMSE | 0.02 | 0.02 | 0.04 | 0.05 | 0.07 | 0.04 | |
| R2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.94 | 0.98 | |
| Dev | nMBE | 1.44% | 1.37% | 0.90% | 0.50% | −0.18% | 0.40% |
| sd nMBE | 0.06 | 0.07 | 0.04 | 0.04 | 0.07 | 0.04 | |
| nRMSE | 6.28% | 6.73% | 3.91% | 3.55% | 7.03% | 3.70% | |
| sd nRMSE | 0.07 | 0.07 | 0.04 | 0.04 | 0.07 | 0.04 | |
| R2 | 0.94 | 0.93 | 0.97 | 0.97 | 0.94 | 0.97 | |
| Test | nMBE | 1.80% | 1.43% | 1.81% | 1.13% | −1.24% | 0.83% |
| sd nMBE | 0.05 | 0.06 | 0.03 | 0.03 | 0.07 | 0.03 | |
| nRMSE | 5.67% | 6.09% | 3.16% | 3.54% | 7.30% | 3.50% | |
| sd nRMSE | 0.06 | 0.07 | 0.02 | 0.04 | 0.08 | 0.04 | |
| R2 | 0.95 | 0.94 | 0.98 | 0.98 | 0.92 | 0.98 |
| Split | Metric | RF | XGBoost | SVR | SNN | RNN | CNN |
|---|---|---|---|---|---|---|---|
| Train | nMBE | 0.60% | 0.53% | 0.10% | 0.77% | −0.09% | 0.25% |
| sd nMBE | 0.02 | 0.03 | 0.05 | 0.05 | 0.09 | 0.04 | |
| nRMSE | 2.44% | 3.15% | 4.59% | 5.04% | 8.82% | 3.76% | |
| sd nRMSE | 0.02 | 0.03 | 0.05 | 0.05 | 0.07 | 0.04 | |
| R2 | 0.99 | 0.99 | 0.97 | 0.97 | 0.91 | 0.98 | |
| Dev | nMBE | 2.14% | 1.99% | 0.13% | 0.90% | −0.42% | 0.24% |
| sd nMBE | 0.08 | 0.08 | 0.04 | 0.04 | 0.10 | 0.04 | |
| nRMSE | 8.04% | 8.82% | 4.42% | 4.58% | 9.62% | 3.76% | |
| sd nRMSE | 0.08 | 0.09 | 0.04 | 0.04 | 0.08 | 0.04 | |
| R2 | 0.93 | 0.90 | 0.97 | 0.97 | 0.91 | 0.98 | |
| Test | nMBE | 3.53% | 2.89% | 1.81% | 2.63% | −2.77% | 0.81% |
| sd nMBE | 0.07 | 0.09 | 0.04 | 0.05 | 0.11 | 0.03 | |
| nRMSE | 8.28% | 8.97% | 4.30% | 5.37% | 11.11% | 3.52% | |
| sd nRMSE | 0.08 | 0.09 | 0.04 | 0.04 | 0.09 | 0.04 | |
| R2 | 0.93 | 0.92 | 0.98 | 0.97 | 0.88 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordeiro-Costas, M.; Villanueva, D.; Eguía-Oller, P.; Granada-Álvarez, E. Machine Learning and Deep Learning Models Applied to Photovoltaic Production Forecasting. Appl. Sci. 2022, 12, 8769. https://doi.org/10.3390/app12178769
Cordeiro-Costas M, Villanueva D, Eguía-Oller P, Granada-Álvarez E. Machine Learning and Deep Learning Models Applied to Photovoltaic Production Forecasting. Applied Sciences. 2022; 12(17):8769. https://doi.org/10.3390/app12178769
Chicago/Turabian StyleCordeiro-Costas, Moisés, Daniel Villanueva, Pablo Eguía-Oller, and Enrique Granada-Álvarez. 2022. "Machine Learning and Deep Learning Models Applied to Photovoltaic Production Forecasting" Applied Sciences 12, no. 17: 8769. https://doi.org/10.3390/app12178769
APA StyleCordeiro-Costas, M., Villanueva, D., Eguía-Oller, P., & Granada-Álvarez, E. (2022). Machine Learning and Deep Learning Models Applied to Photovoltaic Production Forecasting. Applied Sciences, 12(17), 8769. https://doi.org/10.3390/app12178769







