Robust Optimization of Natural Laminar Flow Airfoil Based on Random Surface Contamination
Abstract
:1. Research Background
2. Technical Implementation
2.1. Technical Idea
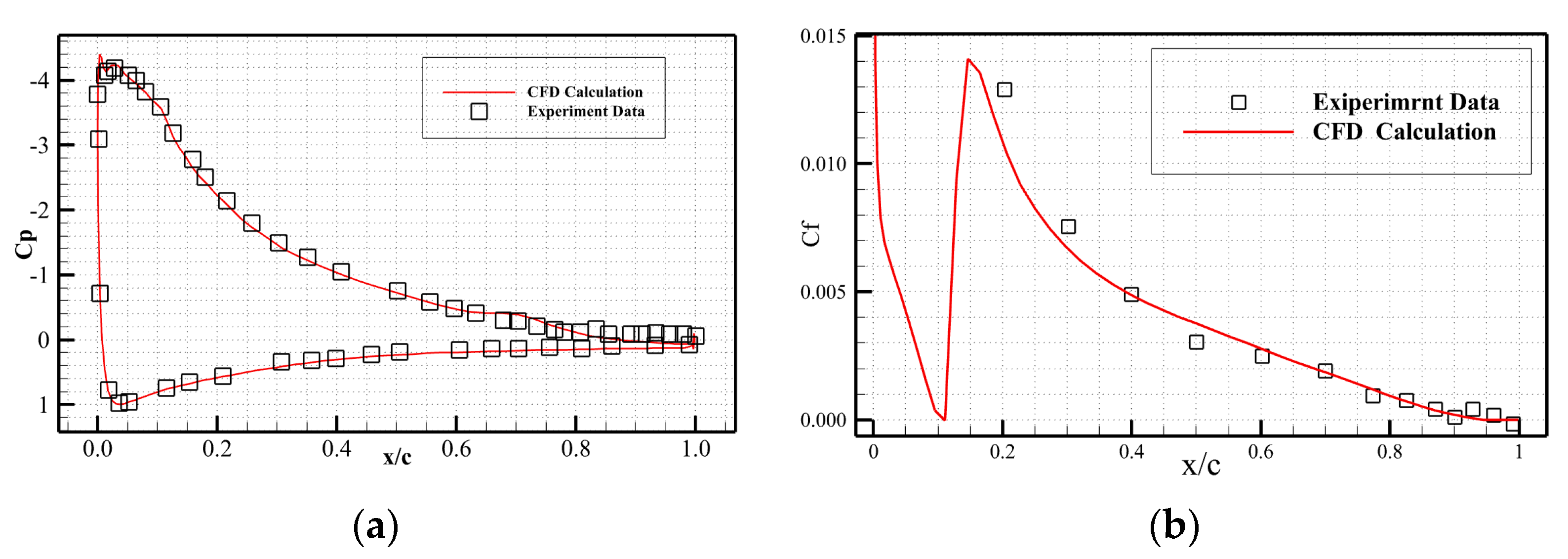
2.2. Case Validation
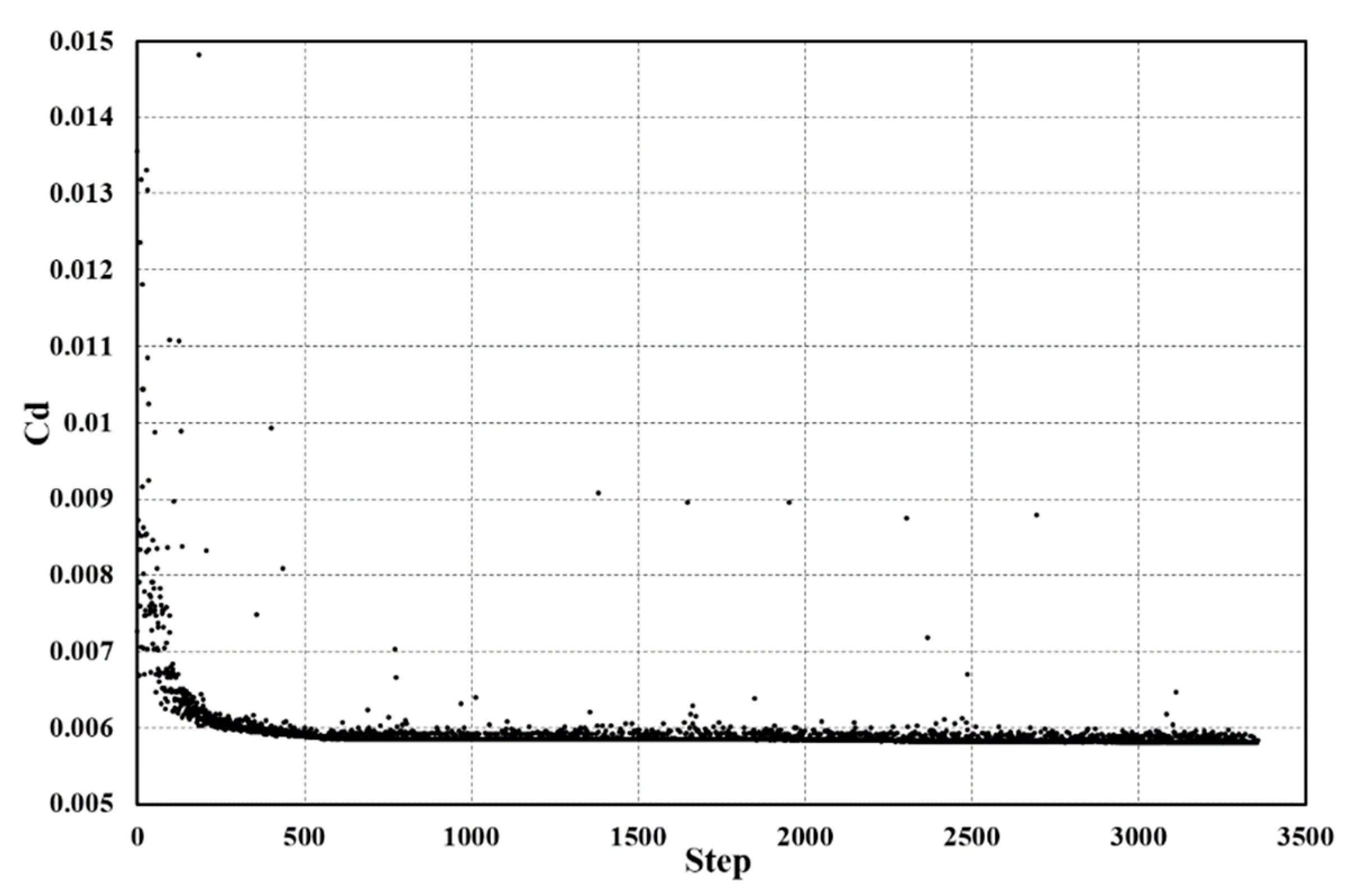
2.3. Optimization Method
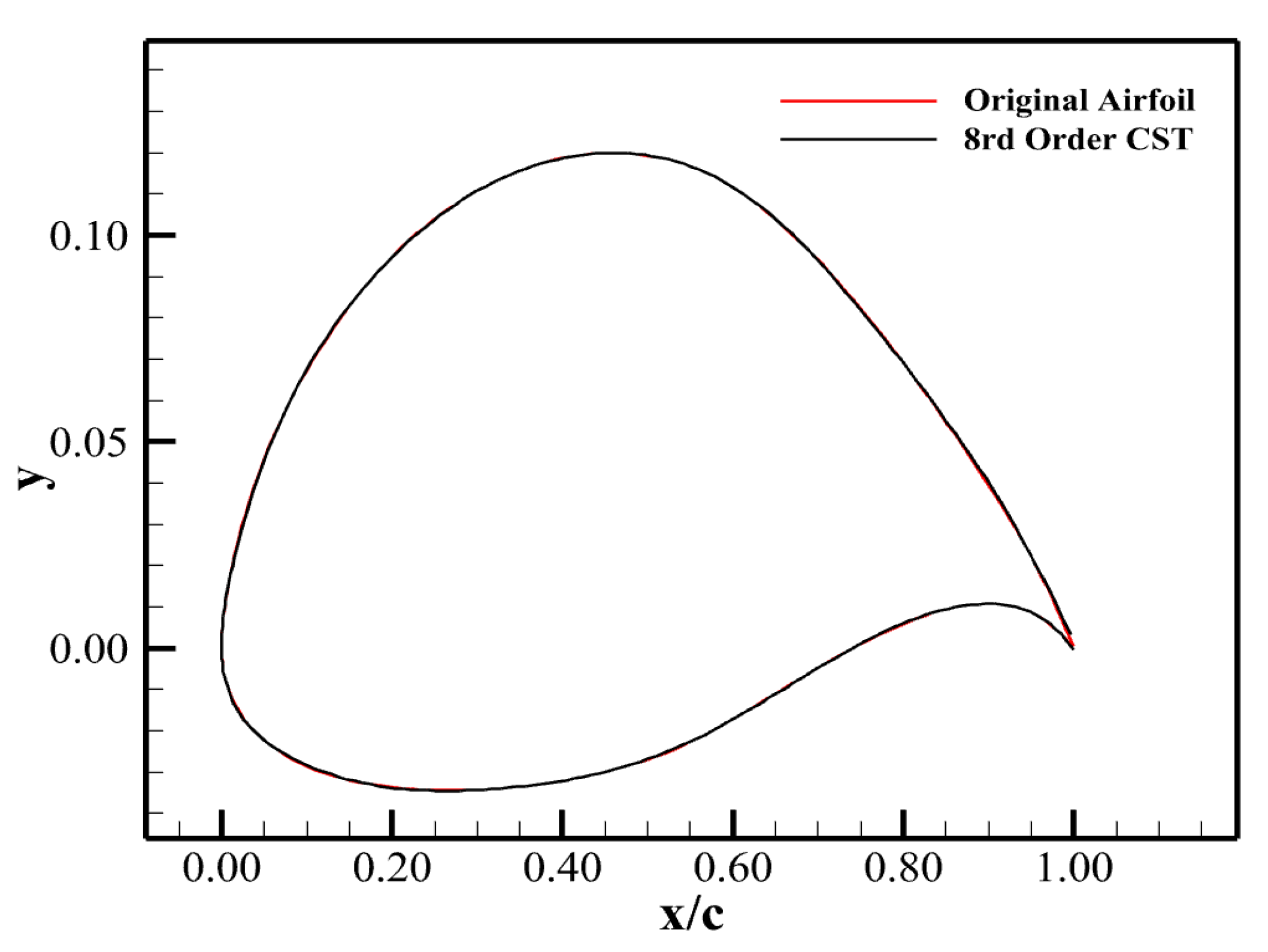
2.4. Parameterization Method
2.5. Monte Carlo Method
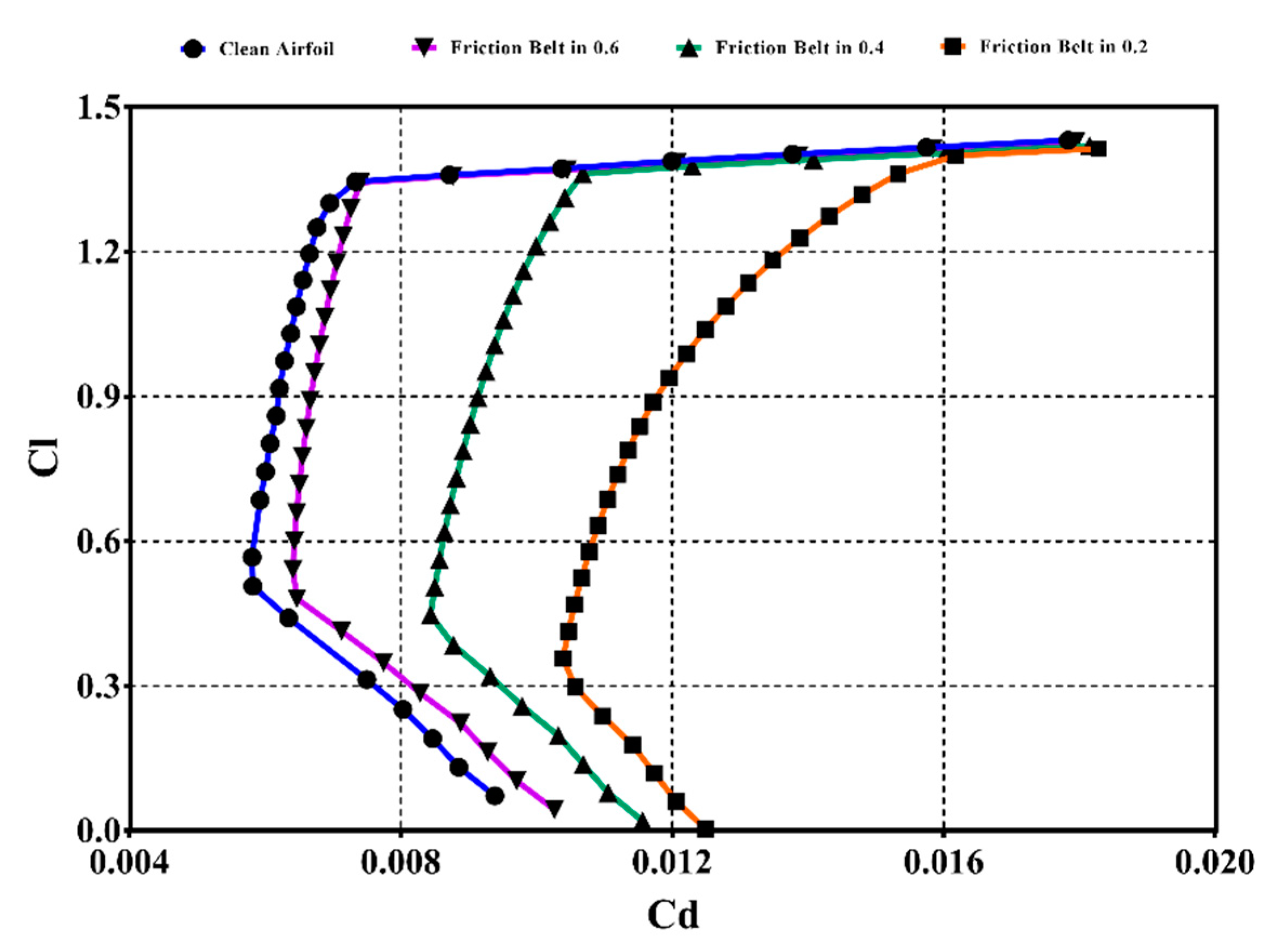
3. Surface Contamination Simulation
4. Normal Optimization
4.1. Optimization Settings
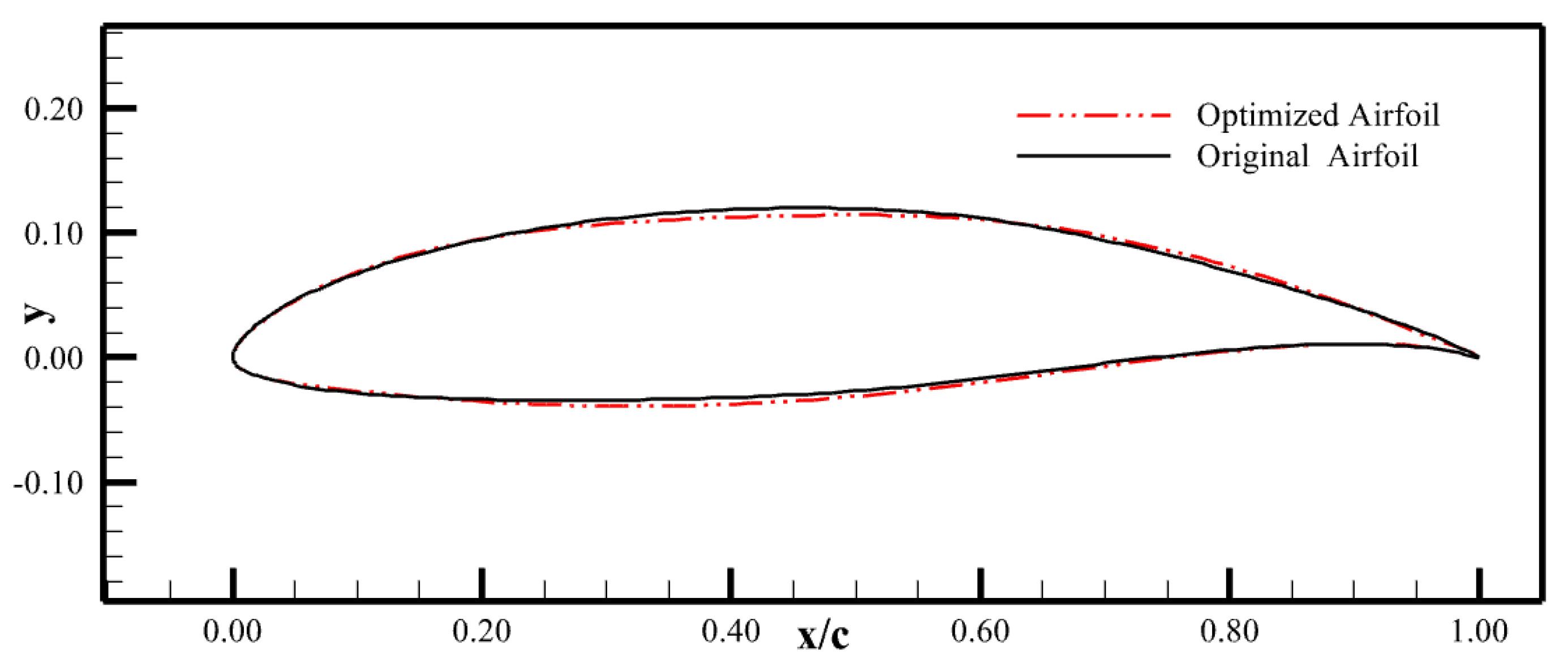
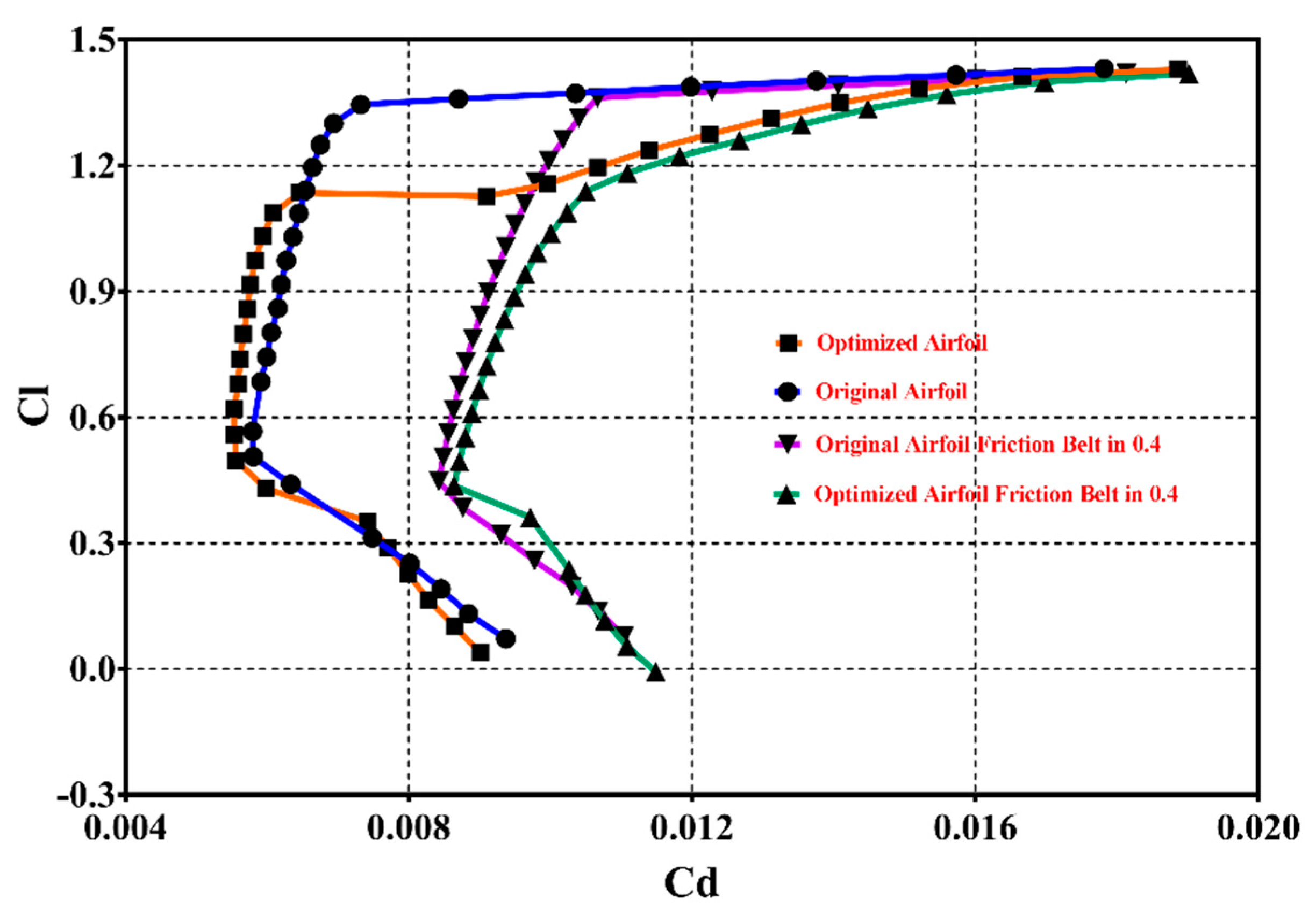
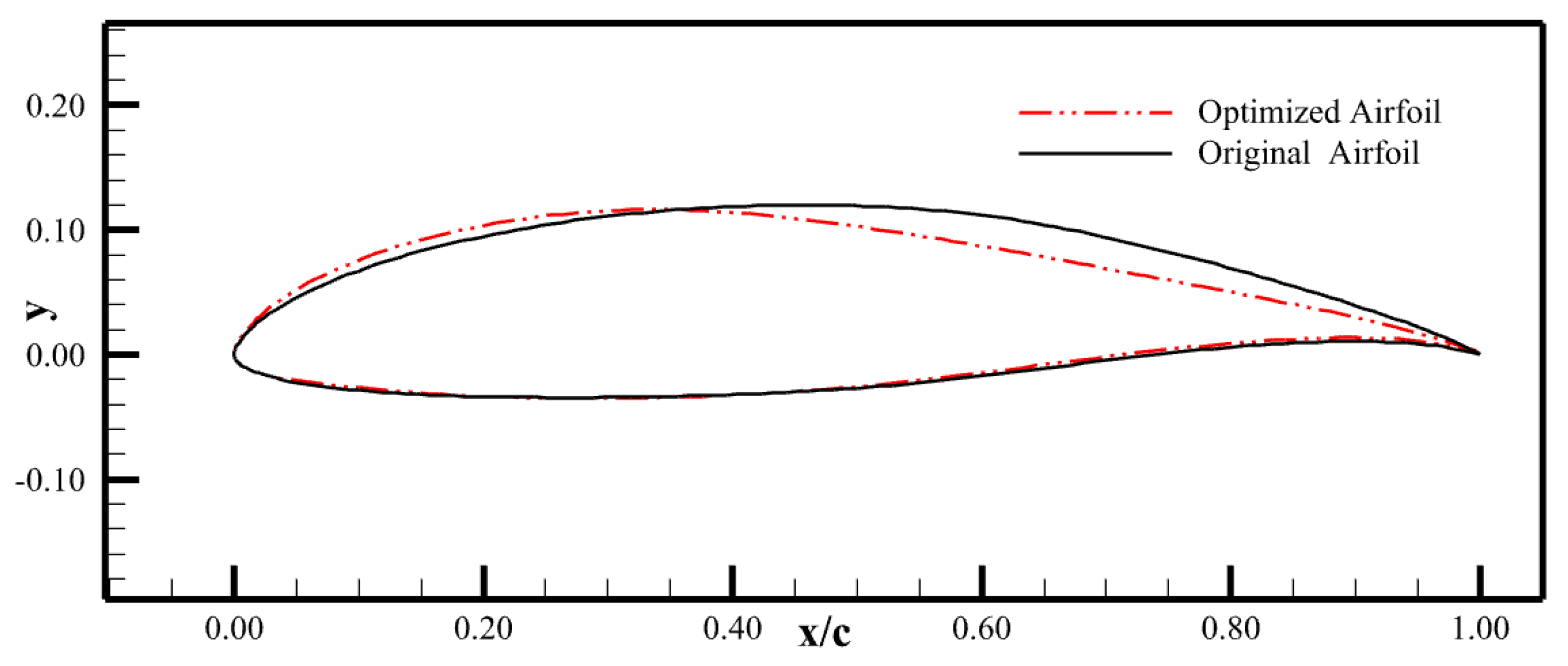
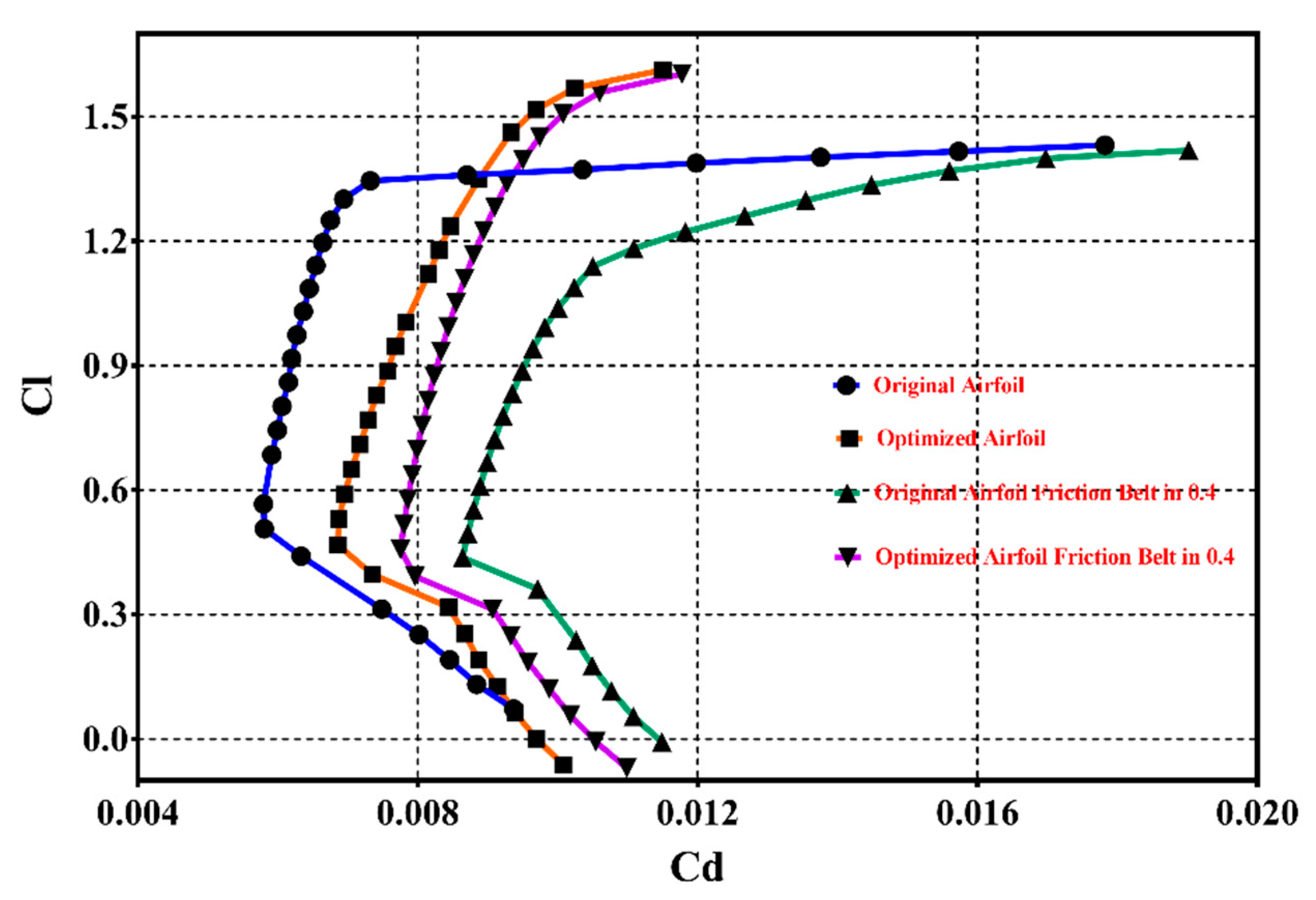
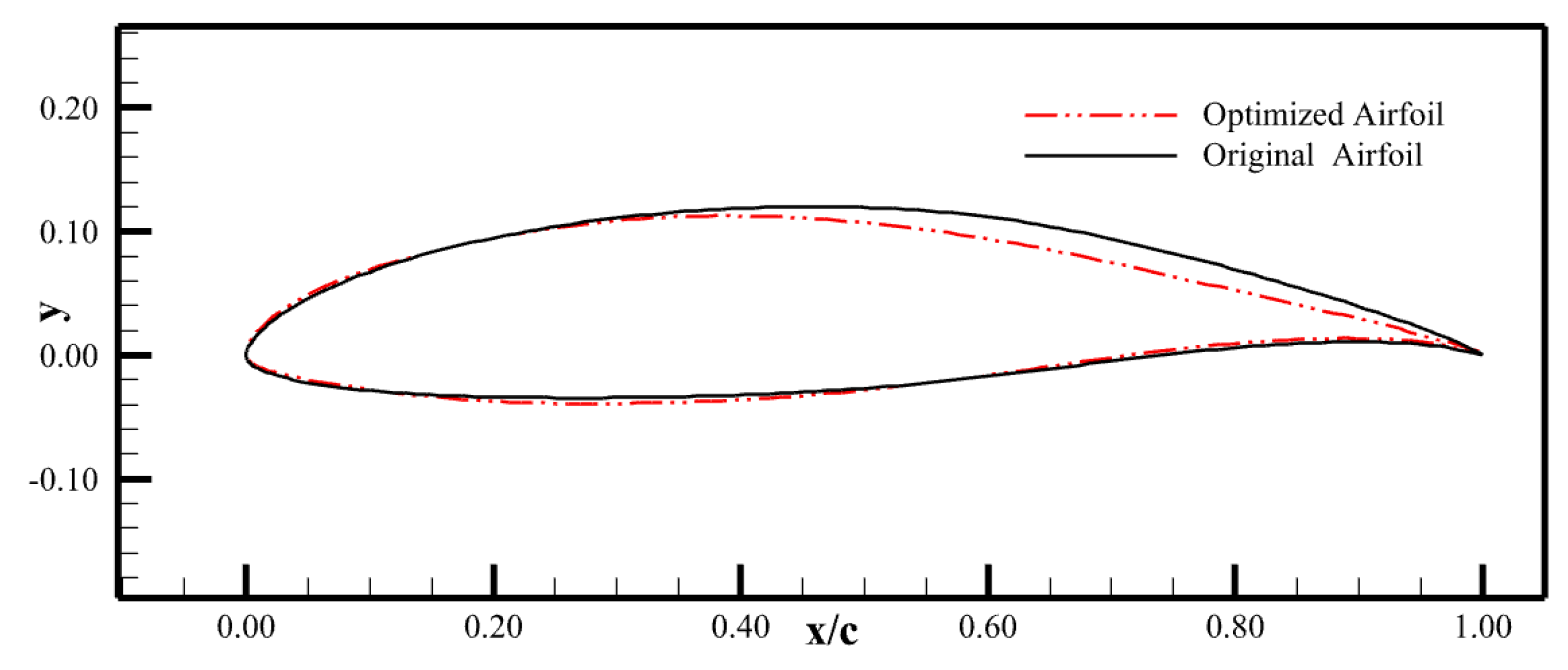
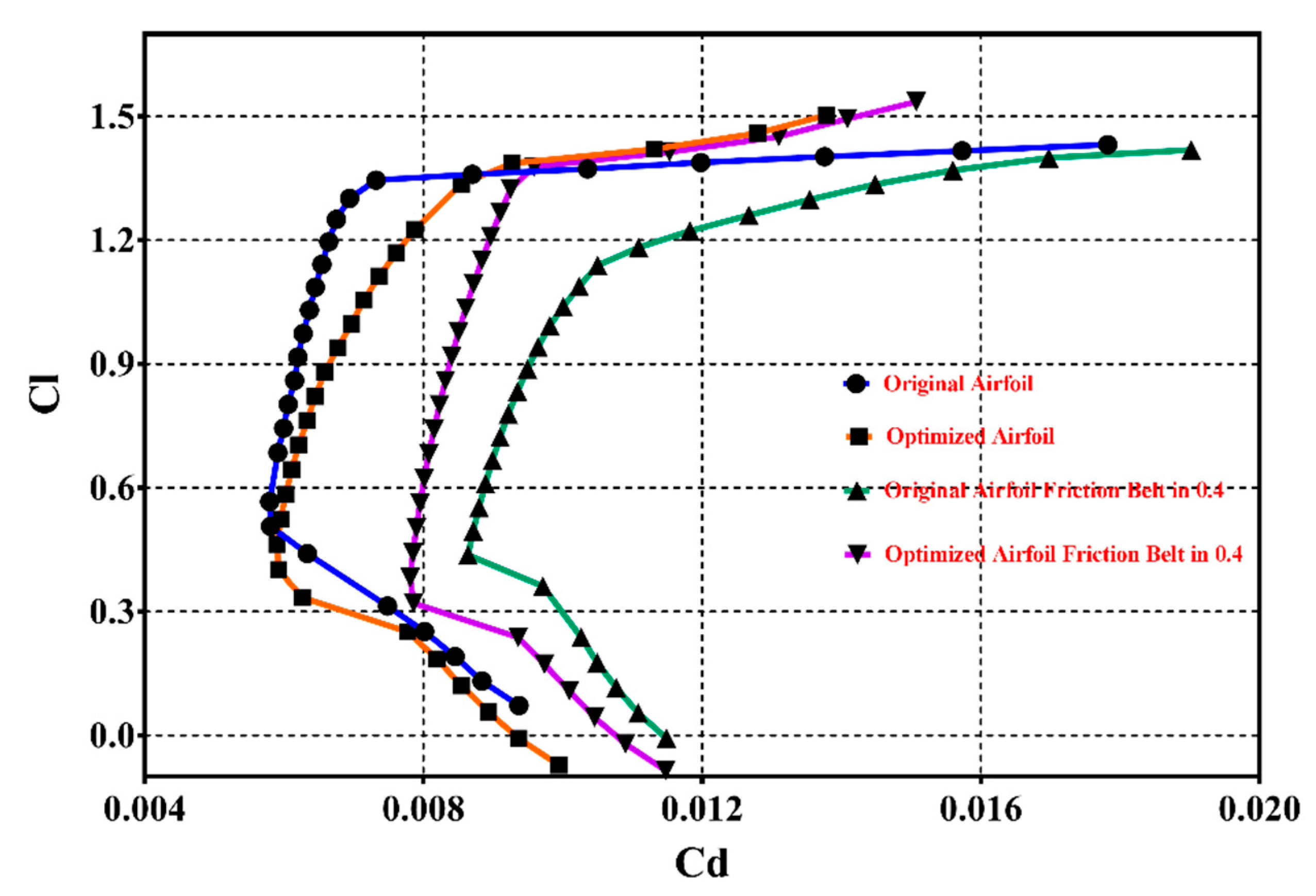
4.2. Optimization Results
5. Robust Optimization
5.1. Uncertainty Modeling
5.2. Optimization Settings
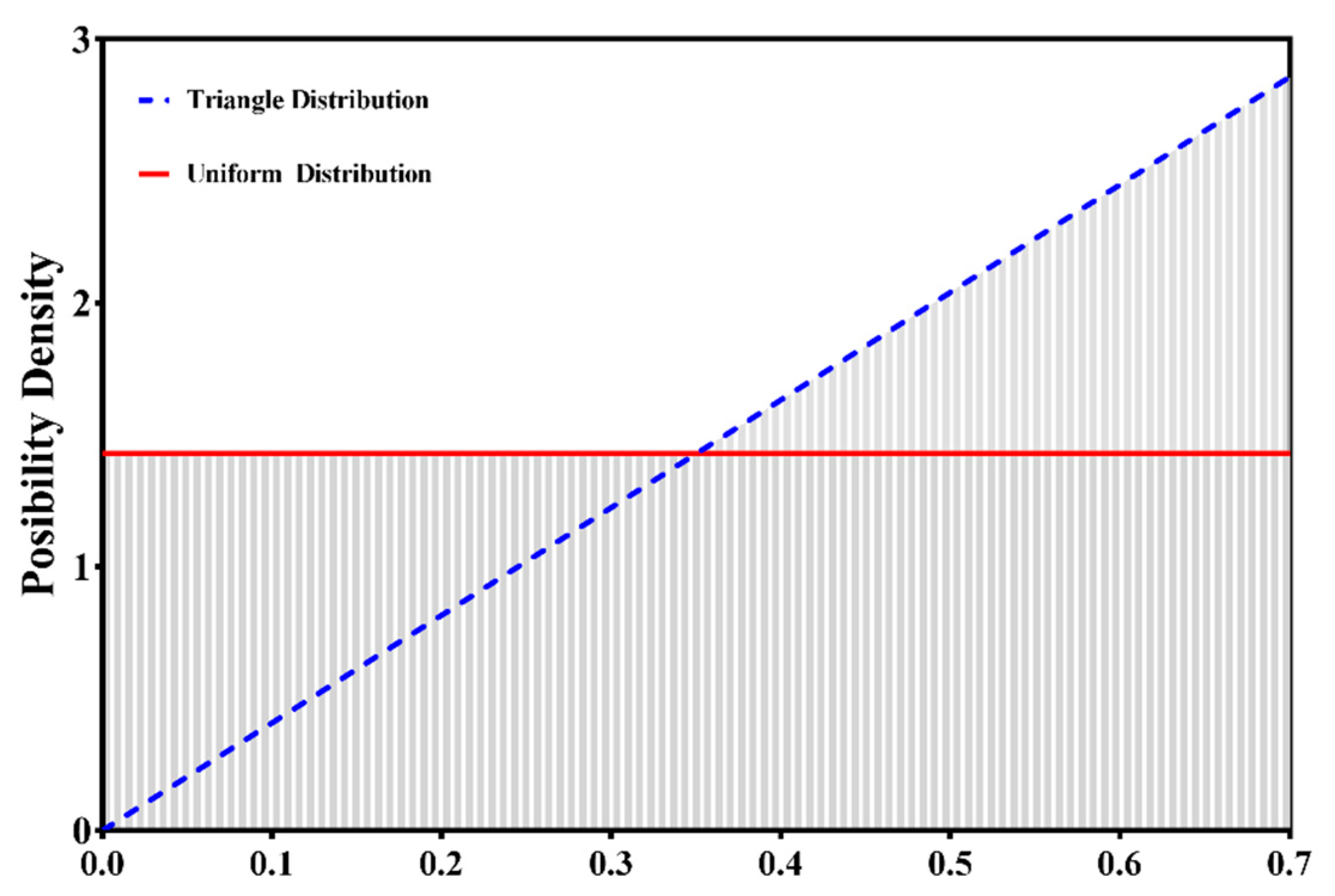
5.3. Triangular Distribution
5.4. Uniform Distribution
6. Conclusions
- (1)
- The normal optimization can reduce the minimum value of the drag coefficient under the set working condition considering the surface contamination, but its mean and standard deviation deteriorate;
- (2)
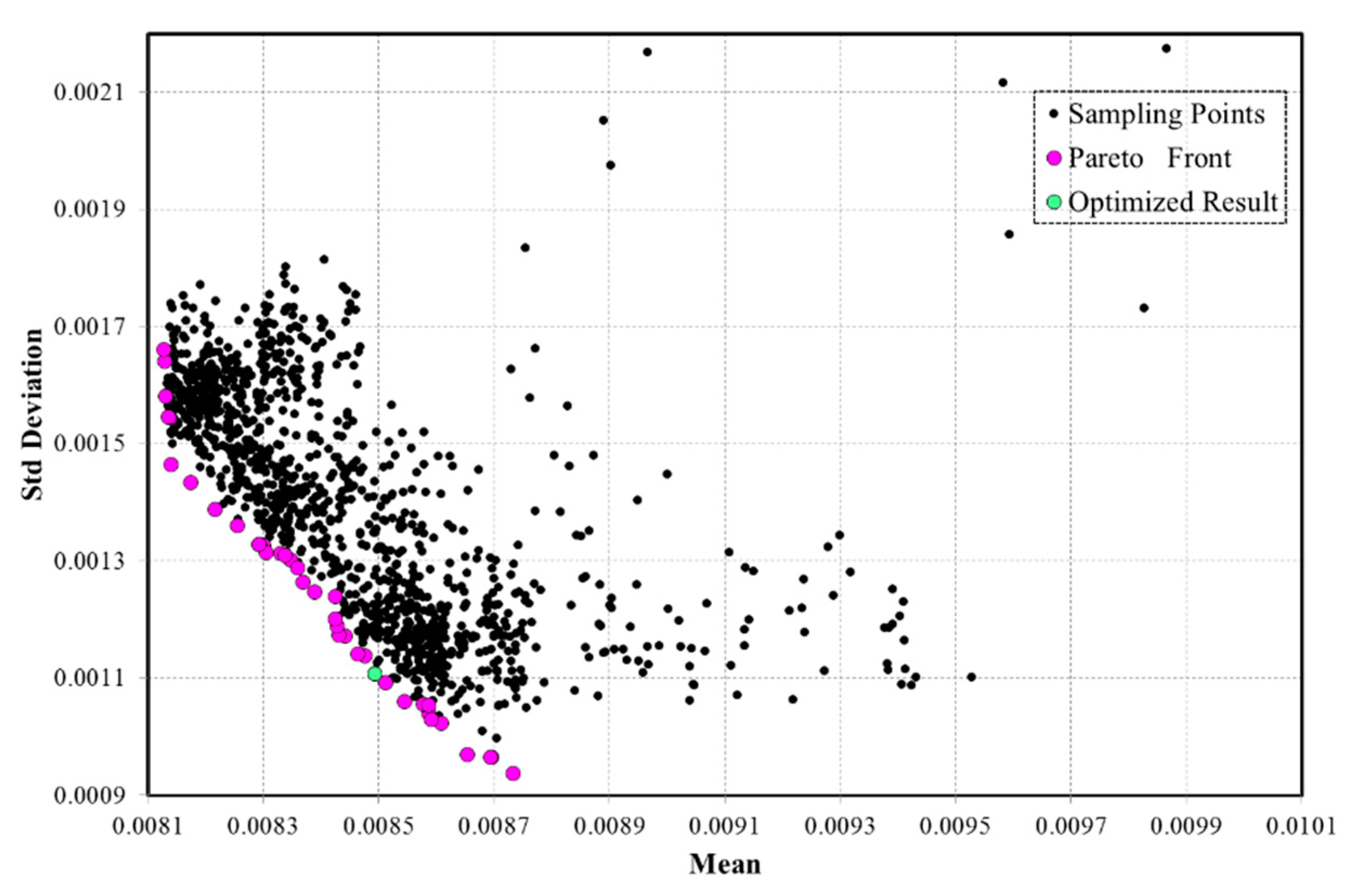
- Under the assumption that the surface contamination is triangularly distributed, the mean value of drag reduces slightly, and standard deviation is reduced by 47% after robust optimization;
- (3)
- Under the assumption of a uniform distribution of surface contamination, the mean value of the drag coefficient is reduced by 7%, and the standard deviation is reduced by 28% after robust optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Tang, Z. Natural laminar flow airfoil shape design at transonic regimes with multi-objective evolutionary algorithms. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 233, 991–999. [Google Scholar] [CrossRef]
- Shi, Y.; Mader, C.A.; He, S.; Halila, G.L.O.; Martins, J.R.R.A. Natural Laminar-Flow Airfoil Optimization Design Using a Discrete Adjoint Approach. AIAA J. 2020, 58, 4702–4722. [Google Scholar] [CrossRef]
- Zhong-Hua, H.; Jing, C.; Ke-Shi, Z.; Xu, Z.-M.; Zhu, Z.; Song, W.P. Aerodynamic Shape Optimization of Natural-Laminar-Flow Wing Using Surrogate-Based Approach. AIAA J. 2018, 56, 2579–2593. [Google Scholar]
- Tao, J.; Sun, G.; Guo, L.; Wang, X. Application of a PCA-DBN-based surrogate model to robust aerodynamic design optimization. Chin. J. Aeronaut. 2020, 33, 1573–1588. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Z.; He, W. An effective approach for robust design optimization of wind turbine airfoils with random aerodynamic variables. Adv. Mech. Eng. 2019, 11, 1687–8132. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Chen, H. Optimization design of airfoils under atmospheric icing conditions for UAV. Chin. J. Aeronaut. 2022, 35, 118–133. [Google Scholar] [CrossRef]
- Kok, M.; Mertens, T.; Raps, D.; Young, T.M. Influence of surface characteristics on insect residue adhesion to aircraft leading edge surfaces. Prog. Org. Coat. 2013, 76, 1567–1575. [Google Scholar] [CrossRef]
- Buzica, A.; Knoth, F.; Breitsamter, C.; Knoth, F.; Breitsamter, C. Leading-Edge Roughness Affecting Diamond-Wing Aerodynamic Characteristics. Aerospace 2018, 5, 98. [Google Scholar] [CrossRef]
- Bak, C.; Gaunaa, M.; Olsen, A.S.; Kruse, E.K. What is the critical height of leading-edge roughness for aerodynamics. J. Phys. Conf. Ser. 2016, 753, 022023. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Proceedings of the Conference on Low Reynolds Number Airfoil Aerodynamics, University of Notre Dame, Notre Dame, IN, USA, 5–7 June 1989. [Google Scholar]
- Drela, M.; Giles, M.B. Viscous-inviscid analysis of transonic and low Reynolds number airfoils. Am. Inst. Aeronaut. Astronaut. 1987, 25, 1347–1355. [Google Scholar] [CrossRef]
- Langtry, R.B. A correlation-Based Transition Model Using Local Variables for Unstructured Parallelized CFD Codes; Stuttgart University Report; Stuttgart University: Stuttgart, Germany, 2006. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Huan, Z.; Zhenghong, G.; Fang, X.; Yidian, Z. Review of Robust Aerodynamic Design Optimization for Air Vehicles. Arch. Comput. Methods Eng. 2018, 26, 685–732. [Google Scholar] [CrossRef]
- Bakar, A.; Li, K.; Liu, H.; Xu, Z.; Alessandrini, M.; Wen, D. Multi-Objective Optimization of Low Reynolds Number Airfoil Using Convolutional Neural Network and Non-Dominated Sorting Genetic Algorithm. Aerospace 2022, 19, 35. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, L.; Wan, Y.; Yang, Z.; Yang, W.; Chen, C.; Zhao, D.; Wang, F.; Guo, Y. An Intelligent Method for Predicting the Pressure Coefficient Curve of Airfoil-Based Conditional Generative Adversarial Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Xiaojing, W.; Zhang, W.; Peng, X.; Wang, Z. Benchmark aerodynamic shape optimization with the POD-based CST airfoil parametric method. Aerosp. Sci. Technol. 2019, 9, 632–640. [Google Scholar]
- Akram, T.; Kim, M.-H. Aerodynamic Shape Optimization of NREL S809 Airfoil for Wind Turbine Blades Using Reynolds-Averaged Navier Stokes Model—Part II. Appl. Sci. 2021, 11, 2211. [Google Scholar] [CrossRef]
- Kulfan, B.M. A Universal Parametric Geometry Representation Method “CST”. Journey Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Mauchmer, M.D.; Somers, D.M. Design and experimental results for a high-altitude, long-endurance airfoil. J. Aircraft 1989, 26, 148–153. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Population size | 12 |
| Crossover rate | 0.9 |
| Number of population generations | 200 |
| Probability of variation | 0.01 |
| Parameter | Initial Value | Range | Parameter | Initial Value | Range |
|---|---|---|---|---|---|
| 0.16 | 0.11~0.21 | −0.12 | −0.16~−0.08 | ||
| 0.35 | 0.25~0.45 | −0.06 | −0.08~−0.03 | ||
| 0.09 | 0.06~0.12 | −0.16 | −0.20~−0.12 | ||
| 0.62 | 0.42~0.82 | 0.00 | −0.05~0.05 | ||
| −0.11 | −0.14~−0.08 | −0.13 | −0.20~0.00 | ||
| 0.84 | 0.60~1.00 | −0.15 | −0.20~−0.10 | ||
| 0.06 | 0.04~0.08 | 0.11 | 0.07~0.15 | ||
| 0.49 | 0.34~0.65 | −0.06 | −0.08~−0.04 | ||
| 0.42 | 0.29~0.55 | 0.30 | 0.20~0.40 |
| Airfoils | ||
|---|---|---|
| Optimized airfoil | 0.00585 | −0.20 |
| Original airfoil | 0.00635 | −0.20 |
| Airfoils | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|
| Original | 0.0086 | 0.0019 | 0.0136 | 0.0064 |
| Normal optimization | 0.0090 | 0.0022 | 0.0155 | 0.0055 |
| Robust optimization | 0.0085 | 0.0010 | 0.0125 | 0.0078 |
| Airfoils | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|
| Original | 0.0102 | 0.0025 | 0.0151 | 0.0063 |
| Normal optimization | 0.0108 | 0.0027 | 0.0159 | 0.0066 |
| Robust optimization | 0.0095 | 0.0018 | 0.0013 | 0.0069 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Guo, Z. Robust Optimization of Natural Laminar Flow Airfoil Based on Random Surface Contamination. Appl. Sci. 2022, 12, 8757. https://doi.org/10.3390/app12178757
Wang S, Guo Z. Robust Optimization of Natural Laminar Flow Airfoil Based on Random Surface Contamination. Applied Sciences. 2022; 12(17):8757. https://doi.org/10.3390/app12178757
Chicago/Turabian StyleWang, Shunshun, and Zheng Guo. 2022. "Robust Optimization of Natural Laminar Flow Airfoil Based on Random Surface Contamination" Applied Sciences 12, no. 17: 8757. https://doi.org/10.3390/app12178757
APA StyleWang, S., & Guo, Z. (2022). Robust Optimization of Natural Laminar Flow Airfoil Based on Random Surface Contamination. Applied Sciences, 12(17), 8757. https://doi.org/10.3390/app12178757






