1. Introduction
This article tackles the problem of path planning and execution of multi-robot search for a static target in urban and indoor environments with teams of heterogeneous robots. In particular, the problem of an efficient search for a static target has a variety of applications related to exploration and Coverage Path Planning (CPP). Search, exploration, and CPP have received attention from the robotics community for a long time to equip robots with the skills to quickly generate high-quality path plans for several tasks requiring the robot’s field of view inspect a region or a portion of a region. These skills are critical to a variety of important real-world tasks including map building [
1,
2,
3,
4], cleaning/covering indoor areas [
5,
6], security, surveillance and information gathering [
7,
8,
9,
10], and reconnaissance or search and rescue [
11,
12,
13].
In traditional CPP, a robot or a team of robots must find the optimal paths such that the sensor footprint, or Field of View (FoV), passes over the entire region or search polygon. A common strategy for CPP and exploration is to find informative next viewpoints or paths using sampling-based approaches to discover unseen regions of the map within some defined search polygon. Static target search is a variation on Coverage Path Planning (CPP) or Exploration, depending on map knowledge, in which the searching agent(s) must additionally detect some predefined target. This manuscript relates closely to the former, where static map information is known a priori. Prior information about the target may also be given. In situations without prior knowledge of the target (i.e., the target prior is a uniform distribution over the search region), we posit that search for a static target and CPP are similar. The team must generate plans optimally to have the FoV, or sensor footprint, cover the entire region of interest. This is the baseline scenario for our simulation and hardware experiments, wherein the target prediction model is uniform over unseen space. In other scenarios, the team may be provided with prior information, for example to search near buildings first in a Search and Rescue (SAR) mission while attempting to help injured people or to leverage the most recent sensor data from a missing team member to determine where on the map they may be lost.
The purpose of this manuscript is to further improve coverage and search speed for situations when the mission completion time is critical, for example SAR or surveillance. We propose an algorithm for generating efficient paths for heterogeneous robot teams, which attempts to maximize the utility of each team member to complete the search in minimum time.
An overview of the path-generation algorithm is given by
Figure 1.
By uniquely combining an H-Clustering step with a TSP step, CONCERTS generates high-quality sample paths for the information-theoretic utility function. We propose a measure of heterogeneity, or coverage competency, which is a score based on the individual robot’s FoV size and movement speed. The H-Clustering step takes advantage of coverage competency and distributes waypoints to each robot to ensure they are assigned a search region that represents their coverage skill with respect to their teammates. We also provide a new metric, Waypoint Allocation Factor (WAF), to measure how evenly waypoints are divided among agents based on their coverage competency score. We demonstrate our algorithm has linear complexity with respect to the number of teammates and provide a complexity analysis. Furthermore, it is shown that CONCERTS is not only resilient to robot failure by re-planning online to re-assign the failed robot’s search region, but also flexible to use prior knowledge of target information.
Finally, we perform indoor experiments with three heterogeneous robots to validate our algorithm’s performance in the real world.
Overall, we present CONCERTS (see Algorithm 1 and
Figure 1), an algorithm for heterogeneous robot teams capable of efficient target search. Our contributions are summarized as follows:
We propose a novel method for sample path generation that uniquely combines H-Clustering for waypoint assignment and TSP for optimal path generation to provide an information-theoretic utility function with high-quality candidates for minimizing search time while maintaining online planning speed.
We propose the metrics coverage competency and Waypoint Allocation Factor (WAF) to capture an agent’s coverage ability to distribute regions equitably and improve search time.
We propose a new Heterogeneous Clustering (H-Clustering) algorithm that leverages coverage competency to efficiently assign search regions to each member of the team and validate that it results in an average of 25% reduction in search time.
CONCERTS is robust to team-member failure and re-plans online by monitoring team progress to guarantee the proposed algorithm always provides paths for complete coverage after the mission starts.
We show that our method outperforms a state-of-the-art CPP algorithm [
7] by 9% in coverage completion time. In situations without prior target information, CONCERTS is a CPP algorithm if not terminated upon target object detection.
We deploy CONCERTS with a team comprised of two quadrupedal and one mobile robot on the floor of a university building to demonstrate that they can find the target rapidly.
This paper is organized as follows.
Section 2 discusses related works. In
Section 3, we give background formulations. In
Section 4, we formally introduce our problem and describe our methods. In
Section 5, we present our experiments with discussion and finally
Section 6 concludes our work.
| Algorithm 1 Multi-Agent Search() |
Input: Entropy Map, Robot Pose, Coverage Competency Output: (A set of paths) for to N do ▹ for each cluster in end for for to N do ▹ for each agent for to do ▹: number of candidate paths ▹ : k-th candidate for n-th agent, Equation ( 8) end for ▹ Get the best path ▹ Save the best path for n-th agent end for return
|
2. Related Works
For decades, CPP has received great attention for its relevance in navigation tasks. Early solutions offered an offline planner given a static map. A traditional method is to decompose the coverage region into cells using Boustrophedon decomposition [
15]. We employ a similar cell decomposition to generate the set of waypoints for complete coverage. A common strategy in this form of the problem is to break down the map and perform simple back-and-forth behaviors. One alternative to such behavior is to generate the set of points to visit and solve a Traveling Salesman Problem (TSP) for optimal visitation order [
6,
11]. Ref. [
16] instead finds the optimal order of visitation using mixed-integer linear programming.
There are also several geometric approaches [
5,
17], which typically give global guarantees with respect to distance traveled during execution. However, such methods often make assumptions about perfect omni-directional sensing. Traditional methods for path planning are insufficient, however, when the goal is to operate in an online fashion to handle robot failure or dynamic environments.
Sampling-based approaches are popular in mapping and exploration [
2,
3,
4,
9,
18]. Such methods account for sensor noise and environment complexity. Early work used frontiers [
19] to explore spaces. Frontiers are the boundaries between explored and unexplored regions of the search polygon. The critical factor in information-theoretic-based strategies [
20,
21] is how to generate subsequent observation paths; i.e., how to provide quality candidates to the utility function. Early work [
2] uses a laser range scanner to map a previously unknown small environment. In [
3,
4], the authors leverage a utility function based on Cauchy–Schwartz quadratic mutual information to more efficiently generate plans to map 3D spaces. Ref. [
9] proposes three planning structures for information-gathering missions such as signal monitoring. Ref. [
18] focuses on mission speed with MAVs by taking a hybrid approach to frontier and sampling-based exploration strategies.
Ref. [
7] addresses the problem of scalable CPP by efficiently generating path plans with up to 150 agents in non-convex areas. The authors propose the robot team conducts auction and conflict resolution steps to determine the region of space they will cover. We benchmark our method against this path planner, which is state of the art in terms of coverage completion time. Our method features agent autonomy for search execution, a target prediction model, and automatic re-planning; however, when the target is static, the path-planning algorithm is equivalently a CPP problem, and therefore we use [
7] as a state-of-the-art comparison in terms of mission completion time (see
Table 1).
There is an abundance of real-time algorithms for multi-robot teams in coverage and exploration tasks. Studies have emphasized resilience to robot failure [
22,
23,
24], management of energy [
25,
26,
27] or communications [
28,
29,
30] constraints, and heterogeneous teaming [
20,
31]. Ref. [
26] also considers an information-gathering mission; however, their future work indicates increasing to
n agents. Ref. [
27] performs search and exploration with UAVs, which are limited in both communication and battery life. They use a state machine to help team members decide between exploring, meeting, sacrificing and relaying. They leverage a frontier-based method. In [
28], they consider a model of communication strength between the agents and a central control strategy, and cleverly use a serial connection of the robots to maximize their exploration area. Instead of constraining the team to constant connectivity, [
30] proposes a method of periodic communications at fixed intervals to update the full team. In [
13], an algorithm for solving Multi-robot Efficient Search Path Planning (MESPP) for finding a non-adversarial moving target is proposed. This method provides theoretical bounds on search performance. However, it only scales up to five agents and does not provide resilience to robot failure.
CONCERTS provides a significant boost in efficiency when compared with the authors’ previous work [
20], which used a greedy sampling-based planner that resulted in overlapping and inefficient paths. The purpose of this manuscript is to improve completion time in multi-robot coverage and search tasks while maintaining online performance and achieving robustness to agent failure—a common scenario during real robot deployment. Reducing search time is critical for SAR or similar applications wherein small improvements in response time may make significant differences for the search target. The proposed method achieves this in three ways. First, by leveraging H-Clustering, each agent is assigned an appropriately sized search region that reflects the team heterogeneity. Second, the proposed method delivers high-quality candidate paths to the information-theoretic utility function using the solution to a TSP in two directions along the assigned waypoints as sample paths, as discussed further in
Section 4.4. Finally, by incorporating each agent’s TSP-based sample paths into a single information-theoretic utility function, final paths are selected as to minimize FoV overlap of agents to search areas faster. Furthermore, the proposed method manages this process while also maintaining robustness to agent failure.
3. Background
3.1. Target Estimation: Bayesian Filtering
We use Bayesian inference to recursively estimate target state
x through sequential observations from each of
n agents,
in a probabilistic manner. This inference model aims to predict the posterior distribution of target position at time
k, namely
. Bayesian filtering uses a prediction stage and a correction stage with incoming sensing information. Assuming that the prior distribution
is available at time
, the prediction step attempts to estimate
from previous observations as follows.
where
is the target’s motion model based on a first-order Markov process. Then, when the measurement
is available, the estimated state can be updated as
where
and
is a sensing model for a multi-agent system that can also be decomposed to
i-th agent’s sensing model
. For the correction stage, the measurements of all agents are used to modify the prior estimate, leading to the target belief. If a static target is assumed, the target prediction can be described as
, only containing a noise term with the previous target state.
3.2. Entropy Map (Search Map)
The entropy map is updated using sensor data of each robot at each instance. The exploration begins under the assumption that the target exists in the search region. We use a 2D occupancy grid map representation in which the search region is discretized into cells. Each cell is assigned a probability of occupancy from 0 to 1. Cells with the value 0 are free space, 0.5 are unknown and 1 are occupied. Local sensor measurements from each agent are used to maintain a local 2D occupancy map, representing its FoV. Entropy map cells are initialized as unknown (i.e., assigned the value 0.5) except those that are known to be occupied by static obstacles. The entropy map
M is constructed by cells with a type
which represent occupied, unknown and free space, respectively. A cell’s occupancy status is used to measure the uncertainty of the target over the total search space (i.e., the map entropy). Entropy is defined here as
where
is the occupancy variable at time step
t and
N denotes the total number of cells. The search map is maintained in this way.
3.3. Target Prediction
In some scenarios, prior information about the target is given and is incorporated into the entropy map using the target prediction model. This prediction model is based on information that can be obtained in advance. For example, in a rescue mission, it might be useful to take advantage of the fact that people are more likely to be near collapsed buildings or the place where the accident occurred. If, on the other hand, a team of robots is searching for a lost robot, it may be useful to consider that teammate’s last known sensor information to determine candidate locations on the map. In this study, the above situations are called context,
c. Context is used to estimate the target’s location. A Gaussian Mixture Model (GMM) is constructed with a finite number of contexts
at time
k using the following equation
where
,
and
are a mixing coefficient, mean vector, and covariance, respectively, for the
i-th distribution. Each component’s density is a 2D Gaussian function of the form as following.
A particle filter is employed to implement the prediction model. If one considers the former scenario of searching near buildings after a disaster, a scene may have more than one building. Then, there exist multiple values representing each collapsed building.
4. Methods
In this section, we detail CONCERTS, a cooperative multi-agent target search algorithm for solving the problem setting described above.
4.1. Overall Framework
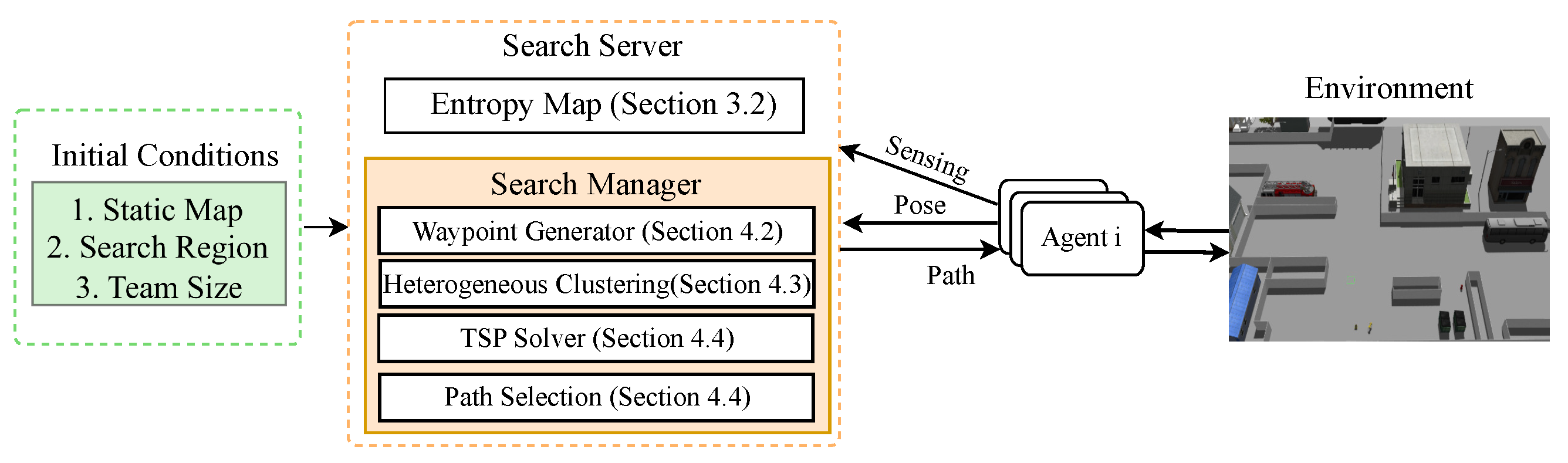
Our search, presented in Algorithm 1 and described in
Figure 1, is as follows:
- 1.
Update entropy map using Bayesian filtering;
- 2.
Generate waypoints from entropy map (Algorithms 2 and A1);
- 3.
Perform Heterogeneous Clustering using coverage competency (Algorithm 3);
- 4.
Solve the Traveling Salesman Problem over clustered waypoints for each agent;
- 5.
Select optimal paths using an information-theoretic approach;
- 6.
If re-plan conditions are met, repeat steps (2)–(5).
| Algorithm 2 WaypointGeneration() |
Input: ▹ (Entropy Map, Current Pose) Output: Waypoint Set take the unknown cell ▹ insert into while is not empty() do ▹ pop from for do ▹ 4-adjacent cells if and then ▹: occupancy value at else if then end if end for end while return
|
| Algorithm 3 HeterogeneousClustering() |
Input: (Waypoints, Centroids(Robot Poses), Sensing Capabilities) Output: A Partition Initiallize ![Applsci 12 08649 i001]() repeat ▹ ▹ if then end if until return
|
4.2. Waypoint Generation
Under the premise that we are given static map information a priori, the entropy map can be used to identify unexplored areas. Algorithm 2 generates a set of waypoints that divide these unexplored portions of the search polygon according to the size of the smallest FoV. Assuming a square-shaped FoV, the number of cells corresponding to the FoV at each moment can be calculated using map resolution. For example, for a square FoV with a sensing range of 5 meters, 100 cells should be collected if the map resolution is 0.5.
Waypoints are found based on the number of cells inside the smallest FoV. Regions of the same number of cells in the map are formed and then waypoints are found by taking the average position of each cell in those regions. However, all cells assigned to a waypoint should be covered by the robot footprint when any team member visits that waypoint (i.e., complete coverage is performed if all waypoints are visited). To this end, when we collect cells to generate waypoints, we restrict those cells which are within the FoV maximum range and exclude those which are further away.
The output of the waypoint-generation algorithm is depicted in
Figure 1b.
4.3. Heterogeneous Clustering
CONCERTS treats the waypoint assignment problem as a clustering problem. Traditional clustering methods partition a set of data into a predefined number of subgroups, K, to minimize the sum of the distance squared between each data point and the centroid of each cluster. These methods use unsupervised learning to determine cluster centroids. In H-Clustering, K is equal to the number of teammates and cluster centroids are the positions of each member of the team.
Then nearest neighbors are computed based on square distance to each centroid and incorporate each robot’s coverage competency.
This formulation is flexible to various initial configurations because clusters are centered about robot initial position. When the robots are evenly distributed in the search region, computed waypoints will easily be distributed among the K agents. However, some situations arise in which robots start next to one another. If two agents with competency gaps begin next to each other, then all the nearby points will be assigned to the more competent teammate. To avoid this situation with only clusters, we compute new clusters when any agent is assigned fewer than some predefined minimum number of waypoints.
In addition, nearby agents are given a new centroid. After clustering, we obtain the waypoints assigned to each agent (centroid) in .
Let
where
is
i-th waypoint extracted from the search map (Algorithm 2) and let
be a set of
K centroids, which correspond to the location of the agents. Suppose
(
) centroids are given as a constraint. The goal is to obtain the remaining number (
) of centroids and to assign each point to the nearest centroid such that sum of weighted 2D Euclidean distance is minimized as follows.
where
is the weighted distance, which reflects the
j-th robot’s sensing capability using the normalized coefficient
and
denotes 2D Euclidean distance between two arbitrary points,
p and
q. We define
coverage competency as
where
is the sensing capacity of
j-th agent and
is the minimum value of robot teams, which is the product of a moving speed and sensing range of agent
j. Because we normalize this coefficient with
, the minimum value of sensing capacity among all agents, we can use it to consider the relative proximity between centroids and points. In this way, we ensure that robots that are fast or have a large FoV are allocated more waypoints than robots that are not.
4.4. Path Selection
After constructing and assigning a cluster of waypoints to each robot, we solve an instance of the Traveling Salesman Problem (TSP) separately for each agent in parallel using the Genetic Algorithm for solving TSP [
14]. The TSP provides the optimal waypoint visitation order with a starting and ending point at the cluster’s centroid (i.e., the robot’s initial position). This optimal visitation order, however, is computed for each agent independently and therefore does not consider the effects of the team. Instead of simply using the TSP solution for each agent, we consider that there are two possible directions along the solution. These two directions are the sample paths we supply to the information-theoretic utility function (see
Figure 2). This approach provides better samples to the utility function than may be generated by traditional or frontier-based methods. Next, the utility function considers the sample paths for each team member sequentially and therefore ensures that the team will choose paths that minimize overlap and maximize the new area searched. By combining the TSP with the information-theoretic utility function, we have optimized each agent’s individual path within their assigned cluster while also allowing the final path selection to consider the full team effort.
We use an A* planner to generate obstacle-free paths and use B-spline to obtain the spline function of it (parameterization). Then we re-parameterize them with respect to the agent’s moving speed using a set of sampled points along the path. This re-parameterization normalizes the process and ensures that the horizon is equivalent for each robot, regardless of movement speed and FoV size. Using this approach, we compute the information gain, denoted as
, with the following equation:
where
denotes the
i-th sampled point and
m is a random variable representing occupancy, while
and
are the number of sampling points and the number of grid cells in the FoV given the sampled points, respectively. Thus, The
is calculated by summing over the FoV regions defined by sampled points through the path. The overall expected utility,
[
], is then computed for the full team as
where
denotes the traveling cost (traveling distance) to move along the path
.
4.5. Re-Planning
The central server monitors team progress to determine when online re-planning is necessary. When a team member fails, finishes their given set of waypoints, or is given new target information, it is desirable to perform re-planning. When a preset percentage of the team covers their region, we generate a new set of waypoints over the full unexplored search map and perform the full process again. This enables the team to continuously search with all its resources. Similarly, if new target information is provided, then re-planning should occur to ensure that the new regions of high entropy are explored with high priority to find the target. On the other hand, re-planning is initialized if a robot loses communication with the server or fails to move for an extended period of time. When re-planning occurs, the process resets to waypoint generation (step (2) in
Section 4.1) to ensure that the team will robustly complete a search of the entire region until the target is found. The scenario of teammate failure is depicted in
Figure 3. Explicitly, re-planning conditions are the following:
Robot failure (stopped operating or lost communication);
New target information is acquired;
Predefined percentage of team completes their search over given waypoints.
By re-planning on these conditions, the proposed method is robust to failure and ensures complete area search, even in situations when only one agent avoids failure. Furthermore, by re-planning upon completion of some teammates, the method avoids wasting resources.
4.6. Waypoint Allocation Factor
We introduce a new metric called Waypoint Allocation Factor (
) to evaluate each agent’s contribution of the search task according to the coverage competency. To compute how evenly the area for coverage is allocated, we take a standard deviation of the total swept area and divide by the
coverage competency of the robot team. Specifically, we apply the following equation:
where
denotes total swept area for agent
i,
is the coverage competency, and
means a normalizing constant. A value close to zero indicates that the waypoints were evenly distributed among the team after competency considerations. We propose this metric to effectively evaluate the area covered with explicit consideration of team heterogeneity. Because it is a standard deviation, a value of 0 means that the search task was perfectly assigned to account for the team heterogeneity.
4.7. Computational Complexity
Computational efficiency is necessary to enable online planning even as the search region and number of teammates increase. Here, we analyze the computational efficiency of the proposed algorithm using the following parameters: number of grid cells (map size ÷ resolution), number of trajectories to sample , and number of agents n. In detail, the complexity of the waypoint-generation Algorithm 2 is .
The clustering has time complexity where i denotes a fixed maximum number of iterations, n is the number of clusters and is equal to the number of agents, is the number of waypoints generated, and d dimension of the data, where d is 2 in this setting. The complexity of the waypoint-generation method can be computed as and represents the worst case of decomposition (i.e., the search region is entirely unknown and divided by the product of number of agents and the number of cells within the smallest FoV, ). The solution of the TSP with the genetic algorithm is of order where j is the number of outer iterations of the genetic algorithm, is the initial size of population, and is the number of waypoints. The sampling-based path selection algorithm takes complexity. The resulting complexity of CONCERTS is .
5. Simulations, Experiments, and Results
5.1. Numerical Simulation Results
We present Python-based simulation results of our proposed approach to demonstrate its scalability. Agent state is represented as
and has two control inputs
as per the equations of motion for a non-holonomic mobile agent. Variables
x and
y represent Cartesian positions while
is yaw angle with respect to the same coordinate frame. Variables
v and
represent forward velocity and angular velocity in the local robot frame. Each agent is equipped with a ray sensor which has a square FoV with limited range. It is assumed that the search region and all static obstacles have a rectangular shape. Obstacle positions are not known in advance. To achieve robust collision avoidance, we use a dynamic window approach [
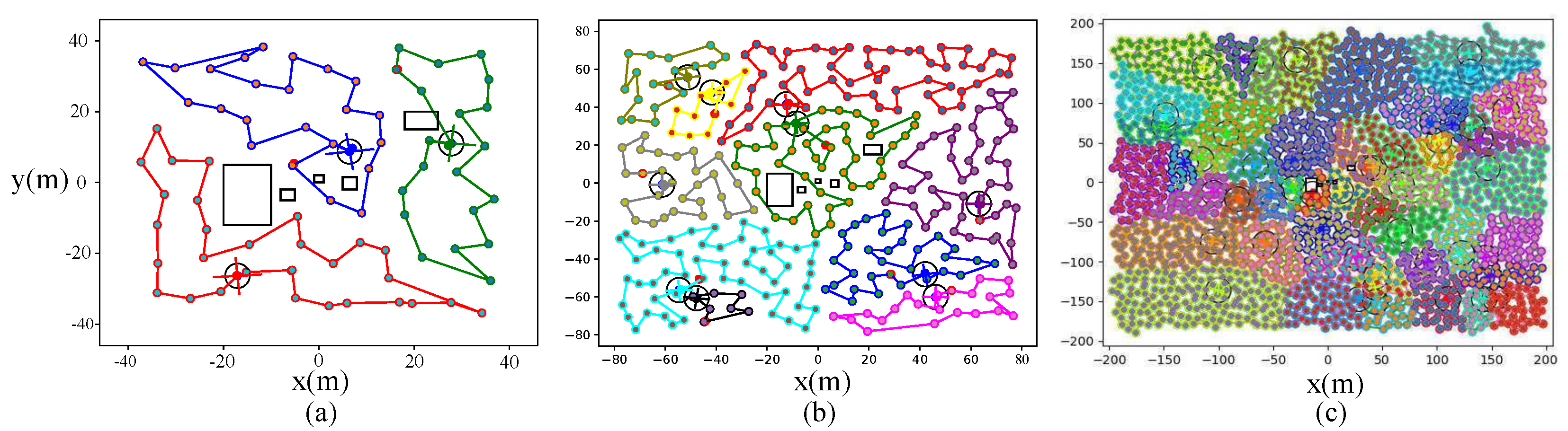
32] to generate each agent’s control input. We tested different initial conditions with a varying number of agents, and we show some example scenarios with up to 50 agents in
Figure 4.
5.2. Comparative Results
We benchmark CONCERTS against a state-of-the-art algorithm, SCoPP [
7], an offline CPP algorithm with the goal to minimize total coverage completion time with the results shown in
Table 1. For a fair comparison, the problem setting is the Python environment with static map information given. CONCERTS is not given prior target information (i.e., uniform prior distribution of target location) and the search does not terminate until the entire area has been explored. Furthermore, each trial uses the same number of agents, and all have the same skill level. The data in
Table 1 is generated from 10 comparative trials with 13 agents, as described in [
7].
In such a setting, CONCERTS performs the same task as a CPP algorithm with the goal of providing complete search as quickly as possible. In this setting, CONCERTS is shown to outperform SCoPP by 9% in coverage completion time.
These results indicate that in scenarios where team heterogeneity cannot be exploited, CONCERTS still is able to outperform a state-of-the-art method. This is a valid comparison because search for a static target assumed to be in the environment has the same goal as a CPP algorithm, i.e., in the worst case, to cover the entire region as quickly as possible. Similar to SCoPP, our method scaled linearly with the number of agents and the slowest step is the path-planning step. However, our method generates plans more quickly, and experimental validation of online re-planning is provided. Finally, CONCERTS also is scalable and is validated with up to 50 agents.
5.3. Gazebo-ROS Simulation
We validate our framework’s ability to transfer to robotic systems in human environments with three high-fidelity Gazebo simulations. The implementation details can be found in
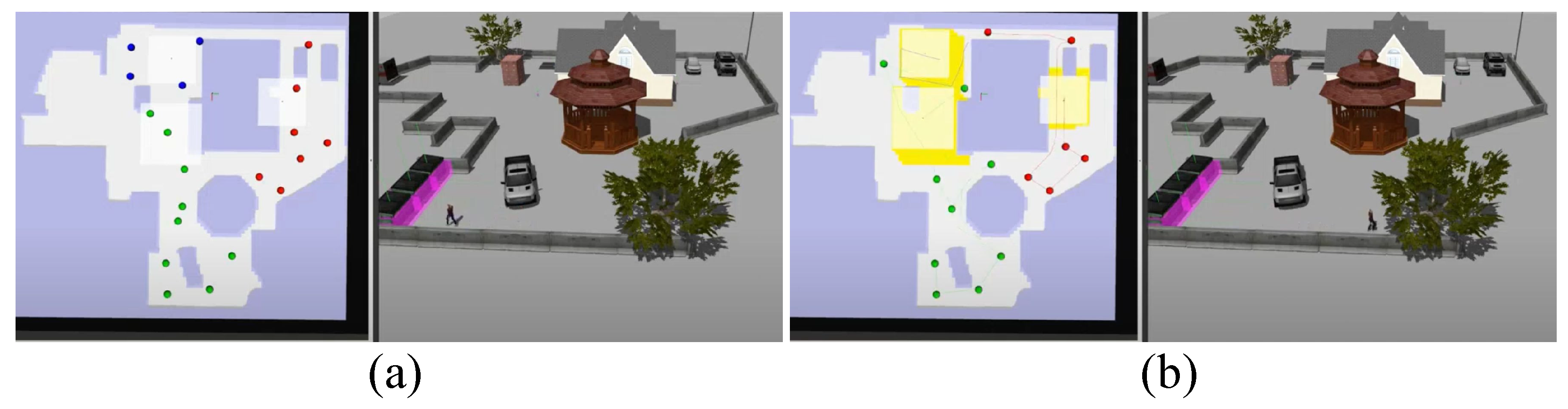
Figure 5. CONCERTS receives a static map, a search region, the number of teammates and their initial positions. The search server manages the entropy map and manages the path planning. Each agent is managed via ROS and receives a path before executing the search. The first environment is a 10 m × 20 m simulation of an apartment in the Anna Hiss Gymnasium Robotics Facility at The University of Texas. The second is a 40 m × 50 m simulation of the area surrounding a home, and the final environment is a 100 m × 100 m town that has been struck by natural disaster. In the home outdoor environment, the team performs robust search and initiates re-planning when one teammate fails. This scenario is depicted in
Figure 6. In (a), three agents begin the search and on the left frame a top-down view of the map in Rviz is shown. Each of 3 agents is assigned a set of waypoints in colors red, green and blue. Soon after starting, the blue agent fails, and re-planning occurs to generate new waypoints and assign each agent to them. The new clustering results are shown in in (b). Here, the yellow regions are those that have been searched by the team. On the other hand, in the case of the disaster map, the team takes advantage of prior target knowledge (see
Figure 7).
Figure 7a shows the visualization of the four-robot search for an injured person. The team is searching for a missing person, and it is given that the person is likely to be near a building. These contexts are represented as particle filters, shown by the four red particle sets. This particle set represents a belief of the target location and is updated based on the team sensor information using Equation (
2). When we use this prior information, our path planner is designed to visit waypoints close to the target belief. As a result, as shown in
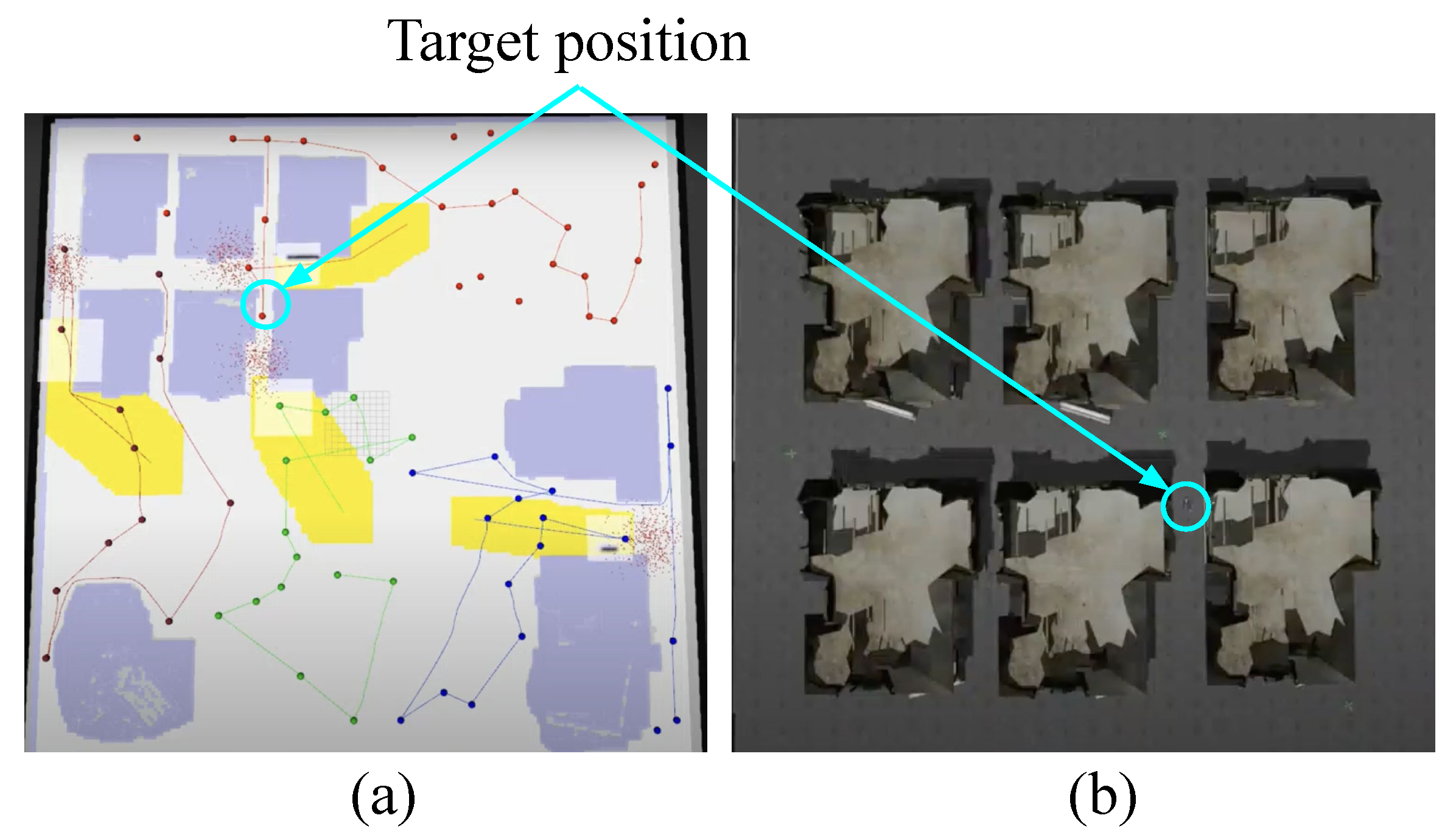
Figure 7, it is shown that each first point of the planned route is set as points near the building. The target location is given by the cyan circles near the destroyed set of homes.
Figure 7b shows a top-down view zoomed in over the homes with the target location indicated in the Gazebo environment. In the case of using such an initial guess, if the guess is correct, the target can be found early, but in the opposite case, it may take a long time. Videos demonstrating these scenarios can be found at the project website.
5.4. Effect of Coverage Competency
We validate the inclusion of coverage competency in the Gazebo-ROS simulation environment and present our findings in
Table 2. The table demonstrates that the inclusion of coverage competency reduces search time by an average of 25% as shown in bold. The results validate that we see a significant performance boost in our metric of interest when coverage competency is considered. Each trial is set with different initial conditions to demonstrate that including coverage competency outperforms in any general setting; however, for a fair comparison, identical initial conditions are considered for each individual trial with and without coverage competency. In all cases, it is confirmed that the search time is significantly reduced by the H-Clustering step.
Additionally, we investigate
to ensure that CONCERTS is effective at incorporating coverage competency. In
Table 2, it is shown that
, as expected, is reduced with the inclusion of coverage competency. WAF equal to zero indicates that the waypoints were distributed perfectly with respect to coverage competency of the team. We note that in
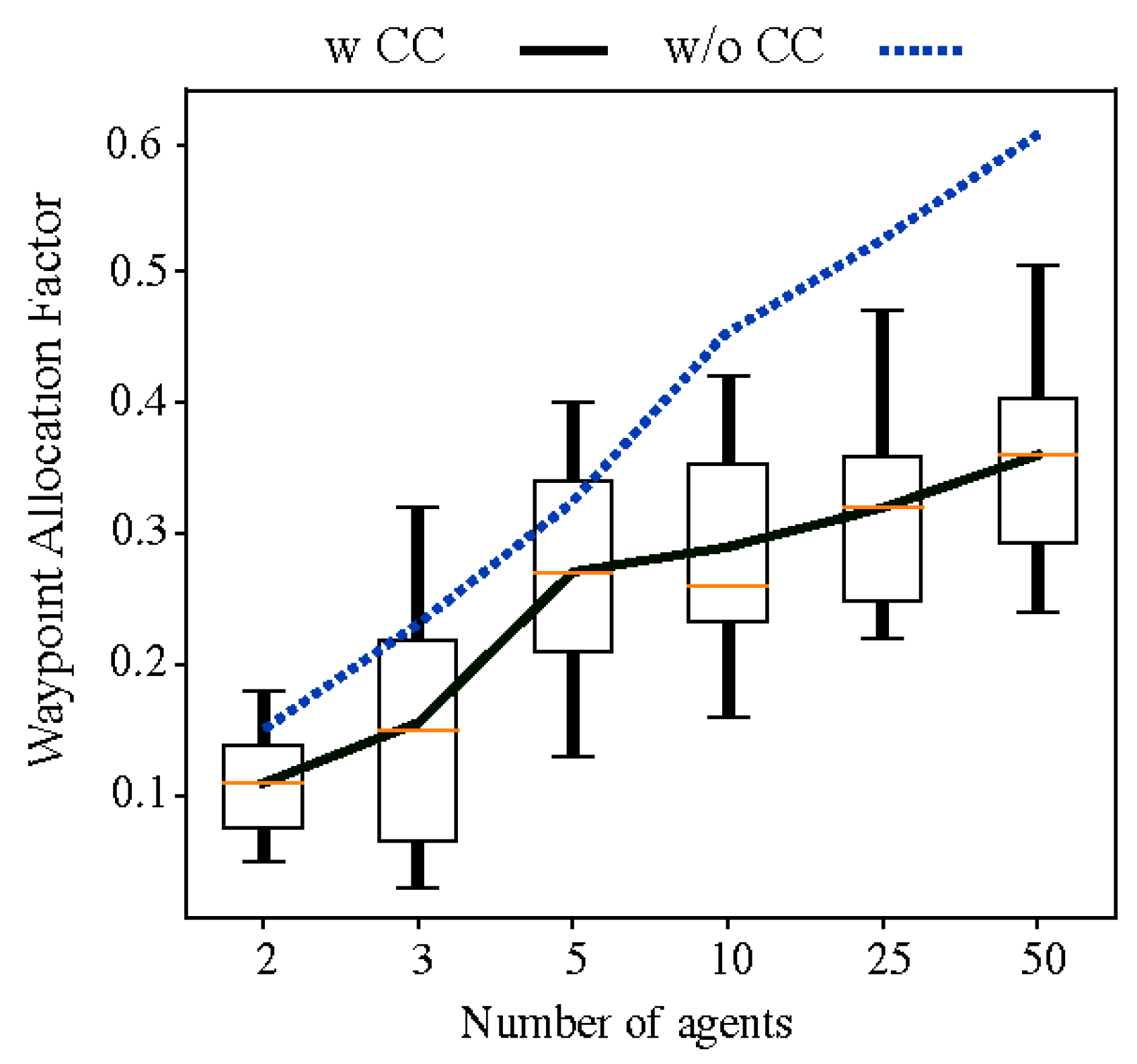
Figure 8 that WAF slightly increases as the number of agents increases. This is expected as a standard deviation, or
will tend to increase as the number of samples, or number of agents, increases.
Figure 8 displays WAF with and without consideration of coverage competency during the H-Clustering stage. As expected, the WAF is lower, or the distribution is fairer, when agent heterogeneity is included. It is clear that regardless of the number of agents, the WAF will be lower when coverage competency is considered and that the overall mission time will be reduced. This implies that leveraging robot characteristics for motion planning increases productivity from the perspective of the entire team.
Ultimately, these results indicate that, while CONCERTS outperforms than the state of the art in area coverage with a homogeneous team, performance is further improved by including coverage competency when the team is heterogeneous. allows measurement of the effectiveness of the inclusion of coverage competency, and it is clear based on the results that by including the term that the efficiency of the search is improved. The term validates the inclusion over 10 separate trials with randomized initial conditions, suggesting that this is a general result.
5.5. Real Robot Environment
The team is comprised of two Unitree A1 quadrupeds with different sensor suites and a Toyota HSR. One A1 quadruped is equipped with a Velodyne Puck 3D LiDAR and a RealSense D435. The other is equipped with a RPLidar A3 2D LiDAR and a Realsense D435. Both quadrupeds have Intel NUC Mini PCs on board which communicate with the robot hardware. The RPLidar A3 has a smaller FoV than the Velodyne Puck LiDAR and the use of different sensors is to introduce heterogeneity within the team for two agents that would otherwise have identical coverage competency scores. The HSR is equipped with Hokuyo 2D LiDAR, RGB-D camera sensing and has an onboard Jetson TK1. All robots run Episodic non-Markov Localization [
33]. The central search server runs on a remote laptop, and we use Robofleet [
34] for efficient communication between the server and agents. The search server receives pose and sensing information from each agent to compute potential paths. Each agent decides the final path based on its own onboard path planner to avoid un-mapped obstacles.
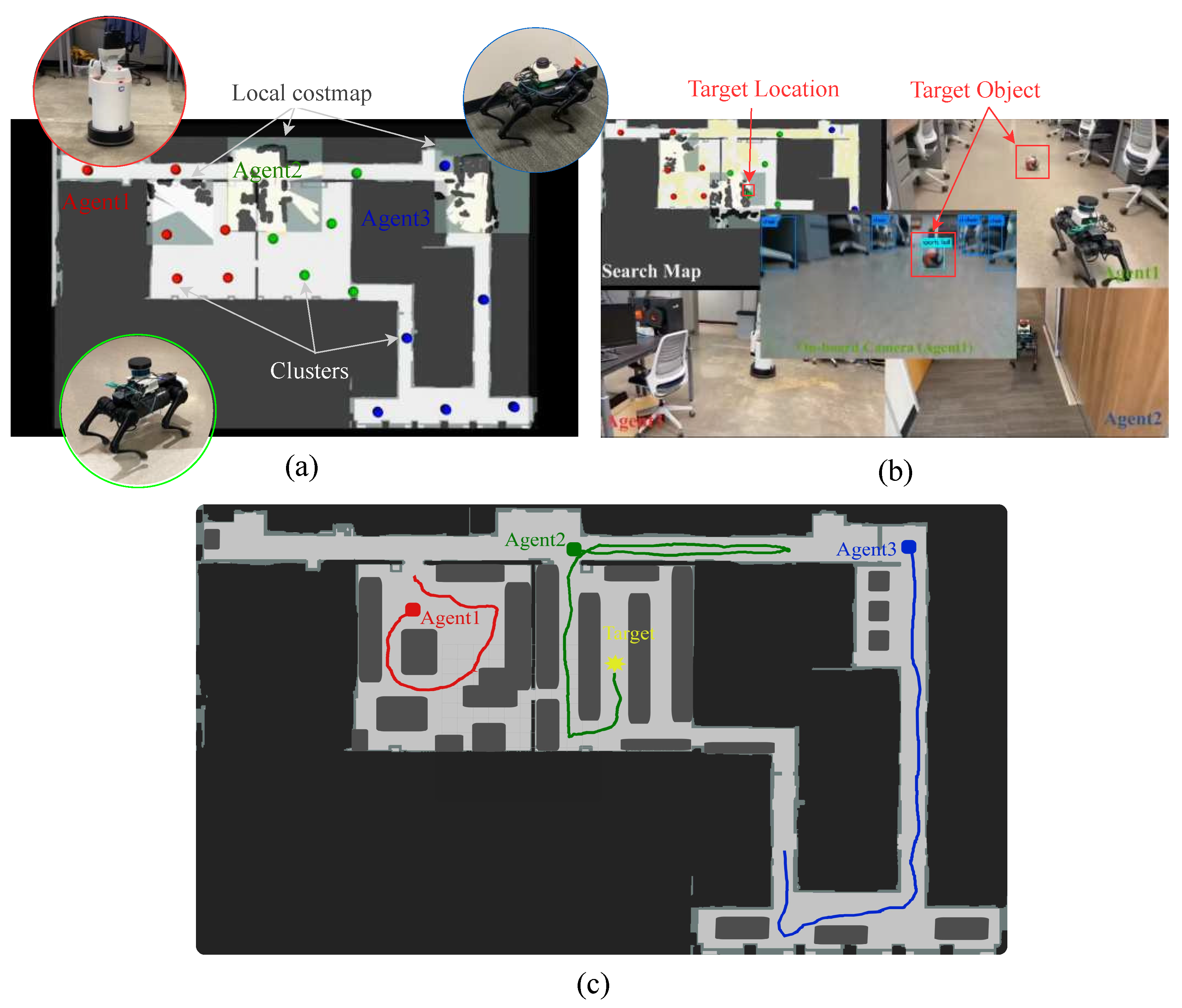
The search experiment is performed in the Aerospace Engineering Building at the University of Texas at Austin while looking for a static volleyball.
Figure 9a shows the initial positions of the robot team members and corresponding waypoints. A snapshot of the experiment is depicted in
Figure 9b and actual paths are visualized in
Figure 9c.
Figure 10 gives snapshots at five different moments during the three-robot search in the Aerospace Engineering Building. The top row depicts the HSR, or Agent 1 in
Figure 9. The second row is the A1 Quadruped with Velodyne Puck LiDAR and is Agent 2 in
Figure 9. This agent is the teammate that finds the target volleyball. Finally, the bottom row is the other A1 Quadruped with the RPLidar A3 and is Agent 3 in
Figure 9. The entire framework is developed in ROS Melodic, and the search server is implemented using ROS actionlib library. At initial planning or during re-planning, the search server generates a set of paths for a robot team and then sends those to each agent (see
Figure 5).
Experiments indicate that search performance is significantly impacted by the initial setting. The main reason for this is that H-Clustering is computed using the initial positions of the robots. For example, if the starting points of all robots are gathered, most waypoints will be allocated to an agent has high coverage competency, leading to uneven distribution. To overcome this undesirable situation, the proposed clustering algorithm flexibly tries to find new centroids for certain agents as shown in the Equation (
6). For example, we use only one robot’s position as a fixed centroid for H-clustering out of three robots, and clustering can be performed to find new centroids for the other two robots by setting
,
. However, in this experiment, robots are distributed evenly throughout the search region and, as a result, the distribution of waypoints neatly reflects coverage competency scores.
The proposed method has room for improvement using path planning with various FoV shapes. In this manuscript, it is assumed that the FoV of each robot is square-shaped based on a 360-degree laser scan. This assumption may not be suitable for a visual-based target search task using a camera, which typically has a cone-shaped FoV. Therefore, search efficiency can be further improved by considering the exact sensor FoV or by only updating the entropy map according to the sensing source.
6. Conclusions
This article explores online search for a general heterogeneous multi-agent system. First, we perform a clustering method which assigns some region of space to each agent given their coverage competency then solves the TSP for each of those agents. We employ an information-theoretic utility function for sampling-based optimization, which results in a path for each of n agents.
We perform baseline testing versus a state-of-the-art algorithm for CPP and verify that our proposed method generates plans faster and results in a quicker overall area coverage time by 9%. We then validate CONCERTS by deploying and executing search in a high-fidelity Gazebo simulation of three different settings to demonstrate how our method works with and without prior target information. Furthermore, we perform Gazebo simulation tests to validate the inclusion of coverage competency for heterogeneous teams. We observed that including coverage competency reduced search completion time by 25%. In addition, as the number of team members of the robot increases, so does the impact of including coverage competency. Specifically, when the team comprises 50 heterogeneous robots then the impact of including coverage competency is doubled, as measured by . The distribution of waypoints is two times closer to a perfect distribution than the case without coverage competency. Finally, we demonstrate the efficacy of this proposed method with real robot experiments in an indoor setting. Overall, results validate the effectiveness and robustness of the proposed algorithm.
Several future works remain; however, current efforts are towards including a target motion model for dynamic targets and performing continuous coverage. Additional future works should involve outdoor field testing of CONCERTS with the addition of planning using an RGB-D camera FoV to replace the square type. Finally, ongoing work should include curiosity regions, where agents are encouraged to explore regions of the FoV that do not match with static mapped obstacles.
Author Contributions
Conceptualization, M.K., R.G. and L.S.; methodology, M.K.; software, M.K. and R.G.; validation, M.K. and R.G.; formal analysis, M.K.; investigation, M.K. and R.G.; data curation, M.K. and R.G.; writing—original draft preparation, M.K. and R.G.; writing—review and editing, M.K., R.G. and L.S.; visualization, M.K. and R.G.; supervision, L.S.; project administration, M.K. and R.G.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
Research was sponsored by the Army Research Office and was accomplished under Cooperative Agreement Number W911NF-19-2-0333. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. This work was also in part supported ONR Grant #N000141512507.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CONCERTS | Coverage cOmpeteNCy-basEd taRgeT Search |
| TSP | Traveling Salesman Problem |
| CPP | Coverage Path Planning |
| FoV | Field of View |
| SAR | Search and Rescue |
| WAF | Waypoint Allocation Factor |
| H-Clustering | Heterogeneous Clustering |
Appendix A
| Algorithm A1 GetWaypoint() |
Input: ▹ (Entropy Map, Current Cell, Visited flag) Output: w ▹ waypoint (average position of cells)
while is not empty() do for do ▹ 4-adjacent cells if and then end if if then w = AveragePos end if end for end while return
|
References
- Cao, C.; Zhu, H.; Choset, H.; Zhang, J. TARE: A hierarchical framework for efficiently exploring complex 3D environments. In Proceedings of the Robotics: Science and Systems Conference (RSS), Virtual, 12–16 July 2021. [Google Scholar]
- Amigoni, F.; Caglioti, V. An information-based exploration strategy for environment mapping with mobile robots. Robot. Auton. Syst. 2010, 58, 684–699. [Google Scholar] [CrossRef]
- Charrow, B.; Kahn, G.; Patil, S.; Liu, S.; Goldberg, K.; Abbeel, P.; Michael, N.; Kumar, V. Information-Theoretic Planning with Trajectory Optimization for Dense 3D Mapping. In Proceedings of the Robotics: Science and Systems, Rome, Italy, 13–17 July 2015; Volume 11. [Google Scholar]
- Charrow, B.; Liu, S.; Kumar, V.; Michael, N. Information-theoretic mapping using cauchy-schwarz quadratic mutual information. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 25–30 May 2015; pp. 4791–4798. [Google Scholar]
- Tokekar, P.R. Placement and Motion Planning Algorithms for Robotic Sensing Systems. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2014. [Google Scholar]
- Bähnemann, R.; Lawrance, N.; Chung, J.J.; Pantic, M.; Siegwart, R.; Nieto, J. Revisiting boustrophedon coverage path planning as a generalized traveling salesman problem. In Field and Service Robotics; Springer: Signapore, 2021; pp. 277–290. [Google Scholar]
- Collins, L.; Ghassemi, P.; Esfahani, E.T.; Doermann, D.; Dantu, K.; Chowdhury, S. Scalable Coverage Path Planning of Multi-Robot Teams for Monitoring Non-Convex Areas. arXiv 2021, arXiv:2103.14709. [Google Scholar]
- McCammon, S.; Hollinger, G.A. Topological path planning for autonomous information gathering. Auton. Robot. 2021, 45, 821–842. [Google Scholar] [CrossRef]
- Hollinger, G.A.; Sukhatme, G.S. Sampling-based robotic information gathering algorithms. Int. J. Robot. Res. 2014, 33, 1271–1287. [Google Scholar] [CrossRef]
- Cavinato, V.; Eppenberger, T.; Youakim, D.; Siegwart, R.; Dubé, R. Dynamic-Aware Autonomous Exploration in Populated Environments. arXiv 2021, arXiv:2104.02696. [Google Scholar]
- Pěnička, R.; Saska, M.; Reymann, C.; Lacroix, S. Reactive dubins traveling salesman problem for replanning of information gathering by uavs. In Proceedings of the 2017 European Conference on Mobile Robots (ECMR), Paris, France, 6–8 September 2017; pp. 1–6. [Google Scholar]
- Kohlbrecher, S.; Kunz, F.; Koert, D.; Rose, C.; Manns, P.; Daun, K.; Schubert, J.; Stumpf, A.; Stryk, O.V. Towards highly reliable autonomy for urban search and rescue robots. In Robot Soccer World Cup; Springer: London, UK, 2014; pp. 118–129. [Google Scholar]
- Hollinger, G.; Singh, S.; Djugash, J.; Kehagias, A. Efficient multi-robot search for a moving target. Int. J. Robot. Res. 2009, 28, 201–219. [Google Scholar] [CrossRef]
- Sedighpour, M.; Yousefikhoshbakht, M.; Darani, N.M. An effective genetic algorithm for solving the multiple traveling salesman problem. J. Optim. Ind. Eng. 2012, 8, 73–79. [Google Scholar]
- Choset, H. Coverage of known spaces: The boustrophedon cellular decomposition. Auton. Robot. 2000, 9, 247–253. [Google Scholar]
- Grotli, E.I.; Johansen, T.A. Path Planning for UAVs Under Communication Constraints Using SPLAT! and MILP. J. Intell. Robot. Syst. 2012, 65, 265–282. [Google Scholar] [CrossRef]
- Premkumar, A.P.; Yu, K.; Tokekar, P. A geometric approach for multi-robot exploration in orthogonal polygons. In Algorithmic Foundations of Robotics XII; Springer: Cham, Switzerland, 2020; pp. 896–911. [Google Scholar]
- Dai, A.; Papatheodorou, S.; Funk, N.; Tzoumanikas, D.; Leutenegger, S. Fast Frontier-based Information-driven Autonomous Exploration with an MAV. arXiv 2020, arXiv:2002.04440. [Google Scholar]
- Yamauchi, B. A frontier-based approach for autonomous exploration. In Proceedings of the Computational Intelligence in Robotics and Automation, CIRA’97, Monterey, CA, USA, 10–11 July 1997; pp. 146–151. [Google Scholar]
- Kim, M.; Gupta, R.; Sentis, L. Information-Theoretic Based Target Search with Multiple Agents. arXiv 2021, arXiv:2107.12715. [Google Scholar]
- Charrow, B. Information-Theoretic Active Perception for Multi-Robot Teams; University of Pennsylvania: Philadelphia, PA, USA, 2015. [Google Scholar]
- Zhou, L.; Tzoumas, V.; Pappas, G.J.; Tokekar, P. Resilient active target tracking with multiple robots. IEEE Robot. Autom. Lett. 2018, 4, 129–136. [Google Scholar]
- Rabban, I.E.; Tokekar, P. Improved Resilient Coverage Maximization with Multiple Robots. arXiv 2020, arXiv:2007.02204. [Google Scholar]
- Ishat-E-Rabban, M.; Tokekar, P. Failure-Resilient Coverage Maximization With Multiple Robots. IEEE Robot. Autom. Lett. 2021, 6, 3894–3901. [Google Scholar] [CrossRef]
- Yu, K.; O’Kane, J.M.; Tokekar, P. Coverage of an environment using energy-constrained unmanned aerial vehicles. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, Canada, 20–24 May 2019; pp. 3259–3265. [Google Scholar]
- Cai, X.; Schlotfeldt, B.; Khosoussi, K.; Atanasov, N.; Pappas, G.J.; How, J.P. Non-Monotone Energy-Aware Information Gathering for Heterogeneous Robot Teams. arXiv 2021, arXiv:2101.11093. [Google Scholar]
- Cesare, K.; Skeele, R.; Yoo, S.H.; Zhang, Y.; Hollinger, G. Multi-UAV exploration with limited communication and battery. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 25–30 May 2015; pp. 2230–2235. [Google Scholar]
- Woosley, B.; Dasgupta, P.; Rogers, J.G.; Twigg, J. Multi-robot information driven path planning under communication constraints. Auton. Robot. 2020, 44, 721–737. [Google Scholar] [CrossRef]
- Shi, G.; Rabban, I.E.; Zhou, L.; Tokekar, P. Communication-Aware Multi-robot Coordination with Submodular Maximization. arXiv 2020, arXiv:2011.01476. [Google Scholar]
- Hollinger, G.A.; Singh, S. Multirobot coordination with periodic connectivity: Theory and experiments. IEEE Trans. Robot. 2012, 28, 967–973. [Google Scholar] [CrossRef]
- Sakamoto, T.; Bonardi, S.; Kubota, T. A Routing Framework for Heterogeneous Multi-Robot Teams in Exploration Tasks. IEEE Robot. Autom. Lett. 2020, 5, 6662–6669. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Biswas, J.; Veloso, M.M. Episodic non-Markov localization. Robot. Auton. Syst. 2017, 87, 162–176. [Google Scholar] [CrossRef]
- Sikand, K.S.; Zartman, L.; Rabiee, S.; Biswas, J. Robofleet: Open Source Communication and Management for Fleets of Autonomous Robots. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 406–412. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
Figure 1.
Four steps to generate a path for each agent. (
a) Given a static map, a search region can be defined using a set of boundary points. (
b) CONCERTS uses cell decomposition to generate a set of waypoints, which, if visited, provide full sensor coverage over the high entropy regions. (
c) We perform a weighted clustering over all waypoints and assign sub-regions (clusters) to each agent based on their coverage competency. (
d) The next step solves instances of the single agent TSP [
14] to provide high-quality candidate paths to the utility function. The utility function selects a direction along the TSP solution to maximize team information gain.
Figure 1.
Four steps to generate a path for each agent. (
a) Given a static map, a search region can be defined using a set of boundary points. (
b) CONCERTS uses cell decomposition to generate a set of waypoints, which, if visited, provide full sensor coverage over the high entropy regions. (
c) We perform a weighted clustering over all waypoints and assign sub-regions (clusters) to each agent based on their coverage competency. (
d) The next step solves instances of the single agent TSP [
14] to provide high-quality candidate paths to the utility function. The utility function selects a direction along the TSP solution to maximize team information gain.
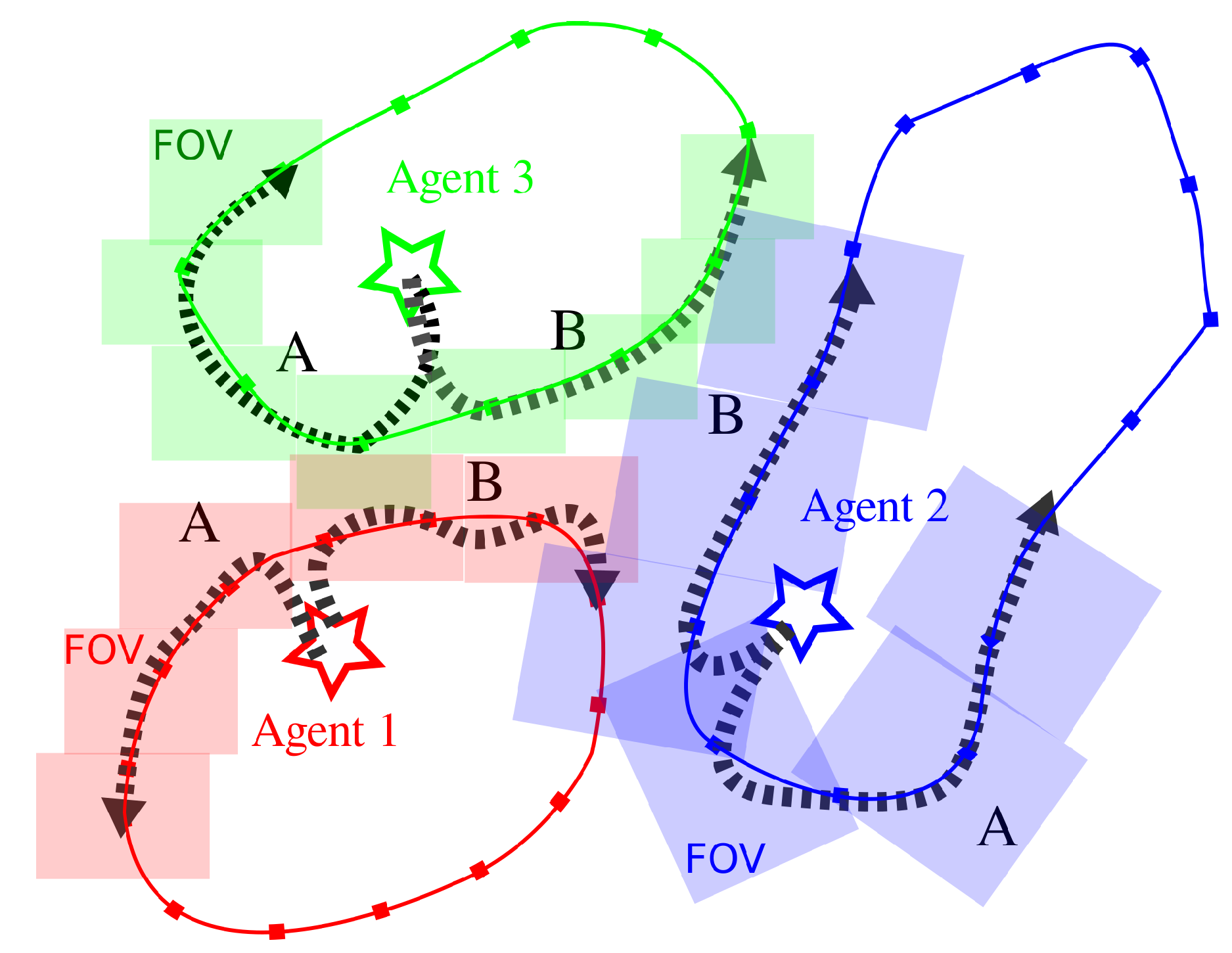
Figure 2.
Sampling paths along the TSP trajectory to calculate the Expected information gain. The three agents each have two candidate paths, A and B. The stars represent robot initial position, shaded rectangles denote the FoV of each agent at points along the path and the arrows represent the robot path from its initial position. If Agent 1 (red) selects path B, then Agent 2 (blue) will choose path A to reduce overlap and increase . It can be seen that Agent 2 in blue has a larger FoV and a higher coverage competency, and therefore covers a larger region than Agent 3 in green.
Figure 2.
Sampling paths along the TSP trajectory to calculate the Expected information gain. The three agents each have two candidate paths, A and B. The stars represent robot initial position, shaded rectangles denote the FoV of each agent at points along the path and the arrows represent the robot path from its initial position. If Agent 1 (red) selects path B, then Agent 2 (blue) will choose path A to reduce overlap and increase . It can be seen that Agent 2 in blue has a larger FoV and a higher coverage competency, and therefore covers a larger region than Agent 3 in green.
Figure 3.
Scenario with six agents. All paths are described in different colors and the effect of coverage competency and H-Clustering is clear. Agent A has the highest competency score and therefore has the largest search region while agent C has the smallest competency score and therefore has the smallest region to cover. (a) Agent E (cyan) failure. Letters A–F are the starting position of each of the 6 agents. (b) Re-planning step: Because the server has access to all robot plans, the waypoints assigned to Agent E can be reassigned to nearby agents. Ellipses represent the assignment of those waypoints to the agent of the same color. (c) CONCERTS guarantees complete coverage by solving a new TSP instance.
Figure 3.
Scenario with six agents. All paths are described in different colors and the effect of coverage competency and H-Clustering is clear. Agent A has the highest competency score and therefore has the largest search region while agent C has the smallest competency score and therefore has the smallest region to cover. (a) Agent E (cyan) failure. Letters A–F are the starting position of each of the 6 agents. (b) Re-planning step: Because the server has access to all robot plans, the waypoints assigned to Agent E can be reassigned to nearby agents. Ellipses represent the assignment of those waypoints to the agent of the same color. (c) CONCERTS guarantees complete coverage by solving a new TSP instance.
Figure 4.
Simulation results with a different number of agents in different size search regions. Agent position is marked by a circle with crossed lines and each agent is given a matching path color. Black rectangles are obstacles to be avoided by the agents. (a) 3-agent case (80 m × 80 m) (b) 10 agents (160 m × 160 m) (c) 50 agents (400 m × 400 m).
Figure 4.
Simulation results with a different number of agents in different size search regions. Agent position is marked by a circle with crossed lines and each agent is given a matching path color. Black rectangles are obstacles to be avoided by the agents. (a) 3-agent case (80 m × 80 m) (b) 10 agents (160 m × 160 m) (c) 50 agents (400 m × 400 m).
Figure 5.
Block diagram detailing the implementation of the proposed method for simulation and real robot experiments. CONCERTS generates the initial set of plans via the search server and ultimately delivers a path to each agent. Each agent manages a full autonomy stack and performs search over the environment.
Figure 5.
Block diagram detailing the implementation of the proposed method for simulation and real robot experiments. CONCERTS generates the initial set of plans via the search server and ultimately delivers a path to each agent. Each agent manages a full autonomy stack and performs search over the environment.
Figure 6.
This figure depicts a side-by-side of the home outdoor environment with three-robot searching. Yellow regions are those that have been covered by the agents. Dots in RGB represent the waypoints assigned to each agent. In (a) the search begins with three agents. The blue agent fails after a short time, then a re-planning step occurs. (b) depicts the results of the re-planning.
Figure 6.
This figure depicts a side-by-side of the home outdoor environment with three-robot searching. Yellow regions are those that have been covered by the agents. Dots in RGB represent the waypoints assigned to each agent. In (a) the search begins with three agents. The blue agent fails after a short time, then a re-planning step occurs. (b) depicts the results of the re-planning.
Figure 7.
The scenario with prior target information. Yellow regions are those that have been covered by the agents. Colored dots and lines represent the waypoints and paths assigned to each agent. Agent current position at that moment is marked by the white costmap ovelayed on the yellow regions. (a) The Rviz interface of the four robots performing search. Red particles represent contexts, or particle filters, to represent possible target locations. (b) A top-down view of the region of destroyed homes where the target is found. The target location is given by the cyan circle in (a,b).
Figure 7.
The scenario with prior target information. Yellow regions are those that have been covered by the agents. Colored dots and lines represent the waypoints and paths assigned to each agent. Agent current position at that moment is marked by the white costmap ovelayed on the yellow regions. (a) The Rviz interface of the four robots performing search. Red particles represent contexts, or particle filters, to represent possible target locations. (b) A top-down view of the region of destroyed homes where the target is found. The target location is given by the cyan circle in (a,b).
Figure 8.
We show analysis of the relationship of WAF and number of agents with and without considering coverage competency in numerical simulations. In all cases, the blue dashed line, which is the average value of WAF w/o CC, is larger than that of the case with CC. The box and whisker plot represents the distribution over 10 trials when considering coverage competency and the black line is the mean value.
Figure 8.
We show analysis of the relationship of WAF and number of agents with and without considering coverage competency in numerical simulations. In all cases, the blue dashed line, which is the average value of WAF w/o CC, is larger than that of the case with CC. The box and whisker plot represents the distribution over 10 trials when considering coverage competency and the black line is the mean value.
Figure 9.
(
a) Experimental validation for a three-robot search in the Aerospace Building fourth floor. The red, green, and blue markers represent the clusters for each agent. (
b) Mission completion with Agent 2 converging to the target of interest. (
a) yellow regions are those which have been explored, while the white areas are regions of uncertainty. Target location is shown as a red box. The object recognition is performed using the YOLO [
35] algorithm to detect a target. (
c) Trajectories of the robot team are visualized in the map.
Figure 9.
(
a) Experimental validation for a three-robot search in the Aerospace Building fourth floor. The red, green, and blue markers represent the clusters for each agent. (
b) Mission completion with Agent 2 converging to the target of interest. (
a) yellow regions are those which have been explored, while the white areas are regions of uncertainty. Target location is shown as a red box. The object recognition is performed using the YOLO [
35] algorithm to detect a target. (
c) Trajectories of the robot team are visualized in the map.
Figure 10.
Snapshots of three robot search experiments in the Aerospace Engineering Building. (a) This row shows the HSR (Agent 1) at different instances performing its search for the target. (b) A1 with Velodyne Puck LiDAR (Agent 2) and in the final frame, it finds the target object (the last frame). (c) The bottom row depicts the other A1 with RPLidar (Agent 3) performing a search.
Figure 10.
Snapshots of three robot search experiments in the Aerospace Engineering Building. (a) This row shows the HSR (Agent 1) at different instances performing its search for the target. (b) A1 with Velodyne Puck LiDAR (Agent 2) and in the final frame, it finds the target object (the last frame). (c) The bottom row depicts the other A1 with RPLidar (Agent 3) performing a search.
Table 1.
Comparative Test.
Table 1.
Comparative Test.
| Method | Completion Time (s) |
|---|
| Guastella’s | 3591.8 ± 0.00 |
| SCoPP | 196.53 ± 14.53 |
| CONCERTS (ours) | 180.22 ± 21.23 |
Table 2.
Search Time (s) with and without coverage competency.
Table 2.
Search Time (s) with and without coverage competency.
| Map (# Robots) | w/o CC | WAF | w CC (Proposed) | WAF |
|---|
| Apartment (2) | 124.8 ± 13.2 | 0.23 | 83.8 ± 22.4 | 0.07 |
| Home Outdoor (3) | 72.8 ± 8.5 | 0.31 | 58.1 ± 12.4 | 0.12 |
| Disaster (4) | 252.2 ± 21.2 | 0.37 | 189.8 ± 29.6 | 0.18 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).