Identification Approach for Nonlinear MIMO Dynamics of Closed-Loop Active Magnetic Bearing System
Abstract
:1. Introduction
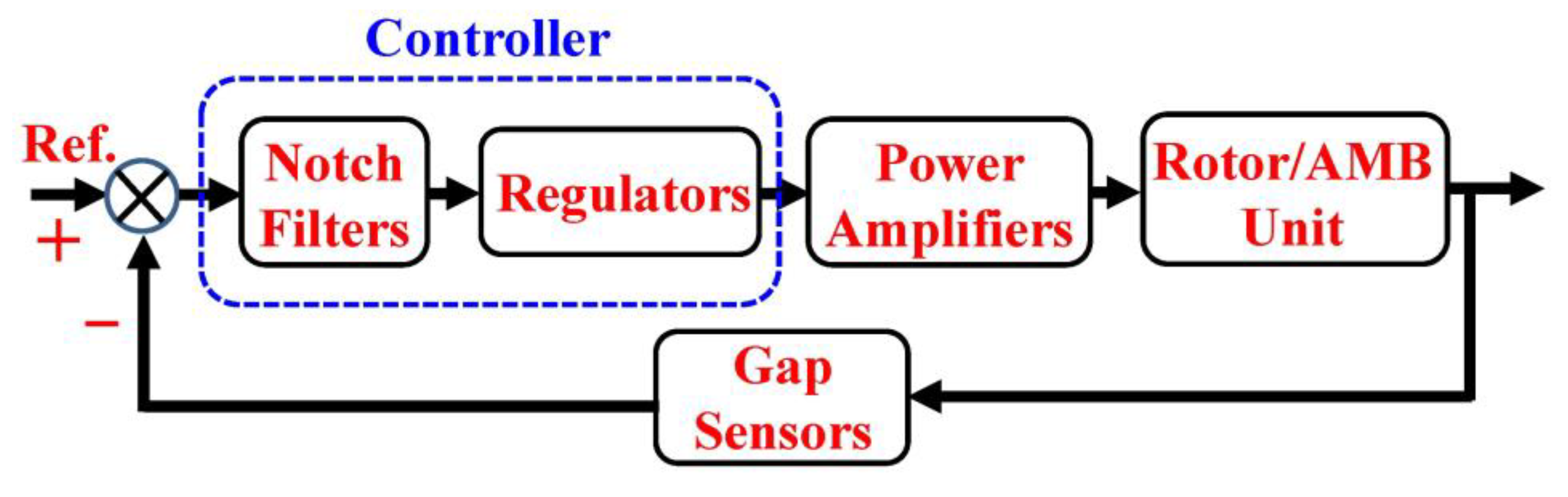
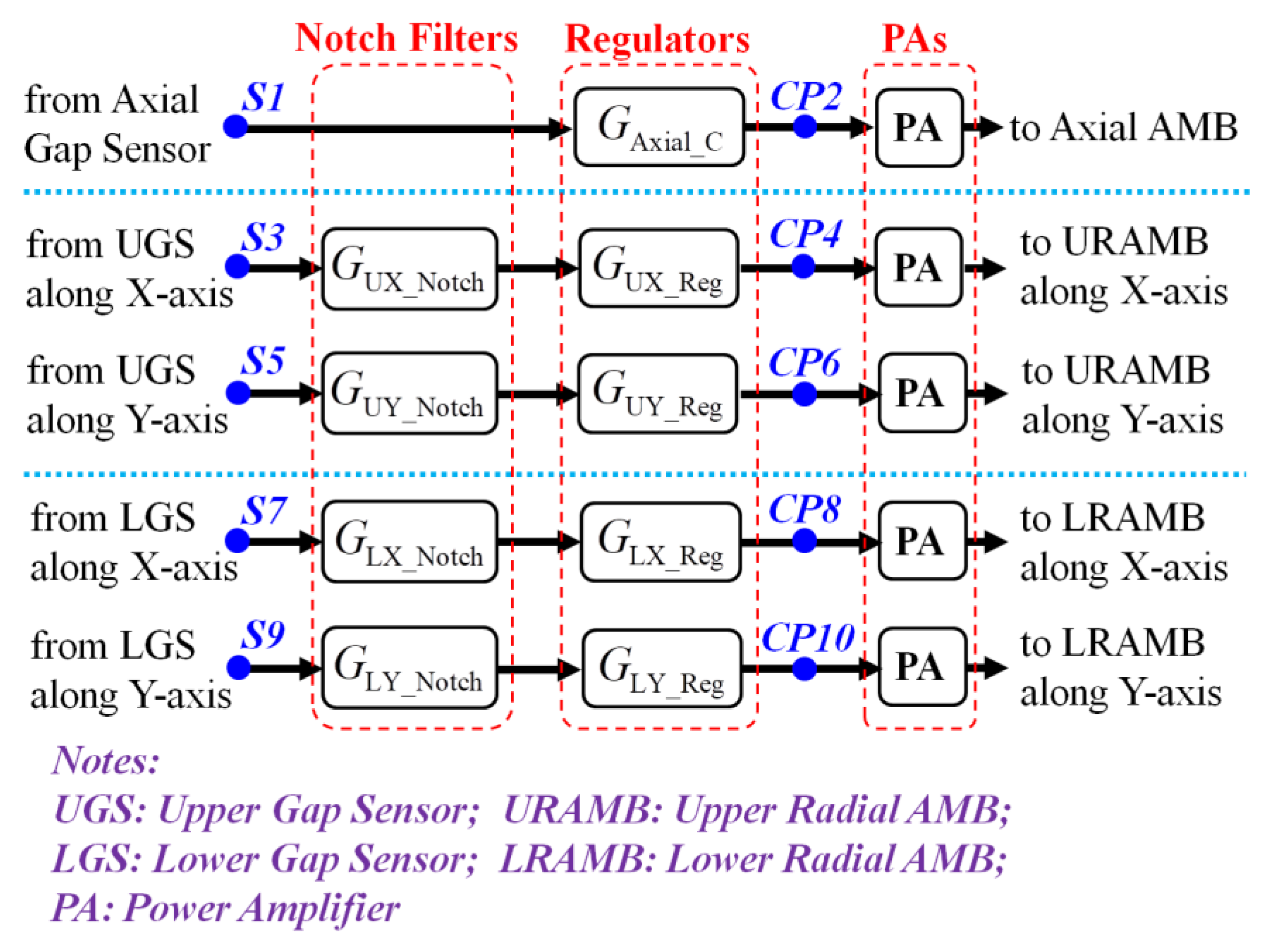
2. System Identification on Controllers for Radial Magnetic Bearings
- Step #1.
- Measure the upper and lower bounds of the control circuit’s input and output signals.
- Step #2.
- Disconnect the control circuit from the control loop of the TMP, but the power is still supplied to the control circuit.
- Step #3.
- Excite the control circuit with the ‘chirp’ perturbation signals and record the corresponding responses.
- Step #4.
- Construct the dynamic model of the controller via the aid of the commercial software, MATLAB.
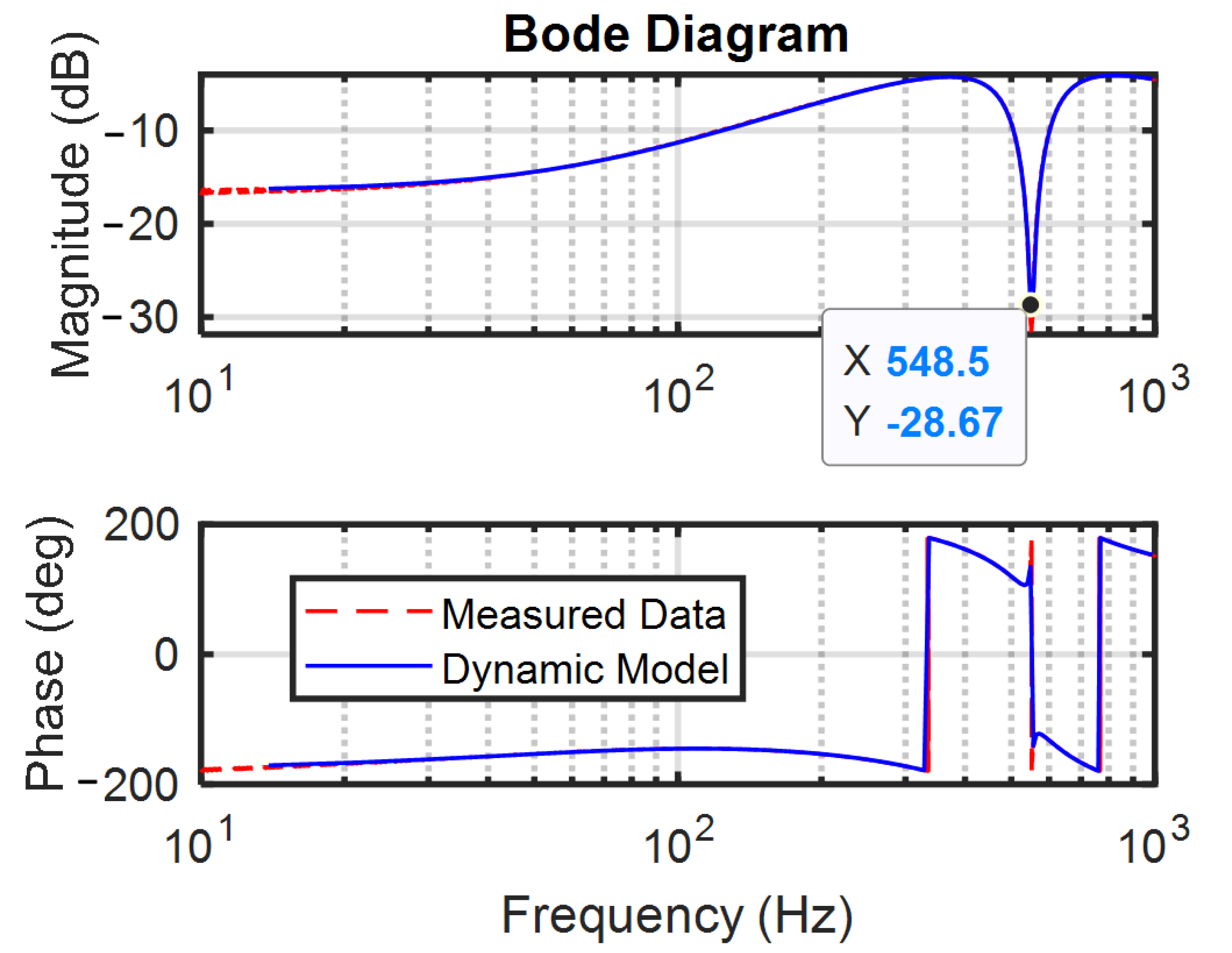
2.1. System Identification on Controllers for URAMB
2.2. System Identification on Controllers for LRAMB
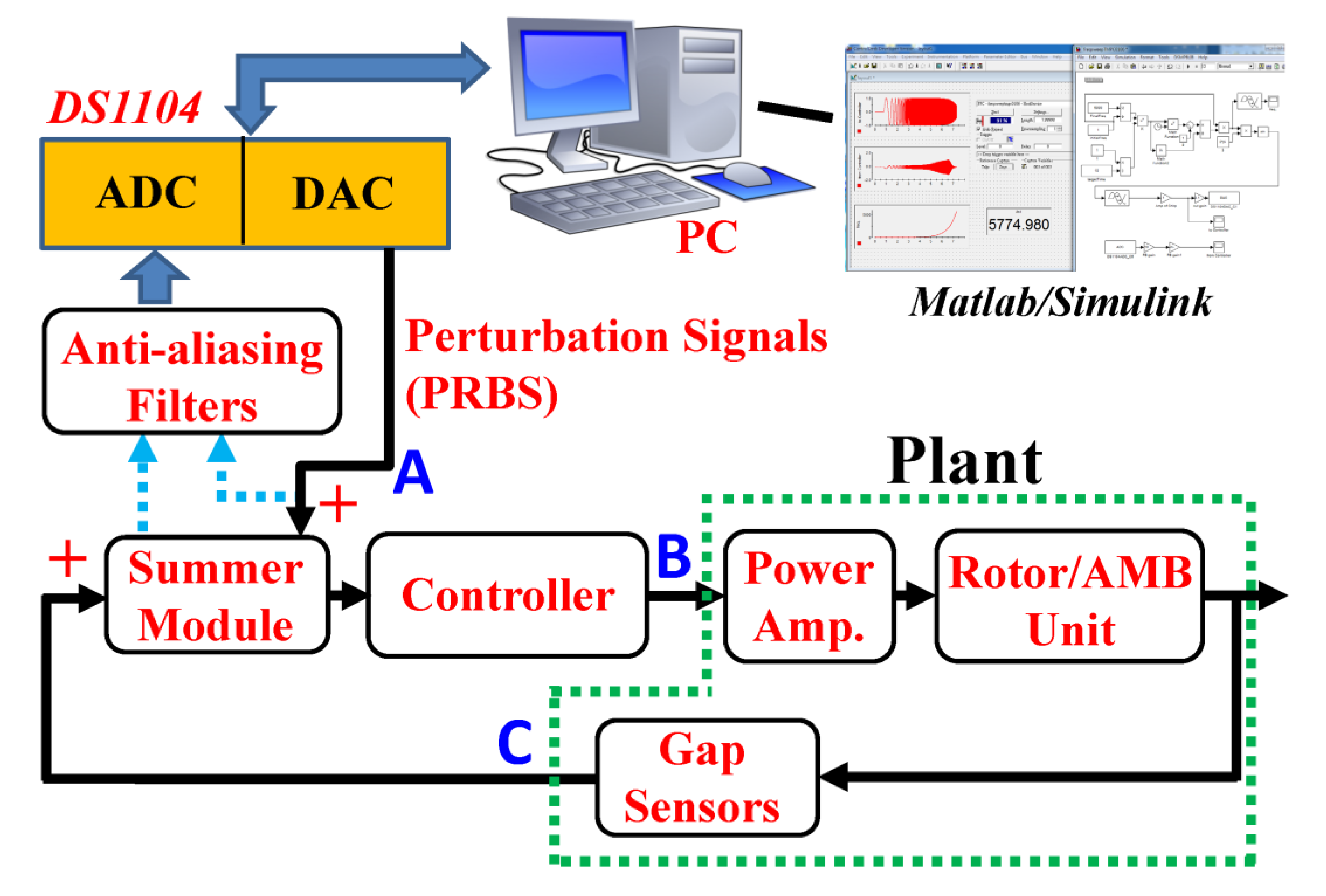
3. Experimental Setup for Identification of Rotor/RAMB Dynamic Model
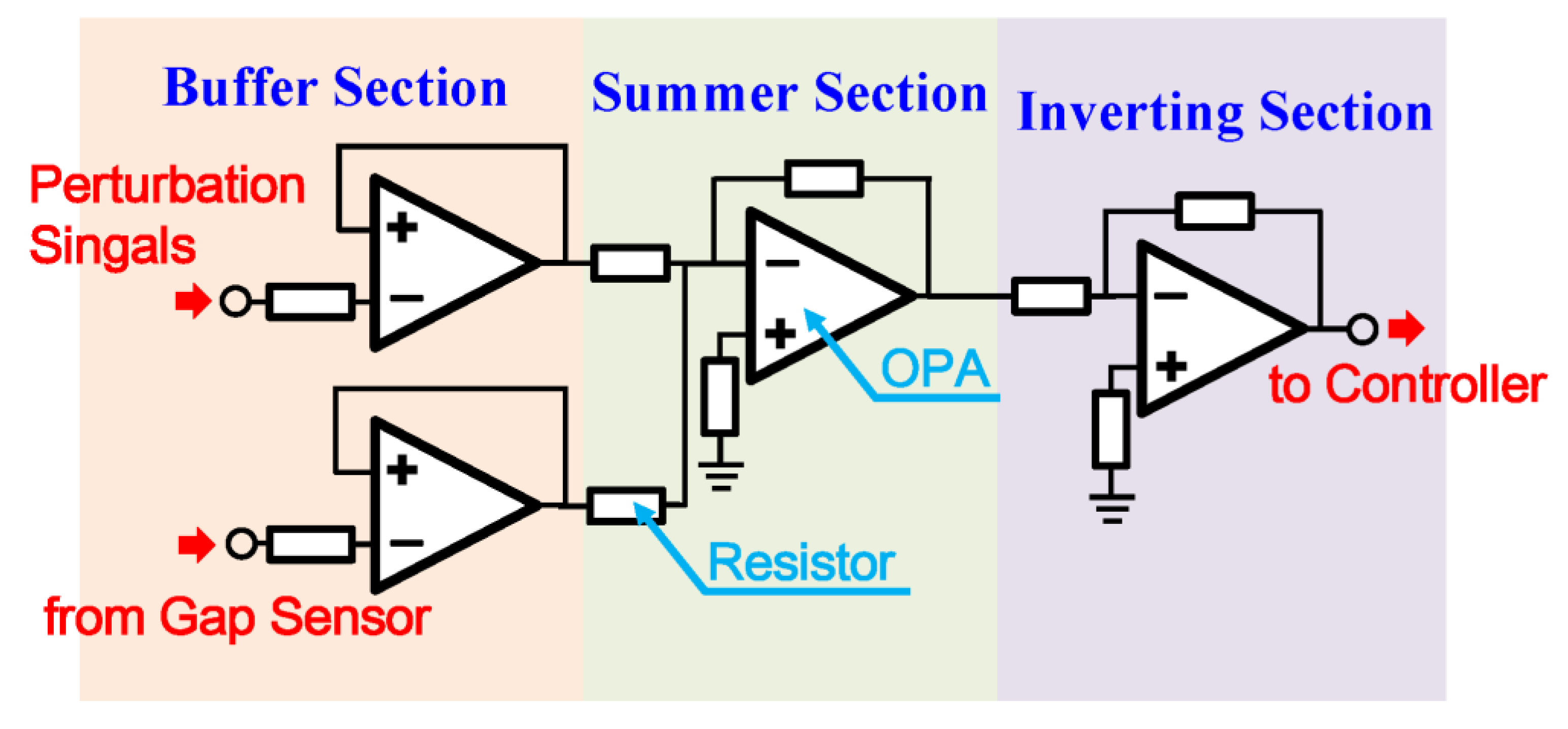
3.1. Design of Summer Module
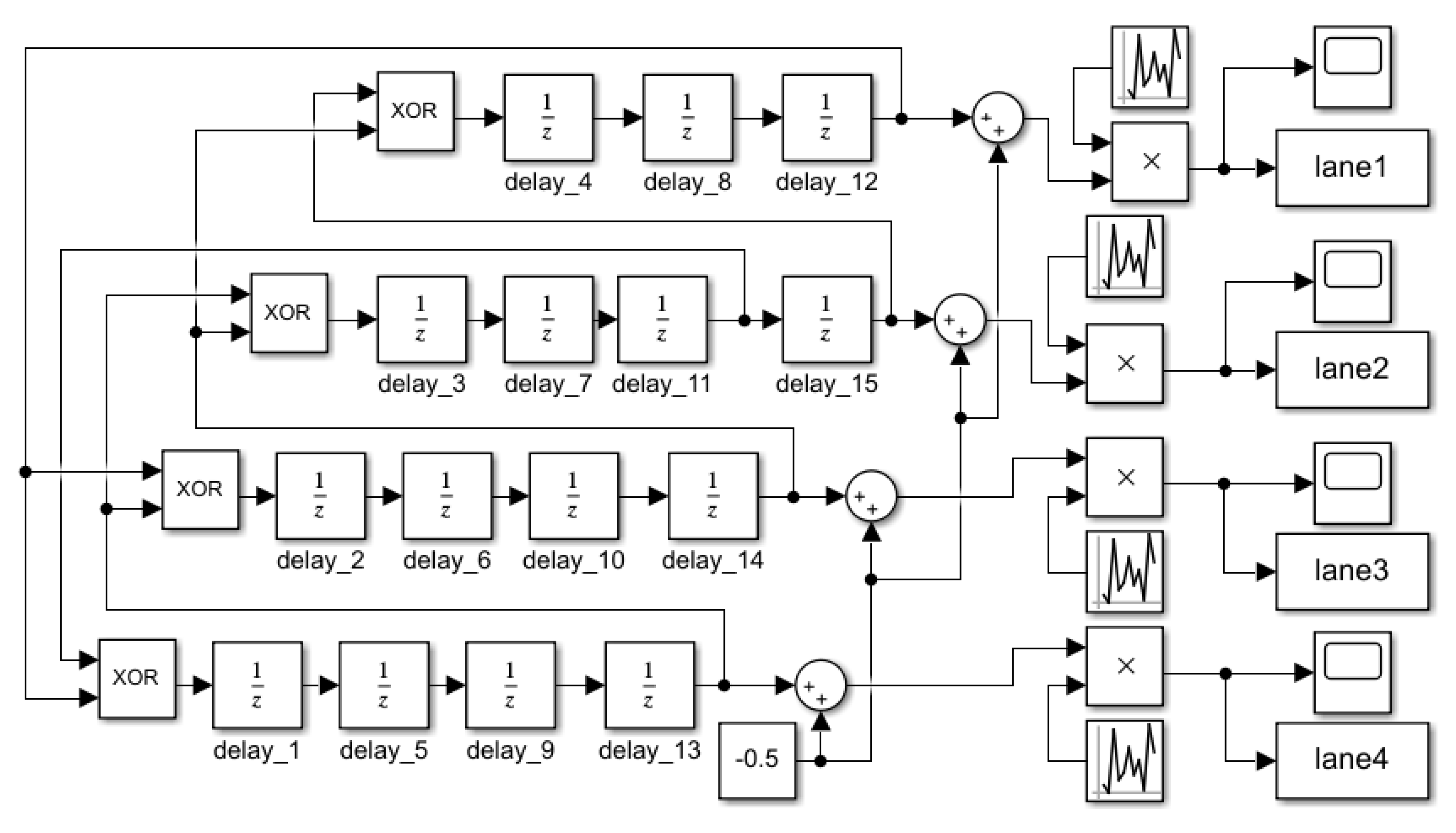
3.2. Parallel Amplitude-Modulated Pseudo-Random Binary Sequence (PAPRBS) Generator
3.3. Parallel Amplitude-Modulated Pseudo-Random Binary Sequence (PAPRBS) Generator
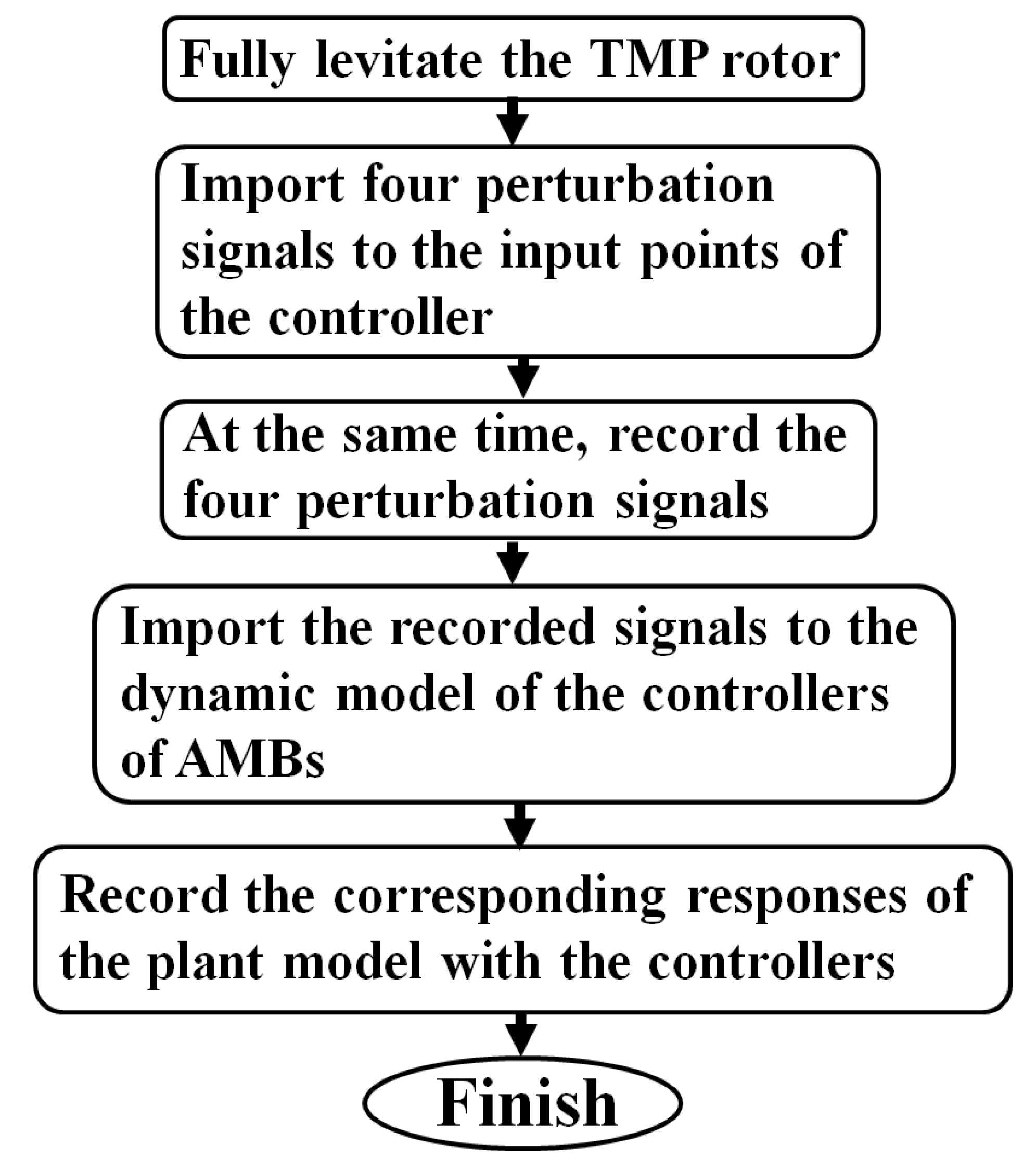
- (i).
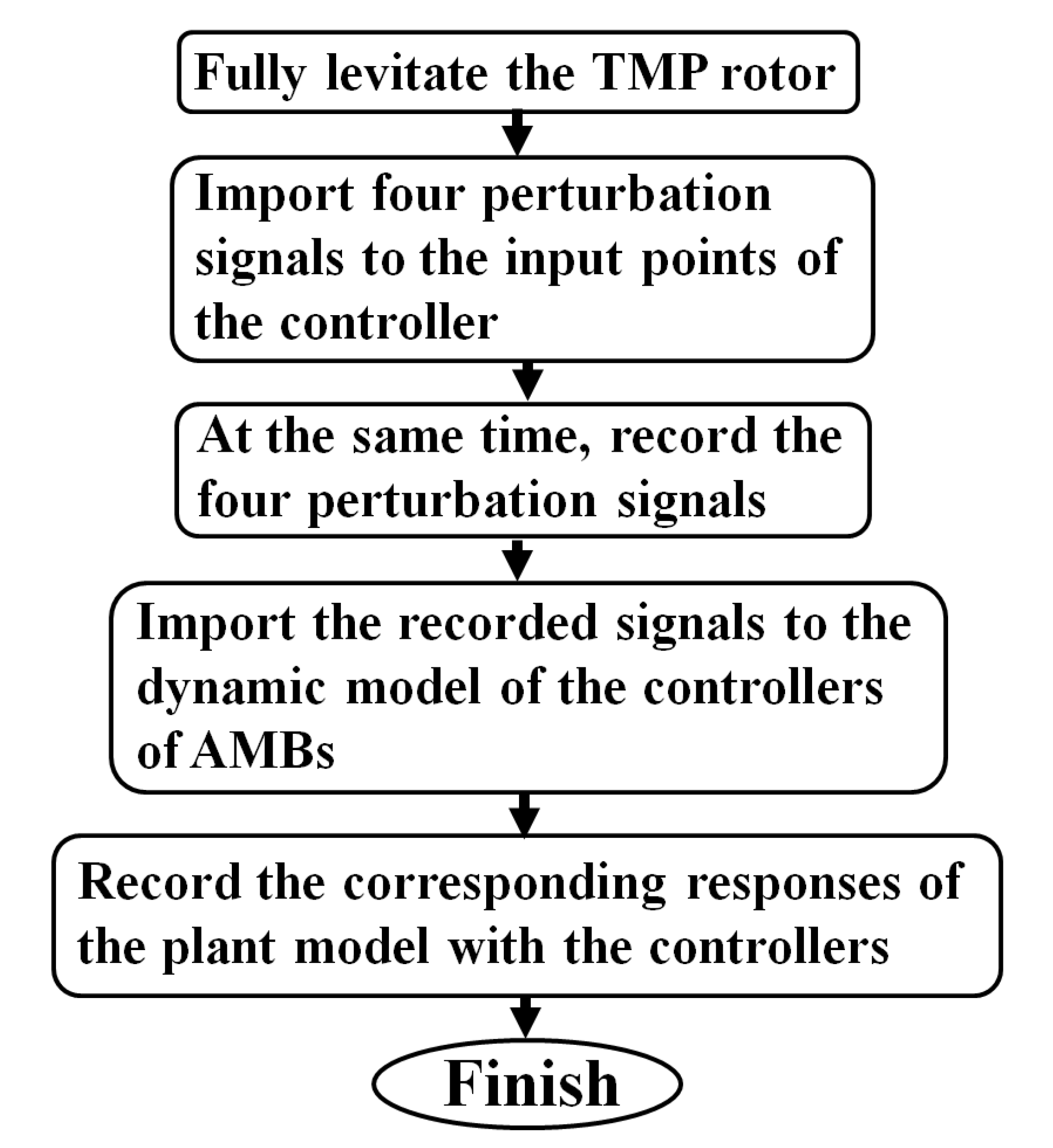
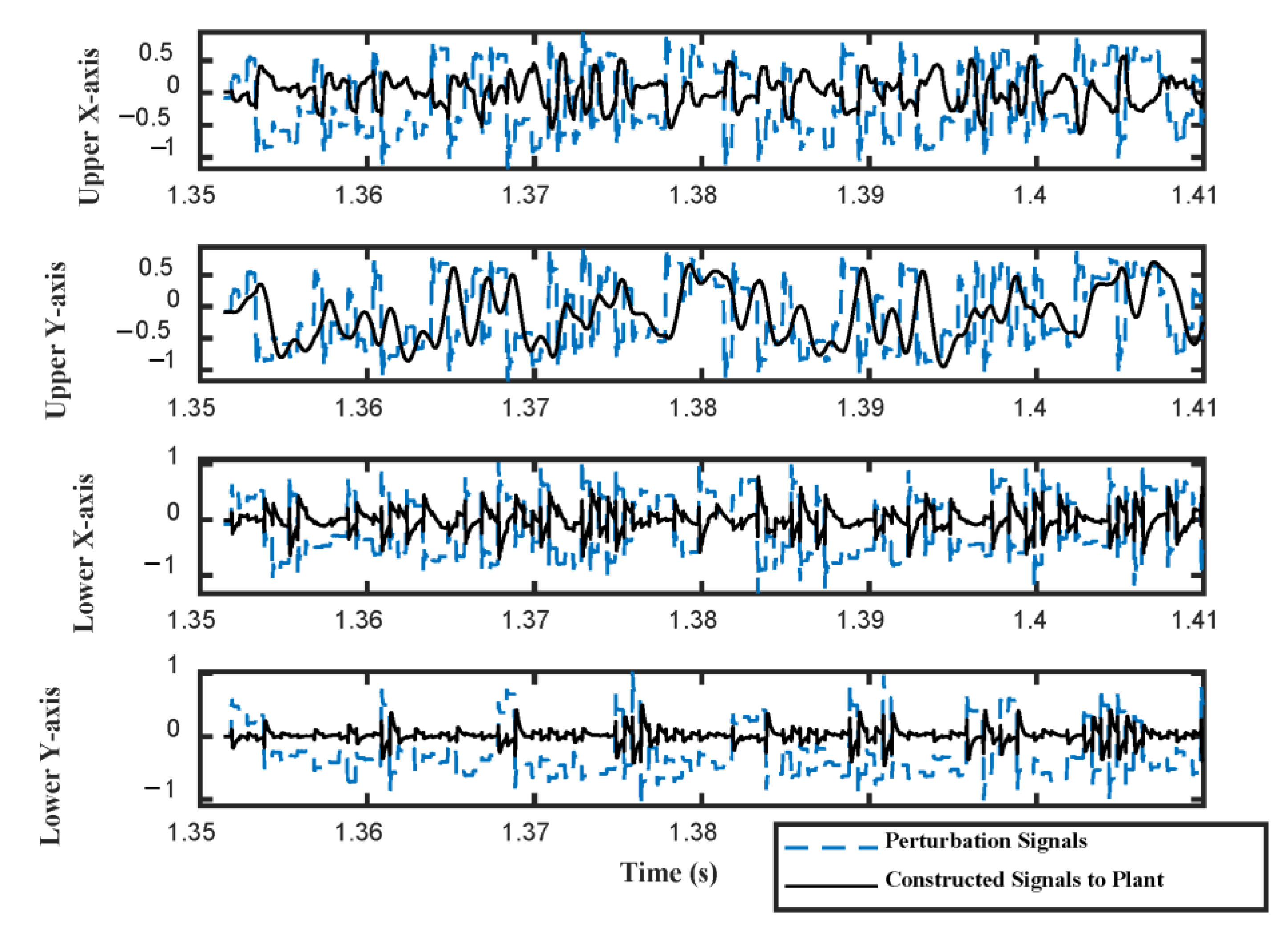
- Four perturbation signals are imported at the input points of the controllers, as the TMP rotor is fully levitated.
- (ii).
- Meanwhile, record the four perturbation signals imported at the input points of the controller, i.e., at Point A, shown in Figure 9.
- (iii).
- Import the recorded four perturbation signals to the dynamic model of the controllers of AMBs, i.e., Equation (5), Equation (10), Equation (15) and Equation (20), respectively.
- (iv).
- Record the corresponding responses of the plant model with the controllers.
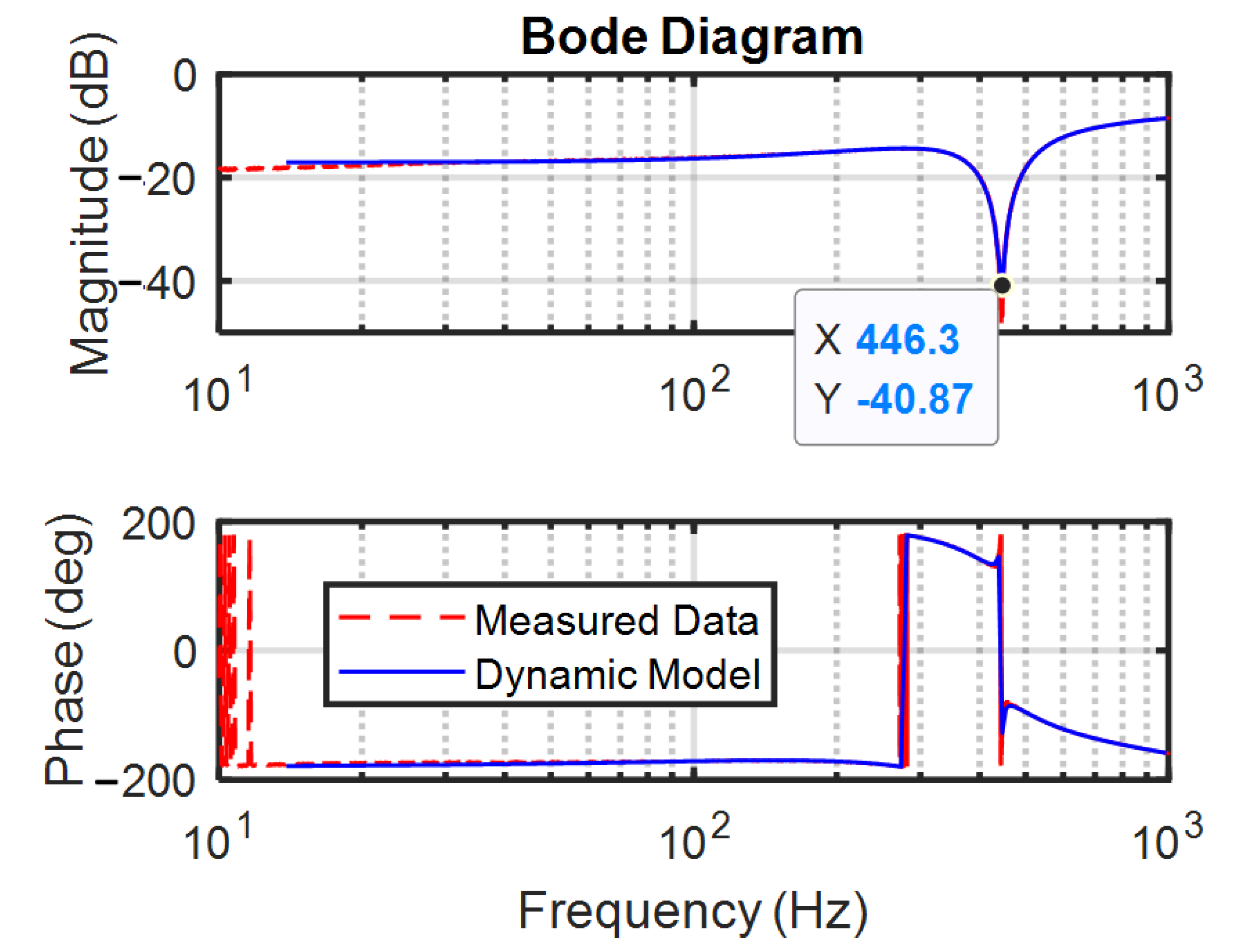
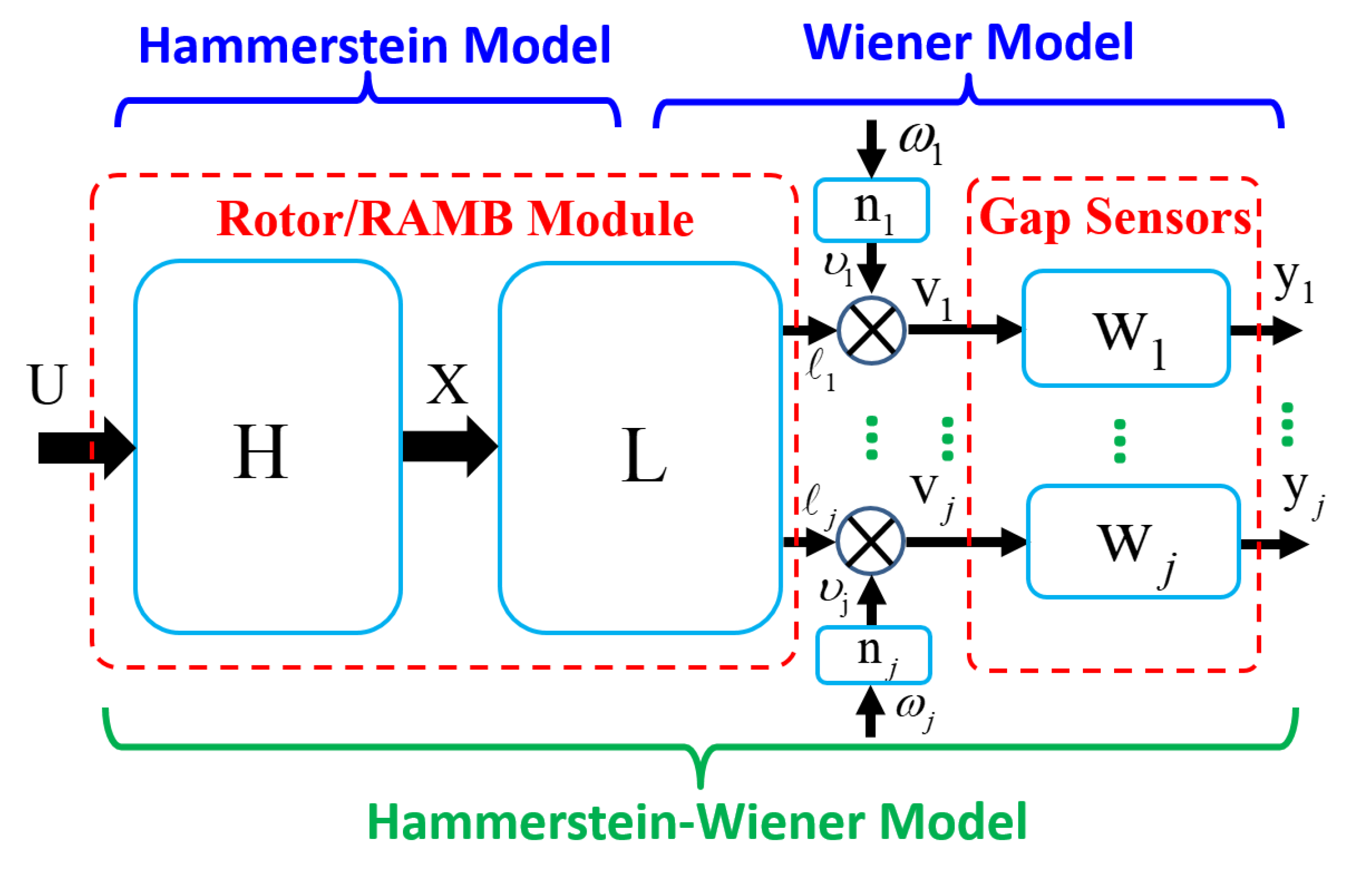
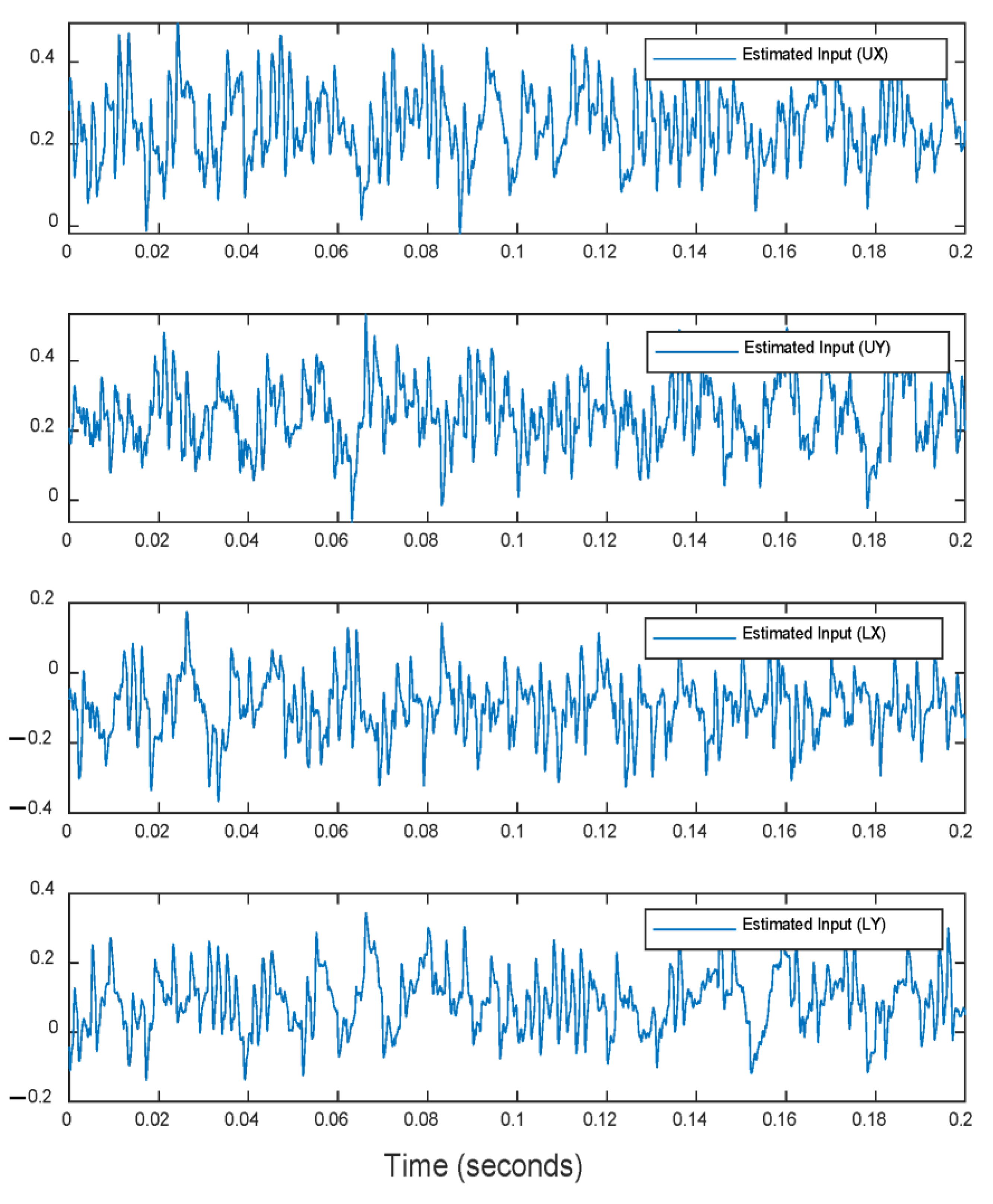
4. System Identification of Rotor/RAMB Dynamics
- By applying the proposed modeling approach presented in Section 4, the mathematical model, i.e., the nonlinear element of the Wiener model, should be estimated prior to the recursive identification algorithm being undertaken. For instance, the static relations between the inputs and outputs of the gap sensor are measured with a high-precision positioning platform.
- As the perturbation signals are being injected into the rotor/RAMB system, the responses of the rotor/RAMB system will be distorted by the vibrations of the surrounding objects. How the engineering of vibration isolation performs will affect the accuracy of the identified model.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Saeed, N.A.; Mohamed, M.S.; Elagan, S.K.; Awrejcewicz, J. Integral Resonant Controller to Suppress the Nonlinear Oscillations of a Two-Degree-of-Freedom Rotor Active Magnetic Bearing System. Processes 2022, 10, 271. [Google Scholar] [CrossRef]
- Ran, S.; Hu, Y.; Wu, H.; Cheng, X. Active Vibration Control of the Flexible High-speed Rotor with Magnetic Bearings via Phase Compensation to Pass Critical Speed. J. Low Freq. Noise Vib. Act. Control 2019, 38, 633–646. [Google Scholar] [CrossRef]
- Zheng, S.; Li, H.; Peng, C.; Wang, Y. Experimental Investigations of Resonance Vibration Control for Noncollocated AMB Flexible Rotor Systems. IEEE Trans. Ind. Electron. 2017, 64, 2226–2235. [Google Scholar] [CrossRef]
- Tang, E.; Fang, J.; Zheng, S.; Jiang, D. Active Vibration Control of the Flexible Rotor to Pass the First Bending Critical Speed in High Energy Density Magnetically Suspended Motor. ASME J. Eng. Gas Turbines Power 2015, 137, 112501. [Google Scholar] [CrossRef]
- Fang, J.; Zheng, S.; Han, B. AMB Vibration Control for Structural Resonance of Double-Gimbal Control Moment Gyro with High-Speed Magnetically Suspended Rotor. IEEE/ASME Trans. Mechatron. 2013, 18, 32–43. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, H.; Wang, W.; Yang, K.; Hu, Y.; Guo, X.; Song, C. Online Unbalance Compensation of a Maglev Rotor with Two Active Magnetic Bearings Based on the LMS Algorithm and the Influence Coefficient Method. Mech. Syst. Signal. Process. 2021, 166, 108460. [Google Scholar]
- Gong, L.; Zhu, C. Vibration Suppression for Magnetically Levitated High-Speed Motors Based on Polarity Switching Tracking Filter and Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 68, 4667–4678. [Google Scholar] [CrossRef]
- Mao, C.; Zhu, C. Unbalance Compensation for Active Magnetic Bearing Rotor System Using a Variable Step Size Real-Time Iterative Seeking Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 4177–4186. [Google Scholar]
- Peng, C.; Sun, J.; Song, X.; Fang, J. Frequency-Varying Current Harmonics for Active Magnetic Bearing via Multiple Resonant Controllers. IEEE Trans. Ind. Electron. 2017, 64, 517–526. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, Q.; Ren, H. Active Balancing Control of AMB-rotor Systems Using a Phase-Shift Notch Filter Connected in Parallel Mode. IEEE Trans. Ind. Electron. 2016, 63, 3777–3785. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Han, B. Suppression of Imbalance Vibration in AMB-rotor Systems Using Adaptive Frequency Estimator. IEEE Trans. Ind. Electron. 2015, 62, 7696–7705. [Google Scholar]
- Darbandi, S.M.; Behzad, M.; Salarieh, H.; Mehdigholi, H. Harmonic Disturbance Attenuation in a Three-pole Active Magnetic Bearing Test Rig using a Modified Notch Filter. J. Vib. Control 2017, 23, 770–781. [Google Scholar] [CrossRef]
- Mu, Y.; Zhou, J.; Di, L.; Zhao, C.; Guo, Q. Active Magnetic Bearing Rotor Model Updating using Resonance and MAC Error. Shock. Vib. 2015, 2015, 263062. [Google Scholar]
- Xu, Y.; Zhou, J.; Lin, Z.; Jin, C. Identification of Dynamic Parameters of Active Magnetic Bearings in a Flexible Rotor System Considering Residual Unbalances. Mechatronics 2018, 49, 46–55. [Google Scholar] [CrossRef]
- Ranjan, G.; Tiwari, R. On-site High-speed Balancing of Flexible Rotor-bearing System Using Virtual Trial Unbalances at Slow Run. Int. J. Mech. Sci. 2020, 183, 105786. [Google Scholar] [CrossRef]
- Molina, L.M.C.; Bonfitto, A.; Tonoli, A.; Amati, N. Identification of Force-Displacement and Force-Current Factors in an Active Magnetic Bearing System. In Proceedings of the 2018 IEEE International Conference on Electro/Information Technology, Rochester, MI, USA, 3–5 May 2018. [Google Scholar]
- Hua, L.; Ming, D. Research on Vibration of Magnetic Suspension Rotor System Caused by Magnetic Bearing Model Error-closed-loop Parameter Identification Method. In Proceedings of the 2nd International Conference on Frontiers of Materials Synthesis and Processing, Sanya, China, 10–11 November 2018. [Google Scholar]
- Lauridsen, J.S.; Voigt, A.J.; Mandrup-Poulsen, C.; Nielsen, K.K.; Santos, I. Identification of Parameters in Active Magnetic Bearing Systems. In Proceedings of the 15th International Symposium on Magnetic Bearings, Kitakyushu, Japan, 3–6 August 2016. [Google Scholar]
- Zhou, J.; Di, L.; Cheng, C.; Xu, Y.; Lin, Z. A Rotor Unbalance Response based Approach to the Identification of the Closed-loop Stiffness and Damping Coefficients of Active Magnetic Bearings. Mech. Syst. Signal Process. 2016, 66, 665–678. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, J.; Di, L.; Zhao, C. Active Magnetic Bearings Dynamic Parameters Identification from Experimental Rotor Unbalance Response. Mech. Syst. Signal Process. 2016, 83, 228–240. [Google Scholar] [CrossRef]
- Prasad, V.; Tiwari, R. Identification of Speed-dependent Active Magnetic Bearing Parameters and Rotor Balancing in High-speed Rotor Systems. J. Dyn. Syst Meas. Control 2019, 141, 041013. [Google Scholar] [CrossRef]
- Martynenko, G. Application of Nonlinear Models for a Well Defined Description of the Dynamics of Rotors in Magnetic Bearings. EUREKA Phys. Eng. 2016, 3, 3–12. [Google Scholar] [CrossRef]
- Khader, S.A.; Liu, B.; Sjöberg, J. System Identification of Active Magnetic Bearing for Commissioning. In Proceedings of the 2014 International Conference on Modelling, Identification & Control, Melbourne, VIC, Australia, 3–5 December 2014. [Google Scholar]
- Aziz, M.H.R.A.; Mohd-Mokhtar, R. Identification of MIMO Magnetic Bearing System Using Continuous Subspace Method with Frequency Sampling Filters Approach. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011. [Google Scholar]
- Mohd-Mokhtar, R.; Wang, L. System Identification of MIMO Magnetic Bearing via Continuous Time and Frequency Response Data. In Proceedings of the 2005 IEEE International Conference on Mechatronics, Taipei, Taiwan, 10–12 July 2005. [Google Scholar]
- Liu, Q.; Wang, L.; Ding, Y. Neural Network Identification of an Axial Zero-Bias Magnetic Bearing. In Proceedings of the International Conference on Intelligent Manufacturing and Internet of Things, Chongqing, China, 21–23 September 2018. [Google Scholar]
- Miranda, J.A.; Manzano, E.A. Parametric Identification of an Active Magnetic Bearing System Using NARMAX Model. In Proceedings of the 2020 IEEE XXVII International Conference on Electronics, Electrical Engineering and Computing (INTERCON), Lima, Peru, 3–5 September 2020. [Google Scholar]
- Noshadi, A.; Shi, J.; Lee, W.S.; Shi, P.; Kalam, A. Genetic algorithm-based system identification of active magnetic bearing system: A frequency-domain approach. In Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA), Taichung, Taiwan, 18–20 June 2014. [Google Scholar]
- Anti-Aliasing Filters and Their Usage Explained, National Instruments Corp. 2019. Available online: http://www.ni.com/zh-tw/innovations/white-papers/18/anti-aliasing-filters-and-their-usage-explained.html (accessed on 6 July 2022).
- Vuojolainen, J.; Nevaranta, N.; Jastrzebski, R.; Pyrhonen, O. Comparison of Excitation Signals in Active Magnetic Bearing System Identification. Model. Identif. Control 2017, 38, 123–133. [Google Scholar] [CrossRef]
- Vilkko, M.; Roinila, T. Designing Maximum Length Sequence Signal for Frequency Response Measurement of Switched Mode Converters. In Proceedings of the Nordic Workshop on Power and Industrial Electronics, Espoo, Finland, 9–11 June 2008. [Google Scholar]
- Bai, J.; Mao, Z.; Pu, T. Recursive Identification for Multi-input-multi-output Hammerstein-Wiener System. Int. J. Control 2017, 92, 1457–1469. [Google Scholar] [CrossRef]
- Wang, L.; Ji, Y.; Wan, L.; Bu, N. Hierarchical Recursive Generalized Extended Least Squares Estimation Algorithms for a Class of Nonlinear Stochastic Systems with Colored Noise. J. Frankl. Inst. 2019, 356, 10102–10122. [Google Scholar]
- Toutounian, F.; Ataei, A. A New Method for Computing Moore-Penrose Inverse Matrices. J. Comput. Appl. Math. 2009, 228, 412–417. [Google Scholar] [CrossRef]




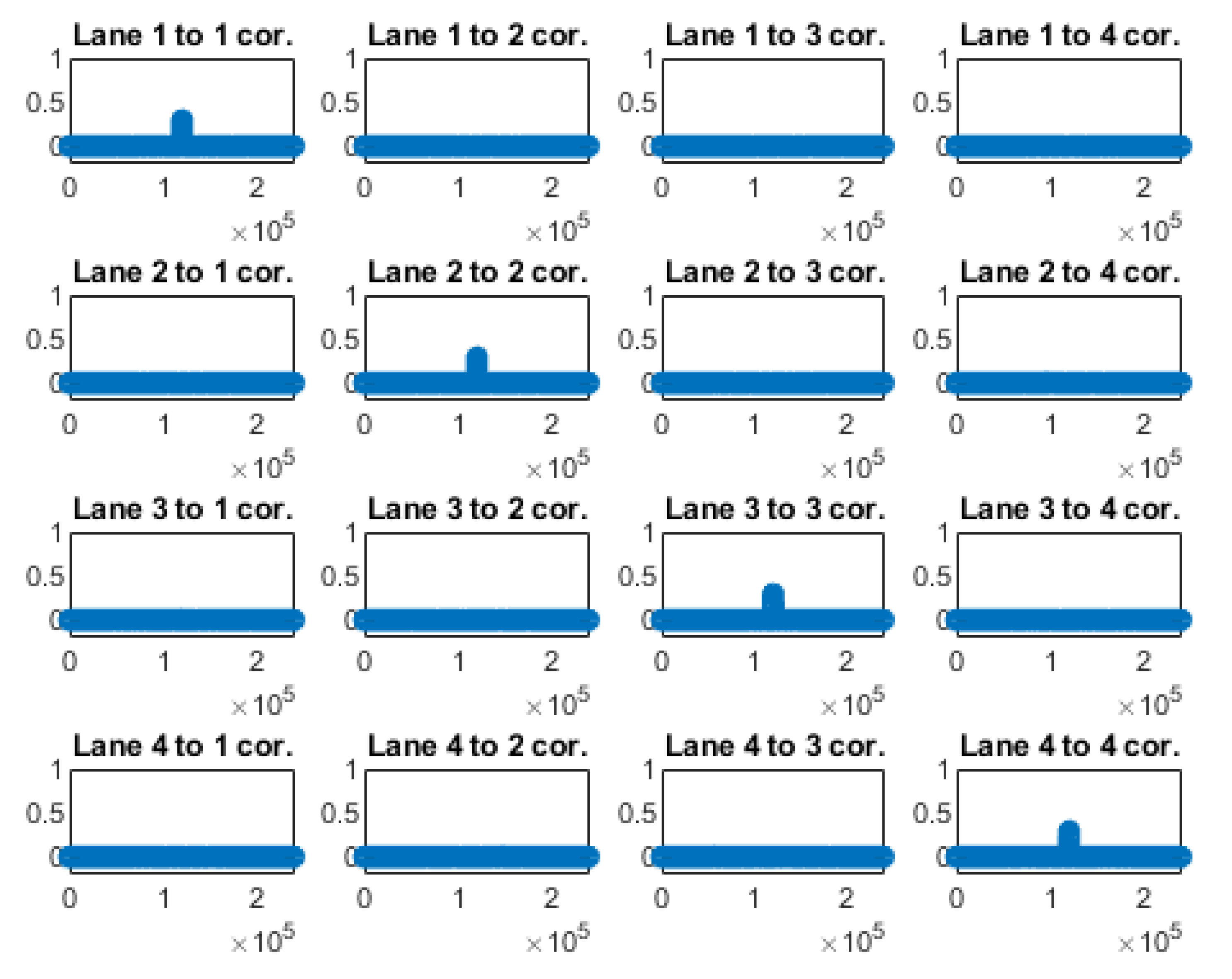


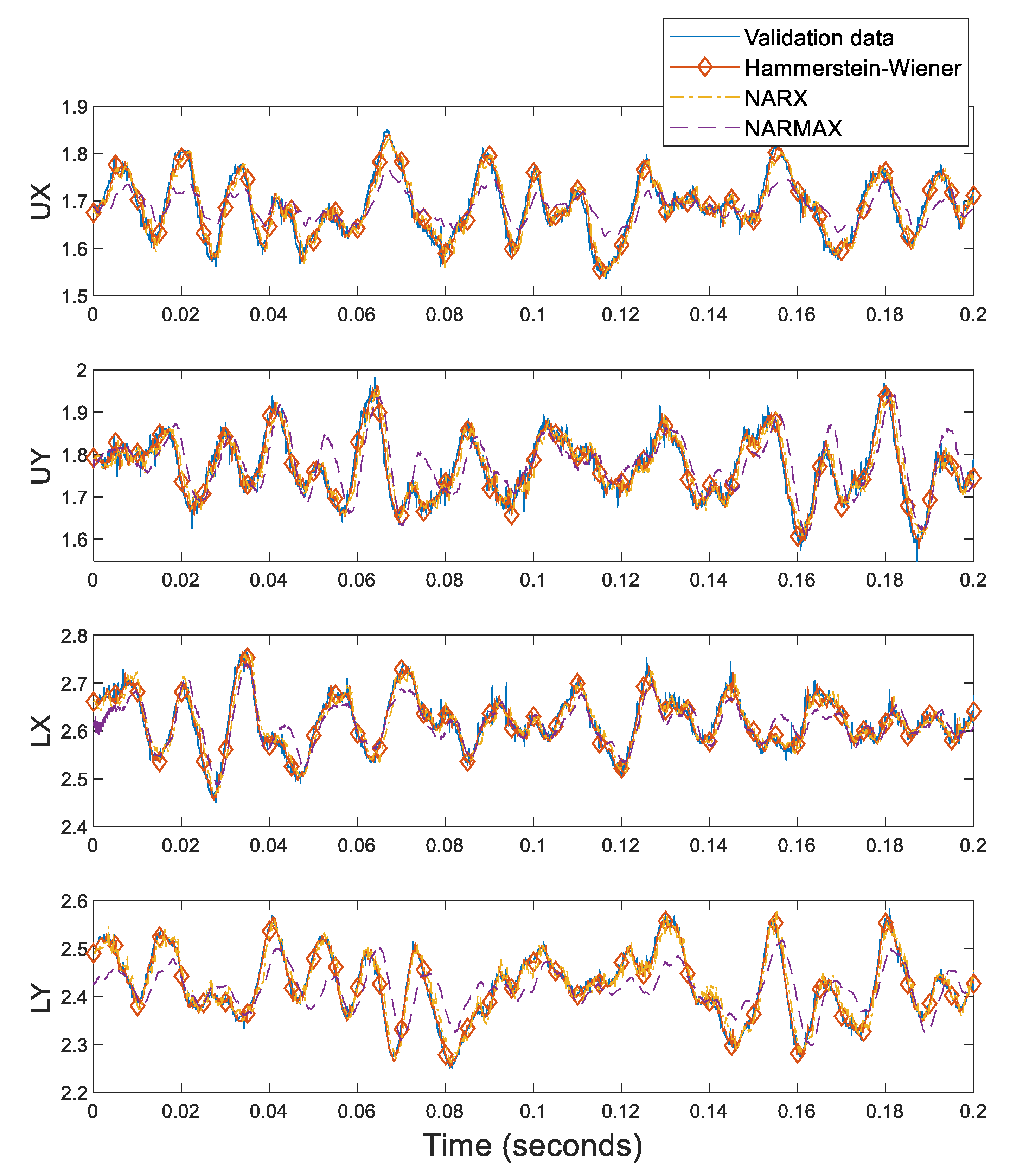
| Fit (%) | Hammerstein–Wiener Model | NARX Model | NARMAX Model |
|---|---|---|---|
| UX | 92.11% | 87.63% | 75.91% |
| UY | 93.38% | 88.88% | 77.88% |
| LX | 91.51% | 85.57% | 78.32% |
| LY | 95.99% | 91.34% | 75.54% |
| Average | 93.25% | 88.36% | 76.91% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, H.-L. Identification Approach for Nonlinear MIMO Dynamics of Closed-Loop Active Magnetic Bearing System. Appl. Sci. 2022, 12, 8556. https://doi.org/10.3390/app12178556
Chiu H-L. Identification Approach for Nonlinear MIMO Dynamics of Closed-Loop Active Magnetic Bearing System. Applied Sciences. 2022; 12(17):8556. https://doi.org/10.3390/app12178556
Chicago/Turabian StyleChiu, Hsin-Lin. 2022. "Identification Approach for Nonlinear MIMO Dynamics of Closed-Loop Active Magnetic Bearing System" Applied Sciences 12, no. 17: 8556. https://doi.org/10.3390/app12178556
APA StyleChiu, H.-L. (2022). Identification Approach for Nonlinear MIMO Dynamics of Closed-Loop Active Magnetic Bearing System. Applied Sciences, 12(17), 8556. https://doi.org/10.3390/app12178556


_Yang.png)




