Calculation for Permanent Displacement of Single Slip Surface of Multi-Stage Loess Slope Based on Energy Method
Abstract
:1. Introduction
2. Influence of the Comprehensive Slope Rate on Permanent Displacement
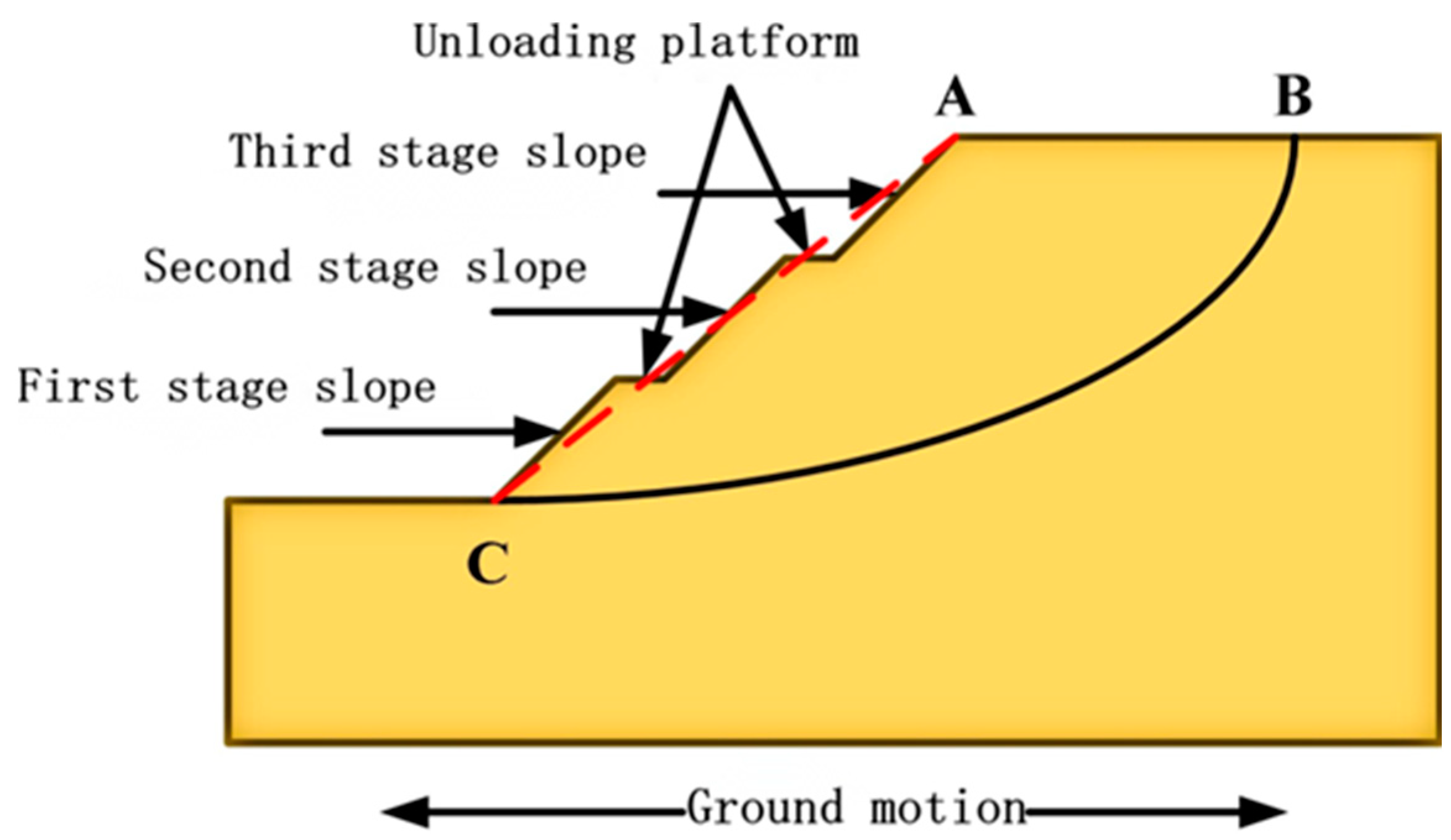
2.1. When the Slope Rate of Each Grade of Multi-Stage Slope Is Changed
2.2. When the Stage of Multi-Stage Slope Is Changed
3. Analysis of Energy Response of Multi-Stage Loess Slope under the Action of Earthquake
3.1. Basic Assumptions
- (1)
- The strength of rock and soil mass obeys the Mohr–Coulomb strength criterion.
- (2)
- When the rock and soil mass fails, the yield surface is convex everywhere and conforms to the relevant flow laws.
- (3)
- When the potential sliding body slides with the lower soil body, its sliding surface is assumed to be a logarithmic spiral along the tangential direction.
- (4)
- When the potential sliding body is in the limit equilibrium state that is about to slide, the acceleration of the potential sliding body is its yield acceleration.
- (5)
- There is no gradual failure of the plastic failure of the soil on the slip surface; that is, the cohesive force of the soil c and the angle of internal friction of the soil φ remain unchanged during the earthquake duration.
3.2. Critical Acceleration of Potential Sliding Soil
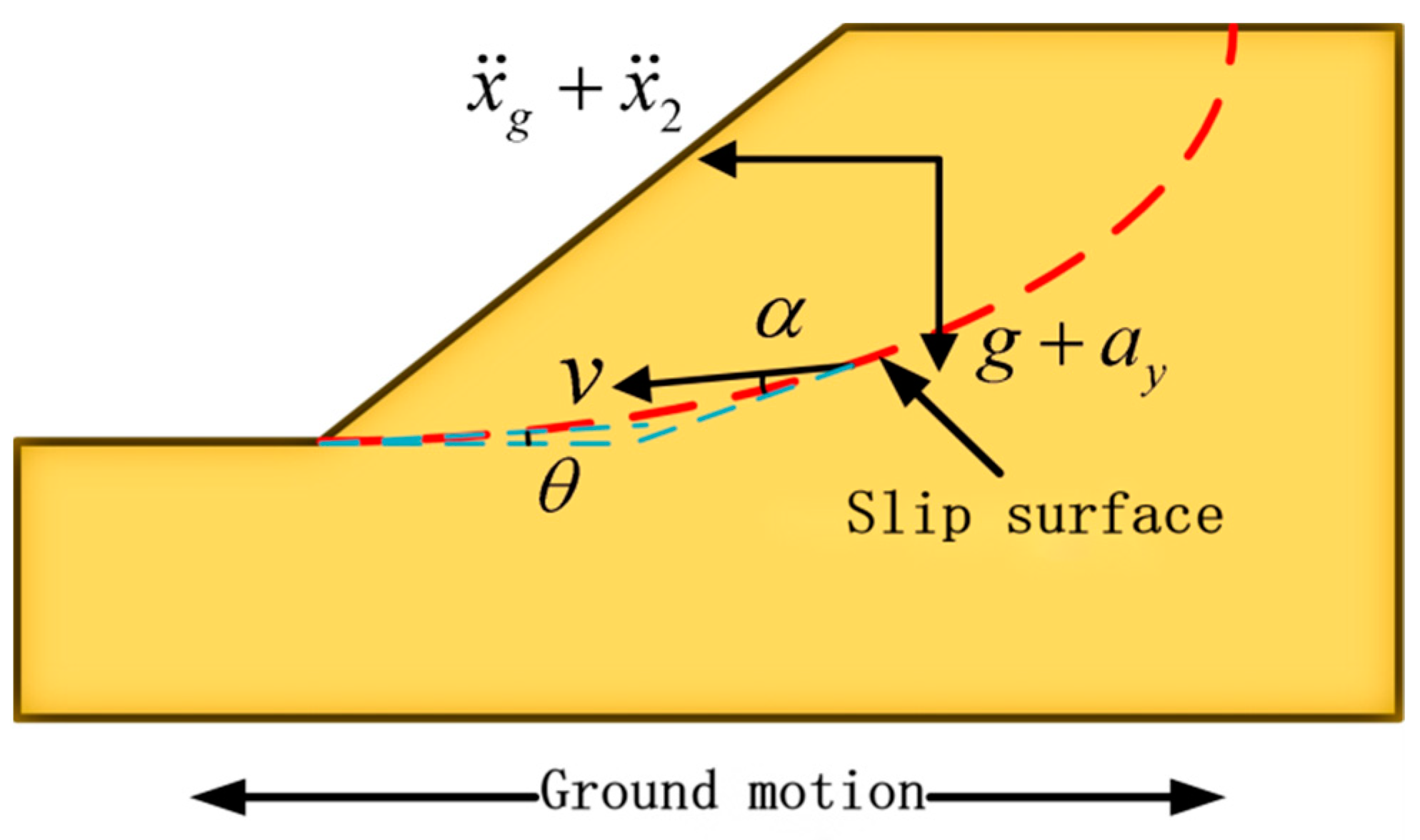
3.2.1. Positive Downward Critical Acceleration
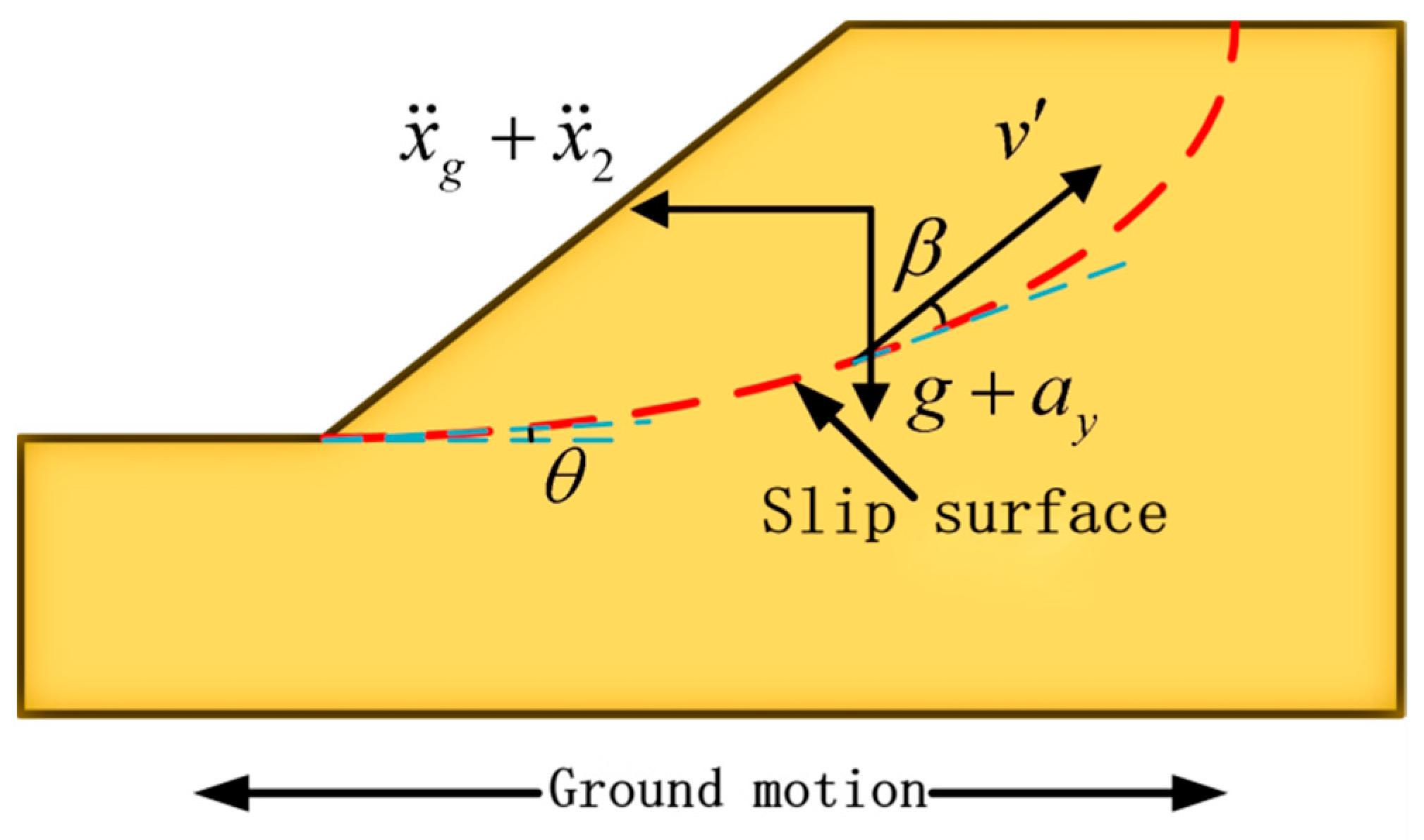
3.2.2. Negative Downward Critical Acceleration
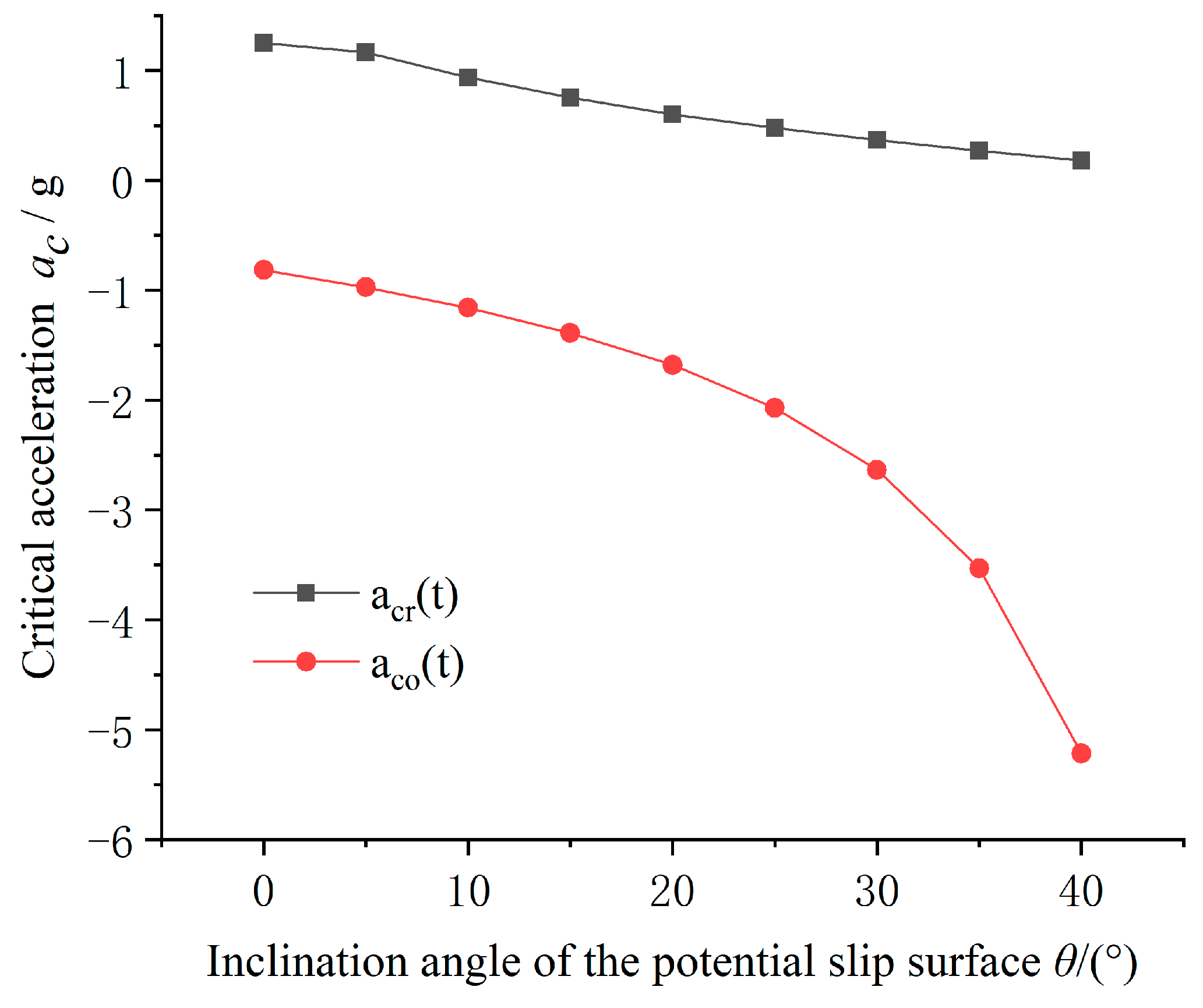
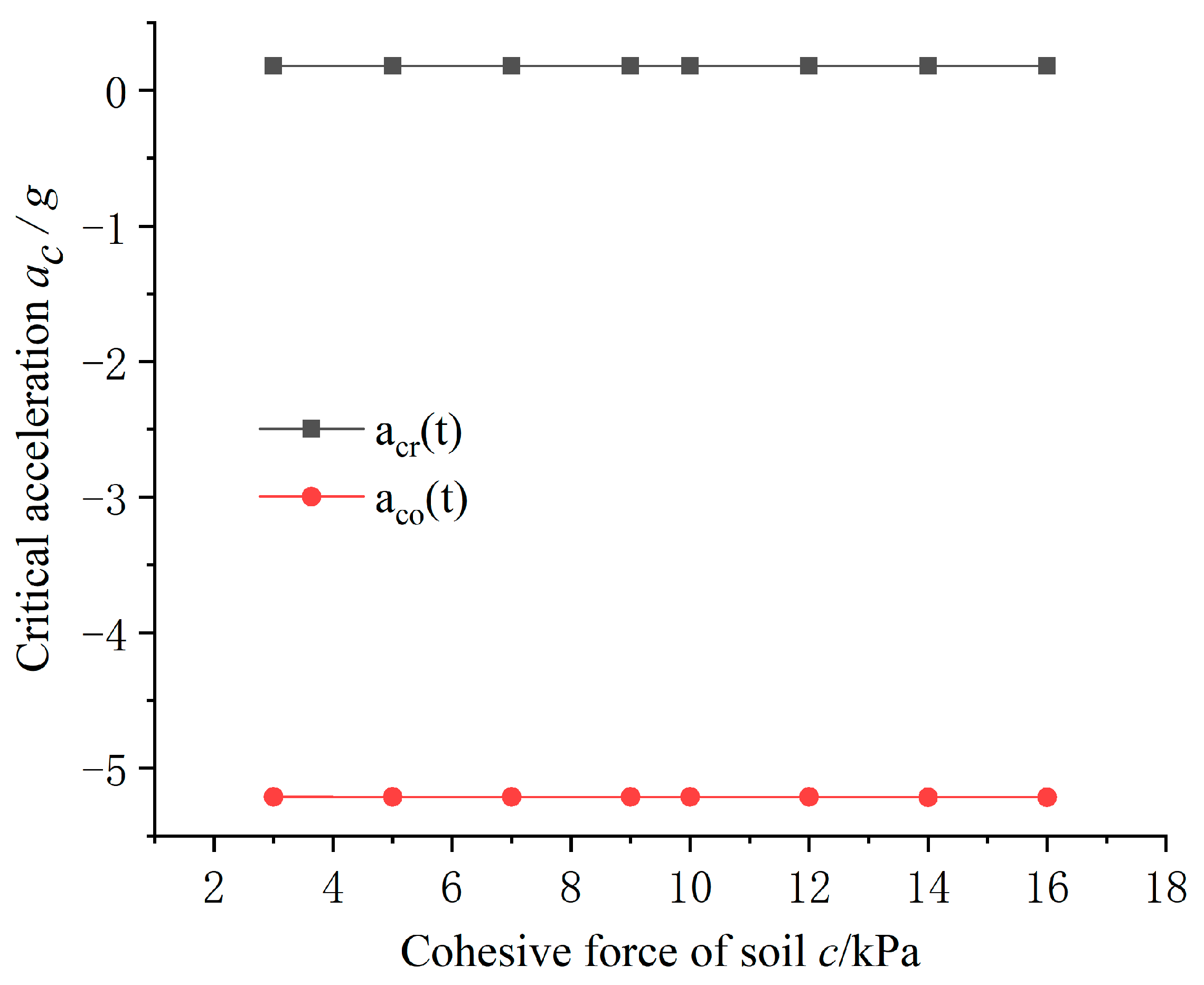
3.3. Influence of Inclination Angle of Slip Surface θ and Soil Parameters on Positive and Negative Critical Acceleration
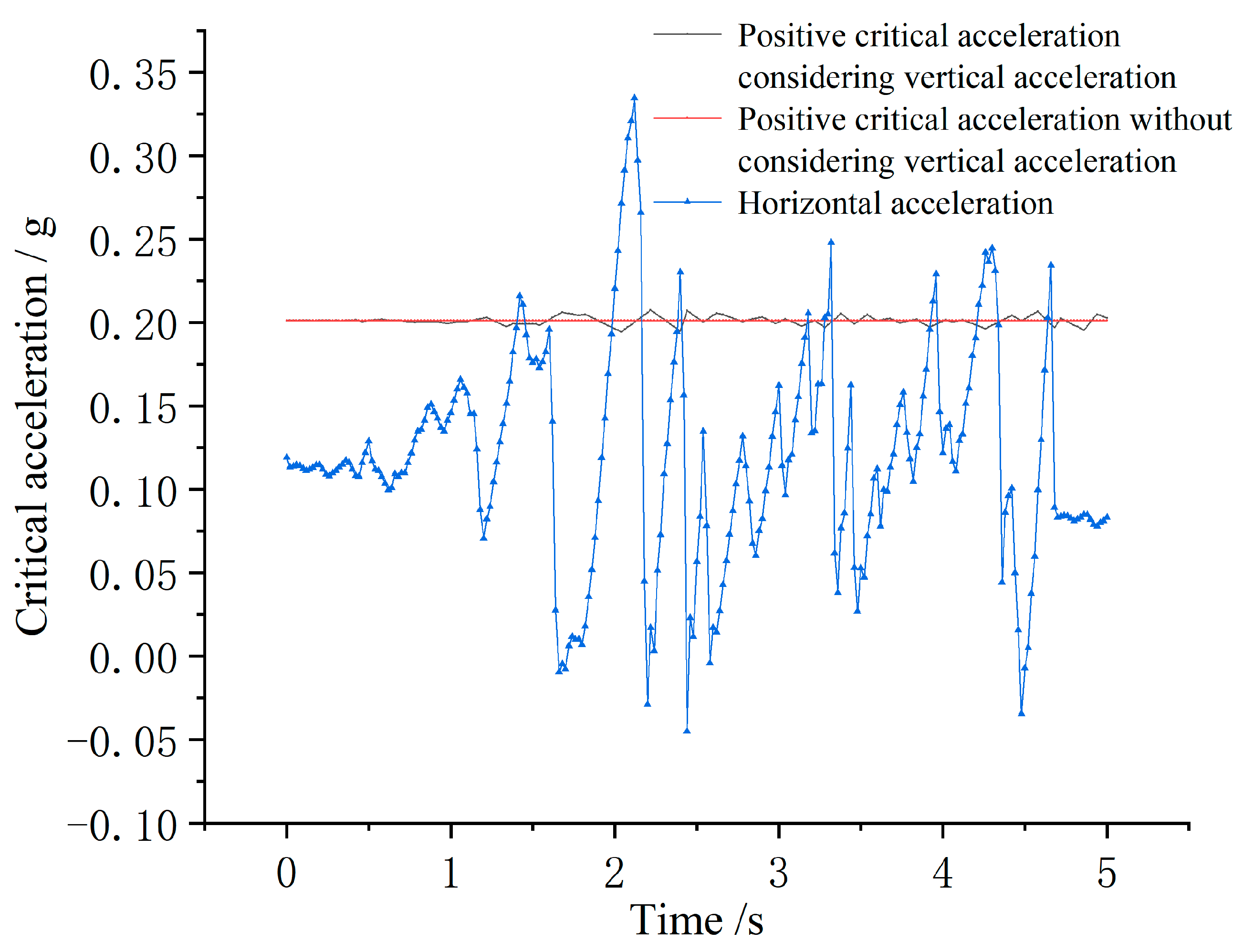
3.4. Influence of Vertical Acceleration on Critical Acceleration in the Action of Earthquake
3.5. Energy Equation of Sliding Soil System
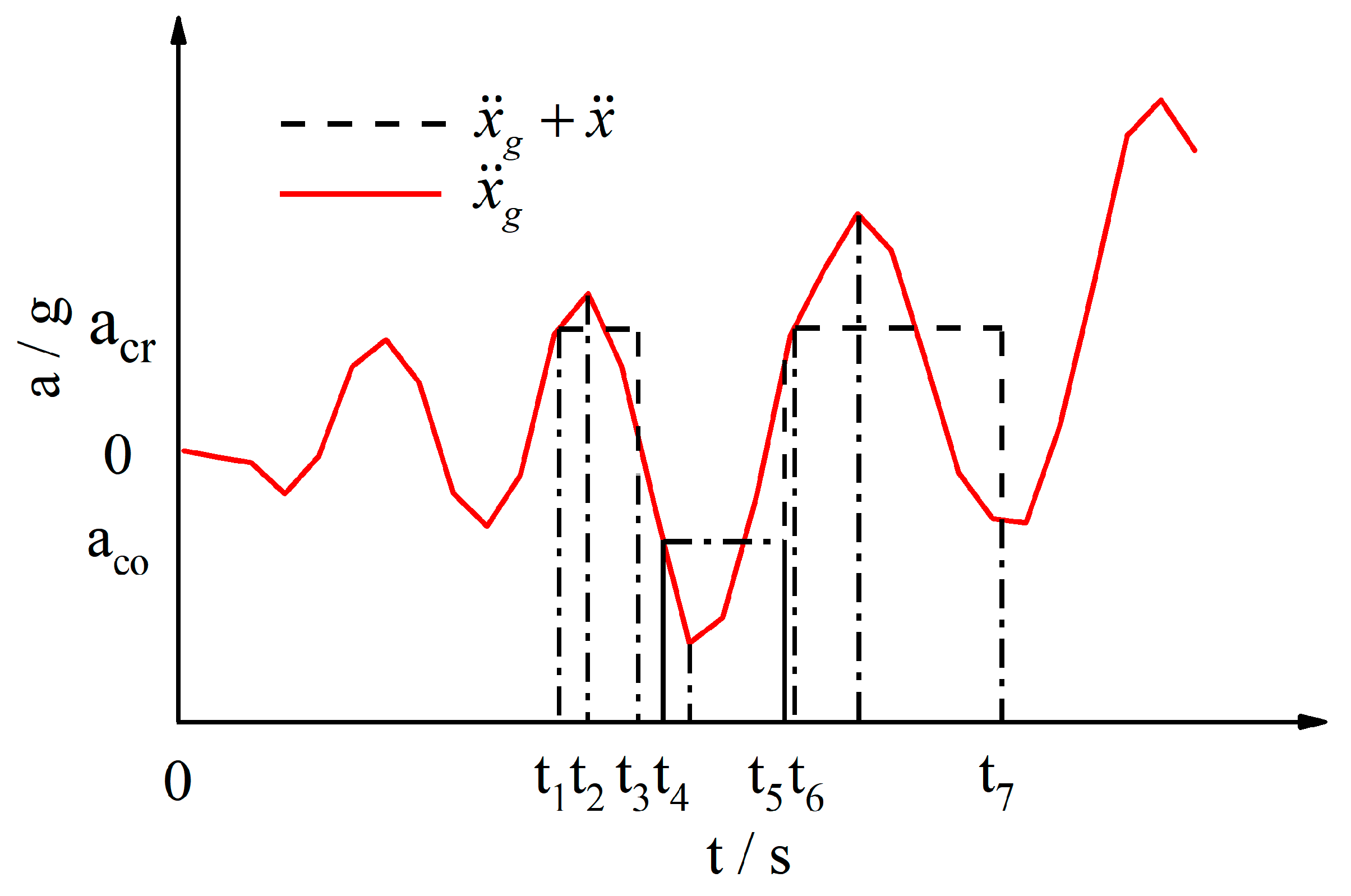
3.6. Critical Input Power and Permanent Displacement
4. Example Verification
4.1. Model Parameters
4.2. Comparison of Calculation Results
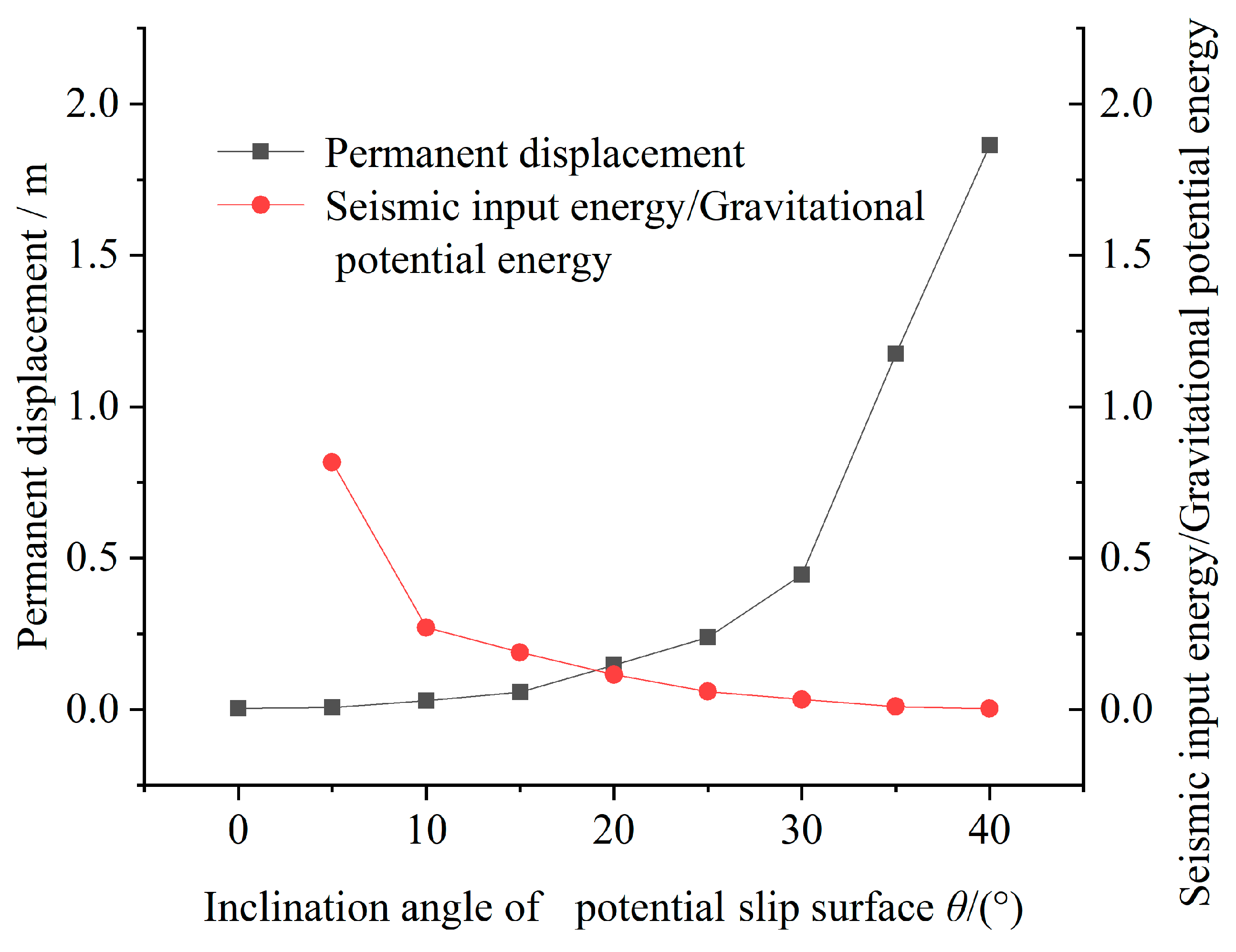
4.3. Influence of the Change in Gravity Potential Energy on Permanent Displacement
5. Conclusions
- Through a large number of numerical simulation tests, it is concluded that the geometric characteristics of the slope cannot be taken into account to a certain extent when calculating the permanent displacement of sliding soil of multi-stage loess slope under the action of earthquake; in addition, it is feasible to use the comprehensive slope to calculate the permanent displacement of the sliding body of multi-stage loess slope under the action of earthquake.
- On the premise of using the comprehensive slope rate to calculate the permanent displacement of multi-stage loess slope under earthquake, based on the energy method, combined with the Newmark slide displacement method, considering soil deformation and damping, the formulas for calculating positive and negative critical acceleration and permanent displacement of sliding soil are reasonable.
- The critical acceleration of the sliding soil is mainly affected by the inclination angle of the sliding surface, but not by the soil parameters. The earthquake is only an inducing factor for the permanent displacement of the sliding soil, and the decrease in gravitational potential energy plays a key role in the permanent displacement.
- The method derived in this paper comprehensively considers the influence of negative critical acceleration on the solution of permanent displacement when the inclination angle of slip surface is small and the seismic acceleration is large, and based on the principle of energy balance in the process of calculation and derivation, the calculation results are thus more accurate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, Y.L.; Liu, X.R.; Yan, C.G.; Yang, Z.P.; Li, J.C.; Zhou, Z.J.; Yue, X.B. Research progress of special soil and rock engineering slopes. China Civ. Eng. J. 2020, 53, 93–105. [Google Scholar]
- Li, Y.R.; Shi, W.H.; Aydin, A.; Beroya-Eitner, M.A.; Gao, G.H. Loess genesis and worldwide distribution. Earth-Sci. Rev. 2020, 201, 1–22. [Google Scholar] [CrossRef]
- Bai, B.; Nie, Q.; Zhang, Y.K.; Wang, X.L.; Hu, W. Cotransport of heavy metals and SiO2 particles at different temperatures by seepage. J. Hydrol. 2021, 597, 125771. [Google Scholar] [CrossRef]
- Ye, S.H.; Huang, A.P. Sensitivity of high fill slope stability factors under seismic conditions. Soil Mech. Found. Eng. 2020, 57, 356–363. [Google Scholar]
- Xu, L.; Gao, C.; Lan, T.; Lei, J.; Zuo, L. Influence of grading on the compressibility of saturated loess soils. Geotech. Lett. 2020, 10, 198–204. [Google Scholar] [CrossRef]
- Tian, W.T.; Sun, J.J.; Wang, L.M.; Xu, S.H.; Liu, K.; Sun, Y. Research progress and frontier scientific problems in loess dynamics. Chin. J. Geotech. Eng. 2015, 37, 2119–2127. [Google Scholar]
- Yan, Z.X.; Guo, B.; He, X.; Jiang, P. Study of effect of platform width on dynamic response and failure mechanism of stepped slopes under earthquake. Rock Soil Mech. 2012, 33, 352–358. [Google Scholar]
- Zhang, F.; Leshchinsky, D.; Gao, Y.F.; Yang, S.C. Corner reinforced slopes: Required strength and length of reinforcement based on internal stability. Geotext. Geomembr. 2019, 47, 408–416. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, C.S.; Gao, Y.F.; Kodikara, J. Effect of 2D spatial variability on slope reliability: A simplified FORM analysis. Geosci. Front. 2018, 9, 1631–1638. [Google Scholar] [CrossRef]
- Bai, B.; Wang, Y.; Rao, D.Y.; Bai, F. The effective thermal conductivity of unsaturated porous media deduced by pore-scale SPH simulation. Front. Earth Sci.-Witz. 2022, 10, 943853. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Makdisi, F.I.; Seed, H.B. Simplified procedure for estimation dam and embankment earthquake induced deformations. Geotech. Eng. Div. 1978, 104, 849–868. [Google Scholar] [CrossRef]
- Steven, L.K. Modified Newmark Model for Seismic Displacements of Compliant Slopes. J. Geotech. Geoenviron. 1997, 123, 635–644. [Google Scholar]
- Ellen, M.R.; Jonathan, D.B. An examination of simplified earthquake-induced displacement procedures for earth structures. Can. Geotech. J. 1999, 36, 72–87. [Google Scholar]
- Ellen, M.R.; Jonathan, D.B. Nonlinear coupled seismic sliding analysis of earth structures. Can. Geotech. J. 2000, 126, 1002–1014. [Google Scholar]
- Bai, B.; Zhou, R.; Cai, G.; Hu, W.; Yang, G. Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotech. 2021, 137, 104272. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Gao, Y.; Pak, R. An exact solution for SH-Wave scattering by a radially multi-layered inhomogeneous semi-cylindrical canyon. Geophys. J. Int. 2019, 217, 1232–1260. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Gao, Y.F.; Pak, R.Y.S.; Yang, J. Site amplification effects of a radially multi-layered semi-cylindrical canyon on seismic response of an earth and rockfill dam. Soil Dyn. Earthq. Eng. 2019, 116, 145–163. [Google Scholar] [CrossRef]
- Bray, J.D.; Travasarou, T. Simplified procedure for estimating earthquake-induced deviatoric slope displacements. J. Geotech. Geoenviron. Eng. 2007, 133, 381–392. [Google Scholar] [CrossRef]
- Hsieh, S.Y.; Lee, C.T. Empirical estimation of the Newmark displacement from the Arias intensity and critical acceleration. Eng. Geol. 2011, 122, 34–42. [Google Scholar] [CrossRef]
- Du, W.Q.; Wang, G.; Huang, D.R. Influence of slope property variabilities on seismic sliding displacement analysis. Eng. Geol. 2018, 242, 121–129. [Google Scholar] [CrossRef]
- Song, J.; Fan, Q.Q.; Feng, T.G.; Chen, Z.Q.; Chen, J.; Gao, Y.F. A multi-block sliding approach to calculate the permanent seismic displacement of slopes. Eng. Geol. 2019, 255, 48–58. [Google Scholar] [CrossRef]
- Ye, S.H.; Zhao, Z.F. Allowable displacement of slope supported by frame structure with anchors under earthquake. Int. J. Geomech. 2020, 20, 04020188. [Google Scholar] [CrossRef]
- Ye, S.H.; Fang, G.W.; Zhu, Y.P. Model Establishment and Response Analysis of Slope Reinforced by Frame with Prestressed Anchors under Seismic Considering the Prestress. Soil Dyn. Earthq. Eng. 2019, 122, 228–234. [Google Scholar] [CrossRef]
- Ye, S.H.; Zhao, Z.F. Seismic response of pre-stressed anchors with frame structure. Math. Probl. Eng. 2020, 2020, 1–15. [Google Scholar]
- Ye, S.H.; Zhao, Z.F.; Zhu, Y.P. Dynamic Response Analysis Of Loess Slope Reinforced By Frame Anchors Based on Numerical Simulation And Shaking Table Test. J. Geoengin. 2020, 15, 89–101. [Google Scholar]
- Zhang, R.H. Stability Analysis of Multistage Loess Slope under Earthquake Action. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2021. [Google Scholar]
- Kokusho, T. Energy-Based Newmark Method for earthquake-induced slope displacements. Soil Dyn. Earthq. Eng. 2019, 121, 121–134. [Google Scholar] [CrossRef]
- Korzec, A.; Jankowski, R. Extended Newmark method to assess stability of slope under bidirectional seismic loading. Soil Dyn. Earthq. Eng. 2021, 143, 106600. [Google Scholar] [CrossRef]
- Shukha, R.; Baker, R. Design implications of the vertical pseudo-static coefficient in slope analysis. Comput. Geotech. 2008, 35, 86–96. [Google Scholar] [CrossRef]
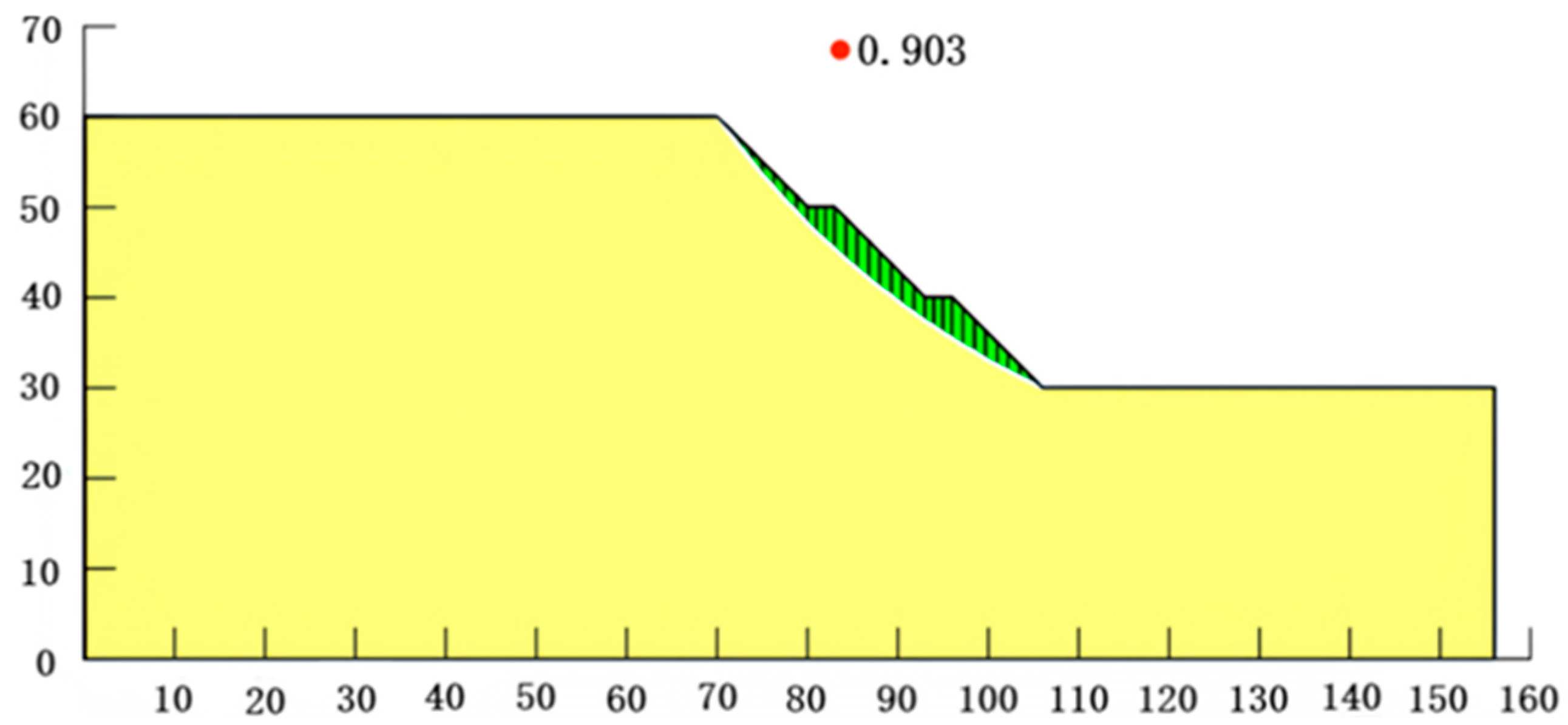
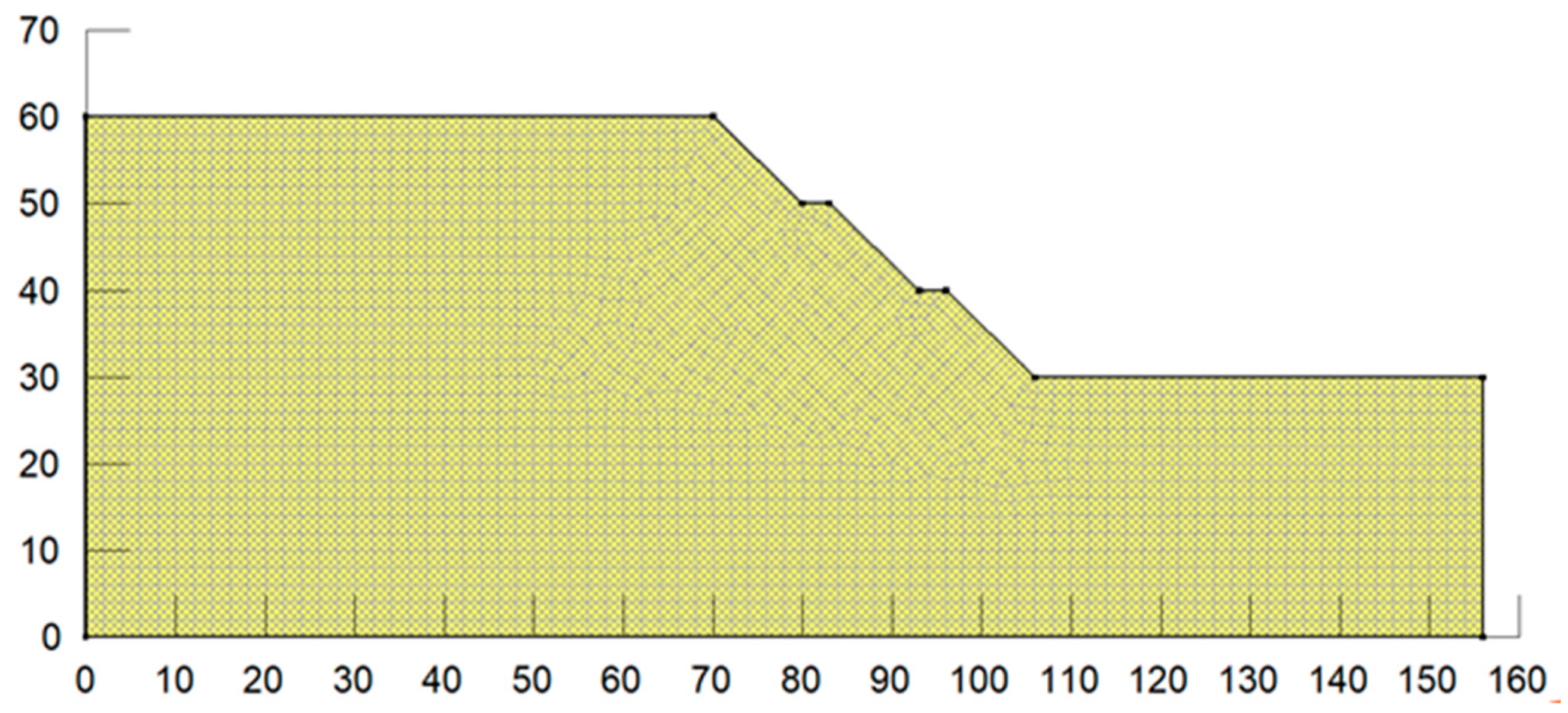
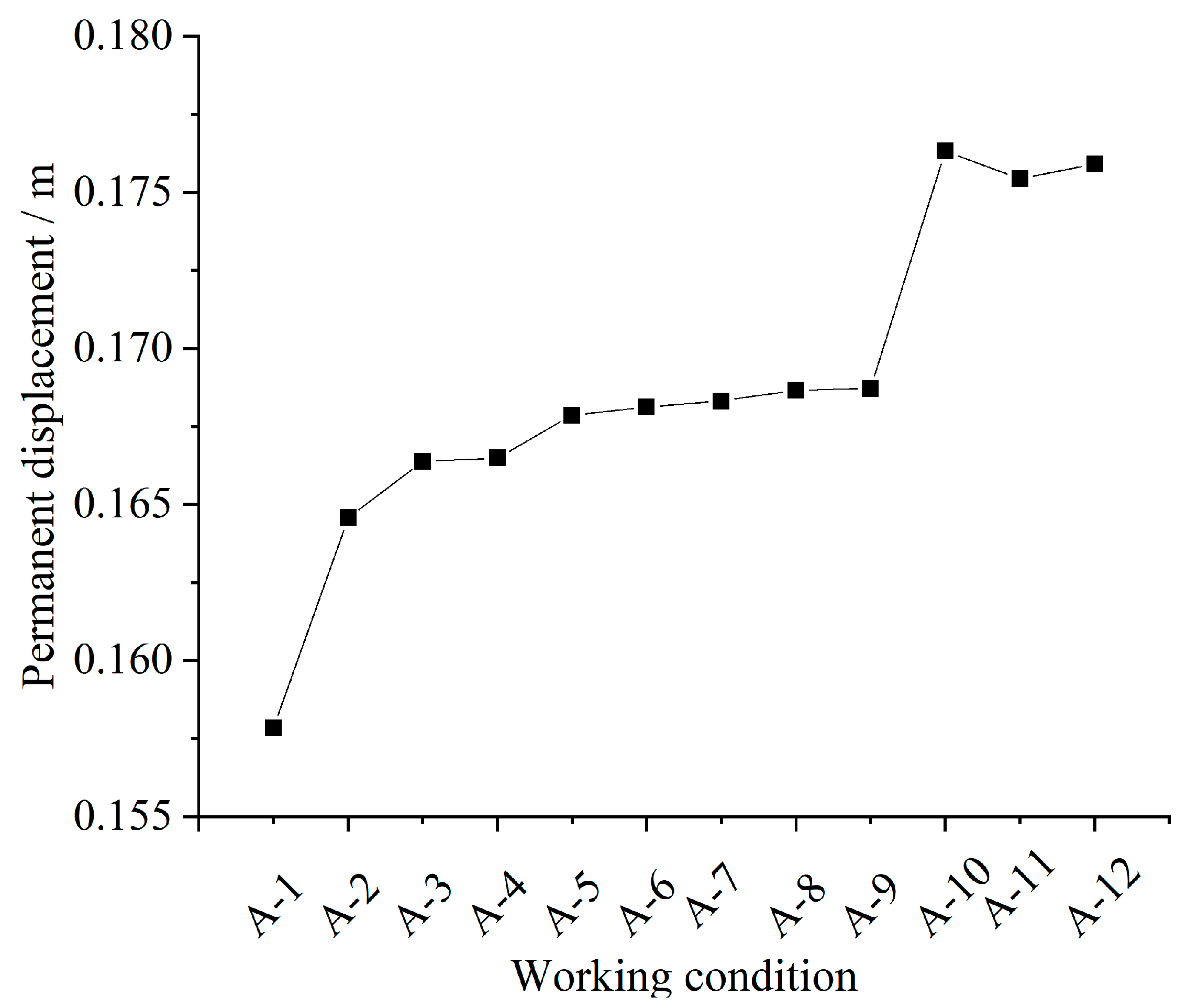
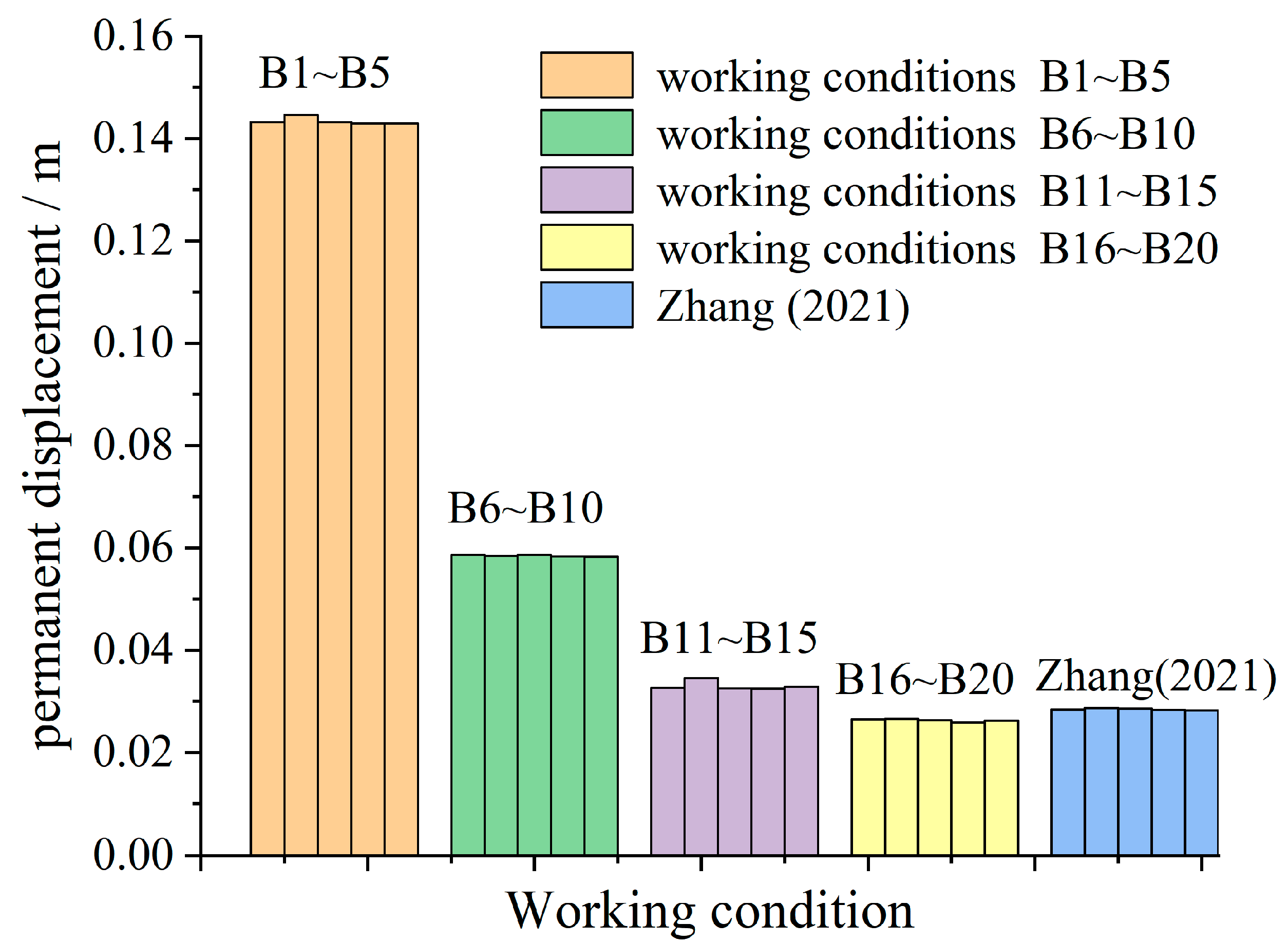


| Working Condition | Slope Rate of Each Grade | Working Condition | Slope Rate of Each Grade | ||||
|---|---|---|---|---|---|---|---|
| A-1 | 1:1 | 1:1 | 1:1 | A-7 | 1:0.85 | 1:0.9 | 1:1.25 |
| A-2 | 1:0.95 | 1:1 | 1:1.05 | A-8 | 1:0.8 | 1:1.1 | 1:1.1 |
| A-3 | 1:0.95 | 1:0.95 | 1:1.1 | A-9 | 1:0.8 | 1:0.95 | 1:1.25 |
| A-4 | 1:0.9 | 1:1.05 | 1:1.05 | A-10 | 1:0.75 | 1:1.1 | 1:1.15 |
| A-5 | 1:0.9 | 1:0.9 | 1:1.2 | A-11 | 1:0.75 | 1:1.05 | 1:1.2 |
| A-6 | 1:0.85 | 1:1.05 | 1:1.1 | A-12 | 1:0.75 | 1:1 | 1:1.25 |
| Working Condition | Slope Stage | Comprehensive Slope Rate | Working Condition | Slope Stage | Comprehensive Slope Rate |
|---|---|---|---|---|---|
| B-1 | 1 | 1:0.75 | B-11 | 1 | 1:1.25 |
| B-2 | 2 | B-12 | 2 | ||
| B-3 | 3 | B-13 | 3 | ||
| B-4 | 4 | B-14 | 4 | ||
| B-5 | 5 | B-15 | 5 | ||
| B-6 | 1 | 1:1 | B-16 | 1 | 1:1.5 |
| B-7 | 2 | B-17 | 2 | ||
| B-8 | 3 | B-18 | 3 | ||
| B-9 | 4 | B-19 | 4 | ||
| B-10 | 5 | B-20 | 5 |
| Parameters | Length of Potential Slippery Surface l/m | Soil Weight γ/(kN/m3) | Dynamic Shear Modulus G/Mpa | Cohesive Force c/kPa | Internal Friction Angle φ/(°) | Inclination Angle of Potential Slip Surface θ/(°) |
|---|---|---|---|---|---|---|
| Numerical value | 172 | 16.6 | 220 | 15 | 32 | 40 |
| Calculation Method | Permanent Displacement/m |
|---|---|
| The method of this paper | 0.186 |
| The method of PLAXIS 3D | 0.118 |
| The method of GEO-Studio | 0.23 |
| The Inclination Angle of the Slip Surface θ/(°) | Critical Acceleration | Permanent Displacement x/m | Gravitational Potential Energy/kJ | Seismic Input Energy/kJ | |
|---|---|---|---|---|---|
| Positive Critical Acceleration acr/g | Negative Critical Acceleration aco/g | ||||
| 0 | 1.25 | −0.81 | 0.003 | 0 | 4.8 |
| 5 | 1.16 | −0.97 | 0.006 | 15.8 | 12.9 |
| 10 | 0.93 | −1.16 | 0.029 | 132 | 35.7 |
| 15 | 0.75 | −1.39 | 0.058 | 458 | 86.4 |
| 20 | 0.60 | −1.68 | 0.147 | 1247 | 143.2 |
| 25 | 0.48 | −2.07 | 0.238 | 2956 | 175.8 |
| 30 | 0.37 | −2.63 | 0.445 | 7234 | 239.6 |
| 35 | 0.27 | −3.53 | 1.175 | 26472 | 257.7 |
| 40 | 0.18 | −5.21 | 1.864 | 125479 | 277.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, X.; Ye, S. Calculation for Permanent Displacement of Single Slip Surface of Multi-Stage Loess Slope Based on Energy Method. Appl. Sci. 2022, 12, 8426. https://doi.org/10.3390/app12178426
Zhang X, Zhang X, Ye S. Calculation for Permanent Displacement of Single Slip Surface of Multi-Stage Loess Slope Based on Energy Method. Applied Sciences. 2022; 12(17):8426. https://doi.org/10.3390/app12178426
Chicago/Turabian StyleZhang, Xiaobing, Xin Zhang, and Shuaihua Ye. 2022. "Calculation for Permanent Displacement of Single Slip Surface of Multi-Stage Loess Slope Based on Energy Method" Applied Sciences 12, no. 17: 8426. https://doi.org/10.3390/app12178426
APA StyleZhang, X., Zhang, X., & Ye, S. (2022). Calculation for Permanent Displacement of Single Slip Surface of Multi-Stage Loess Slope Based on Energy Method. Applied Sciences, 12(17), 8426. https://doi.org/10.3390/app12178426





