Development of Damage Type Viscoelastic Ontological Model for Soft and Hard Materials under High-Strain-Rate Conditions
Abstract
:1. Introduction
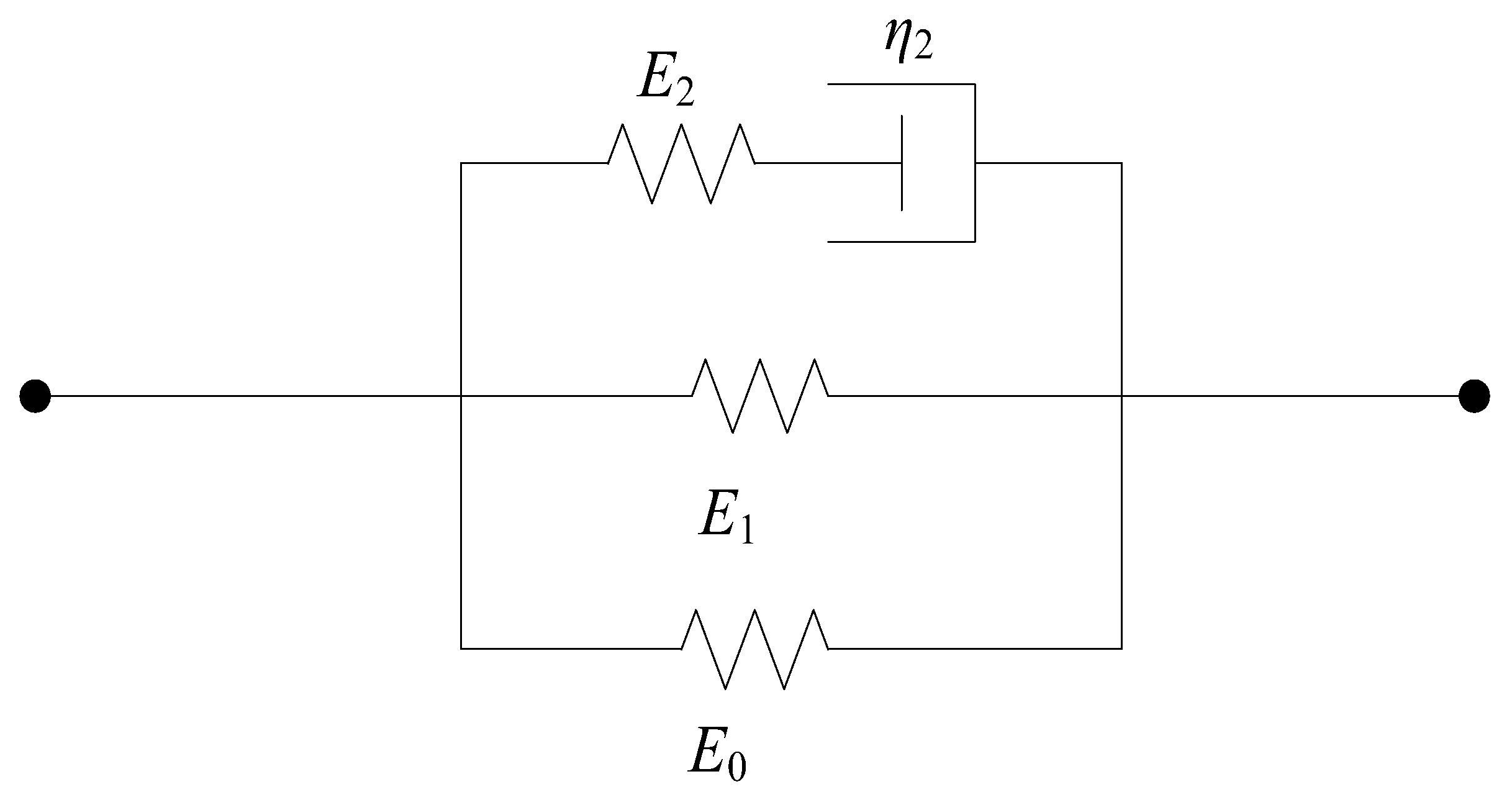
2. Establishment of Constitutive Model
3. Experimental Research
3.1. Preparation of Test Pieces
3.1.1. Preparation of Coal Rock
3.1.2. Preparation of Foam Concrete
3.2. Experimental Method
3.3. Verification of Stress Balance
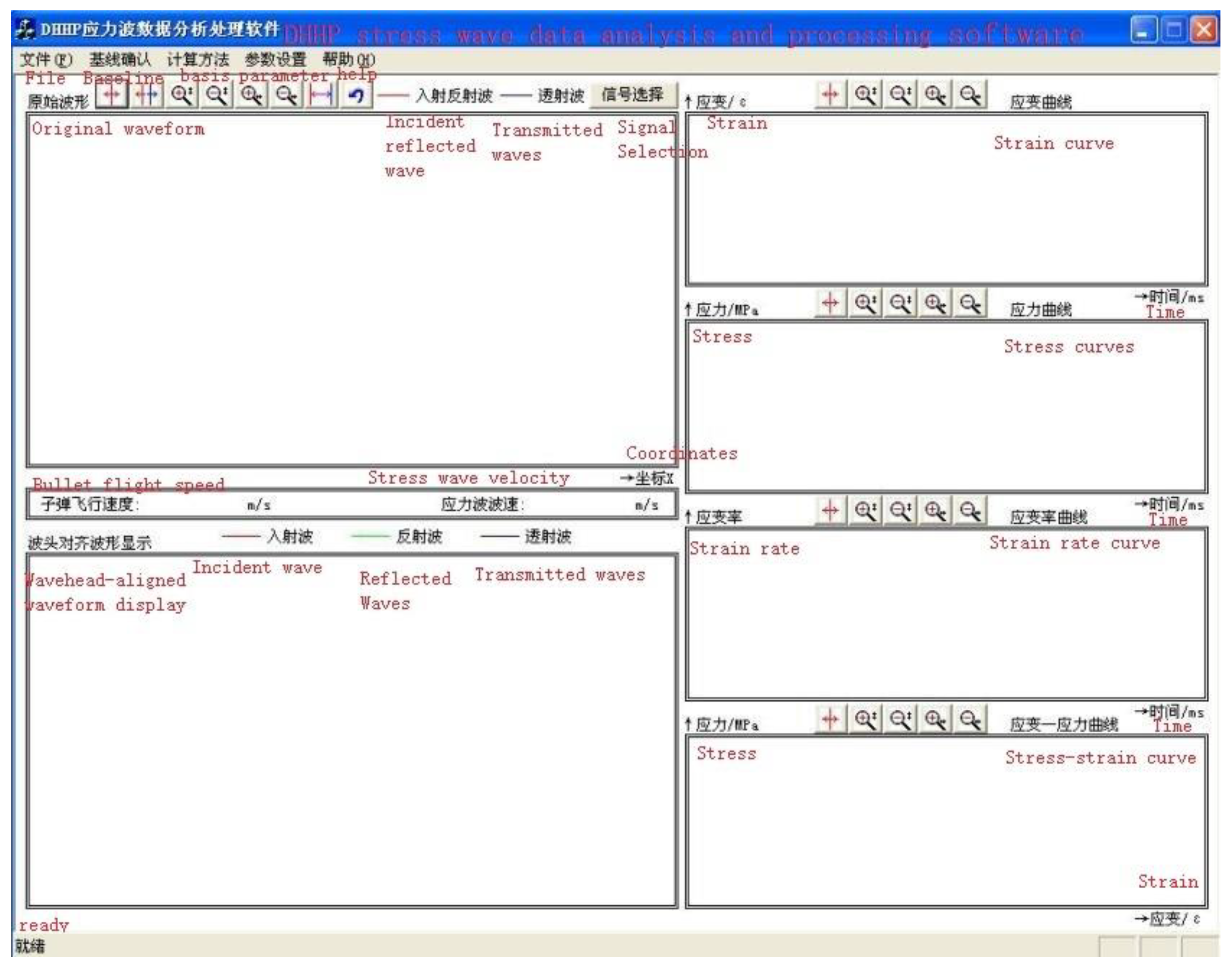
3.4. Data Analysis
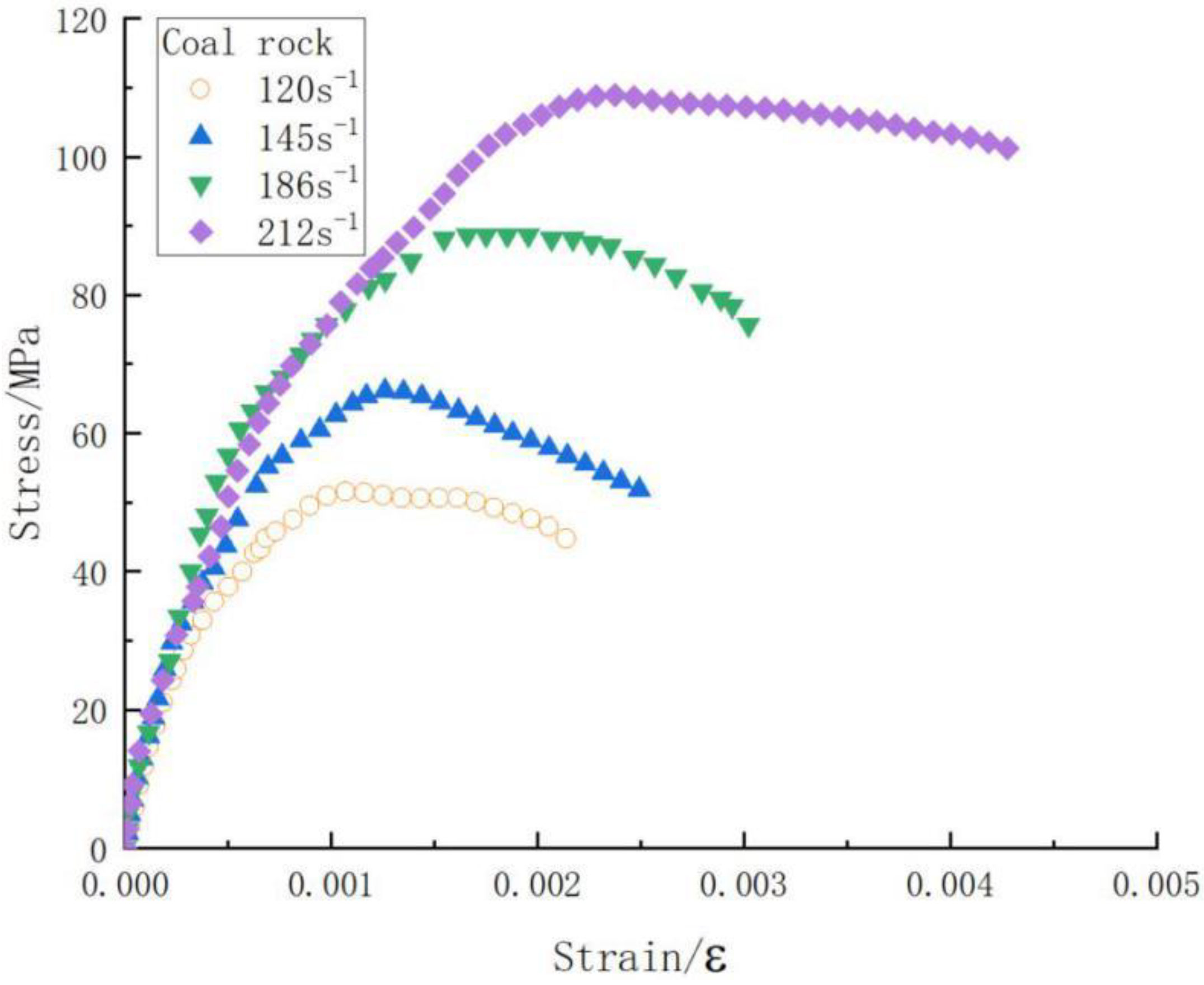
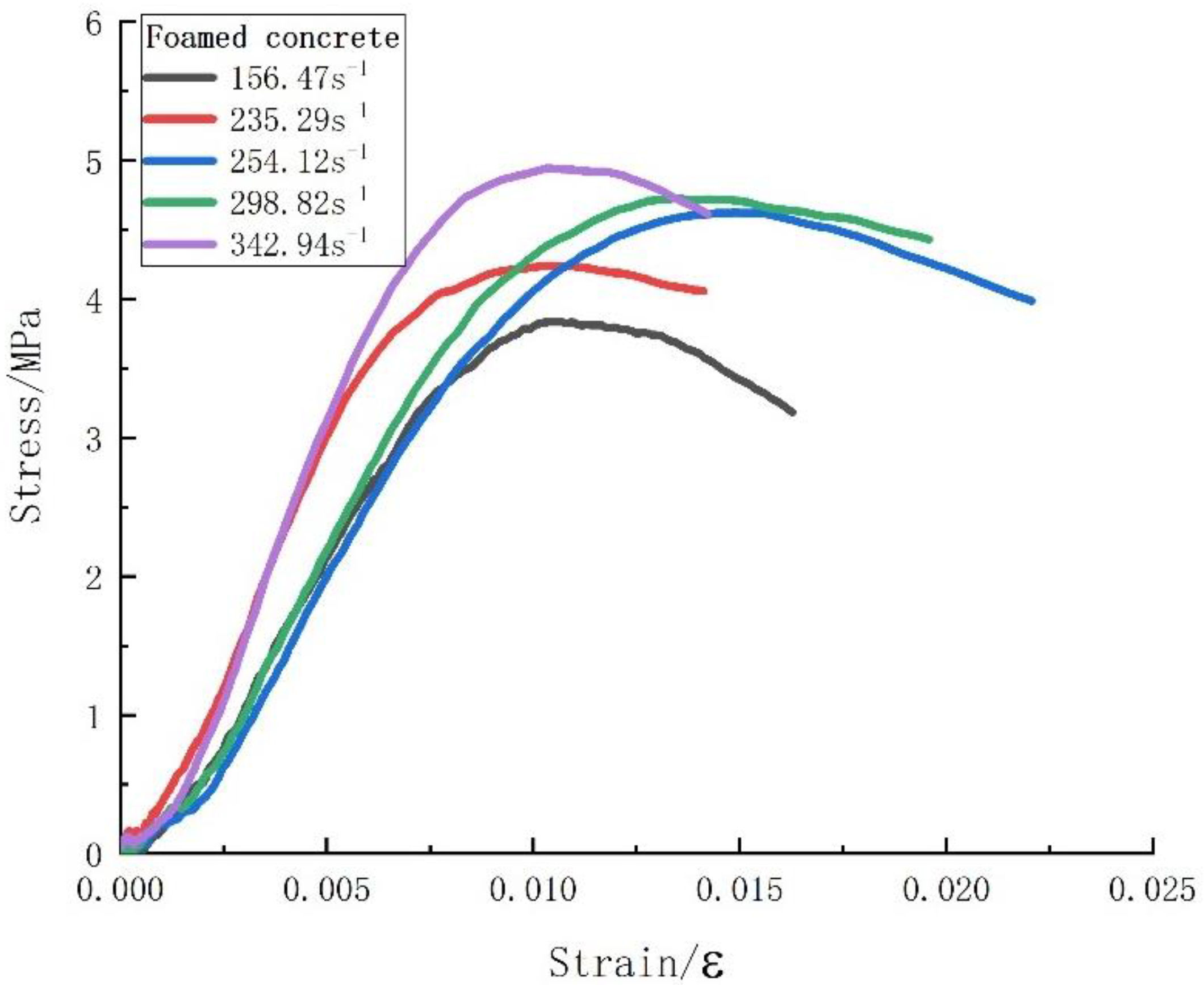
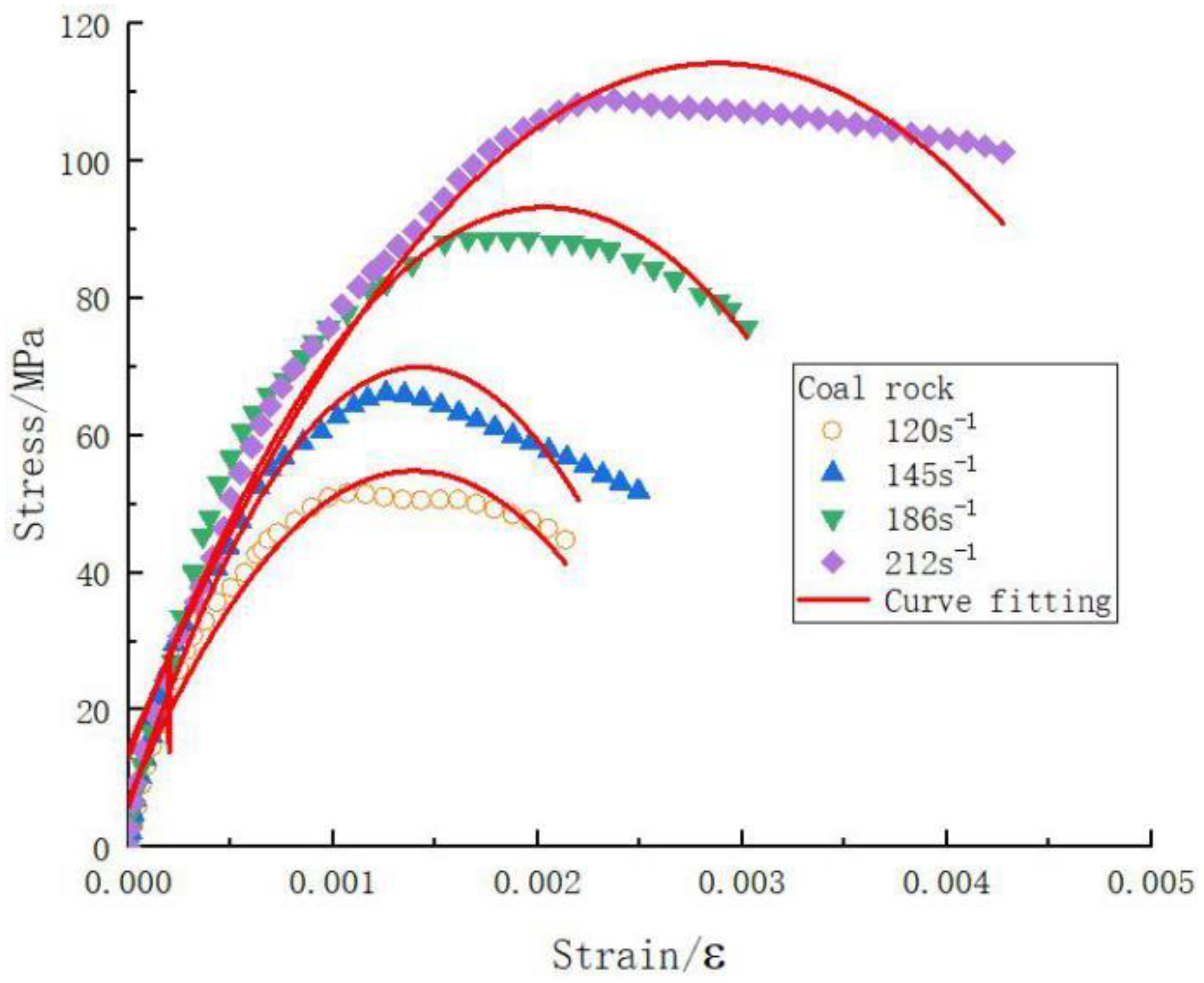
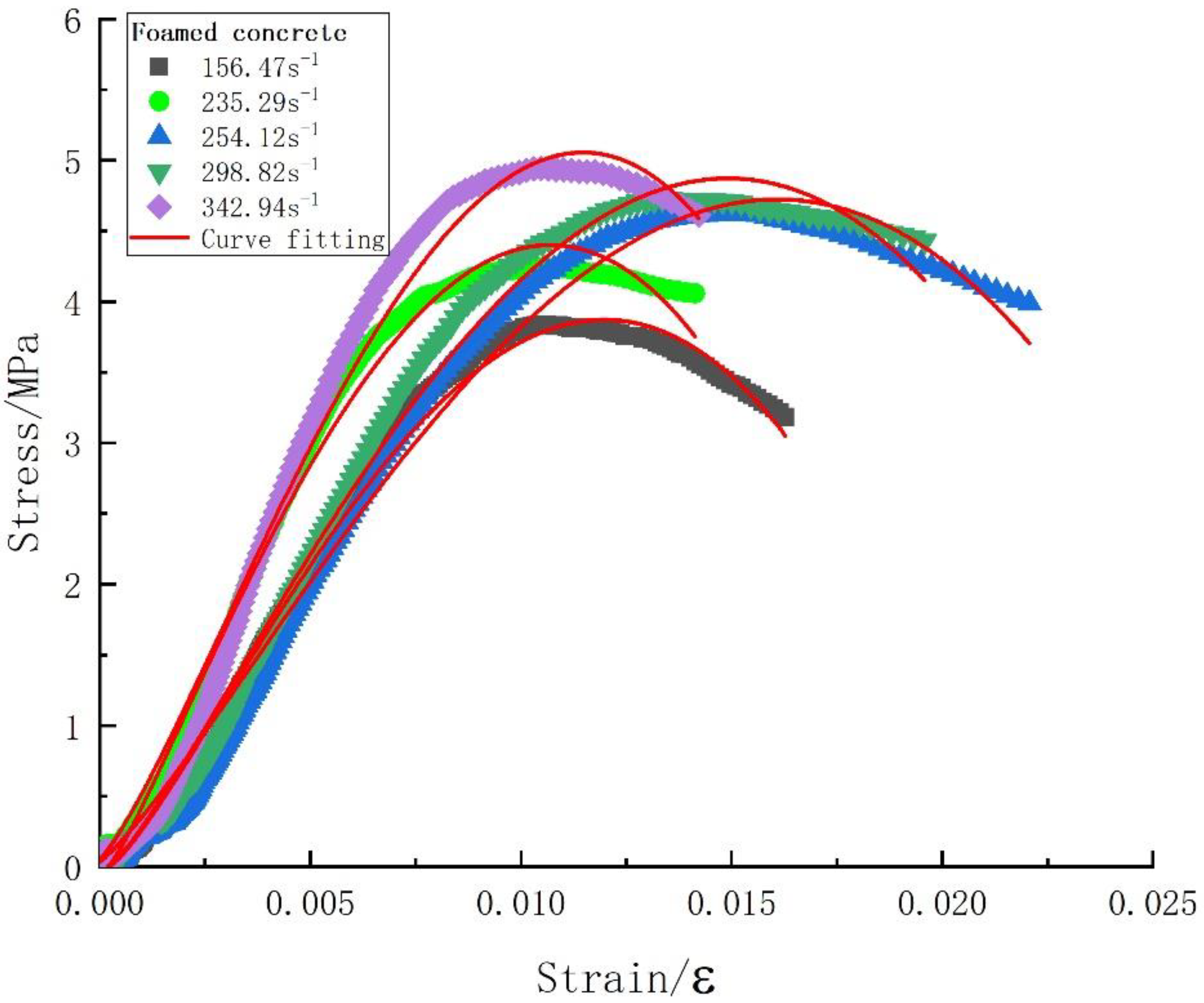
3.5. Experimental Results
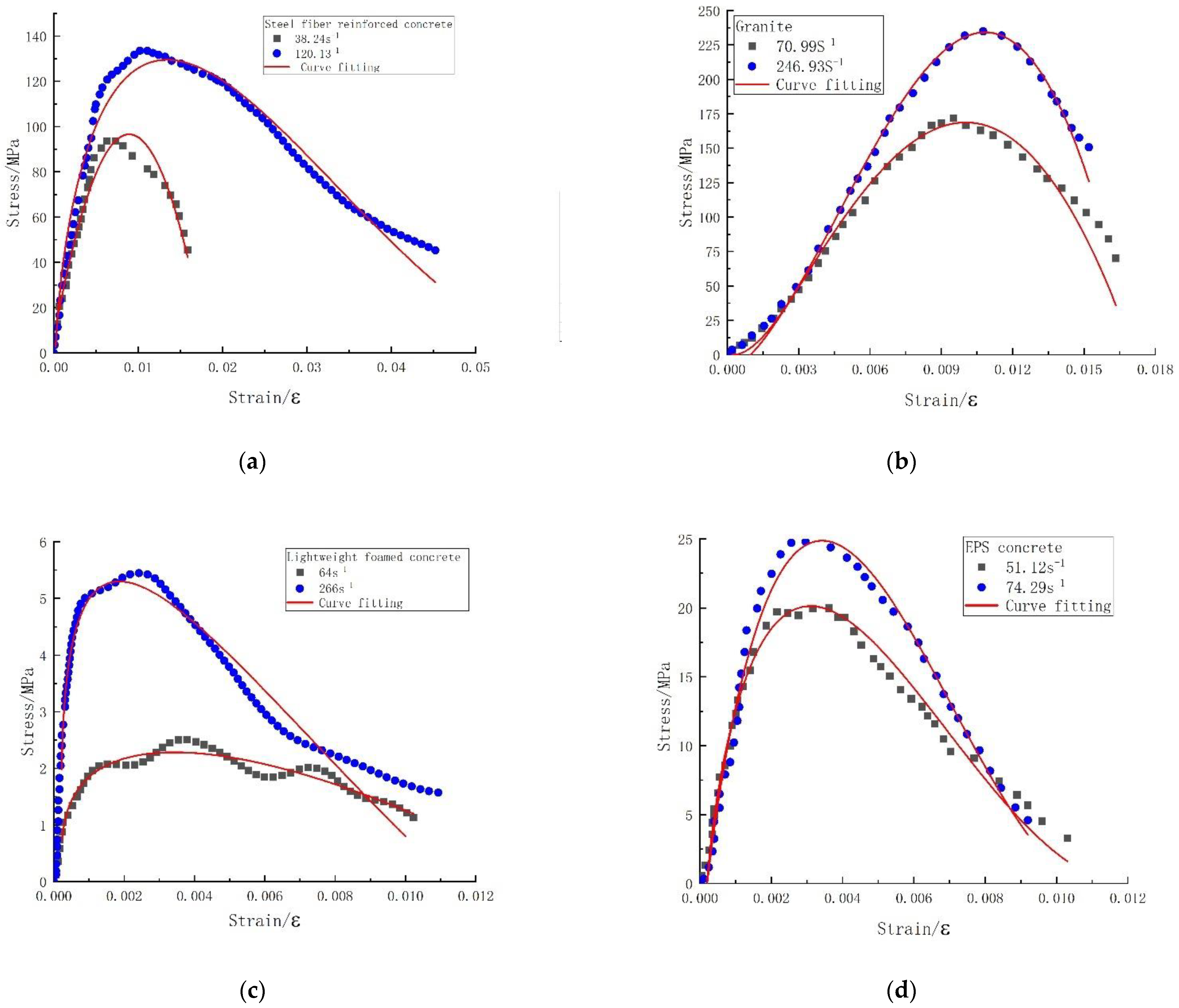
4. Validation of the Viscoelastic Constitutive Model with Damage
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hui, C.; Cheng, C.; Shen, S.; Gao, P.; Chen, J.; Yang, J.; Zhao, M. The Effect of the Wenchuan and Lushan Earthquakes on the Size Distribution of Earthquakes along the Longmenshan Fault. Appl. Sci. 2021, 11, 8534. [Google Scholar] [CrossRef]
- Wei, M.; Cheng, Y.; Lin, Y.; Kuo, W.; Shu, C. Applications of dust explosion hazard and disaster prevention technology. J. Loss Prevent. Proc. 2020, 68, 104304. [Google Scholar] [CrossRef]
- Liu, W.; Mu, C.; Li, Z. Influence of cavity structure on gas explosion characteristics in coal mine. Powder Technol. 2022, 398, 117084. [Google Scholar] [CrossRef]
- Liu, W.; Xu, X.; Mu, C. Experimental Study on Two-Phase Explosion Suppression of Gas/Pulverized Coal by Explosion Suppressant. ACS Omega 2022, 7, 16644–16652. [Google Scholar] [CrossRef]
- Perceka, W.; Liao, W.; Wu, Y. Shear Strength Prediction Equations and Experimental Study of High Strength Steel Fiber-Reinforced Concrete Beams with Different Shear Span-to-Depth Ratios. Appl. Sci. 2019, 9, 4790. [Google Scholar] [CrossRef] [Green Version]
- Iskhakov, I.; Frolov, I.; Ribakov, Y. Experimental Investigation of Concrete Transverse Deformations at Relatively High Loading Rates for Interpretation of High Strength Concrete Behavior. Appl. Sci. 2021, 11, 8460. [Google Scholar] [CrossRef]
- He, Y.; Gao, M.; Zhao, H.; Zhao, Y.; Miguel, N.; Neves, M. Behaviour of Foam Concrete under Impact Loading Based on SHPB Experiments. Shock Vib. 2019, 2019, 2065845. [Google Scholar] [CrossRef]
- Li, L.; Tu, G.; Lan, C.; Liu, F. Mechanical characterization of waste-rubber-modified recycled-aggregate concrete. J. Clean. Prod. 2016, 124, 325–338. [Google Scholar] [CrossRef]
- Bonić, Z.; Ćurčić, G.T.; Trivunić, M.; Davidović, N.; Vatin, N. Some Methods of Protection of Concrete and Reinforcment of Reinforced-Concrete Foundations exposed to Environmental Impacts. Procedia Eng. 2015, 117, 419–430. [Google Scholar] [CrossRef] [Green Version]
- Belyakov, N.; Smirnova, O.; Alekseev, A.; Tan, H. Numerical Simulation of the Mechanical Behavior of Fiber-Reinforced Cement Composites Subjected Dynamic Loading. Appl. Sci. 2021, 11, 1112. [Google Scholar] [CrossRef]
- Thai, D.; Kim, S. Numerical simulation of pre-stressed concrete slab subjected to moderate velocity impact loading. Eng. Fail. Anal. 2017, 79, 820–835. [Google Scholar] [CrossRef]
- Zhao, D.; Yi, W.; Kunnath, S.K. Numerical simulation and shear resistance of reinforced concrete beams under impact. Eng. Struct. 2018, 166, 387–401. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, X.; He, S. Numerical simulation of impact tests on reinforced concrete beams. Mater. Des. 2012, 39, 111–120. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Wang, W.; Tang, L.; Liu, Q.; Cheng, G. Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mec. 2019, 101, 59–66. [Google Scholar] [CrossRef]
- Xie, S.; Lin, H.; Wang, Y.; Chen, Y.; Xiong, W.; Zhao, Y.; Du, S. A statistical damage constitutive model considering whole joint shear deformation. Int. J. Damage Mech. 2020, 29, 988–1008. [Google Scholar] [CrossRef]
- Yanlin, Z.; Lianyang, Z.; Weijun, W.; Wen, W.; Wenhao, M. Separation of Elastoviscoplastic Strains of Rock and a Nonlinear Creep Model. Int. J. Geomech. 2017, 18, 04017129. [Google Scholar]
- Luo, G.; Wu, C.; Xu, K.; Liu, L.; Chen, W. Development of dynamic constitutive model of epoxy resin considering temperature and strain rate effects using experimental methods. Mech. Mater. 2021, 159, 103887. [Google Scholar] [CrossRef]
- Liu, H.T.; Chen, N.; Sun, Y.Z. Experimental and Modelling of Constitutive Equation of Polycarbonate Material. Key Eng. Mater. 2015, 667, 286–291. [Google Scholar] [CrossRef]
- Xu, X.; Gao, S.; Zhang, D.; Niu, S.; Jin, L.; Ou, Z. Mechanical behavior of liquid nitrile rubber-modified epoxy resin: Experiments, constitutive model and application. Int. J. Mech. Sci. 2019, 151, 46–60. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Xie, A.; Qi, Y. Experimental study on dynamic mechanical properties and constitutive model of basalt fiber reinforced concrete. Constr. Build. Mater. 2017, 152, 154–167. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Zheng, K.; Bakura, T.J.; Totakhil, P.G. Research on compressive impact dynamic behavior and constitutive model of polypropylene fiber reinforced concrete. Constr. Build. Mater. 2018, 187, 584–595. [Google Scholar] [CrossRef]
- Li, B.; Zhu, Z.; Ning, J.; Li, T.; Zhou, Z. Viscoelastic–plastic constitutive model with damage of frozen soil under impact loading and freeze–thaw loading. Int. J. Mech. Sci. 2022, 214, 106890. [Google Scholar] [CrossRef]
- Ma, D.; Ma, Q.; Yuan, P. SHPB tests and dynamic constitutive model of artificial frozen sandy clay under confining pressure and temperature state. Cold Reg. Sci. Technol. 2017, 136, 37–43. [Google Scholar] [CrossRef]
- Fu, T.; Zhu, Z.; Zhang, D.; Liu, Z.; Xie, Q. Research on damage viscoelastic dynamic constitutive model of frozen soil. Cold Reg. Sci. Technol. 2019, 160, 209–221. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, Z.; Fu, T.; Jia, J. Damage mechanism and dynamic constitutive model of frozen soil under uniaxial impact loading. Mech. Mater. 2020, 140, 103217. [Google Scholar] [CrossRef]
- Wenqing, Z.; Chaomin, M.; Zhongqing, L. Study on dynamic mechanical properties of coal under impact loading. Coal Sci. Technol. 2019, 47, 198–204. [Google Scholar]
- Song Li, H.S. Two-wave and three-wave method in SHPB data processing. Explos. Shock Waves 2005, 25, 368–373. [Google Scholar]
- Lok, T.S.; Li, X.B.; Liu, D.; Zhao, P.J. Testing and Response of Large Diameter Brittle Materials Subjected to High Strain Rate. J. Mater. Civ. Eng. 2002, 14, 262–269. [Google Scholar] [CrossRef]
- Wang, T.T.; Shang, B. Three-Wave Mutual-Checking Method for Data Processing of SHPB Experiments of Concrete. J. Mech. 2014, 30, N5–N10. [Google Scholar] [CrossRef]
- Ye, Z.B.; Huang, R.Y.; Li, Y.C.; Lv, L.; Zhao, K.; Zhang, Y.L.; Ma, J.; Lin, J.J. Steel fiber-reinforced concrete under impact loading dynamic constitutive equation. Constr. Build. Mater. 2018, 190, 1049–1055. [Google Scholar] [CrossRef]
- Cai, Y.; Yu, S.; Lu, Y. Experimental study on granite and the determination of its true strain-rate effect. Lat. Am. J. Solids Strut. 2015, 12, 675–694. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Zhou, Y.; Wang, Y.; Lei, M. Experimental research on the dynamic mechanical properties and damage characteristics of lightweight foamed concrete under impact loading. Int. J. Impact Eng. 2020, 140, 103558. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Hao, H.; Khan, M.Z.N.; Pham, T.M. Dynamic compressive properties of novel lightweight ambient-cured EPS geopolymer composite. Constr. Build. Mater. 2021, 273, 122044. [Google Scholar] [CrossRef]










| Cement | PO42.5 ordinary Portland cement (PC) with a density of 3150 kg/m3, an initial setting time of 50 min, and a final setting time of 3 h and 30 min |
| Fly ash | Fly ash with an average grain diameter of 1–15 μm, class I parameters, and a density of 2400 kg/m3 |
| Water | Tap water |
| Polypropylene fibers | Density of 0.91 g/m3, Elastic Modulus of 5000 MPa |
| Admixture | Htq-1 compound foaming agent |
| Foam Agent | Calcium stearate (C36H70CaO4) |
| Design Plastic Density (kg/m3) | Fly Ash (kg) | Water (kg) | Cement (kg) | Cement Type | Foam Agent (kg) |
|---|---|---|---|---|---|
| 658 | 164 | 329 | 658 | PC | 5.57 |
| A | α | β | Ea | E2 | θ2 | δ | R2 | ||
|---|---|---|---|---|---|---|---|---|---|
| Coal rock | 120 | 3 | −0.6 | −1 | −1.77042 × 1010 | 1.77042 × 1010 | 3 | −0.0002 | 0.9648 |
| 145 | 3 | −0.59 | −1 | −2.76368 × 1010 | 2.76368 × 1010 | 3 | −0.0002 | 0.9401 | |
| 186 | 3 | −0.545 | −1 | −2.1608 × 1010 | 2.1608 × 1010 | 3 | −0.0002 | 0.9584 | |
| 212 | 3 | −0.51 | −1 | −1.5297 × 1010 | 1.5297 × 1010 | 3 | −0.0002 | 0.9739 | |
| Foamed concrete | 156.47 | 3 | 0.80 | 0.30 | 3005.86 | −3005.93 | 3 | 0.0002 | 0.9953 |
| 235.29 | 3 | 0.68 | 0.20 | 12,479.65 | −12,479.82 | 3 | 0.0002 | 0.9945 | |
| 254.12 | 3 | 0.64 | 0.30 | 14,062.01 | −14,062.27 | 3 | −0.0002 | 0.9946 | |
| 298.82 | 3 | 0.50 | 0.25 | 88,387.15 | −88,388.46 | 3 | 0.0002 | 0.9946 | |
| 342.94 | 3 | 0.70 | 0.35 | 21,752.35 | −21,752.57 | 3 | −0.0002 | 0.9881 | |
| Steel fiber-reinforced concrete | 38.24 | 3 | −0.485 | −1 | −2.58732 × 108 | 2.58731 × 108 | 3 | −0.0002 | 0.9625 |
| 120.13 | 3 | −0.14 | −0.2 | 3.84645 × 108 | −3.84677 × 108 | 3 | −0.0002 | 0.9712 | |
| Granite | 70.99 | 3 | −0.27 | −0.47 | −2.77818 × 109 | 2.77818 × 109 | 3 | −0.0002 | 0.9583 |
| 246.93 | 3 | 0.02 | 0.33 | 2.18859 × 1010 | −2.18859 × 1010 | 3 | −0.0002 | 0.9943 | |
| Lightweight foamed concrete | 64 | 3 | −0.0026 | −0.7 | 155,087.9264 | −155,093.636 | 3 | −0.0002 | 0.9078 |
| 266 | 3 | −0.34 | −0.7 | 5.30233 × 107 | −5.30245 × 107 | 3 | −0.0002 | 0.9105 | |
| EPS concrete | 51.12 | 3 | −0.077 | 0.06 | −2.97949 × 109 | 2.9796 × 109 | 3 | −0.0002 | 0.9776 |
| 74.29 | 3 | 0.1 | 0.5 | −1.00786 × 109 | 1.00788 × 109 | 3 | −0.0002 | 0.9838 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Xu, X.; Mu, C. Development of Damage Type Viscoelastic Ontological Model for Soft and Hard Materials under High-Strain-Rate Conditions. Appl. Sci. 2022, 12, 8407. https://doi.org/10.3390/app12178407
Liu W, Xu X, Mu C. Development of Damage Type Viscoelastic Ontological Model for Soft and Hard Materials under High-Strain-Rate Conditions. Applied Sciences. 2022; 12(17):8407. https://doi.org/10.3390/app12178407
Chicago/Turabian StyleLiu, Wei, Xiangyun Xu, and Chaomin Mu. 2022. "Development of Damage Type Viscoelastic Ontological Model for Soft and Hard Materials under High-Strain-Rate Conditions" Applied Sciences 12, no. 17: 8407. https://doi.org/10.3390/app12178407
APA StyleLiu, W., Xu, X., & Mu, C. (2022). Development of Damage Type Viscoelastic Ontological Model for Soft and Hard Materials under High-Strain-Rate Conditions. Applied Sciences, 12(17), 8407. https://doi.org/10.3390/app12178407






