Seismic Sequence Vulnerability of Low-Rise Special Moment-Resisting Frame Buildings with Brick Infills
Abstract
:1. Introduction
2. Materials and Methods
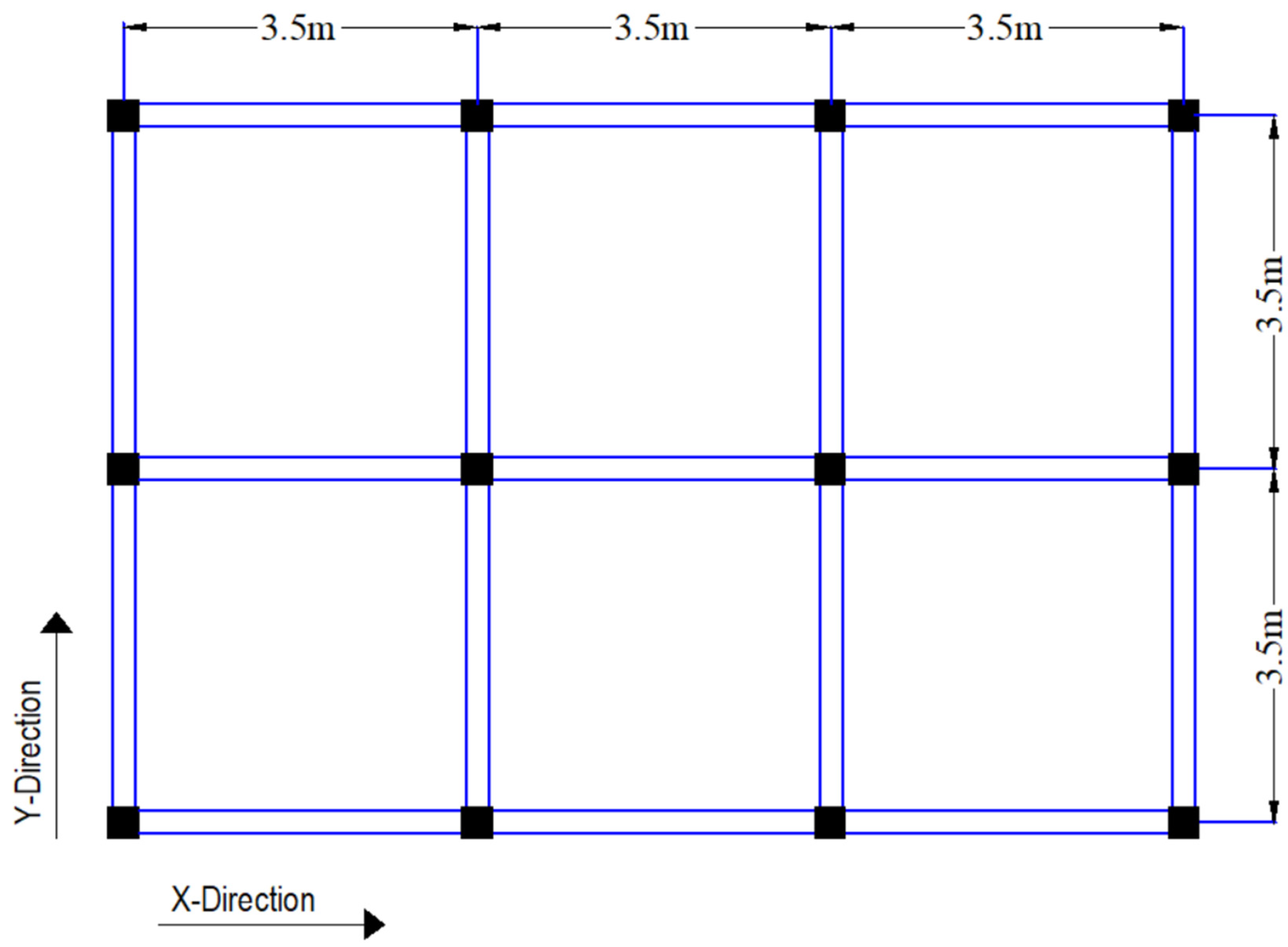
2.1. Case Study Building
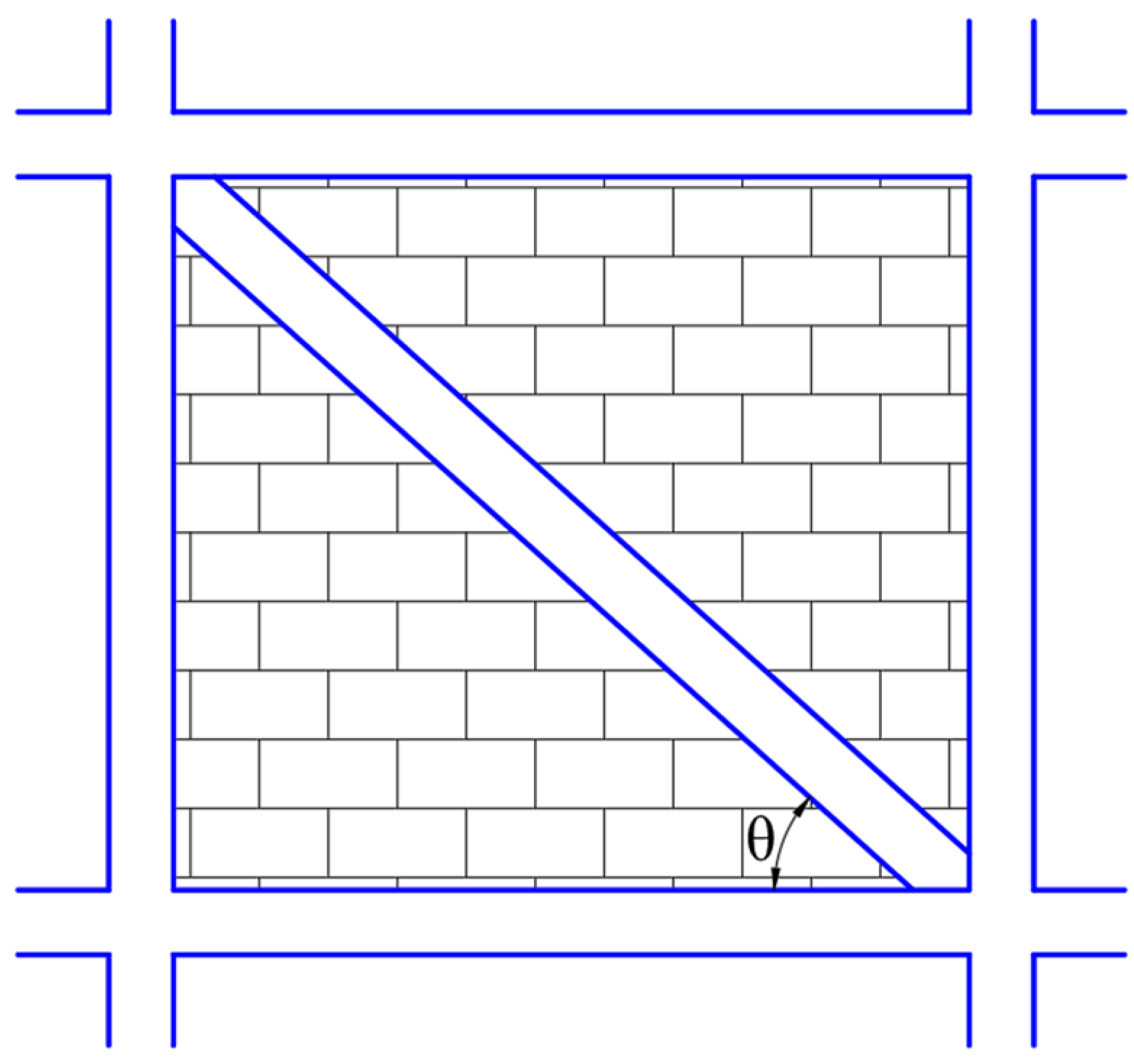
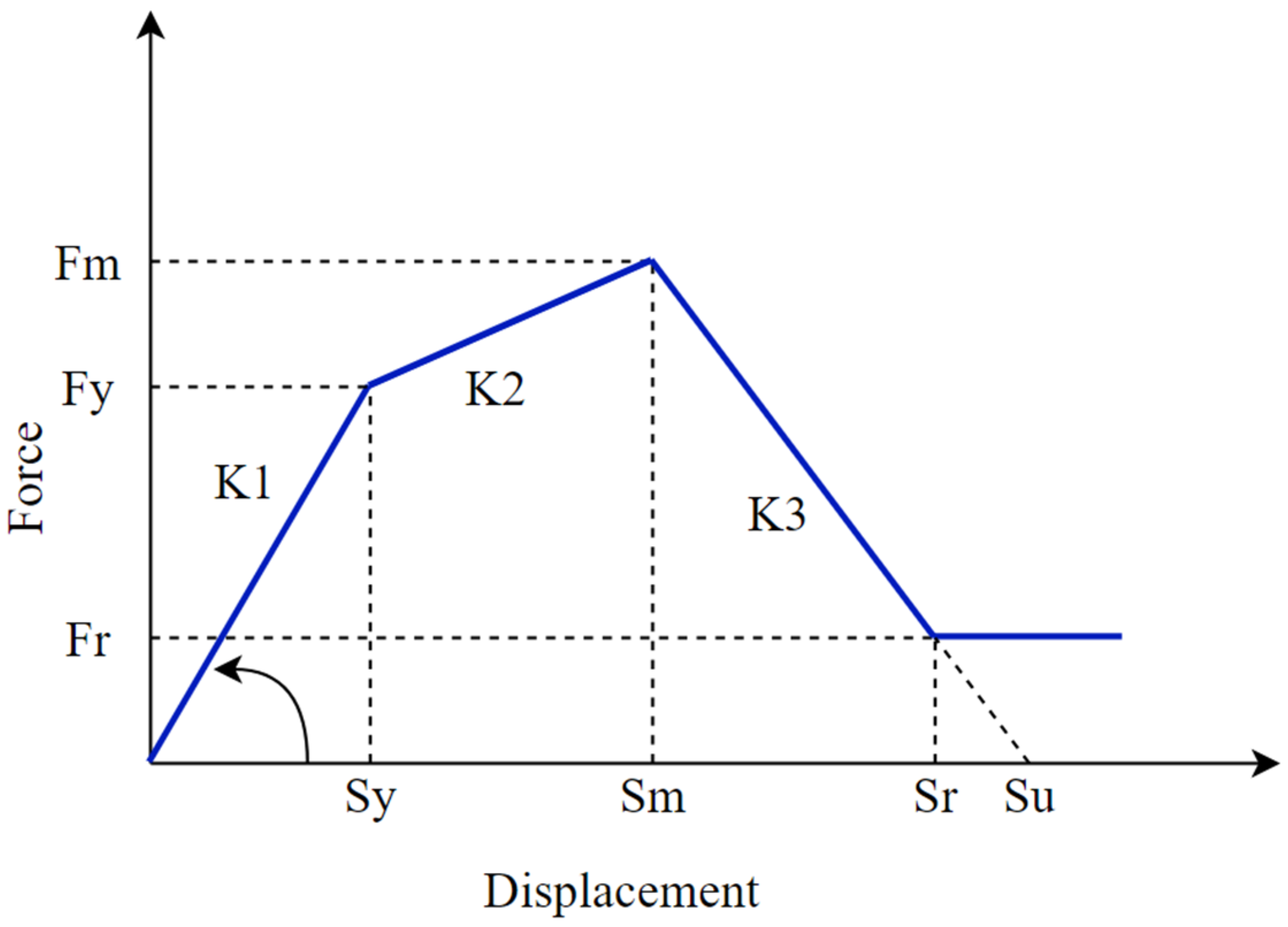
2.2. Infill Modeling
2.3. Finite Element Modeling
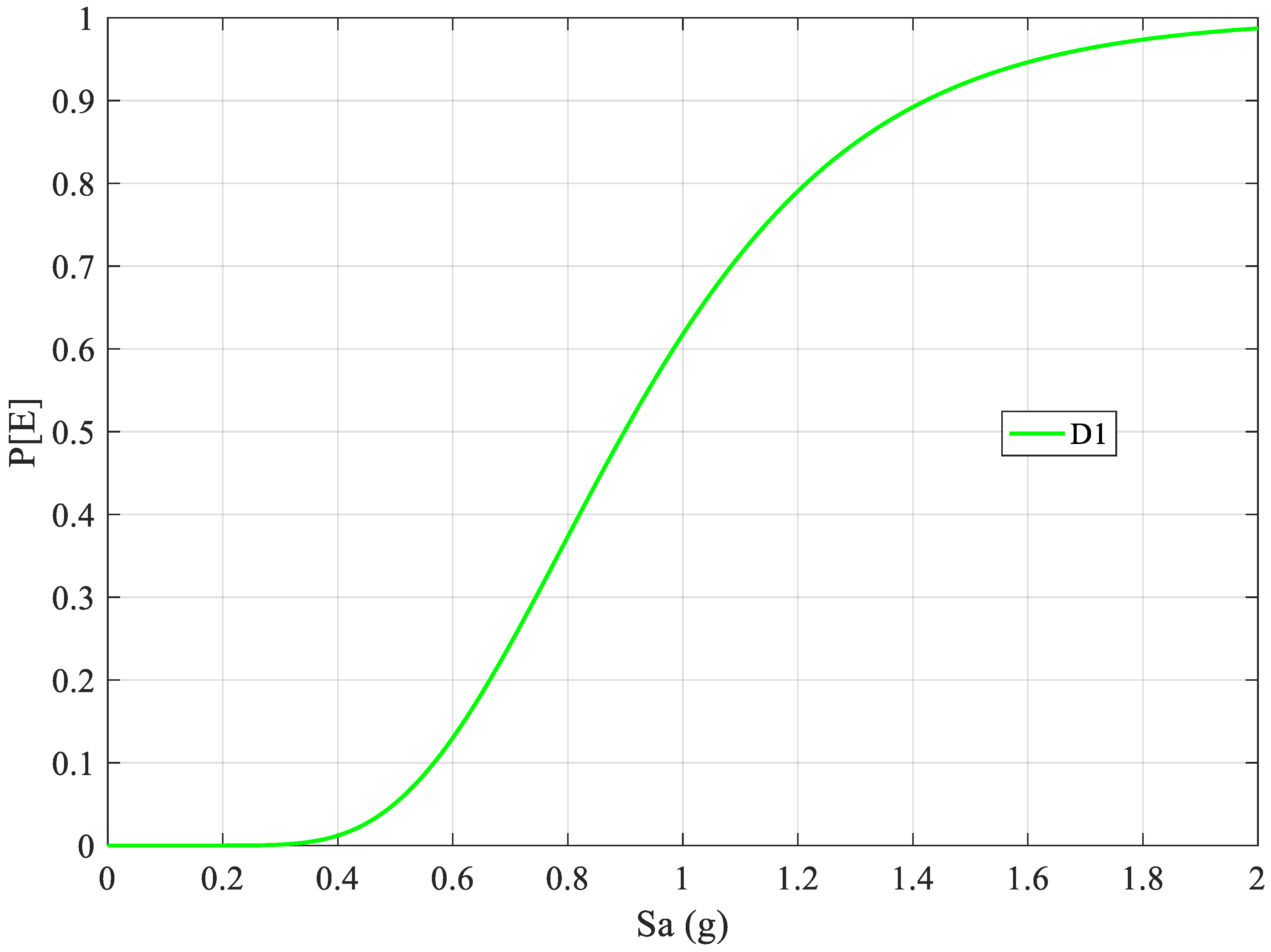
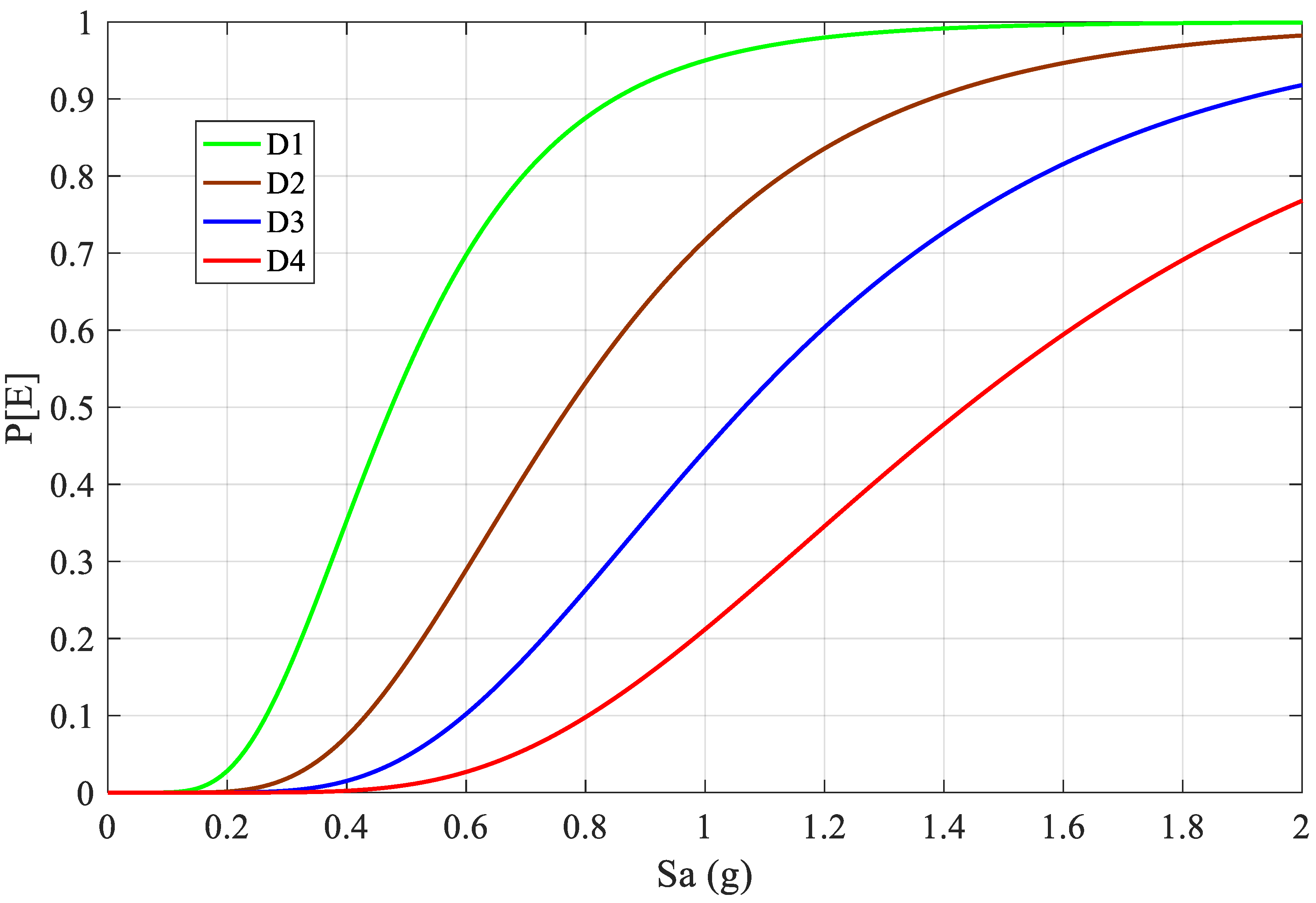
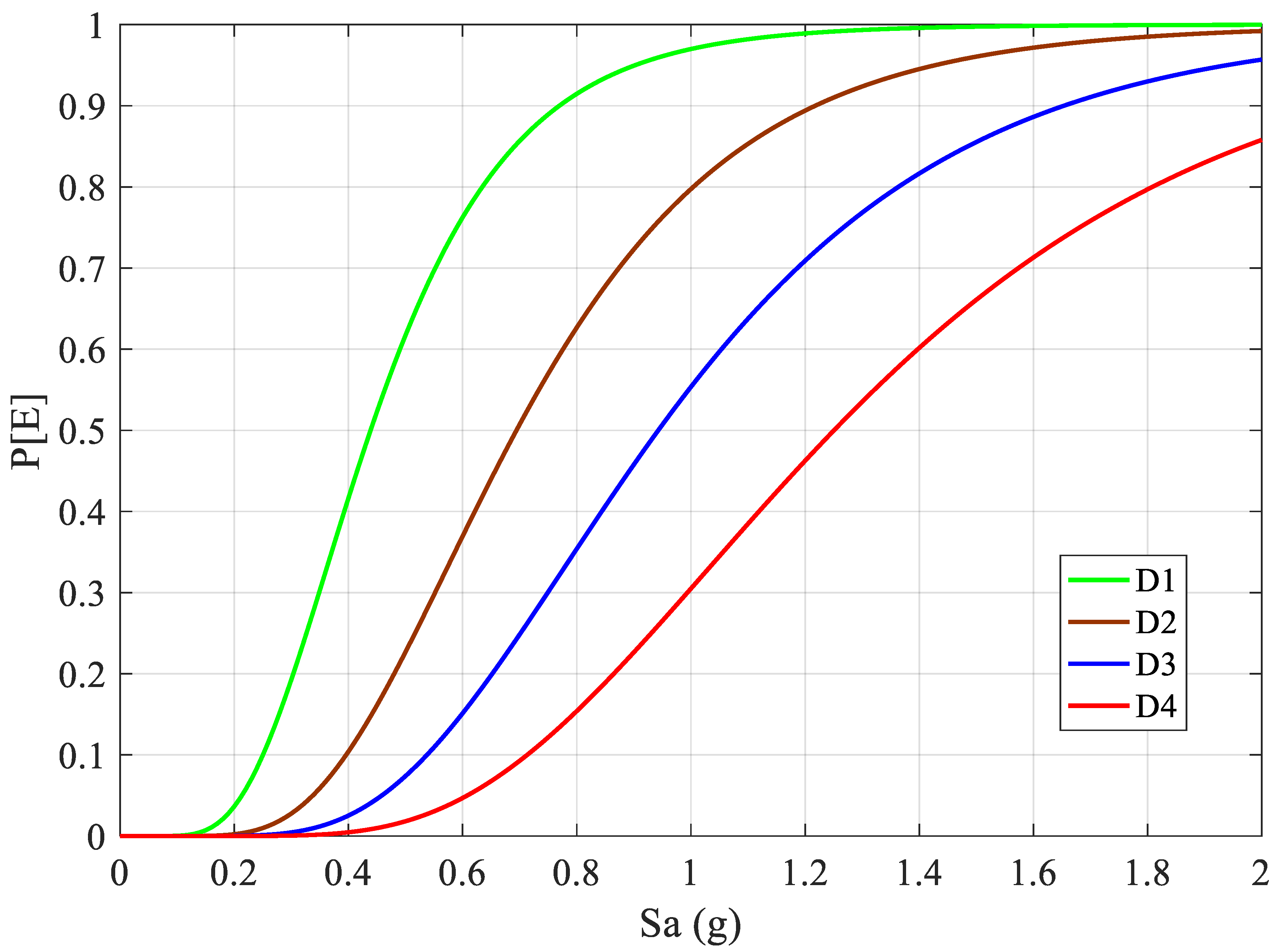
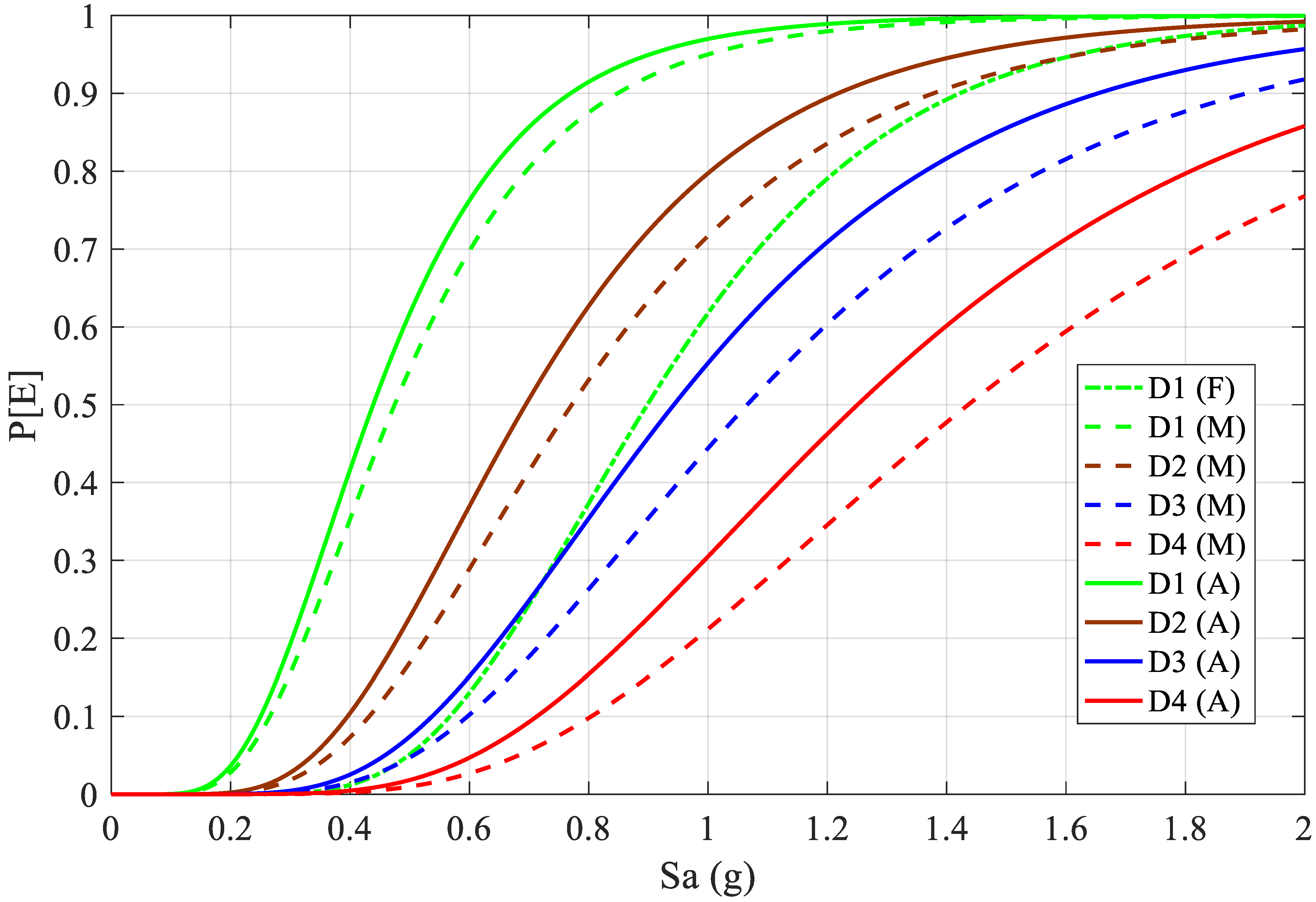
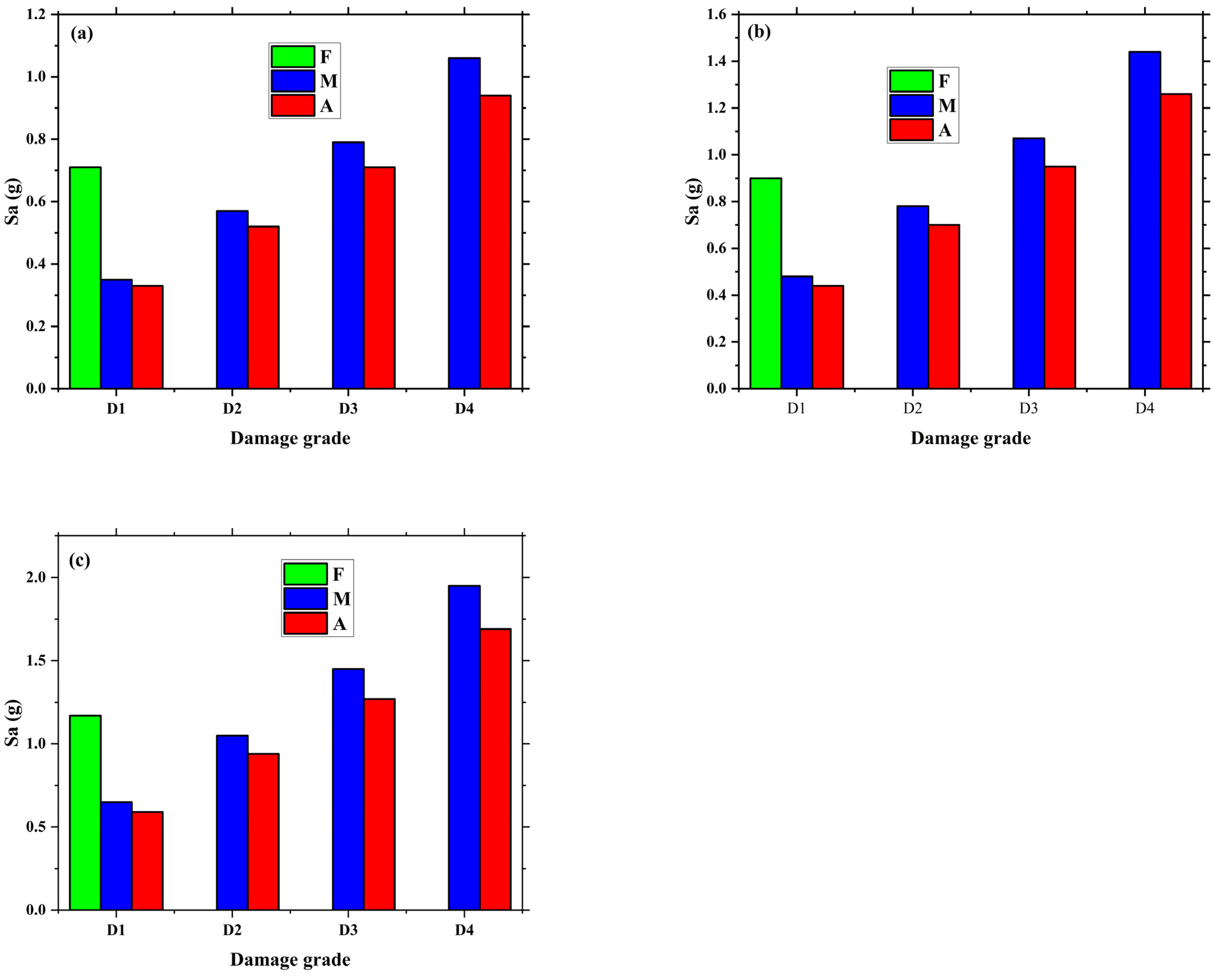
2.4. Fragility Analysis
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grunthal, C. European Macroseismic Scale; European Seimological Commission: Luxembourg, 1998. [Google Scholar]
- Rana, B.S. The Great Earthquake of Nepal 1934; Jorganesh Press: Kathmandu, Nepal, 1935. [Google Scholar]
- Gautam, D.; Fabbrocino, G.; de Magistris, F.S. Derive empirical fragility functions for Nepali residential buildings. Eng. Struct. 2018, 171, 617–628. [Google Scholar] [CrossRef]
- Miano, A.; Jalayer, F.; Forte, G.; Santo, A. Empirical fragility assessment using conditional GMPE-based ground shaking fields: Application to damage data for 2016 Amatrice Earthquake. Bull. Earthq. Eng. 2020, 18, 15. [Google Scholar] [CrossRef]
- Gautam, D.; Adhikari, R.; Rupakhety, R. Seismic fragility of structural and non-structural elements of Nepali RC buildings. Eng. Struct. 2021, 232, 111879. [Google Scholar] [CrossRef]
- Gautam, D.; Adhikari, R.; Rupakhety, R.; Koirala, P. An empirical method for seismic vulnerability assessment of Nepali school buildings. Bull. Earthq. Eng. 2020, 18, 5965–5982. [Google Scholar] [CrossRef]
- Di Sarno, L.; Wu, J.-R. Fragility assessment of existing low-rise steel moment-resisting frames with masonry infills under mainshock-aftershock earthquake sequences. Bull. Earthq. Eng. 2021, 19, 6. [Google Scholar] [CrossRef]
- Di Sarno, L.; Pugliese, F. Effects of mainshock-aftershock sequences on fragility analysis of RC buildings with ageing. Eng. Struct. 2021, 232, 111837. [Google Scholar] [CrossRef]
- Shafaei, H.; Naderpour, H. Collapse Capacity of Ordinary RC Moment Frames Considering Mainshock-Aftershock Effects. J. Earthq. Eng. 2021. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Varum, H.; Arêde, A. Mainshock-aftershock damage assessment of infilled RC structures. Eng. Struct. 2018, 175, 645–660. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Assessment of the mainshock-aftershock collapse vulnerability of RC structures considering the infills in-plane and out-of-plane behaviour. Procedia Eng. 2017, 199, 619–624. [Google Scholar] [CrossRef]
- Iervolino, I.; Chioccarelli, E.; Suzuki, A. Seismic damage accumulation in multiple mainshock–aftershock sequences. Earthq. Eng. Struct. Dyn. 2020, 49, 10. [Google Scholar] [CrossRef]
- Papadopoulos, A.N.; Bazzurro, P. Exploring probabilistic seismic risk assessment accounting for seismicity clustering and damage accumulation: Part II. Risk analysis. Earthq. Spectra 2021, 37, 386–408. [Google Scholar] [CrossRef]
- Bessason, B.; Bjarnason, J. Seismic vulnerability of low-rise residential buildings based on damage data from three earthquakes (Mw6.5, 6.5 and 6.3). Eng. Struct. 2016, 111, 64–79. [Google Scholar] [CrossRef]
- Bessason, B.; Bjarnason, J.; Rupakhety, R. Statistical modelling of seismic vulnerability of RC, timber and masonry buildings from complete empirical loss data. Eng. Struct. 2020, 209, 109969. [Google Scholar] [CrossRef]
- Gautam, D.; Rupakhety, R. Empirical seismic vulnerability analysis of infrastructure systems in Nepal. Bull. Earthq. Eng. 2021, 19, 6113–6127. [Google Scholar] [CrossRef]
- Gautam, D. Observational fragility functions for residential stone masonry buildings in Nepal. Bull. Earthq. Eng. 2018, 16, 4661–4673. [Google Scholar] [CrossRef]
- Gautam, D.; Rupakhety, R.; Adhikari, R. Empirical fragility functions for Nepali highway bridges affected by the 2015 Gorkha Earthquake. Soil Dyn. Earthq. Eng. 2019, 126, 105778. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Z.; Chen, Z. Mainshock-Integrated Aftershock Vulnerability Assessment of Bridge Structures. Appl. Sci. 2020, 10, 6843. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Risk and resilience assessment of bridges under mainshock and aftershocks incorporating uncertainties. Eng. Struct. 2015, 83, 198–208. [Google Scholar] [CrossRef]
- Gautam, D.; Chaulagain, H. Structural performance and associated lessons to be learned from world earthquakes in Nepal after 25 April 2015 (MW 7.8) Gorkha earthquake. Eng. Fail. Anal. 2016, 68, 222–243. [Google Scholar] [CrossRef]
- Nepal Building Code (NBC) 201. Mandatory Rules of Thumb Reinforced Concrete Buildings with Infills; Department of Urban Development and Building Construction, Government of Nepal: Kathmandu, Nepal, 1994. [Google Scholar]
- Nepal Building Code (NBC) 205. Mandatory Rules of Thumb Reinforced Concrete Buildings without Infills; Department of Urban Development and Building Construction, Government of Nepal: Kathmandu, Nepal, 1994. [Google Scholar]
- Gautam, D.; Rodrigues, H.; Bhetwal, K.K.; Neupane, P.; Sanada, Y. Common structural and construction deficiencies of Nepalese buildings. Innov. Infrastruct. Solutions 2016, 1, 1. [Google Scholar] [CrossRef]
- Adhikari, R.; Rupakhety, R.; Giri, P.; Baruwal, R.; Subedi, R.; Gautam, R.; Gautam, D. Seismic Fragility Analysis of Low-Rise RC Buildings with Brick Infills in High Seismic Region with Alluvial Deposits. Buildings 2022, 12, 72. [Google Scholar] [CrossRef]
- Barbosa, A.R.; Fahnestock, L.A.; Fick, D.R.; Gautam, D.; Soti, R.; Wood, R.; Moaveni, B.; Stavridis, A.; Olsen, M.; Rodrigues, H. Performance of Medium-to-High Rise Reinforced Concrete Frame Buildings with Masonry Infill in the 2015 Gorkha, Nepal, Earthquake. Earthq. Spectra 2017, 33, 197–218. [Google Scholar] [CrossRef]
- Varum, H.; Dumaru, R.; Furtado, A.; Barbosa, A.R.; Gautam, D.; Rodrigues, H. Seismic Performance of Buildings in Nepal After the Gorkha Earthquake. In Impacts and Insights of the Gorkha Earthquake; Gautam, D., Rodrigues, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; Chapter 3; pp. 47–63. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arede, A.; Varum, H. Mechanical properties characterization of different types of masonry infill walls. Front. Struct. Civ. Eng. 2020, 14, 411–434. [Google Scholar] [CrossRef]
- De Risi, M.T.; Furtado, A.; Rodrigues, H.; Melo, J.; Verderame, G.M.; António, A.; Varum, H.; Manfredi, G. Experimental analysis of strengthening solutions for the out-of-plane collapse of masonry infills in RC structures through textile reinforced mortars. Eng. Struct. 2020, 207, 110203. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Out-of-plane behavior of masonry infilled RC frames based on the experimental tests available: A systematic review. Constr. Build. Mater. 2018, 168, 831–848. [Google Scholar] [CrossRef]
- Furtado, A.; Vila-Pouca, N.; Varum, H.; Arêde, A. Study of the Seismic Response on the Infill Masonry Walls of a 15-Storey Reinforced Concrete Structure in Nepal. Buildings 2019, 9, 39. [Google Scholar] [CrossRef]
- Computers and Structures Inc. SAP2000; Computers and Structures Inc.: Berkeley, CA, USA, 2018. [Google Scholar]
- Panagiotakos, T.B.; Fardis, M.N. Seismic Response of Infilled RC Frame Structures. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- IS 1893 (Part 1); Criteria for Earthquake Resistant Design of Structures, Part 1: General Provisions and Buildings). Bureau of Indian Standards: New Delhi, India, 2016.
- Maffei, J.; Comartin, C.D.; Kehoe, B.; Kingsley, G.R.; Lizundia, B. Evaluation of Earthquake-Damaged Concrete and Masonry Wall Buildings. Earthq. Spectra 2000, 16, 263–283. [Google Scholar] [CrossRef]
- Elnashai, A.S.; Di Sarno, L. Fundamentals of Earthquake Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Jalayer, F.; Ebrahimian, H.; Miano, A.; Manfredi, G.; Sezen, H. Analytical fragility assessment using unscaled ground motion records. Earthq. Eng. Struct. Dyn. 2017, 46, 2639–2663. [Google Scholar] [CrossRef]

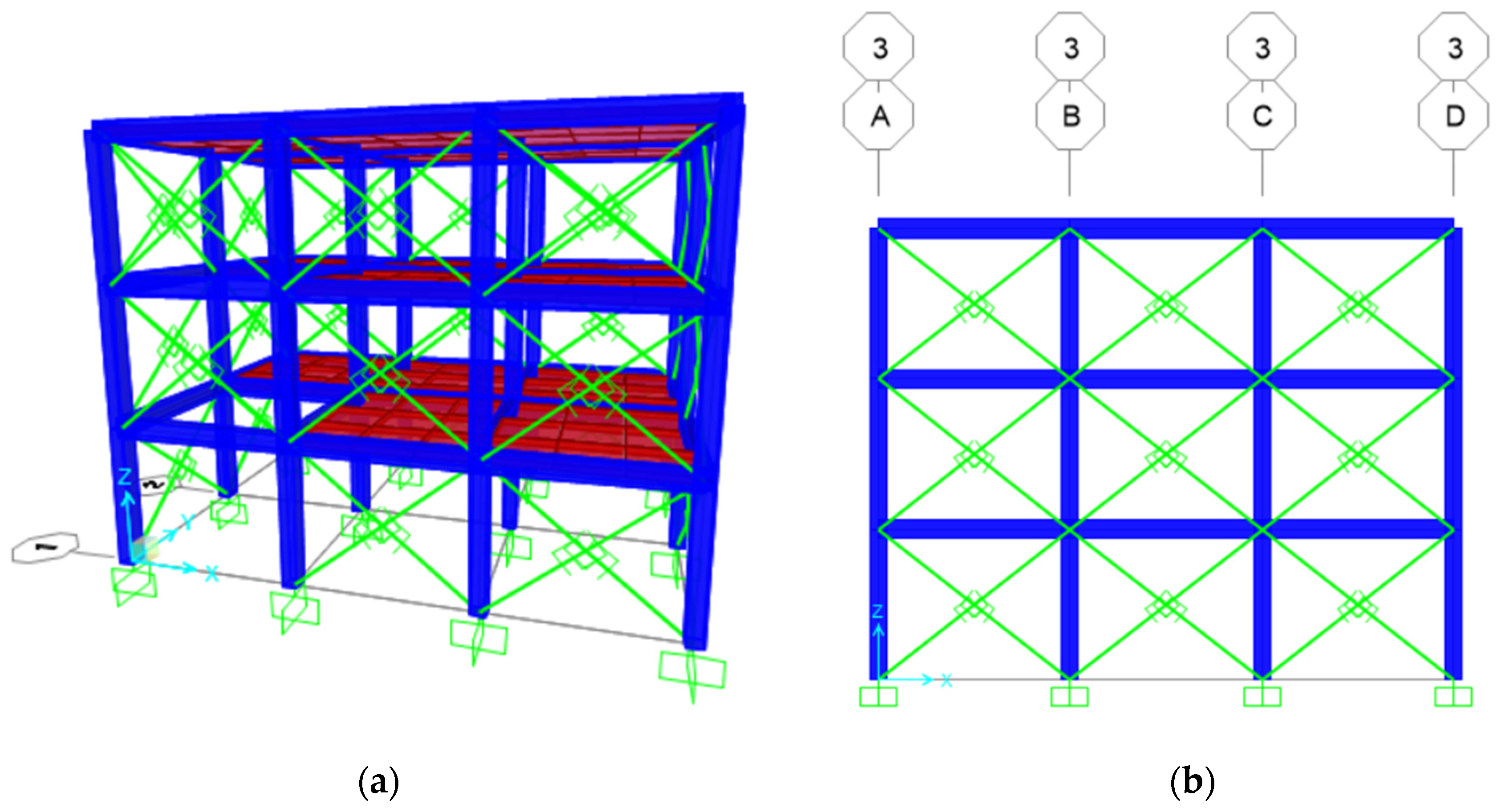
| Component | Description | Details |
|---|---|---|
| Frame | Type | Special moment-resisting frame (SMRF) |
| No. of bays in X-direction | 3 | |
| No. of bays in Y-direction | 2 | |
| Story height | 2.74 m | |
| Total width along x-axis | 10.8 m | |
| Total width along y-axis | 7.3 m | |
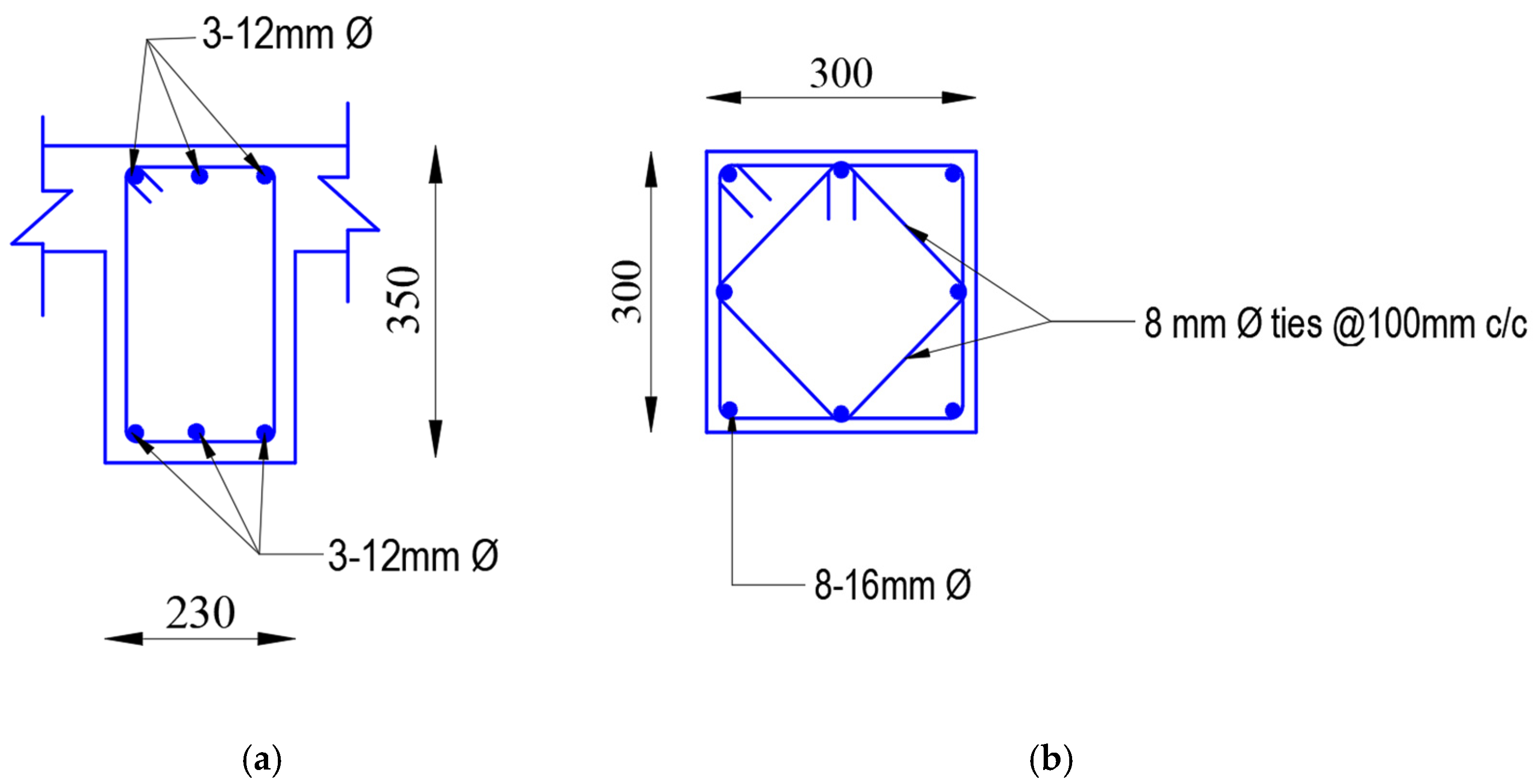
| Beam size | 230 × 350 mm | |
| Column size | 300 × 300 mm | |
| Slab thickness | 125 mm | |
| Plinth area | 78.84 m2 | |
| Load | Live load at floor slab | 2 KN/m2 |
| Live load at roof | 1.5 KN/m2 | |
| Floor finish | 1.0 KN/m2 | |
| Staircase load | 5 KN/m2 | |
| External wall load | 7.844 KN/m | |
| Internal wall load | 5.911 KN/m | |
| Material | Concrete | 20 MPa for all concrete members |
| Rebar | Fe-500 for all RC members | |
| Brickwork | 7.5 MPa bricks in 1:6 cement mortar for 230 mm thick walls |
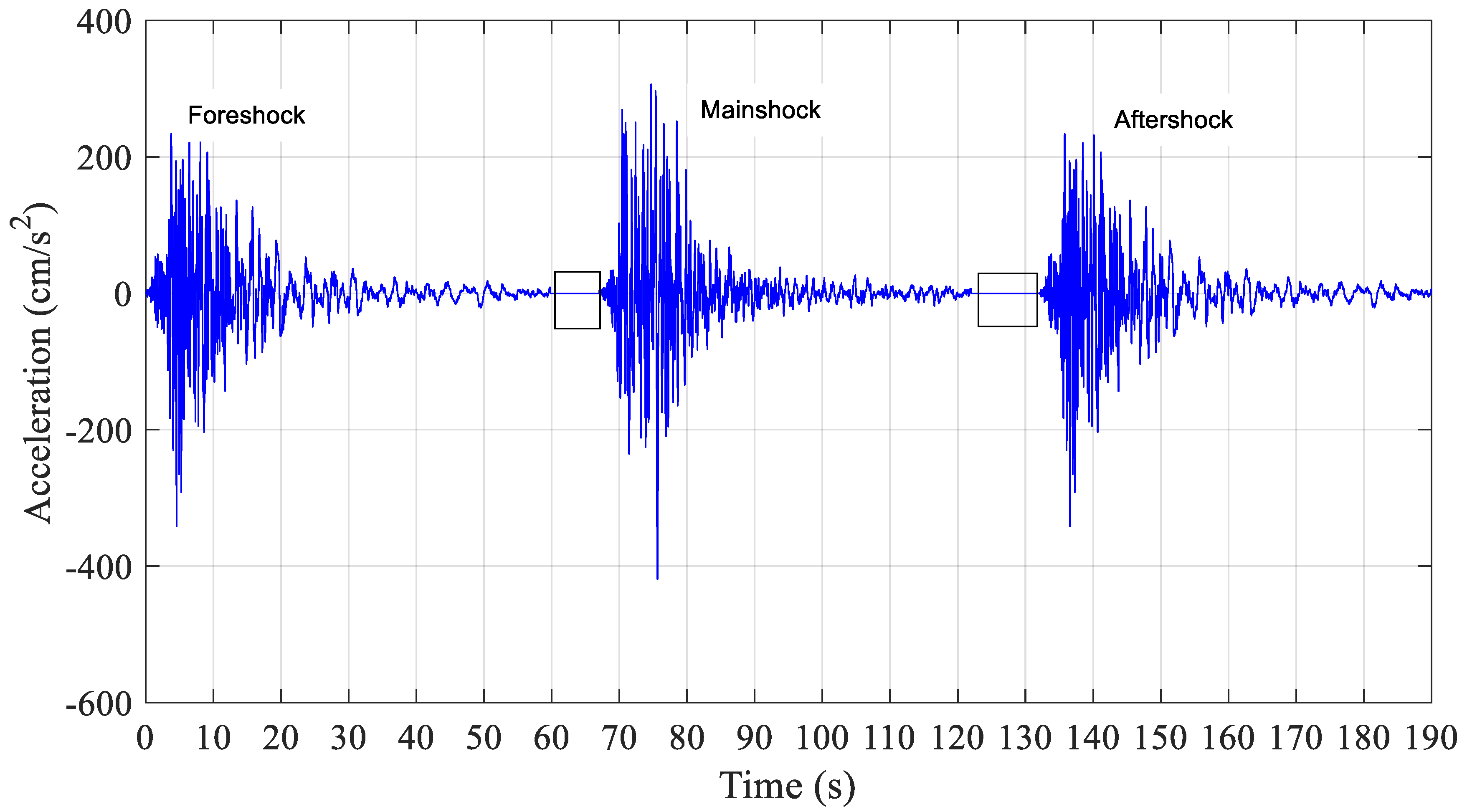
| Earthquake | Station | Date | Event | Magnitude | PGA (g) |
|---|---|---|---|---|---|
| Chalfant Valley | Station: 54428 Chalfant, CA-Zack Bros | 20 July 1986 | Foreshock | 5.9 | 0.23 |
| Station: 54428 Chalfant, CA-Zack Bros | 21 July 1986 | Mainshock | 6.4 | 0.40 | |
| Station: 54171 Bishop, CA-LADWP | 21 July 1986 | Aftershock | 6.4 | 0.17 | |
| Chamoli | Station: IITR gope Gopeshwar, India | 28 March 1999 | Foreshock | 6.6 | 0.19 |
| Station: IITR gope Gopeshwar, India | 28 March 1999 | Mainshock | 6.6 | 0.35 | |
| Station: IITR ukhi Ukhimath, India | 28 March 1999 | Aftershock | 6.6 | 0.09 | |
| Northwest China | Station 19001 Jiashi, China | 6 April 1997 | Foreshock | 5.9 | 0.14 |
| Station: 19001 CBS Jiashi, China | 11 April 1997 | Mainshock | 6.1 | 0.27 | |
| Station: 19001 CBS Jiashi, China | 15 April 1997 | Aftershock | 5.8 | 0.23 | |
| Kozani | Station: ITSAK Chromio Anapsiktirio, Greece | 15 May 1995 | Foreshock | 5.1 | 0.15 |
| Station: ITSAK Kozani, Greece | 13 May 1995 | Mainshock | 6.4 | 0.21 | |
| Station: ITSAK Chromio Anapsiktirio, Greece | 17 May 1995 | Aftershock | 5.3 | 0.12 | |
| Mammoth Lake | Station: 54099 CA-SNARL | 25 May 1980 | Foreshock | 6.0 | 0.18 |
| Station: 54099 CA-SNARL | 25 May 1980 | Mainshock | 6.1 | 0.40 | |
| Station: 54099 CA-SNARL | 25 May 1980 | Aftershock | 5.7 | 0.34 | |
| Northridge | Station: 5303 CA- White Oak Covenant Church | 17 January 1994 | Foreshock | 6.7 | 0.36 |
| Station: 5303 CA- White Oak Covenant Church | 17 January 1994 | Mainshock | 6.7 | 0.47 | |
| Station: 5353 Canoga Park CA | 17 January 1994 | Aftershock | 6.7 | 0.41 | |
| Uttarkashi | Station: ghan Ghansiali, India | 19 October 1991 | Foreshock | 7 | 0.11 |
| Station: utta Uttarkashi India | 19 October 1991 | Mainshock | 7 | 0.30 | |
| Station: bhat Bhatwari, India | 19 October 1991 | Aftershock | 7 | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahat, P.; Pradhan, P.; Adhikari, R.; Furtado, A.; Gautam, D.; Rupakhety, R. Seismic Sequence Vulnerability of Low-Rise Special Moment-Resisting Frame Buildings with Brick Infills. Appl. Sci. 2022, 12, 8231. https://doi.org/10.3390/app12168231
Mahat P, Pradhan P, Adhikari R, Furtado A, Gautam D, Rupakhety R. Seismic Sequence Vulnerability of Low-Rise Special Moment-Resisting Frame Buildings with Brick Infills. Applied Sciences. 2022; 12(16):8231. https://doi.org/10.3390/app12168231
Chicago/Turabian StyleMahat, Pushpa, Piyush Pradhan, Rabindra Adhikari, Andre Furtado, Dipendra Gautam, and Rajesh Rupakhety. 2022. "Seismic Sequence Vulnerability of Low-Rise Special Moment-Resisting Frame Buildings with Brick Infills" Applied Sciences 12, no. 16: 8231. https://doi.org/10.3390/app12168231
APA StyleMahat, P., Pradhan, P., Adhikari, R., Furtado, A., Gautam, D., & Rupakhety, R. (2022). Seismic Sequence Vulnerability of Low-Rise Special Moment-Resisting Frame Buildings with Brick Infills. Applied Sciences, 12(16), 8231. https://doi.org/10.3390/app12168231









