PK-APF: Path-Keeping Algorithm for USVs Based on Artificial Potential Field
Abstract
:1. Introduction
- Traditional APF influences the navigation of USVs through attractive and repulsive forces whereas USVs stop when the attractive and repulsive forces are equal in magnitude and opposite in direction, and the resultant force on USVs is zero—that is, when it falls into a local minimum point;
- Traditional APF only focuses on USVs heading to the goal point and ignores the influences of obstacles and wind on the original planned path, thus, it fails to achieve high-precision path-keeping.
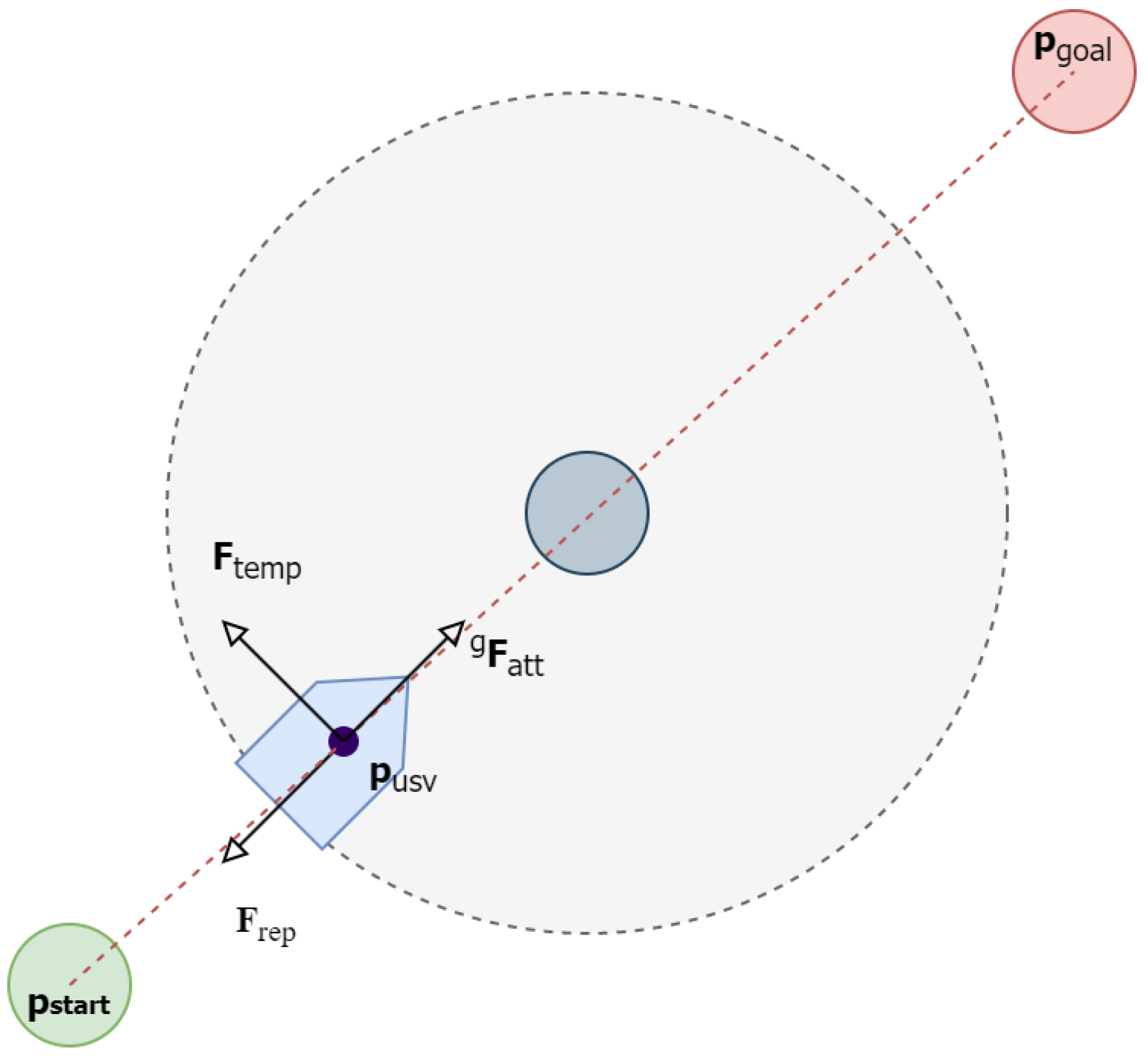
- The idea of temporal force is proposed for USVs to escape from local minimum point and continue the navigation;
- The idea of virtual foot points is proposed to reduce the path deviation between the actual path and the planned path caused by the negative influence of obstacle avoidance, wind, and water waves in the process of autonomous navigation.
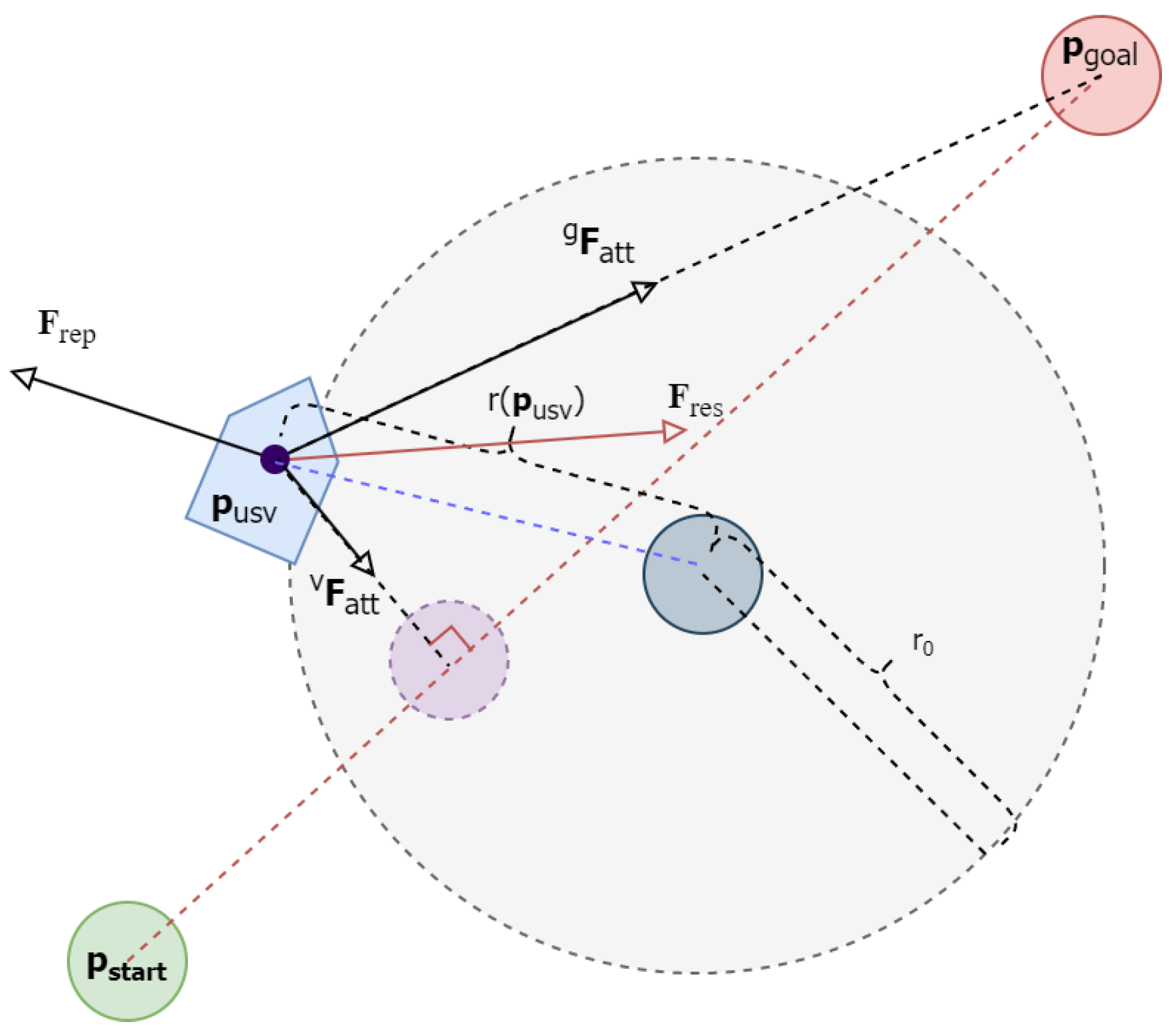
2. PK-APF Methodology
2.1. PK-APF Formulation
2.2. Virtual Attractive Force
2.3. Temporal Force
3. Experiments
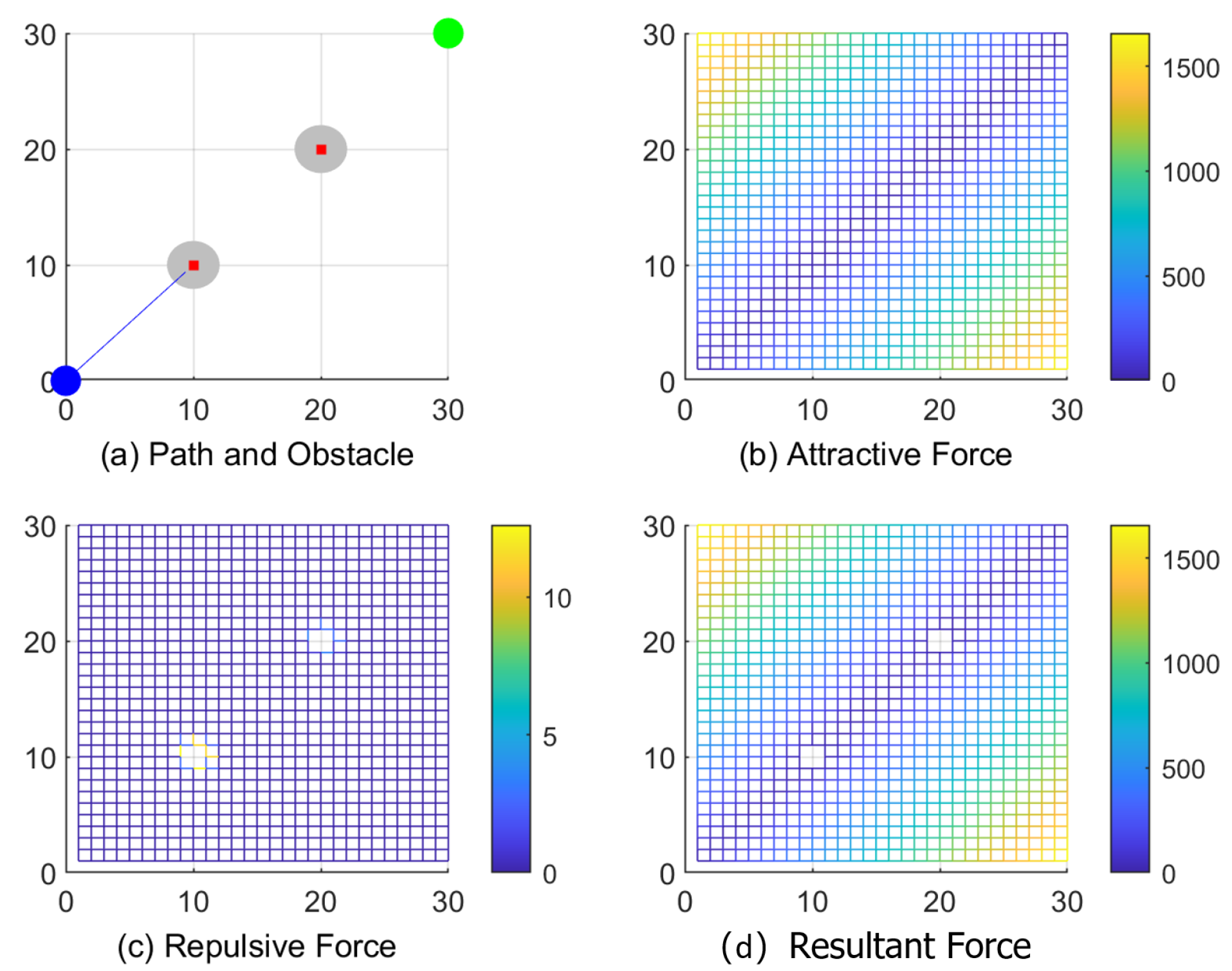
3.1. MATLAB Implementation
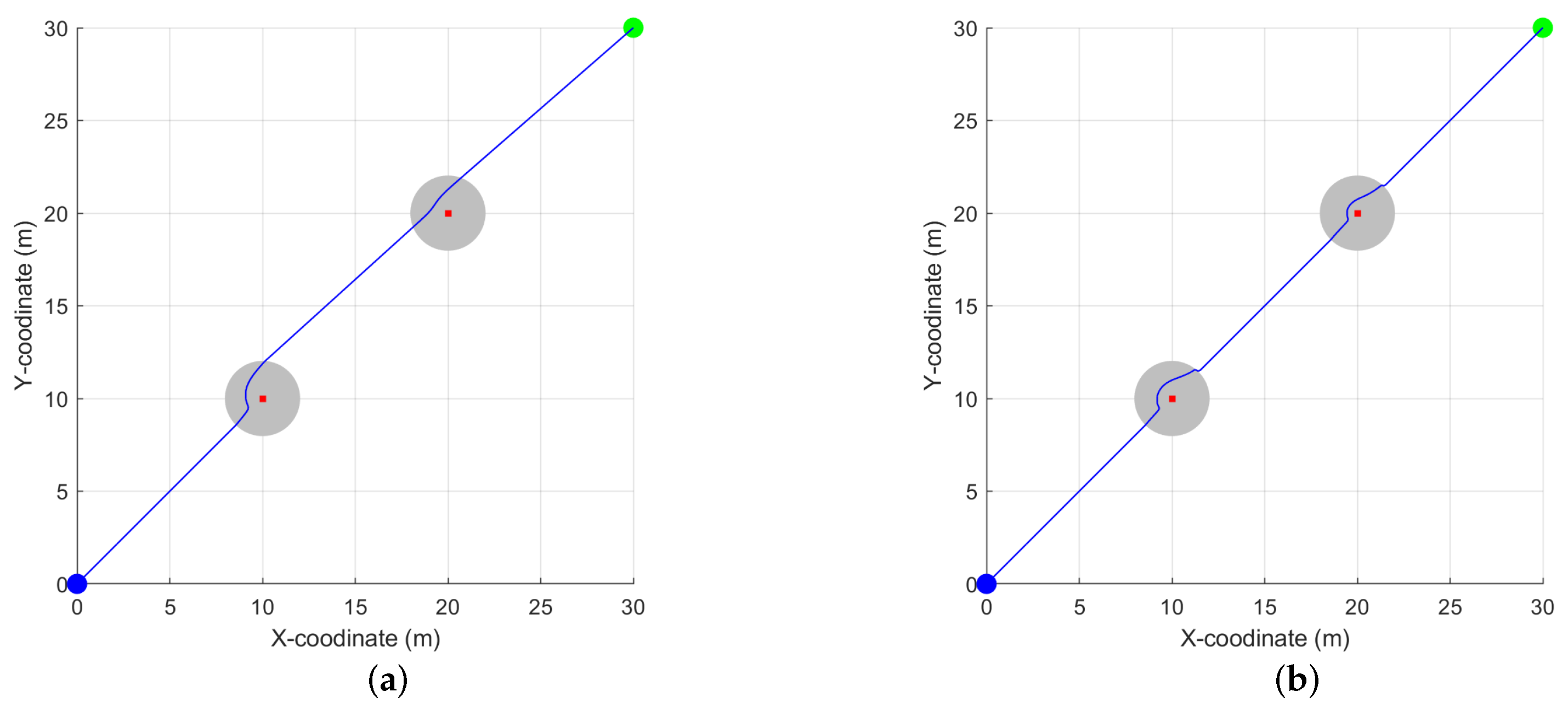
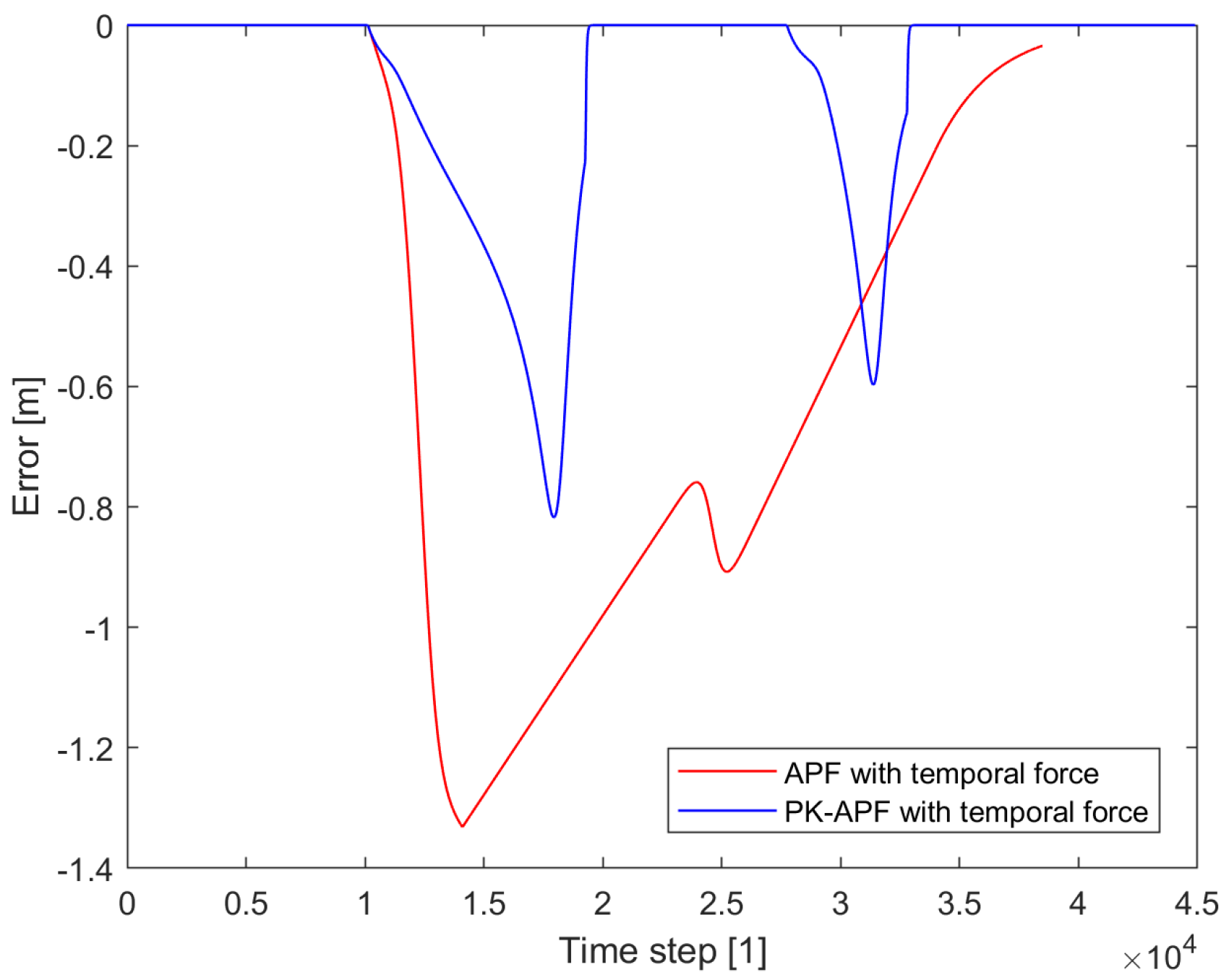
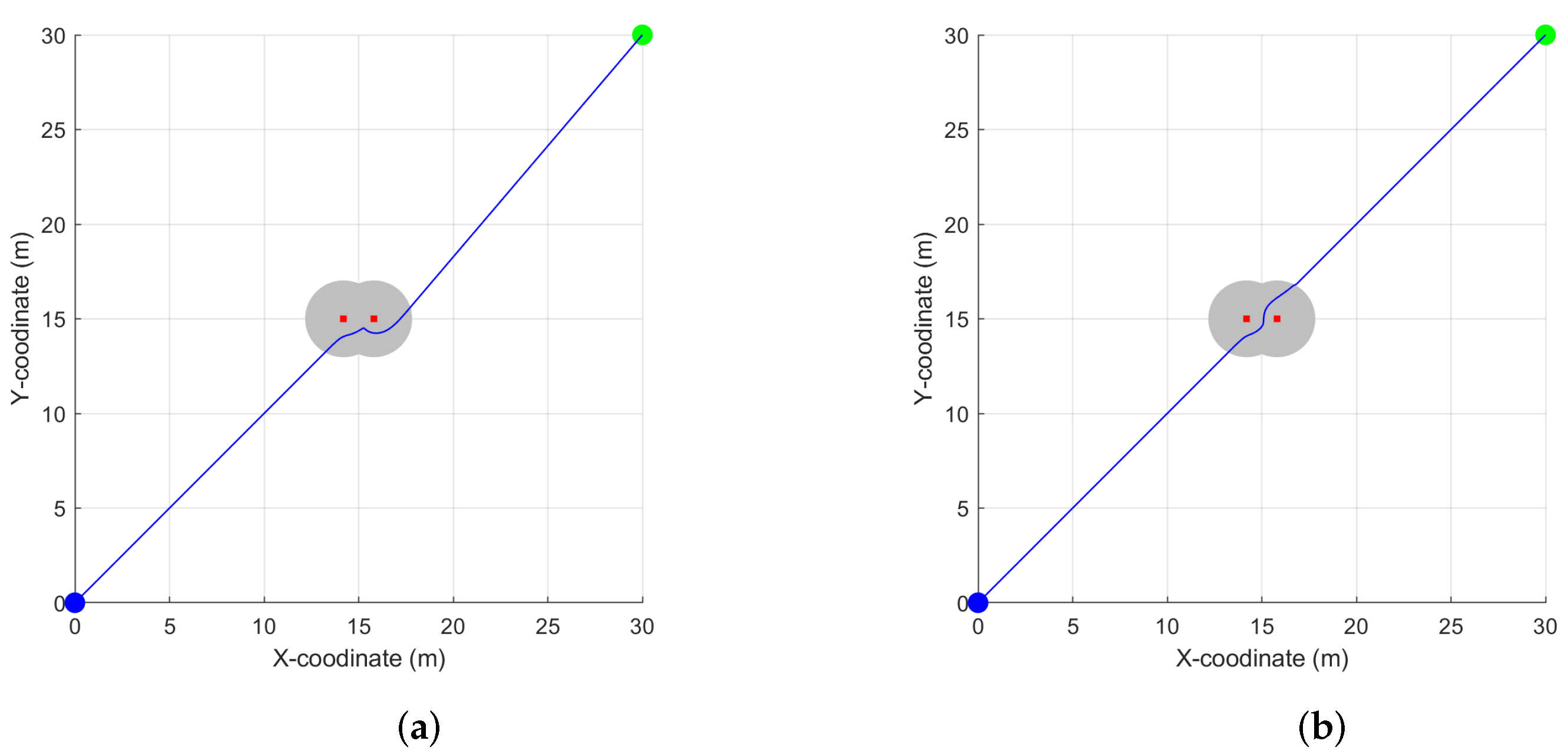
3.1.1. Path Planning with Local Minimum Point
3.1.2. Path Planning in Narrow Corridor
3.1.3. Path Planning with Multiple Obstacles
3.1.4. Conclusion of MATLAB Simulation
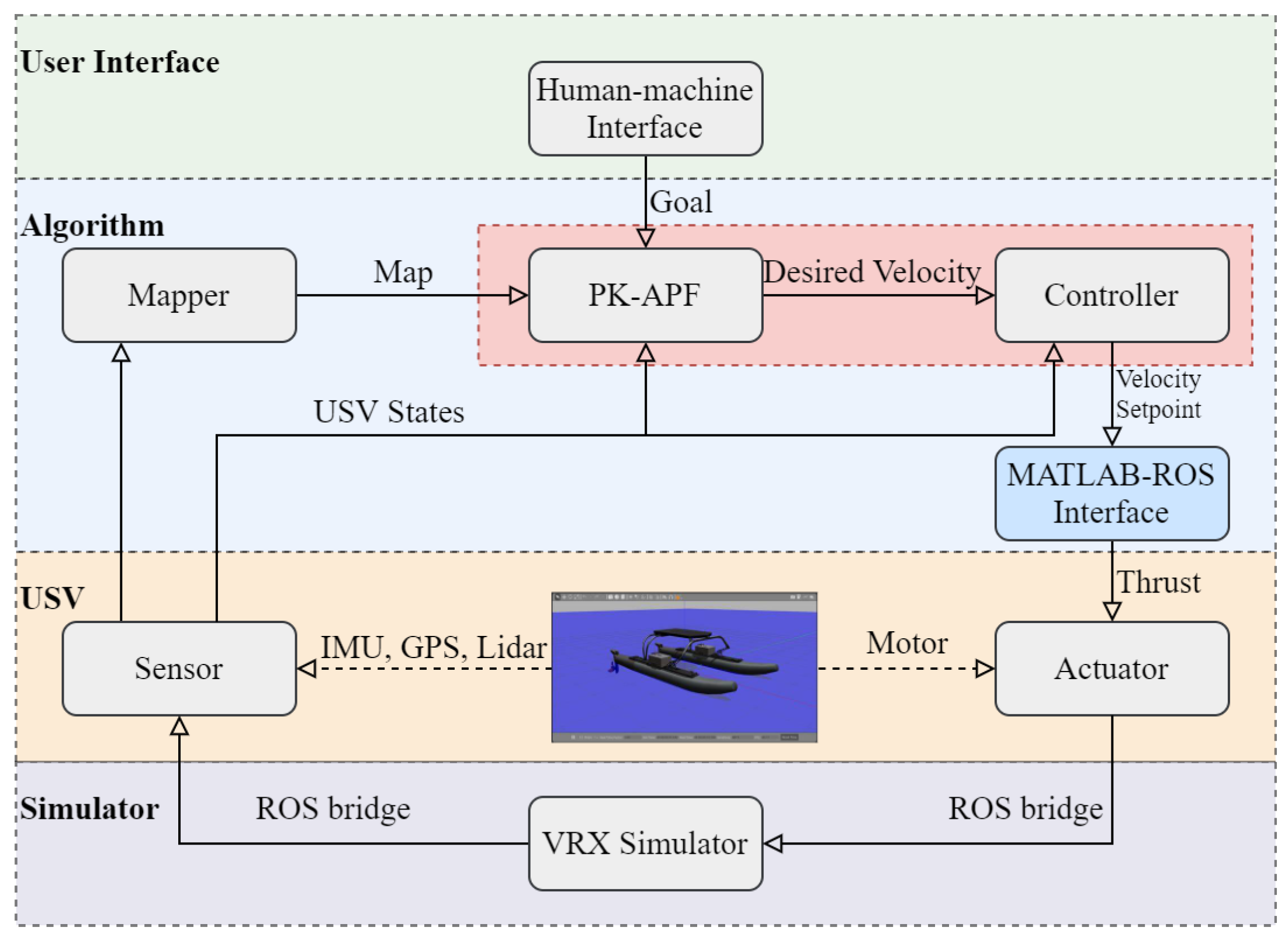
3.2. High-Fidelity ROS Simulation
3.2.1. Virtual RobotX
- Comprehensive wave model to disturb USVs’ motion;
- Stochastic wind representation to disturb USVs’ motion;
- Six degree-of-freedom model for USVs with configurable actuators.
3.2.2. Simulation Parameters and Methods
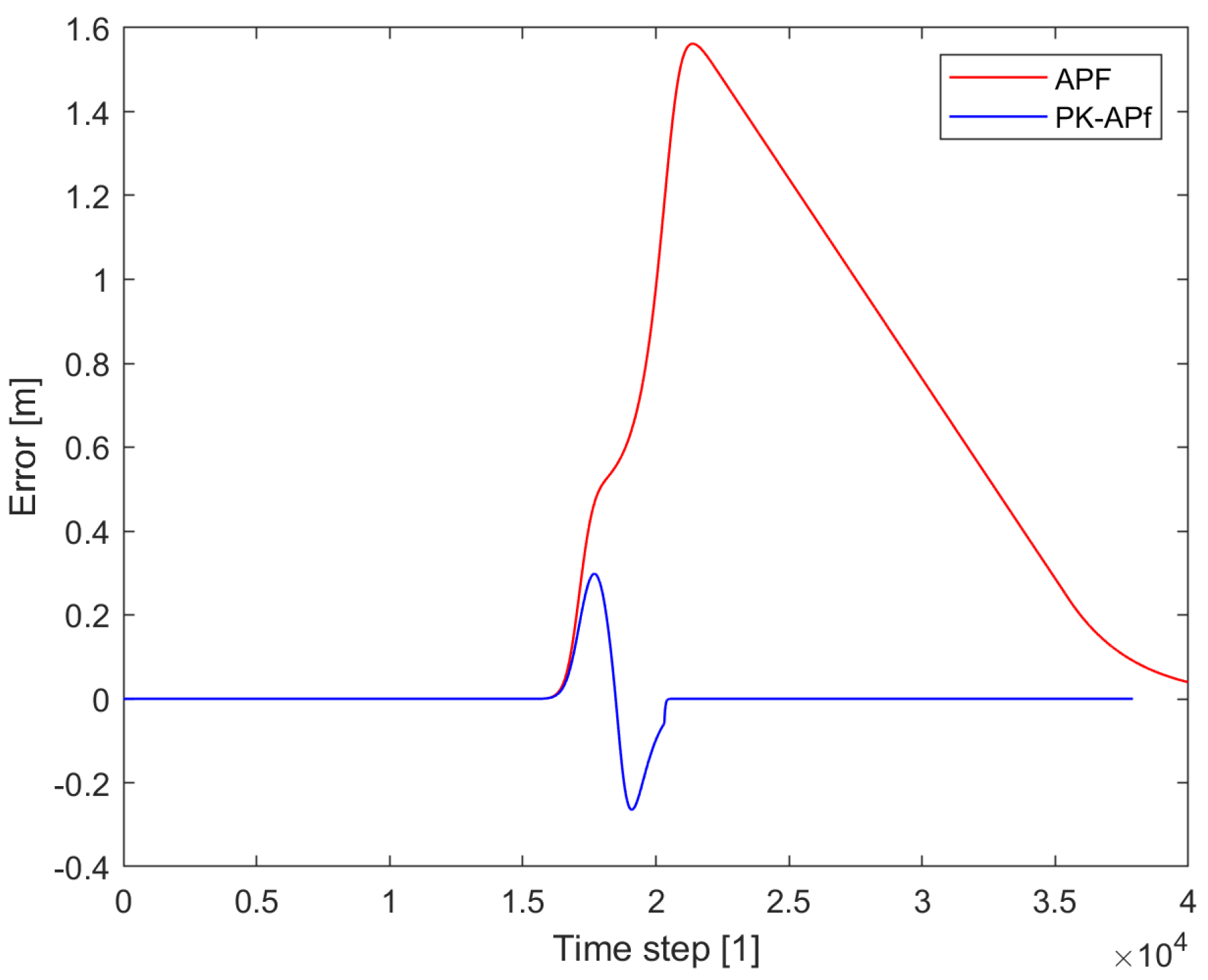
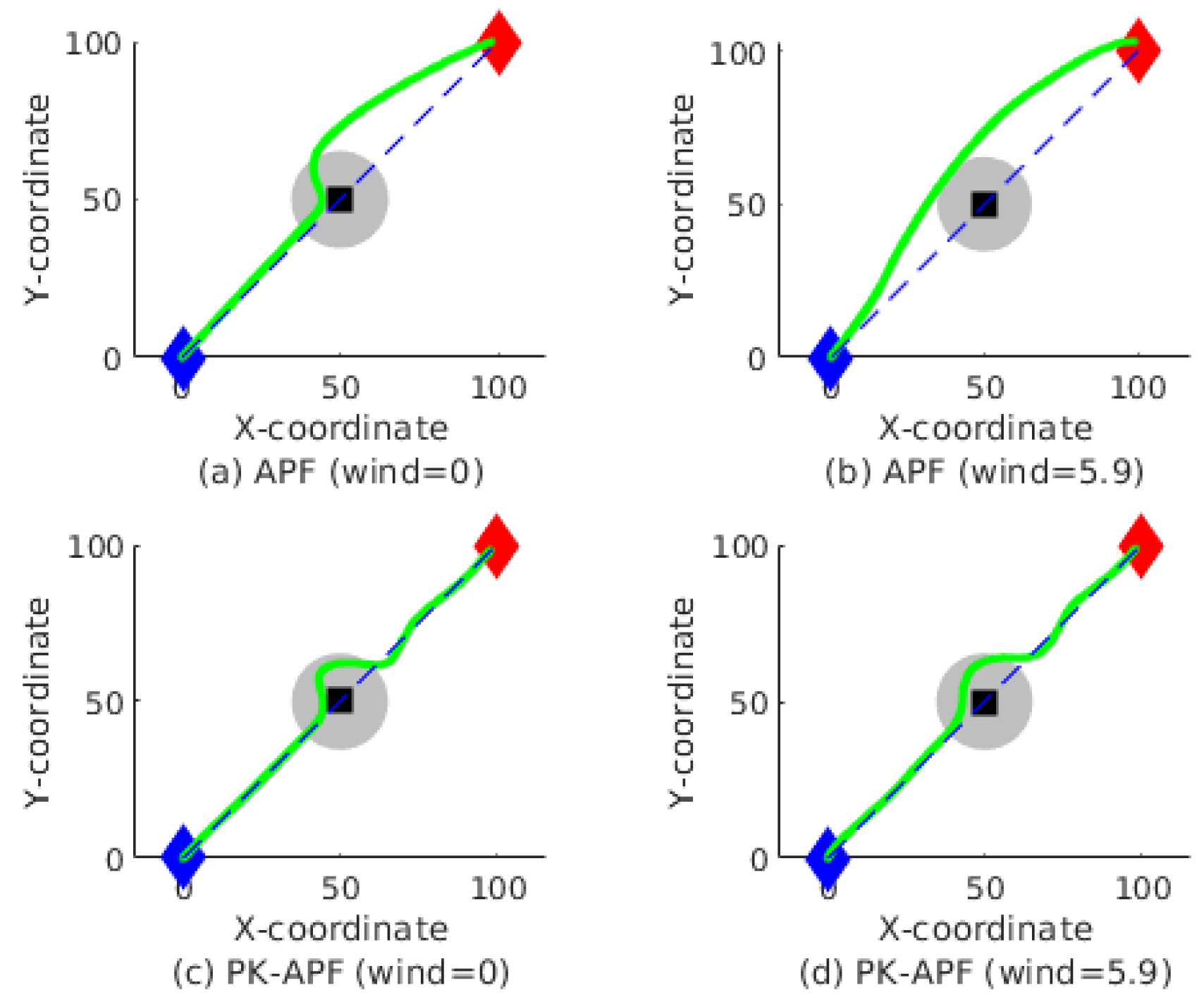
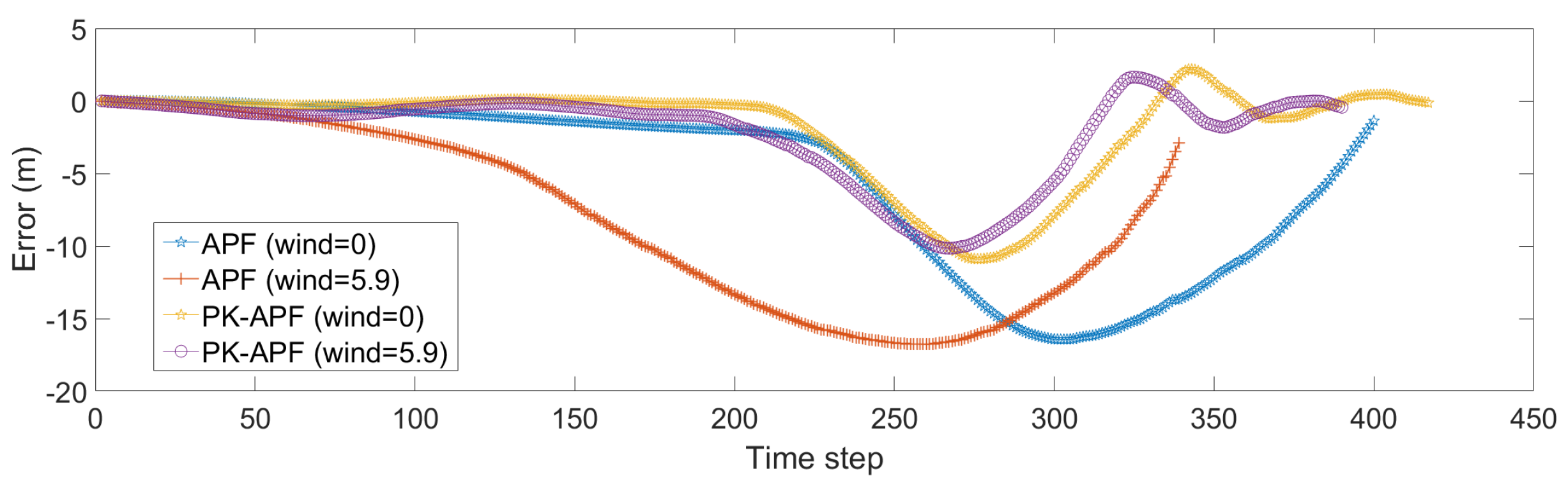
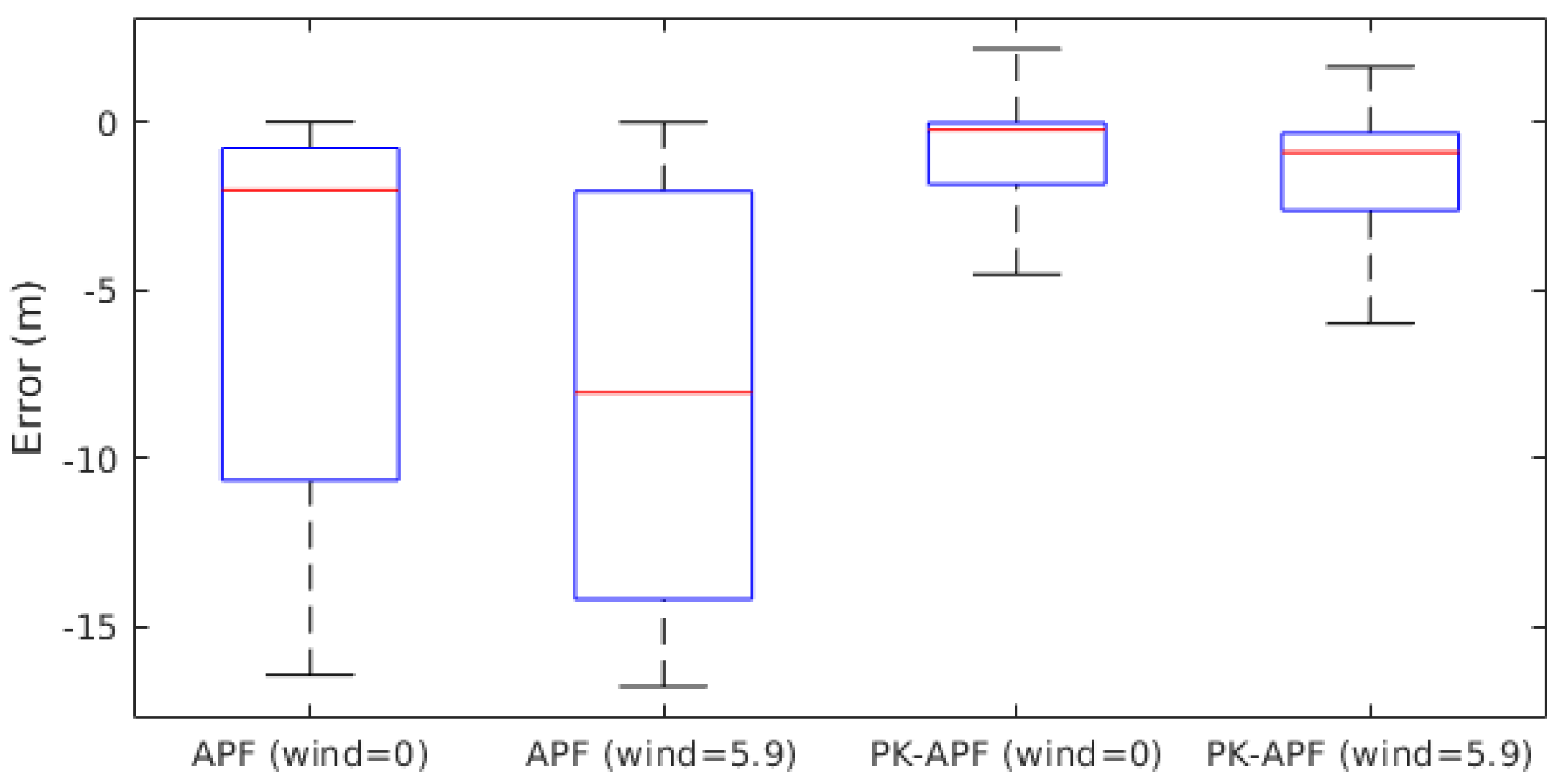
3.2.3. Simulation Result and Discussion
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| USVs | Unmanned surface vehicles |
| PK-APF | Path-keeping artificial potential field |
| APF | Artificial potential field |
| VRX | Virtual RobotX |
| ROS | Robot operating system |
| LPA* | Lifelong planning A* |
| CNN | Convolutional Neural Network |
| MATLAB | Matrix Laboratory |
| PID | Proportion–Integration–Differentiation |
| A* | A Star |
| D* | D Star |
References
- Manley, J.E. Unmanned surface vehicles, 15 years of development. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–4. [Google Scholar]
- Mahacek, P.; Berk, T.; Casanova, A.; Kitts, C.; Kirkwood, W.; Wheat, G. Development and initial testing of a swath boat for shallow-water bathymetry. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–6. [Google Scholar]
- Mousazadeh, H.; Jafarbiglu, H.; Abdolmaleki, H.; Omrani, E.; Monhaseri, F.; Abdollahzadeh, M.R.; Mohammadi-Aghdam, A.; Kiapei, A.; Salmani-Zakaria, Y.; Makhsoos, A. Developing a navigation, guidance and obstacle avoidance algorithm for an Unmanned Surface Vehicle (USV) by algorithms fusion. Ocean Eng. 2018, 159, 56–65. [Google Scholar] [CrossRef]
- Han, J.; Park, J.; Kim, T.; Kim, J. Precision navigation and mapping under bridges with an unmanned surface vehicle. Auton. Robots 2015, 38, 349–362. [Google Scholar] [CrossRef]
- Zhu, X.; Yue, Y.; Wong, P.W.; Zhang, Y.; Ding, H. Designing an optimized water quality monitoring network with reserved monitoring locations. Water 2019, 11, 713. [Google Scholar] [CrossRef]
- Xiao, C.; Zhong, L.; Jianqiang, Z.; Dechao, Z.; Jiao, D. Adaptive sliding-mode path following control system of the underactuated USV under the influence of ocean currents. J. Syst. Eng. Electron. 2018, 29, 1271–1283. [Google Scholar] [CrossRef]
- Shu-Xi, W. The improved dijkstra’s shortest path algorithm and its application. Procedia Eng. 2012, 29, 1186–1190. [Google Scholar] [CrossRef]
- Duchoň, F.; Babinec, A.; Kajan, M.; Beňo, P.; Florek, M.; Fico, T.; Jurišica, L. Path planning with modified a star algorithm for a mobile robot. Procedia Eng. 2014, 96, 59–69. [Google Scholar] [CrossRef]
- Ammar, A.; Bennaceur, H.; Châari, I.; Koubâa, A.; Alajlan, M. Relaxed Dijkstra and A* with linear complexity for robot path planning problems in large-scale grid environments. Soft Comput. 2016, 20, 4149–4171. [Google Scholar] [CrossRef]
- Stentz, A. Optimal and efficient path planning for partially-known environments. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; Volume 4, pp. 3310–3317. [Google Scholar] [CrossRef]
- Zhu, X.; Yue, Y.; Ding, H.; Wu, S.; Li, M.; Hu, Y. An Improved APFM for Autonomous Navigation and Obstacle Avoidance of USVs. In Proceedings of the ICINCO (2), Prague, Czech Republic, 29–31 July 2019; pp. 401–408. [Google Scholar]
- Koenig, S.; Likhachev, M.; Furcy, D. Lifelong planning A*. Artif. Intell. 2004, 155, 93–146. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. D^* lite. AAAI/IAAI 2002, 15, 476–483. [Google Scholar]
- Oral, T.; Polat, F. A multi-objective incremental path planning algorithm for mobile agents. In Proceedings of the 2012 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology, Washington, DC, USA, 4–7 December 2012; Volume 2, pp. 401–408. [Google Scholar]
- Xia, G.; Han, Z.; Zhao, B.; Wang, X. Local path planning for unmanned surface vehicle collision avoidance based on modified quantum particle swarm optimization. Complexity 2020, 2020, 3095426. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Autonomous Robot Vehicles; Springer: Berlin/Heidelberg, Germany, 1986; pp. 396–404. [Google Scholar]
- Yang, Y.; Wang, S.; Wu, Z.; Wang, Y. Motion planning for multi-HUG formation in an environment with obstacles. Ocean Eng. 2011, 38, 2262–2269. [Google Scholar] [CrossRef]
- Pan, W.W.; Jiang, D.P.; Pang, Y.J.; Li, Y.M.; Zhang, Q. A multi-AUV formation algorithm combining artificial potential field and virtual structure. Acta Armamentarii 2017, 38, 326. [Google Scholar]
- Sang, H.; You, Y.; Sun, X.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Chen, Y.; Bai, G.; Zhan, Y.; Hu, X.; Liu, J. Path planning and obstacle avoiding of the USV based on improved ACO-APF hybrid algorithm with adaptive early-warning. IEEE Access 2021, 9, 40728–40742. [Google Scholar] [CrossRef]
- Wang, N.; Xu, H.; Li, C.; Yin, J. Hierarchical path planning of unmanned surface vehicles: A fuzzy artificial potential field approach. Int. J. Fuzzy Syst. 2021, 23, 1797–1808. [Google Scholar] [CrossRef]
- Diab, M.K.; Ammar, H.H.; Shalaby, R.E. Self-Driving Car Lane-keeping Assist using PID and Pure Pursuit Control. In Proceedings of the 2020 International Conference on Innovation and Intelligence for Informatics, Computing and Technologies (3ICT), Sakheer, Bahrain, 20–21 December 2020; pp. 1–6. [Google Scholar]
- Kuo, C.; Lu, Y.; Yang, S. On the image sensor processing for lane detection and control in vehicle lane keeping systems. Sensors 2019, 19, 1665. [Google Scholar] [CrossRef] [PubMed]
- Nose, Y.; Kojima, A.; Kawabata, H.; Hironaka, T. A study on a lane keeping system using CNN for online learning of steering control from real time images. In Proceedings of the 2019 34th International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), Jeju, Korea, 23–26 June 2019; pp. 1–4. [Google Scholar]
- Bingham, B.; Aguero, C.; McCarrin, M.; Klamo, J.; Malia, J.; Allen, K.; Lum, T.; Rawson, M.; Waqar, R. Toward Maritime Robotic Simulation in Gazebo. In Proceedings of the MTS/IEEE OCEANS Conference, Seattle, WA, USA, 27–31 October 2019. [Google Scholar]



| Variable | Value | Variable | Value | |
|---|---|---|---|---|
| [m] | 2.0 | [1] | 0.03 | |
| Planner | [1] | 8.0 | [1] | 70 |
| [1] | 3.0 | [1] | 4 | |
| Conditions | Start [m m] | [0 0] | Goal [m m] | [30 30] |
| MATLAB Scenario | # of Sampling Points | # of 0.5-Error Points | PK Precision | |
|---|---|---|---|---|
| In local minimum point | APF | 38,480 | 20,048 | 52% |
| PK-APF | 44,895 | 41,867 | 93% | |
| In narrow corridor | APF | 37,920 | 23,052 | 61% |
| PK-APF | 37,919 | 37,919 | 100% | |
| In multiple obstacles | APF | 37,920 | 25,021 | 66% |
| PK-APF | 37,920 | 33,390 | 88% |
| Variable | Value | Variable | Value | |
|---|---|---|---|---|
| wave_gain [1] | 0.1 | wind_mean_vel [m/s] | 0, 5.9 | |
| wave_period [s] | 5.0 | wind_direction [deg] | 135 | |
| Simulator | wave_angle [deg] | 0.4 | wind_std [m/s] | 1.5 |
| wave_dx [m] | 1.0 | Obstacle [m m] | [50 50] | |
| wave_dy [m] | 0.0 | |||
| [m] | 15 | [1] | 0.9 | |
| Planner | [1] | 1.8 | [1] | 1.4 |
| [1] | 1.8 | [1] | 0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, Y.; Wu, Z.; Yue, Y.; Zhu, X.; Lim, E.G.; Paoletti, P. PK-APF: Path-Keeping Algorithm for USVs Based on Artificial Potential Field. Appl. Sci. 2022, 12, 8201. https://doi.org/10.3390/app12168201
Chu Y, Wu Z, Yue Y, Zhu X, Lim EG, Paoletti P. PK-APF: Path-Keeping Algorithm for USVs Based on Artificial Potential Field. Applied Sciences. 2022; 12(16):8201. https://doi.org/10.3390/app12168201
Chicago/Turabian StyleChu, Yijie, Ziniu Wu, Yong Yue, Xiaohui Zhu, Eng Gee Lim, and Paolo Paoletti. 2022. "PK-APF: Path-Keeping Algorithm for USVs Based on Artificial Potential Field" Applied Sciences 12, no. 16: 8201. https://doi.org/10.3390/app12168201
APA StyleChu, Y., Wu, Z., Yue, Y., Zhu, X., Lim, E. G., & Paoletti, P. (2022). PK-APF: Path-Keeping Algorithm for USVs Based on Artificial Potential Field. Applied Sciences, 12(16), 8201. https://doi.org/10.3390/app12168201










