A Modal Frequency Estimation Method of Non-Stationary Signal under Mass Time-Varying Condition Based on EMD Algorithm
Abstract
:1. Introduction
2. Theory of EMD and EEMD
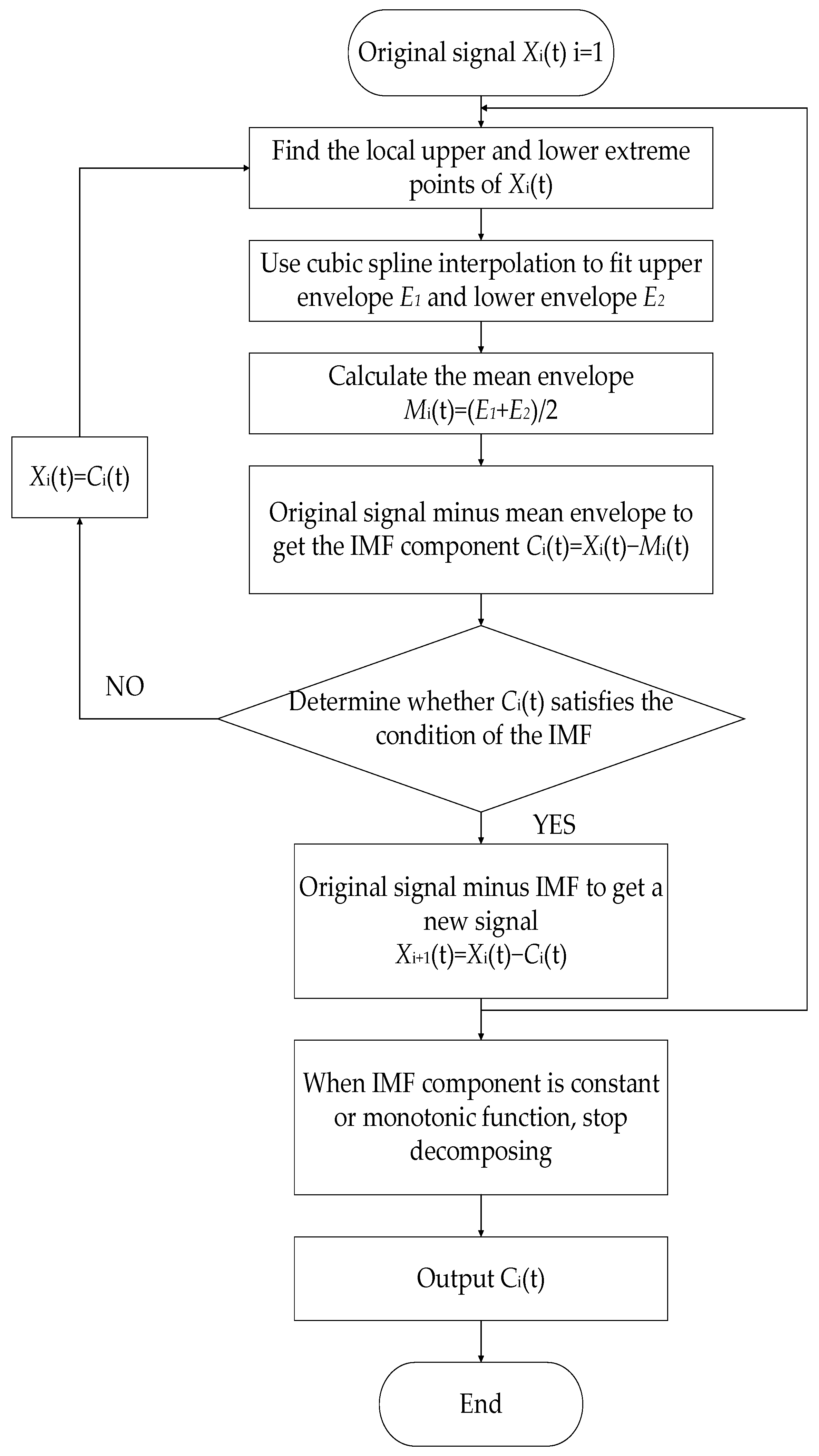
2.1. EMD Method
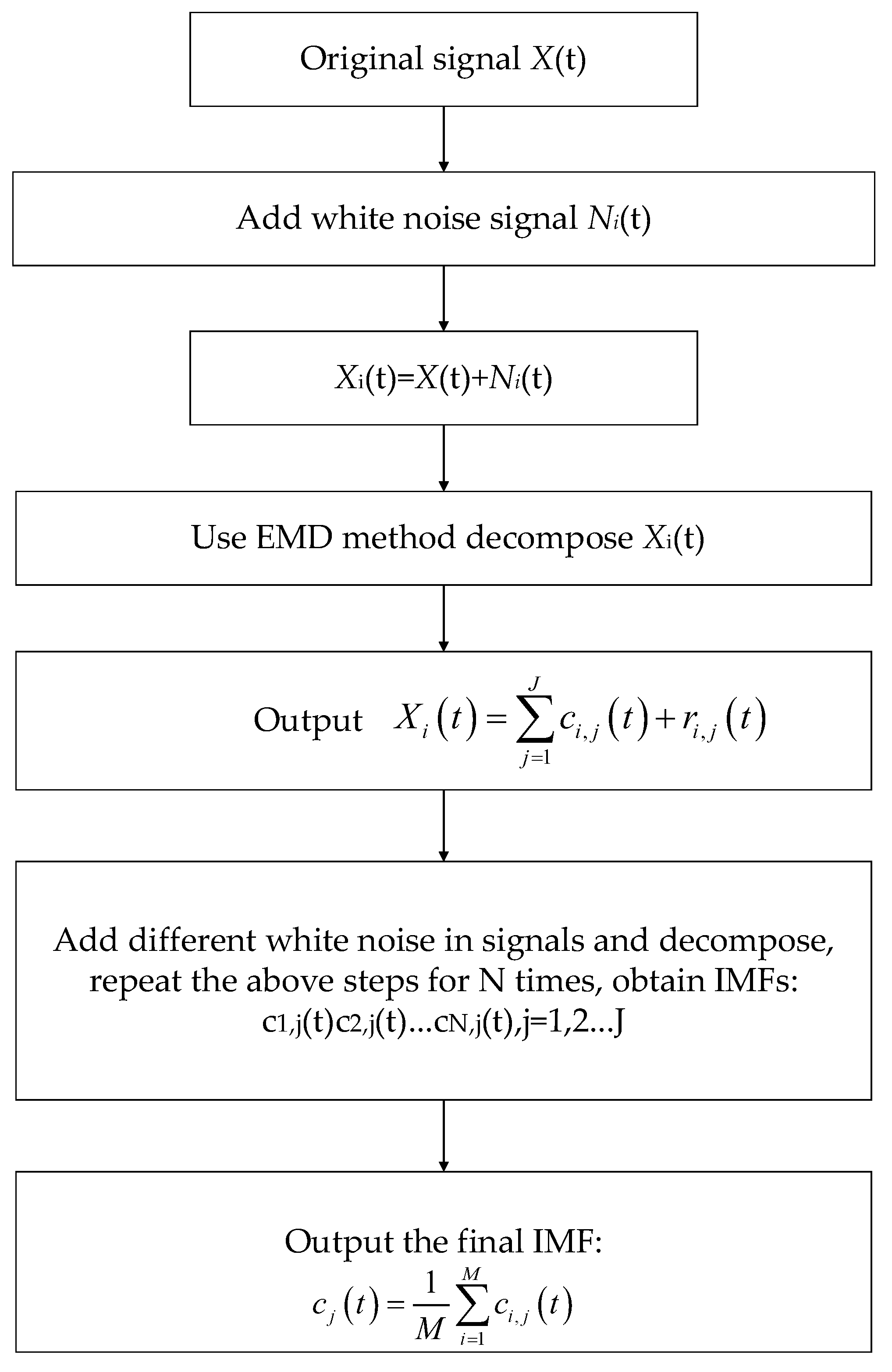
2.2. EEMD Method
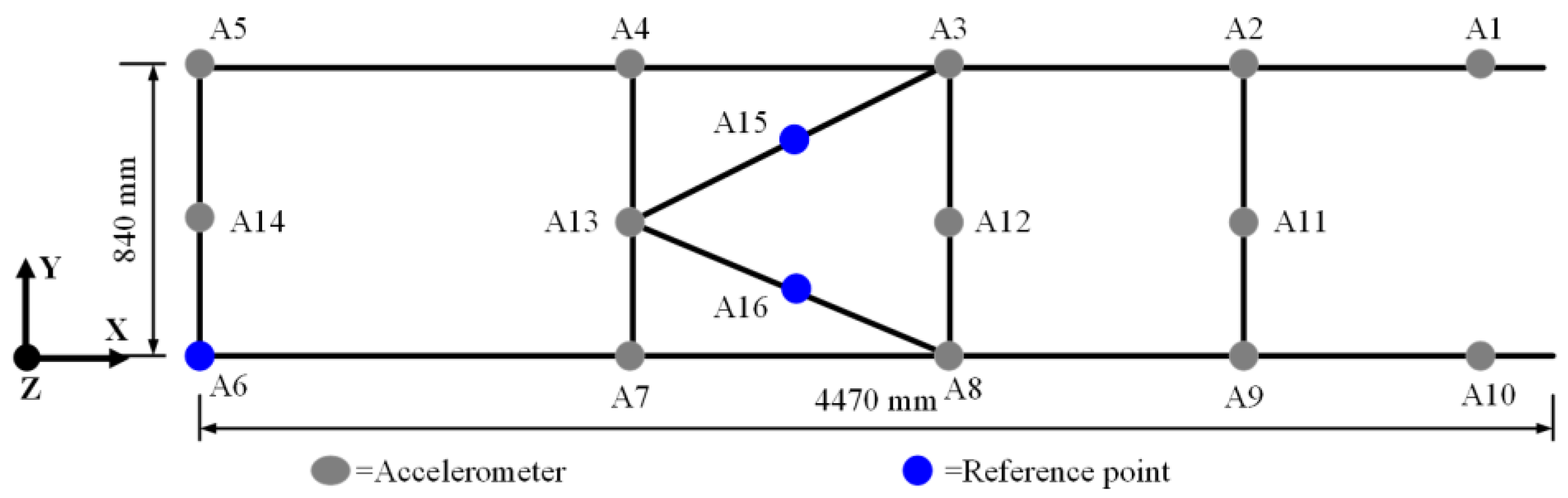
3. Operating Modal Analysis Experiment
4. Vibration Signal Analysis
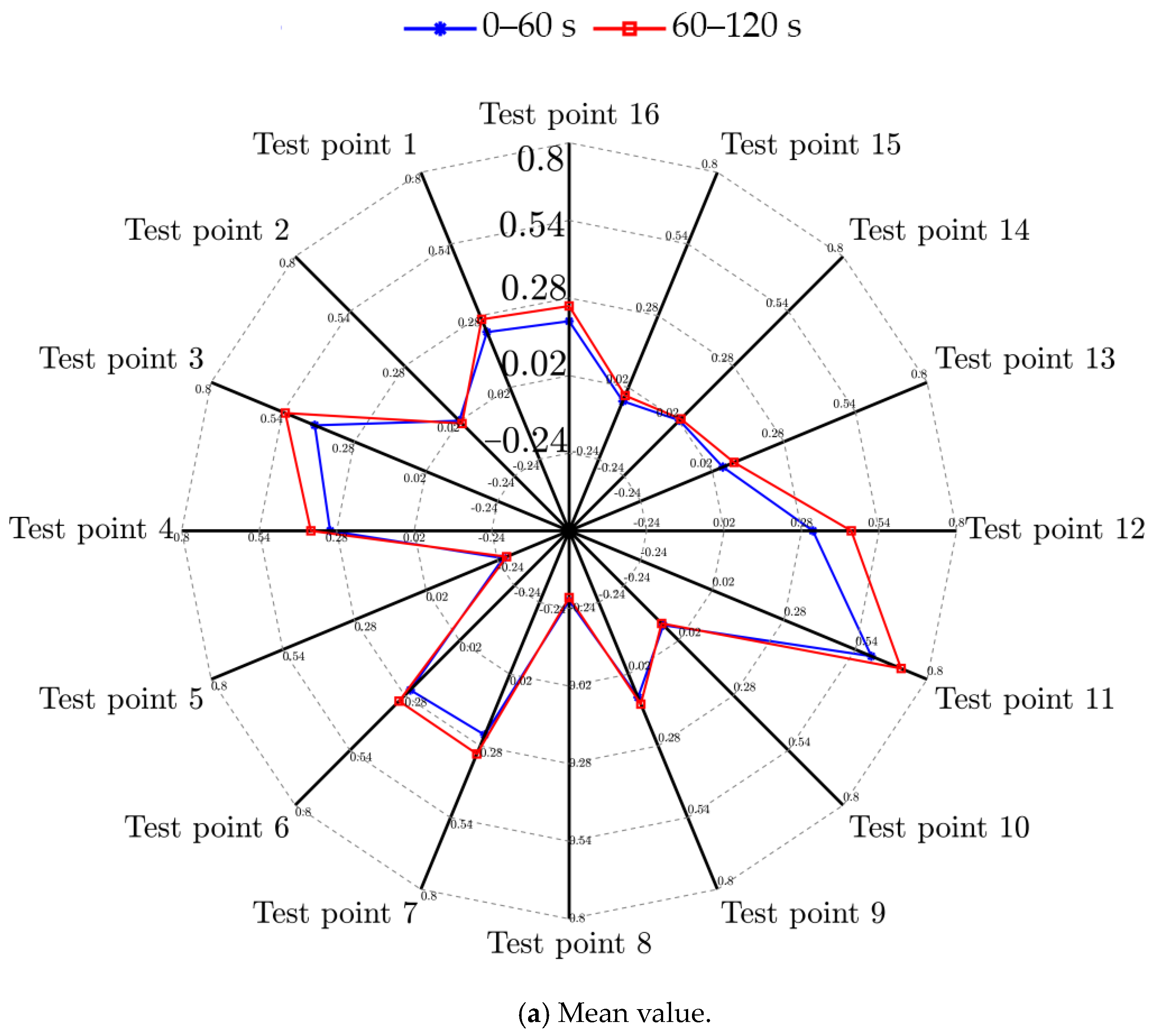
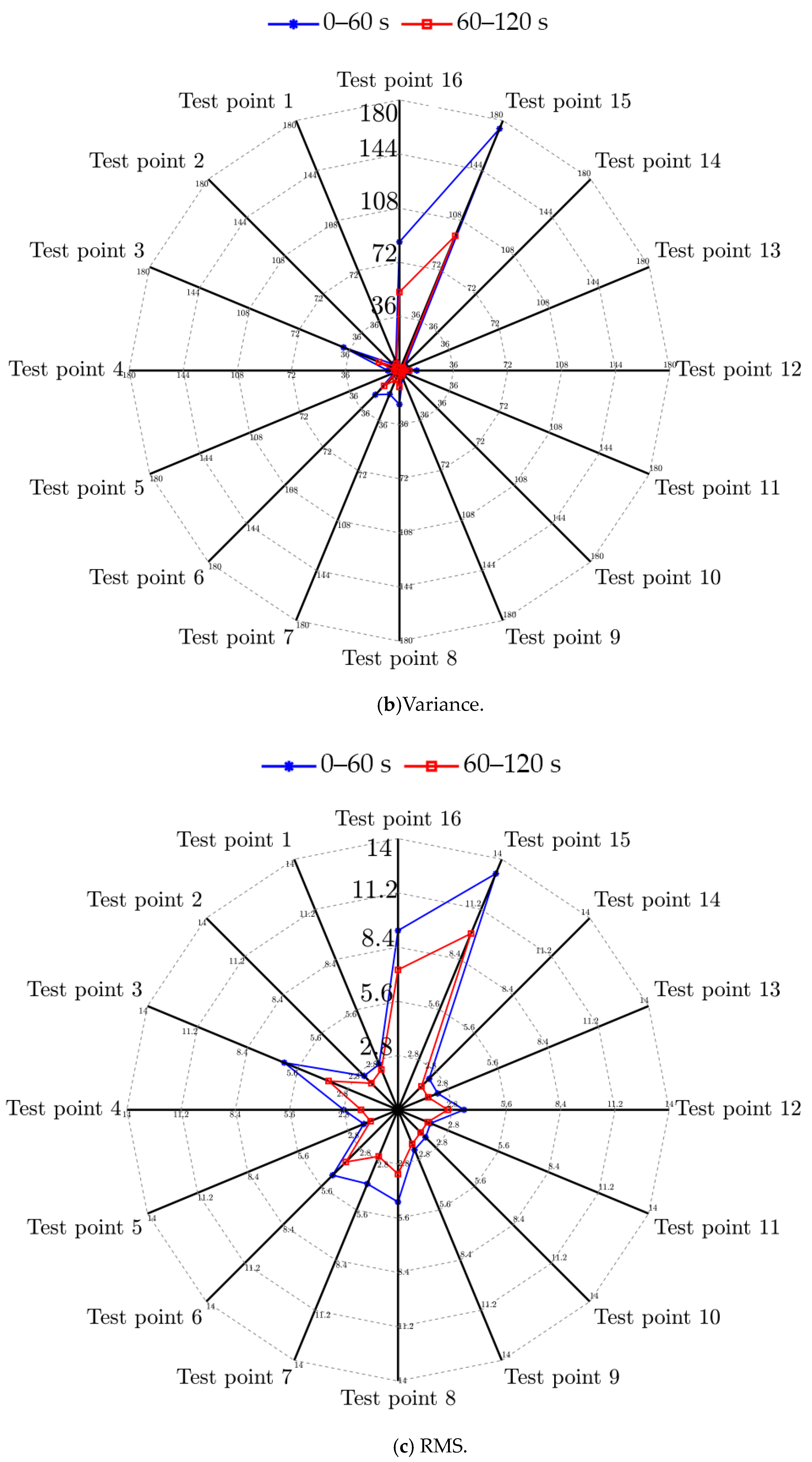
4.1. The Stationarity Analysis of Vibration Signals
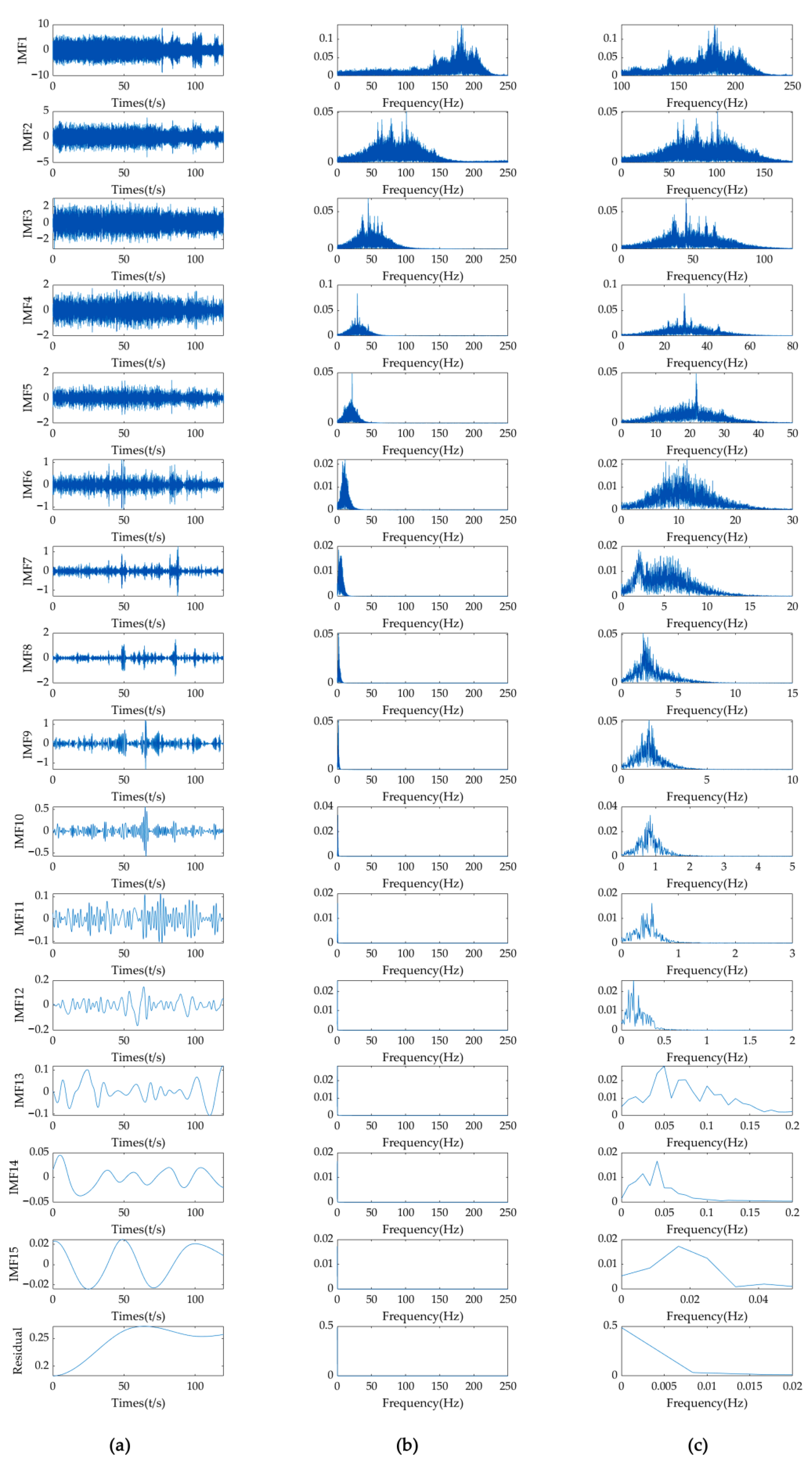
4.2. EMD Frequency Analysis Result
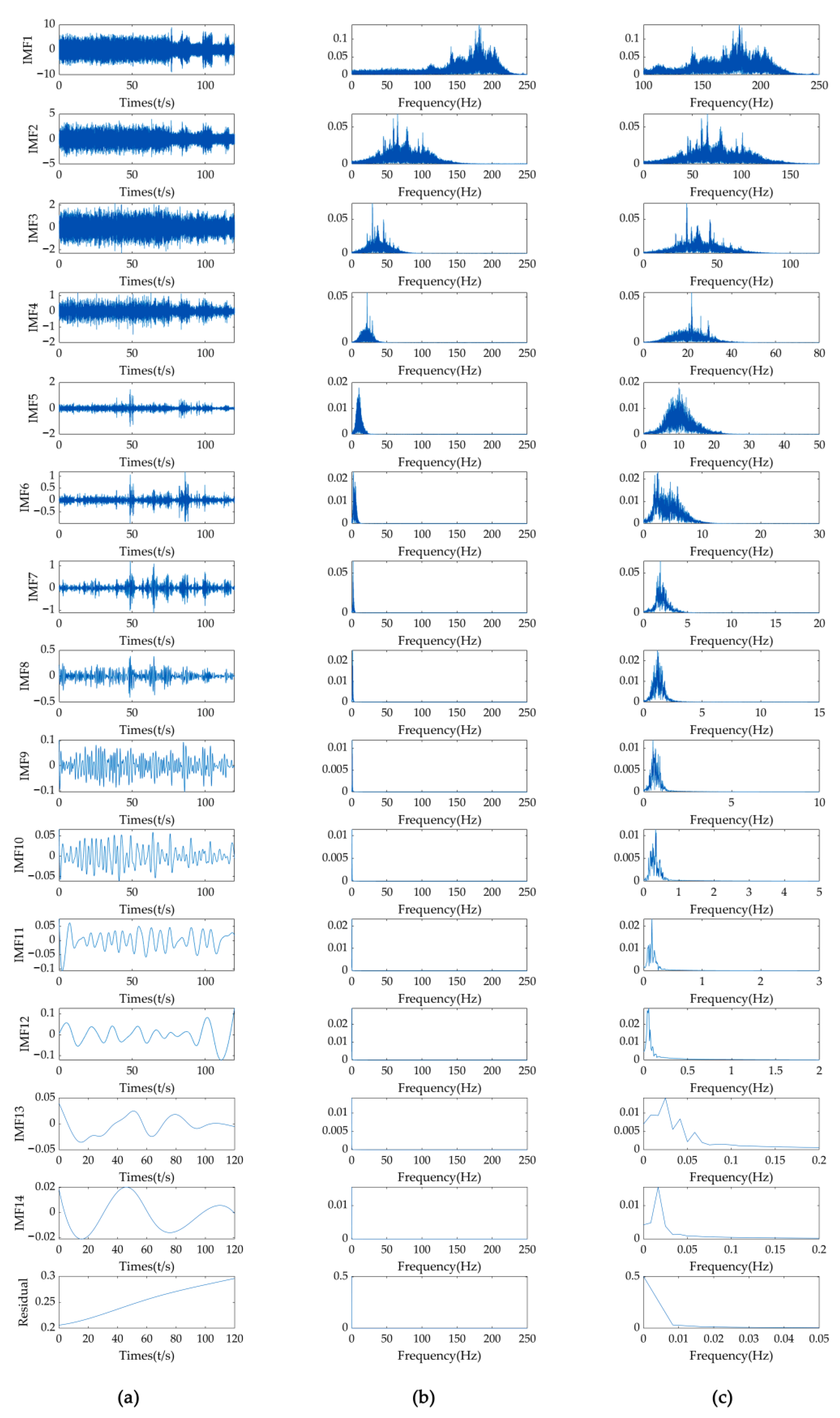
4.3. EEMD Frequency Analysis Result
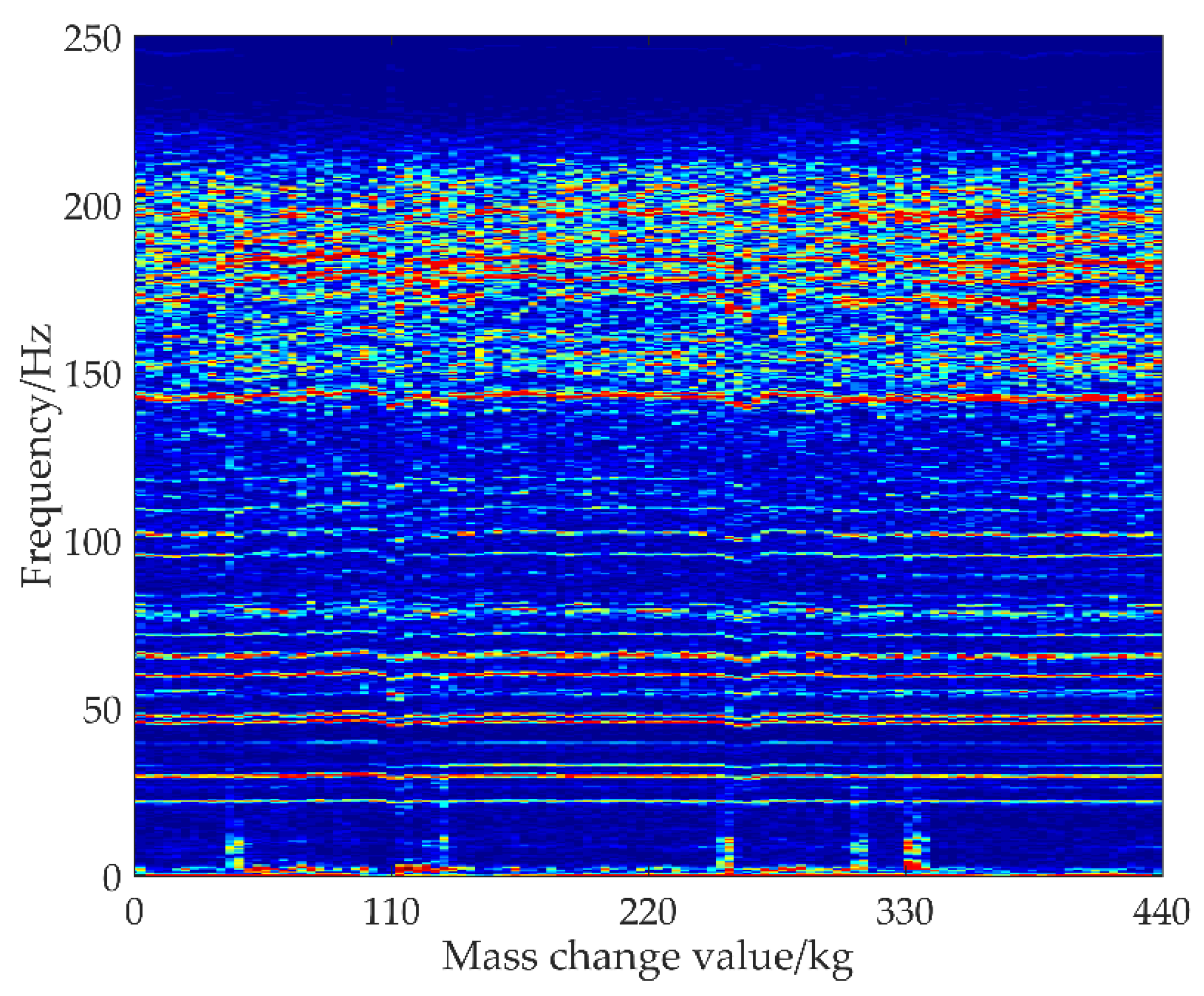
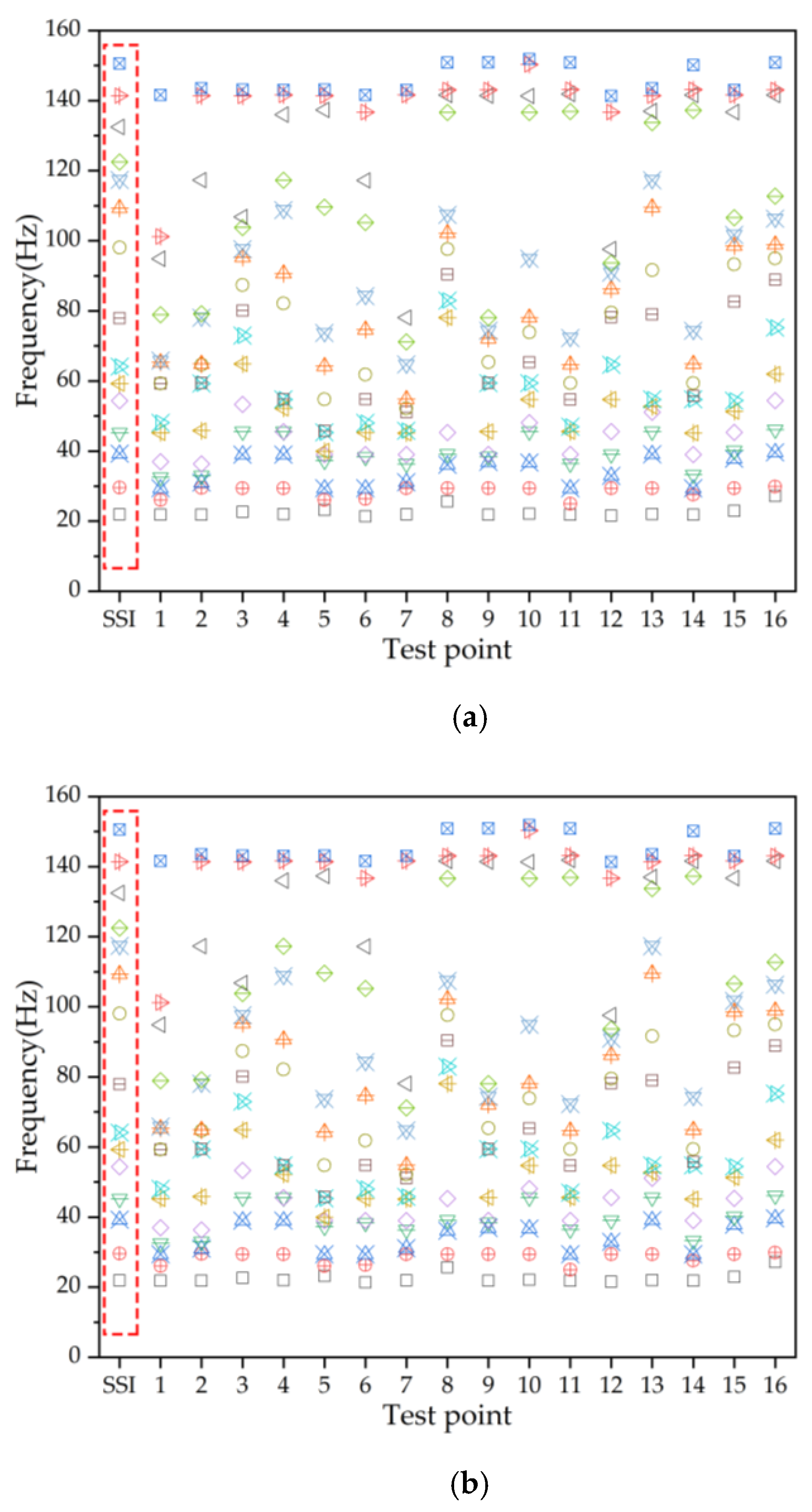
4.4. Frequency Distribution under Different Mass
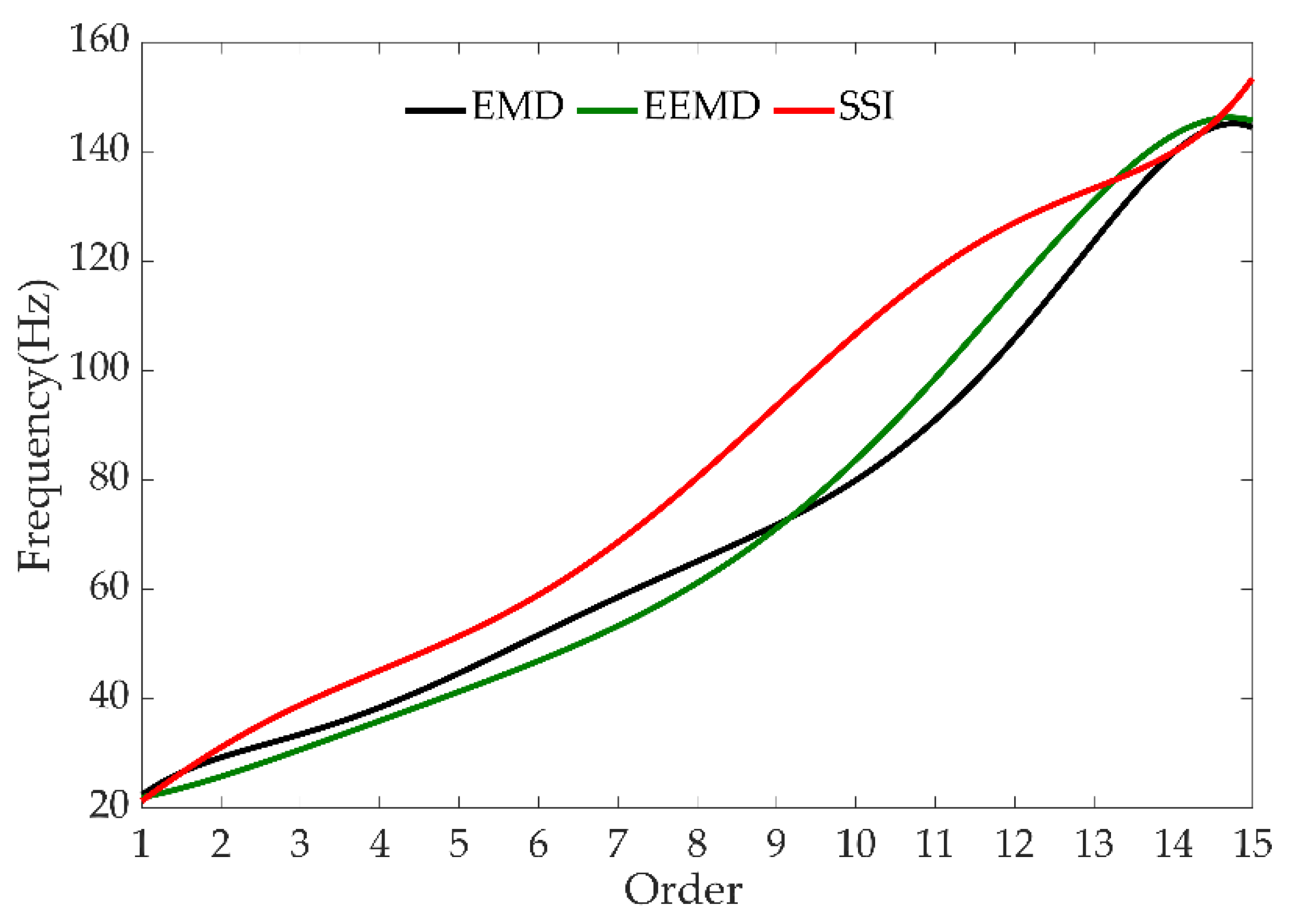
4.5. Comparison of EMD and EEMD Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, Z.H.; Wu, C.Y. Research Progress on Working Vibration problems of Grain Combine. J. Chin. Agric. Mech. 2017, 38, 21–25. [Google Scholar]
- Temmerman, D.J.; Deprez, K.; Anthonis, J.; Ramon, H. Conceptual Cab Suspension System for a Self-propelled Agricultural Machine, Part 1: Development of a Linear Mathematical Model. Biosyst. Eng. 2004, 89, 409–416. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.C.; Chen, Z.; Liang, X.X. The NVH Phenomena Analysis in Corn Harvester-Based on Vibration Dose and A -meter-weight Noise. J. Agric. Mech. Res. 2015, 37, 245–250. [Google Scholar]
- Zhou, M.G.; Zhang, L.; Chen, Y.; Liu, M.Y.; Huang, Y.P. Structural optimization for rack of boat-type tractor based on sensitivity analysis. Trans. Chin. Soc. Agric. Eng. 2016, 32, 54–60. [Google Scholar]
- Li, Y.M.; Sun, P.P.; Pang, J.; Xun, L.Z. Finite element mode analysis and experiment of combine harvester chassis. Trans. Chin. Soc. Agric. Eng. 2013, 29, 38–46. [Google Scholar]
- Quan, L.Z.; Tong, J.; Zeng, B.G.; Chen, D.H. Finite element mode analysis and experiment of corn stubble harvester. Trans. Chin. Soc. Agric. Eng. 2011, 27, 15–20. [Google Scholar]
- Jin, X.; Chen, K.K.; Ji, J.T.; Zhao, K.X.; Du, X.W.; Ma, H. Intelligent vibration detection and control system of agricultural machinery engine. Measurement 2019, 145, 503–510. [Google Scholar] [CrossRef]
- Xie, X.P.; Jiang, B.; Lei, F. Fast calculation method experimental modal analysis and its application. J. Vib. Shock 2015, 34, 46–52. [Google Scholar]
- Mugnaini, V.; Fragonara, L.Z.; Civera, M. A machine learning approach for automatic operational modal analysis. Mech. Syst. Signal Process. 2022, 170, 1–34. [Google Scholar] [CrossRef]
- Fang, D.X.; Wang, X.M. Modal analysis and experimental optimization of the header of rape combine harvester. J. Gansu Agric. Univ. 2019, 54, 232–240. [Google Scholar]
- Chen, S.; Zhou, Y.; Thong, Z.; Lu, S. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Guo, X.F.; Wang, W.B.; Guo, S.L.; Chen, S.J. Modal Analysis and Experimental Study on the Frame of the Potato Harvester. Mach. Des. Manuf. 2018, 54, 154–157. [Google Scholar]
- Tang, Z.; Zhang, B.; Wang, M.L.; Zhang, H.T. Damping behaviour of a prestressed composite beam designed for the thresher of a combine harvester. Biosyst. Eng. 2021, 204, 130–146. [Google Scholar] [CrossRef]
- Yu, Y.C.; Zhang, S.J.; Li, H.; Wang, X.F.; Tang, Y.D. Modal and Harmonic Response Analysis of Key Components of Ditch Device Based on ANSYS. Procedia Eng. 2017, 174, 956–964. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; Zhou, M.G.; Liu, M.Y. Modal testing study on boat-type paddy tractor hull. J. Mech. Strength 2017, 39, 1036–1041. [Google Scholar]
- Guan, Z.H.; Wu, C.Y.; Tang, Q.; Wang, G. Finite Element Mode Analysis and Experiment of Combine Harvester Threshing Cylinder. J. Agric. Mech. Res. 2016, 38, 136–140. [Google Scholar]
- Ryu, S.; Kim, D.; Lee, B.; Han, D.; Jung, I.; Chung, J. Idle Vibration Reduction of a Diesel Sport Utility Vehicle. Appl. Sci. 2022, 12, 5448. [Google Scholar] [CrossRef]
- Silva, R.; Ribeiro, D.; Bragança, C.; Costa, C.; Arêde, A.; Calçada, R. Model Updating of a Freight Wagon Based on Dynamic Tests under Different Loading Scenarios. Appl. Sci. 2021, 11, 10691. [Google Scholar] [CrossRef]
- Yao, Y.C.; Zhao, X.Y.; Du, Y.F.; Song, Z.H.; Yin, Y.Y.; MAO, E.R.; Liu, F. Operating modal analysis and test of harvester induced by mass-varying process. Trans. Chin. Soc. Agric. Eng. 2018, 34, 83–94. [Google Scholar]
- Brewick, P.T.; Smyth, A.W. An investigation of the effects of traffic induced local dynamics on global damping estimates using operational modal analysis. Mech. Syst. Signal Process. 2013, 41, 433–453. [Google Scholar] [CrossRef]
- Lin, C.S.; Wu, Y.X. Response-Only Parametric Estimation of Structural Systems Using a Modified Stochastic Subspace Identification Technique. Appl. Sci. 2021, 11, 11751. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Mirdamadi, H.R.; Ziaei-Rad, S. Operational modal analysis and fatigue life estimation of a chisel plow arm under soil-induced random excitations. Measurement 2018, 116, 451–457. [Google Scholar] [CrossRef]
- Jiao, B.Q.; Cao, J.H.; Lu, B.J.; Zhang, H.Q.; Song, Y.C.; Chen, D.F. Modal test of shaft-mounted brake disc based on polymax modal parameter identification method. China Railw. Sci. 2020, 5, 102–107. [Google Scholar]
- Cong, S.; Hu, S.L.J.; Li, H.J. FRF-based pole-zero method for finite element model updating. Mech. Syst. Signal Process. 2022, 177, 109206. [Google Scholar] [CrossRef]
- Huang, Y.L.; Li, Q.L.; Yao, C.J. Modal analysis and structural parameter optimization of threshing cylinder of combine harvester. J. Agric. Mech. Res. 2019, 12, 30–36. [Google Scholar]
- Geng, J.; Zhang, X.W.; Chen, X.F. High-frequency dynamic response of thin plate with uncertain parameter based on average wavelet finite element method (AWFEM). Mech. Syst. Signal Process. 2018, 110, 180–192. [Google Scholar] [CrossRef]
- Yu, K.P.; Zou, J.X.; Yang, B.Y. Wavelet transform method for mode parameter identification. J. Astronaut. 1999, 4, 72–76. [Google Scholar]
- Harish, C.N.; Sekhar, A.S. Wavelet transform based estimation of modal parameters of rotors during operation. Measurement 2018, 130, 264–278. [Google Scholar]
- Adam, S.A.; Jalil, N.; Rezali, K.; Ng, Y.G. The effect of posture and vibration magnitude on the vertical vibration transmissibility of tractor suspension system. Int. J. Ind. Ergon. 2020, 80, 103014. [Google Scholar] [CrossRef]
- Harmann, T.; Morita, S.; Tanner, G.; Chappell, D.J. High-frequency structure- and air-borne sound transmission for a tractor model using dynamical energy analysis. Wave Motion 2019, 87, 132–150. [Google Scholar] [CrossRef]
- Yan, Z.C.; Jin, Z.H.; Teng, S.; Chen, G.F.; Bassir, D. Measurement of Bridge Vibration by UAVs Combined with CNN and KLT Optical-Flow Method. Appl. Sci. 2022, 12, 5181. [Google Scholar] [CrossRef]
- Ji, J.T.; Xu, L.J.; Pang, J.; Geng, L.X.; Wang, S.S. Minimum amplitude point analysis and optimization of hanging point of miniature grain combine. Trans. Chin. Soc. Agric. Eng. 2017, 12, 28–33. [Google Scholar]
- Zhou, S.D.; Ma, Y.C.; Liu, L.; Kang, J.; Ma, Z.S.; Yu, L. Output-only modal parameter estimator of linear time-varying structural systems based on vector tar model and least squares support vector machine. Mech. Syst. Signal Process. 2018, 98, 722–755. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Mattia, F. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Wang, Y.J.; Kang, S.Q.; Zhang, Y.; Liu, X.; Jiang, Y.C.; Mikulovich, V.I. Condition Recognition Method of Rolling Bearing Based on Ensemble Empirical Mode Decomposition Sensitive Intrinsic Mode Function Selection Algorithm. J. Electron. Inf. Technol. 2014, 36, 595–600. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Fortuna, L.; Mattia, F. Multiple Hysteresis Jump Resonance in a Class of Forced Nonlinear Circuits and Systems. Int. J. Bifurc. Chaos 2020, 30, 13. [Google Scholar] [CrossRef]

| Table | Coding of Sensor | Sensitivity Value (mV/g) | Direction of Z Axis | Mounting Magnetic Pedestal |
|---|---|---|---|---|
| 1 | LW199553 | 10.06 | Down | Yes |
| 2 | LW199811 | 9.97 | Down | Yes |
| 3 | LW199798 | 10.17 | Up | No |
| 4 | LW199436 | 10.15 | Up | No |
| 5 | LW199549 | 9.94 | Up | No |
| 6 | LW199004 | 9.80 | Up | No |
| 7 | LW199988 | 9.93 | Up | No |
| 8 | LW199991 | 9.67 | Up | No |
| 9 | LW199813 | 10.12 | Down | Yes |
| 10 | LW199992 | 9.66 | Down | Yes |
| 11 | LW199438 | 10.04 | Down | Yes |
| 12 | LW199800 | 9.91 | Up | Yes |
| 13 | LW199810 | 10.12 | Down | No |
| 14 | LW199001 | 10.11 | Up | No |
| 15 | LW199002 | 10.31 | Up | No |
| 16 | LW199807 | 10.27 | Up | No |
| Time | 0–120 s | 120–240 s | 240–360 s | |
|---|---|---|---|---|
| Peak | ||||
| 1 | 144.0 Hz | 151.0 Hz | 150.9 Hz | |
| 2 | 141.6 Hz | 141.4 Hz | 141.6 Hz | |
| 3 | 101.2 Hz | 101.3 Hz | 100.8 Hz | |
| 4 | 94.9 Hz | 95.1 Hz | 92.3 Hz | |
| 5 | 78.8 Hz | 79.9 Hz | 79.7 Hz | |
| 6 | 76.2 Hz | 71.3 Hz | 77.5 Hz | |
| 7 | 65.3 Hz | 65.6 Hz | 64.5 Hz | |
| 8 | 59.3 Hz | 59.5 Hz | 59.5 Hz | |
| 9 | 54.5 Hz | 54.9 Hz | 54.5 Hz | |
| 10 | 48.1 Hz | 47.5 Hz | 47.3 Hz | |
| 11 | 45.2 Hz | 45.2 Hz | 45.2 Hz | |
| 12 | 37.0 Hz | 37.4 Hz | 37.2 Hz | |
| 13 | 29.4 Hz | 32.6 Hz | 34.5 Hz | |
| 14 | 26.0 Hz | 29.4 Hz | 29.2 Hz | |
| 15 | 22.1 Hz | 21.9 Hz | 21.8 Hz | |
| Order | Modal Value (Hz) | Order | Modal Value (Hz) |
|---|---|---|---|
| 1 | 21.924 | 9 | 98.090 |
| 2 | 29.578 | 10 | 109.345 |
| 3 | 39.247 | 11 | 117.355 |
| 4 | 45.229 | 12 | 122.489 |
| 5 | 54.385 | 13 | 132.451 |
| 6 | 59.303 | 14 | 141.396 |
| 7 | 64.123 | 15 | 150.583 |
| 8 | 77.930 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Li, X.; Yao, Y.; Wang, Y.; Yang, X.; Zhao, X.; Geng, D.; Li, Y.; Liu, L. A Modal Frequency Estimation Method of Non-Stationary Signal under Mass Time-Varying Condition Based on EMD Algorithm. Appl. Sci. 2022, 12, 8187. https://doi.org/10.3390/app12168187
Gao L, Li X, Yao Y, Wang Y, Yang X, Zhao X, Geng D, Li Y, Liu L. A Modal Frequency Estimation Method of Non-Stationary Signal under Mass Time-Varying Condition Based on EMD Algorithm. Applied Sciences. 2022; 12(16):8187. https://doi.org/10.3390/app12168187
Chicago/Turabian StyleGao, Lei, Xiaoke Li, Yanchun Yao, Yucong Wang, Xuzhe Yang, Xinyu Zhao, Duanyang Geng, Yang Li, and Li Liu. 2022. "A Modal Frequency Estimation Method of Non-Stationary Signal under Mass Time-Varying Condition Based on EMD Algorithm" Applied Sciences 12, no. 16: 8187. https://doi.org/10.3390/app12168187
APA StyleGao, L., Li, X., Yao, Y., Wang, Y., Yang, X., Zhao, X., Geng, D., Li, Y., & Liu, L. (2022). A Modal Frequency Estimation Method of Non-Stationary Signal under Mass Time-Varying Condition Based on EMD Algorithm. Applied Sciences, 12(16), 8187. https://doi.org/10.3390/app12168187





