OGSM: A Parallel Implicit Assembly Algorithm and Library for Overlapping Grids
Abstract
:1. Introduction
- We propose a parallel implicit assembly method that employs a two-step nodes classification scheme to accelerate the hole-cutting operation.
- We implement the proposed method into a convenient library called overlapping grid sewing machine (OGSM) for integration.
- We validate the parallel assembly capability of overlapping multi-component grids with a seven-sphere model.
- We validate the parallel computing efficiency and interpolation accuracy of OGSM with a multi-body trajectory prediction case.
2. Implicit Assembly Algorithm for Overlapping Grid
2.1. Classification of Grid Nodes
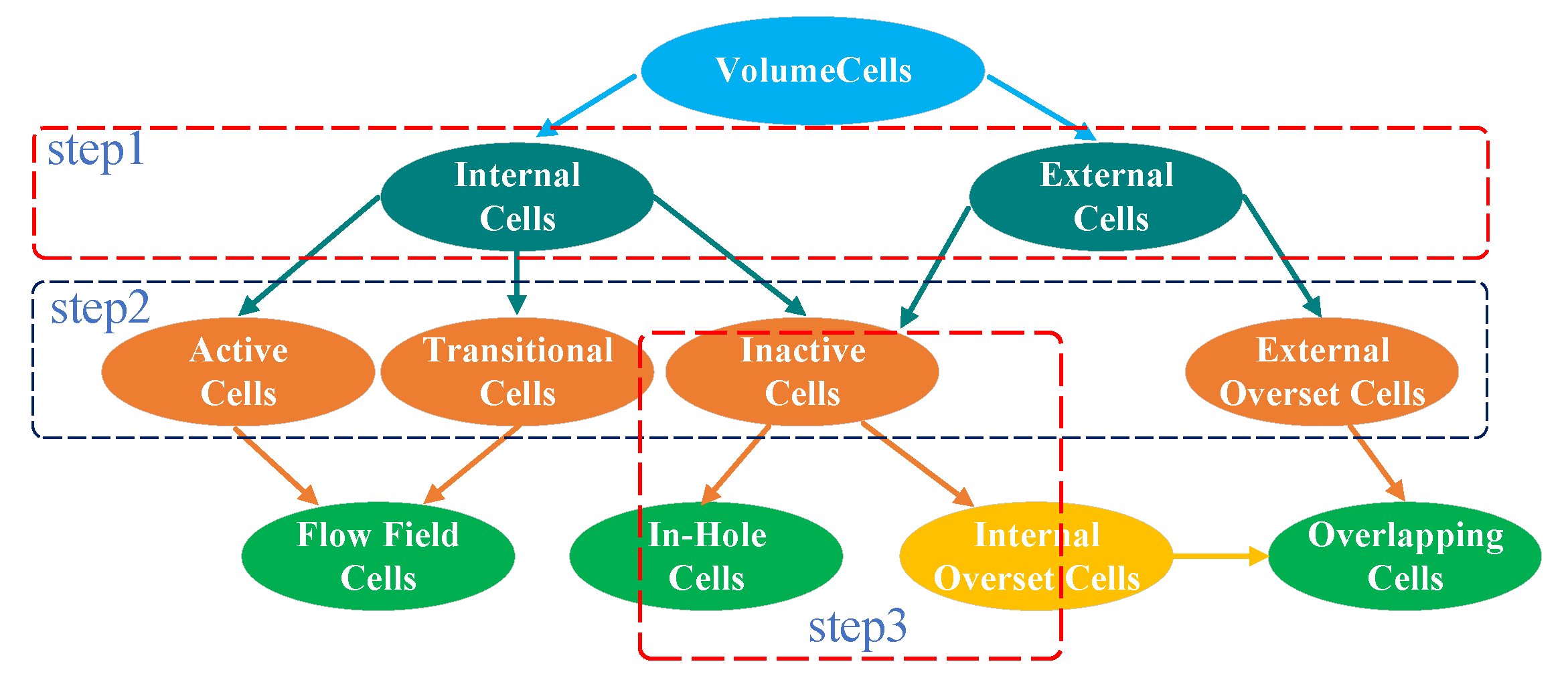
2.2. Classification of Grid Cells
- Classification of internal and external cells. The cells adjacent to the external boundaries of are identified as . Due to their locations, the flow-field properties of these cells have to be obtained by interpolating those on other component grids. These cells do not constitute the donor cells corresponding to the overlapping cells in other component grids. Consequently, all the cells of grid can be partitioned into the internal cells and external cells . Note that and share no common cells.
- Classification of active and inactive cells. If all nodes of cell are inactive (Equation (2)), then c is classified as an inactive cell. As shown in Figure 1, and can both have inactive cells. If all nodes of are active, then c is treated as an active cell; otherwise, c is identified as a transitional cell. For the active and transitional cells in the external cells, we collectively call them external overlapping cells.
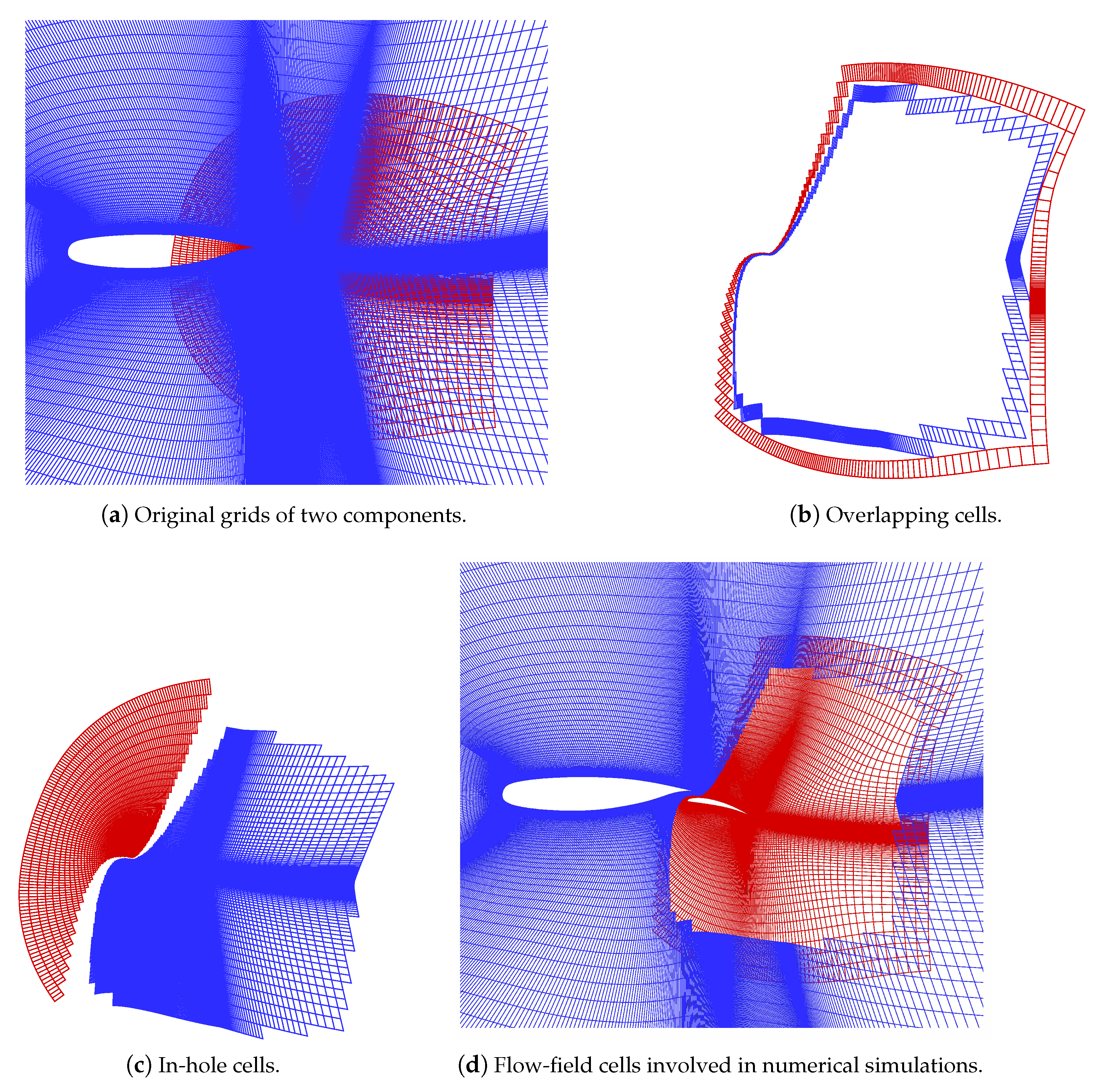
- Classification of inactive cells into in-hole and internal overlapping ones. If an arbitrary inactive cell shares at least one node with a certain transitional cell, then the cell is called an internal overlapping cell. In this way, the inactive cells adjacent to transitional cells are redefined as overlapping cells, while the other inactive ones are in-hole cells.
- Classification of into flow-field, overlapping and in-hole cells. The overlapping cells are constructed with internal overlapping and external overlapping cells. In order to ensure overlapping cells from different grids cannot be donors to each other, we treat transitional cells as flow-field cells, which indicates that flow-field cells consist of active and transitional ones.
3. Parallel Implicit Assembly Method
3.1. Domain-Decomposition Strategy for Overlapping Component Grids
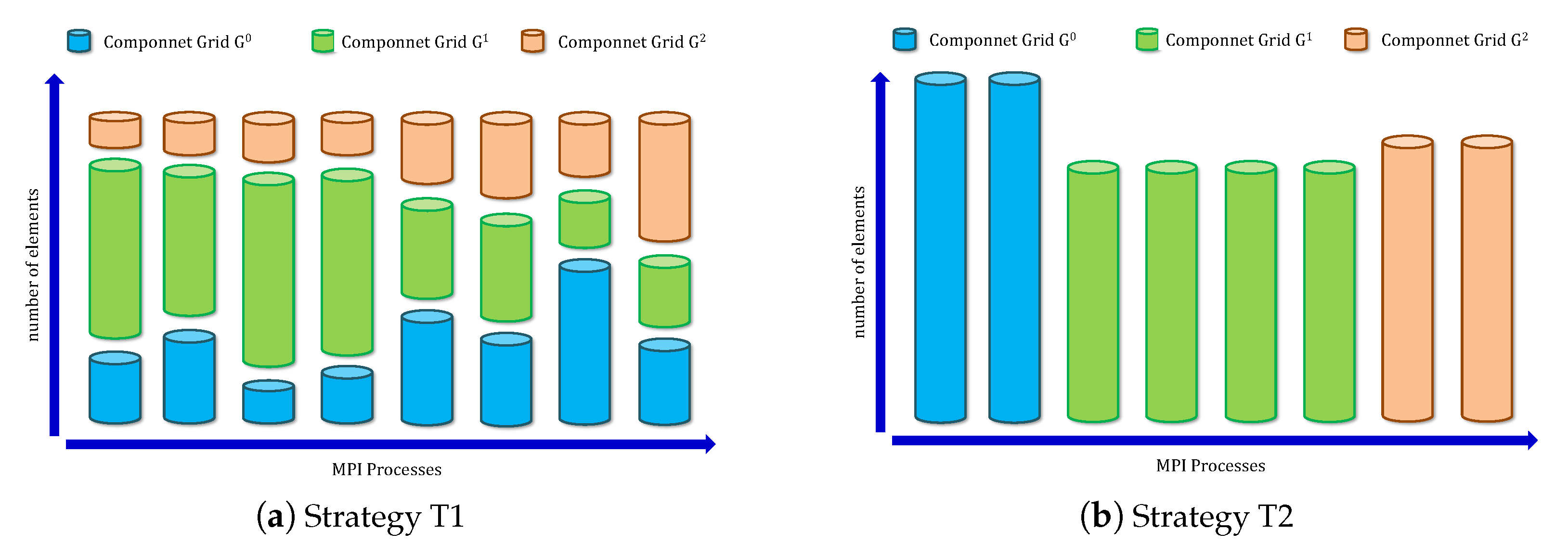
- Strategy (Figure 3a). All the M grids are regarded as a whole grid, and the load measured by the cell amount is distributed across the processes. The domains are consequently decomposed according to the traditional greedy algorithm.
- Strategy (Figure 3b). Based on the ratio of the cell amount in () to that in the total M grids, the required amount of processes for grid is , and the relevant workload is assigned equally among the processes.
3.2. Automatic Determination of Overlapping Relation between Component Grids
3.2.1. Overlapping Relation Determination Based on the OBB Technique
3.2.2. Intersection Relation Judgement between Two Grids
3.3. Parallel Hole-Cutting Based on Two-Step Nodes Classification Scheme
3.3.1. Preliminary Screening Step: Wall Distance Calculation
- Distance screening condition SC1. If the distance of a grid node to its own component is less than that to any other components (i.e., ), then node p is an active node.
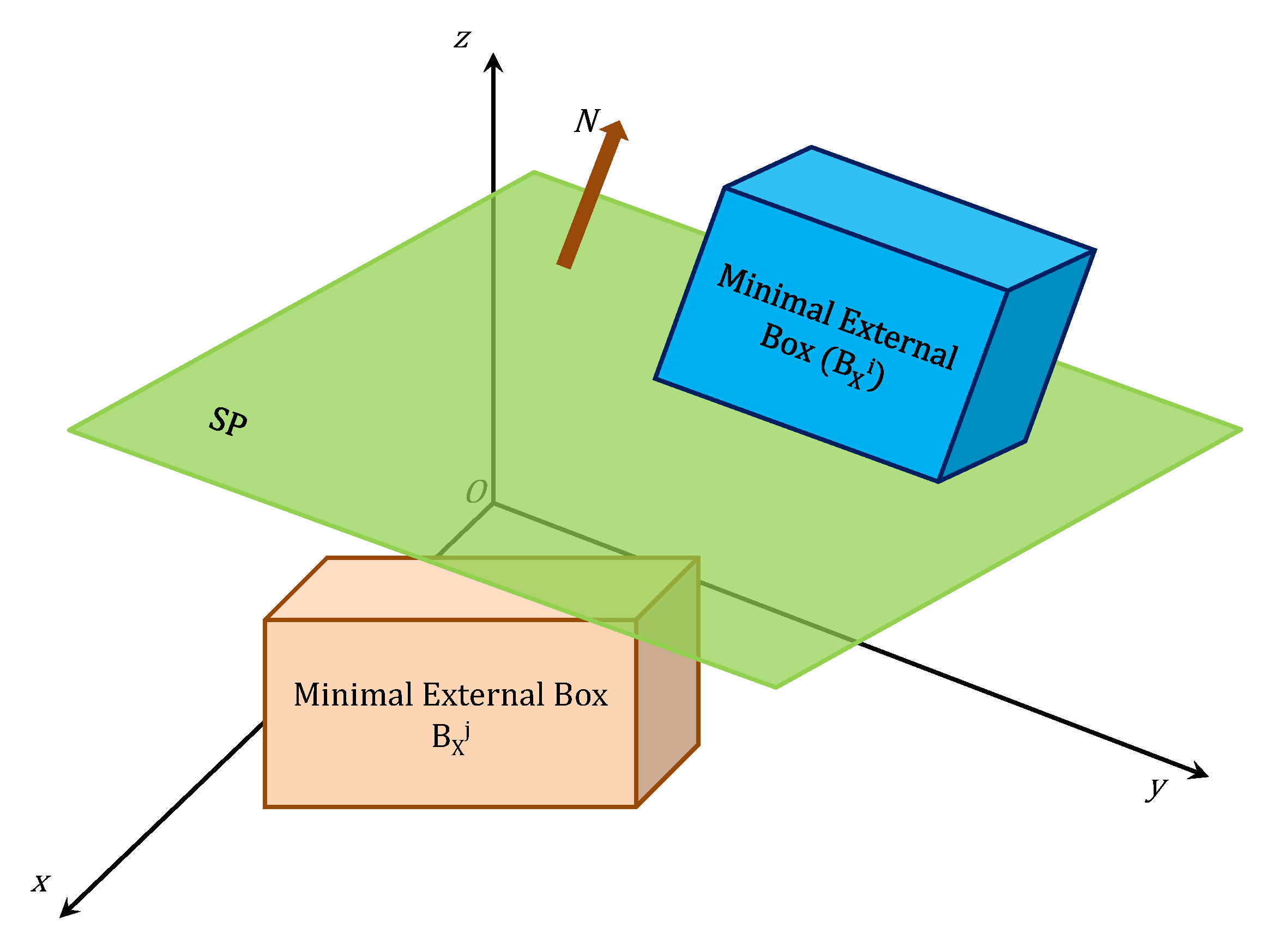
- Coverage screening condition SC2. If grid node p is not surrounded by the minimal external box of any other component grid, it can neither be covered by the corresponding donor cells nor be surrounded by the solid wall boundaries.
- For the solid-wall nodes , the upper and lower bounds can be calculated asThese six spatial planes determine the root box , which is also treated as the current candidate box .
- The ranges of the current candidate box in the x, y and z directions are calculated asWithout loss of generality, we assume and sort the solid-wall nodes in according to the x-coordinate. Along the direction with the largest range, we adopt the bisection method to split into two subsets. The nodes relevant to are correspondingly split into two subsets, i.e., and .
- To minimize the number of solid wall nodes bounded by the box , the operation of step (2) is recursively performed until the the number of elements in is greater than .
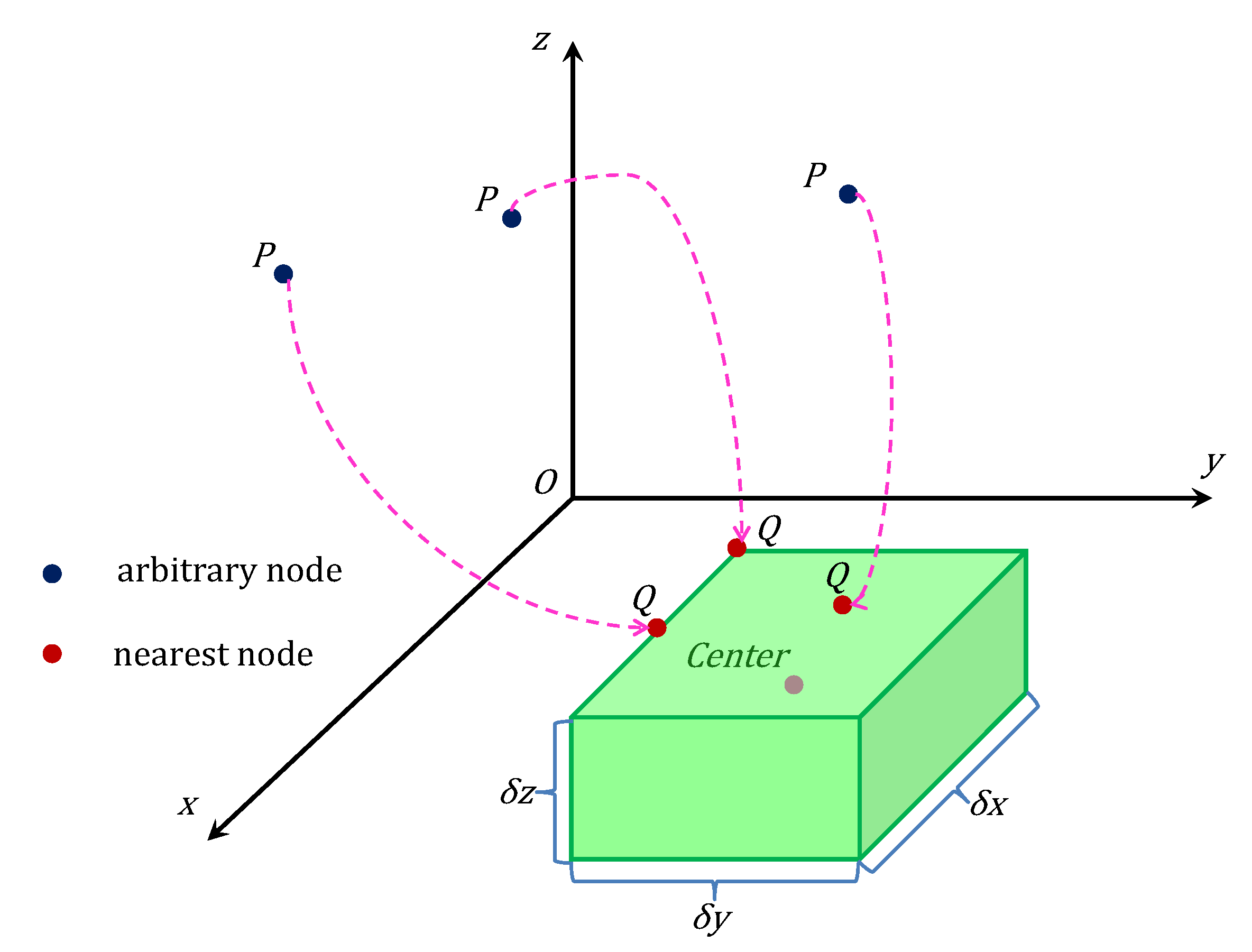
- When all the candidate boxes cannot be further split, the bottom leaves of the box-tree are collected and form cuboid capsules , which can be constructed using the spatial planes of
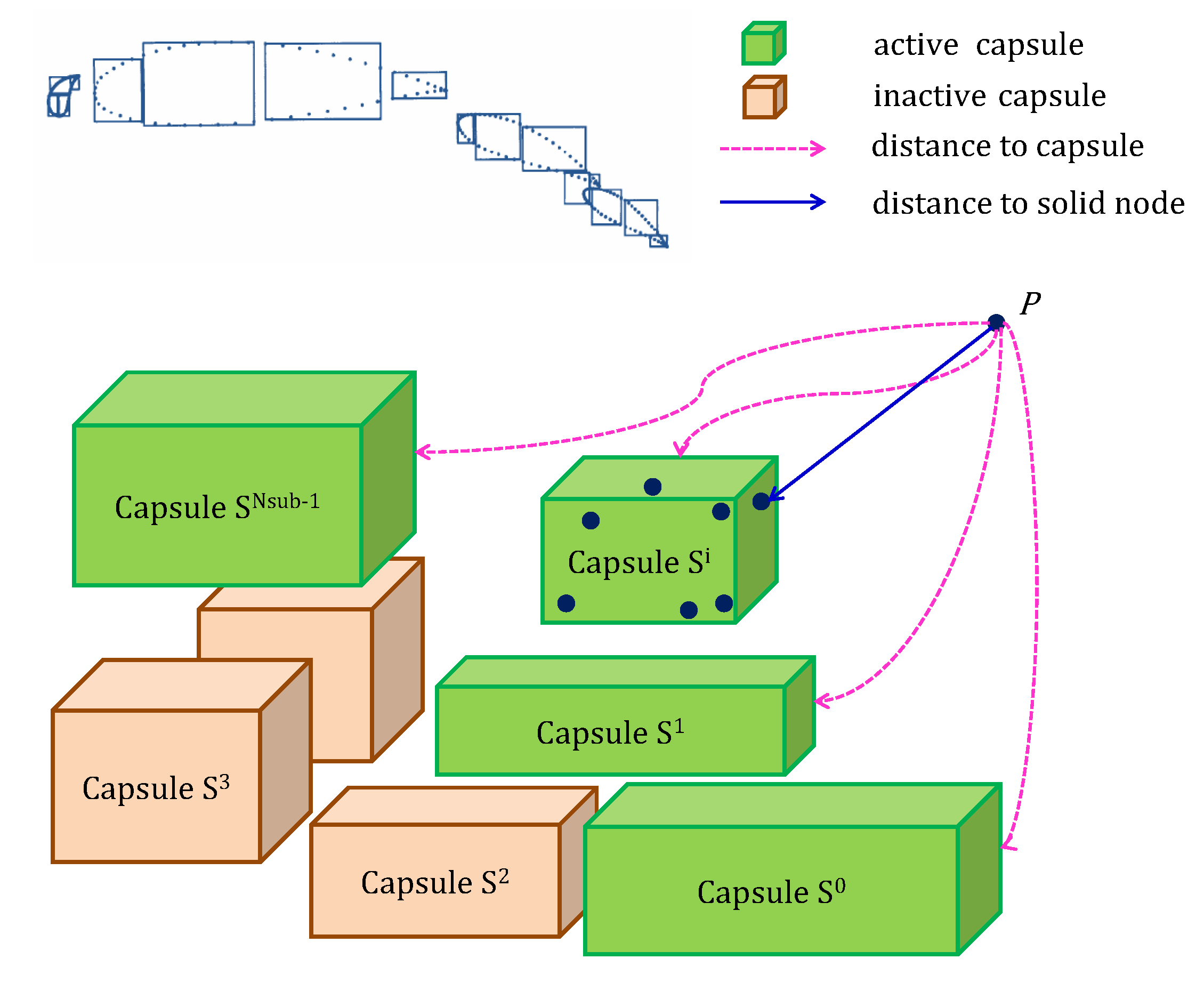
- Calculate the distance from p to each cuboid capsule . Figure 7 shows a schematic of , where the coordinates of p are and the center of is located at . The distance can be calculated aswhereIn addition, each cuboid capsule has a property parameter indicating whether is active and the initial value is set to TRUE. Note that is initialized to .
- Search for the cuboid capsule that makes obtain its minimum among all the active cuboid capsules as shown in Figure 8. Whenever a suitable is found, the index corresponding and are recorded. It is very likely that the capsule contains the desired closest wall node, and a further verification is performed in Step 3. Otherwise, the routine goes directly to Step 4.
- Update the value of asand reset the property parameter of to FALSE. If the cuboid capsule satisfies the conditionthen its property parameter will be assigned to FALSE. The routine goes back to Step 2 and keeps on searching the active cuboid capsules.
- After the above steps are completed, the smallest distance is obtained.
- The solid wall nodes of are collected and shared among processes in the group . Similarly, each process in also has the whole solid-wall nodes for component grid .
- All the processes calculate the distance from p to the wall boundary in parallel.
- Equation (7) indicates that is actually relevant to , and is the minimum of the Ls.
3.3.2. Verification Step: Parallel Treatment of Query Nodes
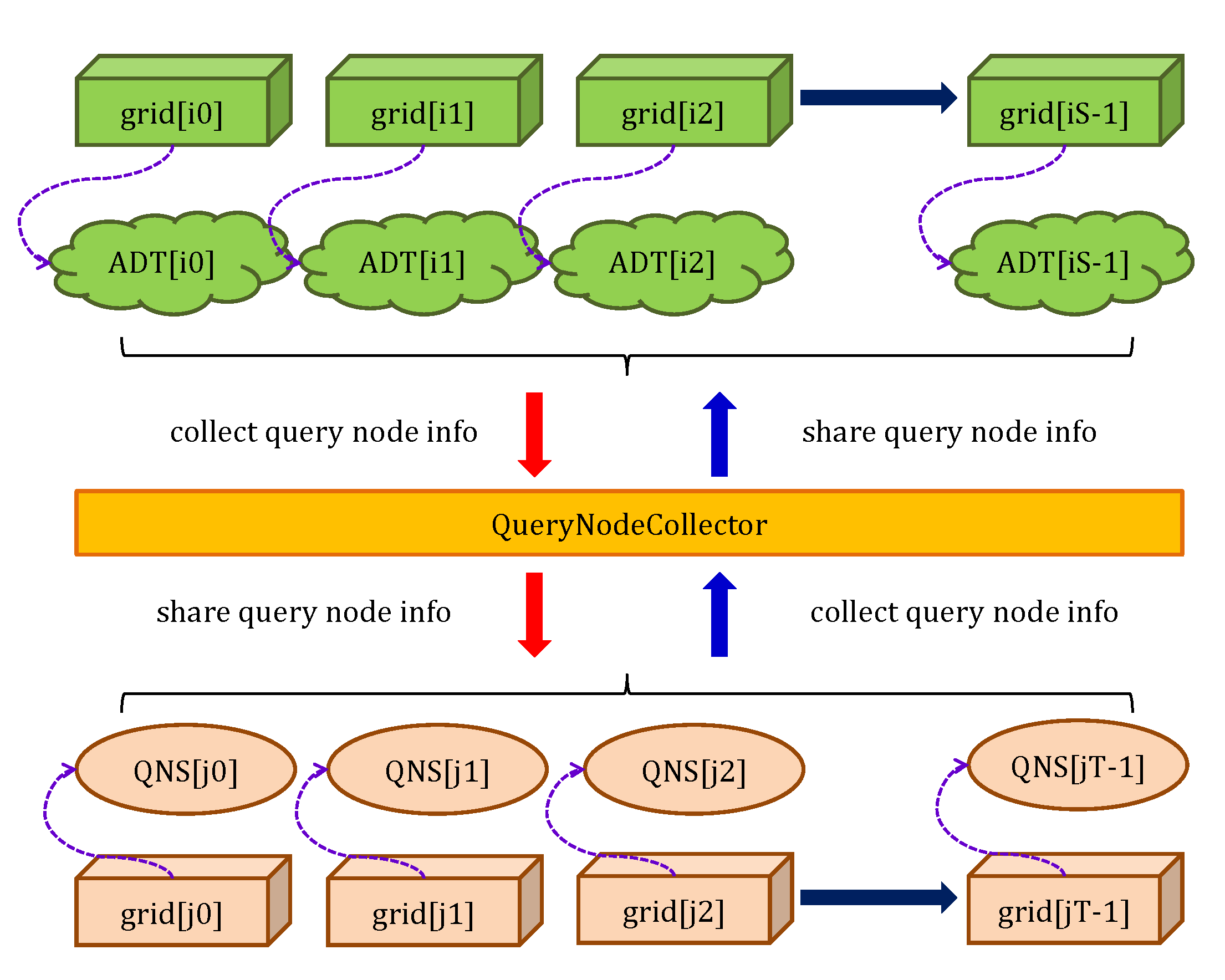
- Parallel query of donor cells and calculation of interpolation information. Each process hosting owns the whole query nodes . On the help of the local ADT, we obtain the information whether an arbitrary query node is covered by any internal cell , i.e., . If holds, the information to be recorded includes the index of process containing , the local index of , the relative coordinates of p in , and . Otherwise, all the information relevant to p is erased from the current process.
- Screening of query nodes. In each process relevant to , the information of query nodes is gathered by the collectors shown in Figure 9 and broadcasted to the T targeting processes. For an arbitrary node , if the stored process index is equal to that of current process P, then is updated in the process P. Furthermore, if holds, then p is an inactive node and excluded from .
- Classification of query nodes. After the above two steps, may still contain inactive node. If p is covered by the minimal internal box of but no donor cells for p can be found on , then we treat p as an inactive node and remove it from . Now all the remaining nodes in are active.
3.4. Identification and Parallel Assembly of the Overlapping Cells
- With the general method in Section 2.2, the cells are preliminarily divided into four categories, namely active cells, inactive cells, transitional cells and external overlapping cells (Figure 1).
- All the nodes in the transitional cells are marked in a black colour, and these nodes are shared among all the processes.
- In each process, the inactive cells containing black nodes are identified as interior overlapping cells, and the other inactive cells are classified as in-hole cells.
- The interior overlapping and the external overlapping cells are unified into a set of overlapping cells. Similarly, the active cells and the transition cells are also unified into flow-field cells.
3.5. Treatment of Defective Cells
- On each process hosting the source grid , the donor cells for the relevant defective cells are independently selected.
- In the non-blocking communication mode, the information about the above selected donor cells is gathered and then broadcasted to those processes (denoted by s) containing the distributed target grids.
- In each process of s, the defective cells are independently screened, and the nearest flow-field cells are taken as donor cells.
4. Implementation and Application of Overlapping-Grid-Sewing-Machine Library
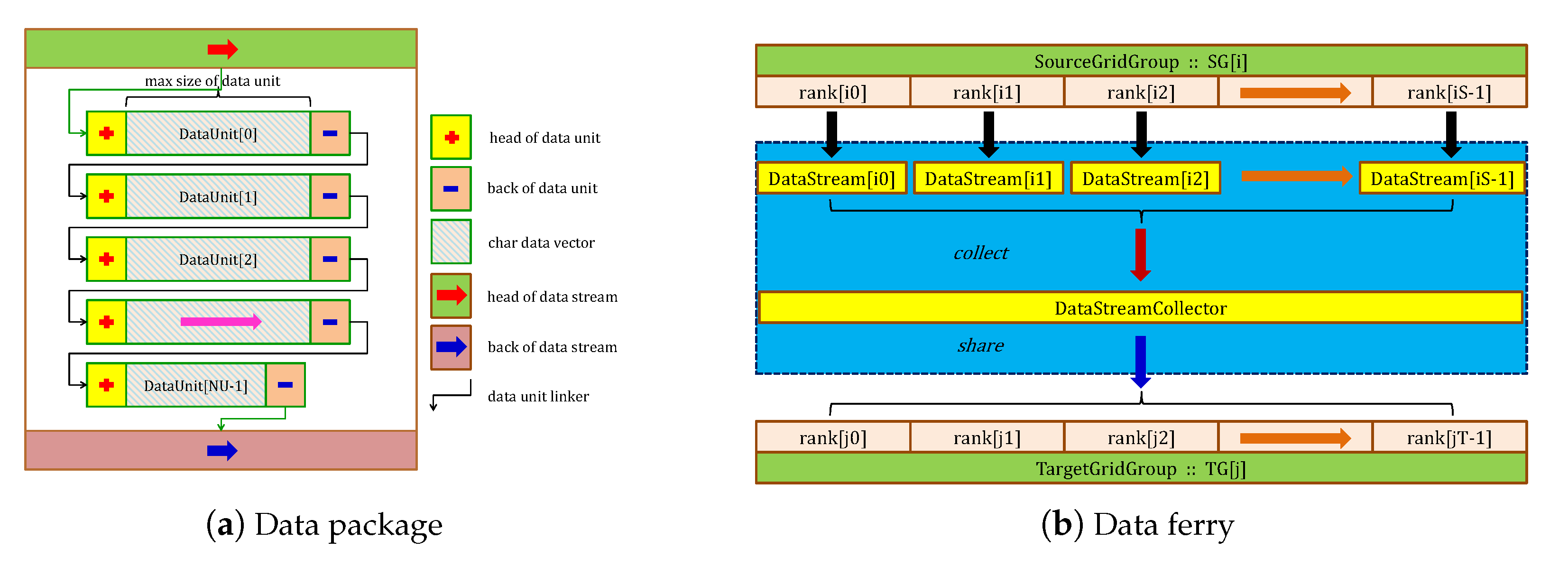
4.1. Data Ferry Technique
4.1.1. Customized Data Packaging Type
4.1.2. Data Ferry
- Each process creates a DataStream object and sends the collected data to the root process .
- Process receives the messages from S DataStream objects and gathers them into a collector of the pointer object.
- The information in collector is broadcasted to the processes . When the sender and the receiver are the same process, a memory-copy operation is called instead to replace the MPI communication.
4.2. Application Programming Interfaces for Simulators
4.2.1. Controlling Parameters of Boundary Conditions
4.2.2. Input and Output Interfaces
4.3. Internal Work-Flow of OGSM Library
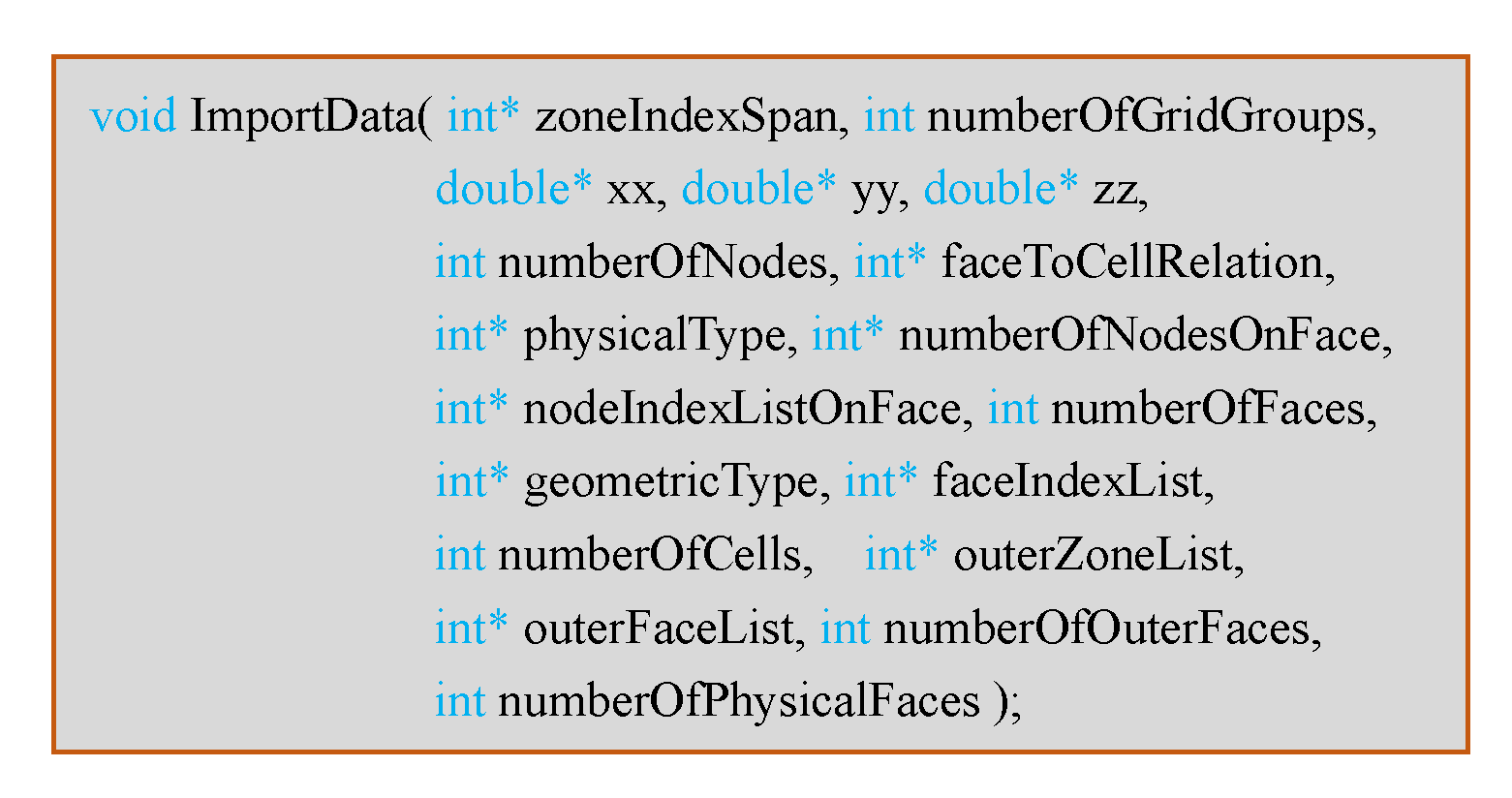
- Import the topology information of the grid distribution in the current process, including the sequence of the spatial nodes, faces and cells. The boundary conditions and the cross-process adjacency relationship between grids are simultaneously attached.
- Recognize solid wall and external boundaries. According to the solidWBC and externalBC parameters assigned by users in “overset.txt”, a quick mapping is performed to identify the solid wall and external boundaries of grids.
- Register face-to-face adjacency relationship. Note that the internal overlapping cells are obtained by extending the transitional cells towards the inactive cells, which may require certain cross-process operations. Therefore, we register the face-to-face adjacency relationship of the sub-grids based on the geometric information obtained in step 1.
- Record the overlapping relationship between multiple component grids. According to the spectral analysis results of the covariance matrix, the minimal internal and external boxes of component grids can be generated in parallel. Then, a spatial planeseparation algorithm is utilized to preliminarily determine the overlapping relation between component grids.
- Initialize the query nodes via the preliminary screening criterion. The recursive-box algorithm is used for the parallel calculation of wall distance parameters and . The query nodes are preliminarily screened according to the distance relation and the coverage relation.
- Update the ADT structures corresponding to the sub-grids. Both the inspection of the coverage relation in Equation (2) and the pairing between overlapping cells and donor cells require cross-process searching. Compared to the traditional recursive query mode, the non-recursive query of ADTs utilized in OGSM can improve the query speed on the ADTs and avoid the stack-overflow effects caused by the large tree structures [27].
- Confirm the types of query nodes. The coverage relationship is judged based on ADT, and the inactive query nodes are excluded. Note that the properties of the nodes to be queried are screened in parallel.
- Classify global volume cells. The hole-cutting boundaries are determined and the global volume cells are classified into flow-field cells, overlapping cells and in-hole cells.
- Query the optimal donor cells for overlapping cells. The tri-linear interpolation coefficients are calculated in parallel. For defective overlapping cells, the recursive-box method is adopted to quickly search for the optimal donor cells, and the other overlapping cells are paired to their donor cells by applying cross-process searching on ADT structures and the Newton–Raphson iterative method.
- Treat the assembly information in parallel. The mapping holds for any overlapping cell in each process. Hereby, and represent the process index and local cell index of the current overlapping cell on the source grid. Meanwhile, , , and represent the process index, the local cell index and the interpolation factors of the corresponding donor cell on the target grid, respectively. Then, the target processes prepares the data for interpolation based on the mapping.
- Count the total number of donor cells in the current process. Strictly speaking, this value is equal to the total number of interpolation operations in the current process. For an unsteady flow field with multi-body relative motion, the assembly state of the overlapping grids changes at each physical time step. Meanwhile, the total number of donor cells on each process varies. OGSM provides the solver with this critical parameter, which enables it to dynamically manage the memory space and perform the interpolation of the physical field.
- Export the information of overlapping interpolation and cell classification. First, the current process outputs the overlapping relations; then the solver interpolates the physical field using the tri-linear factors and exchanges the data across processes for the donor cells. Finally, the type identifiers of volume cells are outputted as an iBlank value (0: in-hole, 1: overlapping, 2: flow-field).
5. Numerical Results
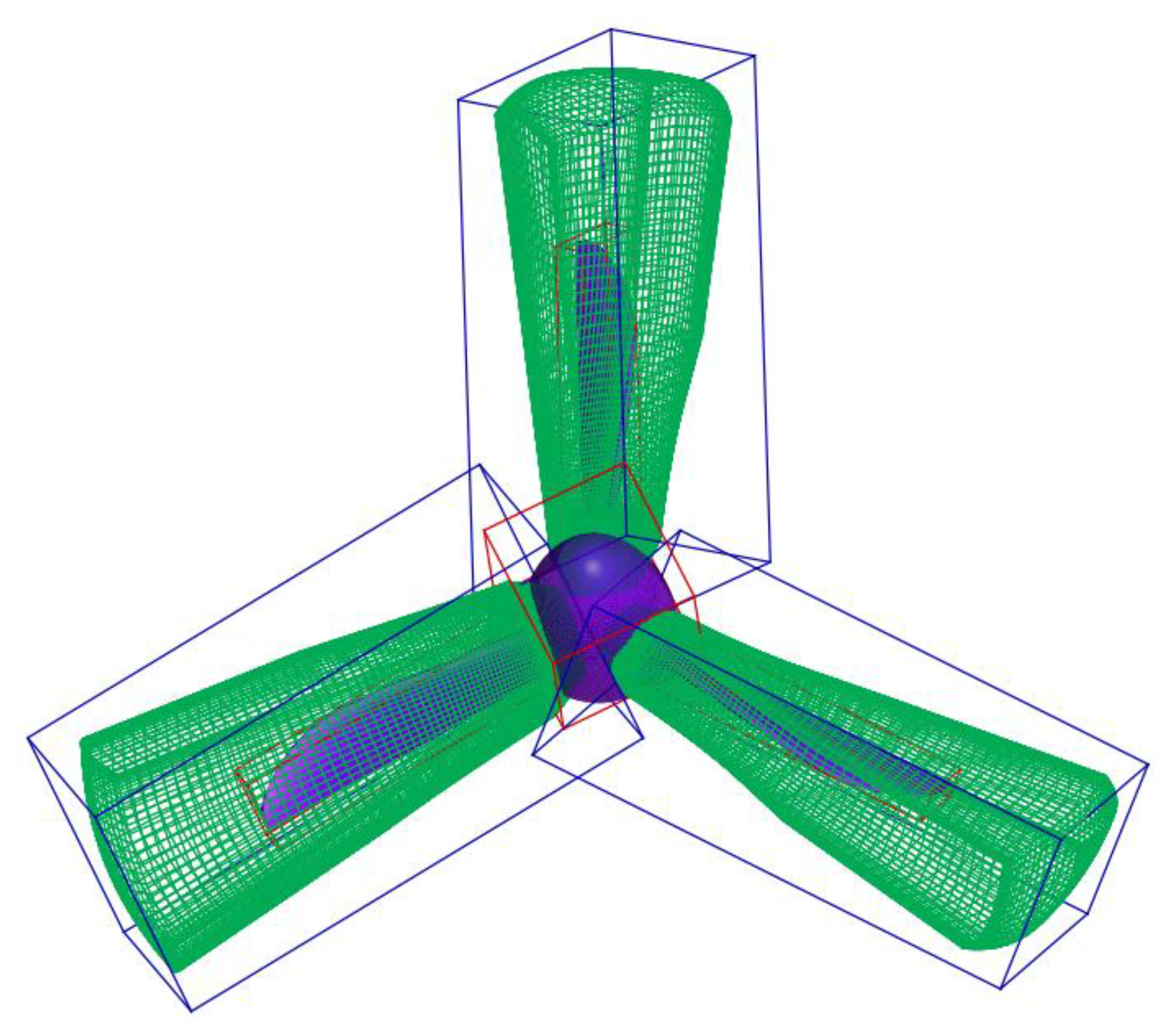
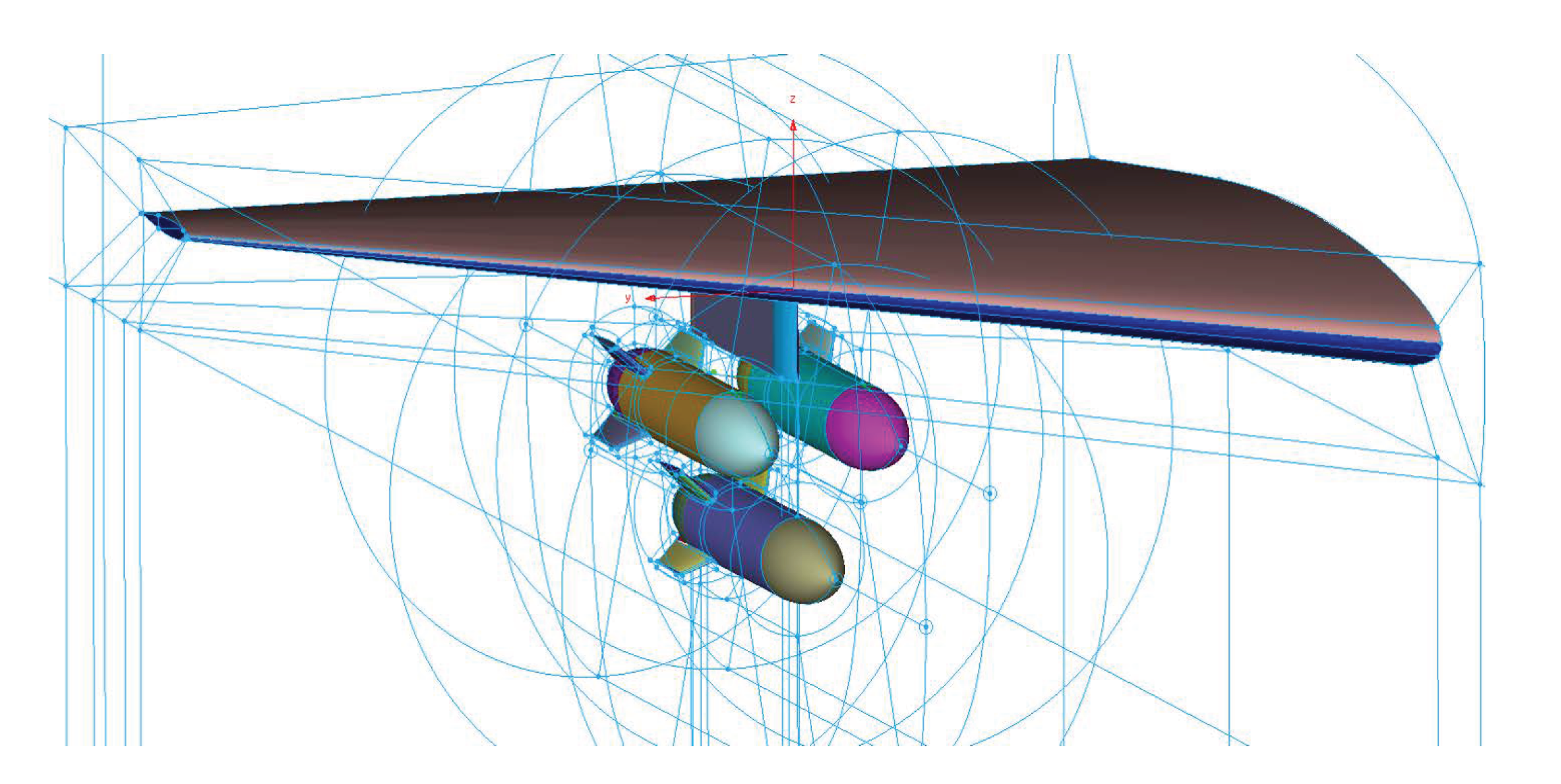
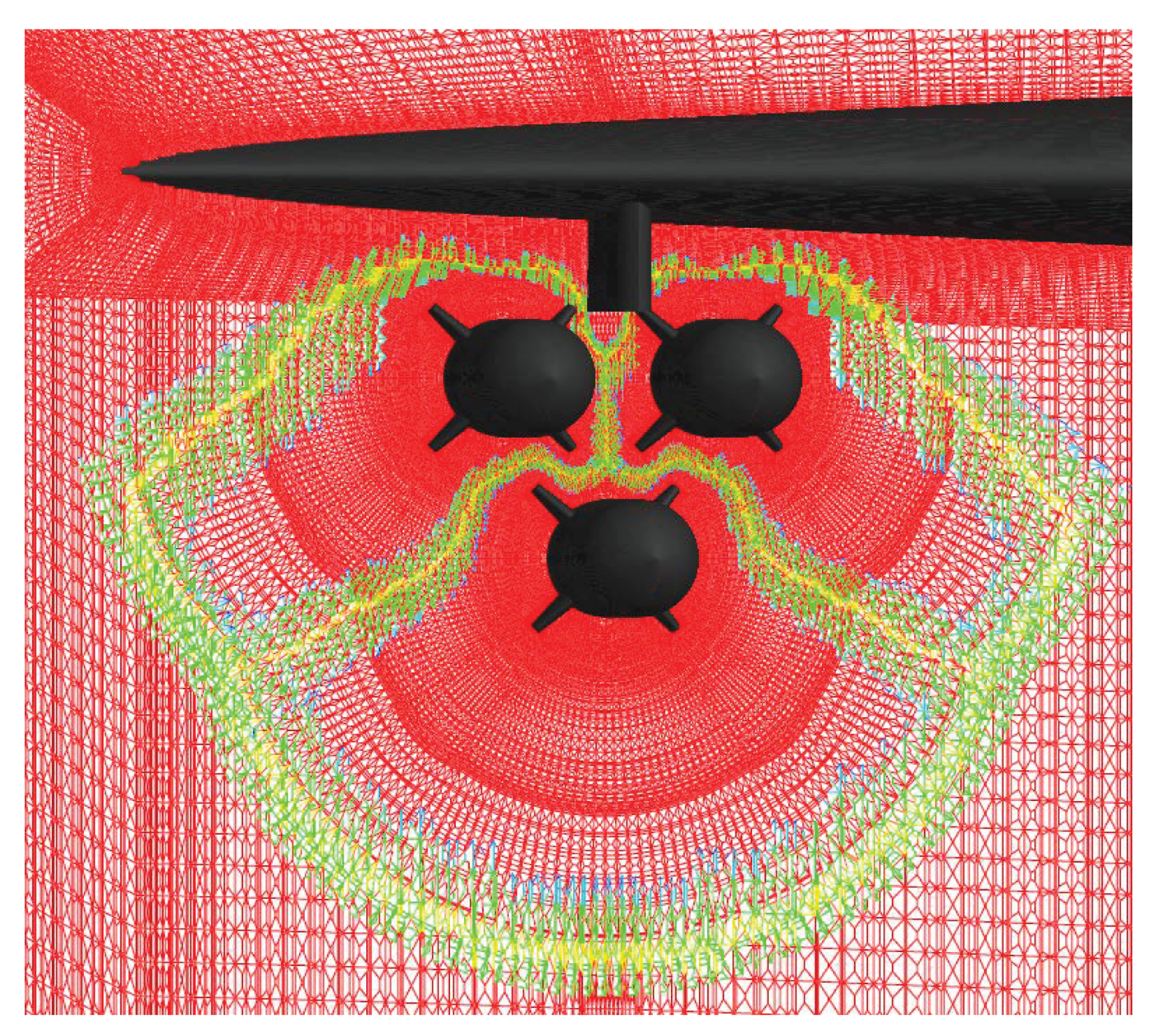
5.1. Assembly for a Seven-Ball Configuration
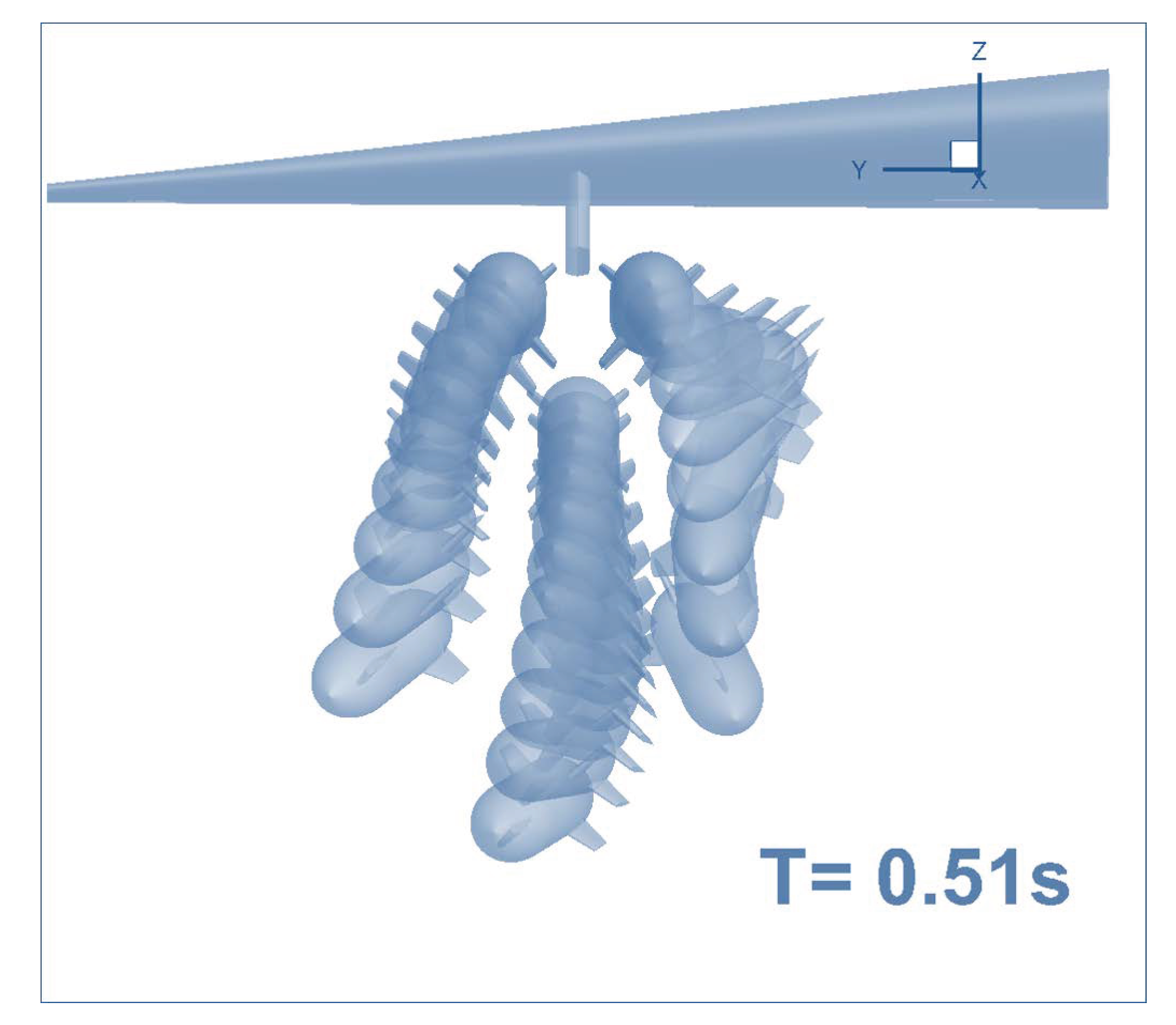
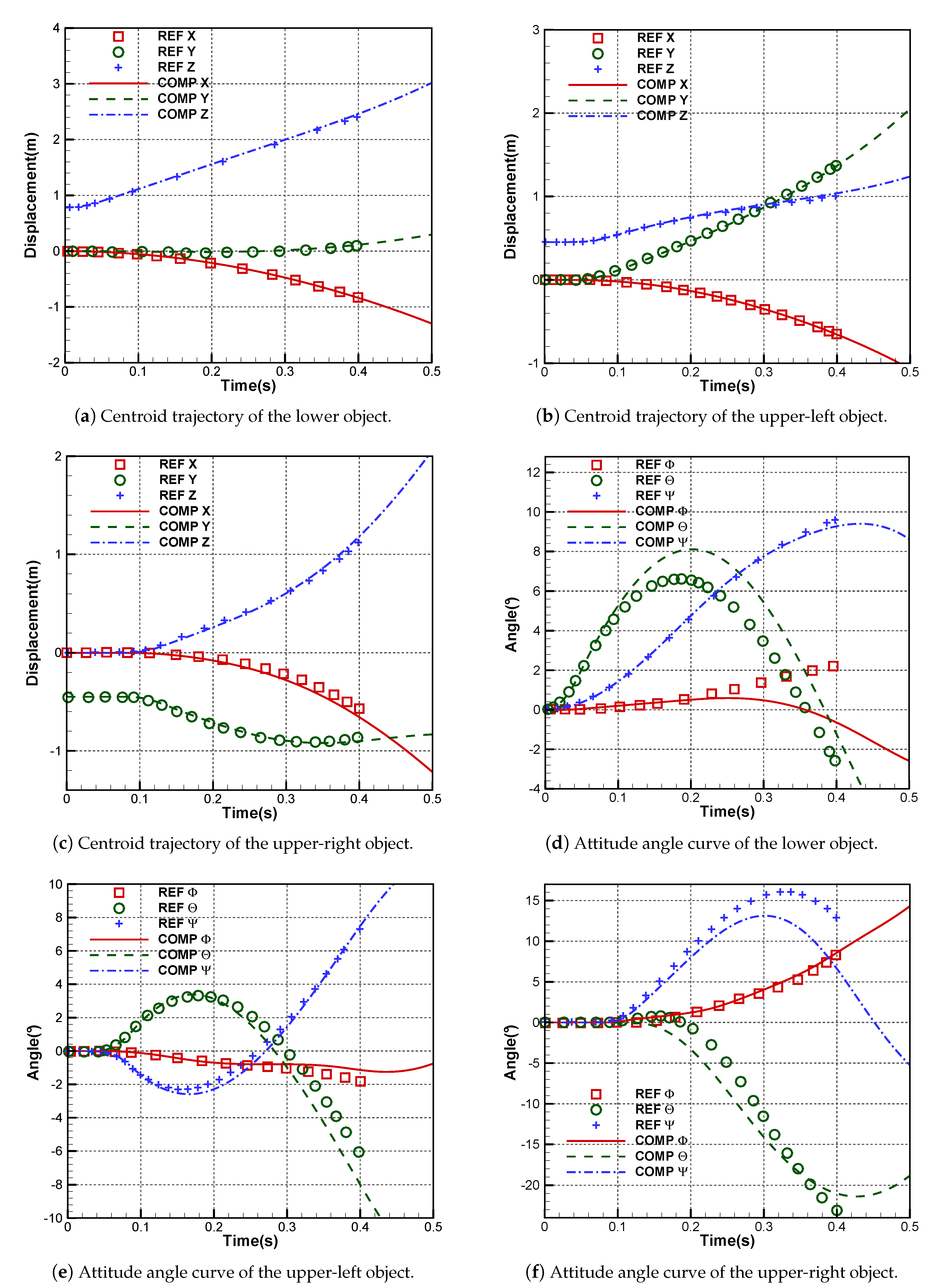
5.2. A Multiple Body Trajectory Prediction Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, C.; Xue, W.; Fu, H. 10M-Core Scalable Fully-Implicit Solver for Nonhydrostatic Atmospheric Dynamics. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Salt Lake City, UT, USA, 13–18 November 2016; pp. 1–12. [Google Scholar]
- Deng, S.; Xiao, T.; van Oudheusden, B.; Bijl, H. A dynamic mesh strategy applied to the simulation of flapping wings. Int. J. Numer. Methods Eng. 2016, 106, 664–680. [Google Scholar] [CrossRef]
- Li, Y.; Paik, K.; Xing, T.; Carrica, P. Dynamic overset cfd simulations of wind turbine aerodynamics. Renew. Energy 2012, 37, 285–298. [Google Scholar] [CrossRef]
- Lu, C.; Shi, Y.; Xu, G. Research on aerodynamic interaction mechanism of rigid coaxial rotor in hover. J. Nanjing Univ. Aeronaut. Astronaut. 2006, 51, 201–207. [Google Scholar]
- Fan, J.; Zhang, H.; Guan, F.; Zhao, J. Studies of aerodynamic interference characteristics for external store separation. J. Natl. Univ. Def. Technol. 2018, 40, 13–21. [Google Scholar]
- Steger, J.; Benek, J. On the use of composite grid schemes in computational aerodynamics. Comput. Methods Appl. Mech. Eng. 1987, 64, 301–320. [Google Scholar] [CrossRef]
- Meakin, R.; Suhs, N. Unsteady aerodynamic simulation of multiple bodies in relative motion. In Proceedings of the 9th Computational Fluid Dynamics Conference, Buffalo, NY, USA, 13–15 June 1989; p. 1996. [Google Scholar]
- Vreman, A. A staggered overset grid method for resolved simulation of incompressible flow around moving spheres. J. Comput. Phys. 2017, 333, 269–296. [Google Scholar] [CrossRef]
- Steger, J.; Dougherty, F.; Benek, J. A Chimera grid scheme. Adv. Grid Gener. ASME 1983, 5, 59–69. [Google Scholar]
- Meakin, R. Object X-rays for cutting holes in composite overset structured grids. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 2537. [Google Scholar]
- Borazjani, I.; Ge, L.; Le, T.; Sotiropoulos, F. A parallel overset-curvilinear-immersed boundary framework for simulating complex 3d incompressible flows. Comput. Fluids 2013, 77, 76–96. [Google Scholar] [CrossRef] [Green Version]
- Lee, Y.L.; Baeder, J. Implicit Hole Cutting—A New Approach to Overset Grid Connectivity. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Liao, W.; Cai, J.; Tsai, H. A multigrid overset grid flow solver with implicit hole cutting method. Comput. Methods Appl. Mech. Eng. 2007, 196, 1701–1715. [Google Scholar] [CrossRef]
- Nakahashi, K.; Togashi, F.; Sharov, D. An Intergrid-boundary definition method for overset unstructured grid approach. AIAA J. 2000, 5, 2077–2084. [Google Scholar] [CrossRef]
- Togashi, F.; Ito, Y.; Nakahashi, K.; Obayashi, S. Extensions of Overset Unstructured Grids to Multiple Bodies in Contact. J. Aircr. 2006, 43, 52–57. [Google Scholar] [CrossRef]
- Landmann, B.; Montagnac, M. A highly automated parallel Chimera method for overset grids based on the implicit hole cutting technique. Int. J. Numer. Methods Fluids 2011, 66, 778–804. [Google Scholar] [CrossRef]
- Meakin, R.; Wissink, A. Unsteady aerodynamic simulation of static and moving bodies using scalable computers. In Proceedings of the 14th AIAA Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1–5 November 1999; p. 3302. [Google Scholar]
- Belk, D.; Maple, R. Automated assembly of structured grids for moving body problems. In Proceedings of the 12th AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995; pp. 381–390. [Google Scholar]
- Suhs, N.; Rogers, S.; Dietz, W. PEGASUS 5: An Automated Pre-Processor for Overset-Grid CFD. AIAA J. 2013, 45, 16–52. [Google Scholar]
- Noack, R.W.; Boger, D.A. Improvements to SUGGAR and DiRTlib for overset store separation simulations. In Proceedings of the 47th AIAA Aerospace Science and Exhibit, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Noack, R.W.; Boger, D.A.; Kunz, R.F.; Carrica, P.M. Suggar++: An improved general overset grid assembly capability. In Proceedings of the 47th AIAA Aerospace Science and Exhibit, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Roget, B.; Sitaraman, J. Robust and Scalable Overset Grid Assembly for Partitioned Unstructured Meshes. In Proceedings of the 51th AIAA Aerospace Science and Exhibit, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Hedayat, M.; Akbarzadeh, A.M.; Borazjani, I. A parallel dynamic overset grid framework for immersed boundary methods. Comput. Fluids 2022, 239, 105378. [Google Scholar] [CrossRef]
- Chang, X.H.; Ma, R.; Zhang, L.P. Parallel implicit hole-cutting method for unstructured overset grid. Acta Aeronaut. Astronaut. Sin. 2018, 39, 121780. [Google Scholar]
- Bergen, G.V.D. A Fast and Robust GJK Implementation for Collision Detection of Convex Objects. J. Graph. Tools 1999, 4, 7–25. [Google Scholar] [CrossRef]
- Bonet, J.; Peraire, J. An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems. Int. J. Numer. Methods Eng. 1991, 31, 1–17. [Google Scholar] [CrossRef]
- Crabill, J.; Witherden, F.D.; Jameson, A. A parallel direct cut algorithm for high-order overset methods with application to a spinning golf ball. J. Comput. Phys. 2018, 374, 692–723. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Qiu, M.; Wang, J.T. Application of CFD in slipstream effect on propeller aircraft research. Acta Aeronaut. Astronaut. Sin. 2019, 40, 1–15. [Google Scholar]
- Prewitt, N.C.; Belk, D.M.; Maple, R.C. Multiple-Body Trajectory Calculations Using the Beggar Code. J. Aircr. 1999, 36, 802–808. [Google Scholar] [CrossRef]
- Davis, D.C.; Howell, K.C. Trajectory evolution in the multi-body problem with applicationsin the Saturnian system. Acta Astronaut. 2011, 69, 1038–1049. [Google Scholar] [CrossRef]





| Name | Type | Description |
|---|---|---|
| numOfSolidWBC | int | the number of solid-wall BC identifiers |
| solidWBC[ ] | int array | the solid-wall identifiers |
| numOfExtBC | int | the number of external BC identifiers |
| externalBC[ ] | int array | the external BC identifiers |
| Name | Type | Description |
|---|---|---|
| zoneIndexSpan | int* | number of processes for each component grid |
| numberOfGridGroups | int | number of component grids |
| xx, yy, zz | double* | coordinates of grid points in current process |
| numberOfNodes | int | number of grid points in current process |
| faceToCellRelation | int* | relationship between two adjacent cells |
| physicalType | int* | boundary condition types for faces |
| numberOfNodesOnFace | int* | number of grid points on each face |
| nodeIndexListOnFace | int* | list of node indexes on face |
| numberOfFaces | int | number of faces on current process |
| geometricType | int* | type of volume cells in current process |
| faceIndexList | int* | list of face indexes around cells in current process |
| numberOfCells | int | number of cells in current process |
| outerZoneList | int* | list of processes owing dual face at border |
| outerFaceList | int* | local indexes of dual faces at border |
| numberOfOuterFaces | int | number of dual faces at domain decomposition border |
| numberOfPhysicalFaces | int | number of physical faces excluding dual faces |
| Name | Type | Description |
|---|---|---|
| sourceRankList | int* | index of process owing interpolation cells |
| sourceCellList | int* | local index of interpolation cells in their processes |
| targetCellList | int* | local index of donor cells in their processes |
| lagrangeFactor | double* | lagrange interpolation factors |
| iblank | int* | type of cells in current process |
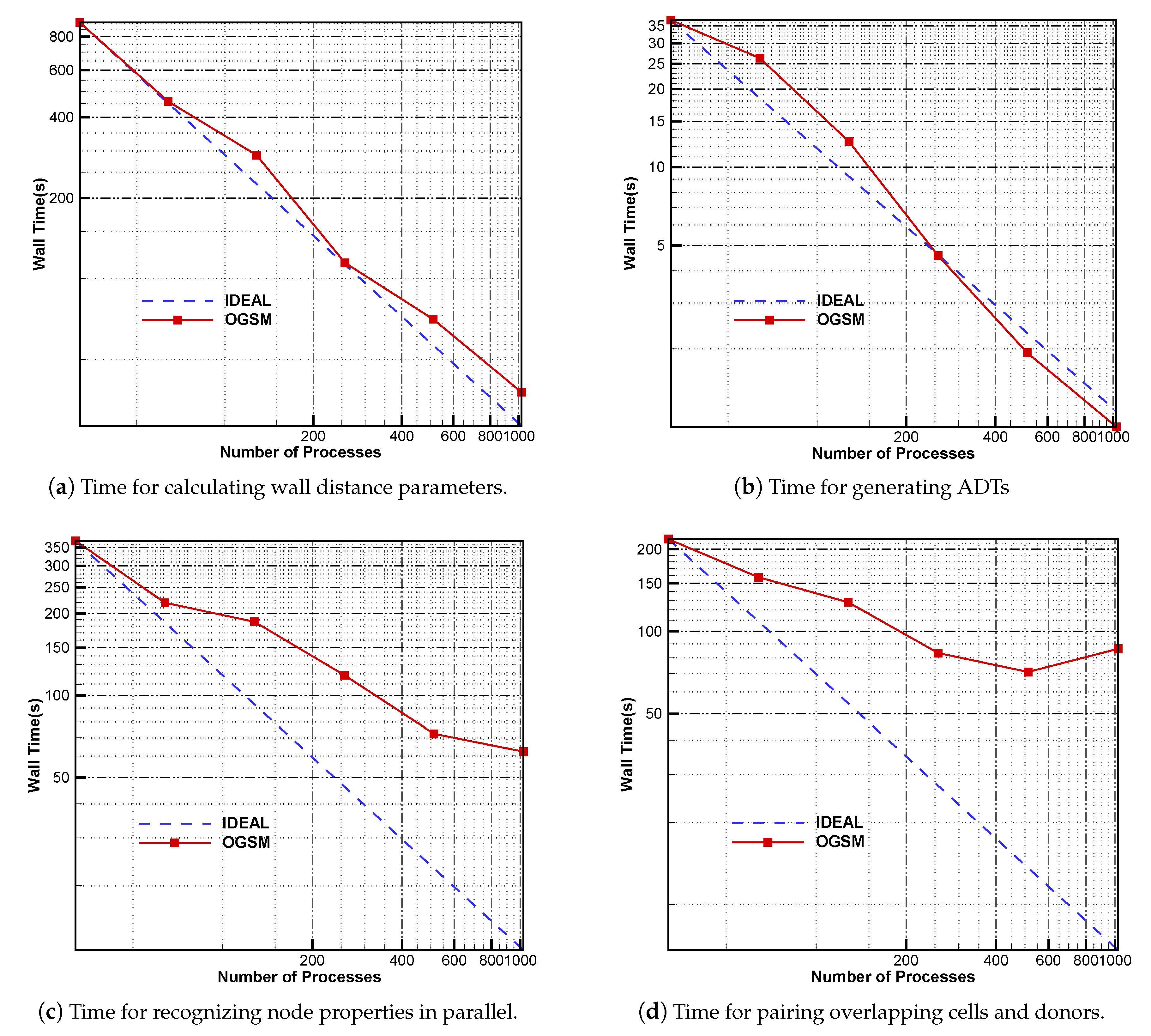
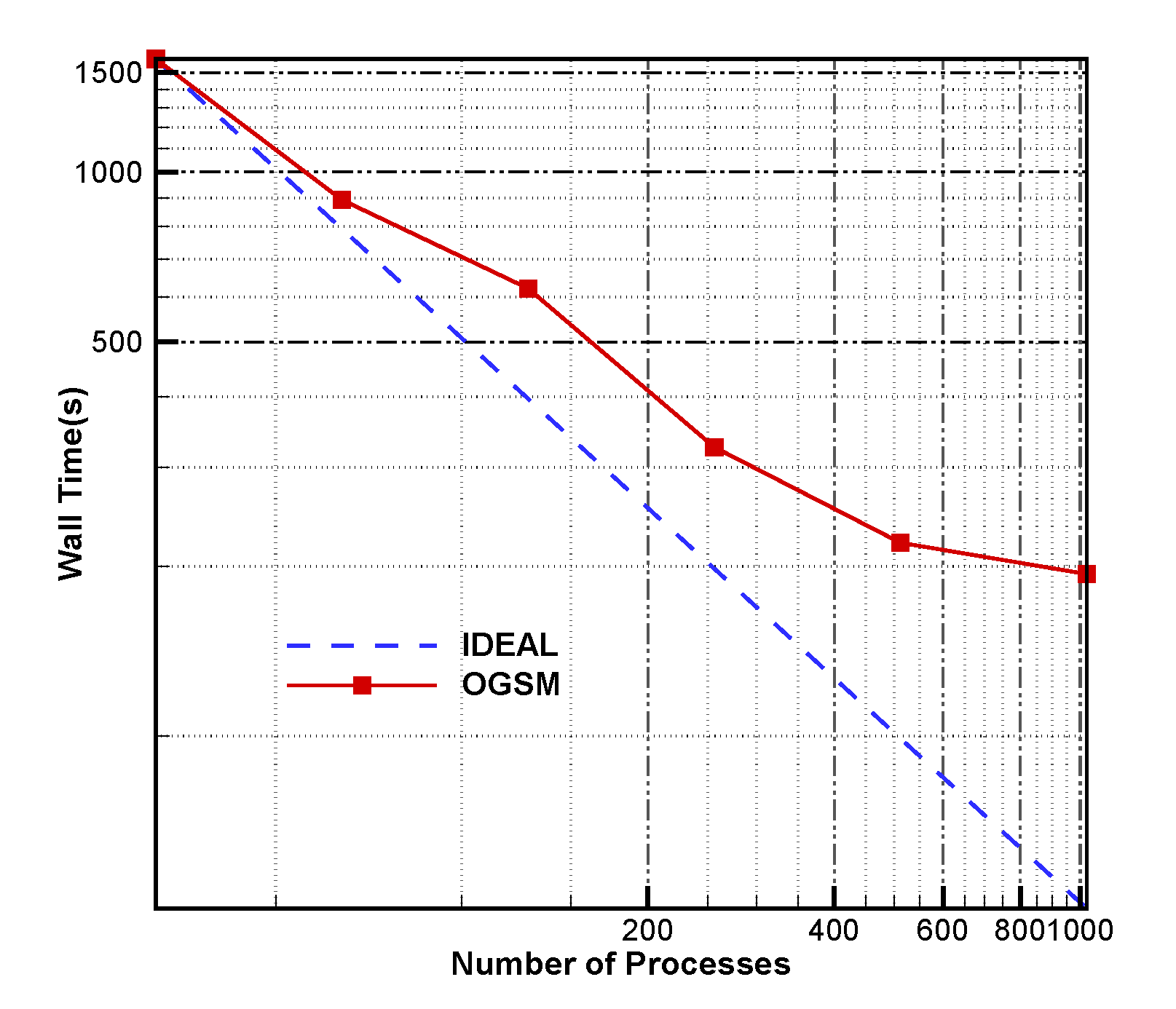
| Subroutine | 32P | 64P | 128P | 256P | 512P | 1024P |
|---|---|---|---|---|---|---|
| ReadGeometry | 19.40 | 31.01 | 21.84 | 8.54 | 13.75 | 0.78 |
| RegContactRel | 53.40 | 28.98 | 4.91 | 3.50 | 3.97 | 6.34 |
| RegOversetRel | 3.09 | 0.98 | 0.57 | 0.37 | 0.33 | 0.20 |
| CalWallDist | 903.95 | 458.84 | 289.34 | 114.76 | 70.61 | 37.71 |
| ExOutQryNode | 0.19 | 0.21 | 0.02 | 0.00 | 0.02 | 0.00 |
| GenBgrdTree | 36.85 | 26.29 | 12.56 | 4.57 | 1.93 | 1.00 |
| ConfrmQryNode | 368.37 | 217.68 | 185.73 | 118.50 | 72.27 | 62.23 |
| ClassifyElems | 2.40 | 1.71 | 0.83 | 0.37 | 0.18 | 0.06 |
| AssemblyElems | 215.92 | 154.91 | 124.19 | 76.95 | 59.20 | 63.28 |
| SewingGrid | 2.11 | 3.23 | 3.70 | 6.38 | 11.84 | 23.10 |
| WritingFile | 169.50 | 115.22 | 160.07 | 148.76 | 148.66 | 138.09 |
| TotalTime | 1775.18 | 1039.06 | 803.76 | 482.70 | 382.76 | 332.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, F.; Guo, Y.; Zhao, B.; Jiang, X.; Chen, B.; Wang, Z.; Xiao, Z. OGSM: A Parallel Implicit Assembly Algorithm and Library for Overlapping Grids. Appl. Sci. 2022, 12, 7804. https://doi.org/10.3390/app12157804
Lu F, Guo Y, Zhao B, Jiang X, Chen B, Wang Z, Xiao Z. OGSM: A Parallel Implicit Assembly Algorithm and Library for Overlapping Grids. Applied Sciences. 2022; 12(15):7804. https://doi.org/10.3390/app12157804
Chicago/Turabian StyleLu, Fengshun, Yongheng Guo, Bendong Zhao, Xiong Jiang, Bo Chen, Ziwei Wang, and Zhongyun Xiao. 2022. "OGSM: A Parallel Implicit Assembly Algorithm and Library for Overlapping Grids" Applied Sciences 12, no. 15: 7804. https://doi.org/10.3390/app12157804
APA StyleLu, F., Guo, Y., Zhao, B., Jiang, X., Chen, B., Wang, Z., & Xiao, Z. (2022). OGSM: A Parallel Implicit Assembly Algorithm and Library for Overlapping Grids. Applied Sciences, 12(15), 7804. https://doi.org/10.3390/app12157804






