A Finite Element Model for Monitoring the Displacement of Pipelines in Landslide Regions by Discrete FBG Strain Sensors

Abstract

This study investigates a system for monitoring displacements of underground pipelines in landslide-prone regions. This information is an important alarm indicator, not only to prevent the failure of the line itself but also to mitigate the direct consequences of landslides on buildings and infrastructures in the affected area. Specifically, a numerical processing tool coupled with a data acquisition system is proposed. The starting point is the measurement of axial strain at three points of discrete sections of the pipeline by Fiber Bragg grating sensors, used to approximate the trend of mean axial strain and bending curvatures along the pipe axis. A finite element analysis based on a 3D geometrically exact beam model is developed for computing the deformed configuration corresponding to the input strain field. After assigning the boundary conditions, a mixed iterative scheme is used for a quick solution to the nonlinear problem. Firstly, the tool is validated theoretically with benchmarks on beam-like structures undergoing large deflections. Then, experimental results are produced on a monitored pipe buried in a wedge of land subject to an artificial slide. The overall sensor-modeling system, with zero displacements far from the landslide as a boundary condition, provides a satisfactory displacement trend with a mean error of about $18\%$ with just three effective monitored sections in the affected pipe stretch of 18 m. The acquisition and processing tool is implemented in a web application as a real-time alarm system.

1. Introduction

Various types of sensors have been developed over the years to obtain real-time measurements of structures. Among the others, we can find those for monitoring vibration, pressure, and strain [1,2,3]. The most widely known strain sensors are those able to provide one-directional values in control points of the structure such as Fiber Bragg grating (FBG) sensors [4], which have been the subject of intense research and development [5] and numerous industry applications for monitoring of bridges, tanks, and concrete structures [6] since this technology overcomes some difficulties related to installation, calibration, and maintenance. A relevant example of application is the monitoring of underground pipelines. These infrastructures are aimed to transport methane gas, petroleum products, water, etc. They are usually designed for a working life of about 25–30 years. However, the lines often remain in service for a much longer time, thanks to technologies of integrity assessment. One of the main sources of risk for such infrastructures is ground movement [3,7]. Indeed, due to the growing difficulties in finding safe routes, engineers are often forced to consider sites with a certain geological instability. In addition, in seismic areas like Italy, the country of the authors, unexpected landslides, liquefaction of sandy soils, and/or significant permanent deformations in the soil can also be caused by earthquakes. Ground movements cause additional stress, strain, and displacement states in the pipeline with respect to those produced by the operating actions such as pressure and temperature variations, which are a possible source of failure, e.g., for a stress exceeding the material strength or for deformations compromising the usability. The trend of stress and deformation states over the years is difficult to estimate reliably in the design stage. This is the reason why tools of structural monitoring are highly requested, especially for mitigating the risk in pipelines intended for fluid transport, considering that a failure may lead to serious consequences.

While many studies on strain monitoring have been reported [8,9], only a very few proposals concern the deflection monitoring of a pipeline caused by a landslide. We can cite, for instance, the proposal in [10], where the deflection curve is reconstructed by exploiting measurements coming from inclinometers. This information is an important alarm indicator, not only to prevent the failure of the line itself but also to mitigate the direct consequences of landslides on buildings and infrastructures in the affected area.

The objective of this work is the development and validation of an integrated sensor-modeling tool for monitoring the displacement trend of pipelines subjected to significant ground motions. Specifically, three FBG sensors are employed at control cross-sections of the pipe. These provide three point values of the axial strain which are used for the evaluation of mean axial strain and the two bending curvatures. The hypotheses of rigid (plane) sections and negligible shear and torsional effects are assumed. Firstly, the trend of mean axial strain and bending curvatures is directly utilized to estimate the maximum normal stress over the structure. In addition, it is shown how this information can be used for predicting the displacement of underground pipelines. The procedure consists in interpolating the values of the discrete control sections in order to estimate the strain field along the pipe. Then, a 3D geometrically exact Simo–Reissner beam model [11] discretized with Lagrangian finite elements is adopted to model the pipeline. A variational formulation is developed for reconstructing the finite kinematics starting from the known strain field. A mixed iterative scheme [12] is employed for a very robust and quick solution of the nonlinear discrete equations. The model can be applied to problems with arbitrarily large displacements and rotations. The use of a simple finite element beam solution is the main difference with the local material basis method proposed [13,14] based on a localized linearization approach. Our proposal can be easily implemented in all well-established commercial finite element codes for structural application to achieve a robust and optimized solution. The tool is firstly validated theoretically with benchmarks on beam-like structures undergoing large deflections. Then, experimental results are produced on a monitored pipe buried in a wedge of land subject to an artificial slide. Negligible displacements are assumed far from the landslide influence as boundary conditions of the model. Finally, the displacements predicted by the sensor-modeling proposal are compared with the displacement trend measured in situ. A web application is also implemented for data acquisition and processing, to provide a real-time alarm detection system.

The novel idea of the proposal can be summarized as follows: how to use FBG sensors for monitoring large displacements of pipelines using a simple and robust finite element model. In addition, experimental validation is provided. The paper is organized using the following structure: Section 2 recalls the FBG technology for the strain measurement; Section 3 introduces the geometrically exact 3D beam model for reconstructing the finite kinematics of the pipeline due to discrete measured strain values; Section 4 describes the finite element model, the efficient solution of the nonlinear discrete equations, and the validation of the numerical model with benchmark structures; Section 5 concerns the experimental setup for a monitored pipe buried in a wedge of land subject to an artificial slide; Section 6 reports and compares experimental and numerical results, in order to assess the proposed monitoring tool; Section 7 shows some details of the web application; conclusions are drawn in the last section.

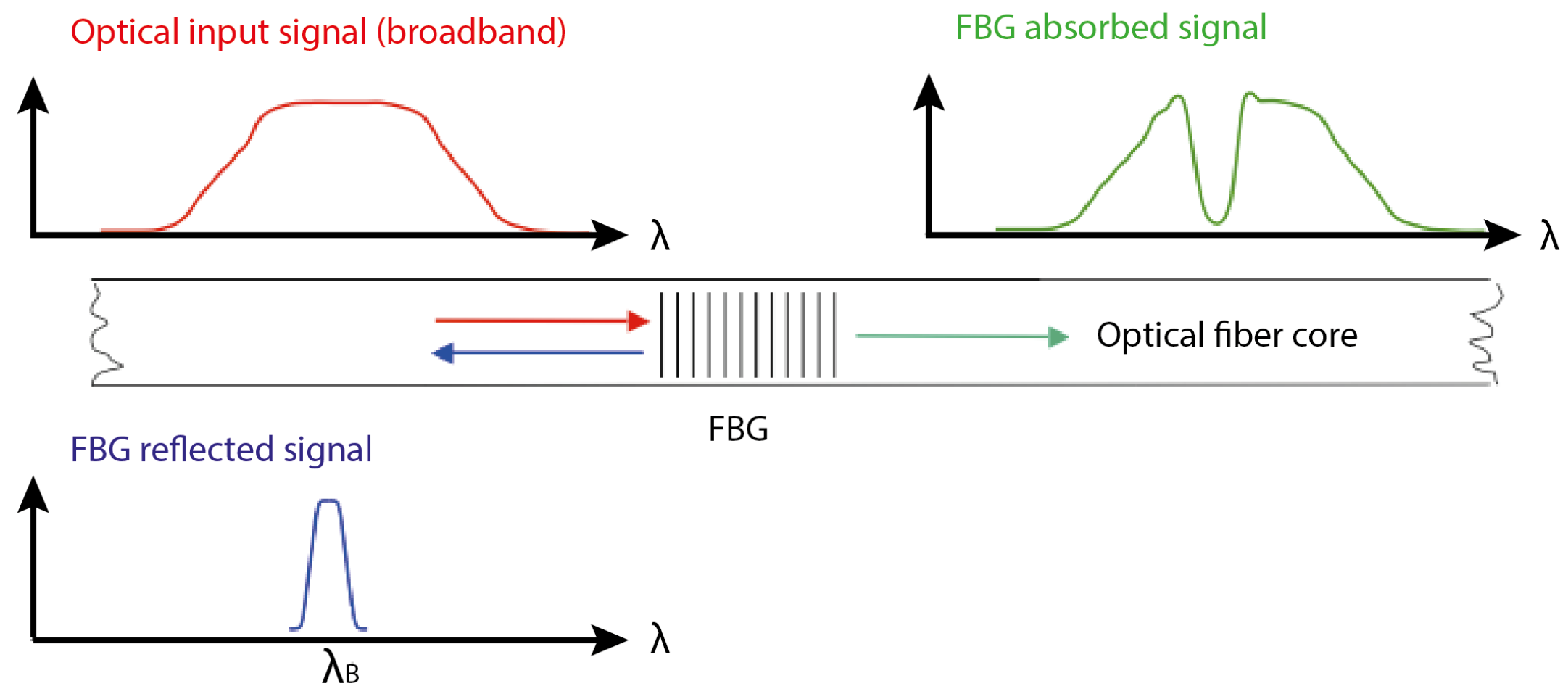
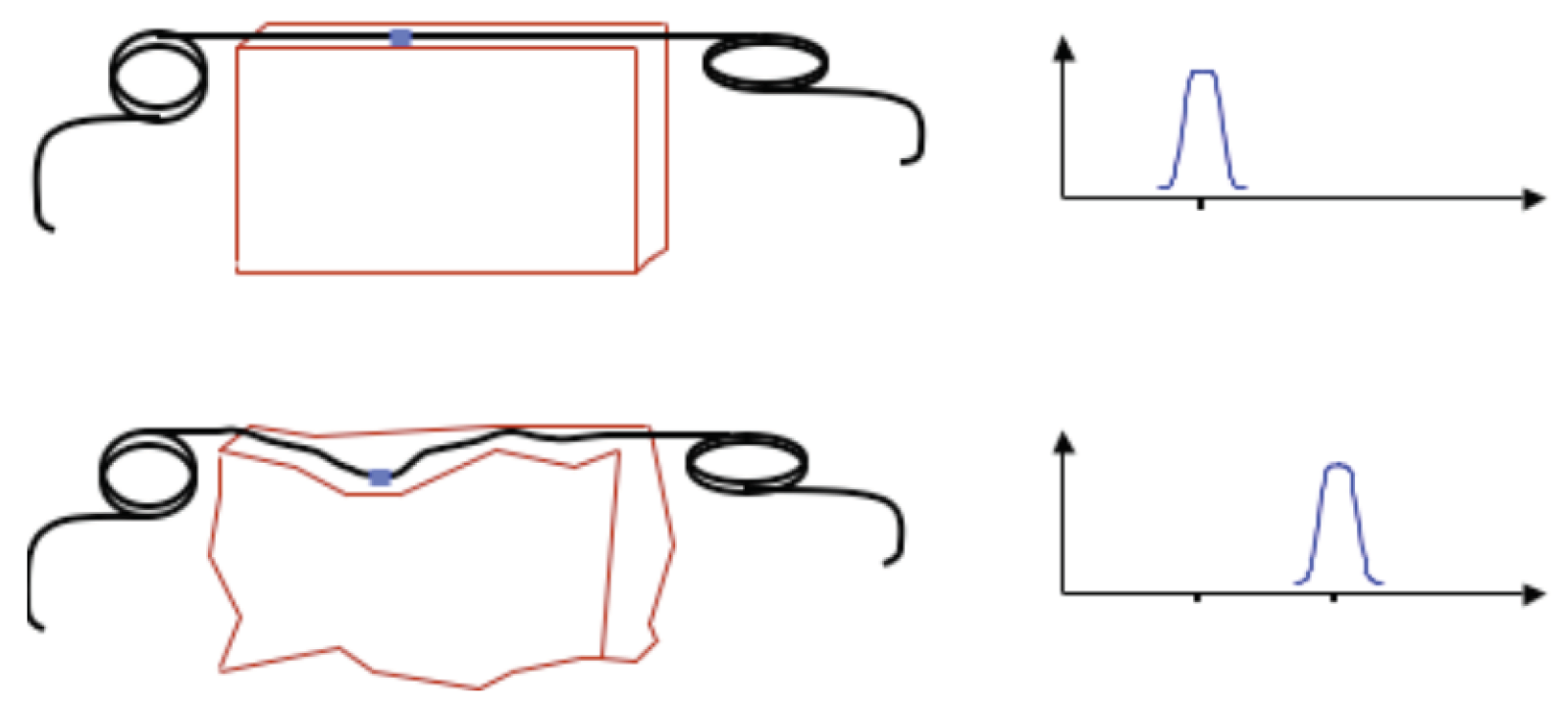
2. FBG Technology

The technology currently used by the main gas network operators in Italy to detect pipeline strains consists of strain gauge bars with vibrating wire. The vibrating string transducer is essentially composed of a wire tensioned at both ends, able to vibrate at its natural frequency. The vibration frequency varies according to the tension of the wire, which is related to small relative movements between the two ends. However, this method presents some strong limitations, including, for example:

• Difficulty to communicate via radio in inaccessible areas, thus requiring installation of repeaters;
• Necessity to install control units locally for processing and sending signals for each strain gauge station;
• Electrical signal attenuation over long-distance transmission;
• Sensor damages due to the high magnetic fields generated by pigging tools.

FBG technology can overcome issues of conventional electrical sensing. In fact:

• Reflected light, used as a signal carrier through the optical cable, is resilient to harsh environments;
• Complexity of monitoring system architecture is reduced since optical cables may embed several gratings, simultaneously interrogated by a single acquisition unit with multiplexing capability.

Moreover, this technology ensures by design:

• Minimal attenuation of the optical signal along the measurement chain;
• Immunity to electromagnetic interference.

The working principle of Bragg grating fiber is based on its ability to reflect wavelengths like a mirror: when the FBG is crossed by the light coming from a broadband source, only a narrow range of wavelength centered on the Bragg wavelength ${\lambda }_B$ is reflected back (see Figure 1). The remaining light continues to propagate along the optical fiber to the next grating without signal loss [3]. Both strain and temperature variations cause changes in the sensor grating period, thus producing a shift of the characteristic wavelength peak ${\lambda }_B$. These changes in the back-reflected spectrum are detected by the same acquisition unit that emits the broadband light. In this way, each frequency acquired can be associated with the corresponding FBG and processed in order to obtain strain (see Figure 2) and temperature measurements. Thanks to the operating principle, it is possible to connect FBG sensors in series, possibly on several channels: since FBG is uniquely identified by its characteristic ${\lambda }_B$, it is then possible to correlate strain and temperature changes to the progressive FBG position along the pipeline.

3. Geometrically Exact 3D Beam Model and Variational Form for Assigned Strains

The nonlinear 3D beam model for large displacements and rotations used for the numerical prediction is a reformulation of that presented in [15], summarized recently in [16], in a variational form able to provide the finite kinematics of the structure from an assigned (measured) strain field.

The parametrization of finite rotations in 3D space is a nontrivial problem, mainly because of the nonlinear character of the 3D rotation space. In order to make the numerical model as simple as possible and to optimize the computational cost, a total Lagrangian formulation based on the parameterization of 3D rotations by means of the pseudo rotation vector is used.

This choice is convenient since it requires a minimal number of parameters, makes the modeling of boundary conditions easy, and allows for additive updates in incremental analysis. On the other hand, the direct interpolation of the total rotation vector has some drawbacks: (i) the singularity of the operators involved for rotation magnitude of $2\pi$; (ii) a numerical non-objective discrete model.

Both these drawbacks are not so significant for this case study since rotations and displacements can be large but their magnitude has to be considered far from the singularity threshold; the objectivity error, which is a discretization error, is very small when a quadratic interpolation is used and for the number of finite elements usually adopted and its effect is practically negligible for the technical application under consideration. Therefore, the use of the total Lagrangian approach with a total rotation vector seems to be the most attractive choice for its simplicity and efficiency.

However, for arbitrarily large rotations, the singularity can be avoided using the incremental rotation vector [17,18,19] or using the corotational strategy with the exact strain measure recently proposed in [16], which also eliminates the objectivity and path-dependence issues of the former.

Other beam models could be also employed, like for instance a 3D Kirchhoff beam [20]. However, a higher continuity of the approximation functions is required in the Kirchhoff model.

3.1. Rotation Tensor

Finite rotation algebra is involved in large deformation analysis of 3D beams. We refer readers to [17,18,21,22,23] among the great amount of work available in the literature on the topic.

Finite 3D rotations can be described by an orthogonal tensor $\mathbf{R}$ belonging to the nonlinear manifold SO₃. The properties ${\mathbf{R}}^{-1}={\mathbf{R}}^T$ and det $\mathbf{R}=1$ allow us to express $\mathbf{R}$ in terms of only three parameters. A useful way to parametrize $\mathbf{R}$ is the use of the rotation vector $\mathbf{\phi }$ because it lies in a vector space:

$${\displaystyle \mathbf{R}}\left(\mathbf{\phi }\right)={\displaystyle \mathbf{I}}+a_1\left(\phi \right){\displaystyle \mathbf{W}}\left(\mathbf{\phi }\right)+\frac{1}{2}{a}_2\left(\phi \right){\displaystyle \mathbf{W}}{\left(\mathbf{\phi }\right)}^2$$

(1)

where $\phi =\sqrt{{\mathbf{\phi }}^T\mathbf{\phi }}$ is the rotation magnitude and $\mathbf{W}\left(\mathbf{\phi }\right)$ is the spin tensor corresponding to $\mathbf{\phi }$, i.e., $\mathbf{W}\left(\mathbf{\phi }\right)\mathbf{v}=\mathbf{\phi }\times \mathbf{v}$ for all vectors $\mathbf{v}$, where × denotes the cross product. As reported in [15], the trigonometric functions $a_1\left(\phi \right)$ and $a_2\left(\phi \right)$ are

$$a_1\left(\phi \right)=\frac{sin\phi }{\phi },a_2\left(\phi \right)=\frac{1-cos\phi }{{\phi }^2}.$$

This parameterization uses the minimal set of parameters to describe the rotation and gives a one-to-one correspondence between $\mathbf{R}$ and $\mathbf{\phi }$ in the range $0\le \phi <2\pi$ [15,18].

For future use, we also introduce the second order tensor $\mathbf{T}$ defined as

$${\displaystyle \mathbf{T}}\left(\mathbf{\phi }\right)={\displaystyle \mathbf{I}}+a_2\left(\phi \right){\displaystyle \mathbf{W}}\left(\mathbf{\phi }\right)+\frac{1}{2}{a}_3\left(\phi \right){\displaystyle \mathbf{W}}{\left(\mathbf{\phi }\right)}^2$$

(2)

with

$$a_3\left(\phi \right)=\frac{\phi -sin\phi }{{\phi }^3}.$$

so that, as reported in [24], we have the equivalence

$$\mathrm{axial}\left({{\displaystyle \mathbf{R}}}^T{\displaystyle \mathbf{R}}{,}_s\right)\equiv {\displaystyle \mathbf{T}}{\left(\mathbf{\phi }\right)}^T\mathbf{\phi }{,}_s$$

where $\mathrm{axial}\left(.\right)$ denotes the extraction of the axial vector from a skew tensor.

3.2. Variations of Rotation and Curvature Tensors with Respect to the Rotation Vector

The variations of $\mathbf{R}$ can be expressed in terms of the rotation vector $\mathbf{\phi }$, which belongs to a vector space. In this case, we can define them more easily by standard directional derivatives [15,22] as

$$\delta {\displaystyle \mathbf{R}}=\frac{d}{dt}{\left[{\displaystyle \mathbf{R}}(\mathbf{\phi }+t\delta \mathbf{\phi })\right]}_{t=0}.$$

(3)

The weak formulation of the beam problem will require the first and second variations of tensors ${\mathbf{R}}^T$ and ${\mathbf{T}}^T$ in terms of the variation of $\mathbf{\phi }$. Following [15], for any constant vectors $\mathbf{a}$ and $\mathbf{c}$, the first variations can be written as

$$\left\{\begin{array}{cc}\hfill \delta {{\displaystyle \mathbf{R}}}^T{\displaystyle \mathbf{a}}& ={{\displaystyle \mathbf{Q}}}_{R^T}({\displaystyle \mathbf{a}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \\ \hfill \delta {{\displaystyle \mathbf{T}}}^T{\displaystyle \mathbf{a}}& ={{\displaystyle \mathbf{Q}}}_{T^T}({\displaystyle \mathbf{a}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \end{array}\right.\mathrm{and}\left\{\begin{array}{cc}\hfill \delta {\displaystyle \mathbf{R}}{\displaystyle \mathbf{a}}& ={{\displaystyle \mathbf{Q}}}_R({\displaystyle \mathbf{a}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \\ \hfill \delta {\displaystyle \mathbf{T}}{\displaystyle \mathbf{a}}& ={{\displaystyle \mathbf{Q}}}_T({\displaystyle \mathbf{a}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \end{array}\right.$$

(4)

with the following equivalences

$$\begin{array}{cc}\hfill & {{\displaystyle \mathbf{a}}}^T{{\displaystyle \mathbf{Q}}}_{R^T}({\displaystyle \mathbf{c}},\mathbf{\phi })\delta \mathbf{\phi }={{\displaystyle \mathbf{c}}}^T{{\displaystyle \mathbf{Q}}}_R({\displaystyle \mathbf{a}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \\ \hfill & {{\displaystyle \mathbf{a}}}^T{{\displaystyle \mathbf{Q}}}_{T^T}({\displaystyle \mathbf{c}},\mathbf{\phi })\delta \mathbf{\phi }={{\displaystyle \mathbf{c}}}^T{{\displaystyle \mathbf{Q}}}_T({\displaystyle \mathbf{a}},\mathbf{\phi })\delta \mathbf{\phi }.\hfill \end{array}$$

(5)

Using a dot to denote a successive variation of $\delta \mathbf{R}$ and $\delta \mathbf{T}$ in direction $\dot{\mathbf{\phi }}$, we have

$$\left\{\begin{array}{cc}\hfill {{\displaystyle \mathbf{a}}}^T\delta \dot{\mathbf{R}}{\displaystyle \mathbf{c}}& ={\dot{\mathbf{\phi }}}^T{{\displaystyle \mathbf{\Gamma }}}_R({\displaystyle \mathbf{a}},{\displaystyle \mathbf{c}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \\ \hfill {{\displaystyle \mathbf{a}}}^T\delta \dot{\mathbf{T}}{\displaystyle \mathbf{c}}& ={\dot{\mathbf{\phi }}}^T{{\displaystyle \mathbf{\Gamma }}}_T({\displaystyle \mathbf{a}},{\displaystyle \mathbf{c}},\mathbf{\phi })\delta \mathbf{\phi }\hfill \end{array}\right.$$

(6)

with ${\mathbf{\Gamma }}_R(\mathbf{a},\mathbf{c},\mathbf{\phi })\ne {\mathbf{\Gamma }}_R(\mathbf{a},\mathbf{c},\mathbf{\phi })$. The expression of the operators ${\mathbf{Q}}_{R^T}$, ${\mathbf{Q}}_{T^T}$, ${\mathbf{Q}}_R$, ${\mathbf{Q}}_T$, ${\mathbf{\Gamma }}_R$, and ${\mathbf{\Gamma }}_T$ is reported explicitly in [15,16].

3.3. Kinematics of the 3D Beam Structural Model

The 3D shear deformable beams represent the structural model under consideration, which is now briefly recalled also in order to introduce some notation. The beam axis in the initial reference configuration is defined by a curve $s\mapsto {\mathbf{r}}_0\left(s\right)\in {\mathbb{R}}^3$ with the curvilinear abscissa $s\in [0,\ell ]$ and ℓ the initial length of the beam axis. The description of the reference configuration is completed by a field of right-handed orthonormal triads $s\mapsto \{{\mathbf{G}}_1\left(s\right),{\mathbf{G}}_2\left(s\right),{\mathbf{G}}_3\left(s\right)\}$ also known as material triads. The triad is attached to the beam cross-section, assumed to be rigid. The first vector of the triad is the unit tangent vector of the initial beam axis

$${{\displaystyle \mathbf{G}}}_1={{\displaystyle \mathbf{r}}}_0{,}_s$$

(7)

where a comma stands for derivative, while ${\mathbf{G}}_2$ and ${\mathbf{G}}_3$ are aligned with the principal axes of the section. Letting $\{{\mathbf{e}}_1,{\mathbf{e}}_2,{\mathbf{e}}_3\}$ the orthonormal vectors of a fixed Cartesian system, the rotation from global frame to material local frame is defined by the rotation matrix ${\mathbf{R}}_0\left(s\right)$:

$${{\displaystyle \mathbf{G}}}_i={{\displaystyle \mathbf{R}}}_0{{\displaystyle \mathbf{e}}}_{i}i=1\cdots 3\Rightarrow {{\displaystyle \mathbf{R}}}_0=\sum _{i=1}^3{{\displaystyle \mathbf{G}}}_i\otimes {{\displaystyle \mathbf{e}}}_i.$$

where ⊗ denotes the tensor product. The initial beam configuration is then defined by the pair $({\mathbf{r}}_0,{\mathbf{R}}_0)\in {\mathbb{R}}^3\times SO\left(3\right)$. Similarly, we can define the current configuration using the current axis positions $\mathbf{r}\left(s\right)={\mathbf{r}}_0\left(s\right)+\mathit{u}\left(s\right)$, with $\mathit{u}\left(s\right)$ the displacement of the beam axis, and the current orientations $\{{\mathbf{g}}_1,{\mathbf{g}}_2,{\mathbf{g}}_3\}$ defined by the rotation $\mathbf{R}\left(s\right)$:

$${{\displaystyle \mathbf{g}}}_i={\displaystyle \mathbf{R}}{{\displaystyle \mathbf{G}}}_i={\displaystyle \mathbf{R}}{{\displaystyle \mathbf{R}}}_0{{\displaystyle \mathbf{e}}}_i,i=1\cdots 3\Rightarrow {\displaystyle \mathbf{R}}=\sum _i{{\displaystyle \mathbf{g}}}_i\otimes {{\displaystyle \mathbf{G}}}_i.$$

The material strain measure [18] for the beam is

$$\mathbf{\epsilon }\left(s\right)\equiv {{\displaystyle \mathbf{R}}}^T{\displaystyle \mathbf{r}}{,}_s-{{\displaystyle \mathbf{G}}}_1,\mathbf{\chi }\left(s\right)=\mathrm{axial}\left({{\displaystyle \mathbf{R}}}^T{\displaystyle \mathbf{R}}{,}_s\right).$$

(8)

In terms of the rotation vector, the curvature can be written as

$$\mathbf{\chi }\left(s\right)\equiv \mathrm{axial}\left({{\displaystyle \mathbf{R}}}^T{\displaystyle \mathbf{R}}{,}_s\right)={\displaystyle \mathbf{T}}{\left(\mathbf{\phi }\right)}^T\mathbf{\phi }{,}_s$$

(9)

with tensor $\mathbf{T}$ defined in Equation (2). Vectors $\mathbf{\epsilon }$ and $\mathbf{\chi }$ collect strain variables work-conjugate to material resultant forces $\mathbf{n}$ and moments $\mathbf{m}$. The constitutive law can be expressed, for hyperelastic materials, as

$$\left[\begin{array}{c}{\displaystyle \mathbf{n}}\left(s\right)\\ {\displaystyle \mathbf{m}}\left(s\right)\end{array}\right]=\left[\begin{array}{cc}{{\displaystyle \mathbf{C}}}_{nn}& {{\displaystyle \mathbf{C}}}_{nm}\\ {{\displaystyle \mathbf{C}}}_{nm}^T& {{\displaystyle \mathbf{C}}}_{mm}\end{array}\right]\left[\begin{array}{c}\mathbf{\epsilon }\left(s\right)\\ \mathbf{\chi }\left(s\right)\end{array}\right].$$

(10)

Defining

$$\mathbf{\rho }=\left[\begin{array}{c}\mathbf{\epsilon }\\ \mathbf{\chi }\end{array}\right]\mathbf{\tau }=\left[\begin{array}{c}{\displaystyle \mathbf{n}}\\ {\displaystyle \mathbf{m}}\end{array}\right]{{\displaystyle \mathbf{C}}}_{\rho }=\left[\begin{array}{cc}{{\displaystyle \mathbf{C}}}_{nn}& {{\displaystyle \mathbf{C}}}_{nm}\\ {{\displaystyle \mathbf{C}}}_{nm}^T& {{\displaystyle \mathbf{C}}}_{mm}\end{array}\right]$$

we can write the constitutive law using the compact notation

$$\mathbf{\tau }={{\displaystyle \mathbf{C}}}_{\rho }\mathbf{\rho }$$

The strain energy of the beam can be expressed in a displacement-based form as

$$\Phi \left(u\right)=\frac{1}{2}{\int }_0^{\ell }\left\{{\mathbf{\rho }}^T{{\displaystyle \mathbf{C}}}_{\rho }\mathbf{\rho }\right\}ds$$

(11)

or, assuming $\mathbf{t}$ as independent variables, in a mixed form as

$$\Phi \left(u\right)={\int }_0^{\ell }\left\{{\mathbf{\tau }}^T\mathbf{\rho }-\frac{1}{2}{\mathbf{\tau }}^T{{\displaystyle \mathbf{C}}}_{\rho }^{-1}\mathbf{\tau }\right\}ds$$

(12)

Equilibrium corresponds to the virtual work equation

$${\Phi }^{\prime }\delta u-{\mathcal{L}}_{ext}=0,\mathit{u}\in \mathcal{U},\delta \mathit{u}\in \mathcal{T}$$

(13)

where ${\mathcal{L}}_{ext}$ is the work of the external loads, $u\in \mathcal{U}$ is the field of configuration variables, $\mathcal{T}$ is the tangent space of $\mathcal{U}$ at u, and a prime is used to denote Frechet’s derivative with respect to u.

3.4. The Beam Model in Case of Measured Strains

The effect of all external loads acting on the pipe, such as the soil pressure and the thermal loads, is taken into account in the proposed formulation through the value of the measured strain $\overline{\mathbf{\rho }}\left(s\right)$, whose distribution over the beam is obtained by means of an interpolation of the measured data at a certain number of cross-sections. This information represents the actual effect of arbitrary distributions of loads.

The variational form of the problem equations in terms of kinematic variables only (displacement form)

$$\Phi \left(u\right)=\frac{1}{2}{\int }_0^{\ell }\left\{{(\mathbf{\rho }-\overline{\mathbf{\rho }})}^T{{\displaystyle \mathbf{C}}}_{\rho }(\mathbf{\rho }-\overline{\mathbf{\rho }})\right\}ds=\mathrm{stationary}$$

(14)

can be seen as a minimization problem, in an energy norm, of the difference between the strain $\mathbf{\rho }$ coming from the kinematic relationships and that obtained from the measurements $\overline{\mathbf{\rho }}$.

A simple and useful way to rewrite the functional in mixed form is to introduce a new stress quantity so defined

$${\displaystyle \mathbf{t}}={{\displaystyle \mathbf{C}}}_{\rho }(\mathbf{\rho }-\overline{\mathbf{\rho }})$$

(15)

that allows to transform the problem as

$$\Phi \left(u\right)={\int }_0^{\ell }\left\{{{\displaystyle \mathbf{t}}}^T(\mathbf{\rho }-\overline{\mathbf{\rho }})-\frac{1}{2}{{\displaystyle \mathbf{t}}}^T{{\displaystyle \mathbf{F}}}_{\rho }{\displaystyle \mathbf{t}}\right\}ds$$

(16)

where ${\mathbf{F}}_{\rho }={\mathbf{C}}_{\rho }^{-1}$ is the cross-section compliance matrix. It is worth noting that the constitutive matrix is not strictly required to obtain the displacements from the assigned strain [13,14], but it is here used just as a metric matrix for homogenizing the different strain components. Obviously, if again we impose a priori the constitutive law, that in this case rewrite as $\mathbf{t}={\mathbf{C}}_{\rho }(\mathbf{\rho }-\overline{\mathbf{\rho }})$, we get the displacement format in Equation (14).

The new variational formulation in Equation (16), if equivalent in solution to those proposed in Equation (14), depends on the measured strains $\overline{\mathbf{\rho }}$ in a linear way, that is only in its first variation. Since it allows a great simplification of the code it will be adopted in the following. For the analysis, furthermore, we will adopt the MIP description of the problem proposed in [12] that allows rendering the Newton method, that we will use to solve the nonlinear problem, very robust and efficient compared to the formulation in displacement variables only.

In particular, the variational problem in Equation (16) is replaced by the following form where a numerical integration is adopted

$$\Phi \left(u\right)=\sum _g\left\{{{\displaystyle \mathbf{t}}}_g^T({\mathbf{\rho }}_g-{\overline{\mathbf{\rho }}}_g)-\frac{1}{2}{{\displaystyle \mathbf{t}}}_g^T{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_g\right\}{w}_g$$

(17)

with $w_g$ the Gauss point weight and the subscript g denotes quantities evaluated at the gth Gauss point of the discrete model.

3.4.1. From Measured Point-Wise Axial Strains to Generalized Strains

For a given cross-section s, we need to evaluate $\overline{\mathbf{\rho }}\left(s\right)$ starting from the values of the axial continuum strain ${\epsilon }_{11}$ measured in three points, using the hypothesis that the strains are small and the cross-section maintains rigid after the deformation.

Let $(s,y_1,z_1)$, $(s,y_2,z_2)$, and $(s,y_3,z_3)$ be the three points of the cross-section, where we have measured the axial strains ${\epsilon }_{11}$. We have

$$\left\{\begin{array}{cc}\hfill {\epsilon }_{11}(s,y_1,z_1)& ={\epsilon }_0+{\chi }_2{z}_1-{\chi }_3{y}_1\hfill \\ \hfill {\epsilon }_{11}(s,y_2,z_2)& ={\epsilon }_0+{\chi }_2{z}_2-{\chi }_3{y}_2\hfill \\ \hfill {\epsilon }_{11}(s,y_3,z_3)& ={\epsilon }_0+{\chi }_2{z}_3-{\chi }_3{y}_3\hfill \end{array}\right.$$

(18)

From the inverse relationship of (18) we are able to find the generalized quantities ${\epsilon }_0,{\chi }_2,{\chi }_3$ and then, from the assumption of negligible tangential strains (slender beams), i.e., ${\chi }_1$, ${\gamma }_2$, and ${\gamma }_3$, we have the generalized strain vector $\overline{\mathbf{\rho }}\left(s\right)={\{{\epsilon }_0\left(s\right),0,0,0,{\chi }_2\left(s\right),{\chi }_3\left(s\right)\}}^T$ required to obtain the body deformation and stress state.

3.4.2. Stress Check

Starting from the three known values of ${\epsilon }_{11}$ in Equation (18) over the cross-section it is possible and easy to evaluate, for this section, the maximum value of the axial strain ${\epsilon }_{11,max}$ (in absolute value) and of the axial stress ${\sigma }_{11,max}$, to be used for the cross-section stress check. In particular, for a circular pipe cross-section, we have

$${\sigma }_{11,max}=E{\epsilon }_{11,max}\mathrm{with}{\epsilon }_{11,max}=\left|{\epsilon }_0\right|+\sqrt{{\chi }_2^2+{\chi }_3^2}R$$

where R is the external radius. Then, the strength check for the elastic limit at this cross-section, is

$${\sigma }_{11,max}\le f_y$$

where $f_y$ is the yield stress of the material reduced by a suitable safety factor.

3.5. Strain Energy Variations

The subsequent derivation of the discrete nonlinear equations and their iterative solution requires the evaluation of the first and second variations of the strain energy. To this aim, let us introduce vector

$$\mathbf{\psi }\left(s\right)=\left[\begin{array}{c}\mathit{u}\\ \mathbf{\phi }\\ \mathbf{\phi }{,}_s\end{array}\right]$$

(19)

which allows us to write the first variation of the strain with respect to the local parameters as

$$\delta \mathbf{\rho }={\displaystyle \mathbf{L}}\delta \mathbf{\psi }{\displaystyle \mathbf{L}}=\left[\begin{array}{c}{{\displaystyle \mathbf{L}}}_{ϵ}\\ {{\displaystyle \mathbf{L}}}_{\chi }\end{array}\right]$$

(20)

where

$$\left\{\begin{array}{cc}\hfill {{\displaystyle \mathbf{L}}}_{ϵ}& =\left[\begin{array}{ccc}{\displaystyle \mathbf{R}}{\left(\mathbf{\phi }\right)}^T& {{\displaystyle \mathbf{Q}}}_{R^T}({{\displaystyle \mathbf{G}}}_1+\mathit{u}{,}_s,\mathbf{\phi })& {\displaystyle \mathbf{0}}\end{array}\right]\hfill \\ \hfill {{\displaystyle \mathbf{L}}}_{\chi }& =\left[\begin{array}{ccc}{\displaystyle \mathbf{0}}& {{\displaystyle \mathbf{Q}}}_{T^T}(\mathbf{\phi }{,}_s,\mathbf{\phi })& {\displaystyle \mathbf{T}}{\left(\mathbf{\phi }\right)}^T\end{array}\right].\hfill \end{array}\right.$$

The first variation of the strain energy in Equation (17) furnishes

$${\Phi }^{\prime }\delta u=0\mathrm{with}{\Phi }^{\prime }\delta u=\sum _g\left\{\delta {{\displaystyle \mathbf{t}}}_g^T({\mathbf{\rho }}_g-{\overline{\mathbf{\rho }}}_g-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_g)+\delta {\mathbf{\psi }}_g^T{{\displaystyle \mathbf{L}}}_g{{\displaystyle \mathbf{t}}}_g\right\}{w}_g$$

(21)

Similarly, the second strain energy variation, by means of the equivalences in Equations (4) and (6), becomes

$$\begin{array}{cc}\hfill {\Phi }^{″}\dot{u}\delta u& =\sum _g\left\{\delta {{\displaystyle \mathbf{t}}}_g^T{{\displaystyle \mathbf{L}}}_g{\dot{\mathbf{\psi }}}_g+{\dot{\mathbf{t}}}_g^T{{\displaystyle \mathbf{L}}}_g\delta {\mathbf{\psi }}_g+{\dot{\mathbf{\psi }}}_g^T{\displaystyle \mathbf{\Gamma }}\left[{{\displaystyle \mathbf{t}}}_g\right]\delta {\mathbf{\psi }}_g-{\dot{\mathbf{t}}}_g{{\displaystyle \mathbf{F}}}_{\rho }\delta {{\displaystyle \mathbf{t}}}_g\right\}ds\hfill \end{array}$$

(22)

where

$${\displaystyle \mathbf{\Gamma }}\left[{{\displaystyle \mathbf{t}}}_g\right]=\left[\begin{array}{ccc}{\displaystyle \mathbf{0}}& {{\displaystyle \mathbf{Q}}}_R({{\displaystyle \mathbf{n}}}_g,\mathbf{\phi })& {\displaystyle \mathbf{0}}\\ {{\displaystyle \mathbf{Q}}}_R{({{\displaystyle \mathbf{n}}}_g,\mathbf{\phi })}^T& {{\displaystyle \mathbf{\Gamma }}}_T(\mathbf{\phi }{,}_s,{{\displaystyle \mathbf{m}}}_g,\mathbf{\phi })+{{\displaystyle \mathbf{\Gamma }}}_R({\displaystyle \mathbf{r}}{,}_s,{{\displaystyle \mathbf{n}}}_g,\mathbf{\phi })& {{\displaystyle \mathbf{Q}}}_T{({{\displaystyle \mathbf{m}}}_g,\mathbf{\phi })}^T\\ {\displaystyle \mathbf{0}}& {{\displaystyle \mathbf{Q}}}_T({{\displaystyle \mathbf{m}}}_g,\mathbf{\phi })& {\displaystyle \mathbf{0}}\end{array}\right]$$

4. Finite Element Model and Solution of the Nonlinear Discrete Equations

4.1. The Beam Finite Element

We use an isoparametric interpolation with the geometry ${\mathbf{r}}_0$ and the kinematic fields u and $\mathbf{\phi }$ interpolated with the same quadratic Lagrangian shape functions. By introducing the approximation functions in Equation (20), we obtain

$$\mathbf{\psi }\left(s\right)={{\displaystyle \mathbf{N}}}_{\psi }\left(s\right){\mathit{u}}_e$$

where vector ${\mathit{u}}_e=\{{\mathit{u}}^i,{\mathbf{\phi }}^i,{\mathit{u}}^m,{\mathbf{\phi }}^m,{\mathit{u}}^j,{\mathbf{\phi }}^j\}$ collects the FE DOFs corresponding to the initial, mid-span, and end node of the element and ${\mathbf{N}}_{\psi }\left(s\right)$ is the interpolation matrix. The element DOFs ${\mathbf{d}}_e$ also include the two Gauss points stresses, assumed as independent variables in the spirit of the MIP formulation [12] so giving the

$${{\displaystyle \mathbf{d}}}_e=\left[\begin{array}{c}{{\displaystyle \mathbf{t}}}_1\\ {{\displaystyle \mathbf{t}}}_2\\ {\mathit{u}}_e\end{array}\right]$$

The discrete form of the residual force vector of the element is

$${{\displaystyle \mathbf{r}}}_e\equiv \frac{\partial \Phi \left({\mathbf{d}}_e\right)}{\partial {\mathbf{d}}_e}=\left[\begin{array}{c}({\mathbf{\rho }}_1-{\overline{\mathbf{\rho }}}_1-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_1)w_1\\ ({\mathbf{\rho }}_2-{\overline{\mathbf{\rho }}}_2-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_2)w_2\\ {\sum }_g{{\displaystyle \mathbf{B}}}_g^T{{\displaystyle \mathbf{t}}}_g{w}_g\end{array}\right]\mathrm{with}{{\displaystyle \mathbf{B}}}_g={{\displaystyle \mathbf{L}}}_g{{\displaystyle \mathbf{N}}}_{\psi }\left(s_g\right).$$

(23)

Vector ${\mathbf{r}}_e$, which represents the residual of the equilibrium equations, can be decomposed in the following form, useful for the application of the Newton method

$${{\displaystyle \mathbf{r}}}_e={{\displaystyle \mathbf{s}}}_e-{{\displaystyle \mathbf{p}}}_e\mathrm{with}{{\displaystyle \mathbf{s}}}_e\equiv \left[\begin{array}{c}({\mathbf{\rho }}_1-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_1)w_1\\ ({\mathbf{\rho }}_2-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_2)w_2\\ {\sum }_g{{\displaystyle \mathbf{B}}}_g^T{{\displaystyle \mathbf{t}}}_g{w}_g\end{array}\right]{{\displaystyle \mathbf{p}}}_e\equiv \left[\begin{array}{c}{\overline{\mathbf{\rho }}}_1{w}_1\\ {\overline{\mathbf{\rho }}}_2{w}_2\\ {\displaystyle \mathbf{0}}\end{array}\right]$$

(24)

It is important to note that in the proposed formulation vector ${\mathbf{p}}_e$, i.e., the load coming from the measured strain, is constant.

Similarly, the local stiffness matrix is

$${{\displaystyle \mathbf{K}}}_e\equiv \frac{{\partial }^2\Phi \left({\mathbf{d}}_e\right)}{\partial {\mathbf{d}}_e^2}=\left[\begin{array}{ccc}-{{\displaystyle \mathbf{F}}}_{\rho }{w}_1& {\displaystyle \mathbf{0}}& {{\displaystyle \mathbf{B}}}_1{w}_1\\ {\displaystyle \mathbf{0}}& -{{\displaystyle \mathbf{F}}}_{\rho }{w}_2& {{\displaystyle \mathbf{B}}}_2{w}_2\\ {{\displaystyle \mathbf{B}}}_1^T{w}_1& {{\displaystyle \mathbf{B}}}_2^T{w}_2& {\sum }_g{{\displaystyle \Xi }}_g{w}_g\end{array}\right]$$

(25)

where

$${{\displaystyle \Xi }}_g={{\displaystyle \mathbf{N}}}_{\psi }^T\left(s_g\right){\displaystyle \mathbf{\Gamma }}\left({{\displaystyle \mathbf{t}}}_g\right){{\displaystyle \mathbf{N}}}_{\psi }\left(s_g\right).$$

(26)

4.2. A Specialized Incremental-Iterative Solution

A specialized numerical solution strategy is now presented, similar to that used for the evaluation of the equilibrium path of geometrically nonlinear structures. It will be used to evaluate the deformed configuration of the pipeline once the assigned generalized strains $\overline{\mathbf{\rho }}$ are known.

Once the standard finite element assembly procedures have been carried out, the equilibrium configuration for assigned strains is obtained from the solution of the following system of nonlinear algebraic equations

$${\displaystyle \mathbf{s}}\left({\displaystyle \mathbf{d}}\right)-{\displaystyle \mathbf{p}}={\displaystyle \mathbf{0}}$$

(27)

where $\mathbf{p}$ and $\mathbf{s}$ represent, respectively, the known vector due to the measured strains and the internal forces vector, which are obtained by means of finite element assemblages of the quantities reported in Equation (24). Vector $\mathbf{d}$ collects all the DOFs of the problem.

To make it possible the solution of the nonlinear system in Equation (27) by means of an incremental formulation based on the Newton method the problem is reformulated as

$${\displaystyle \mathbf{s}}\left({\displaystyle \mathbf{d}}\right)-t{\displaystyle \mathbf{p}}={\displaystyle \mathbf{0}}$$

(28)

with the introduced load factor t which assumes values in $[0,1]$.

In this way it is possible to evaluate a sequence of equilibrium points ${\mathbf{z}}^{\left(k\right)}\equiv \{{\mathbf{d}}^{\left(k\right)},t^{\left(k\right)}\}$ associated to increasing values of t, that is $t^{\left(k\right)}\le t^{(k+1)}$, in order to gradually reach the value of $t=1$. This allows exploiting the properties of the incremental strategy based on the Newton method. The strategy so proposed is then similar to that used to evaluate the equilibrium path of slender elastic structures in case of large deformations and applied external loads [12]. For the problem at hand, since the equilibrium path does not present a limit point for the parameter t, it is possible to use a t-controlled scheme. Assuming a sequence of increasing values of the control parameter $t=t^{\left(k\right)}$ the solution of the nonlinear system

$${\displaystyle \mathbf{r}}({\displaystyle \mathbf{d}},t^{\left(k\right)})\equiv {\displaystyle \mathbf{s}}\left({\displaystyle \mathbf{d}}\right)-t^{\left(k\right)}{\displaystyle \mathbf{p}}={\displaystyle \mathbf{0}}$$

(29)

defines points (steps) ${\mathbf{z}}^{\left(k\right)}\equiv \{{\mathbf{d}}^{\left(k\right)},t^{\left(k\right)}\}$ which satisfy the problem Equation (28).

Starting from a known point ${\mathbf{z}}_0\equiv {\mathbf{z}}^{\left(k\right)}$ which fulfills Equation (29), the first step of the method to evaluate a new point ${\mathbf{z}}^{(k+1)}$ is to obtain a predictor ${\mathbf{z}}_1=\{{\mathbf{d}}_1,t^{\left(k\right)}\}$ using an extrapolation of the previous evaluated point ${\mathbf{d}}_1={\mathbf{d}}^{\left(k\right)}+\beta ({\mathbf{d}}^{\left(k\right)}-{\mathbf{d}}^{(k-1)})$ with $\beta \in \mathbb{R}$ a real number which gives the step amplitude. ${\mathbf{d}}_1$ is evaluated along the initial path tangent for $k=1$. The predictor value is subsequently corrected by means of a sequence of estimates ${\mathbf{z}}_j$ using a Newton–Raphson iteration

$$\left\{\begin{array}{c}{{\displaystyle \mathbf{K}}}_t\dot{\mathbf{d}}=-{{\displaystyle \mathbf{r}}}_j\hfill \\ {{\displaystyle \mathbf{d}}}_{j+1}={{\displaystyle \mathbf{d}}}_j+\dot{\mathbf{d}}\hfill \end{array}\right.$$

(30)

where ${\mathbf{K}}_t$ is the Jacobian of the nonlinear system of Equation (29) evaluated in ${\mathbf{d}}_j$

$${{\displaystyle \mathbf{K}}}_t={\left.\frac{\partial \mathbf{s}\left(\mathbf{d}\right)}{\partial \mathbf{d}}\right|}_{{\mathbf{d}}_j}.$$

obtained by assembling the element contributions in Equation (25). It is worth noting that, due to the high efficiency and robustness of the mixed (stress-displacement) iterations, the method usually converges in a single increment, i.e., the solution is possible directly for $t=1$. The possibility of sub-increments is however maintained for more complex situations with respect to the applications considered in this paper.

Solution in Condensed Form

The system in Equation (30) has a block decoupling due to the local nature of variables ${\mathbf{t}}_g$ which are defined at the element Gauss point level and do not require the imposition of continuity as occurs for the displacement DOFs:

$$\left[\begin{array}{ccc}-{{\displaystyle \mathbf{F}}}_{\rho }{w}_1& {\displaystyle \mathbf{0}}& {{\displaystyle \mathbf{B}}}_1{w}_1\\ {\displaystyle \mathbf{0}}& -{{\displaystyle \mathbf{F}}}_{\rho }{w}_2& {{\displaystyle \mathbf{B}}}_2{w}_2\\ {{\displaystyle \mathbf{B}}}_1^T{w}_1& {{\displaystyle \mathbf{B}}}_2^T{w}_2& {\sum }_g{\displaystyle \Xi }{w}_g\end{array}\right]\left[\begin{array}{c}{\dot{\mathbf{t}}}_1\\ {\dot{\mathbf{t}}}_2\\ {\dot{\mathit{u}}}_e\end{array}\right]=t^{\left(k\right)}\left[\begin{array}{c}{\overline{\mathbf{\rho }}}_1{w}_1\\ {\overline{\mathbf{\rho }}}_2{w}_2\\ {\displaystyle \mathbf{0}}\end{array}\right]-\left[\begin{array}{c}({\mathbf{\rho }}_1-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_1)w_1\\ ({\mathbf{\rho }}_2-{{\displaystyle \mathbf{F}}}_{\rho }{{\displaystyle \mathbf{t}}}_2)w_2\\ {\sum }_g{{\displaystyle \mathbf{B}}}_g^T{{\displaystyle \mathbf{t}}}_g{w}_g\end{array}\right]$$

(31)

We omit the iteration subscript j for simplicity. The correction of stress ${\mathbf{t}}_g$, with $g=1\cdots 2$, at each Gauss point is eliminated from the global operations by means of a static condensation in the displacement correction as follows:

$${\dot{\mathbf{t}}}_g={{\displaystyle \mathbf{C}}}_g({{\displaystyle \mathbf{B}}}_g{\dot{\mathit{u}}}_e+{\mathbf{\rho }}_g-t^{\left(k\right)}{\overline{\mathbf{\rho }}}_g)-{{\displaystyle \mathbf{t}}}_g{{\displaystyle \mathbf{C}}}_{\rho }={{\displaystyle \mathbf{F}}}_{\rho }^{-1}$$

which has the typical structure of the mixed iteration [12,25], in which stresses are coherently updated using a linearized expression.

Once the stress corrections are substituted in the end of Equation (31) we obtain the condensed form of the iteration, where only the correction of kinematic DOFs has to be solved in the global system obtained by assembling globally

$$\left\{\sum _g({{\displaystyle \Xi }}_g+{{\displaystyle \mathbf{B}}}_g^T{{\displaystyle \mathbf{C}}}_g{{\displaystyle \mathbf{B}}}_g)w_g\right\}{\dot{\mathit{u}}}_e=t^{\left(k\right)}{{\displaystyle \mathbf{p}}}_c-{{\displaystyle \mathbf{s}}}_c$$

(32)

with

$${{\displaystyle \mathbf{p}}}_c=\sum _g{{\displaystyle \mathbf{B}}}_g^T{{\displaystyle \mathbf{C}}}_g{\overline{\mathbf{\rho }}}_g{w}_g{{\displaystyle \mathbf{s}}}_c=\sum _g{{\displaystyle \mathbf{B}}}_g^T{{\displaystyle \mathbf{C}}}_g{\mathbf{\rho }}_g{w}_g$$

(33)

Note that, the expression of ${\mathbf{s}}_c$ is the same as that we would have using a purely displacement-based approach. However, the mixed form, with the stress used as an independent variable, improves the efficiency and robustness of the iterative solution, requiring a lower number of iterations i.e., linear systems as shown in [12].

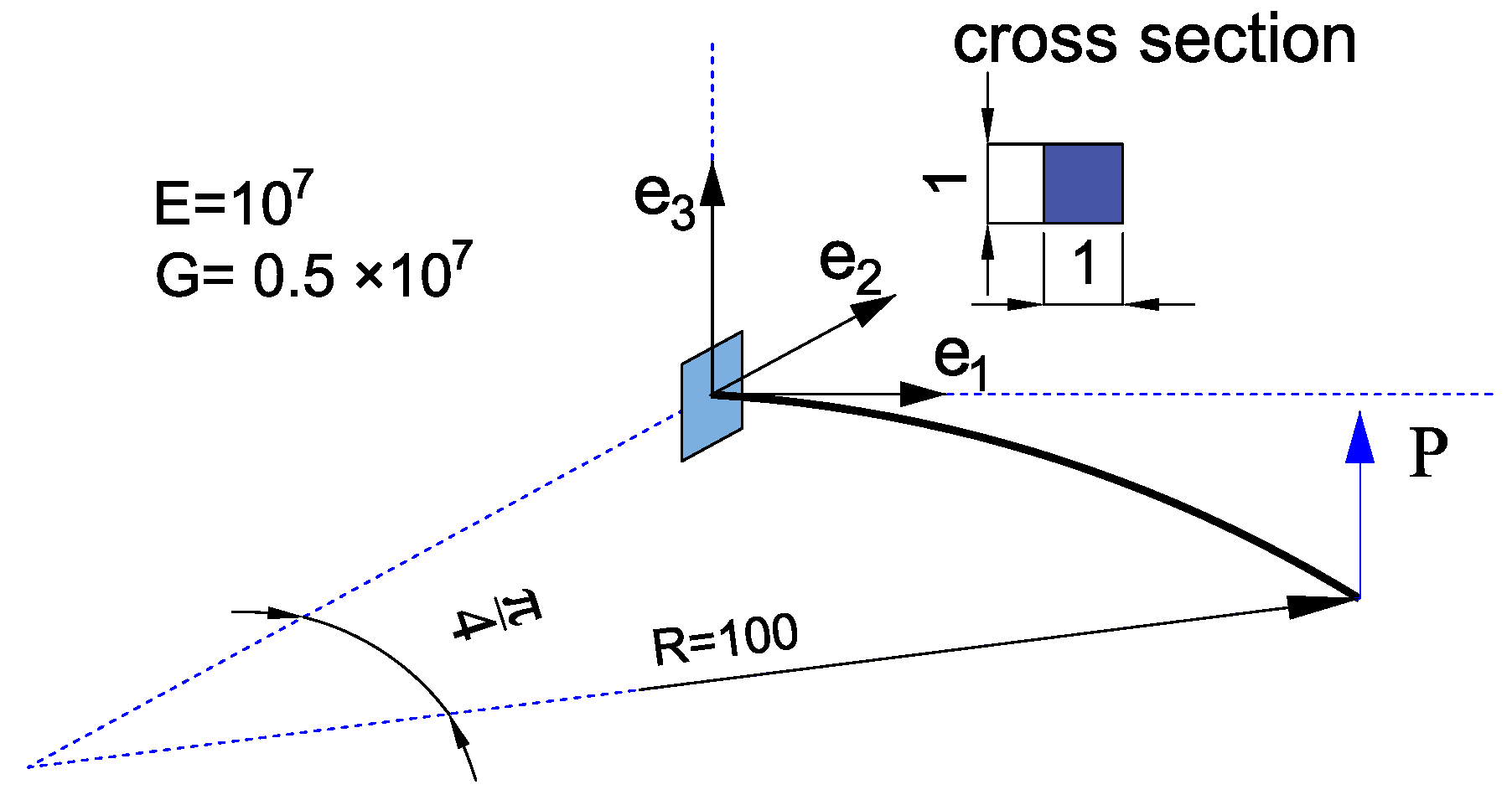
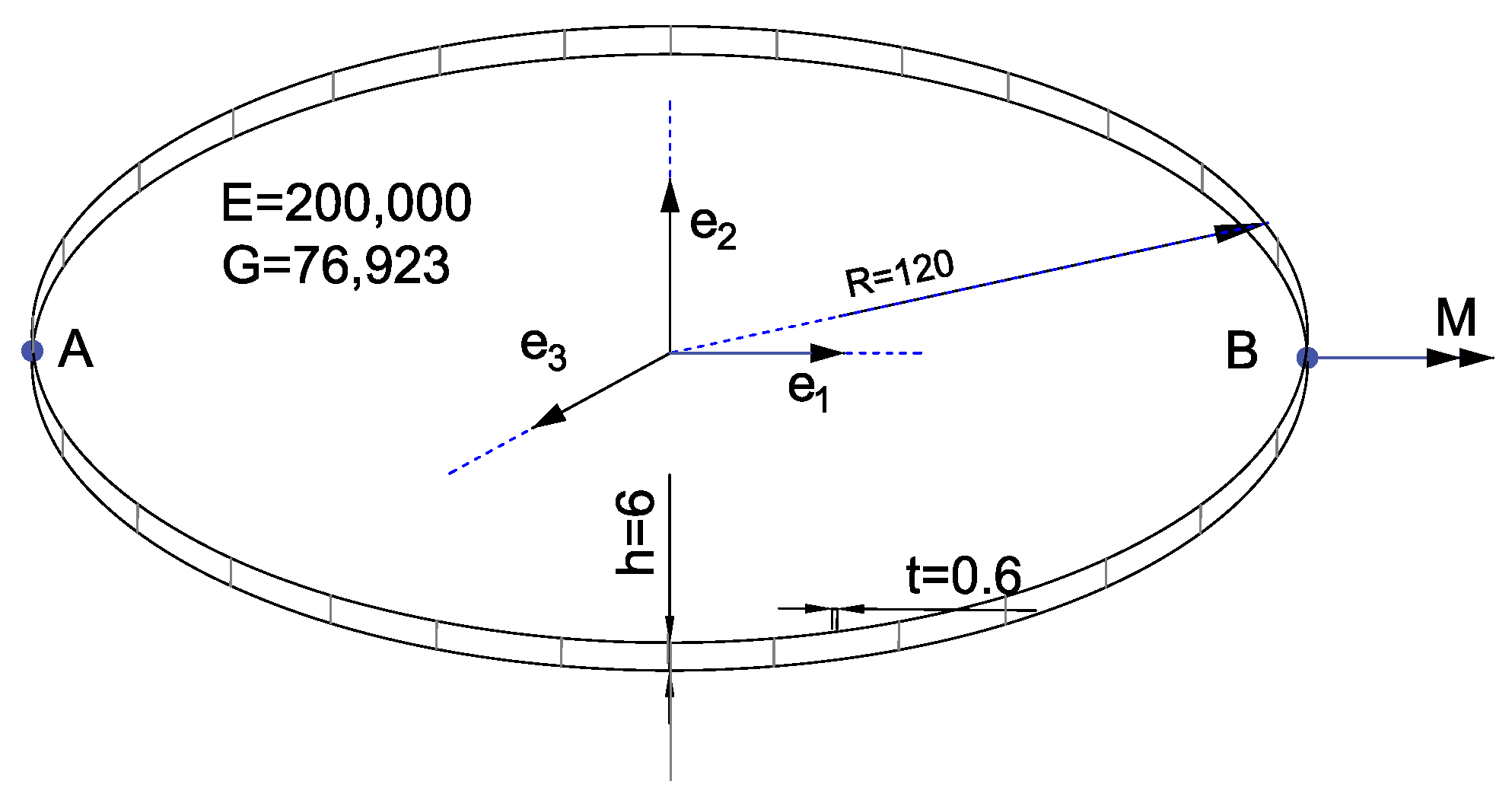
4.3. Numerical Validation in Large Deformation Benchmarks

A validation of the formulation is now carried out using popular benchmarks.

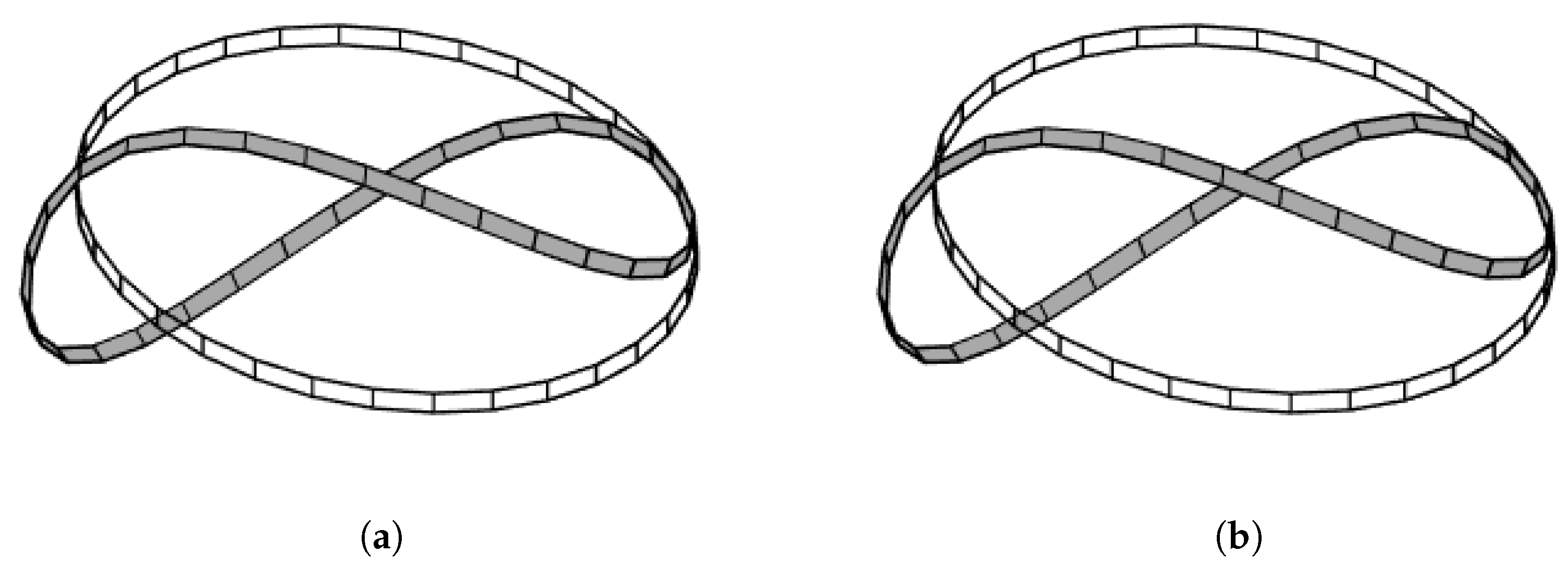
4.3.1. Curved Cantilever Beam under Shear Load

This test regards a well-known 3D cantilever beam, which has been extensively analyzed and documented [26,27], depicted in Figure 3. The beam is initially curved, lies in the ${\mathbf{e}}_1$–${\mathbf{e}}_3$ plane and is clamped at the end-point corresponding to the origin of the reference system. A force $\mathbf{P}$ is applied along ${\mathbf{e}}_2$ with amplitude equal to 600 at the free end-point in order to produce a very large deflection. The discrete model consists of four quadratic elements. The deformed configuration predicted a standard nonlinear load-controlled analysis is shown in Figure 4. The strain field generated by the applied load is stored at the integration points. Then, the proposed numerical method is employed to reconstruct the displacements and rotations directly from the strain field, without any use of the load. In Figure 4 we can see a comparison of the deformed configuration produced by the standard analysis with assigned load and that computed directly from the assigned strain field. A perfect match is obtained in both the deformed shape and the tip displacement. It is worth noting that, despite the nonlinearity due to the extremely large deflection, the proposed strain-based analysis with a mixed iterative scheme is able to provide the kinematic solution in a single step and only two iterations.

4.3.2. Ring under Torsion

The second test in Figure 5 is another famous benchmark for the validation of finite element models with large rotations. It is a thin circular ring clamped at point A and subjected to a torque $M=800$ on the opposite point labeled as B. A total of 16 finite elements are used for the mesh. A load-controlled nonlinear analysis is used to compute the deformed configuration for the applied load. The resulting strain field is stored at the integration points and used as input for the proposed strain-based algorithm for evaluating the kinematics without using the load information. Figure 6 shows the perfect match of the load-based and the strain-based algorithm. Again, notwithstanding the significant nonlinearity of the problem due to large 3D rotations, the strain-based algorithm with mixed iteration is very efficient and robust, with convergence achieved in a single step and only three iterations.

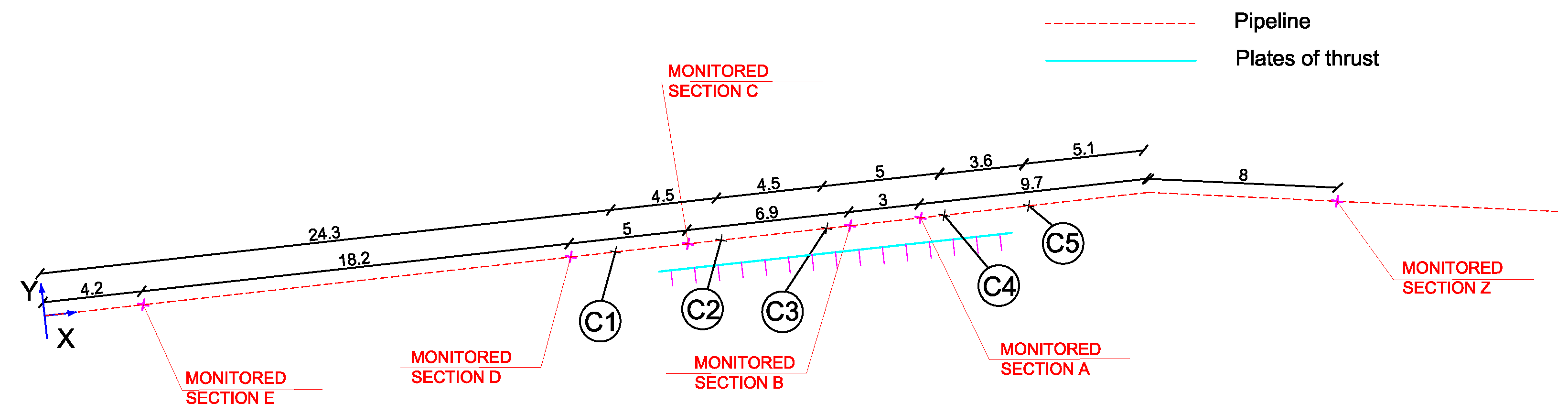
5. Experimental Setup

As we can see in Figure 7, the prototype pipeline is buried in a wedge of land subject to an artificial landslide generated by 15 actuators started by a hydraulic unit. The actuators, positioned with the rod parallel to the sliding surface, are placed in an excavation parallel to the pipeline and constrained to a retaining wall. The thrust action of the actuators used to induce the landslide is transmitted to the ground by means of steel ribbed plates. The pipe has a circular section with an inner radius equal to 154.1 mm and thickness equal to 7.1 mm. It is made of steel with Young modulus $E=206,000$ N/mm${}^2$ and Poisson coefficient $\nu =0.3$.

Figure 8 shows the position of the sections along the pipeline where strain is monitored in real time. From left to right, the monitored sections are:

-

section E

-

section D

-

section F

-

section B

-

section A

-

section Z

The position of the three FBG sensors on each monitored cross-section of the pipe is depicted in Figure 9. The sensors parameters are available at https://www.sylex.sk/product/sws-03-spot-weldable-strain-sensor (accessed on 20 July 2022), with the strain range extend to $\pm 2000\mu \epsilon$.

In order to validate the evolution of the deformed configuration predicted by the proposed numerical processing methodology starting from the strain measurements, the displacements of the pipeline are measured in situ by means of marker rods (see Figure 10 and Figure 11) welded to the pipe and translating with it. These rods can slide along a graduated metric scale (Figure 12) constrained to the retaining wall, making it possible to read the actual values of the displacement component in the thrust direction. The marker rods are named C1, C2, C3, C4, and C5. They are located at five points in the area of the induced landslide as displayed in Figure 8. Clearly, the deformed configuration will have 3D kinematics as highlighted by the strain measurements, while the markers only give information about one displacement component which, however, is expected to be the most significant one.

6. Experimental and Numerical Results

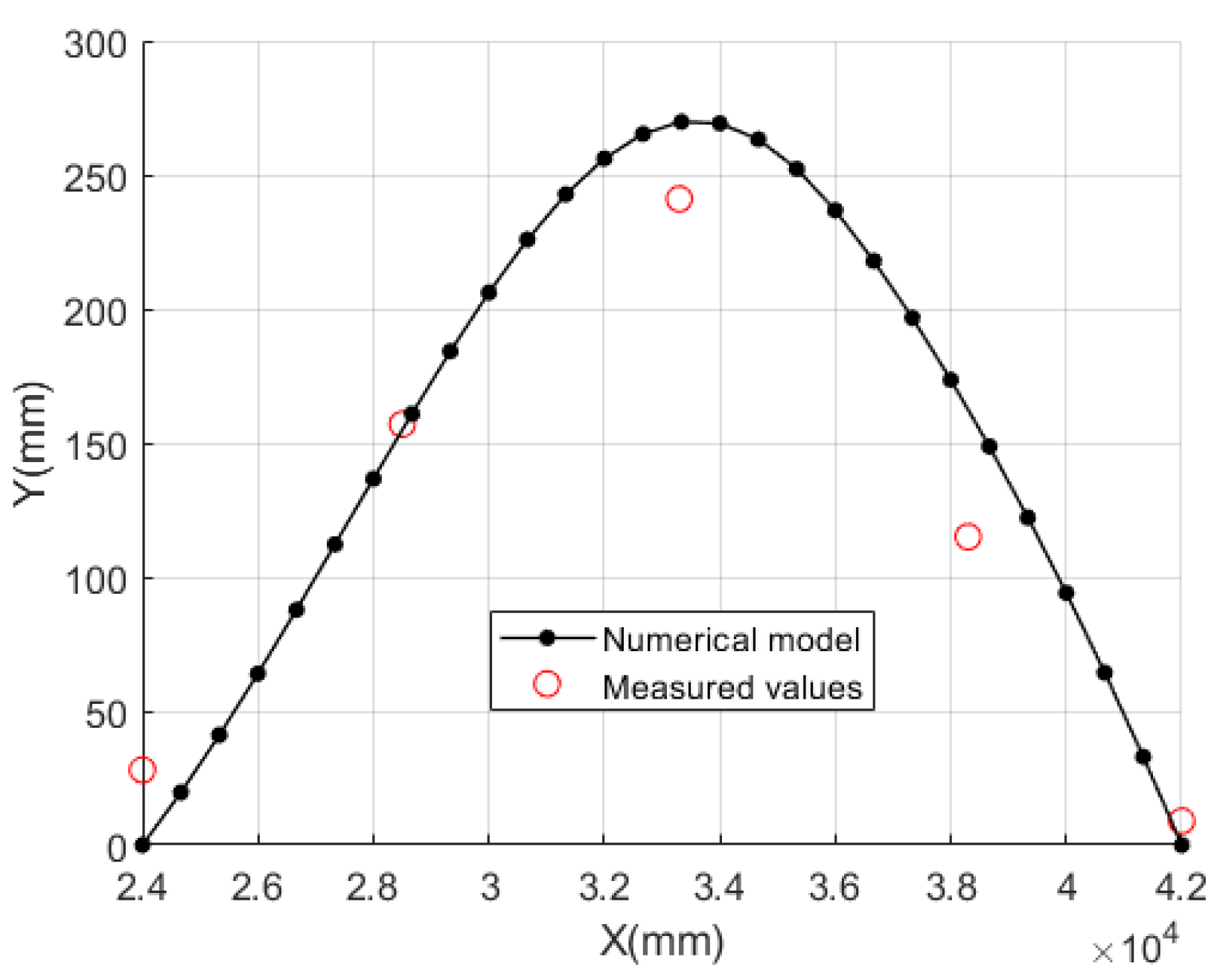
Comparison between Predicted and Measured Displacements on the Prototype Test Bench

For the purpose of model validation, various experimental tests are performed. During each test, a landslide is induced artificially by means of actuators using different setup parameters of displacement.

Table 1. Strain measured at each cross-section at 2 instants of the experiment test.

	Test 1 ($\mathit{\mu }\mathit{\epsilon }$)	Test 2 ($\mathit{\mu }\mathit{\epsilon }$)
$A_1$	225	150
$A_2$	405	395
$A_3$	770	1205
$B_1$	−900	−963
$B_2$	807	1297
$B_3$	1308	1425
$D_1$	369	440
$D_2$	−17	37
$D_3$	−497	−452
$E_1$	−8	6
$E_2$	−145	−151
$E_3$	−46	−30
$F_1$	352	483
$F_2$	222	140
$F_3$	530	715
$Z_1$	483	239
$Z_2$	484	242
$Z_3$	470	224

shows strain measurements of the most significant tests, named test 1 and test 2, for each cross-section. Specifically, the strain value in microstrains (m$\epsilon$) is reported for each of the three control points on the monitored sections along the pipeline. For example, $B_3$ refers to sensor number 3 according to Figure 9 of the section labeled as B in Figure 8.

A finite element model is constructed for the pipe sector delimited by C1 and C5 of length equal to 18 m and discretized with 27 beam finite elements. At each control section, the mean axial strain and the two bending curvatures are obtained from the values in Table 1 by solving the linear system in Equation (18). The corresponding values at the Gauss integration points of each finite element are obtained by interpolation using the pchip (piecewise cubic Hermite interpolating polynomial) function of the software Matlab. The predictive model needs six equations as boundary conditions since the strain field can define the kinematics except for a rigid motion of the body. These are obtained using the assumption that the displacement is restrained at the endpoints C1 and C5 external to the area directly affected by the landslide. Actually, these points have a non-null displacement as proved by the real measurements but with a small value compared to those of the inner part.

The comparison between the measured and predicted values are reported in

Table 2. Test 1: predicted and measured displacements.

	C1	C2	C3	C4	C5
X (m)	24	28.5	33.3	38.3	42
Y (mm) meas.	24	144	209	97	6
Y (mm) pred.	0	143	244	133	0
rel. error (%)	-	−1	17	37	-

and

Table 3. Test 2: predicted and measured displacements.

	C1	C2	C3	C4	C5
X (m)	24	28.5	33.3	38.3	42
Y (mm) meas.	28	157	241	115	9
Y (mm) pred.	0	155	270	162	0
rel. error (%)	-	−1	12	41	-

for the two tests. In particular, for each marker rod, the tables report:

• label of the markers used to read the actual displacements: C1, C2, C3, C4, C5;
• the position X (mm) of each marker rod along the pipeline axis;
• the displacement Y (mm) measured by each marker rod in the thrust direction;
• the displacement Y (mm) at the marker rod position predicted by the numerical model based on the strain measurements;
• the relative error percentage calculated as $({\mathrm{Y}}_{\mathrm{predicted}}-{\mathrm{Y}}_{\mathrm{measured}})/{\mathrm{Y}}_{\mathrm{measured}}\times 100$.

In addition, the deformed configuration in the plane X-Y is also illustrated in Figure 13 and Figure 14 for the two tests respectively. We can observe a satisfactory estimate of the displacement trend provided by the proposed finite element model coupled with the strain acquisition system. A mean error in the displacement of about $18\%$ was obtained with practically just three effectively monitored sections (A, B, and F) in the pipe stretch of 18 m mainly affected by the landslide. This demonstrates the feasibility of using the proposal as an effective alarm indicator. The error is mainly attributed to the very few discrete strain measurements, which can only approximate the actual complex strain field along the pipeline, in addition to instrumental errors in the point-wise strain. Another possible approximation consists in neglecting the tangential strains in the measurements, although their effects are unlikely to be significant given the slenderness of the problem.

The finite element analysis also predicts a displacement along Z of about 1/4 of the Y component showing the necessity of a 3D model. Furthermore, a linear analysis gives 343 mm and 404 mm as maximum displacement in Y for the two tests respectively, proving the necessity of a geometrically nonlinear model that takes into account the cable-like effect of the axial stiffness in reducing the transversal displacement.

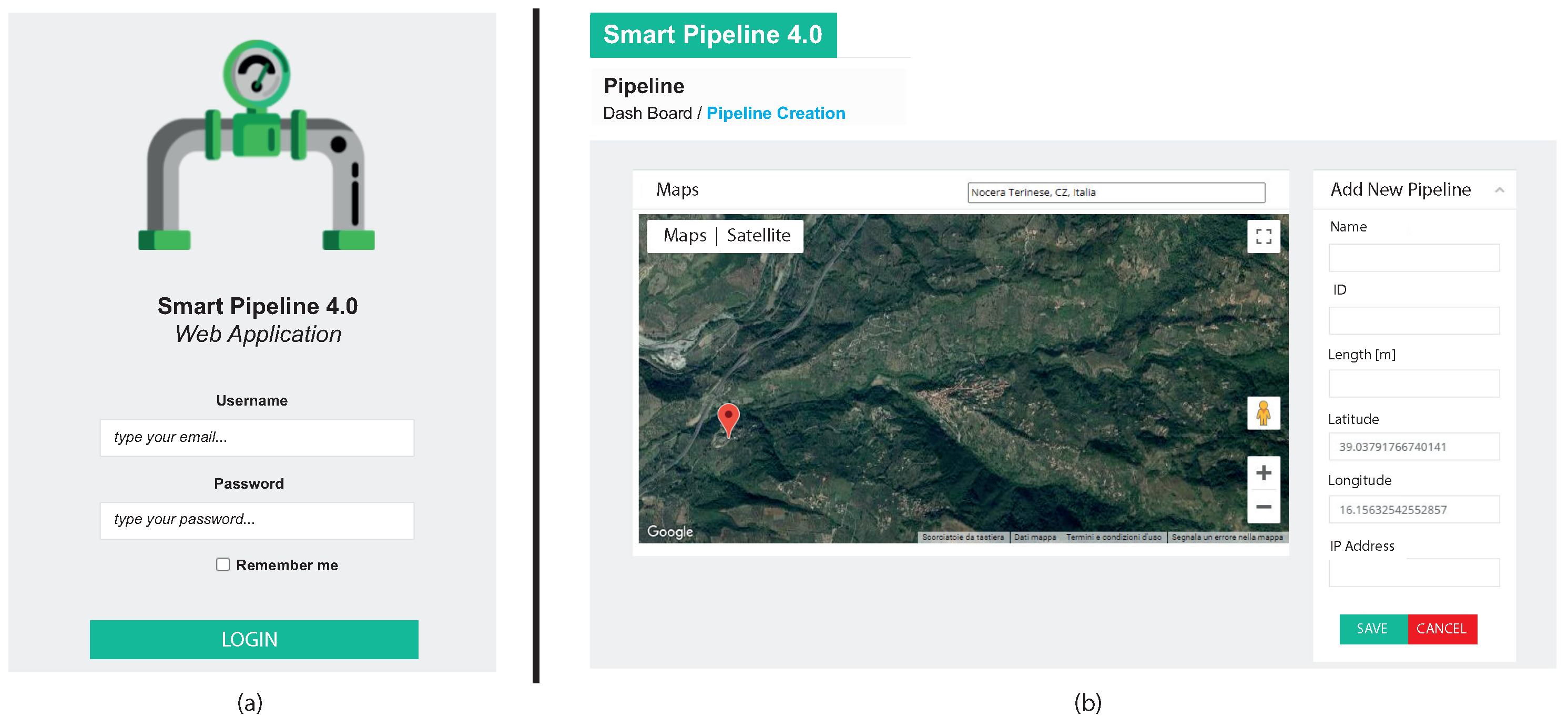
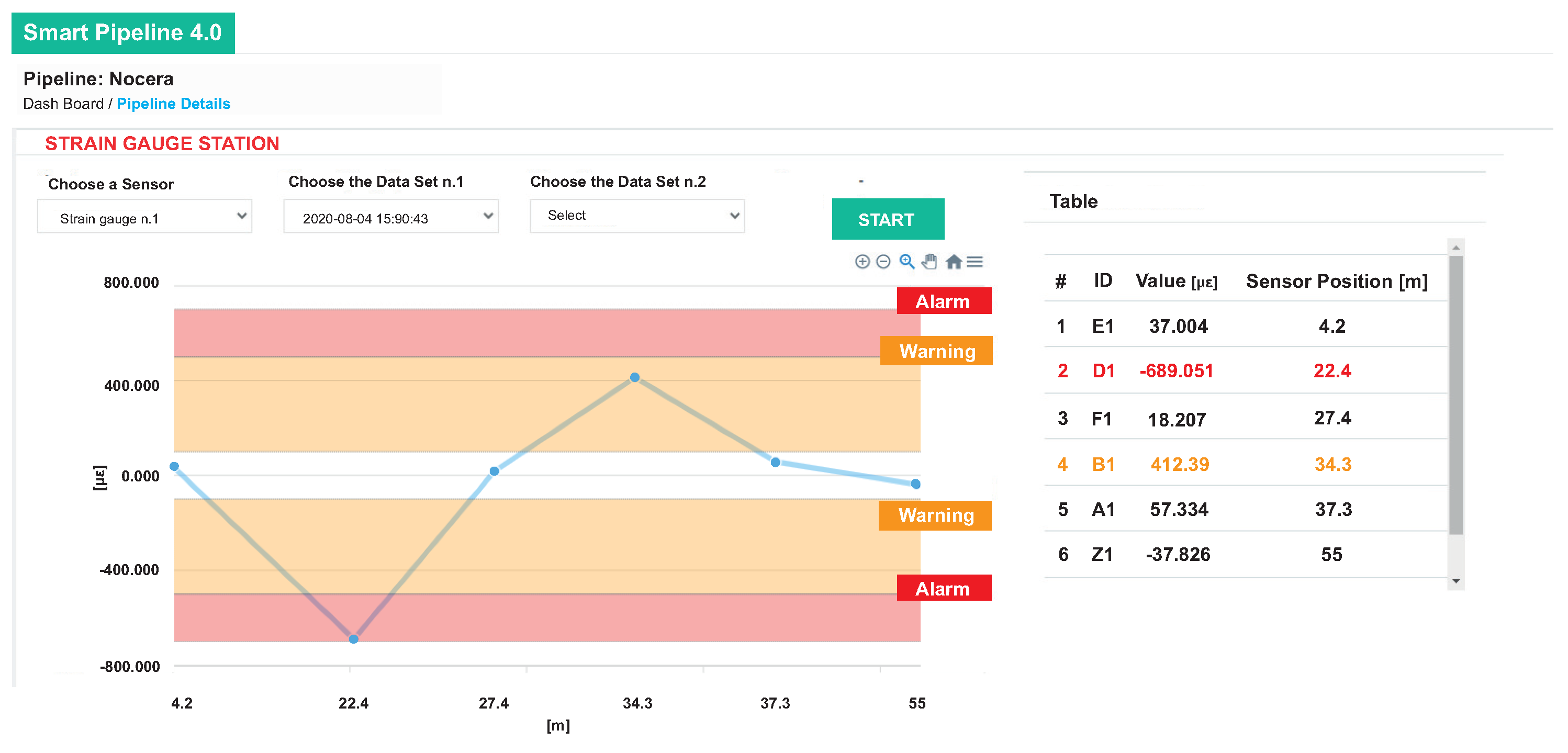
7. Web Application for Real-Time Monitoring and Alarm Management

The web application is designed mainly for ensuring:

• remote management of the pipelines;
• smart monitor of pipeline health status based on acquired measures.

Figure 15 depicts the infrastructure concept that exploits the design idea described in [28]. In this figure, we highlight the presence of local devices (properly placed in the measuring stations) that can exchange data (control commands and information requests) with the remote management web application through a gateway. The infrastructure exploits local and remote communication channels for data exchange. The local communication channel allows data exchange amongst the local devices distributed on the installation site. On the other hand, the remote communication channel enables data exchange between the local devices and the remote server and, consequently, allows the centralized consultation of the collected data.

An important aspect of the smart pipeline system is the friendliness level of interactions between the system managers and the infrastructure. For instance, the web application provides the following services:

• Account management that allows the administrator to define permissions and access levels to the web application (i.e., system manager, user, etc.);
• Multiple pipeline configurations and geo-referencing properties;
• Pipeline monitoring;
• Sensors configuration and deployment;
• Anomalous conditions detection and alarms generation;
• Sensor data monitoring;
• Finite element analysis for the displacement reconstruction.

The web application also provides access to the smart pipeline system settings. For instance, it is possible to set warning and alarm thresholds for each sensor deployed on the pipeline. It is also possible to configure the type and number of sensors to be deployed on the pipeline. Moreover, the user can evaluate the information related to the measured data, pipeline conditions, and other warnings and alarms.

The web application, in addition to the typical access control based on user credentials checking, can be configured to adopt the hypertext transfer protocol secure (HTTPS) to improve the protection of the privacy and the integrity of the exchanged data while in transit. hypertext transfer protocol secure (HTTPS) is a variant of the standard web transfer protocol (HTTP) that adds a layer of security to the data in transit through a secure socket layer (SSL) or transport layer security (TLS protocol connection). Thanks to the HTTPS properties, the web application enables encrypted communications and secure connections between the remote users and the web server. Figure 16 and Figure 17 show some illustrative pages of the web application. In particular, the log page is depicted in Figure 16a whilst Figure 16b shows the pipeline system configuration, where the user can operate in order to set the basic installation properties (e.g., installation name, ID, GPS coordinate, etc.). Moreover, information about the pipeline status and data trends are displayed as in the example shown in Figure 17, where white, orange, and red areas represent safe, early warning, and alarm conditions respectively. Early warning and alarm limits for strain and deflections can be set by the user depending on material strength, service requirements, and the presence of other buildings and infrastructures in the surrounding area. Finally, the web application makes it possible to define the finite element model, select the strain data set (with different time-stamps), and, consequently, run the analysis for computing the displacement of the pipeline. The displacement outputs are similar to those already shown in Figure 13 and Figure 14. In this respect, the web application only adds information about the displacement trends and warning and fault alarms.

8. Conclusions

This study investigated a system for monitoring displacements of underground pipelines in regions prone to landslides. It consists of a real time measurement of the axial strain through FBG sensors located at three points of some cross-sections of the pipe. The displacement field along the pipeline is reconstructed from the strain field by means of a nonlinear finite element model exploiting, as boundary conditions, the assumption of negligible displacement at the end-points of the model external to the affected area. The finite element analysis is based on a geometrically exact 3D beam model and a variational formulation that makes it possible to find the finite displacement and rotation fields corresponding to the measured strains and satisfy the boundary conditions. The nonlinear discrete problem is solved efficiently by a high-performing mixed iterative scheme. Some theoretical assessments were firstly carried out on large deformation benchmarks found in the literature. Subsequently, experimental results were produced on an underground monitored pipeline subject to an artificially induced landslide. A satisfactory agreement was found between predicted and actual displacements. Specifically, a mean displacement error of about $18\%$ was obtained with just three effective monitored sections in the pipe stretch of 18 m affected by the landslide. Finally, a web application was developed for real-time monitoring and alarm management.

In a future work, it would be interesting to optimize the distribution of the sensors along the pipeline using, for example, direct finite element simulations to estimate the strain distribution caused by assumed landslides [29,30].

Finally, although the finite element model application was validated on a pipeline subjected to landslide movements, it is important to specify that this model is applicable to underground pipelines subjected to the movement produced by different causes (for example seismic movement) and also for sub-sea pipelines. In this last case, a different model of sensors with waterproof properties has to be selected.