Accurate Evaluation of Feature Contributions for Sentinel Lymph Node Status Classification in Breast Cancer

Abstract

The current guidelines recommend the sentinel lymph node biopsy to evaluate the lymph node involvement for breast cancer patients with clinically negative lymph nodes on clinical or radiological examination. Machine learning (ML) models have significantly improved the prediction of lymph nodes status based on clinical features, thus avoiding expensive, time-consuming and invasive procedures. However, the classification of sentinel lymph node status represents a typical example of an unbalanced classification problem. In this work, we developed a ML framework to explore the effects of unbalanced populations on the performance and stability of feature ranking for sentinel lymph node status classification in breast cancer. Our results indicate state-of-the-art AUC (Area under the Receiver Operating Characteristic curve) values on a hold-out set ($67\%$) while providing particularly stable features related to tumor size, histological subtype and estrogen receptor expression, which should therefore be considered as potential biomarkers.

1. Introduction

Current recommendations advise sentinel lymph node biopsy (SLNB) for breast cancer patients experiencing clinically negative lymph nodes on clinical or radiological evaluation [1]. While this procedure is currently the most accurate assessment, it is also the most expensive and time-consuming, as well as the most invasive, with a variety of potential adverse effects [2,3]. In addition, in patients with early-stage breast cancer, the incidence of axillary metastases is around 10–25% [4,5], therefore SLNB is often an unnecessary procedure. In this context, the definition of less expensive and invasive alternative procedures for the prediction of lymph node involvement represents a current task of interest for the clinical and scientific community.

In literature, several models have been proposed to predict non-sentinel lymph nodes status by using different features [6,7]. On the other side, a small number of studies with the goal of predicting the sentinel lymph nodes status have yielded promising findings [8,9,10].

Nevertheless, the classification of sentinel lymph nodes provides a typical example of an unbalanced classification problem. In healthcare data analysis applications including cancer diagnosis and disease risk prediction, classifying unbalanced datasets has been identified as a major challenge. When the quantity of samples in a dataset is substantially uneven, an unbalanced classification problem emerges. In binary classification tasks, the unbalanced classification problem occurs when one class (i.e., the minority class) has much fewer observations than the other class (i.e., the majority class) [11]. For unbalanced datasets, most of the machine learning (ML) algorithms usually perform poorly since they aim to optimize overall classification accuracy and thus assume an equal incidence of all classes. As a result, these methods exhibit classification bias towards the majority class, failing to identify examples of the minority class [12].

Several strategies have been proposed to overcome these limitations. Resampling methods have been introduced to rebalance the datasets. Resampling schemes include random oversampling of the minority class, undersampling (or subsampling) of the majority class and some advanced synthetic sampling methods that aim at rebalancing the class distribution at the data level. These rebalancing solutions, however, present several drawbacks. For example, loss of information is an inherent consequence of undersampling [13], but oversampling by randomly repeating the minority class sample could result in overfitting [14].

Although several works have investigated the effect of different data balancing strategies on the overall classification performance [15,16,17,18], there is a lack of work exploring the effect of these methods on feature ranking. This issue is particularly crucial in clinical contexts, where the interpretability of decisions and therefore the accurate identification of the feature contribution to the decisions of the algorithms is a key requirement [19,20].

In this work, we developed a ML framework to explore the effects of unbalanced populations on the performance and stability of feature ranking for sentinel lymph node status classification in breast cancer. In particular, we assessed the predictive power of different clinical and immunohistochemical features by exploiting two classifiers. We embedded a module specifically devoted to analysis the importance of features in relation to the variation of the training set obtained by different sampling techniques. Our work aims to address some questions: (i) How do the different models perform? (ii) What are the most important predictors? (iii) Are they stable across populations?

2. Materials

2.1. Data

From 2015 to 2017, we collected 635 patients enrolled at Istituto Tumori “Giovanni Paolo II” in Bari (Italy) according to the following eligibility criteria: (i) no evidence of metastatic lymph nodes on palpation or radiological examination, and (ii) patient undergoing SBLN. In particular, the one-step nucleic acid amplification (OSNA) procedure is performed in our Institute. OSNA is the intra-operative exam with a sensitivity and specificity of 87.5–100% and 90.5–100%, respectively [21], but it is an expensive and time-consuming process. Overall, 214 patients had clinically positive lymph nodes, whereas 421 patients resulted negative. For each patient, we collected age at breast cancer diagnosis and several prognostic factors related to the tumor evaluated on pre-operative stage. The retrospective observational study was approved by the Scientific Board of the Istituto Tumori “Giovanni Paolo II” and carried out according the Helsinki Statement. All patients who agreed to have their data used for research were enrolled.

2.2. Histological Features

We gathered information from our pathological anatomy department’s immunohistochemistry analyses, such as: tumor size stage (T: staging system classify), histological grade (G, Elston–Ellis scale: 1, 2, 3), estrogen receptor expression (ER, Pos/Neg), histological subtype (i.e., ductal, lobular, other special types), progesterone receptor expression (PgR, Pos/Neg), cellular marker for proliferation (Ki67, Pos/Neg with cut-off 20%), tumor multiplicity (Pos/Neg), human epidermal growth factor receptor-2 (HER2/neu: 0, 1+, 2+, 3+), presence of carcinoma in situ associated with invasive component (Pos/Neg), and the sentinel lymph nodes status (N, Pos/Neg) required in the classification approach. A lower grade denotes a better prognosis, and the Elston–Ellis adaptation of the Scarff–Bloom–Richardson grading system uses a three-grade scale to describe the tumor grade G: G1 (low grade), G2 (intermediate grade), or G3 (high grade) [22]. The histological examination was carried out using multiple 14–16 G core biopsy sampling while being guided by ultrasound. The characteristics of the samples are summarized in

Table 1. Characteristics of the samples collected in this study.

	N. Patients	N. Positive/ N. Negative
Overall	635	$214/421$
Histologic Type
Ductal	512	$185/327$
Lobular	67	$20/47$
Special type	56	$9/47$
Diameter
T1a	31	$3/28$
T1b	125	$18/107$
T1c	281	$88/193$
T2	198	$105/93$
ER
Positive	571	$193/378$
Negative	64	$21/43$
Grading
G1	175	$35/140$
G2	287	$111/176$
G3	173	$68/105$
HER2
0	471	$161/310$
1	78	$23/55$
2	46	$21/25$
3	39	$9/30$
Multifocality
Positive	143	$61/82$
Negative	492	$153/339$
In situ component
Positive	369	$114/255$
Negative	266	$100/166$

.

3. Methods

In this work, we investigated the effectiveness of two classification methods (Random Forest and Logit Lasso) with three training strategies, i.e., unbalanced strategy, oversampling of the minority class and subsampling of the majority class. As depicted in Figure 1, we adopted a hold-out approach, randomly selecting $M=100$ samples for the independent test (i.e., the hold-out test). A repeated k-fold validation ($N=10$ iterations, $k=10$ folds) was selected as cross-validation approach on the training set. In detail, each of the three strategies was combined with each of the two classification algorithms resulting in six training schemes. For each scheme, we evaluated both the importance and variability of the features. In addition, the consensus degree on the probability scores of the different strategies was assessed as the correlation between each couple of schemes. Each step is detailed in the following sections. We used a PC with the following hardware configuration: Intel Core i7-8550U CPU @ 1.99GHz x 4, and 16GB RAM to run the experiments. All the analyses were performed by using R Statistical Software (v4.1.1., R Core Team 2021) with a run-time of 9.8 min for the execution of the entire framework.

3.1. Training Strategies

The simple subsampling strategy involves randomly eliminating samples from the majority class in order to match a certain fixed percentage of samples from the minority class. In this work, we selected the parameter of 50% of the samples in the minority class to achieve a reasonable trade-off between sample representativeness and computational efficiency.

On the other hand, SMOTE (Synthetic Minority Over-sampling Technique) creates artificial samples from the minority class leveraging the information in the data [23]. For each sample from the minority class $x_i$, firstly $R=5$ samples from the minority class with the smallest Euclidean distance from the original sample were identified (i.e., the top R nearest neighbors $x_j^{NN}$, $j=1,\cdots ,R$), then, one of these samples is randomly chosen ($x_s^{NN}$) and a new synthetic SMOTE sample is defined as:

$$x^{SMOTE}=x+u·(x_s^{NN}-x),$$

(1)

where u is randomly chosen from the uniform distribution $U(0,1)$ and is the same for all variables, but differs for each SMOTE sample in order to ensure that the SMOTE sample is on the line joining the two original samples used to generate it [24]. Thus, SMOTE is an augmentation technique to increase the minority class resulting in an output balanced training set.

3.2. Classification Algorithms

3.2.1. Logistic LASSO

In binary classification studies, the dichotomous response variable $y_i$ is usually coded as 1 for cases and 0 for controls. In order to model logistic regression, the probability $p_i=Pr(y_i=1)$ of case i given the predictor vector $x_i$ can be expressed as:

$$p_i=\frac{e^{{\beta }_0+x_i^T\beta }}{1+e^{{\beta }_0+x_i^T\beta }},$$

(2)

The parameter vector $\Theta ={({\beta }_0,{\beta }_1,\dots ,{\beta }_p)}^T$ is usually estimated by maximizing the log-likelihood function:

$$L(\Theta )=\sum _{i=1}^N[y_{i}log\left(p_i\right)+(1-y_i)log(1-p_i)]$$

(3)

Regularization methods such as shrinkage or penalized regression could reduce the likelihood of overfitting by modifying the loss function with a penalty term to shrink the coefficients in the regression towards zero and selecting the nonzero variables in the final model [25]. This approach has the additional advantage of selecting the most important variables for the predictions from a large and potentially multicollinear set of features, resulting in a more relevant and interpretable set of predictors [26,27,28]. The logistic LASSO model involves L1 penalty term, resulting in:

$$L(\Theta )+\lambda \sum _{j=1}^P\left|{\beta }_j\right|$$

(4)

In order to tune the penalty constant $\lambda$, without introducing bias and overfitting, we used an inner round of k-fold validation within each training round, with $k=3$. The AUC metric was computed for the test set as the performance measure to tune $\lambda$. We used the “glmnet” package to fit the logistic LASSO regression.

3.2.2. Random Forest

Random Forest (RF) is also recognized as bagged decision trees. This algorithm works on using different weak learners to implement strong learners [29]. The target outcome for each sample $y_i$ is individually forecast by each tree, while the final predictions are based on the majority of trees voting.

Two types of randomization are included: (I) a subset of observations is picked at random for each tree, and (II) a random set of $mtry$ candidate predictors is chosen to produce a split within each tree. As a result, a purity measure and a decision threshold are used to divide the node input samples into two groups. Each tree is built until the nodes have divided their inputs into subsets and assigned a single final label to each of them. The out-of-the-bag (OOB) set for that tree contains the samples that were not utilized for that tree [30]. The accuracy of RF is assessed by using the samples of the OOB as:

$$MS{E}_{OOB}=\frac{1}{N}\sum _{i=1}^N{(y_i-y_{\overline{\widehat{i}}O})}^2,$$

(5)

where $y_{\overline{\widehat{i}}O}$ denotes the average prediction for the ith observation from all trees for which this observation has been OOB. We used the “RandomForest” R Package with the default parameter $mtry=P/3$ and number of trees = 100.

3.3. Performance Evaluation

The model decisions that arise may be categorized into four different groups: true positives (TP), which occur when the model correctly predicts the positive class, true negatives (TN), which occur when the model correctly predicts the negative class, and false positives (FP) and false negatives (FN), which occur when the model incorrectly predicts the positive and negative classes, respectively. Given these four cases, we considered the following metrics to evaluate the performance of the classification models:

• Accuracy

  $$\frac{TP+TN}{TP+TN+FP+FN};$$
• Sensitivity

  $$\frac{TP}{TP+FN};$$
• Specificity

  $$\frac{TN}{TN+FP};$$
• Area Under the Receiver Operating Characteristics (ROC) Curve (AUC) that adjusts the decision threshold to plot sensitivity versus specificity.

3.4. Feature Ranking Analysis

Both RF and Lasso Logistic regression provide embedded feature selection techniques. As a result of the model, a subset of the features with non-zero weights could be retrieved, and the coefficients of the least relevant features are shrunk to zero [31]. Moreover, the absolute values of the Lasso coefficients could be used for feature ranking since the weight ${\beta }_i$ quantifies the impact that each feature has in the regression model. We exploited the averaged absolute values of the weights across the validation rounds in order to obtain a final feature ranking, regardless of the specific training fold.

On the other side, RF feature importance can be assessed by applying the permutation-based MSE reduction criterion [32]. The relevance of each feature per each tree is determined by permuting the feature’s OOB data for the tree and calculating the difference between the permuted and true OOB-MSE. By averaging these differences over all of the forest’s trees, the final MSE decrease for each feature is produced. The basic logic behind this technique is that if a feature has no effect on performance, the difference in accuracy estimated using the true values of the feature and that computed using its permuted values is unlikely to be significant.

For each classification scheme (i.e., each sampling algorithm with each of the two machine learning methods), we averaged the importance scores of the features across the rounds to obtain a single feature importance vector. In addition, the quartile coefficient of dispersion [33] was used to assess the variability across rounds of each feature.

4. Results and Discussion

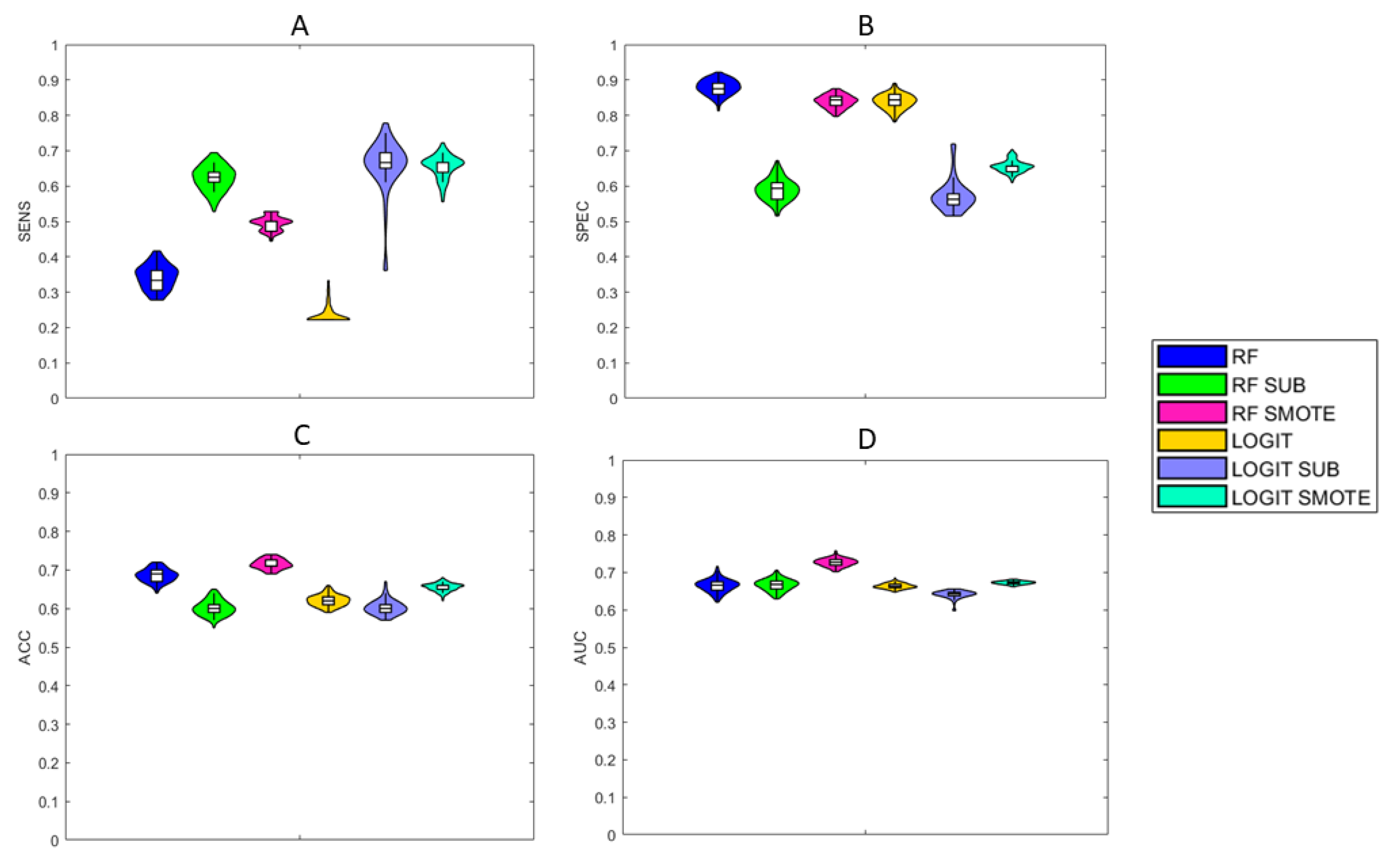
4.1. Performance

Figure 2 and Figure 3 show the performance metrics across the cross-validation rounds and for the independent hold-out test for each classification scheme, respectively.

Table 2. Performance of the ML models for for the cross-validation sets (mean ± std).

Classification Scheme	SENS	SPEC	ACC	AUC
RF	$0.37\pm 0.1$	$0.85\pm 0.05$	$0.7\pm 0.05$	$0.66\pm 0.07$
RF SUB	$0.59\pm 0.11$	$0.67\pm 0.11$	$0.63\pm 0.07$	$0.66\pm 0.08$
RF SMOTE	$0.89\pm 0.03$	$0.98\pm 0.01$	$0.93\pm 0.01$	$0.98\pm 0.005$
Logit Lasso	$0.39\pm 0.1$	$0.85\pm 0.05$	$0.70\pm 0.05$	$0.72\pm 0.08$
Logit Lasso SUB	$0.67\pm 0.1$	$0.67\pm 0.12$	$0.67\pm 0.07$	$0.72\pm 0.07$
Logit Lasso SMOTE	$0.73\pm 0.04$	$0.72\pm 0.04$	$0.73\pm 0.03$	$0.77\pm 0.03$

and

Table 3. Performance of the ML models for for the hold-out set (mean ± std).

Classification Scheme	SENS	SPEC	ACC	AUC
RF	$0.34\pm 0.03$	$0.87\pm 0.02$	$0.69\pm 0.01$	$0.66\pm 0.01$
RF SUB	$0.62\pm 0.003$	$0.58\pm 0.03$	$0.60\pm 0.01$	$0.66\pm 0.01$
RF SMOTE	$0.49\pm 0.03$	$0.83\pm 0.01$	$0.71\pm 0.01$	$0.73\pm 0.01$
Logit Lasso	$0.23\pm 0.02$	$0.84\pm 0.02$	$0.62\pm 0.01$	$0.66\pm 0.006$
Logit Lasso SUB	$0.65\pm 0.08$	$0.57\pm 0.04$	$0.60\pm 0.01$	$0.64\pm 0.01$
Logit Lasso SMOTE	$0.65\pm 0.03$	$0.65\pm 0.01$	$0.65\pm 0.01$	$0.67\pm 0.004$

list the mean and standard deviation for each performance metric for cross-validation sets and hold-out test, respectively. The Logit Lasso algorithm is less affected by model overfitting as it can be noted from the smaller difference between training and test performance. Moreover, it is worth noting that among the various strategies, the SMOTE technique provides the best balance between sensitivity and specificity.

Overall, the achieved performance compares favorably with that obtained in our previous work [34]. In particular, in this analysis, we also found the logistic regression model as the method with the most stable performance between the training and test sets. However, in contrast to our previous work, here we used different training sampling strategies that showed that SMOTE represents a promising method for this clinical challenge and that simply undersampling does not guarantee equally effective results.

Other works addressed similar classification tasks, showing that the performance can be significantly improved by adding predictors extracted from imaging [35,36], genetics [9] and nomograms of clinical and pathologic variables [37] with more complex nonlinear models such as deep neural networks [38]. In our analysis, we used simpler and therefore more interpretable models in combination with known sampling strategies in order to highlight different effects on performance. In future developments, we will expand the presented framework to investigate the impact of other features and predictive models.

4.2. Feature Ranking Analysis

We computed the feature ranking list resulting from each classification scheme over the cross-validation rounds for the clinical interpretability of the results. Figure 4A shows the feature ranking for the six schemes. It can be noted that only the diameter results are relevant, regardless of the adopted scheme. The correlation between tumor size and lymph node status has been evaluated in several studies. In patients with breast cancer, increasing tumor diameter at diagnosis is associated with an increasing number of metastatic lymph nodes [39,40].

Moreover, it is worth noting that the three Lasso Logit models agree much more with each other on the final average feature ranking, outlining the features histology, diameter, ER and multifocality as the most important features. As a matter of fact, Logit Lasso exhibits greater stability of feature ranking compared to RF. Stability refers to the feature ranking’s sensitivity to perturbation of training samples and it is associated with the reproducibility power of the feature selection method [41]. When analyzing feature selection algorithms in different clinical scenarios, high stability could be just as crucial as high classification accuracy [42,43,44]. We used the quartile coefficient to objectively measure the stability of these features for each classification scheme. It can be seen in Figure 4B that the feature diameter is the most stable among all the features, regardless of the adopted scheme, while the HER2 feature exhibits the highest dispersion coefficient, showing high instability. Moreover, the weights of Age, PgR and Ki67 are shrunk to zero from the Lasso algorithm, highlighting their low impact on the classification task.

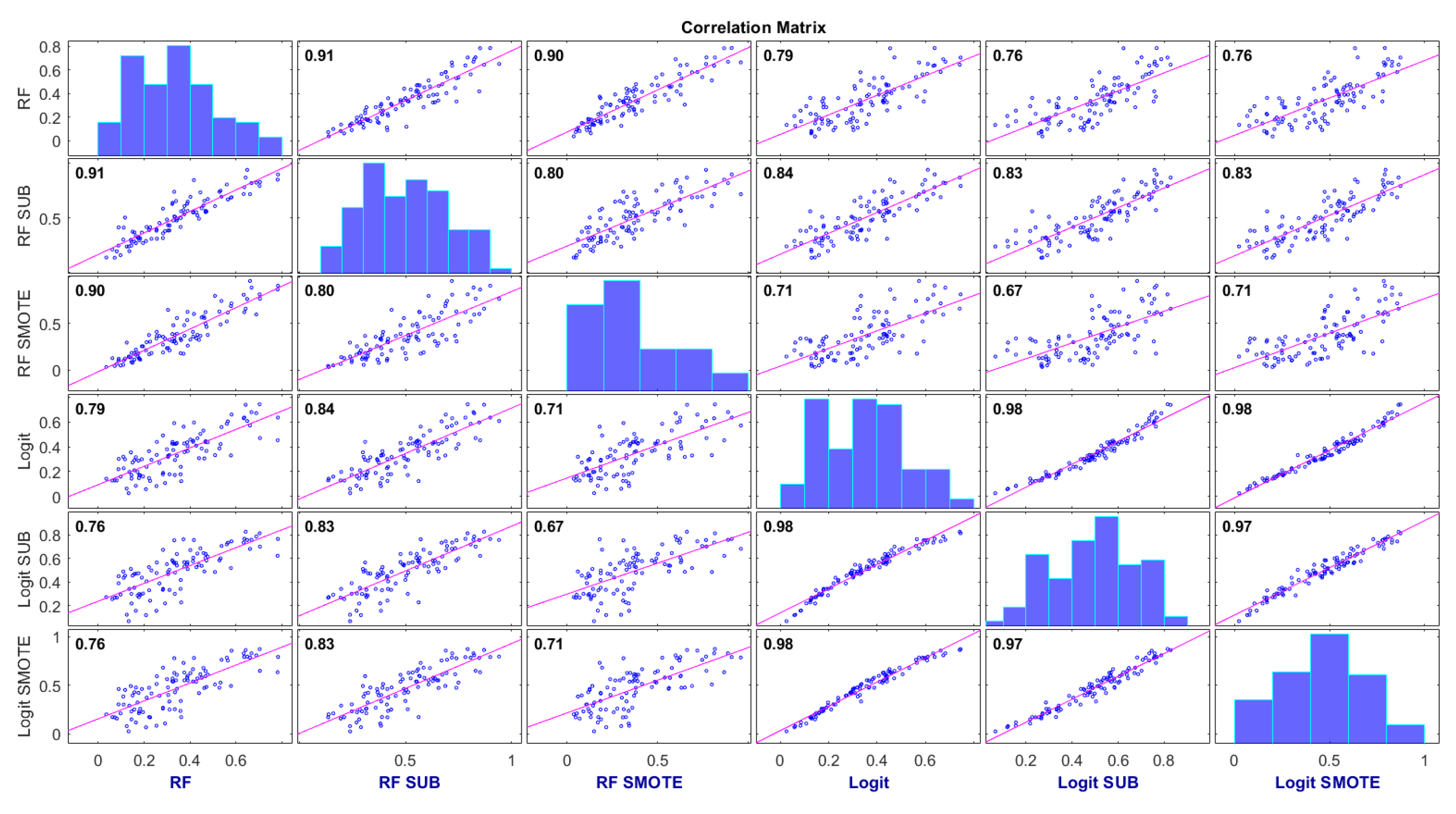
4.3. Consensus Degree of the Probability Scores

We better analyzed the behavior of the classification schemes on the independent hold-out test set, by inspecting the correlation between the probability scores resulting from each couple of schemes as shown in Figure 5. It is important to underline that the RF algorithm exhibits the lowest correlations between the probability scores for the different training strategies, showing an inherent instability with respect to the sampling methods; on the contrary, the Logit Lasso algorithm shows the highest correlations between the probability scores, underlining better stability of performance and less variability among the sampling strategies. This issue is of paramount importance in the clinical setting, where stability and generalization of algorithms supporting diagnosis are highly recommended. These two aspects are closely linked to each other since we need to evaluate how changes in the composition of the learning set (i.e., sampling randomness) influence the function produced by the algorithm (i.e., the probability scores) [45,46,47].

5. Landscape

Most of the studies proposed in the literature aimed at predicting the lymph node status in general terms (i.e., non-sentinel lymph nodes) using nomograms of clinical and pathological variables [6,7,48,49]. On the contrary, to the best of our knowledge, few works aimed at predicting the status of the sentinel lymph node [9,50]. The model proposed in [9] reached an average AUC value of 88.3%. by using genetic characteristics, tumor size and lymph vascular invasion. In [50], the authors proposed an analogous model for patients with ductal carcinoma in situ by stating an AUC value of 75%. In our preliminary works, comparable results were reached to the-state-of-the-art [10,34]. Recent studies, radiomic features extracted from magnetic resonance images [35,36,51] or ultrasounds [52] were exploited to identify a better performing customized model. However, none of the works reported in the literature specifically addressed the issue of class imbalance, as proposed in this work.

6. Limitations and Future Perspectives

In this work, we analyzed a dataset of limited size, therefore we avoided more sophisticated strategies such as those based on deep neural networks that require large sample sizes, preferring two simpler methods such as RF and Lasso. Such methods are rather well established in the literature for classification tasks in various clinical contexts. Moreover, these methods offer the advantage of providing the most important features for the algorithm’s decisions proving a higher explainability of the impact of the clinical predictors on the overall performance. This issue is particularly relevant as it enables the integration of the perspectives of both clinical specialists and algorithm developers, allowing synergy between the different entities and improving the machine learning paradigms in each specific clinical context.

Although our methodological choices were conditioned by the dimensionality of the dataset, it should be emphasised that for high-dimensional datasets, other approaches should be evaluated in conjunction with Lasso. As an example, Ren et al. [53] proposed a network constrained regularization approach for classification exploiting networks to model interconnections among features, overcoming the existing shortcomings in addressing the correlations among features. In addition, when the number of features increases, robust feature selection techniques are critical for successful performance since these methods usually have better stability and reproducibility [54]. Accordingly, with higher dimensionality of the features and complex data structure, more feature selection algorithms should be evaluated in order to avoid the oversimplification of the predictive models. On the other hand, although the proposed framework is fully scalable and would allow a larger number of machine learning algorithms combined with different sampling strategies to be compared for future developments, it should be noted that the computational complexity and the execution time increase with the number of algorithms to be compared. Further analyses will be carried out to identify the best combinations of ML algorithms and sampling strategies that ensure the best balance among classification accuracy, computational complexity and interpretability of the models.

7. Conclusions

In this work, we presented a simple ML framework to explore the effect of different sampling strategies on both performance and feature stability for the prediction of the sentinel lymph node status in breast cancer. Due to the unbalanced configuration of the classification problem, we trained two different machine learning algorithms on tumor histopathology and clinical features in combination with the random undersampling method and a synthetic augmentation technique (SMOTE) to balance the training set. We found that the best combination of techniques consists in the use of the simpler Lasso classifier and the SMOTE strategy both in terms of the ability to generalize the predictive models on the hold-out test set and the stability of the clinical features. Although the proposed framework does not yet allow the implementation of a diagnosis support system due to moderate performance, it provides a set of clinical features worthy of attention, which should be considered as possible biomarkers alongside other imaging and genetic features.