Time-Dependent Reliability Assessment Method for RC Simply Supported T-Beam Bridges Based on Lateral Load Distribution Influenced by Reinforcement Corrosion
Abstract
:1. Introduction
2. Reinforcement Steel Corrosion Model
2.1. Corrosion Time and Rate of Reinforcement
2.2. Degree of Reinforcement Corrosion
2.3. Flexural Stiffness of Bridge with Corroded Reinforcement
3. Load Effect Calculation Method of Corroded Reinforcement Bridges
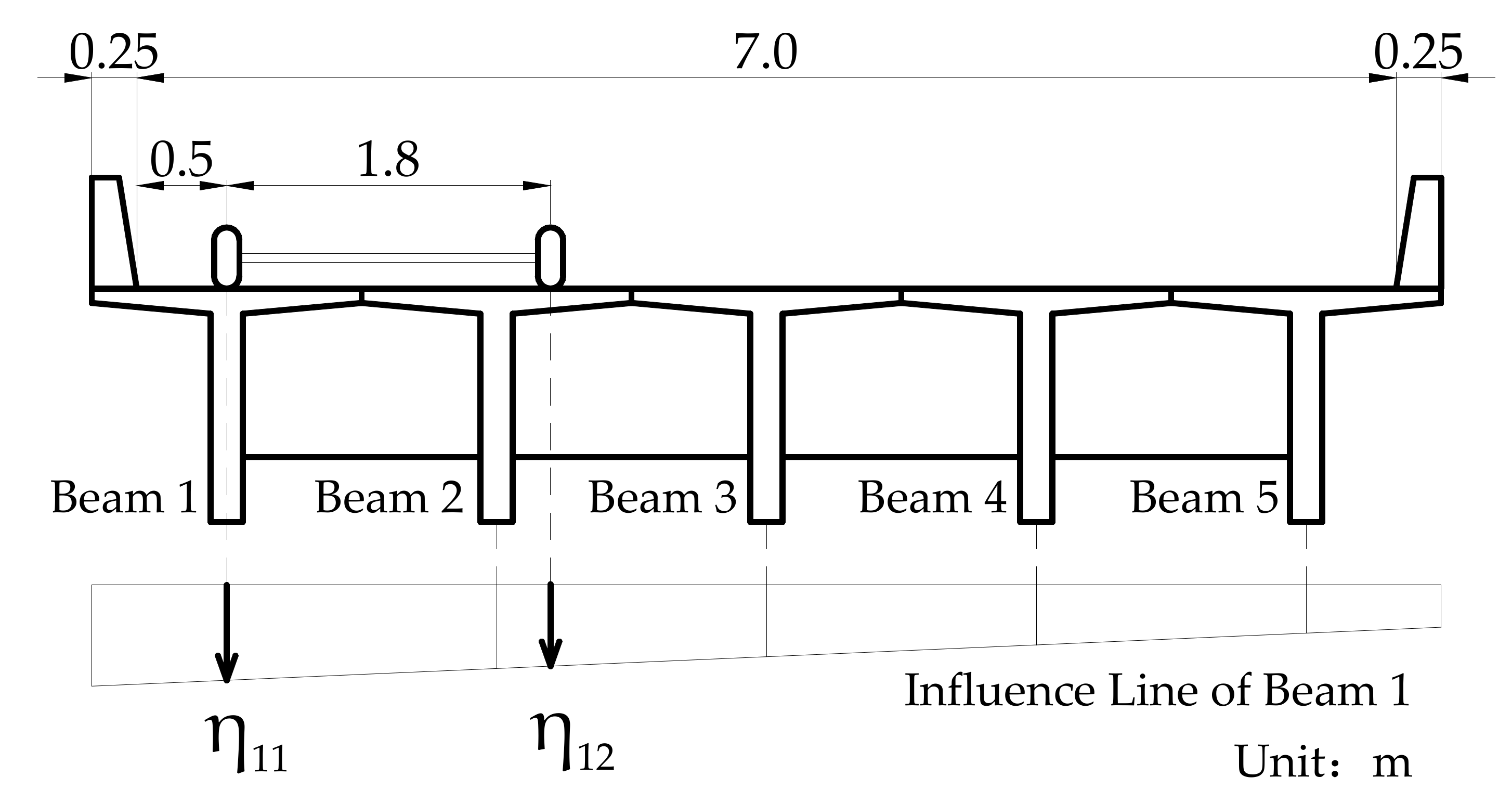
3.1. Influence Lines of Lateral Load Distribution Considering Reinforcement Corrosion
3.2. Vehicle Load Effect Calculation Model
3.3. Performance Function of Flexural Bearing Capacity
4. Results and Analysis
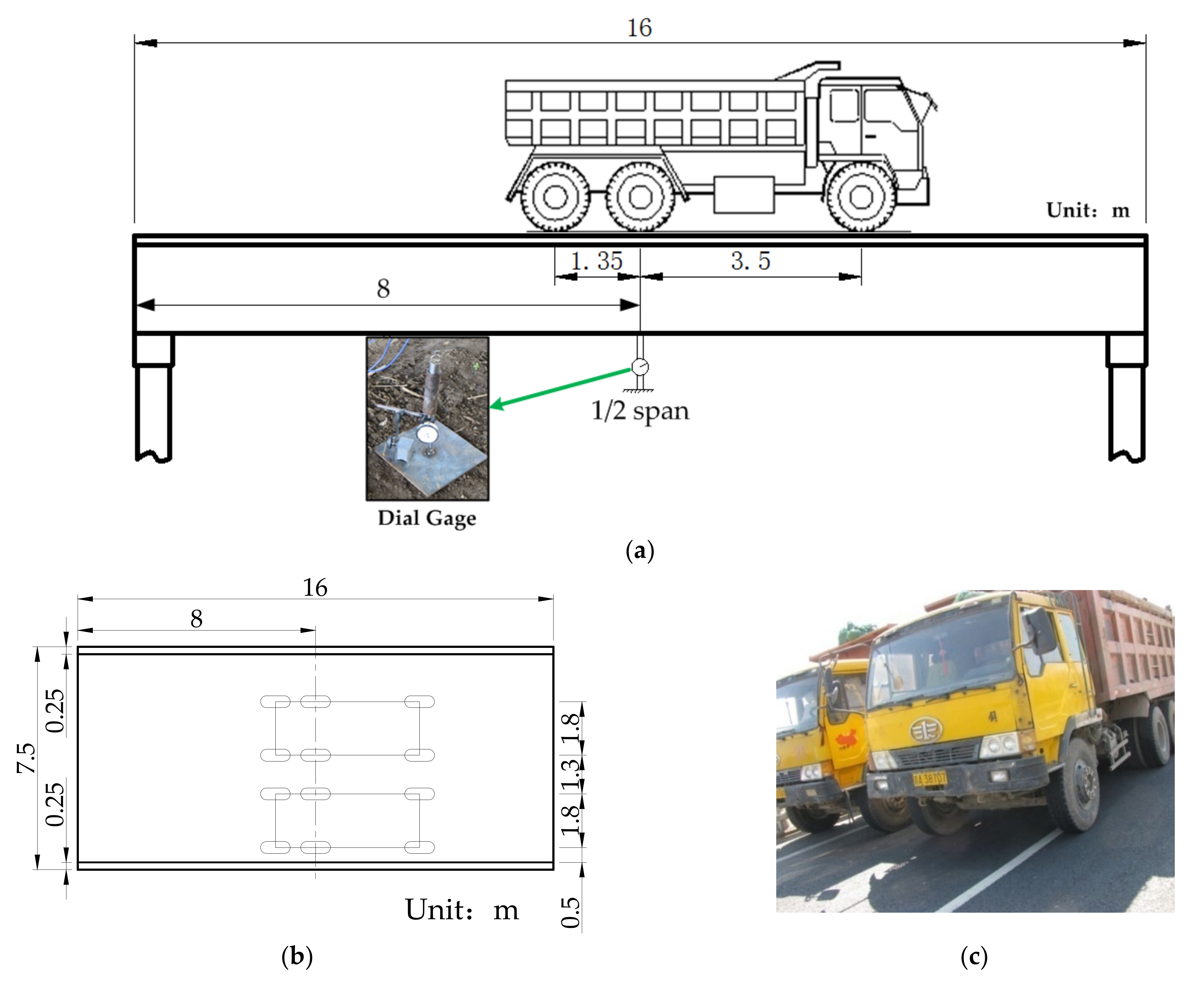
4.1. Overview of the Simply Supported T-Beam Bridge
4.2. Bridge Detection Data and Probability Distribution Information of Influencing Factors
4.3. Analysis of Bridge Load Effect Considering Reinforcement Corrosion
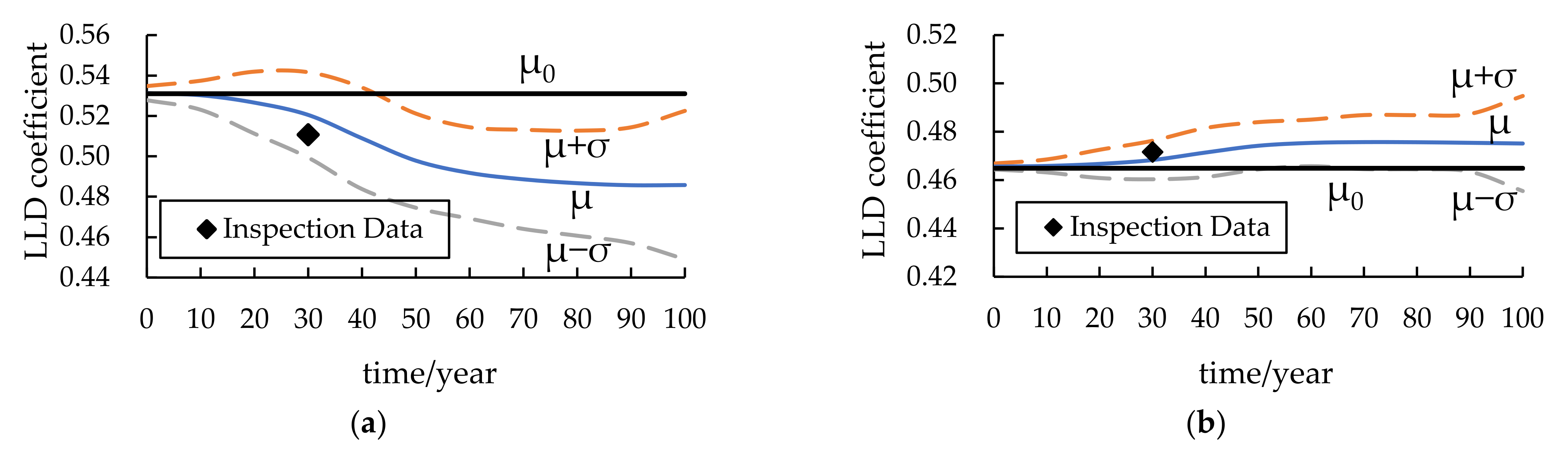
4.4. Reliability Analysis Considering LLD Affected by Reinforcement Corrosion
5. Discussion
6. Conclusions
- (1)
- Reinforcement corrosion due to chloride ingress not only reduces the bearing capacity of simply supported T-beam bridges but also results in the deterioration of stiffness. As a result, the vehicle load effect will be changed, which will conversely aggravate the reinforcement corrosion process. The traditional LLD theory is no longer suitable for actual bridge engineering.
- (2)
- Reinforcement corrosion can lead to the redistribution of vehicle load effect. In both the theoretical and experimental analysis, the load effect of Beam 1 decreases gradually with the increase in reinforcement corrosion, and part of the load effect is redistributed to the internal beam. Due to the coincidence of the computational and experimental results, the correctness of the LLD calculation method for corroded reinforcement bridges is verified.
- (3)
- The LLD coefficient also possesses time-dependent properties. Because the reinforcement of the bridge is not corroded at the initial stage of service, there is little fluctuation with increasing time. After that, the LLD coefficients of T-beams will observably increase or decrease according to the position on the bridge and the reinforcement corrosion degree.
- (4)
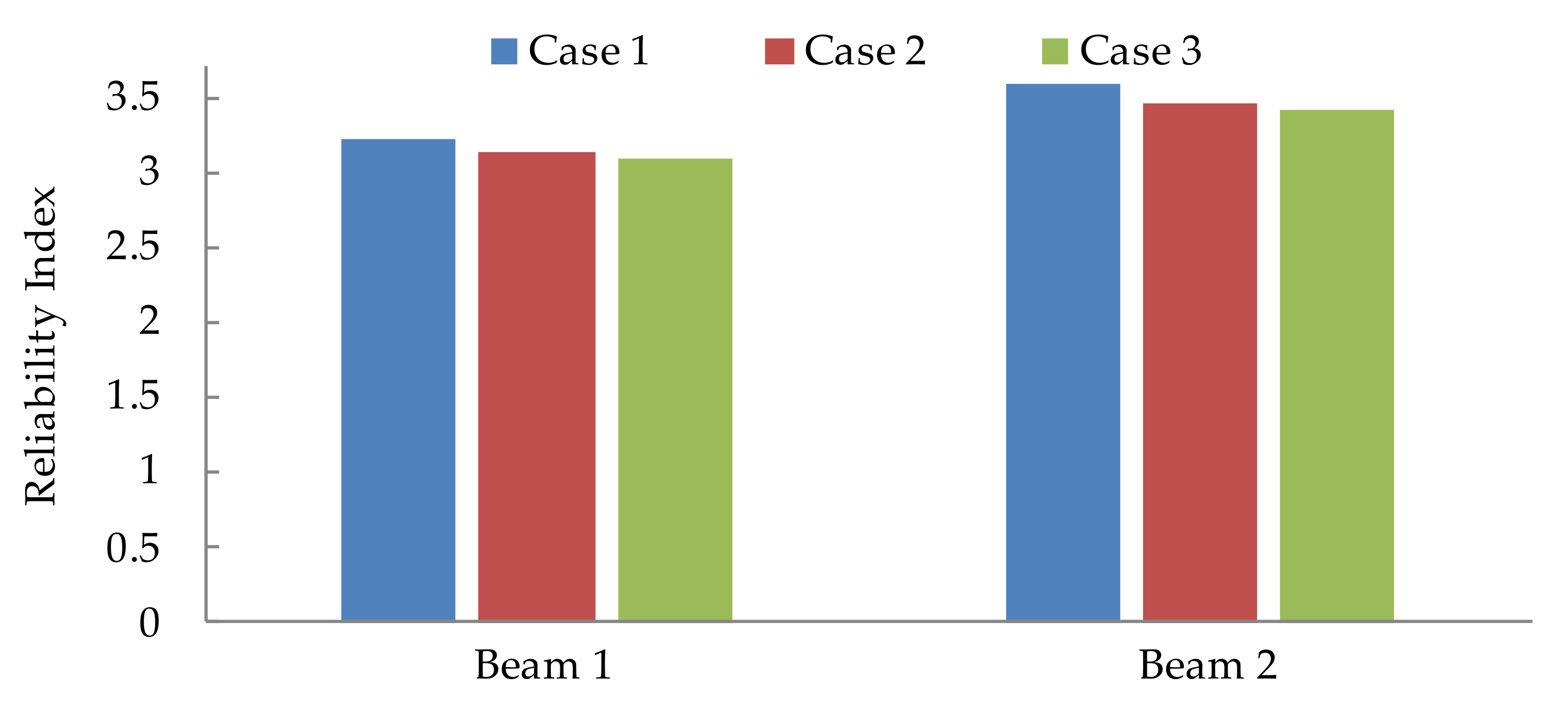
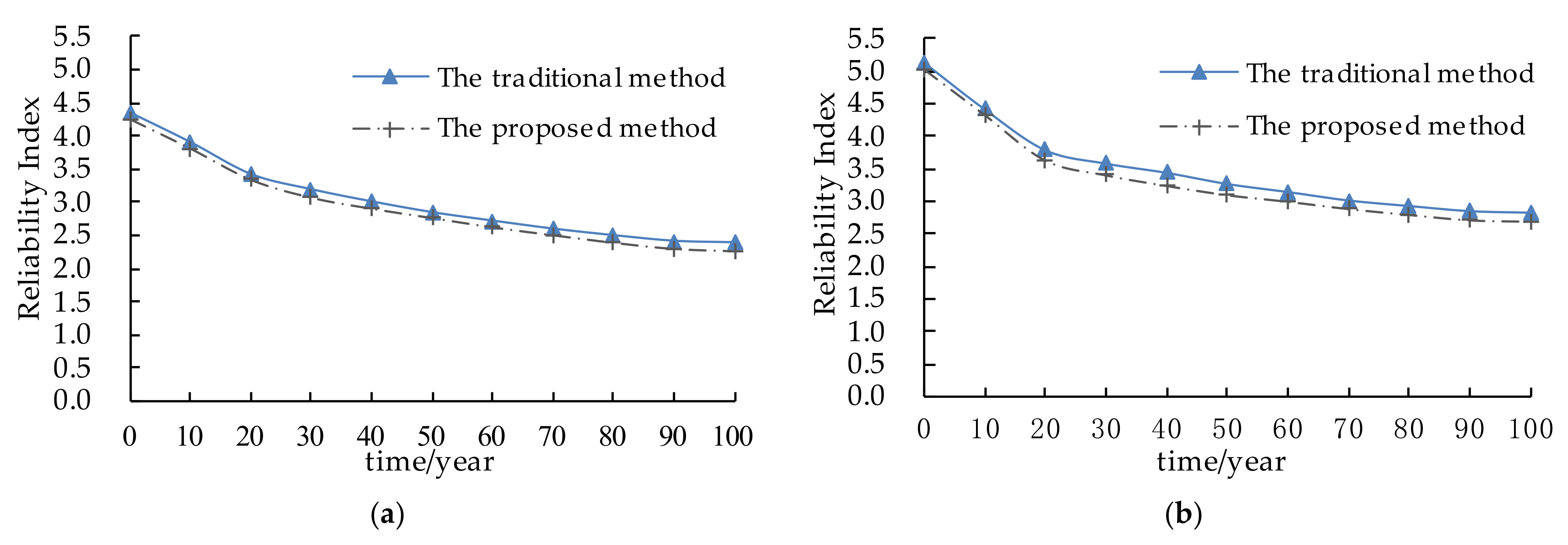
- The traditional reliability analysis method for corroded reinforcement bridges only focuses on the bridge bearing capacity change. The interaction between the effective bending moment of inertia and the LLD coefficient caused by reinforcement corrosion is ignored. It increases the reliability calculation model error. The comparison results demonstrate the reliability index calculated by the traditional method is greater than that of the method proposed in this paper. This indicates the traditional method is too conservative and does not consider the influence of reinforcement corrosion on the LLD of simply supported T-beam bridges.
- (5)
- In this paper, the influence of reinforcement corrosion on the superstructure of simply supported bridges was researched based on bridge inspection data. For future study, the reinforcement corrosion influence on vehicle effects for other types of bridges will be extended. Moreover, modal parameters are used as important indicators for structural health monitoring, and they are also influenced by reinforcement corrosion. If the relationship between modal parameters and reinforcement corrosion is explicit, structural health monitoring data can be employed to accurately evaluate the reinforcement corrosion degree and the reliability of corroded bridges.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melhem, M.M.; Caprani, C.C.; Stewart, M.G. Reliability of Super-T PSC Girders at Serviceability Limit State Stresses across All Span Ranges. Struct. Infrastruct. Eng. 2019, 15, 812–821. [Google Scholar] [CrossRef]
- Murad, M.O.F.; Chik, Z.; Mustafa, A.; Absar, B.M.N.; Shikdar, K.H.; Nayan, K.A.M. A Comparative Study between Structural Properties of Pre-Tensioned Inverted T-Girder and Actual Post-Tensioned Box Girder in Bridge Construction. KSCE J. Civ. Eng. 2016, 20, 2403–2409. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Y.; Gong, J.; Liu, M.; Yang, X. Effect of Global Warming on Chloride Ion Erosion Risks for Offshore RC Bridges in China. KSCE J. Civ. Eng. 2018, 22, 3600–3606. [Google Scholar] [CrossRef]
- Huang, C.; Huang, S. Seismic Resilience Assessment of Aging Bridges with Different Failure Modes. Structures 2021, 33, 3682–3690. [Google Scholar] [CrossRef]
- Zambon, I.; Santamaria Ariza, M.P.; Campos e Matos, J.; Strauss, A. Value of Information (VoI) for the Chloride Content in Reinforced Concrete Bridges. Appl. Sci. 2020, 10, 567. [Google Scholar] [CrossRef] [Green Version]
- Crespi, P.; Zucca, M.; Valente, M. On the Collapse Evaluation of Existing RC Bridges Exposed to Corrosion under Horizontal Loads. Eng. Fail. Anal. 2020, 116, 104727. [Google Scholar] [CrossRef]
- Crespi, P.; Zucca, M.; Valente, M.; Longarini, N. Influence of Corrosion Effects on the Seismic Capacity of Existing RC Bridges. Eng. Fail. Anal. 2022, 140, 106546. [Google Scholar] [CrossRef]
- Chen, C.; Yang, C. Experimental and Simulation Studies on the Mechanical Performance of T-Girder Bridge Strengthened with Transverse Connection. J. Perform. Constr. Fac. 2019, 33, 04019055. [Google Scholar] [CrossRef]
- El Hassan, J.; Bressolette, P.; Chateauneuf, A.; El Tawil, K. Reliability-Based Assessment of the Effect of Climatic Conditions on the Corrosion of RC Structures Subject to Chloride Ingress. Eng. Struct. 2010, 32, 3279–3287. [Google Scholar] [CrossRef]
- Darmawan, M.S.; Stewart, M.G. Spatial Time-Dependent Reliability Analysis of Corroding Pretensioned Prestressed Concrete Bridge Girders. Struct. Saf. 2007, 29, 16–31. [Google Scholar] [CrossRef]
- Naito, C.; Fox, J.; Bocchini, P.; Khazaali, M. Chloride Migration Characteristics and Reliability of Reinforced Concrete Highway Structures in Pennsylvania. Constr. Build. Mater. 2020, 231, 117045. [Google Scholar] [CrossRef]
- Bautista, A.; Pomares, J.C.; Gonzalez, M.N.; Velasco, F. Influence of the Microstructure of TMT Reinforcing Bars on Their Corrosion Behavior in Concrete with Chlorides. Constr. Build. Mater. 2019, 229, 116899. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Li, G.; Yi, T.; Li, H. A Performance-Based Service Life Design Method for Reinforced Concrete Structures under Chloride Environment. Constr. Build. Mater. 2016, 124, 453–461. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, H.; Hao, Y. Blast Fragility Analysis of RC Columns Considering Chloride-Induced Corrosion of Steel Reinforcement. Struct. Saf. 2022, 96, 102200. [Google Scholar] [CrossRef]
- Chehade, F.E.; Younes, R.; Mroueh, H.; Chehade, F.H. Time-Dependent Reliability Analysis for A Set of RC T-Beam Bridges under Realistic Traffic Considering Creep and Shrinkage. Eur. J. Environ. Civ. Eng. 2021, 1, 1–25. [Google Scholar] [CrossRef]
- Saad, L.; Aissani, A.; Chateauneuf, A.; Raphael, W. Reliability-Based Optimization of Direct and Indirect LCC of RC Bridge Elements under Coupled Fatigue-Corrosion Deterioration Processes. Eng. Fail. Anal. 2016, 59, 570–587. [Google Scholar] [CrossRef]
- Lu, X.; Xu, L.; Wei, K.; Xu, L. Transverse Seismic Damage Mode Identification of Deteriorating Simply-Supported Highway Bridges. Structures 2022, 38, 1529–1541. [Google Scholar] [CrossRef]
- Val, D.V.; Stewart, M.G.; Melchers, R.E. Effect of Reinforcement Corrosion on Reliability of Highway Bridges. Eng. Struct. 1998, 20, 1010–1019. [Google Scholar] [CrossRef]
- Duprat, F. Reliability of RC Beams under Chloride-Ingress. Constr. Build. Mater. 2007, 21, 1605–1616. [Google Scholar] [CrossRef]
- Tu, B.; Dong, Y.; Fang, Z. Time-Dependent Reliability and Redundancy of Corroded Prestressed Concrete Bridges at Material, Component, and System Levels. J. Bridge Eng. 2019, 24, 04019085. [Google Scholar] [CrossRef]
- Yogalakshmi, N.J.; Rao, K.B.; Anoop, M.B. Safety Assessment of In-Service Reinforced Concrete T-Girders of Bridge Decks. Struct. Concr. 2017, 18, 733–746. [Google Scholar] [CrossRef]
- Kim, T.H. Seismic Performance Assessment of Deteriorated Two-Span Reinforced Concrete Bridges. Int. J. Concr. Struct. Mater. 2022, 16, 4. [Google Scholar] [CrossRef]
- Ghosh, P.; Konecny, P.; Lehner, P.; Tikalsky, P.J. Probabilistic Time-Dependent Sensitivity Analysis of HPC Bridge Deck Exposed to Chlorides. Comput. Concr. 2017, 19, 305–313. [Google Scholar] [CrossRef]
- Hajkova, K.; Smilauer, V.; Jendele, L.; Cervenka, J. Prediction of reinforcement corrosion due to chloride ingress and its effects on serviceability. Eng. Struct. 2018, 174, 768–777. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Yi, J. Effect of Uneven Multilane Truck Loading of Multigirder Bridges on Component Reliability. Struct. Concr. 2020, 21, 1644–1661. [Google Scholar] [CrossRef]
- Liberati, E.A.P.; Nogueira, C.G.; Leonel, E.D.; Chateauneuf, A. Nonlinear Formulation Based on FEM, Mazars Damage Criterion and Fick’s Law Applied to Failure Assessment of Reinforced Concrete Structures Subjected to Chloride Ingress and Reinforcements Corrosion. Eng. Fail. Anal. 2014, 46, 247–268. [Google Scholar] [CrossRef]
- Tu, B.; Fang, Z.; Dong, Y.; Frangopol, D.M. Time-Variant Reliability Analysis of Widened Deteriorating Prestressed Concrete Bridges Considering Shrinkage and Creep. Eng. Struct. 2017, 153, 1–16. [Google Scholar] [CrossRef]
- Sajedi, S.; Huang, Q. Reliability-Based Life-Cycle-Cost Comparison of Different Corrosion Management Strategies. Eng. Struct. 2019, 186, 52–63. [Google Scholar] [CrossRef]
- Ballim, Y.; Reid, J.C. Reinforcement Corrosion and the Deflection of RC Beams—An Experimental Critique of Current Test Methods. Cement Concr. Comp. 2003, 25, 625–632. [Google Scholar] [CrossRef]
- Malumbela, G.; Moyo, P.; Alexander, M. Longitudinal Strains and Stiffness of RC Beams under Load as Measures of Corrosion Levels. Eng. Struct. 2012, 35, 215–227. [Google Scholar] [CrossRef]
- Li, C.; Hao, H.; Li, H.; Bi, K. Seismic Fragility Analysis of Reinforced Concrete Bridges with Chloride Induced Corrosion Subjected to Spatially Varying Ground Motions. Int. J. Struct. Stab. Dyn. 2016, 16, 1550010. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Q.; Ren, Y. Performance deterioration of corroded RC beams and reinforcing bars under repeated loading. Constr. Build. Mater. 2015, 96, 404–415. [Google Scholar] [CrossRef]
- ACI 3188-05; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2005.
- Ma, Y. Reliability Assessment and Life Prediction for Existing RC Bridges Under Multi-Source Uncertainties. Ph.D. Thesis, Changsha University of Science & Technology, Changsha, China, 2014. (In Chinese). [Google Scholar]
- Cui, J.; Xie, H.; Cui, P.; Kim, D. Seismic Performance Evaluation of Existing RC Structures Based on Hybrid Sensing Method. Neural Comput. Appl. 2018, 31, 4653–4663. [Google Scholar] [CrossRef]
- Suo, Q.; Stewart, M.G. Corrosion Cracking Prediction Updating of Deteriorating RC Structures using Inspection Information. Reliab. Eng. Syst. Safe 2009, 94, 1340–1348. [Google Scholar] [CrossRef]
- Specification for Mix Proportion Design of Ordinary Concrete, 1st ed.; China Architecture & Building Press: Beijing, China, 2011. (In Chinese)
- Stewart, M.G. Mechanical Behaviour of Pitting Corrosion of Flexural and Shear Reinforcement and Its Effect on Structural Reliability of Corroding RC Beams. Struct. Saf. 2009, 31, 19–30. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Structural Reliability of Concrete Bridges Including Improved Chloride-Induced Corrosion Models. Struct. Saf. 2000, 22, 313–333. [Google Scholar] [CrossRef]
- Stewart, M.G.; Al-Harthy, A. Pitting Corrosion and Structural Reliability of Corroding RC Structures: Experimental Data and Probabilistic Analysis. Reliab. Eng. Syst. Safe 2008, 93, 373–382. [Google Scholar] [CrossRef]
- General Code for Design of Highway Bridges and Culverts, 1st ed.; China Communications Press: Beijing, China, 2015. (In Chinese)
- Guo, T.; Chen, Z.; Liu, T.; Han, D. Time-Dependent Reliability of Strengthened PSC Box-Girder Bridge using Phased and Incremental Static Analyses. Eng. Struct. 2016, 117, 358–371. [Google Scholar] [CrossRef]
- Mao, S.; Tang, Y. Bayesian Statistics, 2nd ed.; China Statistics Press: Beijing, China, 2012; pp. 82–87. (In Chinese) [Google Scholar]



| Number | Concrete Cover Thickness/mm | Concrete Strength/MPa | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Beam 1 | Beam 2 | Beam 3 | Beam 4 | Beam 5 | Beam 1 | Beam 2 | Beam 3 | Beam 4 | Beam 5 | |
| 1 | 28.1 | 32.5 | 29.9 | 29.6 | 32.5 | 24.6 | 35.8 | 34.1 | 35.3 | 33.3 |
| 2 | 27.9 | 30.4 | 30.7 | 30.2 | 33.1 | 28.8 | 30.6 | 36.6 | 27.9 | 26.1 |
| 3 | 29.3 | 30.3 | 29.6 | 33.5 | 29.5 | 33.6 | 30.0 | 28.1 | 30.2 | 32.6 |
| 4 | 25.6 | 32.7 | 29.8 | 30.6 | 33.2 | 27.7 | 36.3 | 34.5 | 29.3 | 29.5 |
| 5 | 27.5 | 29.8 | 30.0 | 31.3 | 30.5 | 26.9 | 29.9 | 28.8 | 36.5 | 31.4 |
| 6 | 28.5 | 32.8 | 29.4 | 31.5 | 31.4 | 32.1 | 36.7 | 34.5 | 37.3 | 28.3 |
| 7 | 27.0 | 30.9 | 28.4 | 30.7 | 30.9 | 28.4 | 30.8 | 33.2 | 31.4 | 28.7 |
| 8 | 27.5 | 30.1 | 31.9 | 33.7 | 31.5 | 34.6 | 35.6 | 27.9 | 34.1 | 33.2 |
| 9 | 28.9 | 30.1 | 31.8 | 32.9 | 29.9 | 32.3 | 28.1 | 35.5 | 33.7 | 35.8 |
| 10 | 27.3 | 29.2 | 29.8 | 31.9 | 30.5 | 27.6 | 30.8 | 33.8 | 35.0 | 28.9 |
| Parameter | Unit | Dispersion Pattern | Mean Value | Coefficient of Variation | Explanation | Reference |
|---|---|---|---|---|---|---|
| % | Lognormal distribution | 0.12 | 0.10 | Chloride concentration on concrete surface | [42] | |
| m2/year | Lognormal distribution | 0.5 | 0.10 | Diffusion coefficient of chloride | [42] | |
| % | Lognormal distribution | 0.045 | 0.10 | Critical chloride centration | [42] | |
| MPa | Normal distribution | 335 | 0.0719 | Tensile strength of reinforcement steel | [40] | |
| mm | Normal distribution | 16 | 0.035 | Initial diameter of reinforcement steel | [40] | |
| mm | Normal distribution | 32 | 0.035 | [40] |
| Influence Factor | Beam 1 | Beam 2 | Beam 3 | Beam 4 | Beam 5 | ||
|---|---|---|---|---|---|---|---|
| Concrete strength/MPa | Statistic | Mean value | 29.7 | 32.5 | 32.7 | 33.1 | 30.8 |
| Standard deviation | 3.274 | 3.237 | 3.203 | 3.190 | 2.952 | ||
| Bayesian estimation | Mean value | 29.7 | 32.5 | 32.7 | 33.1 | 30.8 | |
| Standard deviation | 2.353 | 2.351 | 2.349 | 2.348 | 2.335 | ||
| Concrete cover thickness/mm | Statistic | Mean value | 27.8 | 30.9 | 30.1 | 31.6 | 31.3 |
| Standard deviation | 1.050 | 1.307 | 1.086 | 1.406 | 1.295 | ||
| Bayesian estimation | Mean value | 27.8 | 30.9 | 30.1 | 31.6 | 31.3 | |
| Standard deviation | 1.228 | 1.238 | 1.229 | 1.243 | 1.237 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Tan, G.; Chu, W.; Wang, W.; Kong, Q. Time-Dependent Reliability Assessment Method for RC Simply Supported T-Beam Bridges Based on Lateral Load Distribution Influenced by Reinforcement Corrosion. Appl. Sci. 2022, 12, 7028. https://doi.org/10.3390/app12147028
He X, Tan G, Chu W, Wang W, Kong Q. Time-Dependent Reliability Assessment Method for RC Simply Supported T-Beam Bridges Based on Lateral Load Distribution Influenced by Reinforcement Corrosion. Applied Sciences. 2022; 12(14):7028. https://doi.org/10.3390/app12147028
Chicago/Turabian StyleHe, Xin, Guojin Tan, Wenchao Chu, Wensheng Wang, and Qingwen Kong. 2022. "Time-Dependent Reliability Assessment Method for RC Simply Supported T-Beam Bridges Based on Lateral Load Distribution Influenced by Reinforcement Corrosion" Applied Sciences 12, no. 14: 7028. https://doi.org/10.3390/app12147028
APA StyleHe, X., Tan, G., Chu, W., Wang, W., & Kong, Q. (2022). Time-Dependent Reliability Assessment Method for RC Simply Supported T-Beam Bridges Based on Lateral Load Distribution Influenced by Reinforcement Corrosion. Applied Sciences, 12(14), 7028. https://doi.org/10.3390/app12147028









