An Explosive Driven Shock Tube-Based Laboratory Scale Test for Combined Blast and Fragment Impact Loading
Abstract
:1. Introduction
2. Experimental Setup Using the Explosive Driven Shock Tube
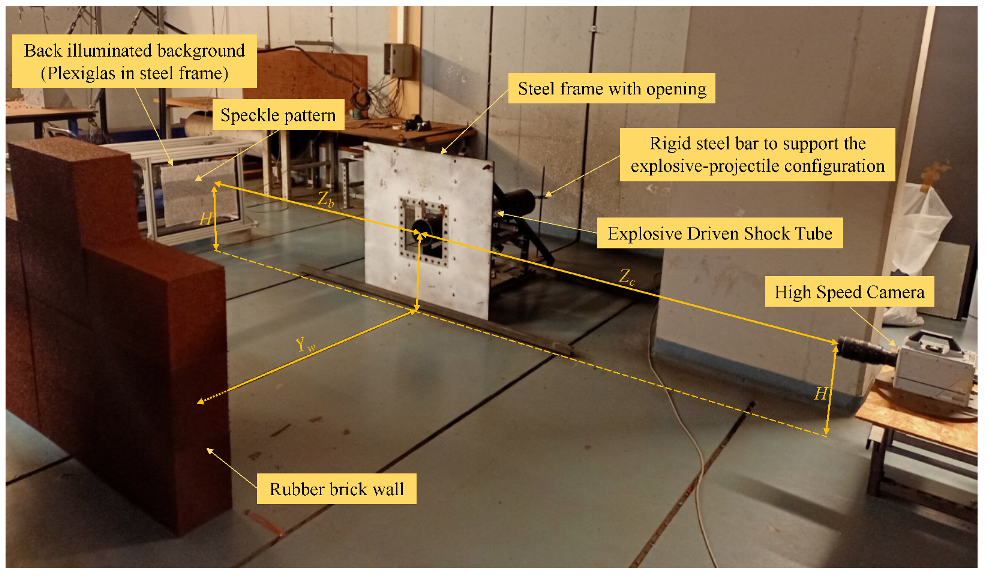
2.1. Description of the Experimental Setup
2.2. Control of the Projectile Flight Trajectory
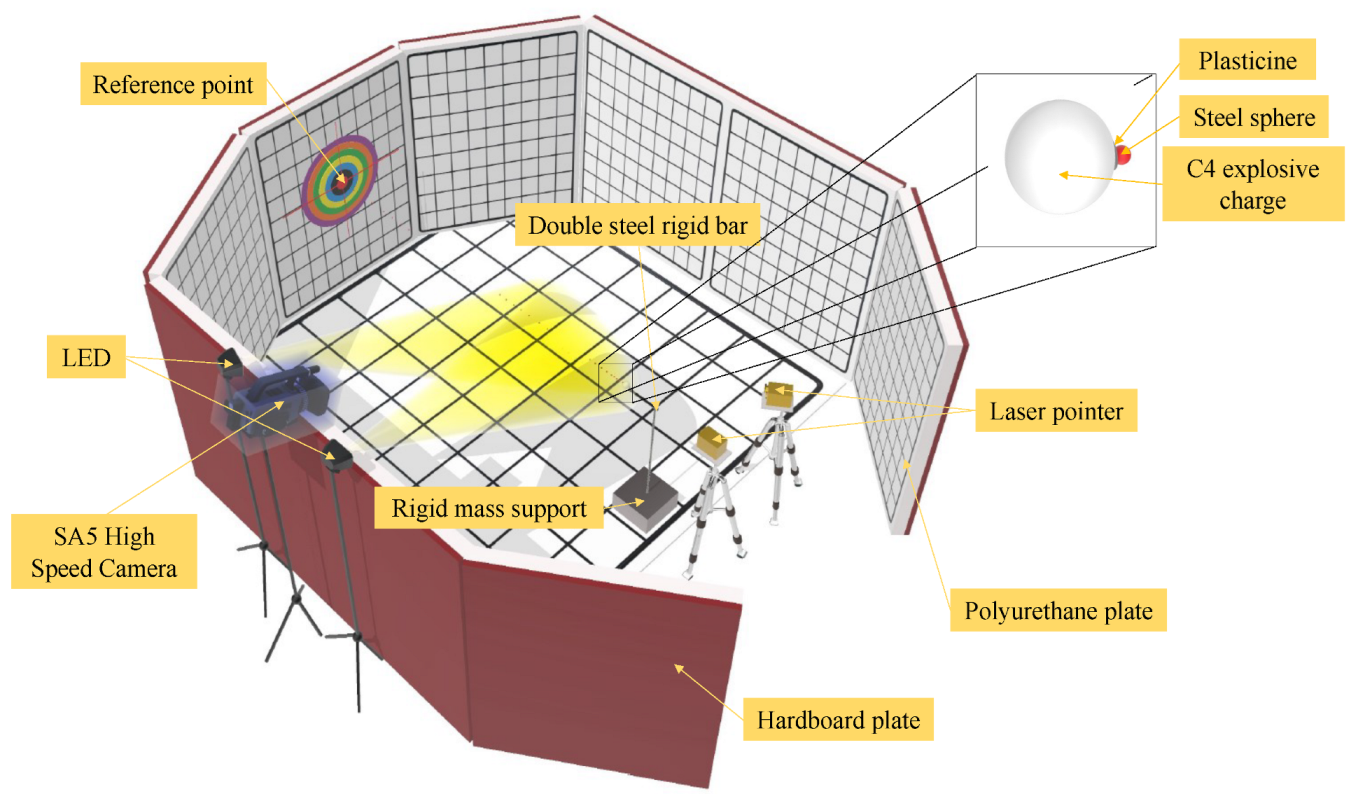
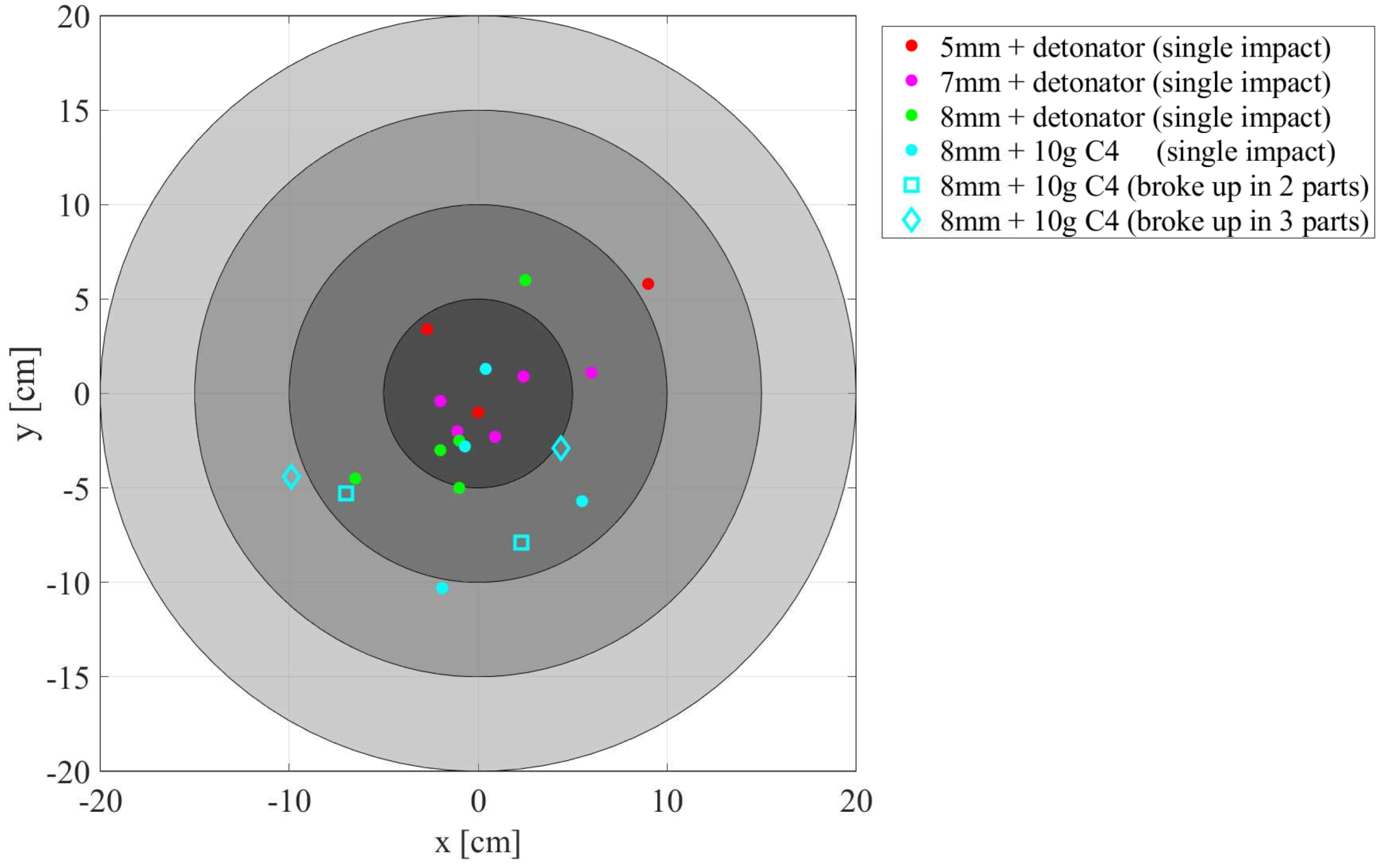
2.2.1. Projectile Flight Trajectory and Dispersion of Impacts in Free Air
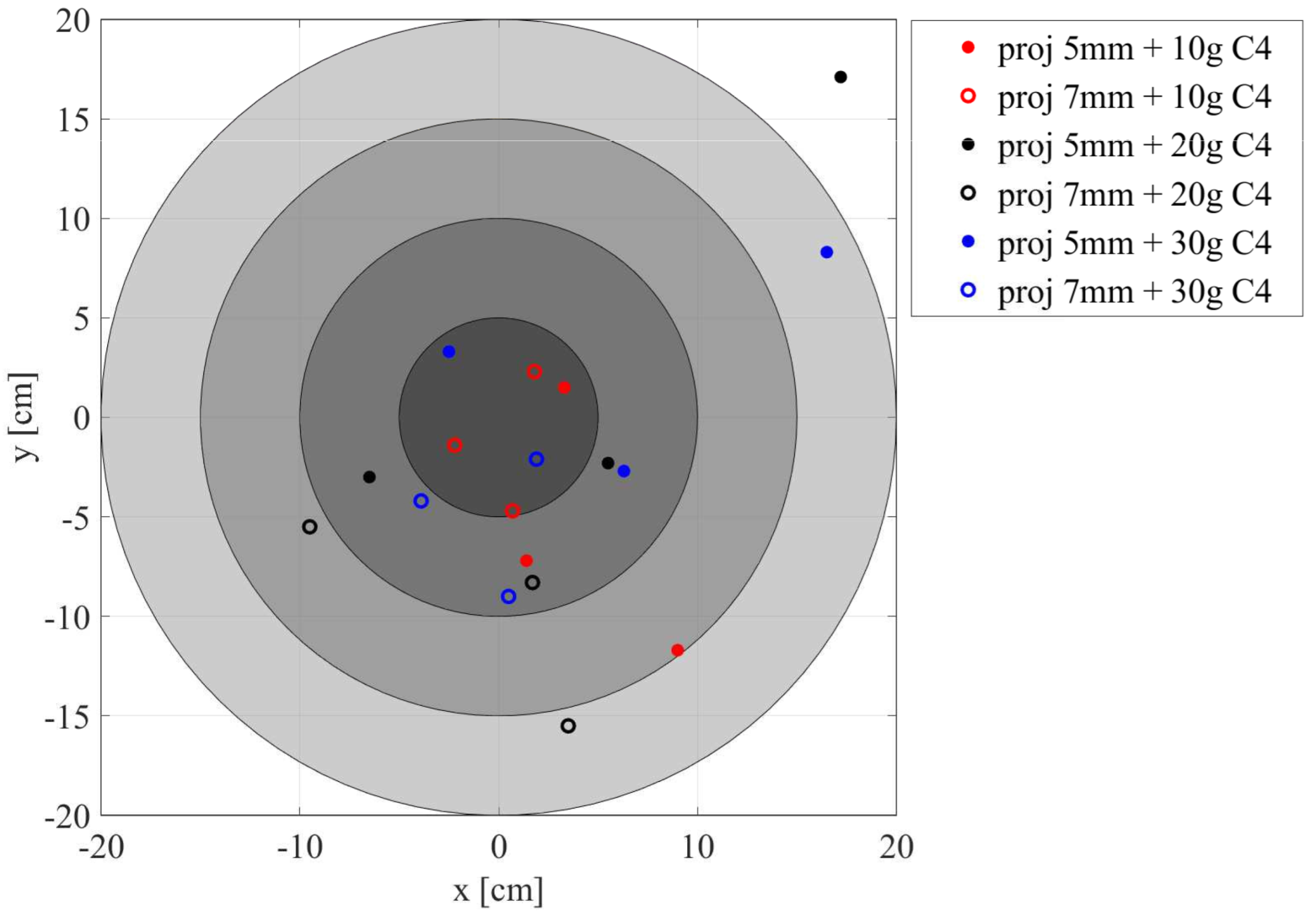
2.2.2. Projectile Flight Trajectory and Dispersion of Impacts Using the EDST
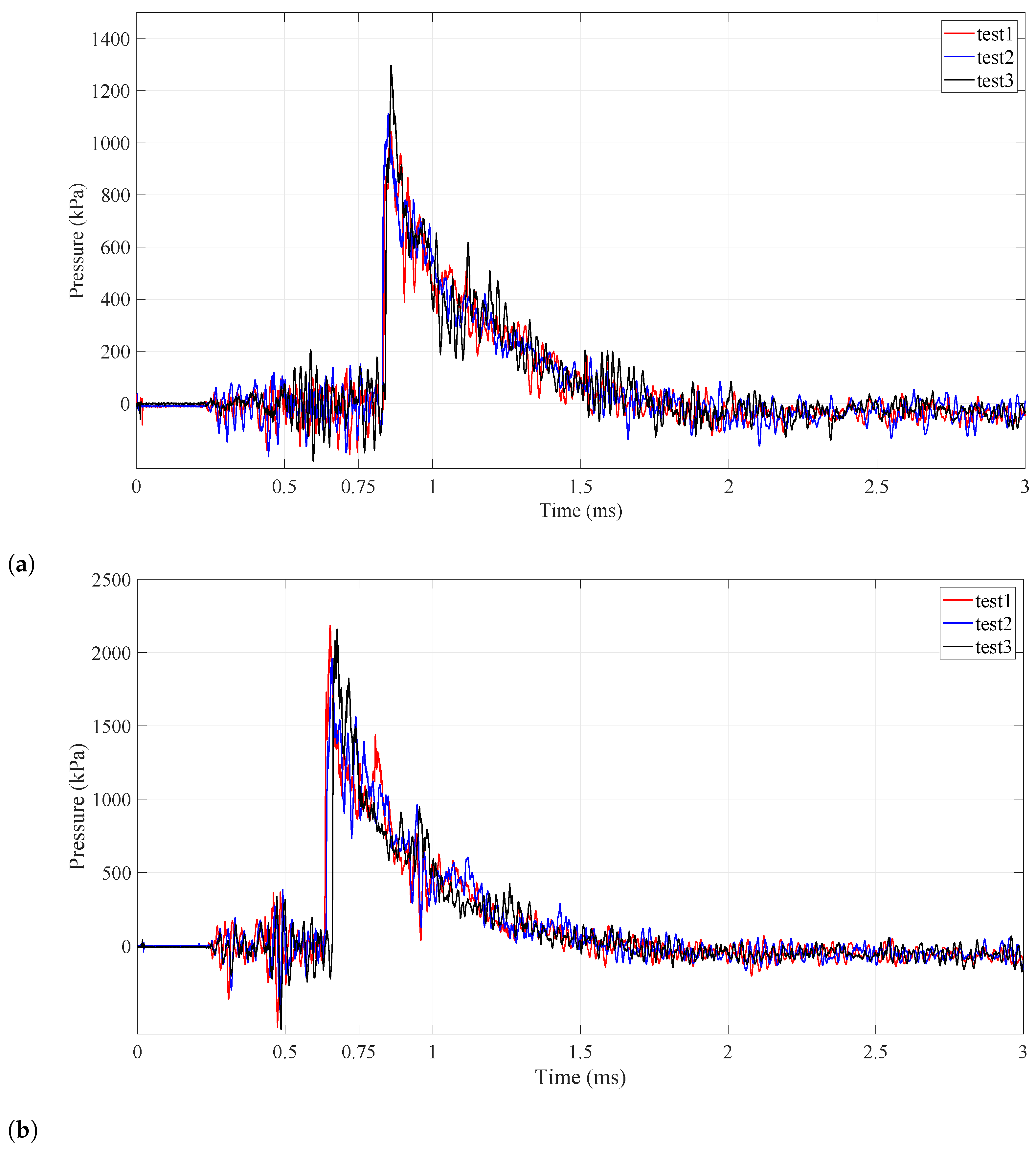
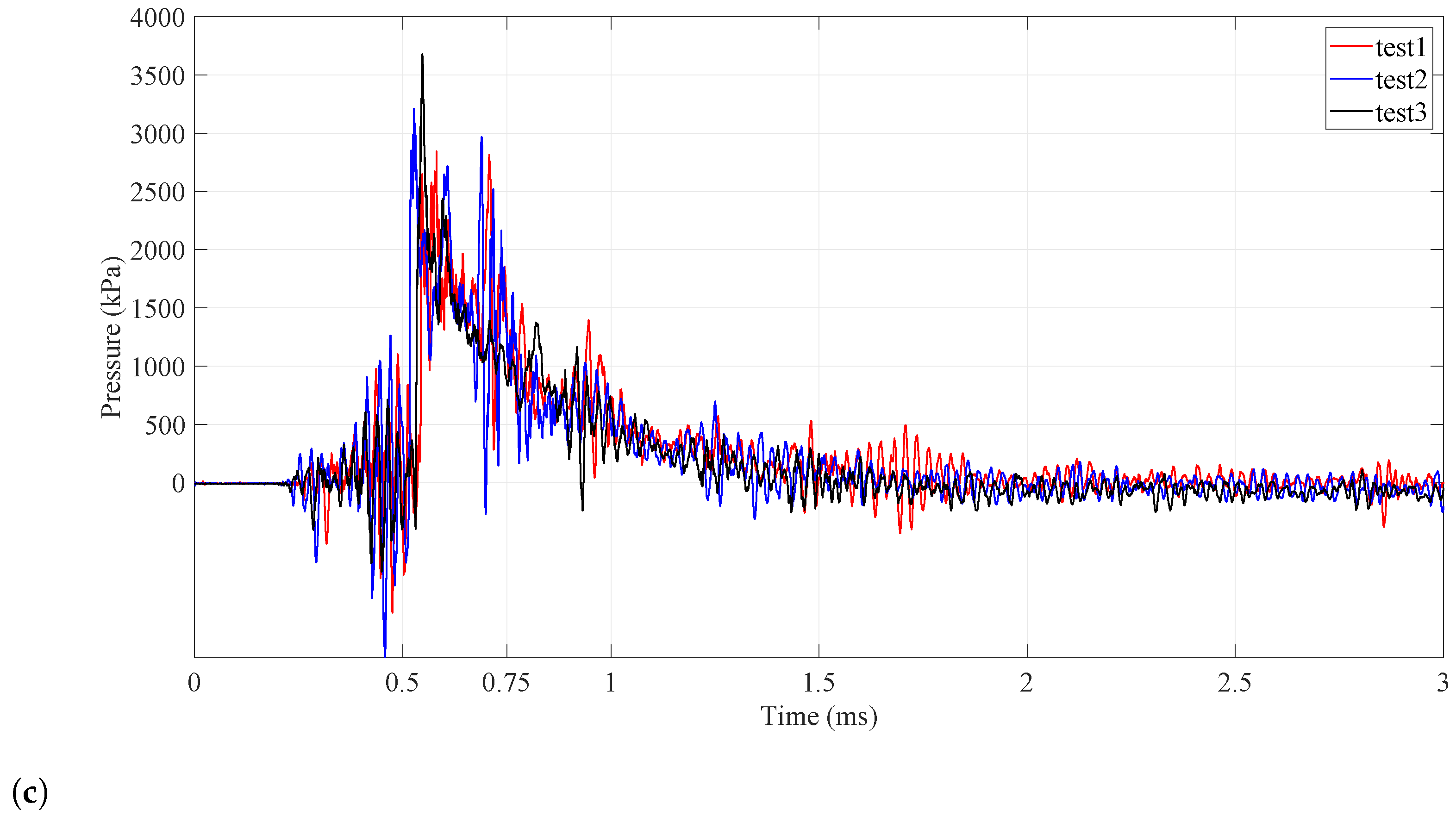
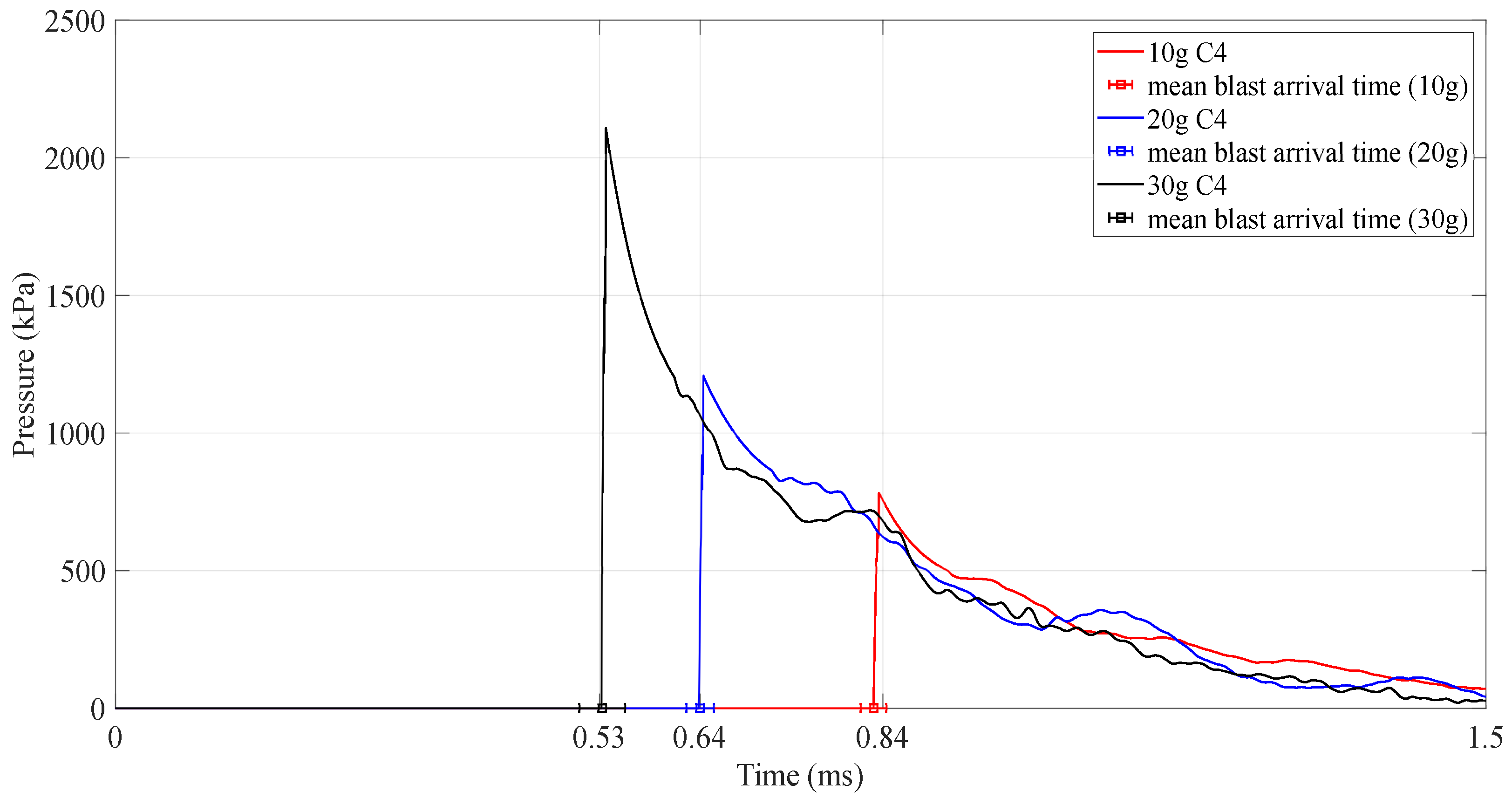
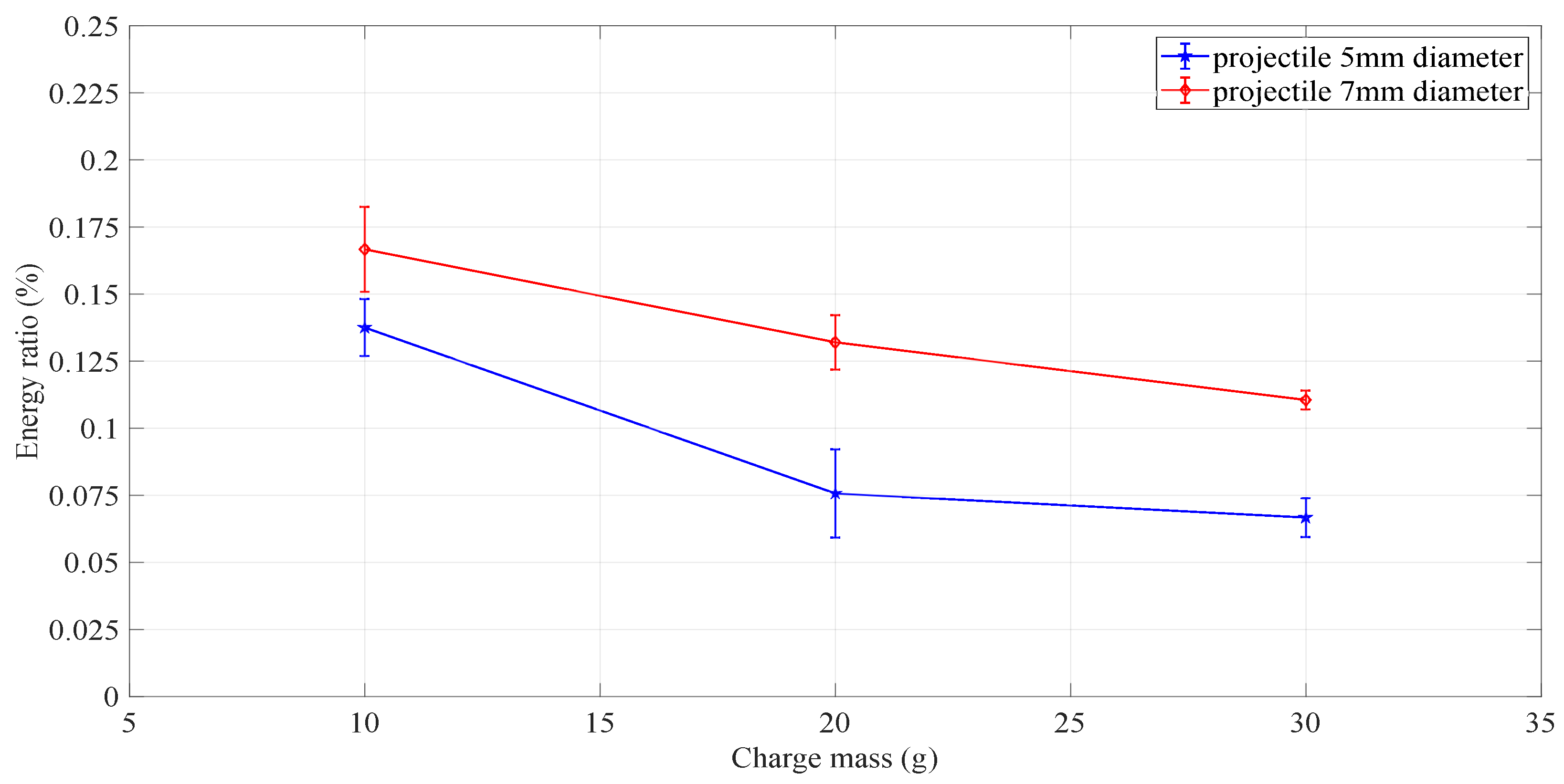
2.3. Blast Loading Characteristics
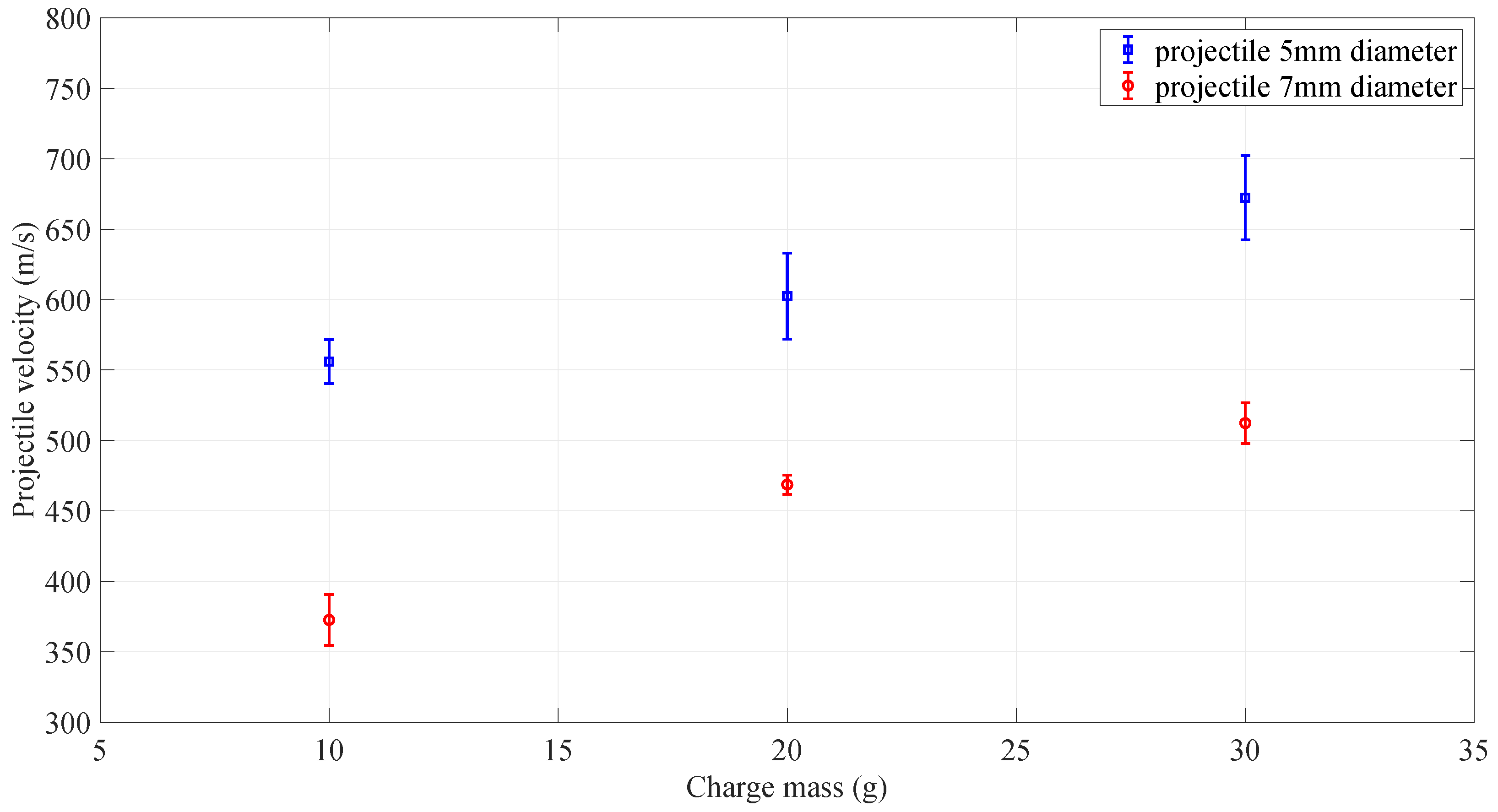
2.4. Projectile Characteristics
2.5. Time Interval
2.6. Combined Effect of Blast Wave and Projectile Impact Loading on a Plate: Case Study Application
3. Computational Modeling
3.1. Formulation Approach
3.2. Model Setup
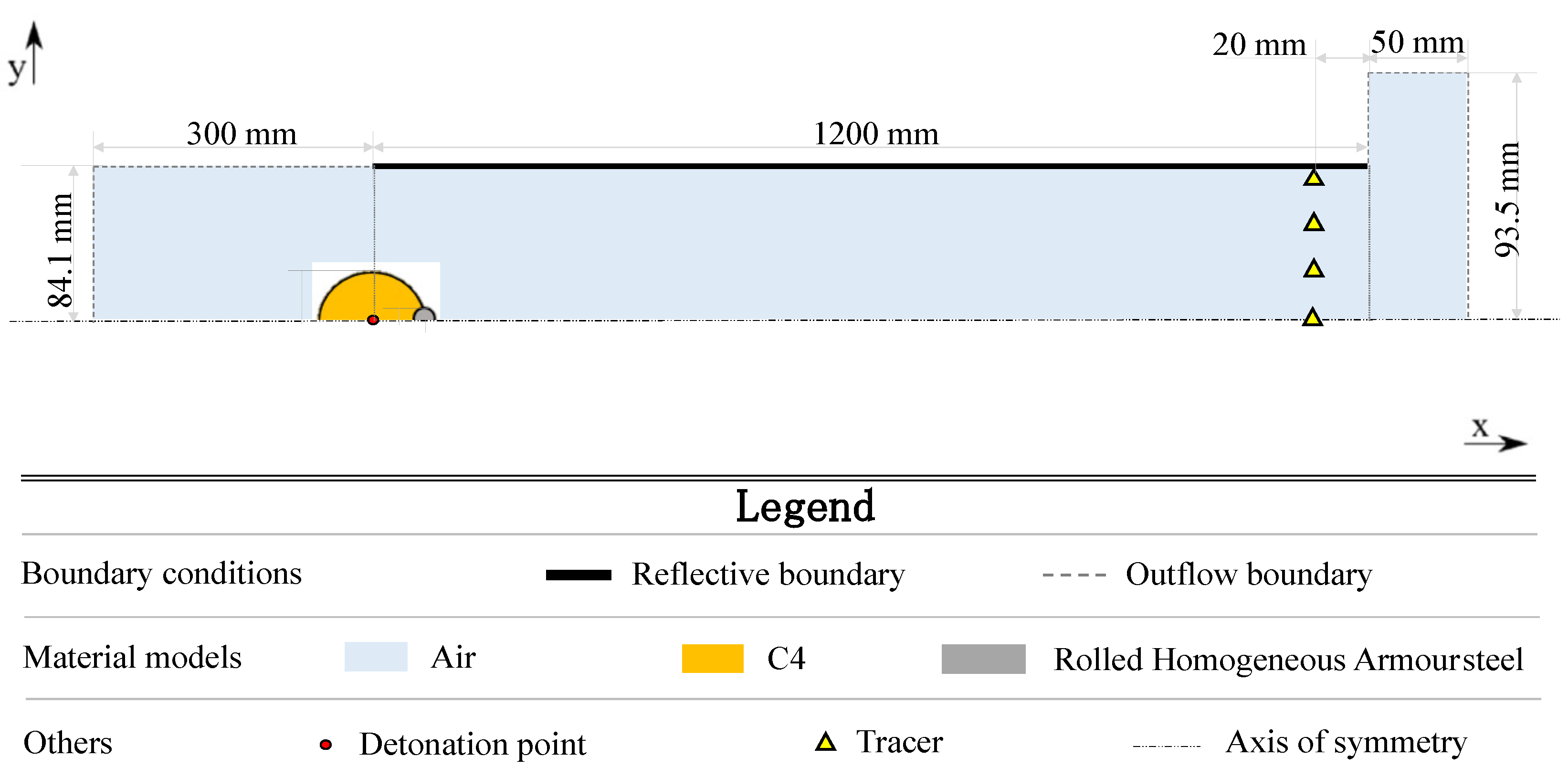
3.2.1. Geometry and Boundary Conditions
3.2.2. Material Formulation
3.2.3. Simulation Control Parameters
3.3. Simulation Results
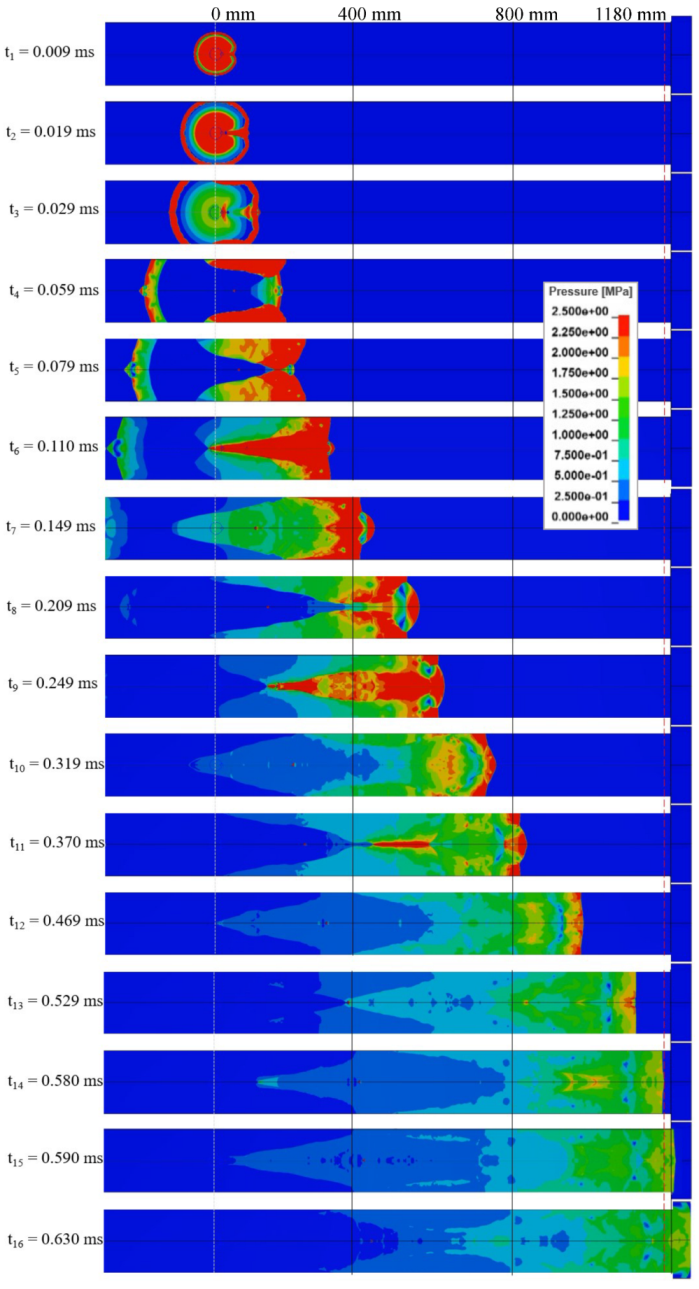
3.3.1. Blast Wave and Projectile Flight Characteristics
3.3.2. Comparison between Experimental and Numerical Results
4. Conclusions
- The capability of the steel spheres to maintain an oriented path in free air until impact on the target. The dispersion of impacts is circumscribed within an area which corresponds to the cross-sectional area of the used EDST.
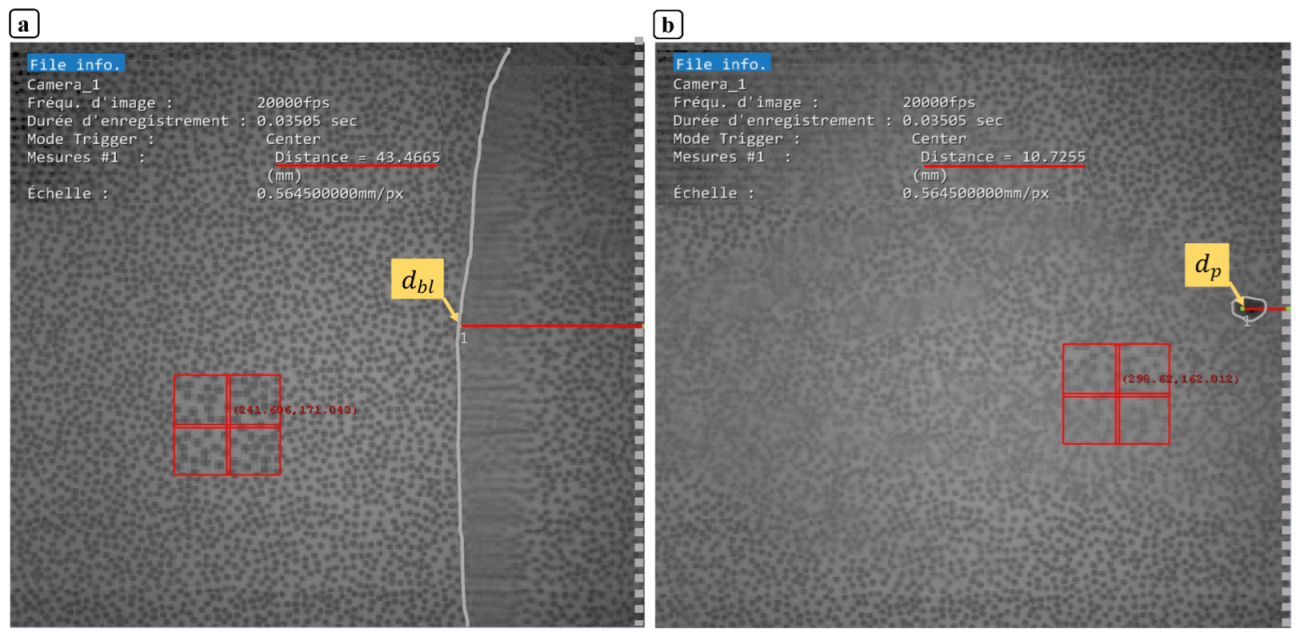
- The optical measurement technique is able to determine the spatiotemporal evolution of the shock wave and the projectile in all different flight phases.
- The established laboratory scale technique is able to generate a repeatable combined blast and single projectile impact loading on the target.
- The capability of the steel spheres to maintain an oriented path inside the explosive driven shock tube when aiming a structure placed at its exit and to limit the dispersion of impacts on the target.
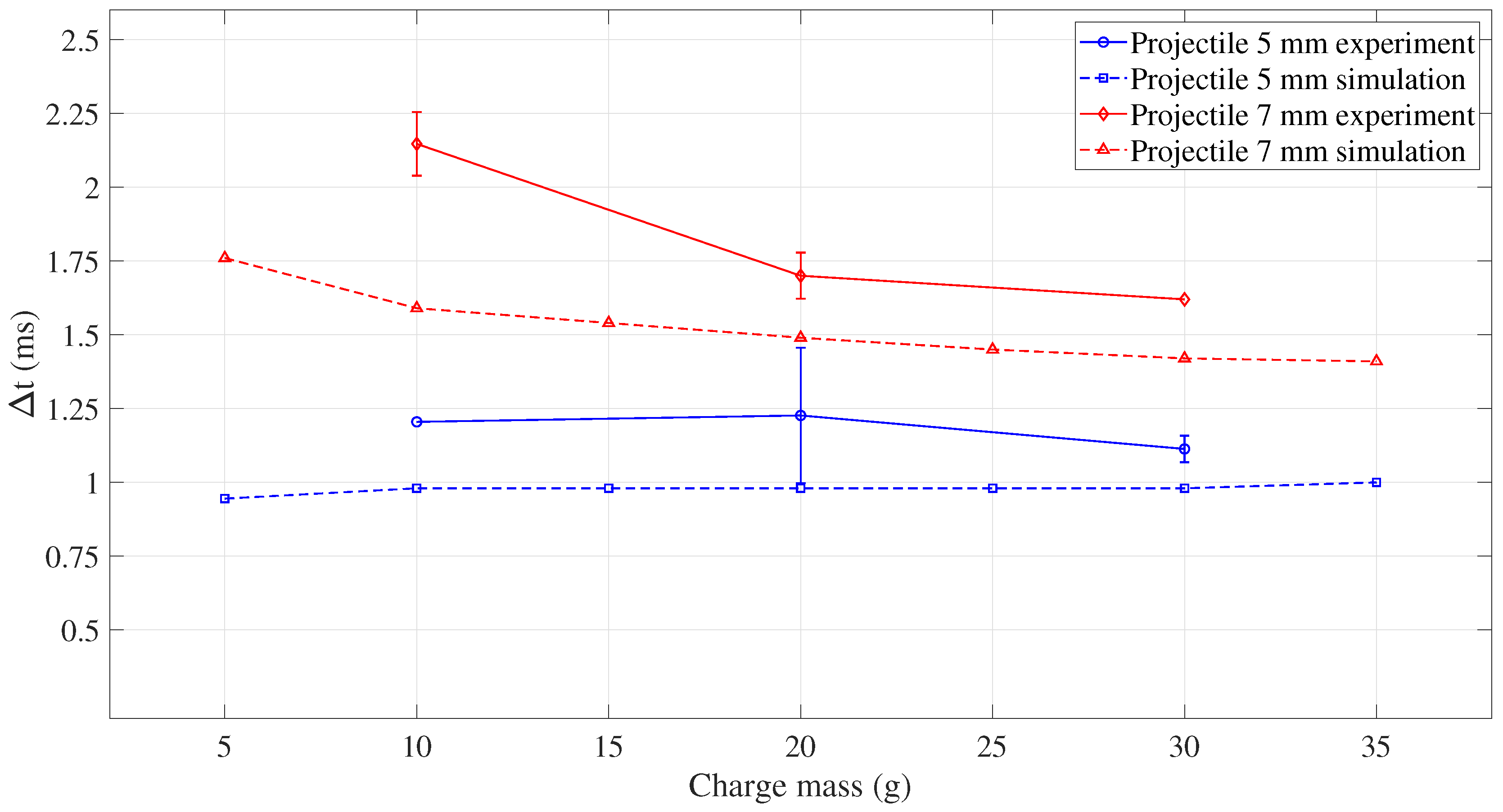
- The setup guarantees the reproducibility of a planar blast wave (magnitude and arrival time) applied on a target plate placed at the tube’s exit. For the same charge mass, the time interval increases with increasing projectile diameter.
- The FE model is able to reproduce the peak pressures, the blast wave and projectile arrival times, the projectile velocity, and the time interval.
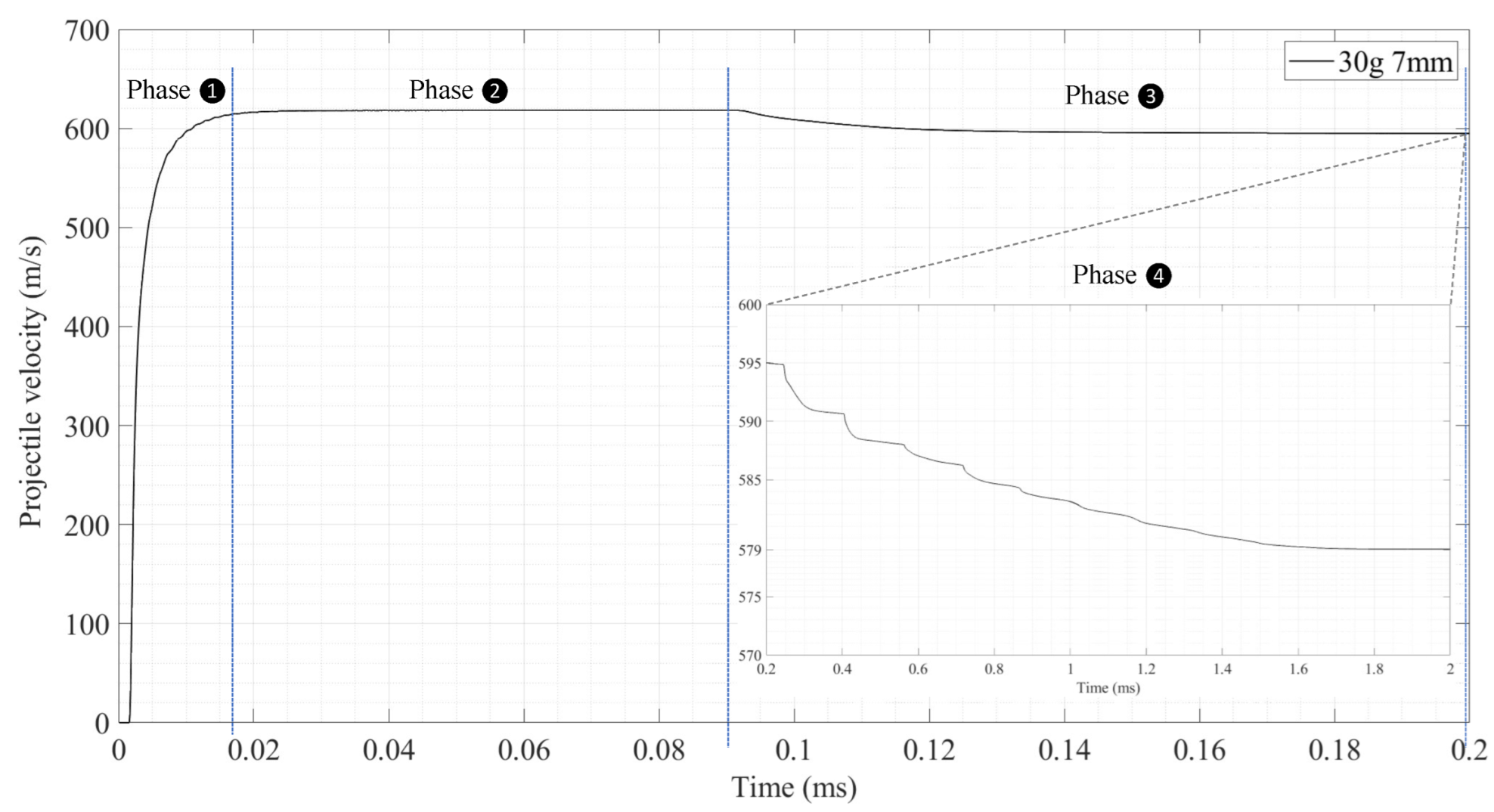
- The FE model allows to uncover details about the projectile flight characteristics (three flight phases) and driving mechanism inside the tube.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Explosive Violence Monitor: 2020. Available online: https://aoav.org.uk/2021/explosive-violence-in-2020/ (accessed on 21 March 2022).
- Improvised Explosive Device (IED) Monitor. Available online: https://reliefweb.int/sites/reliefweb.int/files/resources/IED-Monitor-Report-for-web-final.pdf (accessed on 21 March 2022).
- Marchand, K.A.; Vargas, M.; Nixon, J.D. The Synergistic Effects of Combined Blast and Fragment Loadings; Technical Report; Southwest Research Inst.: San Antonio, TX, USA, 1992. [Google Scholar]
- Kong, X.S.; Wu, W.G.; Li, J.; Chen, P.; Liu, F. Experimental and Numerical Investigation on a Multi-Layer Protective Structure under the Synergistic Effect of Blast and Fragment Loadings. Int. J. Impact Eng. 2013, 65, 146–162. [Google Scholar] [CrossRef]
- Gotts, P. International ballistic and blast specifications and standards. In Lightweight Ballistic Composites; Elsevier: Amsterdam, The Netherlands, 2016; pp. 115–156. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, W.; Kuang, N.; Li, D.; Huang, W.; Gao, Y.; Ye, N.; Guo, L.; Ren, P. Experimental investigation of normal and oblique impacts on CFRPs by high velocity steel sphere. Compos. Part B Eng. 2016, 99, 483–493. [Google Scholar] [CrossRef]
- Lozano, E. Design and Analysis of a Personnel Blast Shield for Different Explosives Applications; Colorado School of Mines: Golden, CO, USA, 2016. [Google Scholar]
- Nurick, G.; Martin, J. Deformation of thin plates subjected to impulsive loading—A review Part II: Experimental studies. Int. J. Impact Eng. 1989, 8, 171–186. [Google Scholar] [CrossRef]
- Maazoun, A.; Belkassem, B.; Reymen, B.; Matthys, S.; Vantomme, J.; Lecompte, D. Blast response of RC slabs with externally bonded reinforcement: Experimental and analytical verification. Compos. Struct. 2018, 200, 246–257. [Google Scholar] [CrossRef]
- Zhu, W.; Huang, G.; Liu, H.; Lai, W.; bin Bian, X.; Shan, F.S. Experimental and numerical investigation of a hollow cylindrical water based barrier against internal blast induced fragment loading. Int. J. Impact Eng. 2020, 138, 103503. [Google Scholar] [CrossRef]
- Grisaro, H.D.A. Towards a better understanding of the response of RC barriers to combined loading of blast and fragments. In Proceedings of the The 11th fib International PhD Symposium in Civil Engineering, Tokyo, Japan, 29–31 August 2016; pp. 353–360. [Google Scholar]
- Zhang, C.; Cheng, Y.; Zhang, P.; Duan, X.; Liu, J.; Li, Y. Numerical investigation of the response of I-core sandwich panels subjected to combined blast and fragment loading. Eng. Struct. 2017, 151, 459–471. [Google Scholar] [CrossRef]
- Cai, S.; Liu, J.; Zhang, P.; Li, C.; Cheng, Y.; Chen, C. Experimental study on failure mechanisms of sandwich panels with multi-layered aluminum foam/UHMWPE laminate core under combined blast and fragments loading. Thin-Walled Struct. 2021, 159, 107227. [Google Scholar] [CrossRef]
- Grisaro, H.Y.; Dancygier, A.N. Dynamic Response of RC Elements Subjected to Combined Loading of Blast and Fragments. Eng. Struct. 2021, 147, 04020315. [Google Scholar] [CrossRef]
- Nyström, U.; Gylltoft, K. Numerical studies of the combined effects of blast and fragment loading. Int. J. Impact Eng. 2009, 36, 995–1005. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Gholipour, G.; Mousavi, A.A. Nonlinear dynamic behavior of simply-supported RC beams subjected to combined impact-blast loading. Eng. Struct. 2019, 181, 124–142. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Ren, X.; Tao, R.; Gao, R.; Fang, D. Experimental and numerical study on damage mode of RC slabs under combined blast and fragment loading. Int. J. Impact Eng. 2020, 142, 103579. [Google Scholar] [CrossRef]
- Lai, E.; Zhao, J.; Li, X.; Hu, K.; Chen, G. Dynamic responses and damage of storage tanks under the coupling effect of blast wave and fragment impact. J. Loss Prev. Process Ind. 2021, 73, 104617. [Google Scholar] [CrossRef]
- Price, M.A.; Nguyen, V.T.; Hassan, O.; Morgan, K. An approach to modeling blast and fragment risks from improvised explosive devices. Appl. Math. Model. 2017, 50, 715–731. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zhang, Q.C.; Zhang, R.; Wang, X.; Zhao, Z.Y.; He, S.Y.; Han, B.; Lu, T.J. A laboratory experimental technique for simulating combined blast and impact loading. Int. J. Impact Eng. 2019, 134, 103382. [Google Scholar] [CrossRef]
- Qi, R.; Langdon, G.S.; Cloete, T.J.; Yuen, S.C.K. Behaviour of a blast-driven ball bearing embedded in rear detonated cylindrical explosive. Int. J. Impact Eng. 2020, 146, 103698. [Google Scholar] [CrossRef]
- LS-DYNA Keyword User’s Manual Volume I. Available online: https://lstc.com/pdf/ls-dyna_971_manual_k.pdf (accessed on 21 March 2022).
- Mellen, P.; Shanahan, C.; Bennett, T. Blast and fragmentation loading indicative of a VBIED surrogate for structural panel response analysis. Int. J. Impact Eng. 2019, 126, 172–184. [Google Scholar] [CrossRef]
- Louar, M.; Belkassem, B.; Ousji, H.; Spranghers, K.; Kakogiannis, D.; Pyl, L.; Vantomme, J. Explosive driven shock tube loading of aluminium plates: Experimental study. Int. J. Impact Eng. 2015, 86, 111–123. [Google Scholar] [CrossRef]
- PCB Dynamic Pressure Sensors for High Frequency Measurements. Available online: https://www.pcb.com/Contentstore/MktgContent/LinkedDocuments/Pressure/TM-PRS-113B-102B_lowres.pdf (accessed on 21 March 2022).
- Moumen, A.; Grossen, J.; Ndindabahizi, I.; Gallant, J.; Hendrick, P. Visualization and Analysis of Muzzle Flow Fields Using the Background-Oriented Schlieren Technique. J. Vis. 2020, 23, 409–423. [Google Scholar] [CrossRef]
- Atoui, O.; Lecompte, D.; Belkassem, B. Tests Showing the Projectile Flight Trajectory of 5, 7 and 8 mm Diameter Steel Spheres Attached to Either a Detonator or a Rear Detonated C4 Spherical Explosive Charge. Zenodo 2022. [Google Scholar] [CrossRef]
- Robbe, C.; Nsiampa, N.; Oukara, A.; Papy, A. Quantification of the uncertainties of high-speed camera measurements. Int. J. Metrol. Qual. 2014, 5, 201. [Google Scholar] [CrossRef] [Green Version]
- Robbe, C.; Nsiampa, N.; Papy, A.; Oukara, A. Practical considerations for using high-speed camera to measure dynamic deformation occurring at the impact of a kinetic energy non-lethal weapon projectile on ballistic simulant. In Proceedings of the Personal Armour System Symposium (PASS) Conference Proceedings, Nuremberg, Germany, 17–21 September 2012. [Google Scholar]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 7, 14. [Google Scholar] [CrossRef] [Green Version]
- Photron FASTCAM Viewer Operation Manual. Available online: https://www.techimaging.com/downloads/docs/Photron_FASTCAM_Viewer_Manual_Rev2437en.pdf (accessed on 21 March 2022).
- Langdon, G.; Curry, R.; Rigby, S.; Pickering, E.; Clarke, S.; Tyas, A. Optical diagnostics in near-field blast measurements. Fire Blast Inf. Group Tech. Newsl. 2021, 82, 25–30. [Google Scholar]
- Peton, N.; Lardjane, N. An Eulerian version of geometrical blast dynamics for 3D simulations. Shock Waves 2022, 32, 241–259. [Google Scholar] [CrossRef]
- Chen, M.; Liu, M.; Tang, Y. Comparison of Euler-Euler and Euler-Lagrange approaches for simulating gas-solid flows in a multiple-spouted bed. Int. J. Chem. Reactor Eng. 2019, 17, 20180254. [Google Scholar] [CrossRef]
- Ma, T.; Wang, C.; Ning, J. Multi-material eulerian formulations and hydrocode for the simulation of explosions. Comp. Model. Eng. Sci. CMES 2008, 33, 155–178. [Google Scholar] [CrossRef]
- Gao, C.; Kong, X.-z.; Fang, Q.; Hong, J.; Wang, Y. Numerical investigation on free air blast loads generated from center-initiated cylindrical charges with varied aspect ratio in arbitrary orientation. Def. Technol. 2021. [Google Scholar] [CrossRef]
- Schwer, L.; Rigby, S. Secondary and height of burst shock reflections: Application of afterburning. In Proceedings of the 25th International Symposium on Military Aspects of Blast and Shock, Paper, The Hague, The Netherlanders, 21–25 September 2018. [Google Scholar]
- Ning, P.; Tang, D. Influence of explosive density on small scale internal blast experiments. J. Chongqing Univ. 2012, 11, 119–126. [Google Scholar]
- Dobratz, B.M. LLNL Explosives Handbook: Properties of Chemical Explosives and Explosive Simulants; Technical Report; Lawrence Livermore National Lab.: Livermore, CA, USA, 1981.
- Riegel, J.J.P.; Davison, D. Consistent constitutive modeling of metallic target penetration using empirical, analytical, and numerical penetration models. Def. Technol. 2016, 126, 172–184. [Google Scholar] [CrossRef] [Green Version]







| Test n | Charge Mass [g] | Projectile Diameter [mm] | [mm] | [m/s] | [mm] | [m/s] | [ms] | Mean [ms] | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 5 | ND * | ND | ND | ND | ND | ND | 1.21 |
| 2 | 10 | 5 | 27 | 32.74 | 925.78 | 19.76 | 533.21 | 1.27 | |
| 3 | 10 | 5 | 24 | 34.43 | 835.46 | 5.64 | 564.5 | 1.14 | |
| 4 | 20 | 5 | 23 | 53.62 | 1129.06 | 15.8 | 620.95 | 1.07 | |
| 5 | 20 | 5 | 24 | 48.54 | 1467.7 | 27.66 | 598.37 | 1.12 | |
| 6 | 20 | 5 | 31 | 35.56 | 1174.16 | 14.11 | 501.35 | 1.49 | |
| 7 | 30 | 5 | 24 | 31.61 | 1332.27 | 5.08 | 643.53 | 1.16 | |
| 8 | 30 | 5 | 24 | 66.04 | 1230.61 | 18.62 | 641.52 | 1.11 | |
| 9 | 30 | 5 | 22 | 21.45 | 1264.48 | 6.20 | 700.79 | 1.07 | |
| 10 | 10 | 7 | 43 | 29.91 | 880.62 | 16.38 | 383.86 | 2.07 | |
| 11 | 10 | 7 | 47 | 43.46 | 891.91 | 10.72 | 350.17 | 2.27 | |
| 12 | 10 | 7 | 44 | 47.98 | 890.21 | 15.25 | 361.28 | 2.1 | |
| 13 | 20 | 7 | 35 | 71.12 | 1264.48 | 14.68 | 440.31 | 1.66 | |
| 14 | 20 | 7 | 37 | 45.16 | 1230.61 | 6.79 | 474.18 | 1.79 | |
| 15 | 20 | 7 | 35 | 64.35 | 1117.71 | 11.85 | 463.02 | 1.65 | |
| 16 | 30 | 7 | ND * | ND | ND | ND | ND | ND | 1.62 |
| 17 | 30 | 7 | 32 | 80.72 | 1478.99 | 3.38 | 521.3 | 1.53 | |
| 18 | 30 | 7 | 35 | 20.88 | 1388.67 | 11.29 | 508.05 | 1.71 |
| [kJ.kg−1] | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 0.2534 | 1 |
| EOS-JWL | Mat High Explosive Burn | |||||||
|---|---|---|---|---|---|---|---|---|
| [GPa] | [GPa] | [kJ.kg−1] | [kg/m3] | [GPa] | [m/s] | |||
| 609.77 | 12.95 | 4.5 | 1.4 | 0.25 | 9 | 1601 | 28 | 8193 |
| Property Name | Symbol | Value | Unit | |
|---|---|---|---|---|
| Elastic constants | Mass density | 7850 | [kg/m] | |
| Young’s modulus | E | [MPa] | ||
| Poisson’s ratio | 0.3 | [-] | ||
| Johnson–Cook parameters | Yield stress | A | 1225 | [MPa] |
| Strain-hardening constant | B | 1575 | [MPa] | |
| Strain-hardening coefficient | n | 0.768 | [-] | |
| Strengthening coefficient of strain rate | C | 0.0049 | [-] |
| Simulation ID | Simulation Inputs | At 1180 mm from the Center of Detonation | At 1200 mm from the Center of Detonation | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Charge Mass (g) | Charge Diameter (mm) | Projectile Diameter (mm) | (ms) | Peak Pressure (MPa) | (ms) | (ms) | Time Interval(ms) | Projectile Velocity (m/s) | |||||||||
| Num | Exp | Relative Error (%) | Num | Exp | Relative Error (%) | Num | Exp | Relative Error (%) | Num | Exp | Relative Error (%) | ||||||
| 1 | 5 | 18.12 | 5 | 1.24 | * VE | 0.32 | * VE | 1.28 | 2.22 | 0.94 | * VE | 536 | * VE | ||||
| 2 | 7 | 1.24 | 0.34 | 1.28 | 3.04 | 1.76 | 388 | ||||||||||
| 3 | 10 | 22.84 | 5 | 0.90 | 0.84 | +7.14 | 0.61 | 0.78 | −21.59 | 0.92 | 1.90 | 0.98 | 1.21 | −19.10 | 632 | 549 | +15.22 |
| 4 | 7 | 0.91 | 0.84 | +8.33 | 0.60 | 0.78 | −22.21 | 0.96 | 2.56 | 1.60 | 2.14 | −25.23 | 465 | 365 | +27.40 | ||
| 5 | 15 | 26.14 | 5 | 0.75 | * VE | 0.87 | * VE | 0.78 | 1.76 | 0.98 | * VE | 666 | * VE | ||||
| 6 | 7 | 0.78 | 0.88 | 0.80 | 2.34 | 1.54 | 505 | ||||||||||
| 7 | 20 | 28.78 | 5 | 0.68 | 0.64 | +6.25 | 1.15 | 1.21 | −4.72 | 0.69 | 1.67 | 0.98 | 1.23 | −20.32 | 703 | 573 | +22.70 |
| 8 | 7 | 0.68 | 0.64 | +6.25 | 1.13 | 1.21 | −6.37 | 0.70 | 2.19 | 1.49 | 1.70 | −12.40 | 538 | 459 | +17.21 | ||
| 9 | 25 | 31 | 5 | 0.62 | * VE | 1.39 | * VE | 0.63 | 1.61 | 0.98 | * VE | 727 | * VE | ||||
| 10 | 7 | 0.62 | 1.38 | 0.64 | 2.09 | 1.45 | 562 | ||||||||||
| 11 | 30 | 32.94 | 5 | 0.58 | 0.54 | +7.40 | 1.64 | 2.11 | −22.16 | 0.59 | 1.58 | 0.98 | 1.11 | −11.71 | 739 | 662 | +11.63 |
| 12 | 7 | 0.58 | 0.54 | +7.40 | 1.62 | 2.11 | −23.11 | 0.59 | 2.01 | 1.42 | 1.62 | −12.34 | 579 | 514 | +12.64 | ||
| 13 | 35 | 34.68 | 5 | 0.54 | * VE | 1.88 | * VE | 0.55 | 1.55 | 1.00 | * VE | 749 | * VE | ||||
| 14 | 7 | 0.54 | 1.86 | 0.56 | 1.97 | 1.41 | 593 | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atoui, O.; Kechagiadakis, G.; Moumen, A.; Maazoun, A.; Belkassem, B.; Pyl, L.; Lecompte, D. An Explosive Driven Shock Tube-Based Laboratory Scale Test for Combined Blast and Fragment Impact Loading. Appl. Sci. 2022, 12, 6854. https://doi.org/10.3390/app12146854
Atoui O, Kechagiadakis G, Moumen A, Maazoun A, Belkassem B, Pyl L, Lecompte D. An Explosive Driven Shock Tube-Based Laboratory Scale Test for Combined Blast and Fragment Impact Loading. Applied Sciences. 2022; 12(14):6854. https://doi.org/10.3390/app12146854
Chicago/Turabian StyleAtoui, Oussama, Georgios Kechagiadakis, Abdelhafidh Moumen, Azer Maazoun, Bachir Belkassem, Lincy Pyl, and David Lecompte. 2022. "An Explosive Driven Shock Tube-Based Laboratory Scale Test for Combined Blast and Fragment Impact Loading" Applied Sciences 12, no. 14: 6854. https://doi.org/10.3390/app12146854
APA StyleAtoui, O., Kechagiadakis, G., Moumen, A., Maazoun, A., Belkassem, B., Pyl, L., & Lecompte, D. (2022). An Explosive Driven Shock Tube-Based Laboratory Scale Test for Combined Blast and Fragment Impact Loading. Applied Sciences, 12(14), 6854. https://doi.org/10.3390/app12146854







