Application of Machine Learning Tools for Long-Term Diagnostic Feature Data Segmentation
Abstract
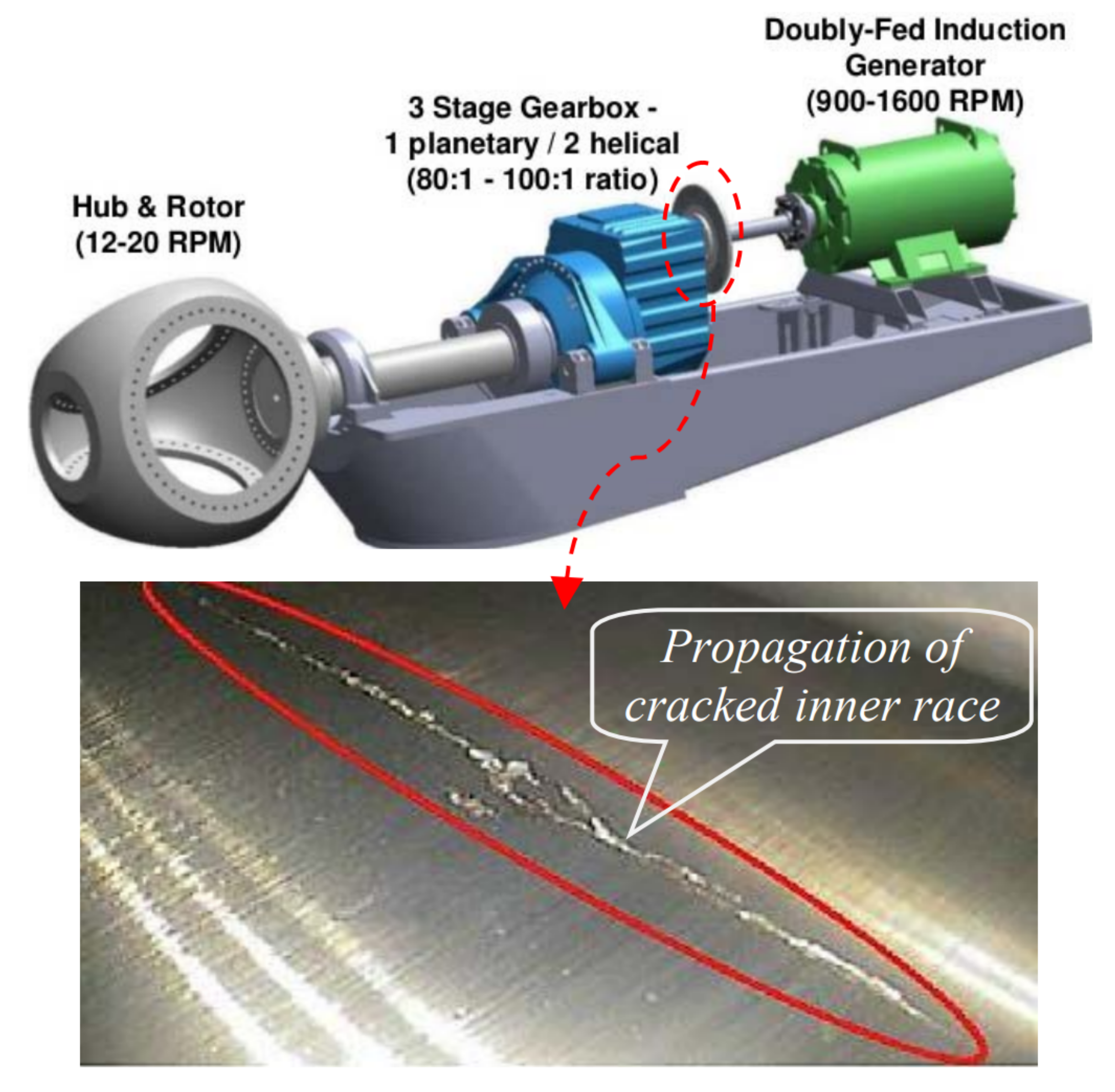
1. Introduction
2. State of the Art
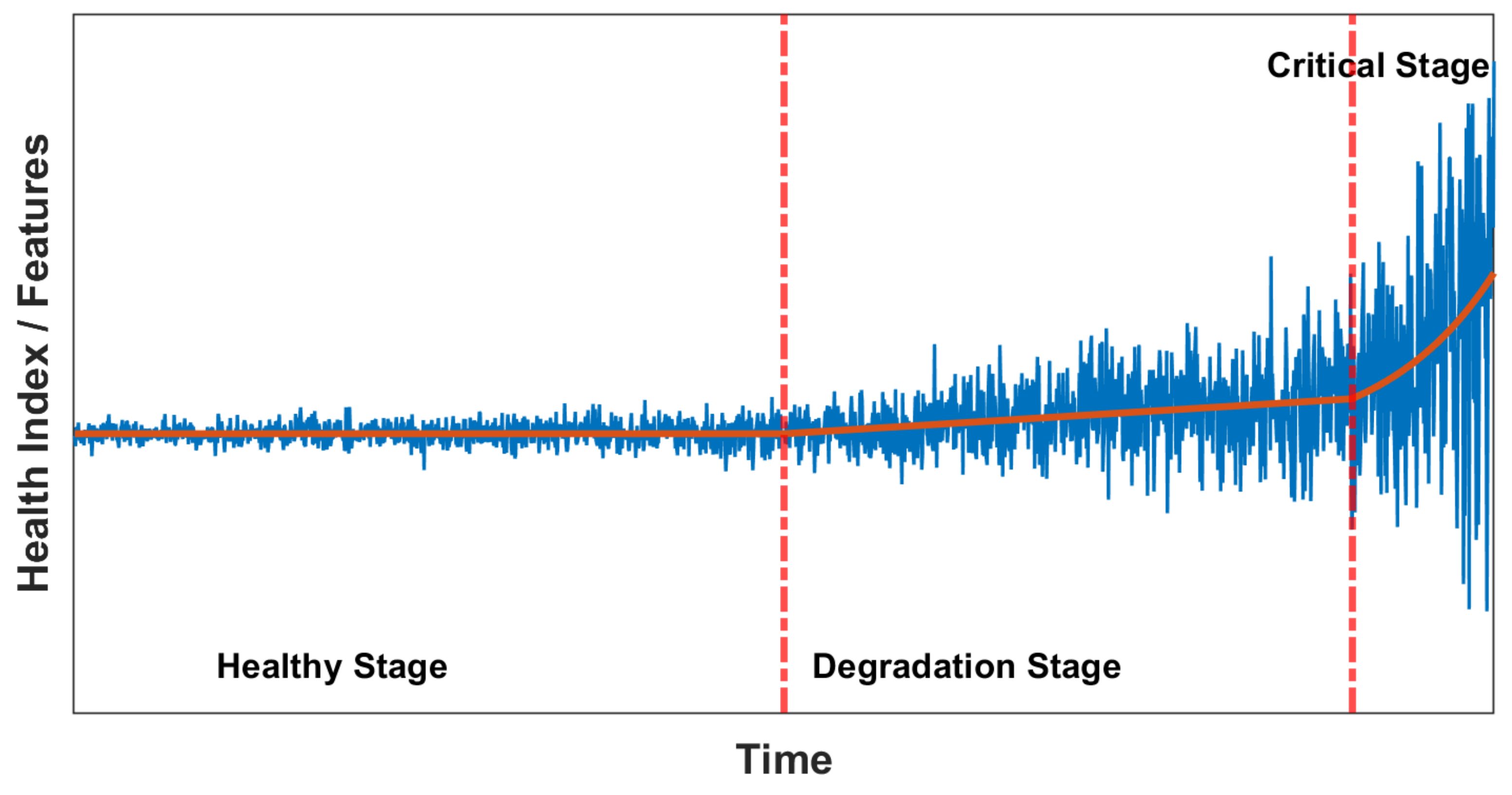
3. Problem Formulation
- (a)
- Good condition, where HI is nearly constant (no degradation);
- (b)
- Slow degradation (HI is increasing slowly and approximately linearly);
- (c)
- Fast degradation (HI is rapidly growing like exponential function).
4. Methodology
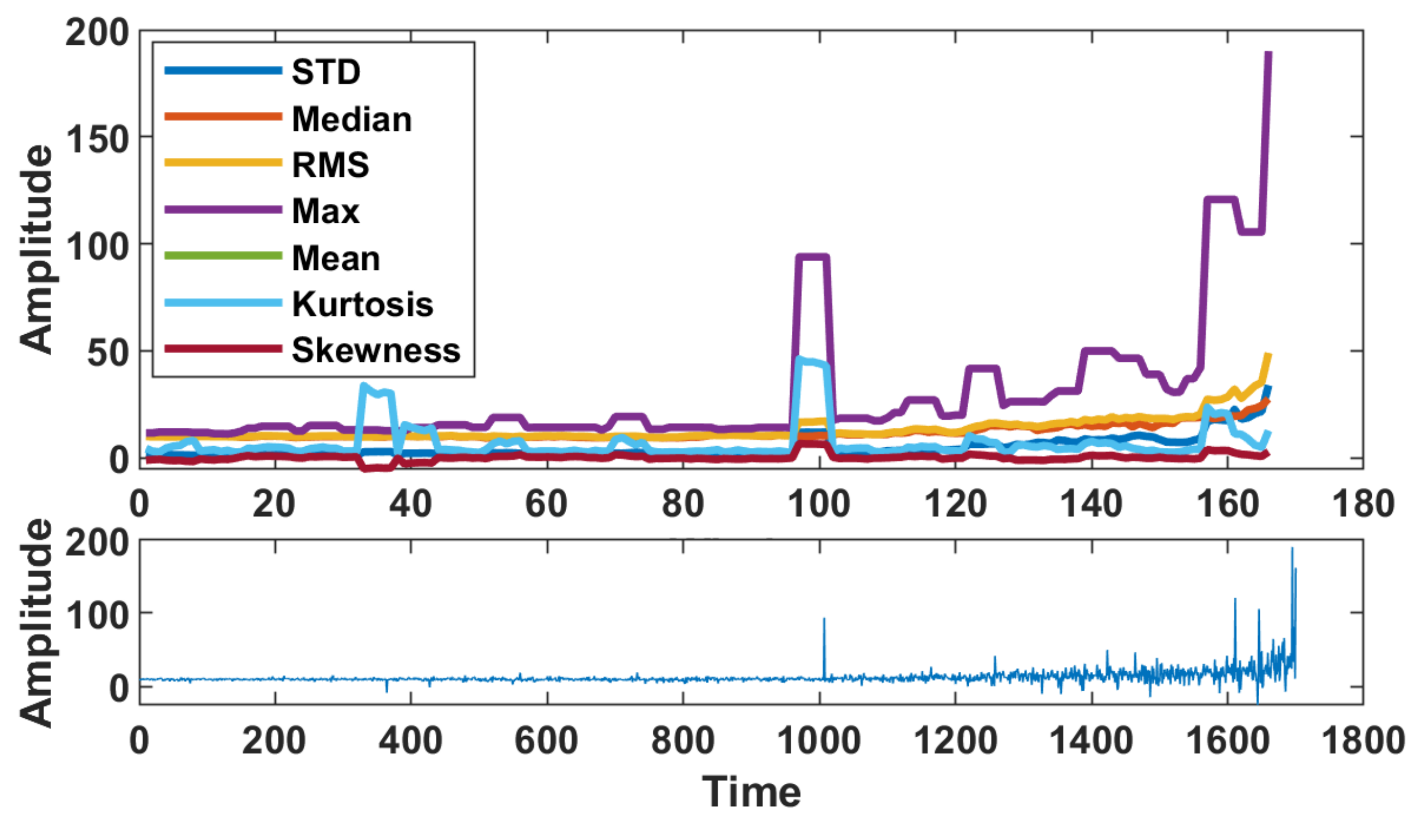
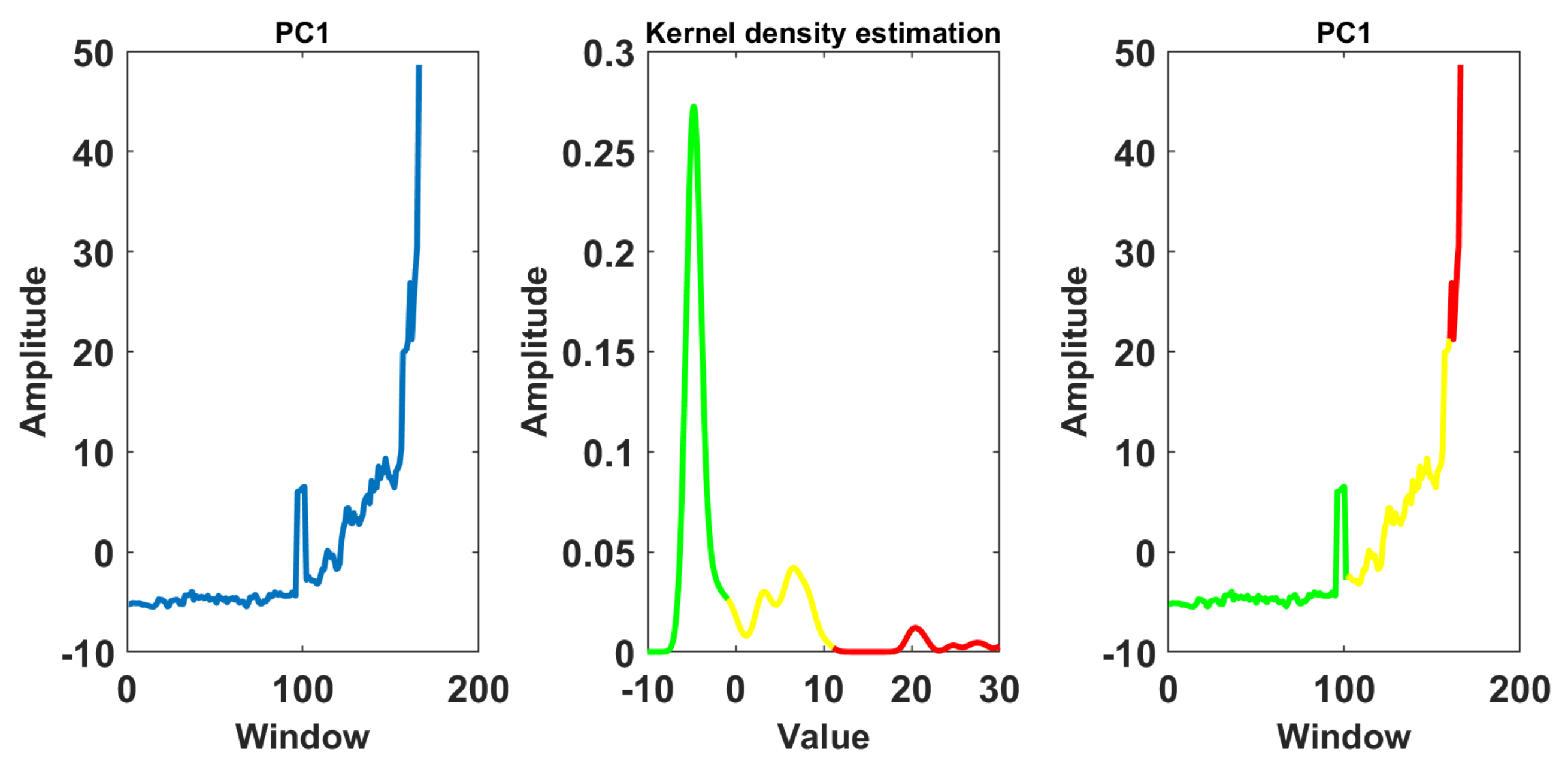
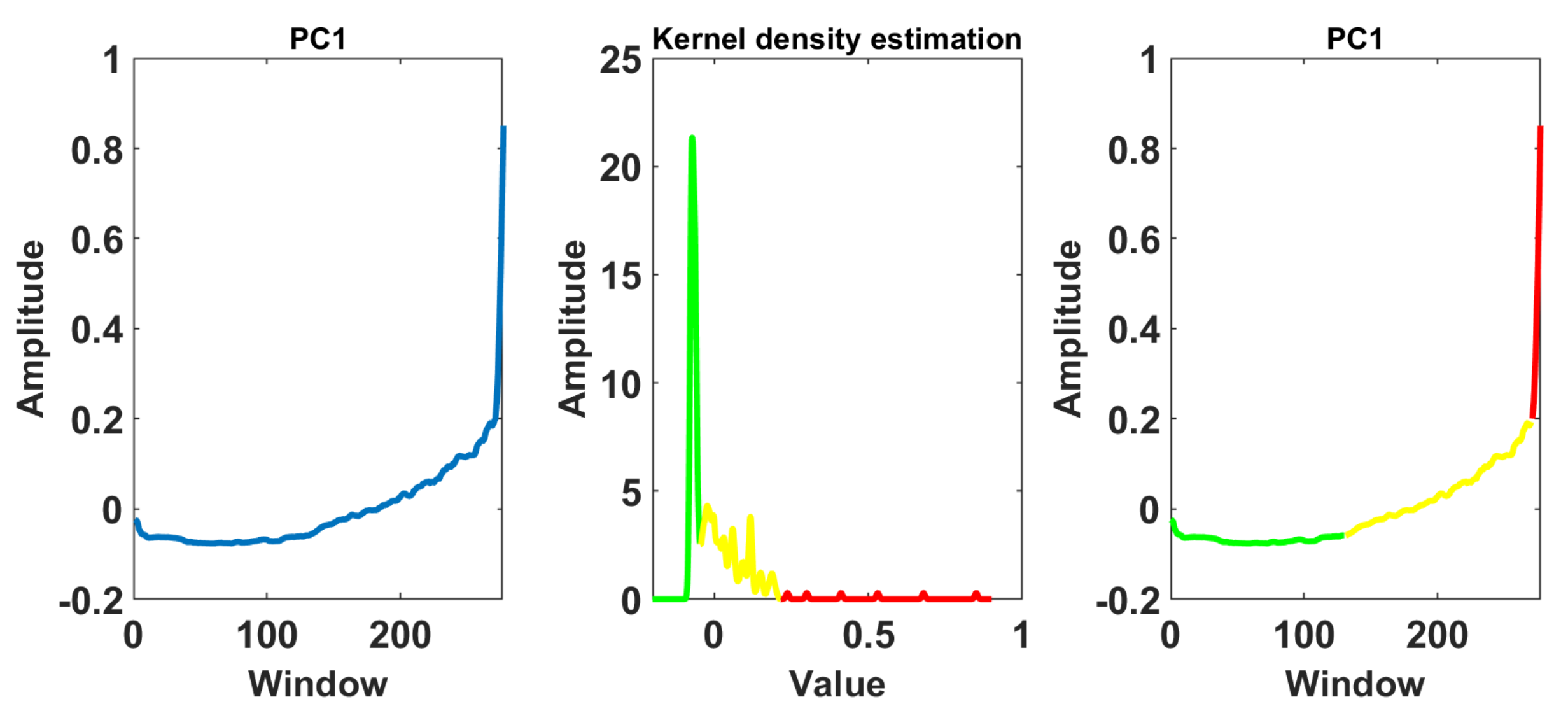
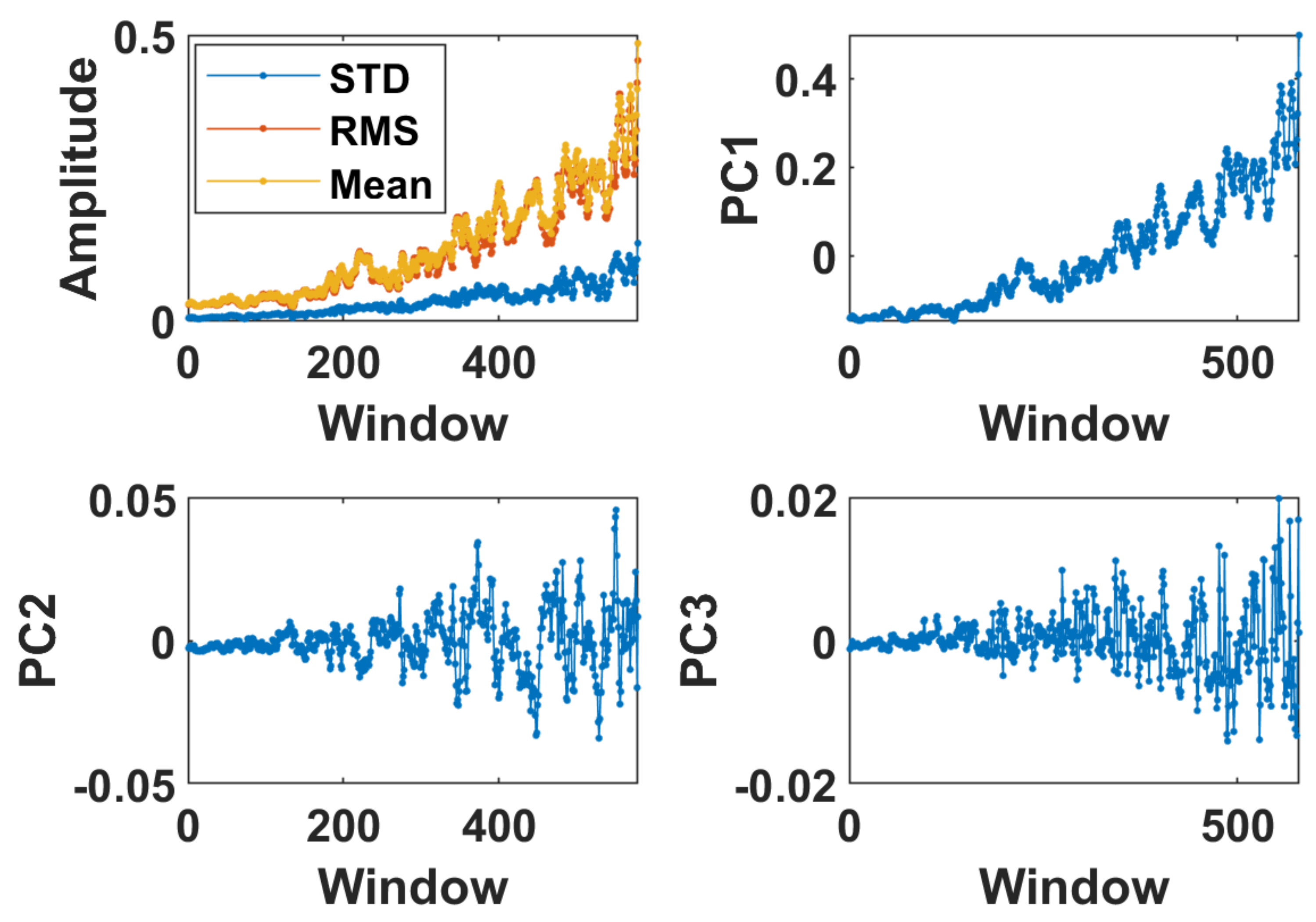
4.1. Segmentation and Descriptive Statistics Used as Features
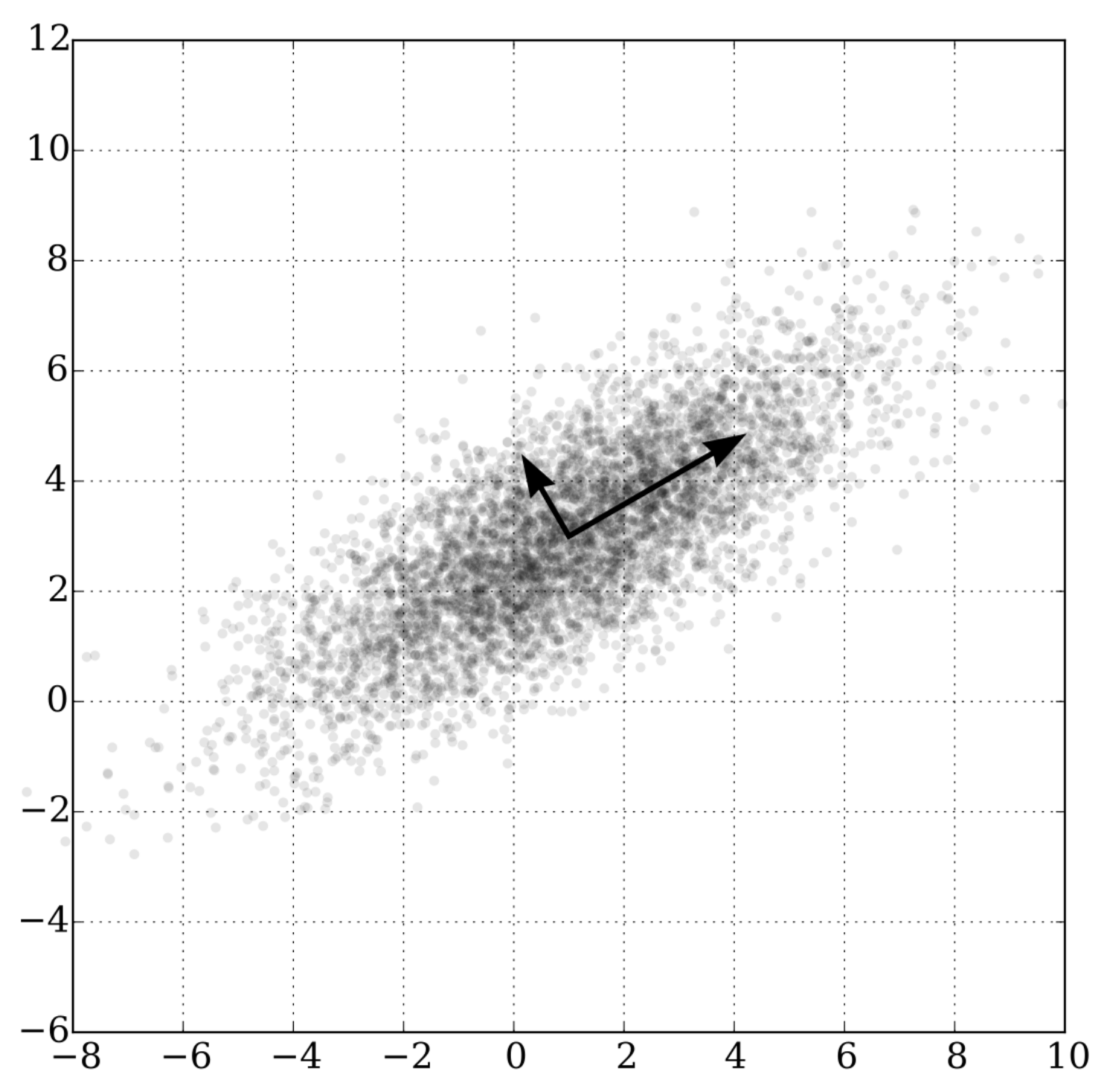
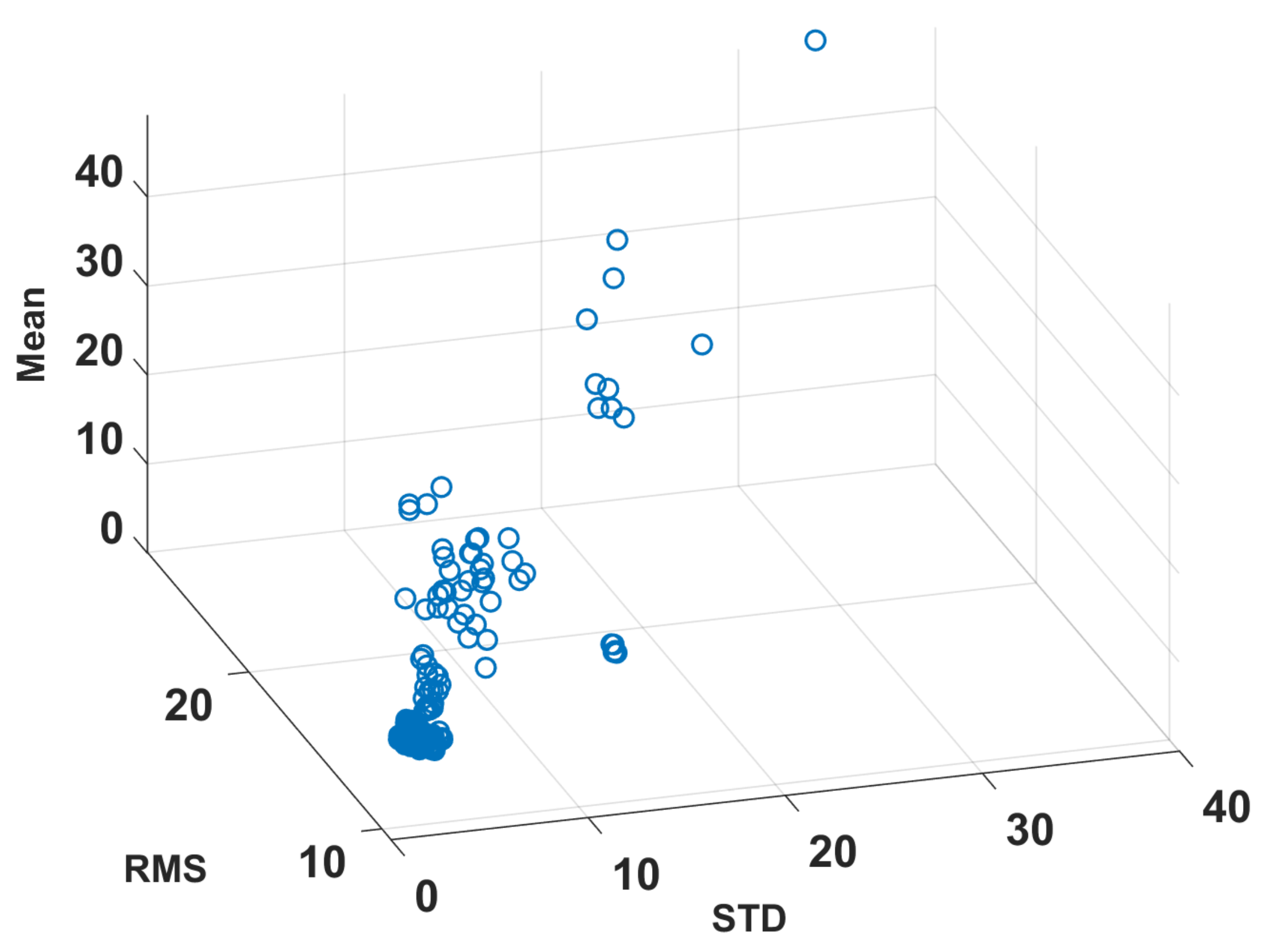
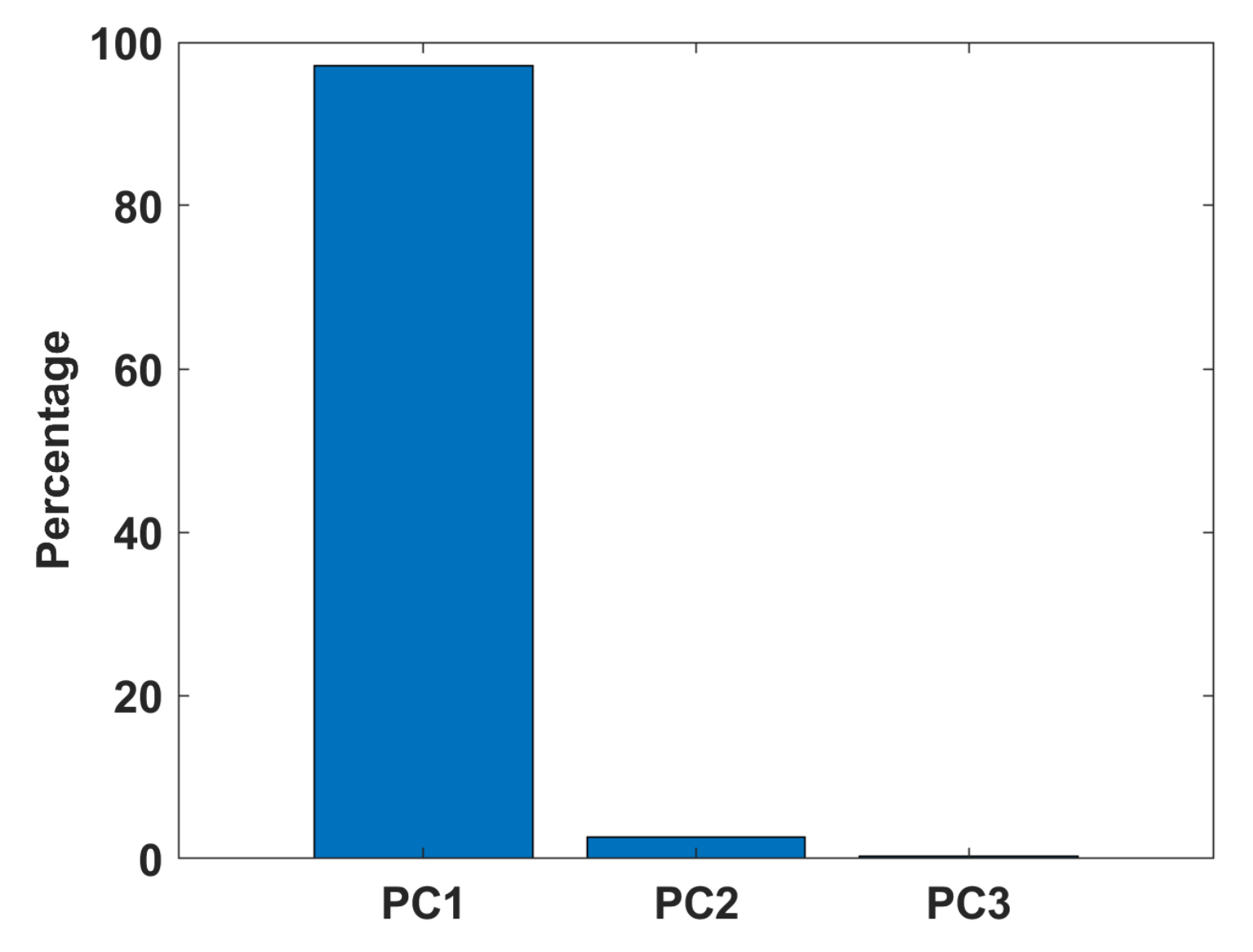
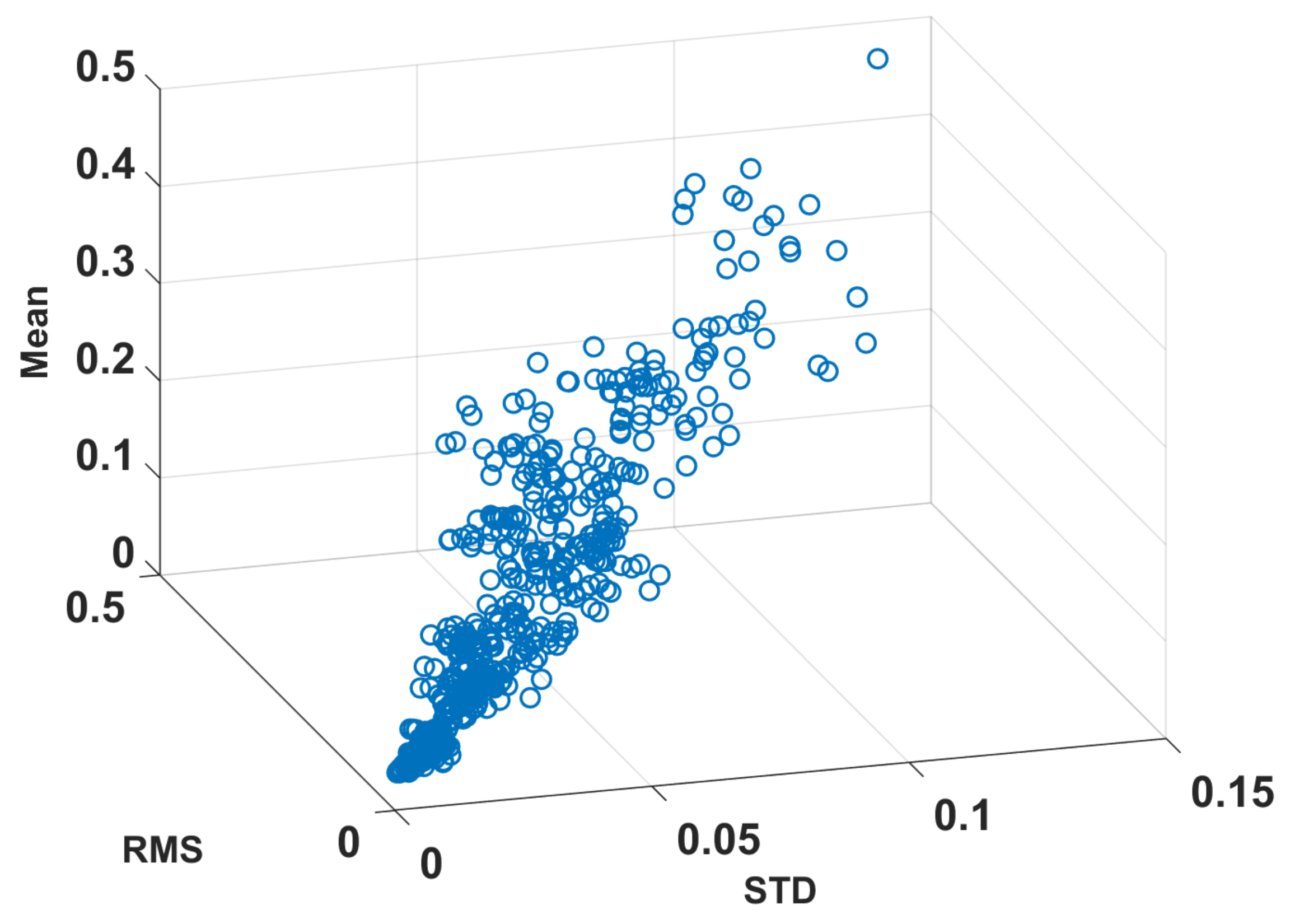
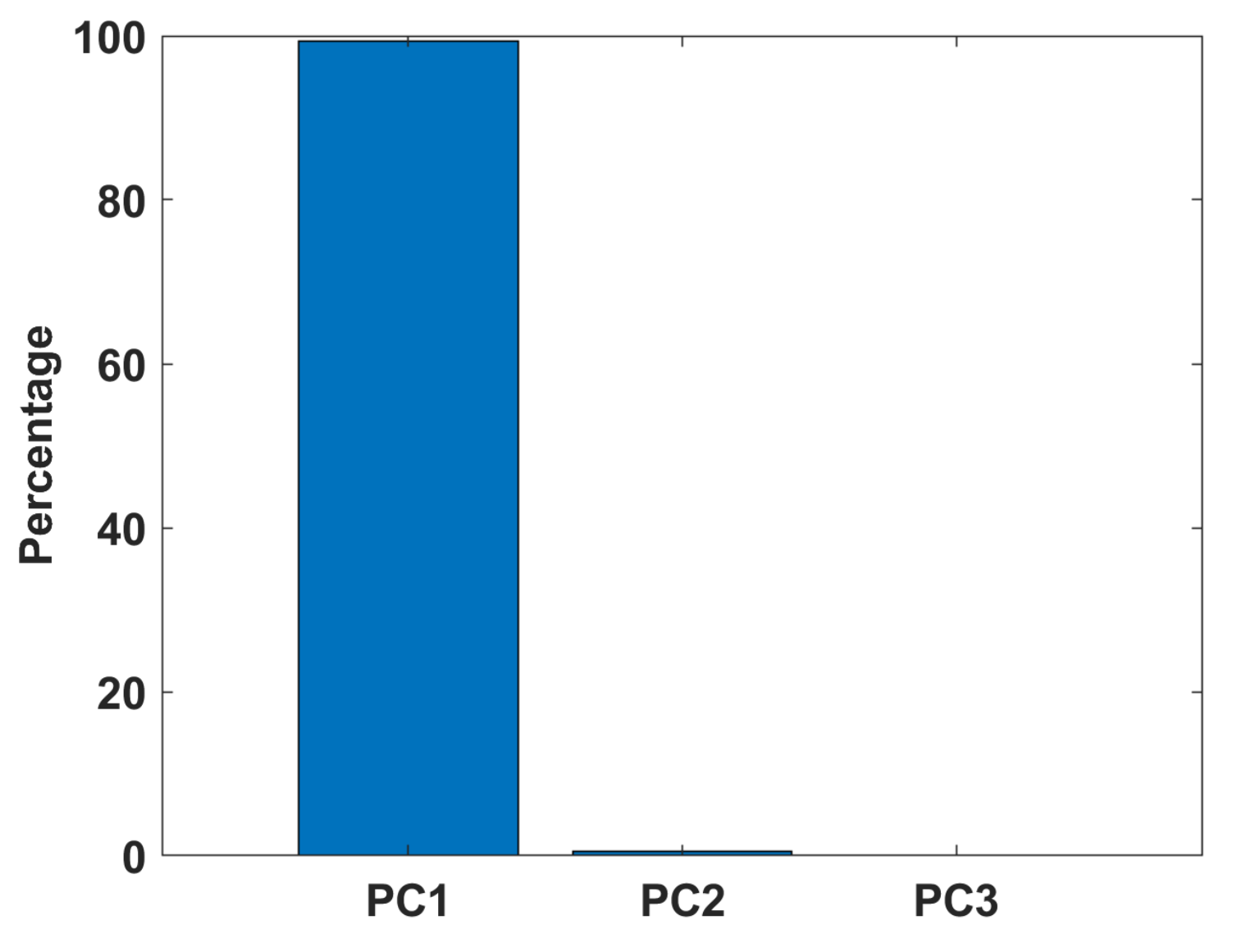
4.2. Principal Component Analysis
4.3. Kernel Density Estimation
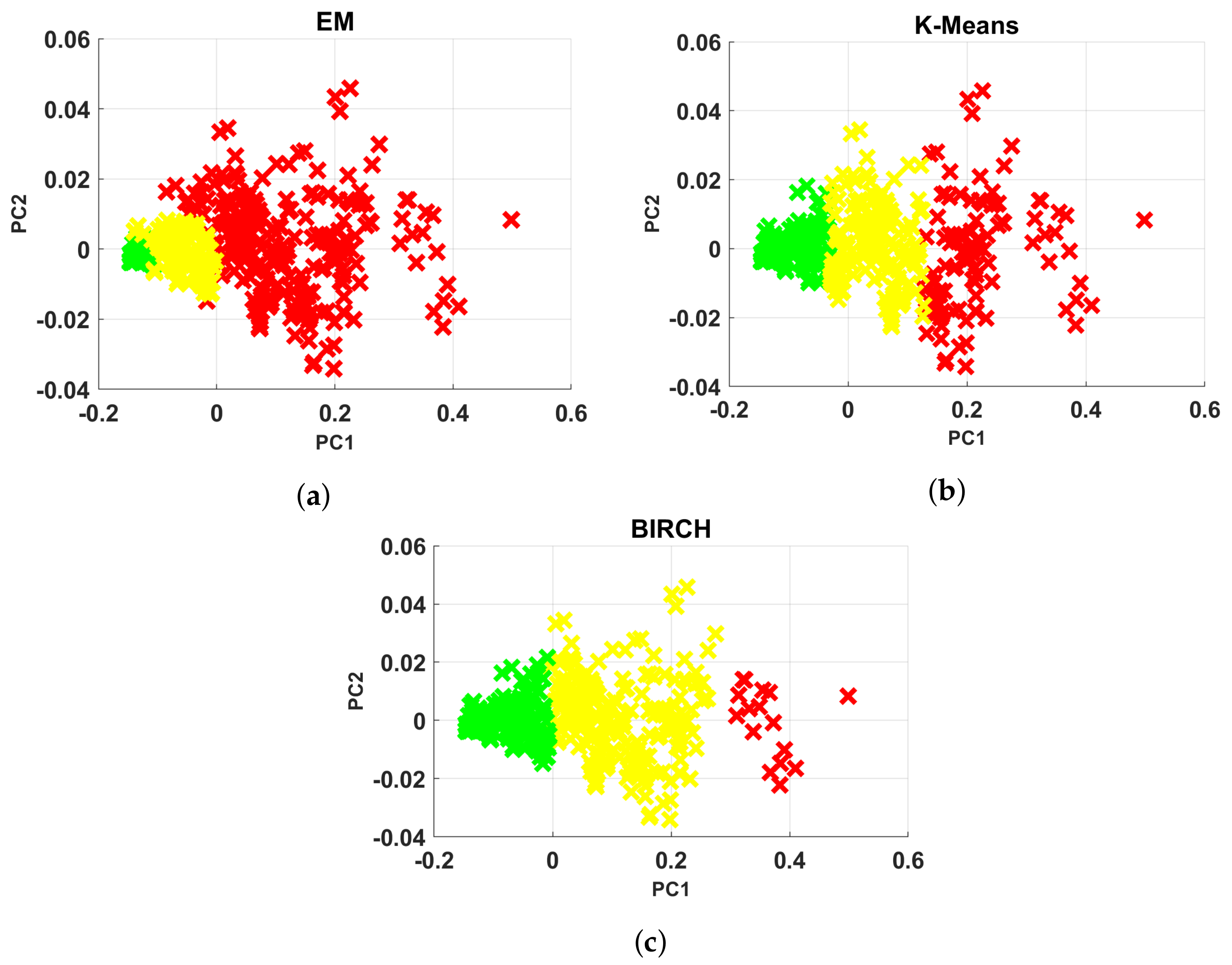
4.4. Cluster Analysis Techniques
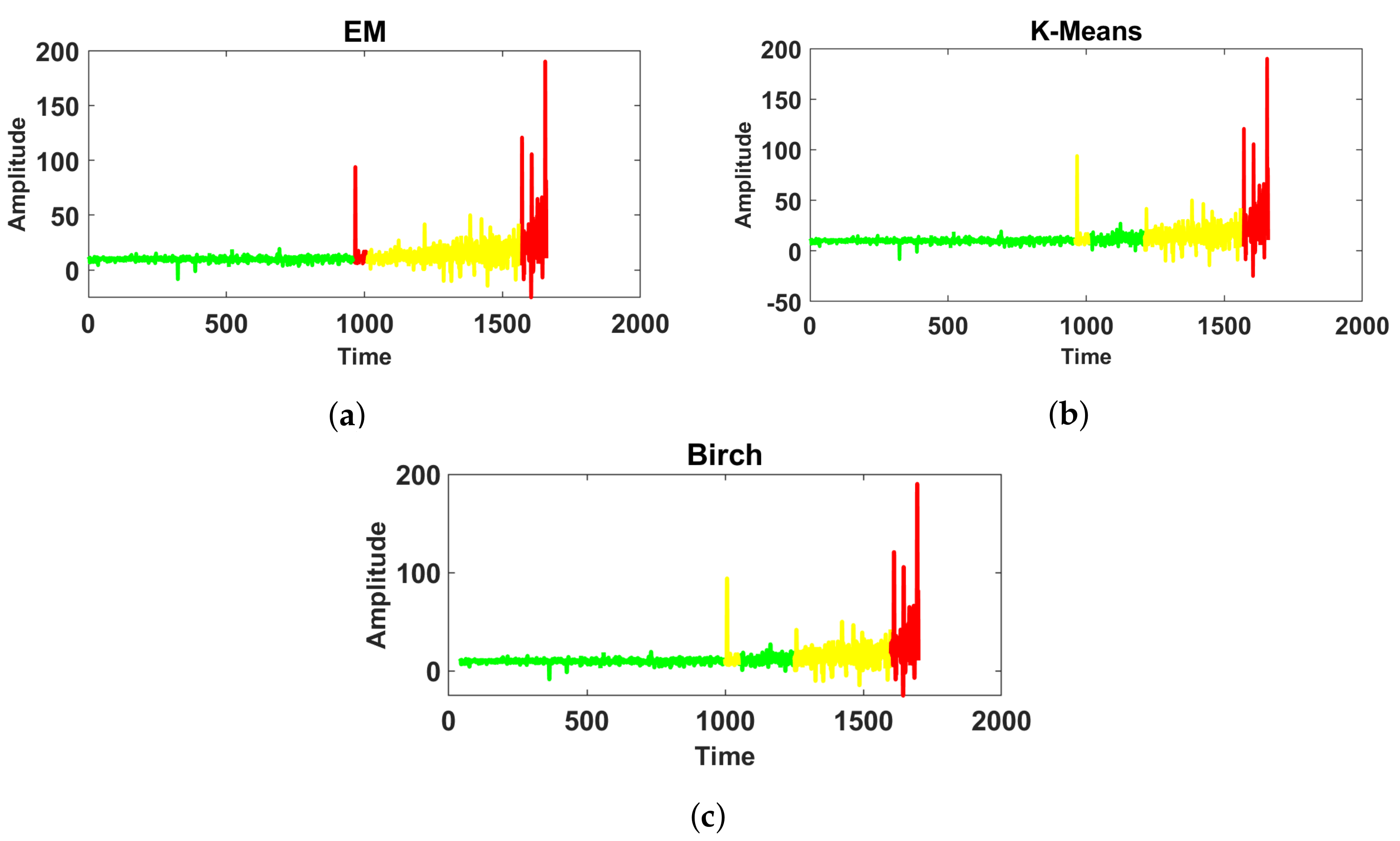
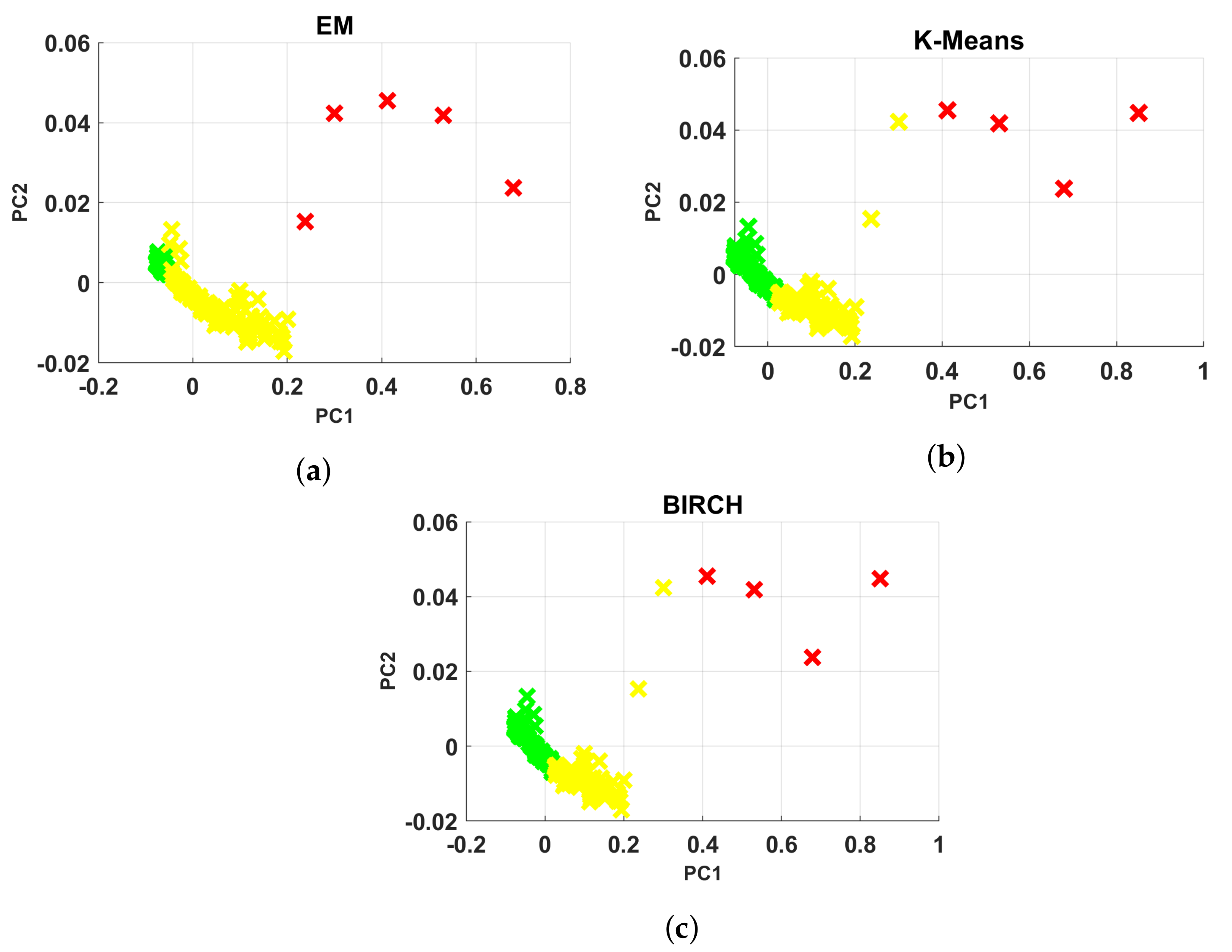
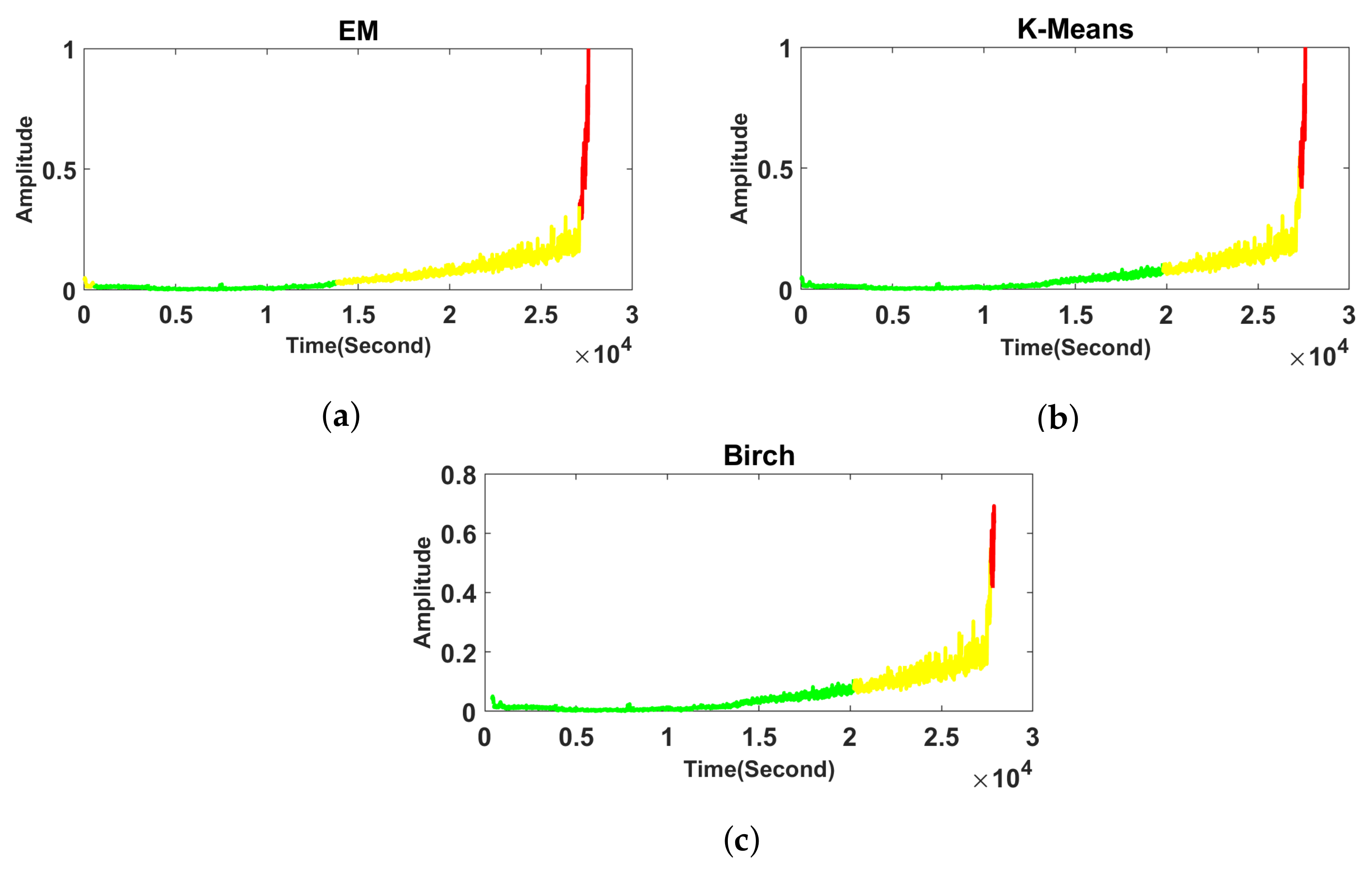
- K-means clustering is a method of vector quantification that is originally derived from signal processing, and it is famous approach for clustering in data mining [55,56,57,58]. K-means clustering is used to decompose the n observations into k clusters whose observations belong to a cluster with its closest mean. According to the set of observations where each observation is a M dimension vector. The target of K-means clustering is to divide N observation to collection such that the sum of the squares of the difference from the mean (i.e., variance) is minimized for each cluster.
- BIRCH (balanced iterative reducing and clustering using hierarchies) is one of the fastest clustering algorithms, introduced in refs. [59,60,61]. The main advantage of BIRCH is that it clusters incrementally and dynamically, attempting to produce the best quality given the time and memory constraints, with the requirement of only a single scan of the data set. However, it needs to specify the cluster count as an input variable. Additionally, BIRCH clustering is used in engineering applications. Lu et al. [62] introduced automatic fault detection based on BIRCH.
- Gaussian mixture modeling (GMM) is one of the popular methods used for unbalanced data clustering. The GMM is a probabilistic model that is based on the assumption that M-dimensional data X are arranged as a number of spatially-distributed Gaussian distribution modes with unknown parameters (list of M-dimensional means) and (list of covariance matrices).The expectation–maximization (EM) algorithm is used to estimate the parameters of GMM, thus allowing to cluster the data [63,64,65,66,67,68]. This method can be divided into two parts. At first, the expectation step (E-step) is used to estimate the probabilities for every point to be assigned to every cluster. Then the maximization step (M-step) is utilized to estimate the distributions based on the probabilities from E-step. Those two steps are iterated for a given number of iterations or until convergence.
5. Simulated Data Analysis
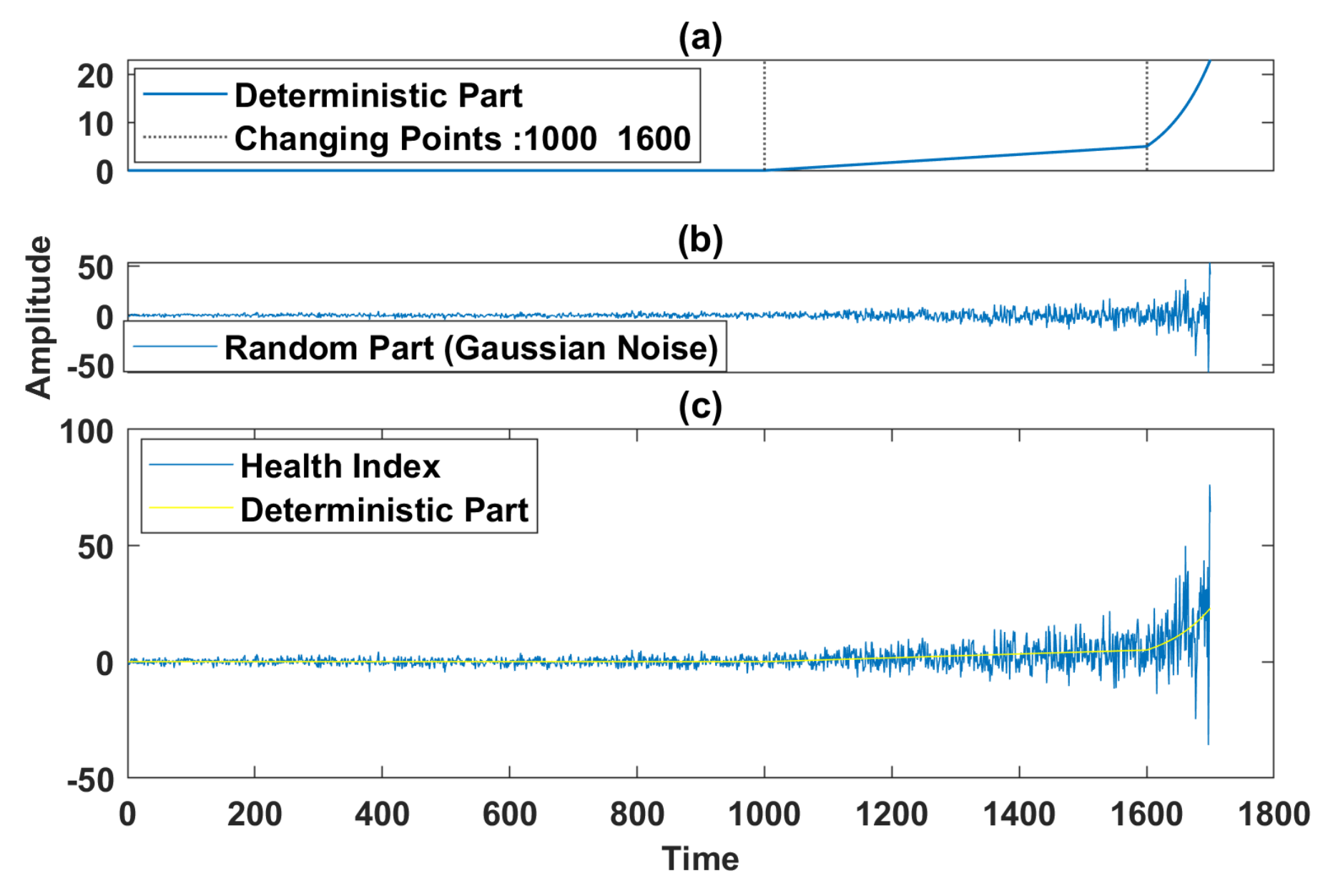
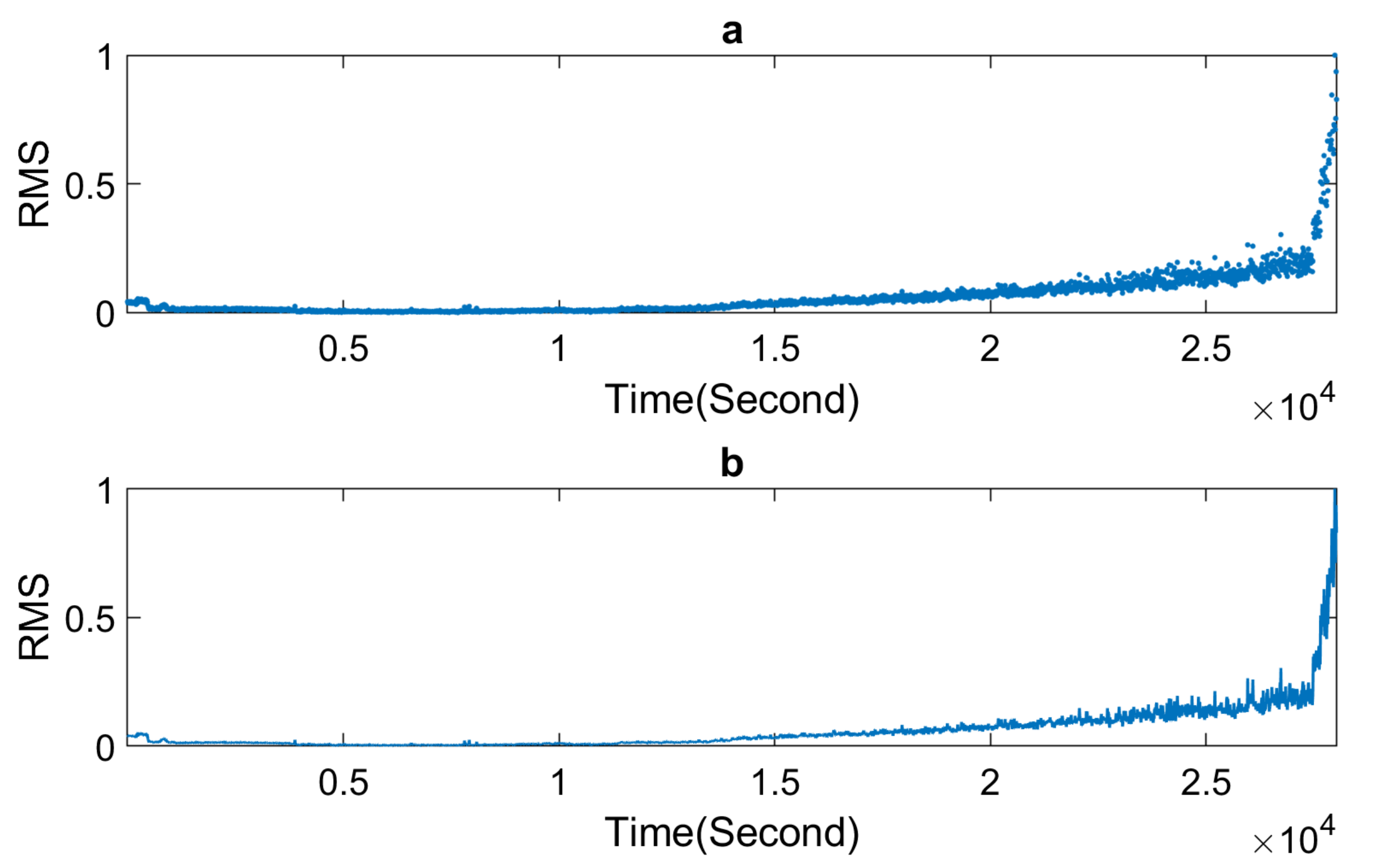
5.1. Signal Simulation for Gaussian and Non-Gaussian Noise
5.2. Extraction of Features for Simulated Signal for Gaussian Noise Case
5.3. Extraction of Features from Simulated Signal for Non-Gaussian Noise Case
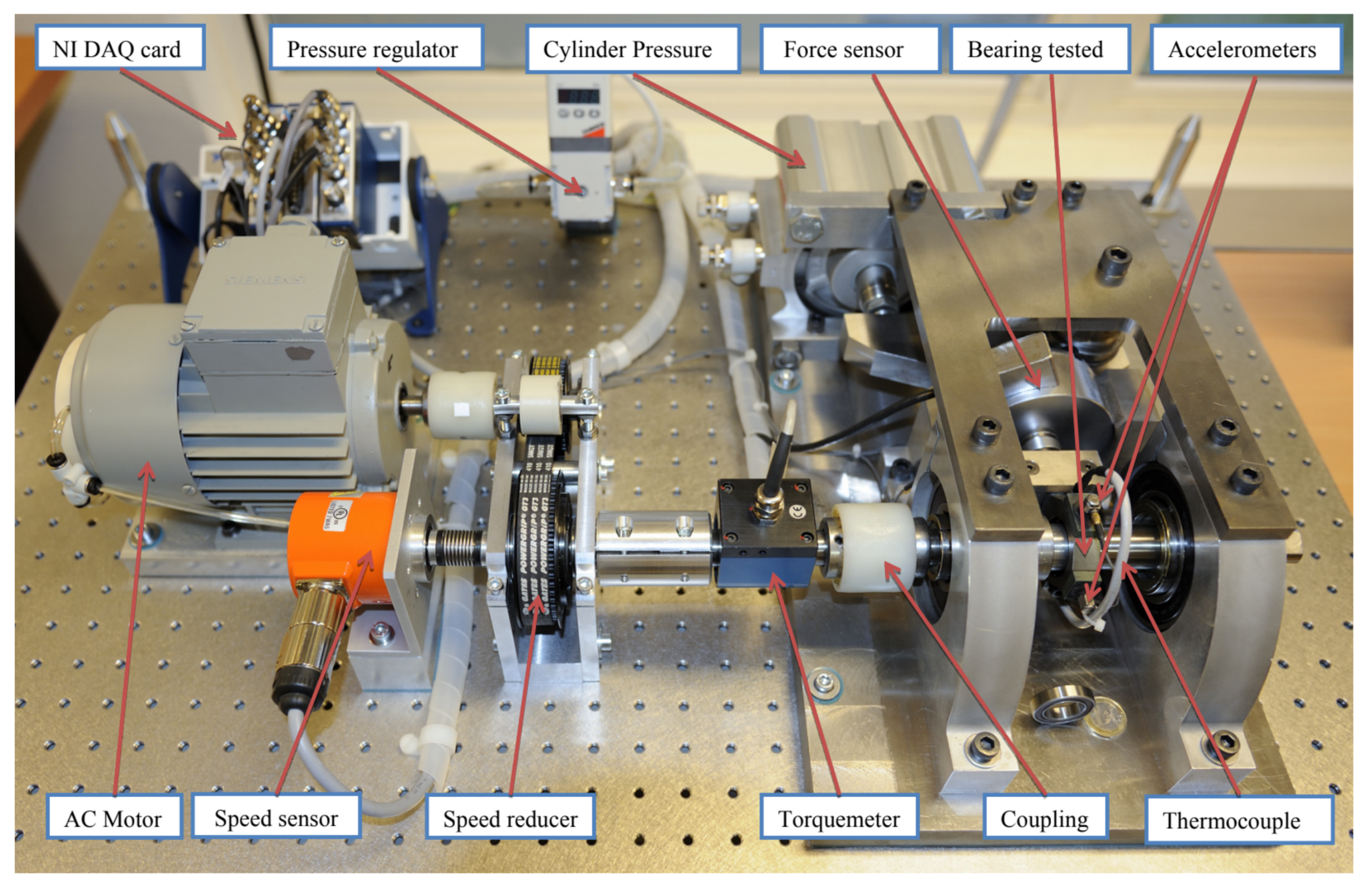
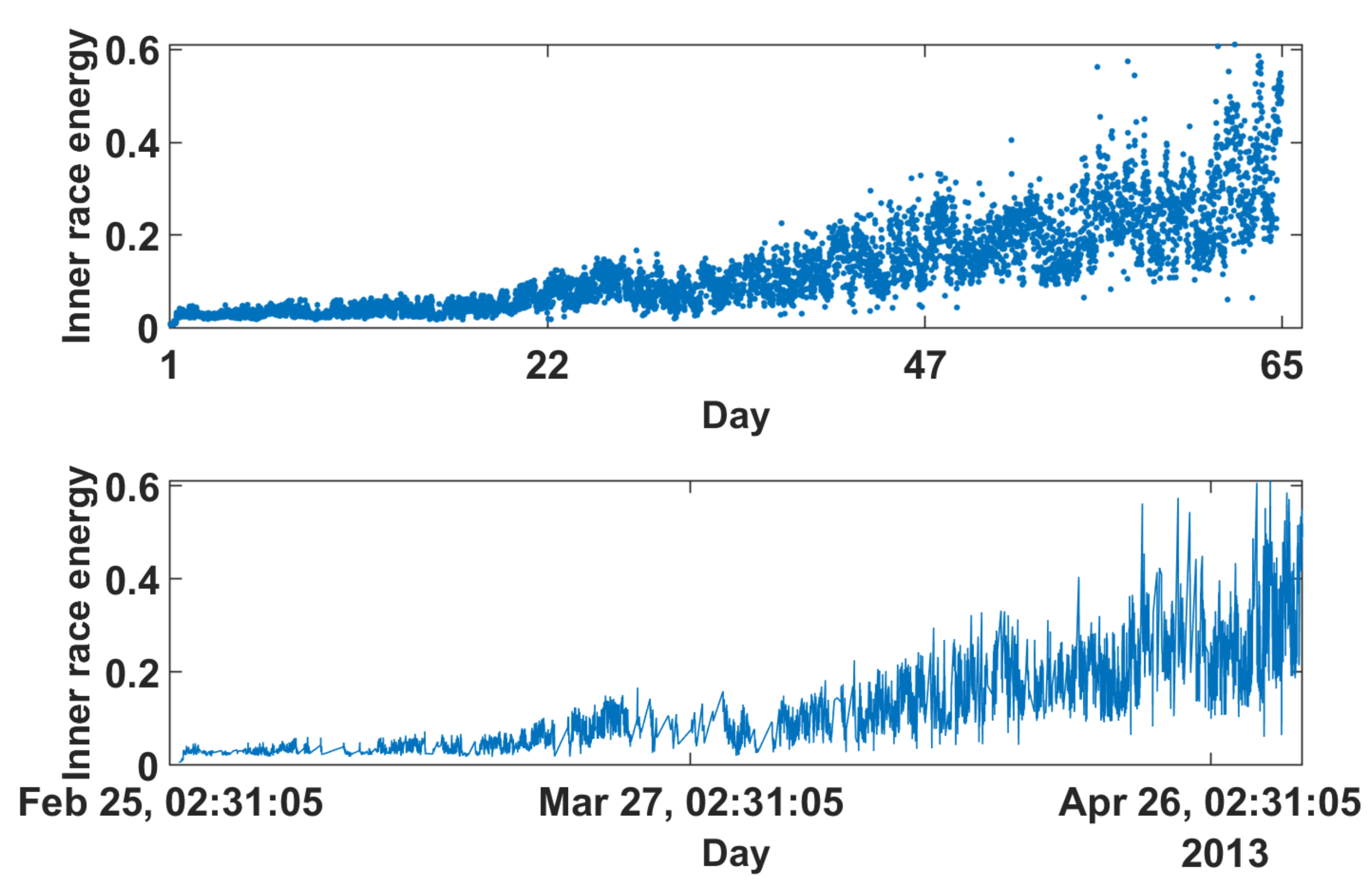
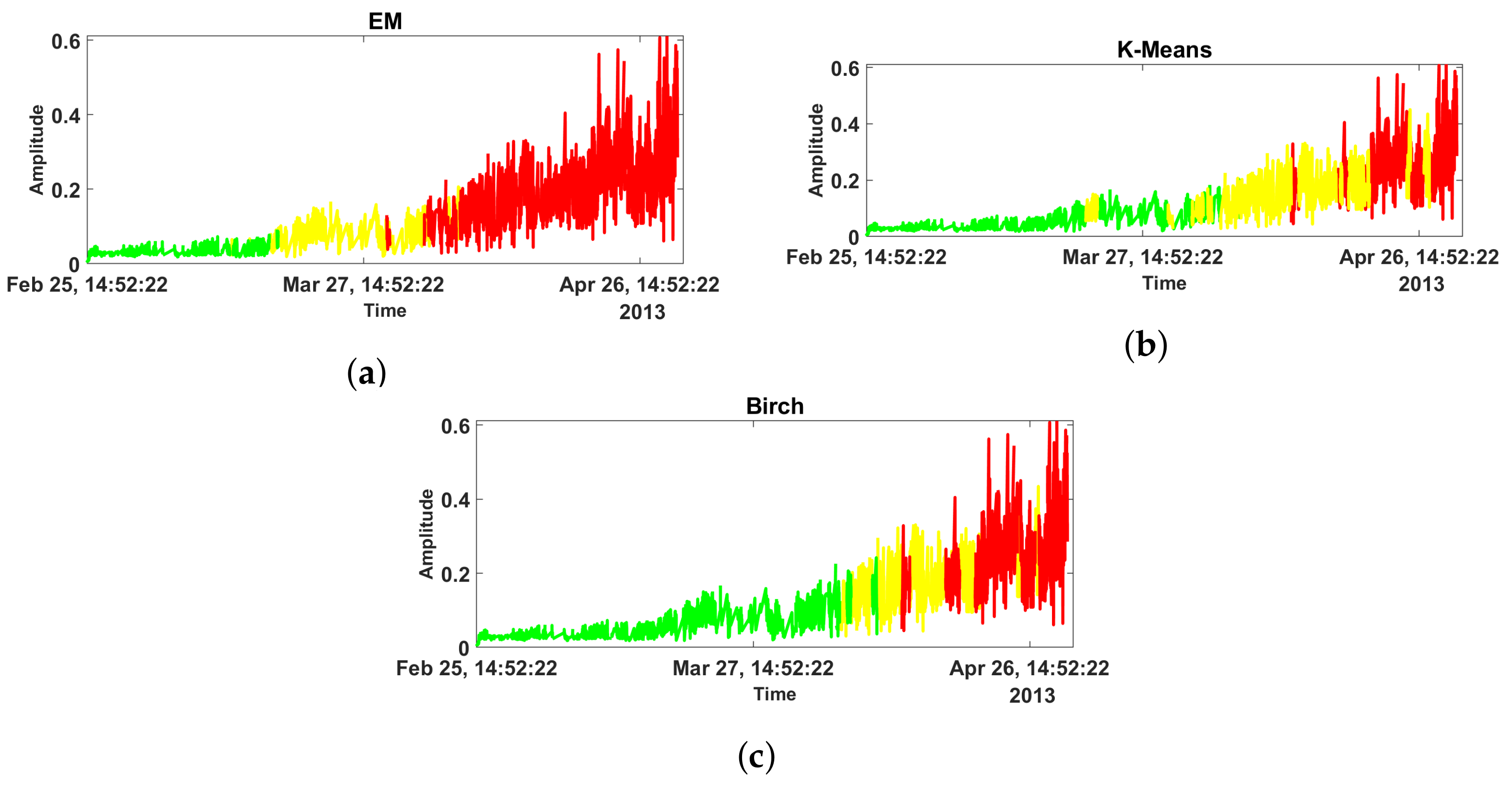
6. Real Data Analysis
6.1. Real Data with Almost Gaussian Noise
6.2. Real Data with Strong Non-Gaussian Noise
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sikora, G.; Michalak, A.; Bielak, L.; Miśta, P.; Wyłomańska, A. Stochastic modeling of currency exchange rates with novel validation techniques. Phys. A Stat. Mech. Appl. 2019, 523, 1202–1215. [Google Scholar] [CrossRef]
- Szarek, D.; Bielak, L.; Wyłomańska, A. Long-term prediction of the metals’ prices using non-Gaussian time-inhomogeneous stochastic process. Phys. A Stat. Mech. Appl. 2020, 555. [Google Scholar] [CrossRef]
- Tapia, C.; Coulton, J.; Saydam, S. Using entropy to assess dynamic behaviour of long-term copper price. Resour. Policy 2020, 66, 101597. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Zimroz, R.; Bartelmus, W.; Barszcz, T.; Urbanek, J. Diagnostics of bearings in presence of strong operating conditions non-stationarity—A procedure of load-dependent features processing with application to wind turbine bearings. Mech. Syst. Signal Process. 2014, 46, 16–27. [Google Scholar] [CrossRef]
- Ignasiak, A.; Gomolla, N.; Kruczek, P.; Wylomanska, A.; Zimroz, R. Long term vibration data analysis from wind turbine—Statistical vs. energy based features. Vibroeng. Procedia 2017, 13, 96–102. [Google Scholar] [CrossRef]
- Wodecki, J.; Stefaniak, P.; Michalak, A.; Wyłomańska, A.; Zimroz, R. Technical condition change detection using Anderson–Darling statistic approach for LHD machines–engine overheating problem. Int. J. Min. Reclam. Environ. 2018, 32, 392–400. [Google Scholar] [CrossRef]
- Grzesiek, A.; Zimroz, R.; Śliwiński, P.; Gomolla, N.; Wyłomańska, A. Long term belt conveyor gearbox temperature data analysis—Statistical tests for anomaly detection. Meas. J. Int. Meas. Confed. 2020, 165, 108124. [Google Scholar] [CrossRef]
- Wang, P.; Long, Z.; Wang, G. A hybrid prognostics approach for estimating remaining useful life of wind turbine bearings. Energy Rep. 2020, 6, 173–182. [Google Scholar] [CrossRef]
- Li, W.; Jiao, Z.; Du, L.; Fan, W.; Zhu, Y. An indirect RUL prognosis for lithium-ion battery under vibration stress using Elman neural network. Int. J. Hydrogen Energy 2019, 44, 12270–12276. [Google Scholar] [CrossRef]
- Staszewski, W.; Tomlinson, G. Local tooth fault detection in gearboxes using a moving window procedure. Mech. Syst. Signal Process. 1997, 11, 331–350. [Google Scholar] [CrossRef]
- Marcjasz, G.; Serafin, T.; Weron, R. Selection of calibration windows for day-ahead electricity price forecasting. Energies 2018, 11, 2364. [Google Scholar] [CrossRef]
- Allen, J. Short Term Spectral Analysis, Synthesis, and Modification by Discrete Fourier Transform. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 235–238. [Google Scholar] [CrossRef]
- Yan, H.; Qin, Y.; Xiang, S.; Wang, Y.; Chen, H. Long-term gear life prediction based on ordered neurons LSTM neural networks. Measurement 2020, 165, 108205. [Google Scholar] [CrossRef]
- Tamilselvan, P.; Wang, Y.; Wang, P. Deep belief network based state classification for structural health diagnosis. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–11. [Google Scholar]
- Liu, J.; Lei, F.; Pan, C.; Hu, D.; Zuo, H. Prediction of remaining useful life of multi-stage aero-engine based on clustering and LSTM fusion. Reliab. Eng. Syst. Saf. 2021, 214, 107807. [Google Scholar] [CrossRef]
- Singh, J.; Darpe, A.; Singh, S.P. Bearing remaining useful life estimation using an adaptive data-driven model based on health state change point identification and K-means clustering. Meas. Sci. Technol. 2020, 31, 085601. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Sun, B.; Wang, L. Prediction of Bearings Remaining Useful Life Across Working Conditions Based on Transfer Learning and Time Series Clustering. IEEE Access 2021, 9, 135285–135303. [Google Scholar] [CrossRef]
- Sharanya, S.; Venkataraman, R.; Murali, G. Estimation of Remaining Useful Life of Bearings Using Reduced Affinity Propagated Clustering. J. Eng. Sci. Technol. 2021, 16, 3737–3756. [Google Scholar]
- Javed, K.; Gouriveau, R.; Zerhouni, N. A new multivariate approach for prognostics based on extreme learning machine and fuzzy clustering. IEEE Trans. Cybern. 2015, 45, 2626–2639. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine remaining useful life prediction via an attention-based deep learning approach. IEEE Trans. Ind. Electron. 2020, 68, 2521–2531. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Abdullah, S.; Niaki, S.T.A.; Banihashemi, S. An intelligent hybrid classification algorithm integrating fuzzy rule-based extraction and harmony search optimization: Medical diagnosis applications. Knowl.-Based Syst. 2021, 220, 106943. [Google Scholar] [CrossRef]
- Yu, W.; Kim, I.Y.; Mechefske, C. Analysis of different RNN autoencoder variants for time series classification and machine prognostics. Mech. Syst. Signal Process. 2021, 149, 107322. [Google Scholar] [CrossRef]
- Baptista, M.L.; Henriques, E.M.; Prendinger, H. Classification prognostics approaches in aviation. Measurement 2021, 182, 109756. [Google Scholar] [CrossRef]
- Stock, S.; Pohlmann, S.; Günter, F.J.; Hille, L.; Hagemeister, J.; Reinhart, G. Early quality classification and prediction of battery cycle life in production using machine learning. J. Energy Storage 2022, 50, 104144. [Google Scholar] [CrossRef]
- Buchaiah, S.; Shakya, P. Bearing fault diagnosis and prognosis using data fusion based feature extraction and feature selection. Measurement 2022, 188, 110506. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef] [PubMed]
- Prakash, A.; James, N.; Menzies, M.; Francis, G. Structural clustering of volatility regimes for dynamic trading strategies. Appl. Math. Financ. 2022, 28, 236–274. [Google Scholar] [CrossRef]
- Das, S. Blind Change Point Detection and Regime Segmentation Using Gaussian Process Regression. Ph.D. Thesis, University of South Carolina, Columbia, SC, USA, 2017. [Google Scholar]
- Abonyi, J.; Feil, B.; Nemeth, S.; Arva, P. Fuzzy clustering based segmentation of time-series. In Proceedings of the International Symposium on Intelligent Data Analysis, Berlin, Germany, 28–30 August 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 275–285. [Google Scholar]
- Tseng, V.S.; Chen, C.H.; Huang, P.C.; Hong, T.P. Cluster-based genetic segmentation of time series with DWT. Pattern Recognit. Lett. 2009, 30, 1190–1197. [Google Scholar] [CrossRef]
- Samé, A.; Chamroukhi, F.; Govaert, G.; Aknin, P. Model-based clustering and segmentation of time series with changes in regime. Adv. Data Anal. Classif. 2011, 5, 301–321. [Google Scholar] [CrossRef]
- Keogh, E.J.; Pazzani, M.J. An Enhanced Representation of Time Series Which Allows Fast and Accurate Classification, Clustering and Relevance Feedback. Proc. KDD 1998, 98, 239–243. [Google Scholar]
- Tseng, V.S.; Chen, C.H.; Chen, C.H.; Hong, T.P. Segmentation of time series by the clustering and genetic algorithms. In Proceedings of the Sixth IEEE International Conference on Data Mining-Workshops (ICDMW’06), Hong Kong, China, 18–22 December 2006; pp. 443–447. [Google Scholar]
- Wood, K.; Roberts, S.; Zohren, S. Slow momentum with fast reversion: A trading strategy using deep learning and changepoint detection. J. Financ. Data Sci. 2022, 4, 111–129. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T. Estimating change-point latent factor models for high-dimensional time series. J. Stat. Plan. Inference 2022, 217, 69–91. [Google Scholar] [CrossRef]
- Ge, X.; Lin, A. Kernel change point detection based on convergent cross mapping. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106318. [Google Scholar] [CrossRef]
- Kucharczyk, D.; Wyłomańska, A.; Obuchowski, J.; Zimroz, R.; Madziarz, M. Stochastic Modelling as a Tool for Seismic Signals Segmentation. Shock Vib. 2016, 2016, 8453426. [Google Scholar] [CrossRef][Green Version]
- Gąsior, K.; Urbańska, H.; Grzesiek, A.; Zimroz, R.; Wyłomańska, A. Identification, decomposition and segmentation of impulsive vibration signals with deterministic components—A sieving screen case study. Sensors 2020, 20, 5648. [Google Scholar] [CrossRef]
- Grzesiek, A.; Gasior, K.; Wyłomańska, A.; Zimroz, R. Divergence-based segmentation algorithm for heavy-tailed acoustic signals with time-varying characteristics. Sensors 2021, 21, 8487. [Google Scholar] [CrossRef]
- Wen, Y.; Wu, J.; Das, D.; Tseng, T.L. Degradation modeling and RUL prediction using Wiener process subject to multiple change points and unit heterogeneity. Reliab. Eng. Syst. Saf. 2018, 176, 113–124. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Heng, A.; Zhang, S.; Tan, A.; Mathew, J. Rotating machinery prognostics: State of the art, challenges and opportunities. Mech. Syst. Signal Process. 2009, 23, 724–739. [Google Scholar] [CrossRef]
- Sikorska, J.; Hodkiewicz, M.; Ma, L. Prognostic modelling options for remaining useful life estimation by industry. Mech. Syst. Signal Process. 2011, 25, 1803–1836. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Kan, M.; Tan, A.; Mathew, J. A review on prognostic techniques for non-stationary and non-linear rotating systems. Mech. Syst. Signal Process. 2015, 62, 1–20. [Google Scholar] [CrossRef]
- Reuben, L.; Mba, D. Diagnostics and prognostics using switching Kalman filters. Struct. Health Monit. 2014, 13, 296–306. [Google Scholar] [CrossRef]
- Lim, C.; Mba, D. Switching Kalman filter for failure prognostic. Mech. Syst. Signal Process. 2015, 52-53, 426–435. [Google Scholar] [CrossRef]
- Wodecki, J.; Stefaniak, P.; Obuchowski, J.; Wylomanska, A.; Zimroz, R. Combination of principal component analysis and time-frequency representations of multichannel vibration data for gearbox fault detection. J. Vibroeng. 2016, 18, 2167–2175. [Google Scholar]
- Wikipedia. Principal Component Analysis. 2016. Available online: https://en.wikipedia.org/wiki/Principal_component_analysis (accessed on 9 May 2022).
- Peter, D.H. Kernel estimation of a distribution function. Commun. Stat.-Theory Methods 1985, 14, 605–620. [Google Scholar] [CrossRef]
- Silverman, B.W. Density estimation for statistics and data analysis. In Monographs on Statistics and Applied Probability; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- Jin, R.; Goswami, A.; Agrawal, G. Fast and exact out-of-core and distributed k-means clustering. Knowl. Inf. Syst. 2006, 10, 17–40. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. 2013, 1, 90–95. [Google Scholar]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A new data clustering algorithm and its applications. Data Min. Knowl. Discov. 1997, 1, 141–182. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large databases. ACM Sigmod Rec. 1996, 25, 103–114. [Google Scholar] [CrossRef]
- Madan, S.; Dana, K.J. Modified balanced iterative reducing and clustering using hierarchies (m-BIRCH) for visual clustering. Pattern Anal. Appl. 2016, 19, 1023–1040. [Google Scholar] [CrossRef]
- Liu, S.; Cao, D.; An, P.; Yang, X.; Zhang, M. Automatic fault detection based on the unsupervised seismic attributes clustering. In Proceedings of the SEG 2018 Workshop: SEG Maximizing Asset Value Through Artificial Intelligence and Machine Learning, Beijing, China, 17–19 September 2018; Society of Exploration Geophysicists: Houston, TX, USA; Chinese Geophysical Society: Beijing, China, 2018; pp. 56–59. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar]
- Sundberg, R. Maximum likelihood theory for incomplete data from an exponential family. Scand. J. Stat. 1974, 1, 49–58. [Google Scholar]
- Maugis, C.; Celeux, G.; Martin-Magniette, M.L. Variable selection for clustering with Gaussian mixture models. Biometrics 2009, 65, 701–709. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Basford, K.E. Mixture Models: Inference and Applications to Clustering; M. Dekker: New York, NY, USA, 1988; Volume 38. [Google Scholar]
- Biernacki, C.; Celeux, G.; Govaert, G. Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 719–725. [Google Scholar] [CrossRef]
- Kruczek, P.; Wodecki, J.; Wyłomanska, A.; Zimroz, R.; Gryllias, K.; Grobli, N. Multi-fault diagnosis based on bi-frequency cyclostation-ary maps clustering. In Proceedings of the ISMA2018-USD2018, Leuven, Belgium, 17–19 September 2018; pp. 981–990. [Google Scholar]
- Hebda-Sobkowicz, J.; Zimroz, R.; Wyłomańska, A.; Antoni, J. Infogram performance analysis and its enhancement for bearings diagnostics in presence of non-Gaussian noise. Mech. Syst. Signal Process. 2022, 170, 108764. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Wyłomańska, A.; Zimroz, R. Influence of non-Gaussian noise on the effectiveness of cyclostationary analysis—Simulations and real data analysis. Measurement 2021, 171, 108814. [Google Scholar] [CrossRef]
- Kruczek, P.; Zimroz, R.; Antoni, J.; Wyłomańska, A. Generalized spectral coherence for cyclostationary signals with α-stable distribution. Mech. Syst. Signal Process. 2021, 159, 107737. [Google Scholar] [CrossRef]
- Khinchine, A.Y.; Lévy, P. Sur les lois stables. CR Acad. Sci. Paris 1936, 202, 374–376. [Google Scholar]
- Burnecki, K.; Wyłomańska, A.; Beletskii, A.; Gonchar, V.; Chechkin, A. Recognition of stable distribution with Lévy index α close to 2. Phys. Rev. E 2012, 85, 056711. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]
- Liu, Z.; Zuo, M.J.; Qin, Y. Remaining useful life prediction of rolling element bearings based on health state assessment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 314–330. [Google Scholar] [CrossRef]
- Kimotho, J.K.; Sondermann-Wölke, C.; Meyer, T.; Sextro, W. Machinery Prognostic Method Based on Multi-Class Support Vector Machines and Hybrid Differential Evolution–Particle Swarm Optimization. Chem. Eng. Trans. 2013, 33, 619–624. [Google Scholar]
- Zurita, D.; Carino, J.A.; Delgado, M.; Ortega, J.A. Distributed neuro-fuzzy feature forecasting approach for condition monitoring. In Proceedings of the 2014 IEEE Emerging Technology and Factory Automation (ETFA), Barcelona, Spain, 16–19 September 2014; pp. 1–8. [Google Scholar]
- Guo, L.; Gao, H.; Huang, H.; He, X.; Li, S. Multifeatures fusion and nonlinear dimension reduction for intelligent bearing condition monitoring. Shock Vib. 2016, 2016, 4632562. [Google Scholar] [CrossRef]
- Jin, X.; Sun, Y.; Que, Z.; Wang, Y.; Chow, T.W. Anomaly detection and fault prognosis for bearings. IEEE Trans. Instrum. Meas. 2016, 65, 2046–2054. [Google Scholar] [CrossRef]
- Mosallam, A.; Medjaher, K.; Zerhouni, N. Time series trending for condition assessment and prognostics. J. Manuf. Technol. Manag. 2014, 25, 550–567. [Google Scholar] [CrossRef]
- Loutas, T.H.; Roulias, D.; Georgoulas, G. Remaining useful life estimation in rolling bearings utilizing data-driven probabilistic e-support vectors regression. IEEE Trans. Reliab. 2013, 62, 821–832. [Google Scholar] [CrossRef]
- Javed, K.; Gouriveau, R.; Zerhouni, N.; Nectoux, P. Enabling health monitoring approach based on vibration data for accurate prognostics. IEEE Trans. Ind. Electron. 2014, 62, 647–656. [Google Scholar] [CrossRef]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. Extended Kalman filtering for remaining-useful-life estimation of bearings. IEEE Trans. Ind. Electron. 2014, 62, 1781–1790. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, L.; Xu, J. Degradation feature selection for remaining useful life prediction of rolling element bearings. Qual. Reliab. Eng. Int. 2016, 32, 547–554. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z.; Zio, E.; Wang, W. An adaptive method for health trend prediction of rotating bearings. Digit. Signal Process. 2014, 35, 117–123. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A model-based method for remaining useful life prediction of machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Nie, Y.; Wan, J. Estimation of remaining useful life of bearings using sparse representation method. In Proceedings of the 2015 Prognostics and System Health Management Conference (PHM), Beijing, China, 21–23 October 2015; pp. 1–6. [Google Scholar]
- Li, H.; Wang, Y. Rolling bearing reliability estimation based on logistic regression model. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013; pp. 1730–1733. [Google Scholar]
- Huang, Z.; Xu, Z.; Ke, X.; Wang, W.; Sun, Y. Remaining useful life prediction for an adaptive skew-Wiener process model. Mech. Syst. Signal Process. 2017, 87, 294–306. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.; Zi, Y.; Jin, X.; Tsui, K.L. A two-stage data-driven-based prognostic approach for bearing degradation problem. IEEE Trans. Ind. Inform. 2016, 12, 924–932. [Google Scholar] [CrossRef]
- Pan, Y.; Er, M.J.; Li, X.; Yu, H.; Gouriveau, R. Machine health condition prediction via online dynamic fuzzy neural networks. Eng. Appl. Artif. Intell. 2014, 35, 105–113. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Wang, X.z. Reliability estimation and remaining useful lifetime prediction for bearing based on proportional hazard model. J. Cent. South Univ. 2015, 22, 4625–4633. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, X.; Zhang, X.; Liu, M. A novel approach for bearing remaining useful life estimation under neither failure nor suspension histories condition. J. Intell. Manuf. 2017, 28, 1893–1914. [Google Scholar] [CrossRef]
- Bechhoefer, E.; Schlanbusch, R. Generalized Prognostic Algorithm Implementing Kalman Smoother. IFAC-PapersOnLine 2015, 48, 97–104. [Google Scholar] [CrossRef]
- Saidi, L.; Ali, J.B.; Bechhoefer, E.; Benbouzid, M. Particle filter-based prognostic approach for high-speed shaft bearing wind turbine progressive degradations. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 8099–8104. [Google Scholar]
- Saidi, L.; Ali, J.B.; Bechhoefer, E.; Benbouzid, M. Wind turbine high-speed shaft bearings health prognosis through a spectral Kurtosis-derived indices and SVR. Appl. Acoust. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Saidi, L.; Bechhoefer, E.; Ali, J.B.; Benbouzid, M. Wind turbine high-speed shaft bearing degradation analysis for run-to-failure testing using spectral kurtosis. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 267–272. [Google Scholar]
- Ali, J.B.; Saidi, L.; Harrath, S.; Bechhoefer, E.; Benbouzid, M. Online automatic diagnosis of wind turbine bearings progressive degradations under real experimental conditions based on unsupervised machine learning. Appl. Acoust. 2018, 132, 167–181. [Google Scholar]

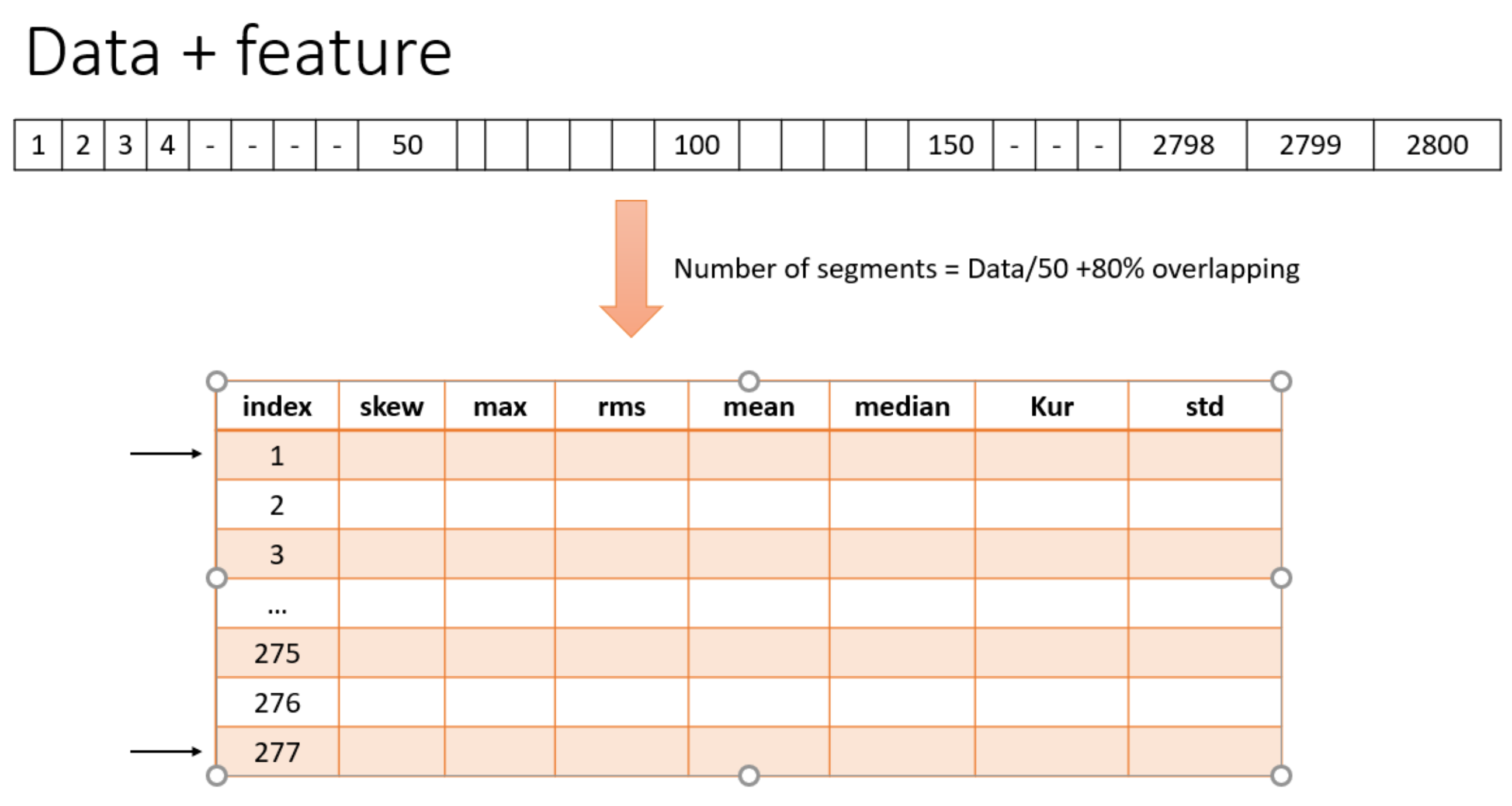

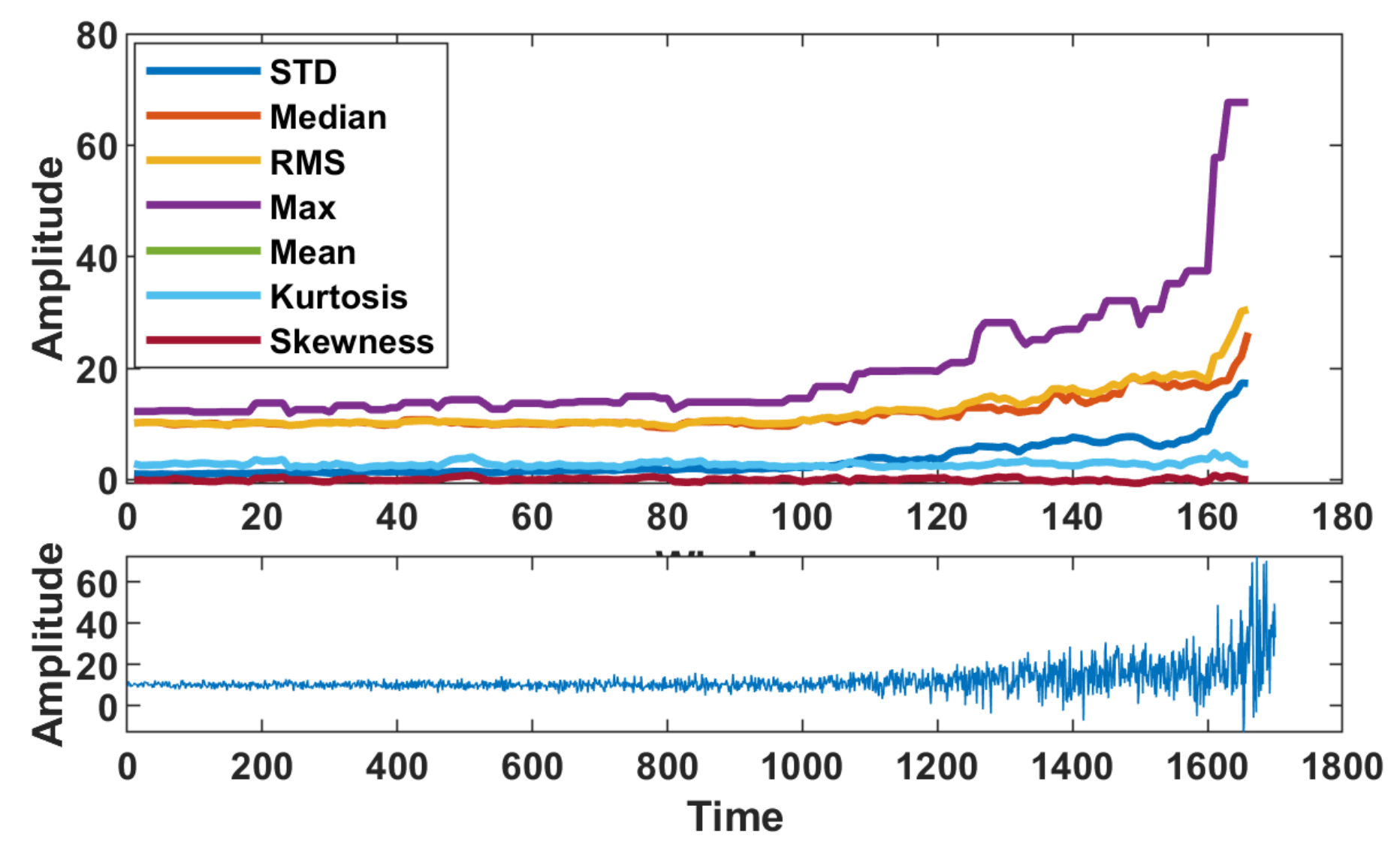
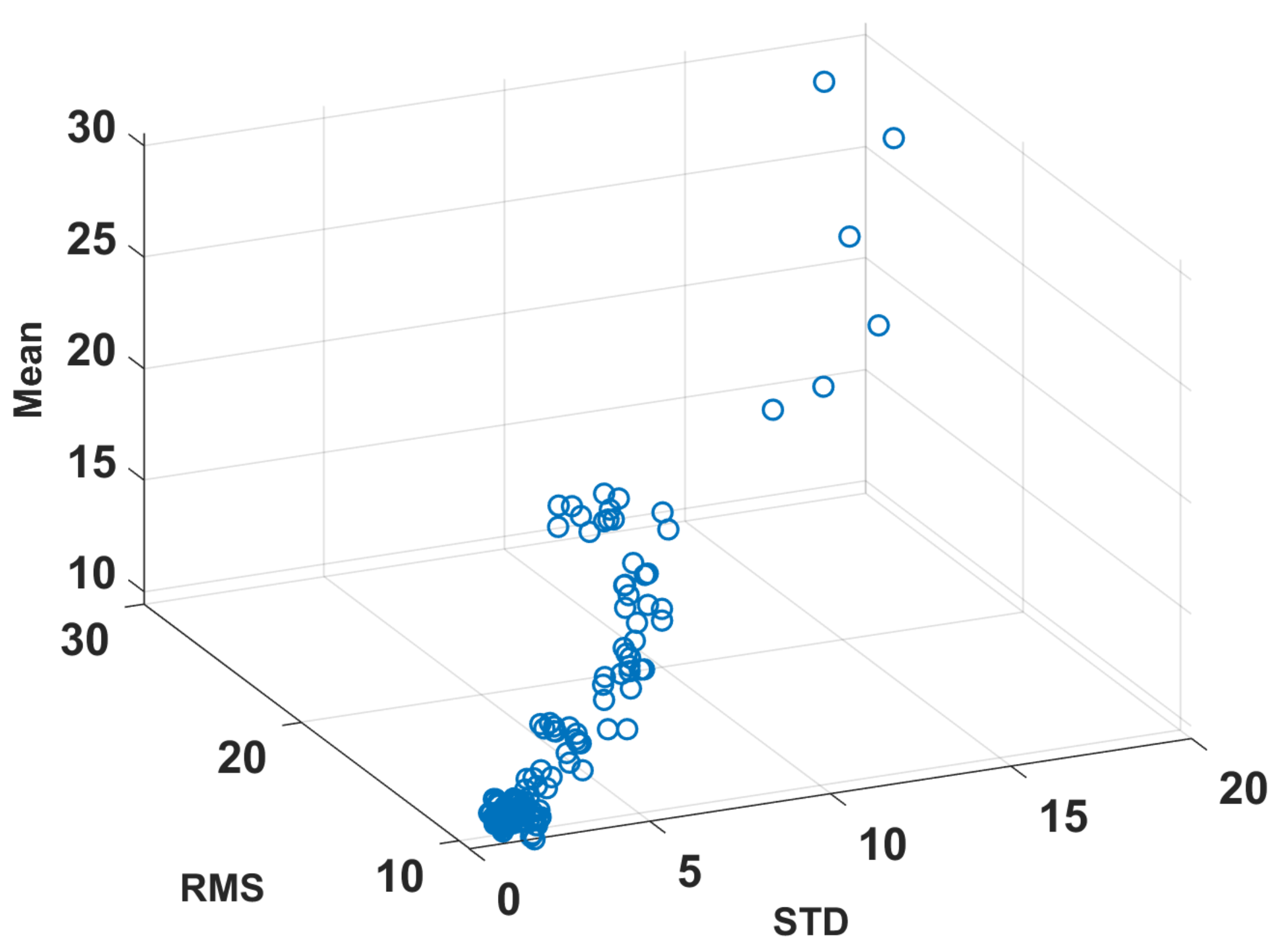

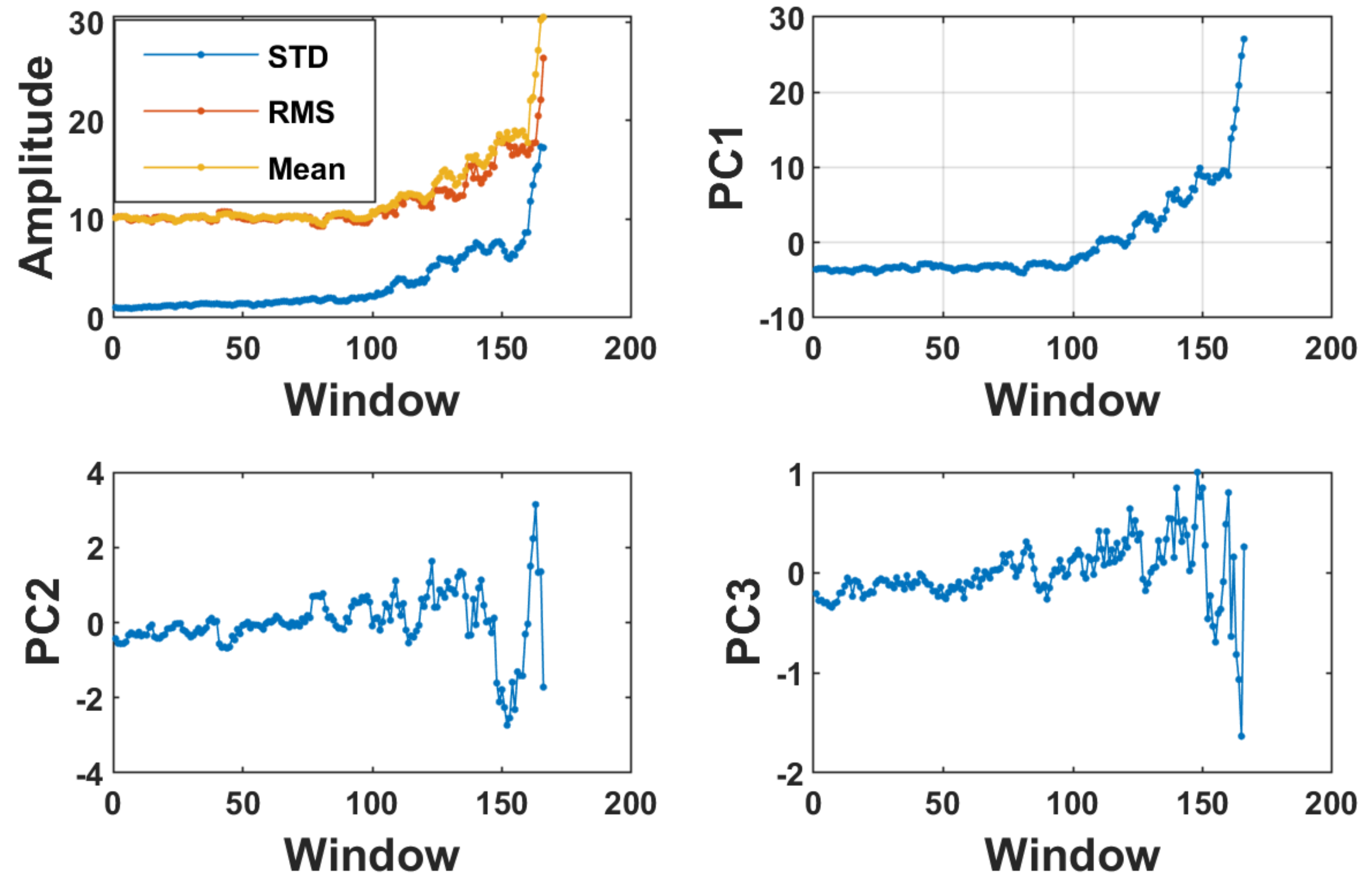
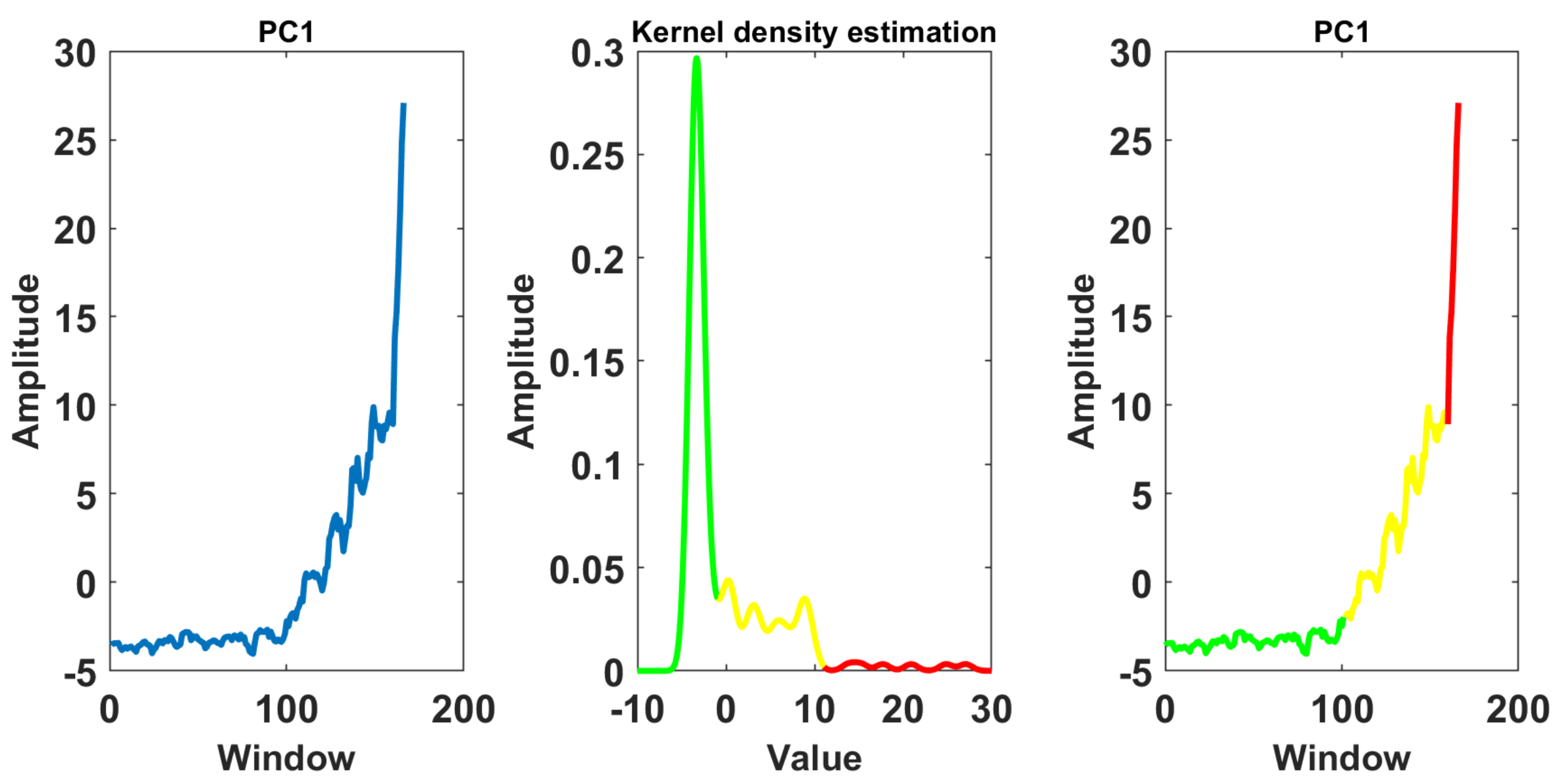



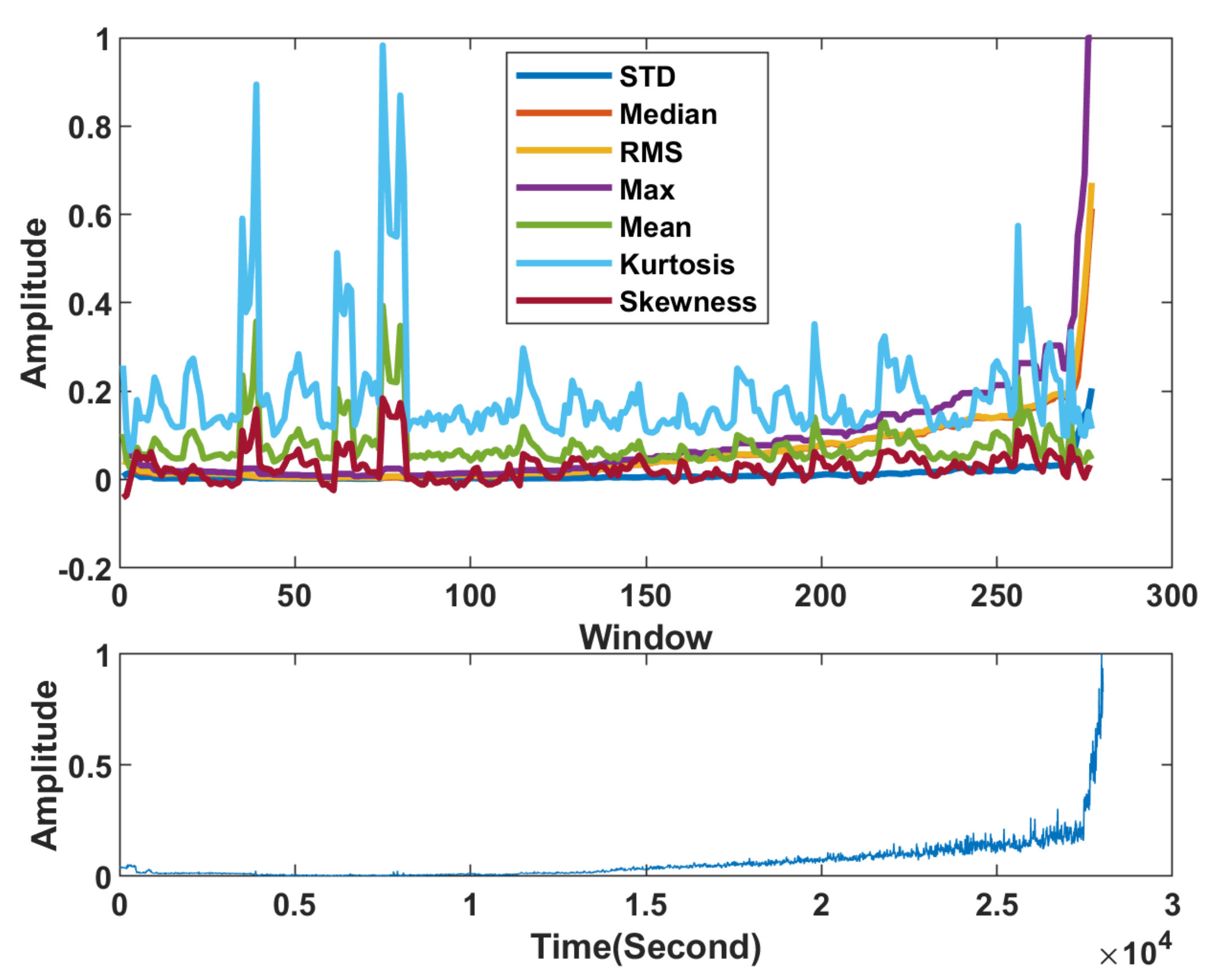
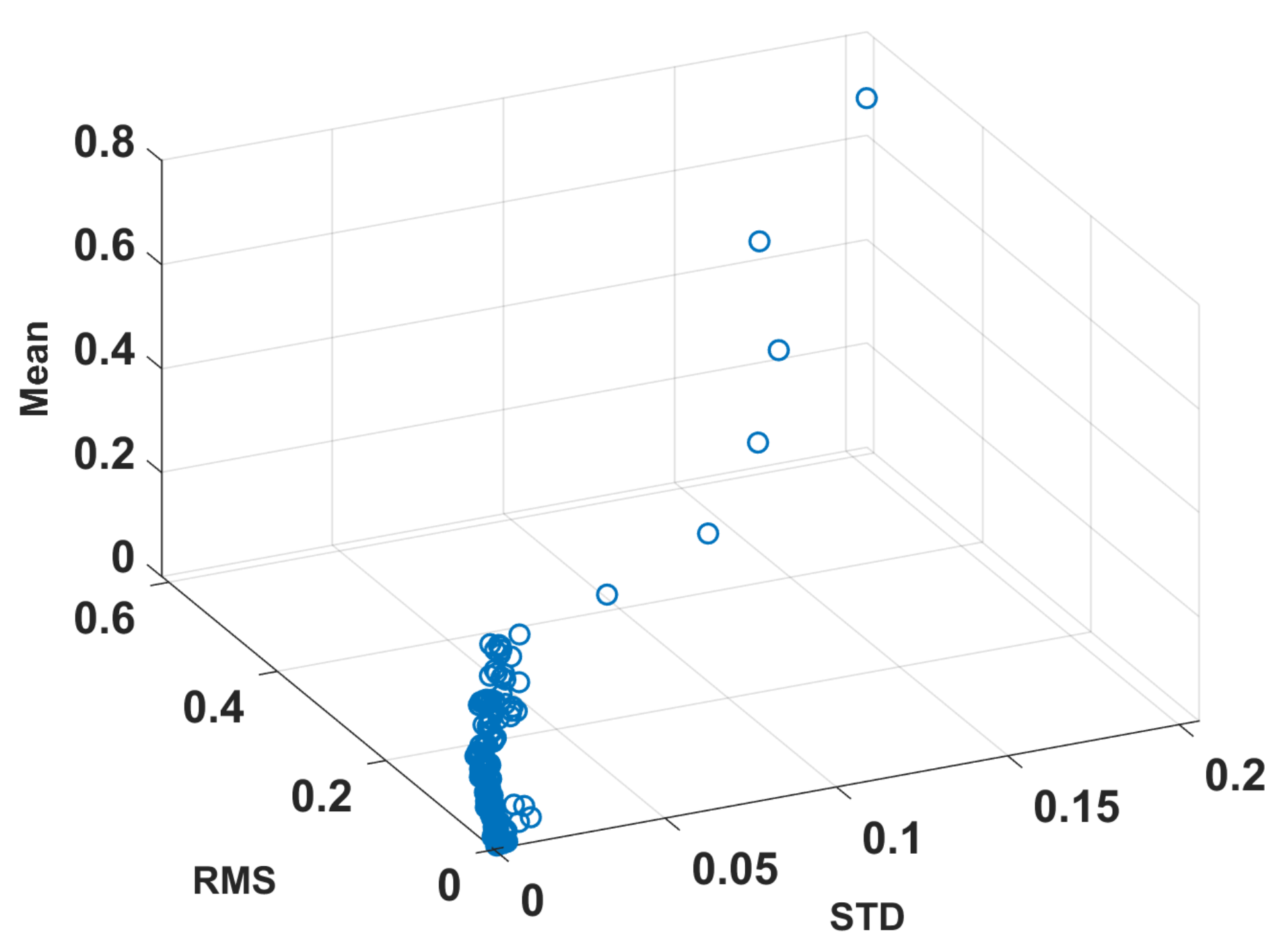
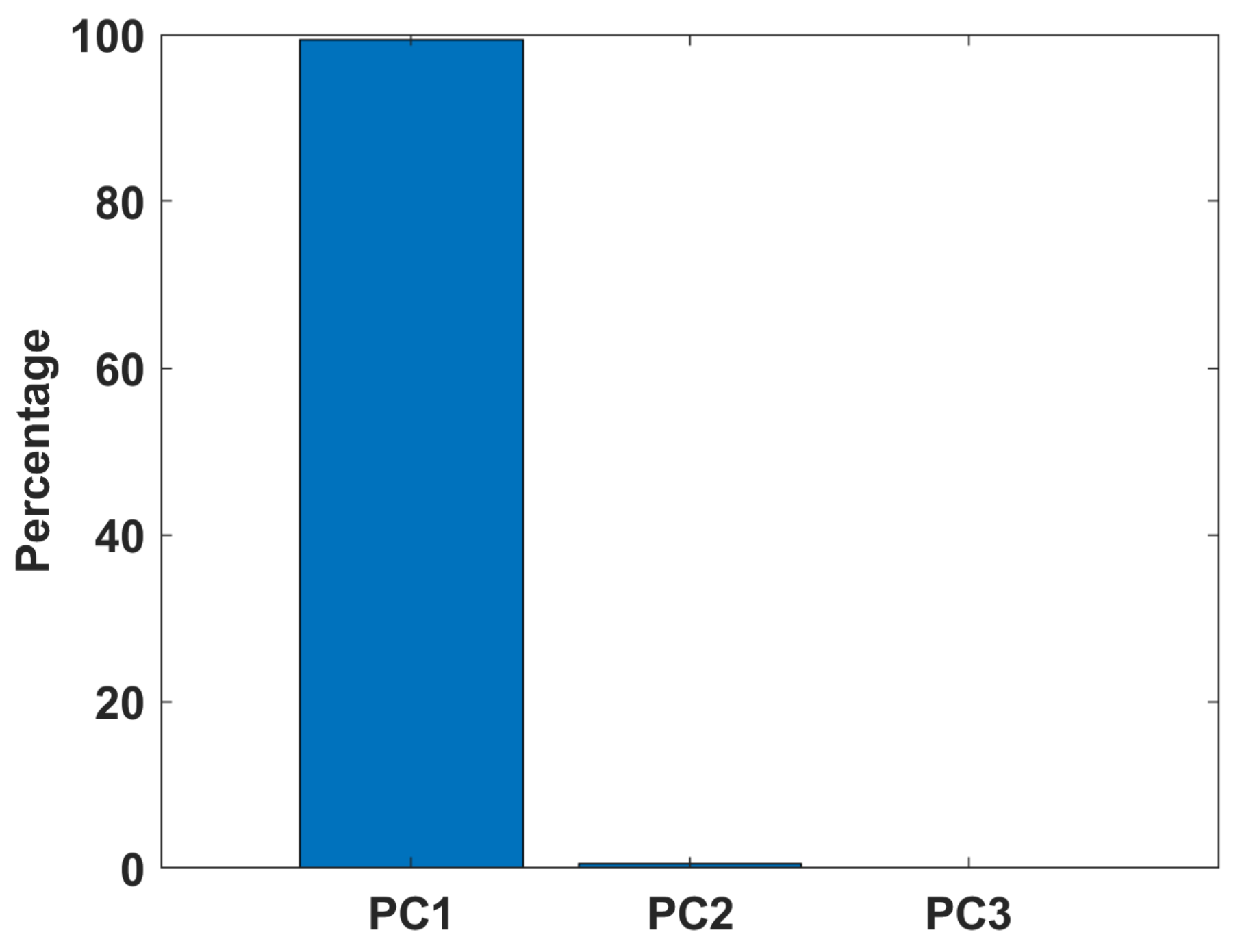
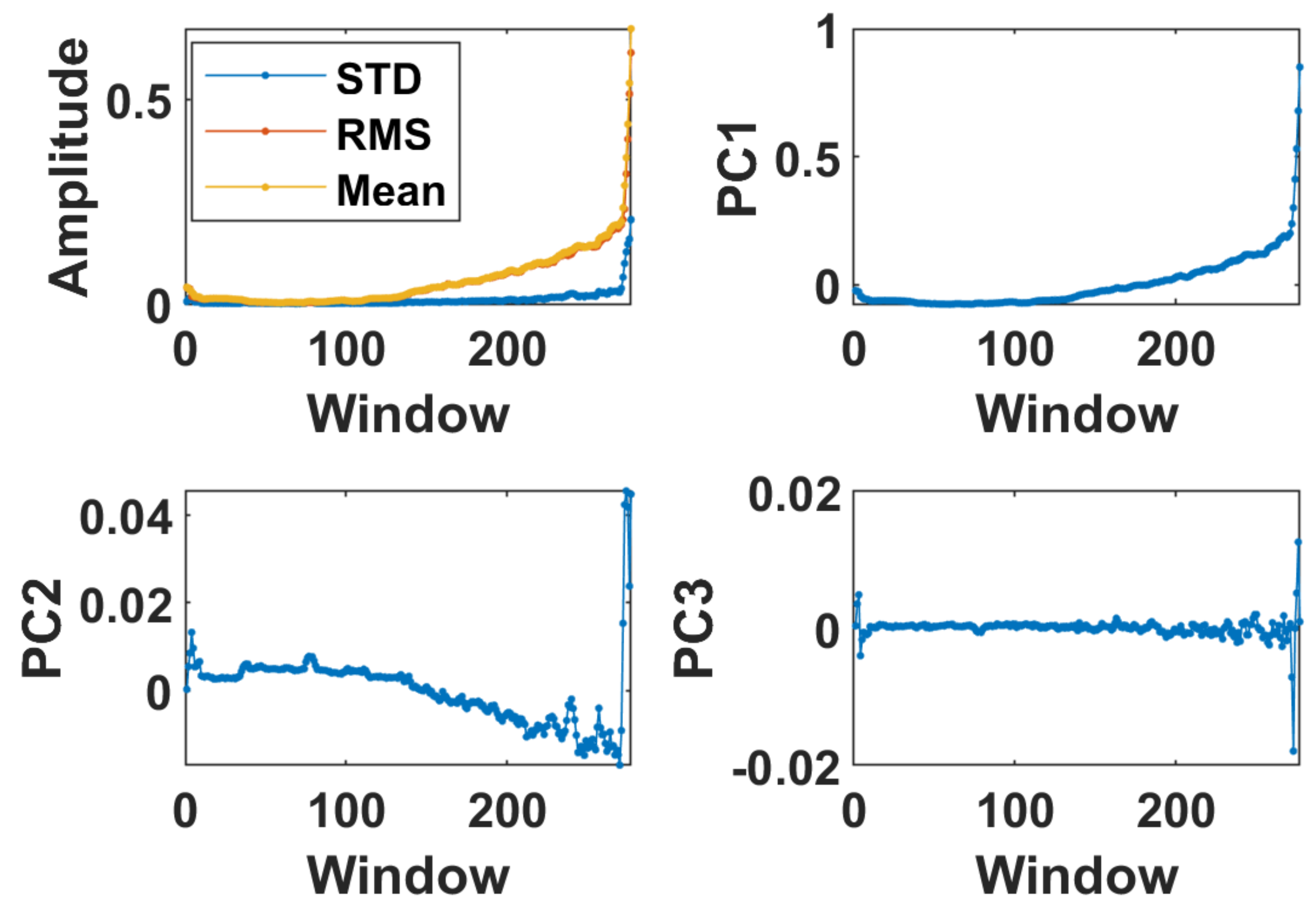
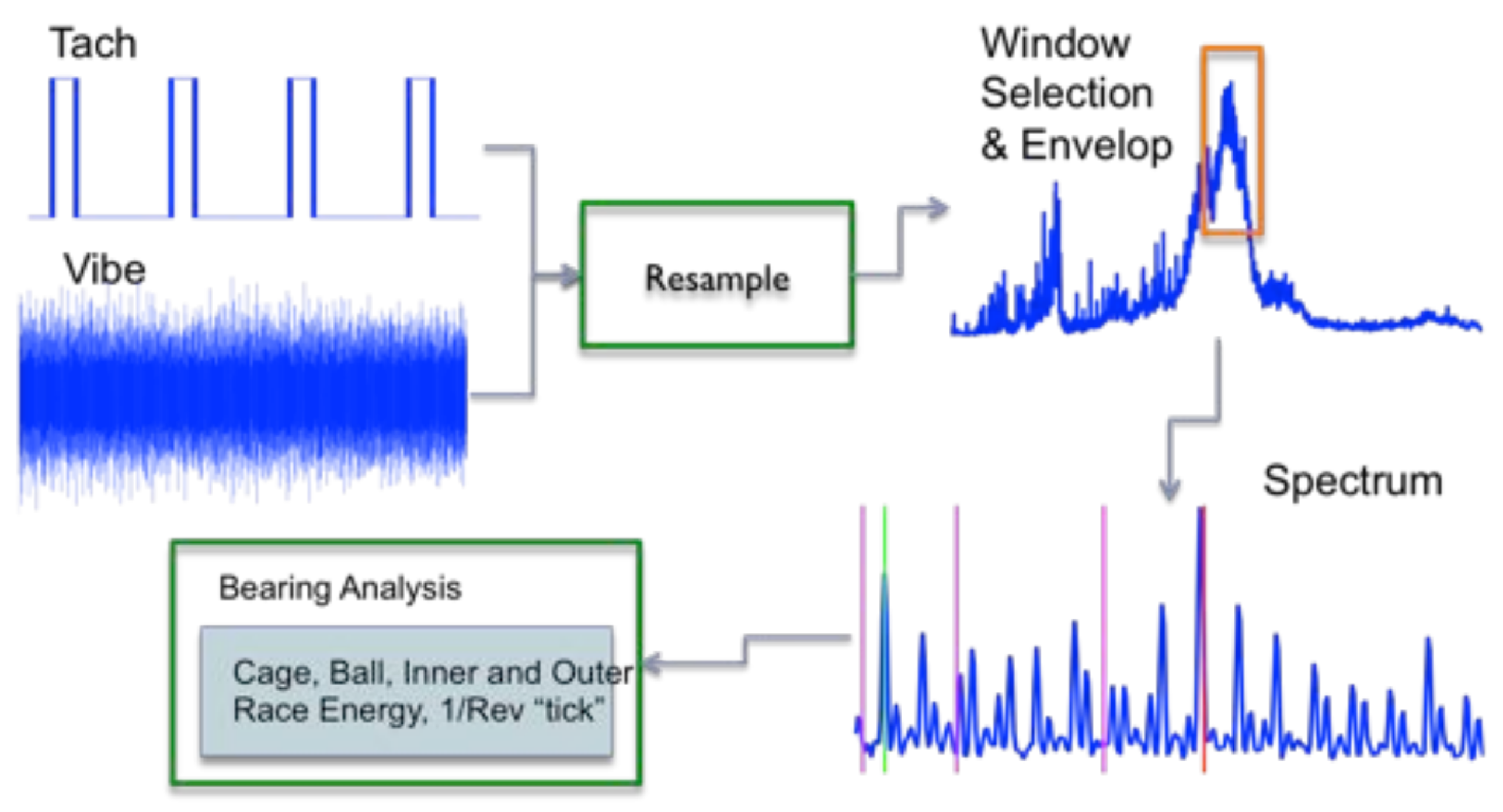
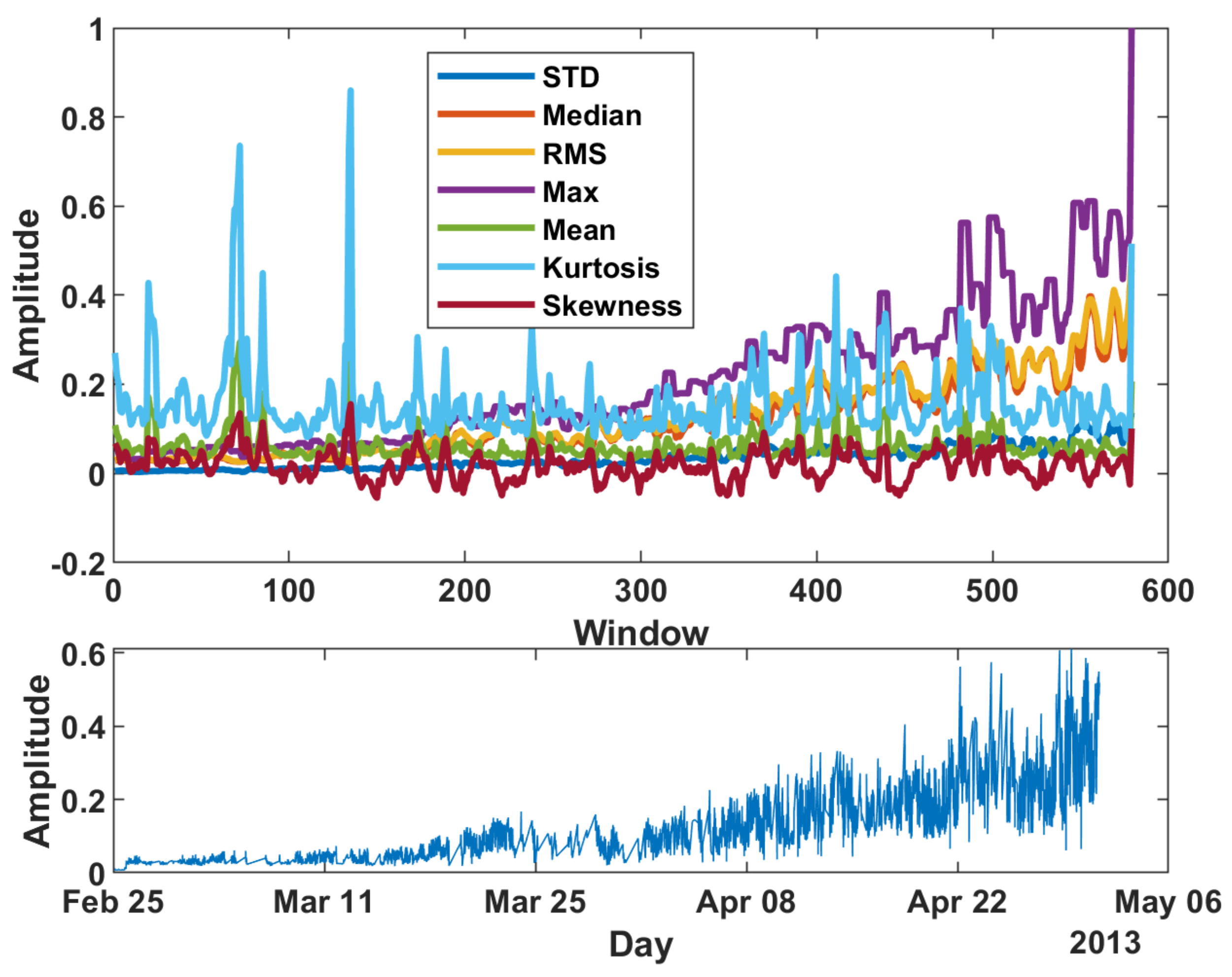

| Feature | Formula |
|---|---|
| Max value | M = max() |
| Sample median | |
| Sample mean value | |
| Sample standard deviation (STD) | |
| Sample kurtosis | |
| Sample skewness | |
| root mean square |
| Algorithm | 1st Point | 2nd Point |
|---|---|---|
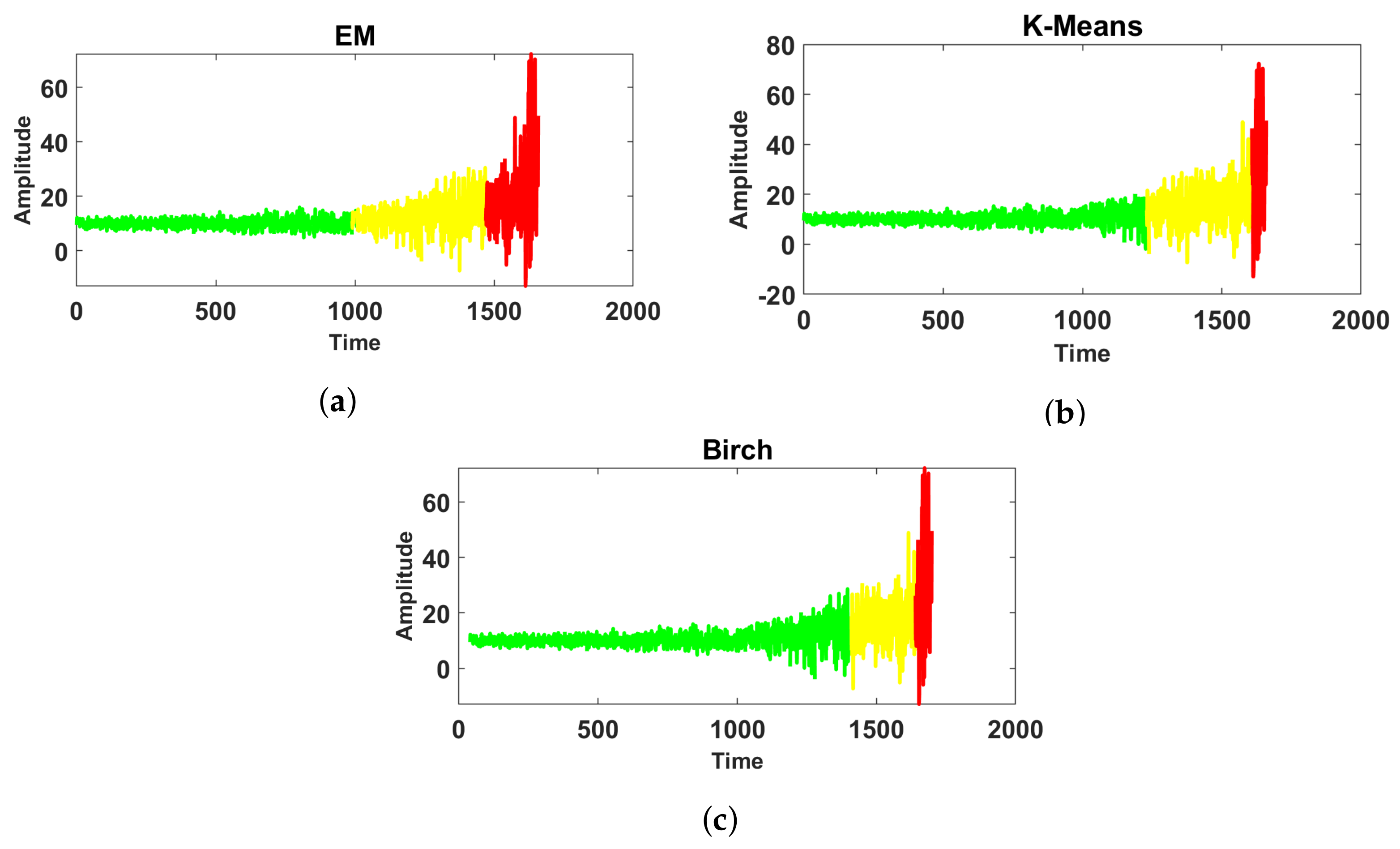
| EM | 998 | 1500 |
| K-Means | 1240 | 1570 |
| BIRCH | 1390 | 1580 |
| Algorithm | 1st Point | 2nd Point |
|---|---|---|
| EM | 1050 | 1610 |
| K-Means | 1240 | 1590 |
| BIRCH | 1252 | 1592 |
| Algorithm | 1st Point | 2nd Point |
|---|---|---|
| EM | 13,170 | 27,120 |
| K-Means | 19,780 | 27,400 |
| BIRCH | 20,200 | 27,800 |
| Algorithm | 1st Point | 2nd Point |
|---|---|---|
| EM | Undefine | Undefine |
| K-Means | Undefine | Undefine |
| BIRCH | Undefine | Undefine |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moosavi, F.; Shiri, H.; Wodecki, J.; Wyłomańska, A.; Zimroz, R. Application of Machine Learning Tools for Long-Term Diagnostic Feature Data Segmentation. Appl. Sci. 2022, 12, 6766. https://doi.org/10.3390/app12136766
Moosavi F, Shiri H, Wodecki J, Wyłomańska A, Zimroz R. Application of Machine Learning Tools for Long-Term Diagnostic Feature Data Segmentation. Applied Sciences. 2022; 12(13):6766. https://doi.org/10.3390/app12136766
Chicago/Turabian StyleMoosavi, Forough, Hamid Shiri, Jacek Wodecki, Agnieszka Wyłomańska, and Radoslaw Zimroz. 2022. "Application of Machine Learning Tools for Long-Term Diagnostic Feature Data Segmentation" Applied Sciences 12, no. 13: 6766. https://doi.org/10.3390/app12136766
APA StyleMoosavi, F., Shiri, H., Wodecki, J., Wyłomańska, A., & Zimroz, R. (2022). Application of Machine Learning Tools for Long-Term Diagnostic Feature Data Segmentation. Applied Sciences, 12(13), 6766. https://doi.org/10.3390/app12136766








