Mechanical Test of Sleeve Grouted Lapping Connectors under Uniaxial Tension and High-Stress Repeated Tension and Compression Loading
Abstract
:Featured Application
Abstract
1. Introduction
2. Experimental Program
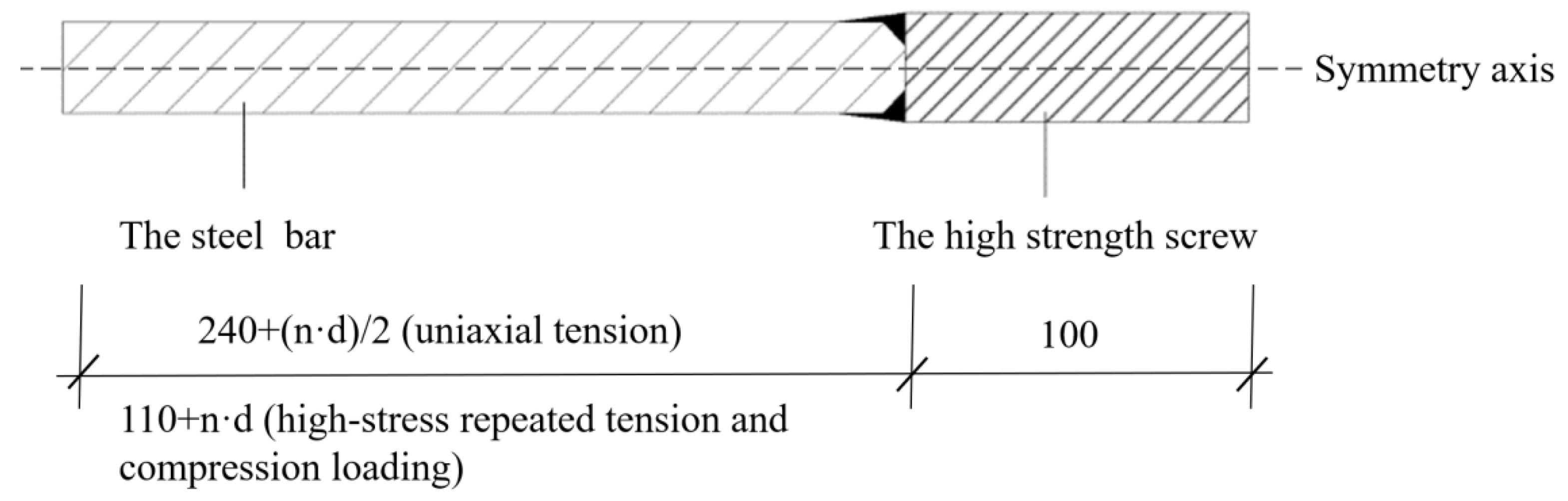
2.1. Design and Production of APC Connector Specimens
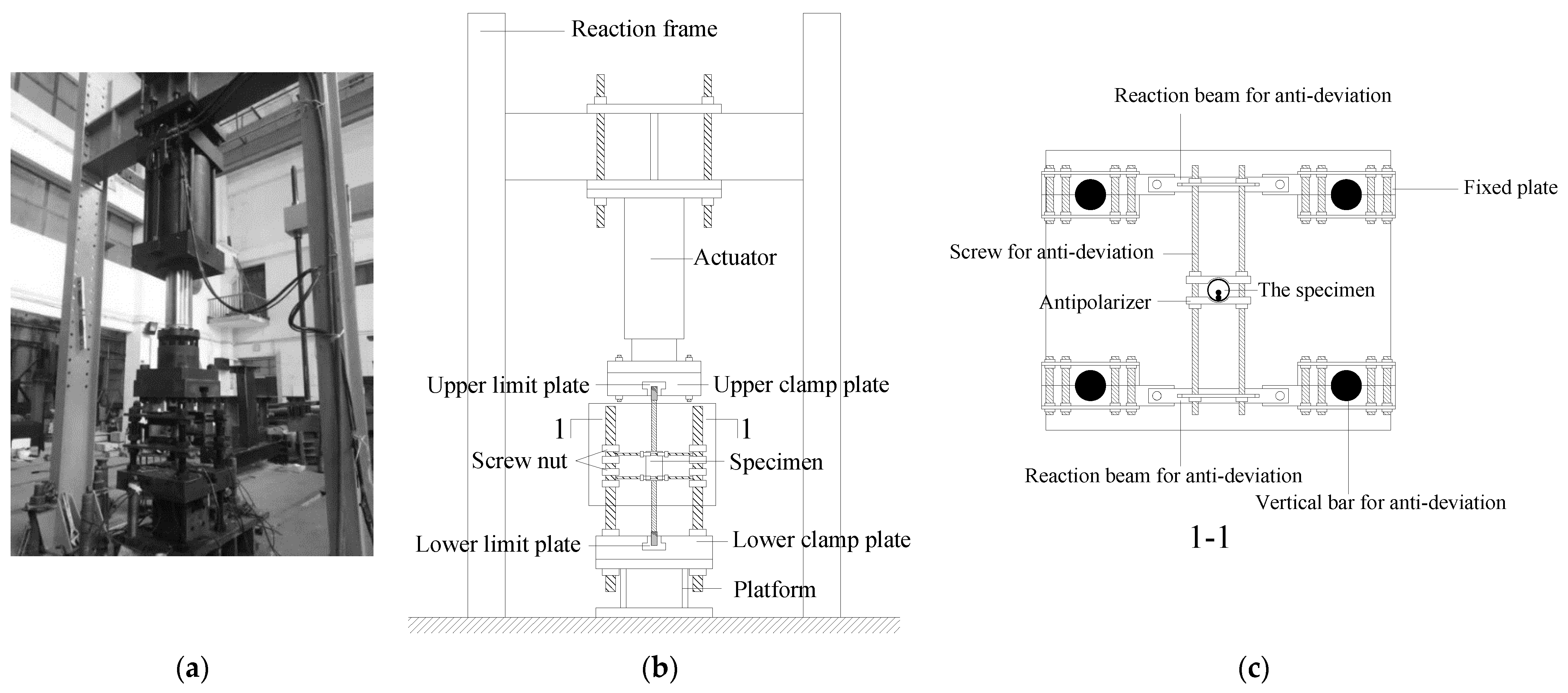
2.2. Material Properties and Experimental Setup
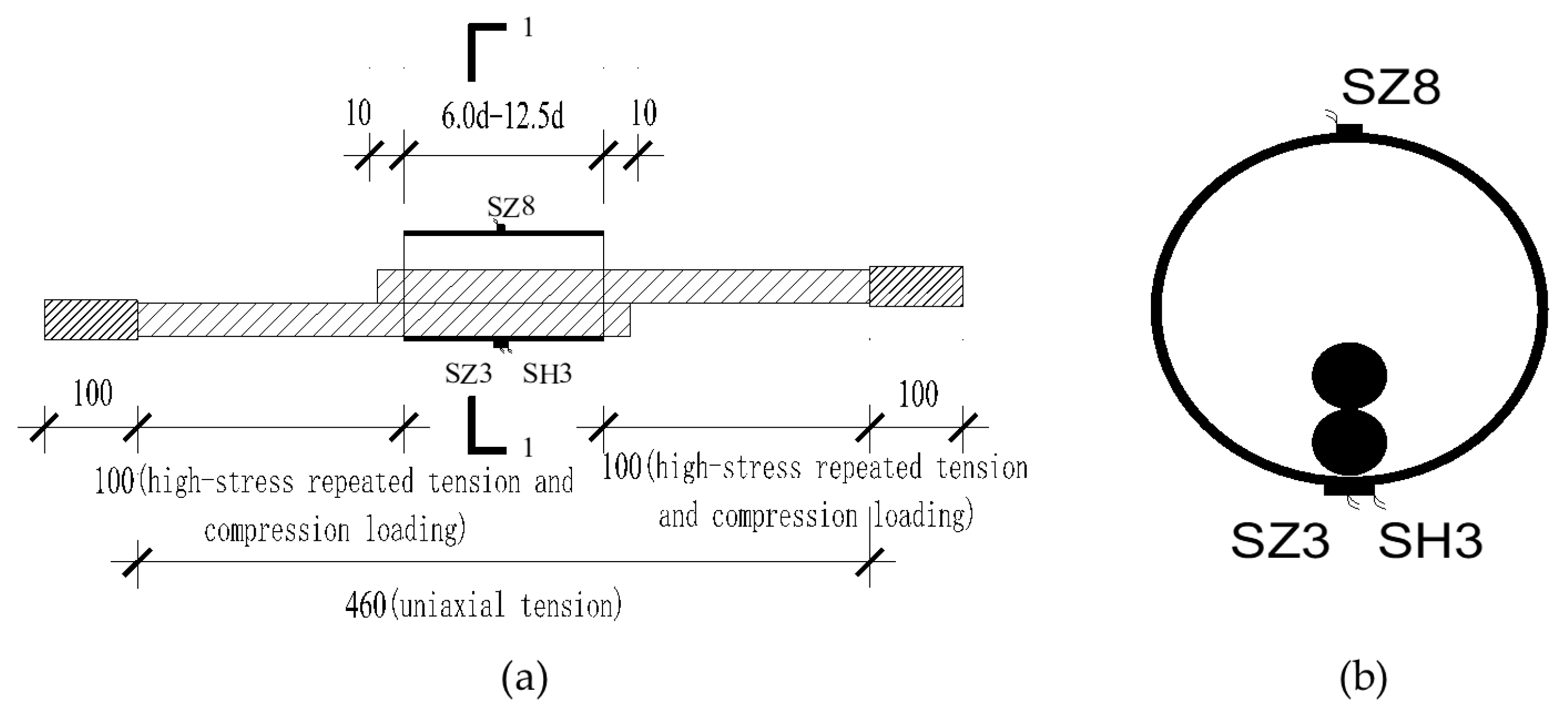
2.3. Scheme and Measurement of the Specimen
3. Experimental Results and Failure Modes
4. Mechanical Properties
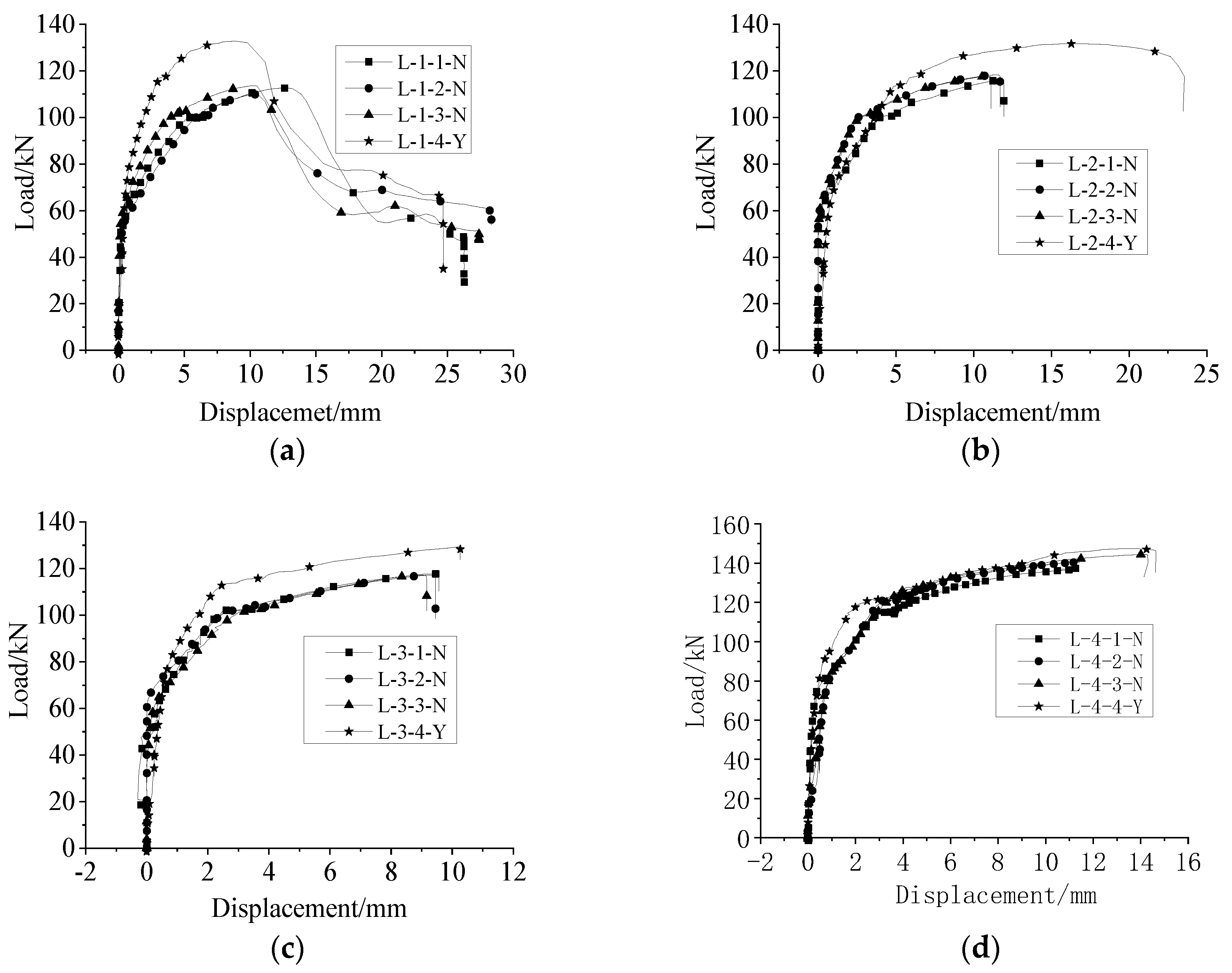
4.1. Load–Displacement Curves
4.1.1. Uniaxial Tension
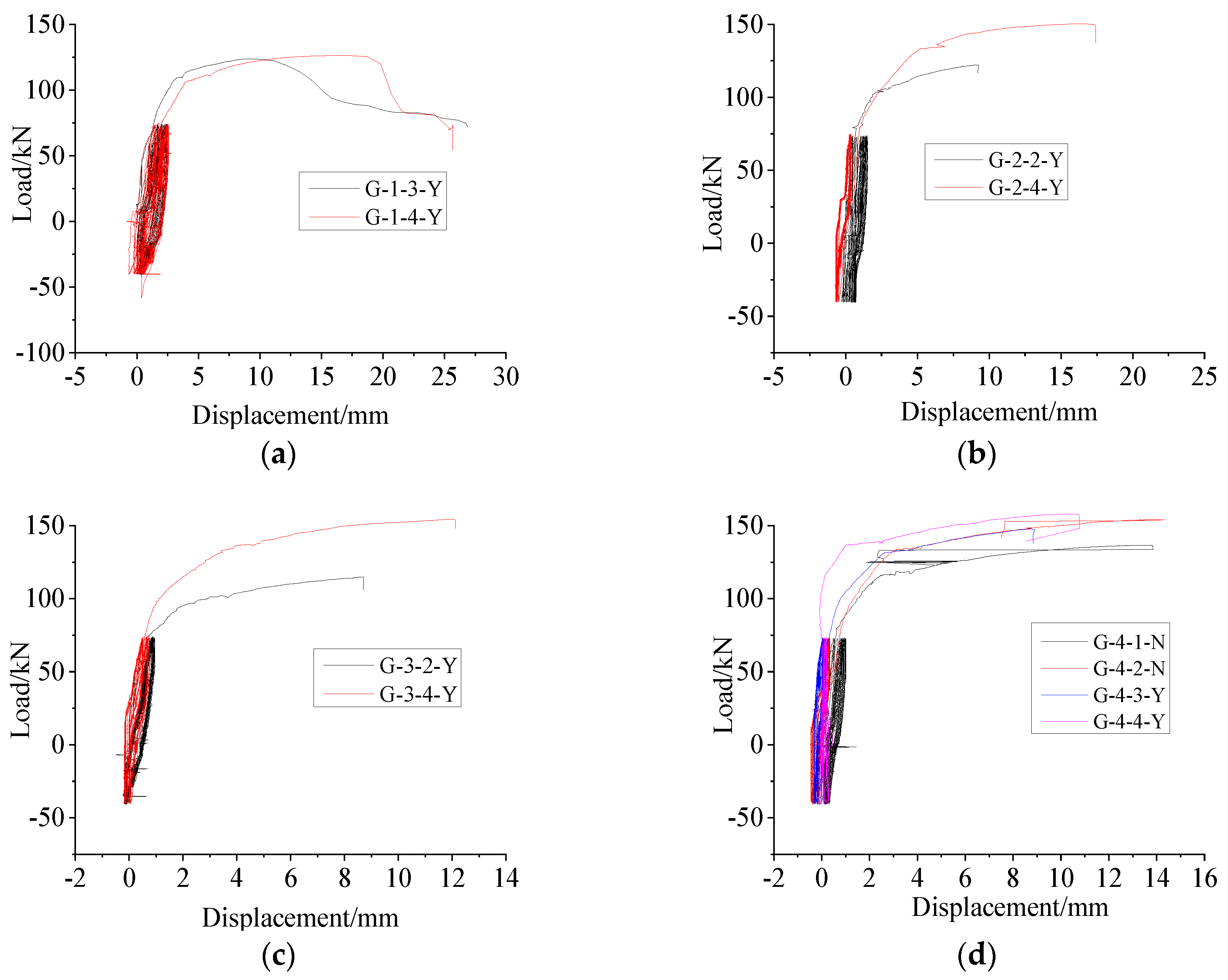
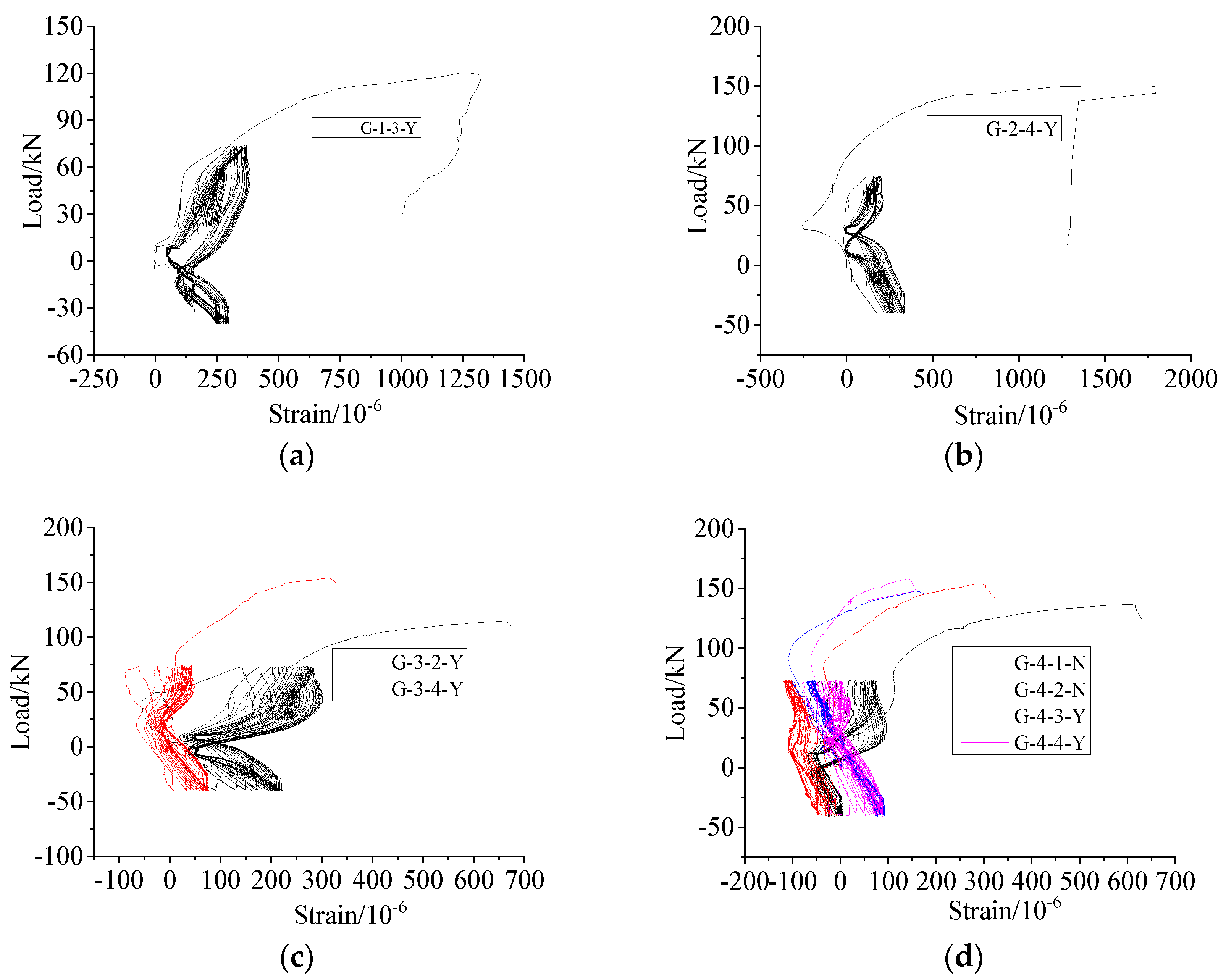
4.1.2. High-Stress Repeated Tension and Compression
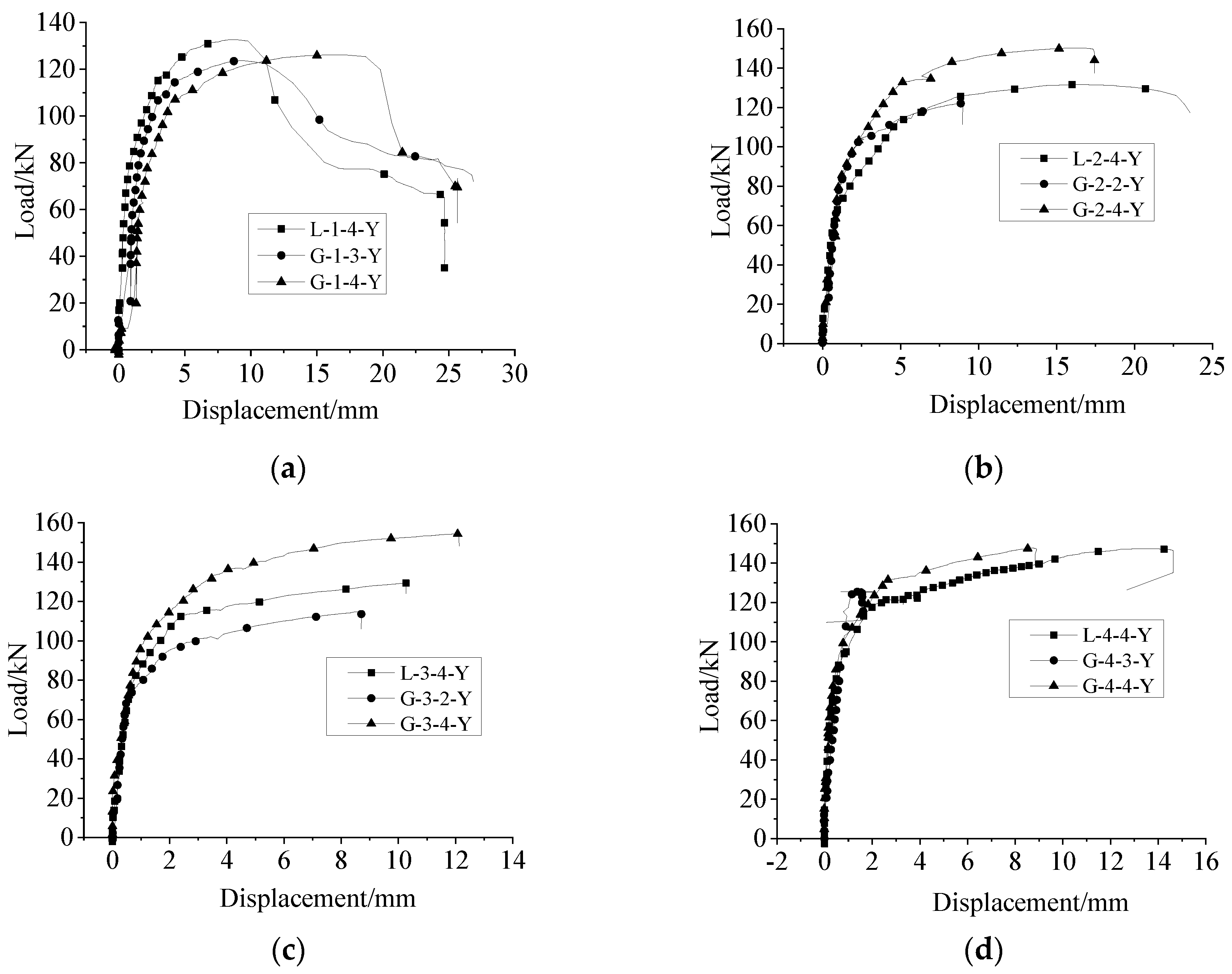
4.1.3. Comparison between Uniaxial Tension and Repeated Tension and Compression Loading
4.2. Bearing Capacity
4.3. Ductility and Residual Deformation
4.3.1. Ductility
4.3.2. Residual Deformation
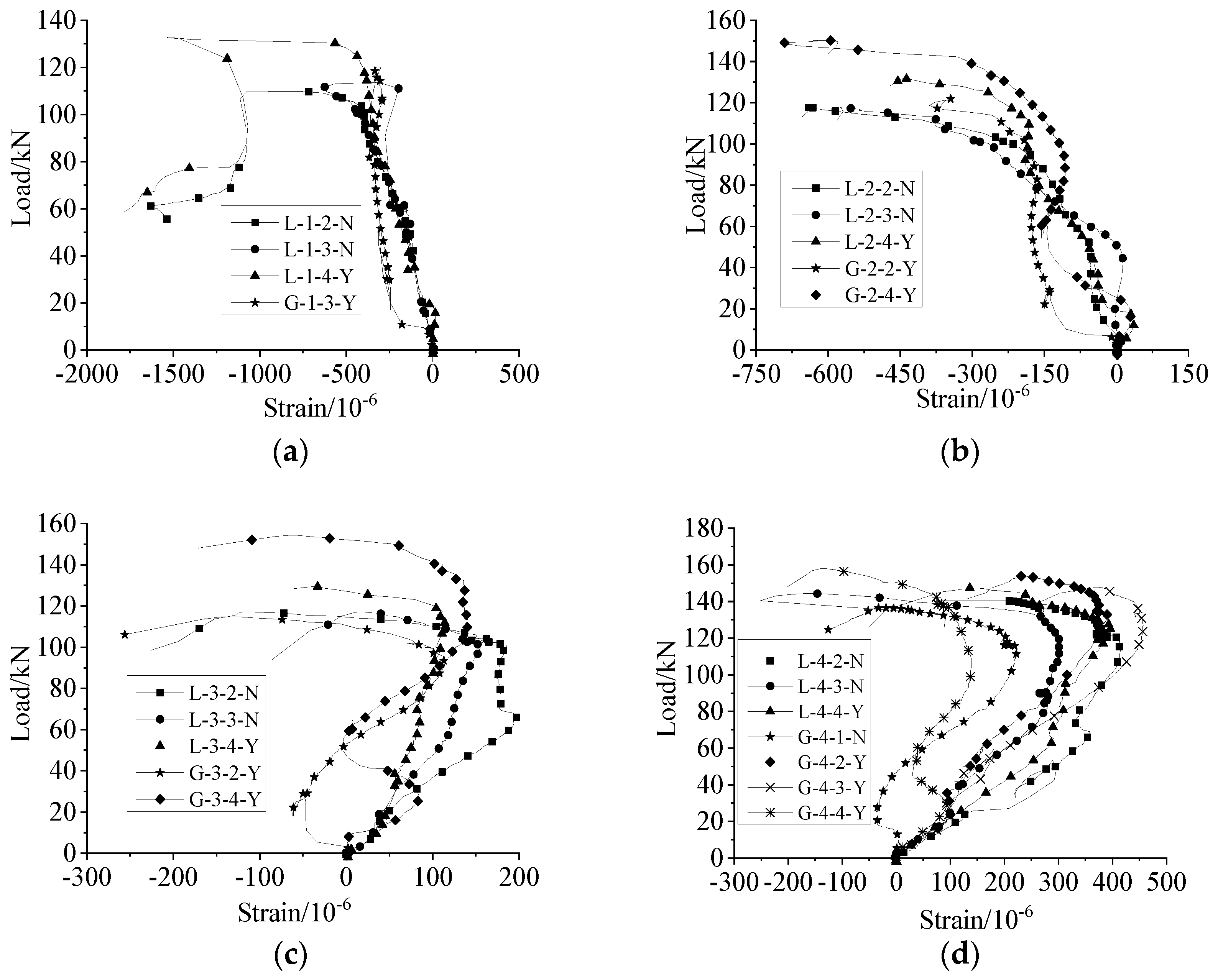
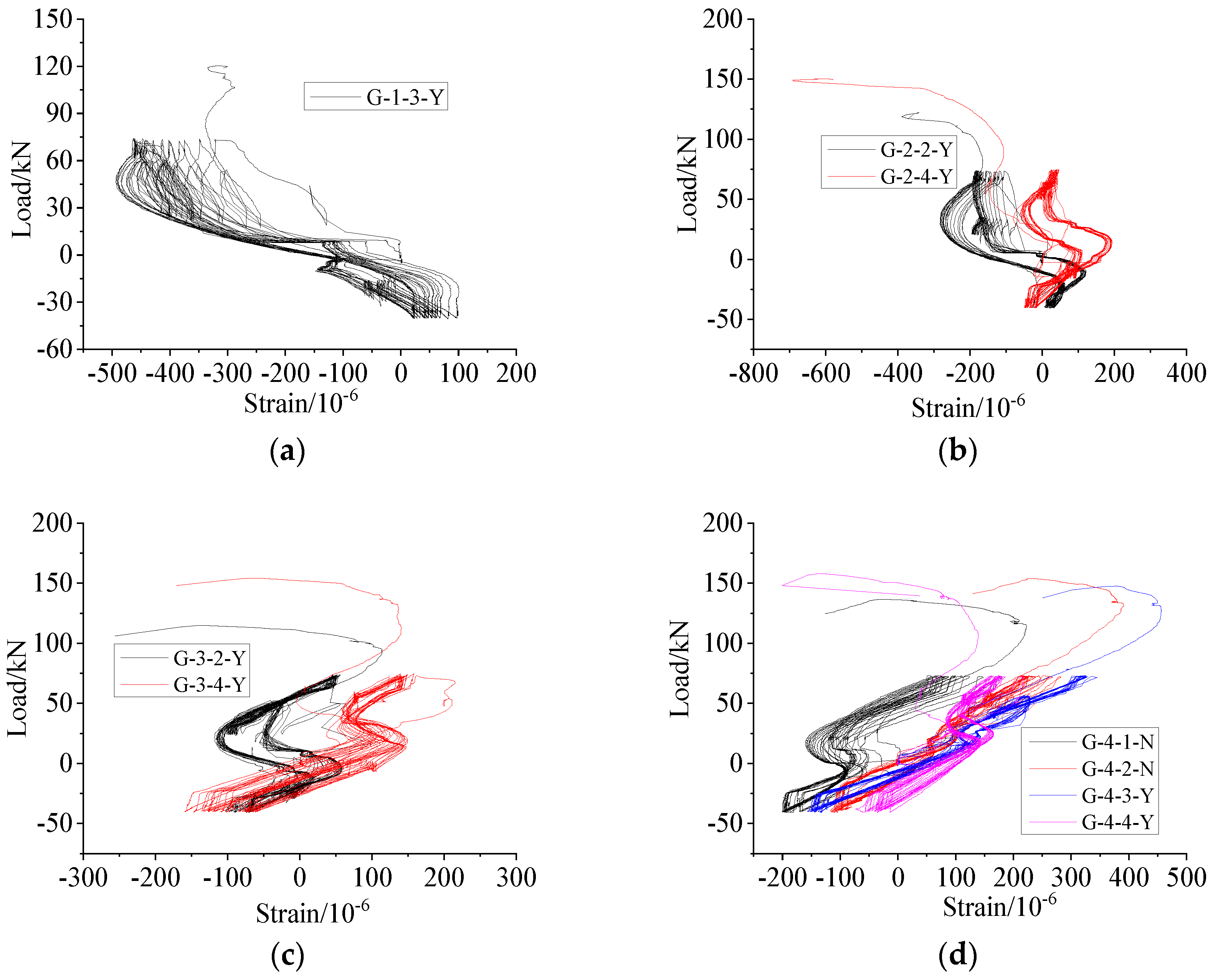
4.4. Longitudinal and Hoop Stress Distributions of Sleeve
4.4.1. Longitudinal and Hoop Strain Curves for the Middle Section of the Sleeve near Steel Bar under Uniaxial Tension and Repeated Tension and Compression (Only Final Tension Process) Loading
4.4.2. Longitudinal and Hoop Strain Curves of the Middle Section of the Sleeve near Steel Bar Side under High-Stress Repeated Tension and Compression Loading
5. Mechanical Mechanism of the Connector
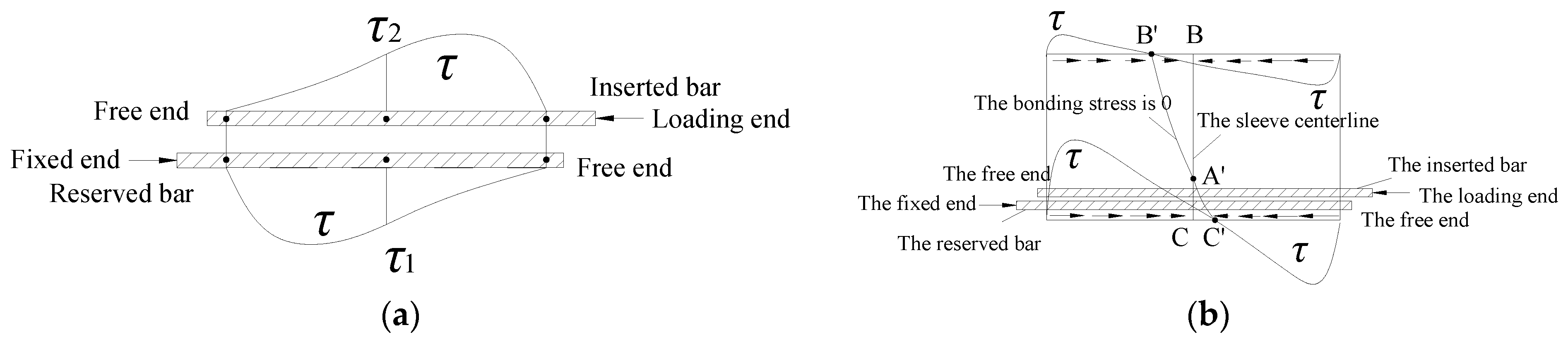
5.1. Stress Analysis of Connection under Tension
5.2. Stress Analysis of Connection under Compression
6. Calculation of Bonding Strength and Critical Lapping Length
6.1. Grey Correlation Analysis of Bonding Factors
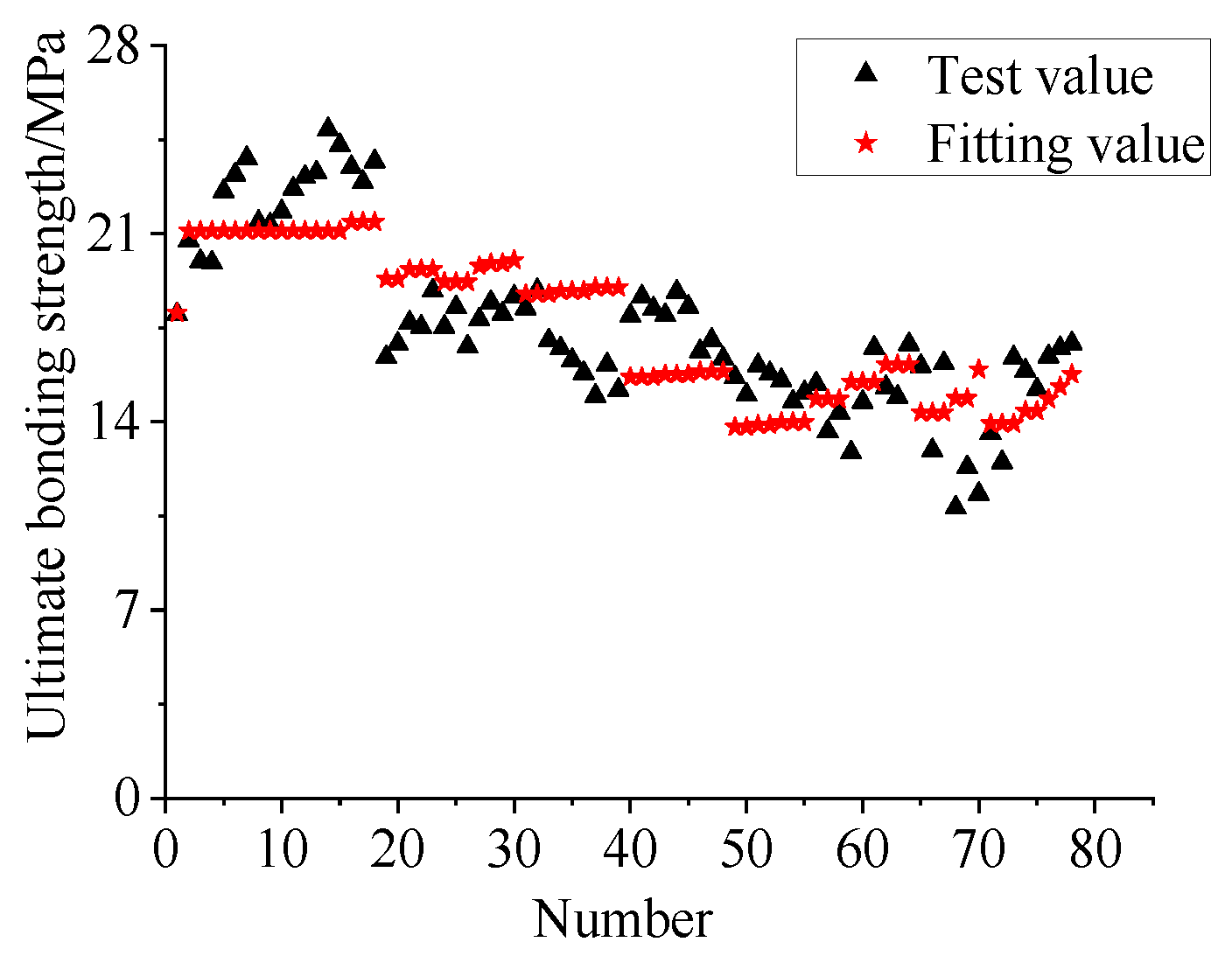
6.2. Calculation of Ultimate Bonding Stress Considering the Influence of Defects
6.3. Critical Lapping Length Considering Grouting Defect
7. Conclusions
- There were two failure modes of the APC connector specimens under uniaxial tension: steel bar tensile failure and steel bar pull out. There were three failure modes of the specimens under high-stress repeated tension and compression: steel bar tensile failure, steel bar pull out, and steel bar bending.
- The bearing capacity of specimens was strengthened after repeated high-stress tension and compression, so the ultimate bearing capacity increased compared with specimens under uniaxial tension. Because of anti-deflection measures, the bearing capacities of specimens without anti-deflection measures were lower than those of specimens with anti-deflection measures.
- When the connector was broken via the steel bar being pulled out under uniaxial tension, the effects of the lapping length and anti-deflection measures on the ductility of the specimens were not evident under repeated tension and compression. As the steel bar was hardened and the cracks of the grout were fully developed under repeated tension and compression loading, the yield displacement of the specimens increased, and the ductility of the specimens was less than that of the specimens under uniaxial tension.
- The values of the residual deformation u0 and u20 decreased with the increase in the lapping length. The stiffness values before yielding of the specimens with anti-deflection measures were higher than those without anti-deflection measures, whereas the values of the residual deformation u0 and u20 were lower.
- Under uniaxial tension and repeated tension and compression (only the final tension process) loading, the longitudinal compressive strain, and the hoop tensile strain near the steel bar side of the middle section of the sleeve decreased with the increase in the lapping length of the sleeve under the ultimate load. After repeated tension and compression loading, the longitudinal strain in the middle of the sleeve changed from compression to tension under tension and from tension to compression under compression with the increase in the lapping length.
- When the lapping length was small, the sleeve was subjected to longitudinal compression in the early stage and tension in the late stage, which agreed with the test results. The distribution of the bonding stress of the steel bar and the sleeve changed with the increase in the lapping length, which needs further research.
- The correlation between the variables and the bonding strength of the APC connector was analysed by using Grey correlation analysis. It was found that the correlation between the simplified steel content t/D and the ultimate bonding strength was the greatest. Formulas for the ultimate bonding strength and the critical lapping length for the steel bar fracture were proposed considering the grouting defect coefficient ω. The theoretical calculation results agreed well with the test results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Yee, A.A. Structural and Economic Benefits of Precast/Prestressed Concrete Construction. PCI J. 2001, 46, 34–42. [Google Scholar] [CrossRef]
- Holden, T.; Restrepo, J.; Mander, J.B. Seismic Performance of Precast Reinforced and Prestressed Concrete Walls. J. Struct. Eng. 2003, 129, 286–296. [Google Scholar] [CrossRef]
- Alias, A.; Sapawi, F.; Kusbiantoro, A.; Zubir, M.A.; Rahman, A.B.A. Performance of grouted splice sleeve connector under tensile load. J. Mech. Eng. Sci. 2014, 7, 1094–1102. [Google Scholar] [CrossRef]
- Ameli, M.J.; Pantelides, C.P. Seismic analysis of precast concrete bridge columns connected with grouted splice sleeve connectors. J. Struct. Eng. 2017, 143, 04016176. [Google Scholar] [CrossRef]
- Rahman, A.B.A.; Yoon, L.H.; Ibrahim, I.S.; Mohamed, R.N.; Mohammad, S.; Saim, A.A. Performance of grouted splice sleeves with tapered bars under axial tension. Appl. Mech. Mater. 2015, 4113, 1176–1180. Available online: https://www.scientific.net/AMM.789-790.1176 (accessed on 30 April 2022).
- Sayadi, A.A.; Rahman, A.B.A.; Jumaat, M.Z.B.; Alengaram, U.J.; Ahmad, S. The relationship between interlocking mechanism and bond strength in elastic and inelastic segment of splice sleeve. Constr. Build. Mater. 2014, 55, 227–237. [Google Scholar] [CrossRef]
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S. Feasibility study of grouted splice connector under tensile load. Constr. Build. Mater. 2014, 50, 530–539. [Google Scholar] [CrossRef]
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S.; Hamid, Z.A. Behaviour of grouted pipe splice under incremental tensile load. Constr. Build. Mater. 2012, 33, 90–98. [Google Scholar] [CrossRef]
- Alias, A.; Zubir, M.A.; Shahid, K.A.; Rahman, A.B.A. Structural Performance of Grouted Sleeve Connectors with and without Transverse Reinforcement for Precast Concrete Structure. Procedia Eng. 2013, 53, 116–123. [Google Scholar] [CrossRef] [Green Version]
- Ling, J.H.; Rahman, A.B.A.; Ibrahim, I.S.; Hamid, Z.A. Tensile capacity of grouted splice sleeves. Eng. Struct. 2016, 111, 285–296. [Google Scholar] [CrossRef]
- Henin, E.; Morcous, G. Non-proprietary bar splice sleeve for precast concrete construction. Eng. Struct. 2015, 83, 154–162. [Google Scholar] [CrossRef]
- Li, F.R.; Abruzzese, D.; Milani, G.; Li, S.C. Influence of internal defects of semi grouted sleeve connections on the seismic performance of precast monolithic concrete columns. J. Build. Eng. 2022, 49, 104009. [Google Scholar] [CrossRef]
- Belleri, A.; Riva, P. Seismic performance and retrofit of precast concrete grouted sleeve connections. PCI J. 2012, 57, 97–109. [Google Scholar] [CrossRef]
- Yuan, H.; Zhu, Z.G.; Naito, C.J.; Yi, W.J. Tensile behavior of half grouted sleeve connections: Experimental study and analytical modeling. Constr. Build. Mater. 2017, 152, 96–104. [Google Scholar] [CrossRef]
- Dai, Z.Q.; Pang, S.D.; Liew, J.Y.R. Axial load resistance of grouted sleeve connection for modular construction. Thin-Walled Struct. 2020, 154, 106883. [Google Scholar] [CrossRef]
- Espoir, K.K.; Xie, F.Z.; Geng, H.J. Grouted Sleeve Connection for Precast Concrete Members. Civ. Eng. J. 2020, 30, 435–447. [Google Scholar] [CrossRef]
- Zheng, G.Y.; Kuang, Z.P.; Xiao, J.Z.; Pan, Z.F. Mechanical performance for defective and repaired grouted sleeve connections under uniaxial and cyclic loadings. Constr. Build. Mater. 2020, 233, 117233. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.H.; Zhu, Q.H. Experimental study on mechanical properties of reinforcement sleeving grouting joint. J. N. China Inst. Sci. Technol. 2018, 15, 80–86. [Google Scholar] [CrossRef]
- Xu, C.S.; Liu, H.T.; Du, X.L. Experimental study on connection performance of reinforced sleeve grouting under repeated tension and compression under high stress. J. Build. Struct. 2018, 39, 178–184+193. [Google Scholar] [CrossRef]
- Zhao, X.L.; Grundy, P.; Lee, Y.T. Grout sleeve connections under large deformation cyclic loading. In Proceedings of the Twelfth International Offshore and Polar Engineering Conference, Kyushu, Japan, 26–31 May 2002. [Google Scholar]
- Wang, T.; Yu, M.; Li, X.Y.; Yan, Z.G.; Saafi, M.; Ye, J.Q. Experimental investigation on the post-fire cyclic behavior of grouted sleeve connections. Constr. Build. Mater. 2021, 279, 122394. [Google Scholar] [CrossRef]
- Yu, Q. A New Confined Lapping Sleeve. C.N. Patent 201420656653.0, 1 April 2015. [Google Scholar]
- Yu, Q.; Zhang, L.; Tang, P.Y.; Li, L.Z.; Zhang, X.K.; Fan, B.X.; Zhang, Z.; Chen, Z.H. Experimental Study and In-depth Tensile Mechanism Analysis of Grouted Sleeve Lapping Conectors. Lat. Am. J. Solids Struct. 2022, 19, e428. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.M.; Gong, X.; Bai, S.H.; Fan, B.X. Comparison of mechanical properties of reinforced sleeve grouting butt joint and lap joint. J. Harbin Inst. Technol. 2020, 52, 140–150. [Google Scholar] [CrossRef]
- Yu, Q.; Xu, X.J.; Yuan, W.H.; Xu, Z.Y.; Lv, X.L. Mechanical experimental study on sleeve binding slurry anchor lap joints with different lap lengths. J. Hunan Univ. 2017, 44, 82–91. [Google Scholar] [CrossRef]
- GB/T 17671-1999; Test Method for Strength of Cement Mortar. State Administration of Quality and Technical Supervision; China Standardization Press: Beijing, China, 1999. (In Chinese)
- GB50081-2002; Standard Test Method for Mechanical Properties of Ordinary Concrete. Ministry of Construction of the People’s Republic of China, China Architecture and Building Press: Beijing, China, 2003. (In Chinese)
- GB/T228.1-2010; Metallic Materials Tensile Test Part 1: Test Method at Room Temperature. National Standardization Committee of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, China Standard Press: Beijing, China, 2010. (In Chinese)
- Yu, Q. A Kind of Single Tensile and Reciprocating Tensile and Compression Loading Device for Reinforcement Slepe Grouting Lap Connection. C.N. Patent 202021155373.3, 26 February 2021. [Google Scholar]
- JGJ 107-2016. Technical Specification for Mechanical Joint of Reinforcement. Ministry of Housing and Urban-Rural Development, China Building Industry Press: Beijing, China, 2016. (In Chinese)
- ACI 318M-11. Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2011.
- Xu, Y.L. Experimental Study on Bonding Anchorage Performance of Deformed Reinforcement and Concrete. Ph.D. Thesis, Tsinghua University, Beijing, China, 1990. [Google Scholar]
- Xu, Y.L.; Shen, W.D.; Wang, H. An experimental study of bond-anchorage properties of bars in concrete. J. Build. Mater. Struct. 1994, 15, 26–37. [Google Scholar] [CrossRef]
- Zhou, X.W. Research and Application of Grey Relation Degree. Master’s Thesis, Jilin University, Changchun, China, 2007. [Google Scholar]
- Xu, K. Influence of Sleeve Section Size on Tensile Performance of Sleeve Lapping Connectors. Master’s Thesis, Tongji University, Shanghai, China, 2018. [Google Scholar]
- Shan, X.B. Experimental Study on Bonding Anchorage between Deformed Reinforcement and Self-compacting Concrete. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Yu, Q.; Xu, Z.Y.; Yuan, W.H.; Lv, X.L. Tensile test of sleeve grouting lap joint under the influence of two factors. J. Harbin Inst. Technol. 2016, 48, 34–42. [Google Scholar] [CrossRef]














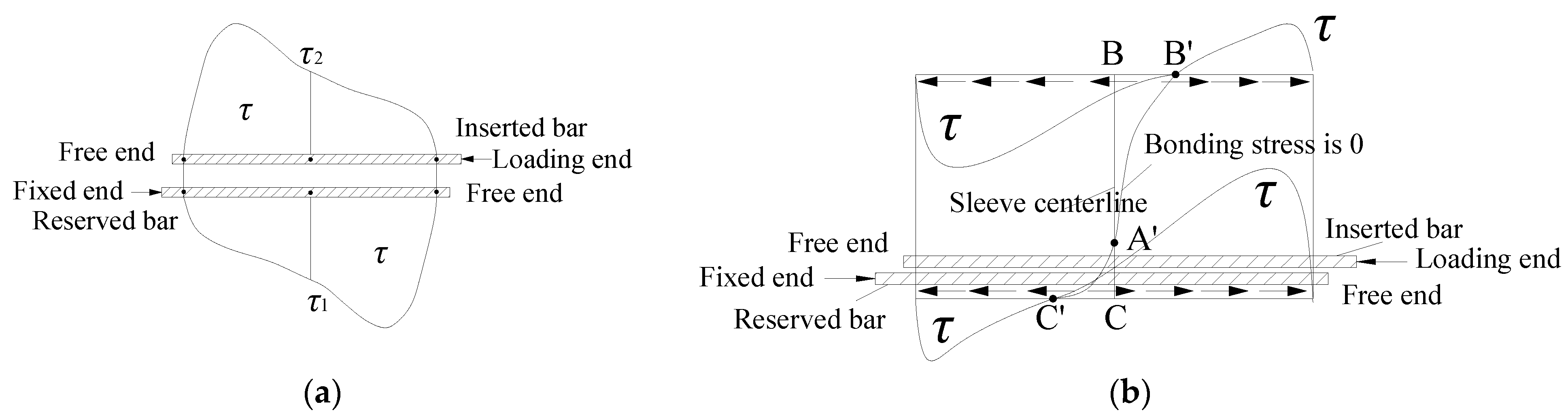
| Number | Cross-Sectional Area (mm2) | Yield Load (kN) | Ultimate Load (kN) | Yield Strength (MPa) | Average Yield Strength (MPa) | Ultimate Strength (MPa) | Average Ultimate Strength (MPa) |
|---|---|---|---|---|---|---|---|
| T-1 | 37.23 | 8.84 | 15.71 | 237.44 | 266.99 | 422.24 | 417.16 |
| T-2 | 38.62 | 10.57 | 14.55 | 273.69 | 376.75 | ||
| T-3 | 37.57 | 10.89 | 17.00 | 289.86 | 452.49 |
| Loading Method | Loading Scheme | Limit of Residual Deformation in Accordance with Grade-I Connection Standard (mm) |
|---|---|---|
| Uniaxial tension | 0 (measurement of residual deformation) → maximum tension (record of ultimate tensile strength)→ damaged (measurement of total elongation at maximum force) | bu0 ≤ 0.10 (d ≤ 32) |
| High-stress repeated tension and compression | cu20 ≤ 0.3 |
| Specimen | Failure Pattern | Lapping Length | Relative Lapping Length | Pub/kN | fyc/MPa | fud/MPa | Whether the Strength Meets the Requirements of [28] | Whether the Strength Meets the Requirements of [29] |
|---|---|---|---|---|---|---|---|---|
| L-1-1-N a | Steel bar pulled out at fixed end | 96 | 6.0 | 112.54 | 492.39 | 559.9 | N g | N |
| L-1-2-N | Steel bar pulled out at fixed end | 96 | 6.0 | 109.84 | 493.58 | 546.47 | N | N |
| L-1-3-N | Steel bar pulled out at fixed end | 96 | 6.0 | 113.54 | 485.97 | 564.88 | N | N |
| L-1-4-Y | Steel bar pulled out at loading end | 96 | 6.0 | 132.7 | 568.71 | 660.2 | Y f | Y |
| L-2-1-N | Steel bar tensile failure at weld at fixed end | 128 | 8.0 | 116.01 | 482.44 | 577.16 | Y | Y |
| L-2-2-N | Steel bar tensile failure at weld at fixed end | 128 | 8.0 | 118.29 | 489.65 | 588.51 | Y | Y |
| L-2-3-N | Steel bar tensile failure at weld at fixed end | 128 | 8.0 | 117.64 | 484.28 | 585.27 | Y | Y |
| L-2-4-Y | Steel bar tensile failure at sleeve end at loading end | 128 | 8.0 | 131.4 | 573.33 | 653.73 | Y | Y |
| L-3-1-N | Steel bar tensile failure at weld at fixed end | 160 | 10.0 | 117.67 | 493.58 | 585.42 | Y | Y |
| L-3-2-N | Steel bar tensile failure at weld at fixed end | 160 | 10.0 | 117.23 | 486.72 | 583.23 | Y | Y |
| L-3-3-N | Steel bar tensile failure at weld at fixed end | 160 | 10.0 | 117.13 | 489.85 | 582.74 | Y | Y |
| L-3-4-Y | Steel bar tensile failure at weld at loading end | 160 | 10.0 | 129.4 | 566.67 | 643.78 | Y | Y |
| L-4-1-N | Steel bar tensile failure at reinforcing base at fixed end | 200 | 12.5 | 138.2 | 576.12 | 687.56 | Y | Y |
| L-4-2-N | Steel bar tensile failure at weld at loading end | 200 | 12.5 | 140.7 | 599 | 700 | Y | Y |
| L-4-3-N | Steel bar tensile failure at weld at fixed end | 200 | 12.5 | 145.2 | 633.83 | 722.39 | Y | Y |
| L-4-4-Y | Steel bar tensile failure at weld at fixed end | 200 | 12.5 | 147.8 | 609.45 | 735.32 | Y | Y |
| G-1-1-N | Steel bar bending after repeated tension and compression for first cycle | 96 | 6.0 | —— e | —— | —— | —— | —— |
| G-1-2-Y | Steel bar bending after repeated tension and compression for first cycle | 96 | 6.0 | —— | —— | —— | —— | —— |
| G-1-3-Y | Steel bar pulled out at loading end | 96 | 6.0 | 123.7 | 535.47 | 615.42 | Y | Y |
| G-1-4-Y | Steel bar pulled out at loading end | 96 | 6.0 | 126.2 | 524.48 | 627.86 | Y | Y |
| G-2-1-N | Steel bar bending after repeated tension and compression for first cycle | 128 | 8.0 | —— | —— | —— | —— | —— |
| G-2-2-Y | Steel bar tensile failure at weld at loading end | 128 | 8.0 | 122.1 | 529 | 607.46 | Y | Y |
| G-2-3-Y | Steel bar tensile failure at weld at loading end (steel bar bending after repeated tension and compression for 14th cycle) | 128 | 8.0 | —— | —— | —— | —— | —— |
| G-2-4-Y | Steel bar tensile failure at weld at loading end | 128 | 8.0 | 150.3 | 643.88 | 747.76 | Y | Y |
| G-3-1-N | Steel bar bending after repeated tension and compression for first cycle | 160 | 10.0 | —— | —— | —— | —— | —— |
| G-3-2-Y | Steel bar tensile failure at weld at loading end | 160 | 10.0 | 114.8 | 481.19 | 571.14 | Y | Y |
| G-3-3-Y | Steel bar tensile failure at weld at fixed end (steel bar bending after repeated tension and compression for the 6th cycle, Anti-polarizer damaged) | 160 | 10.0 | —— | —— | —— | —— | —— |
| G-3-4-Y | Steel bar tensile failure at weld at loading end | 160 | 10.0 | 154.3 | 652.34 | 767.66 | Y | Y |
| G-4-1-N | Steel bar tensile failure at reinforcing base at loading end | 200 | 12.5 | 136.8 | 573.13 | 680.6 | Y | Y |
| G-4-2-N | Steel bar tensile failure at reinforcing base at loading end | 200 | 12.5 | 154.1 | 661.19 | 766.67 | Y | Y |
| G-4-3-Y | Steel bar tensile failure at reinforcing base at loading end | 200 | 12.5 | 147.8 | 683.58 | 735.32 | Y | Y |
| G-4-4-Y | Steel bar tensile failure at weld at loading end | 200 | 12.5 | 157.3 | 658.21 | 782.59 | Y | Y |
| Specimen | Asgt | u0/u20 (mm) | Whether the Residual Deformation Met the Requirements of [30] | |
|---|---|---|---|---|
| L-1-1-N | —— | 0.22 | N c | —— |
| L-1-2-N | —— | 0.33 | N | —— |
| L-1-3-N | —— | 0.52 | N | —— |
| L-1-4-Y | —— | 0.25 | N | —— |
| L-2-1-N | 8.93 | 0.37 | N | 3.29 |
| L-2-2-N | 10.65 | 0.35 | N | 4.72 |
| L-2-3-N | 8.93 | 0.08 | Y a | 4.59 |
| L-2-4-Y | 8.47 | 0.06 | Y | 3.81 |
| L-3-1-N | 9.01 | 0.25 | N | 4.21 |
| L-3-2-N | 8.27 | 0.25 | N | 4.24 |
| L-3-3-N | 9.31 | 0.07 | Y | 4.30 |
| L-3-4-Y | 8.72 | 0.05 | Y | 3.66 |
| L-4-1-N | 10.14 | .0.13 | N | 4.07 |
| L-4-2-N | 7.84 | 0.09 | Y | 4.82 |
| L-4-3-N | 7.98 | 0.15 | N | 4.02 |
| L-4-4-Y | 8.59 | 0.05 | Y | 4.33 |
| G-1-1-N | —— | —— | —— | —— |
| G-1-2-Y | —— | —— | —— | —— |
| G-1-3-Y | —— | 0.53 | N | —— |
| G-1-4-Y | —— | 0.76 | N | —— |
| G-2-1-N | —— | —— | —— | —— |
| G-2-2-Y | —— | 0.51 | N | 2.83 |
| G-2-3-Y | —— | —— | —— | —— |
| G-2-4-Y | —— | 0.7 | N | 3.73 |
| G-3-1-N | —— | —— | —— | —— |
| G-3-2-Y | —— | 0.5 | N | 3.86 |
| G-3-3-Y | —— | —— | —— | —— |
| G-3-4-Y | —— | 0.19 | Y | 3.49 |
| G-4-1-N | —— | 0.39 | N | 5.09 |
| G-4-2-N | —— | 0.45 | N | 3.24 |
| G-4-3-Y | —— | 0.31 | AY b | 2.58 |
| G-4-4-Y | —— | 0.31 | AY | 3.00 |
| Influencing Factors | d | l | t | D | l/d | D/d | t/D | Steel Content ρv |
|---|---|---|---|---|---|---|---|---|
| Correlation r | 0.7624 | 0.7195 | 0.7466 | 0.7782 | 0.7255 | 0.7559 | 0.7921 | 0.7903 |
| Data Source | d (mm) | t (mm) | D (mm) | ft (MPa) | lcrx/d | lcre/d |
|---|---|---|---|---|---|---|
| ω = 0.85 | ||||||
| Value from this test | 20 | 3 | 70 | 4.12 | 13 | About 8–10 |
| Value from Xu’s test | 18 | 3 | 70 | 4.63 | 11 | 10.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Tang, P.; Tang, Z.; Zhang, X.; Fan, B.; Zhang, Z.; Chen, Z. Mechanical Test of Sleeve Grouted Lapping Connectors under Uniaxial Tension and High-Stress Repeated Tension and Compression Loading. Appl. Sci. 2022, 12, 6736. https://doi.org/10.3390/app12136736
Yu Q, Tang P, Tang Z, Zhang X, Fan B, Zhang Z, Chen Z. Mechanical Test of Sleeve Grouted Lapping Connectors under Uniaxial Tension and High-Stress Repeated Tension and Compression Loading. Applied Sciences. 2022; 12(13):6736. https://doi.org/10.3390/app12136736
Chicago/Turabian StyleYu, Qiong, Peiyan Tang, Ziming Tang, Xingkui Zhang, Baoxiu Fan, Zhi Zhang, and Zhenhai Chen. 2022. "Mechanical Test of Sleeve Grouted Lapping Connectors under Uniaxial Tension and High-Stress Repeated Tension and Compression Loading" Applied Sciences 12, no. 13: 6736. https://doi.org/10.3390/app12136736
APA StyleYu, Q., Tang, P., Tang, Z., Zhang, X., Fan, B., Zhang, Z., & Chen, Z. (2022). Mechanical Test of Sleeve Grouted Lapping Connectors under Uniaxial Tension and High-Stress Repeated Tension and Compression Loading. Applied Sciences, 12(13), 6736. https://doi.org/10.3390/app12136736





