Dynamic Analysis of the Musical Triangles—Experimental and Numerical Approaches
Abstract
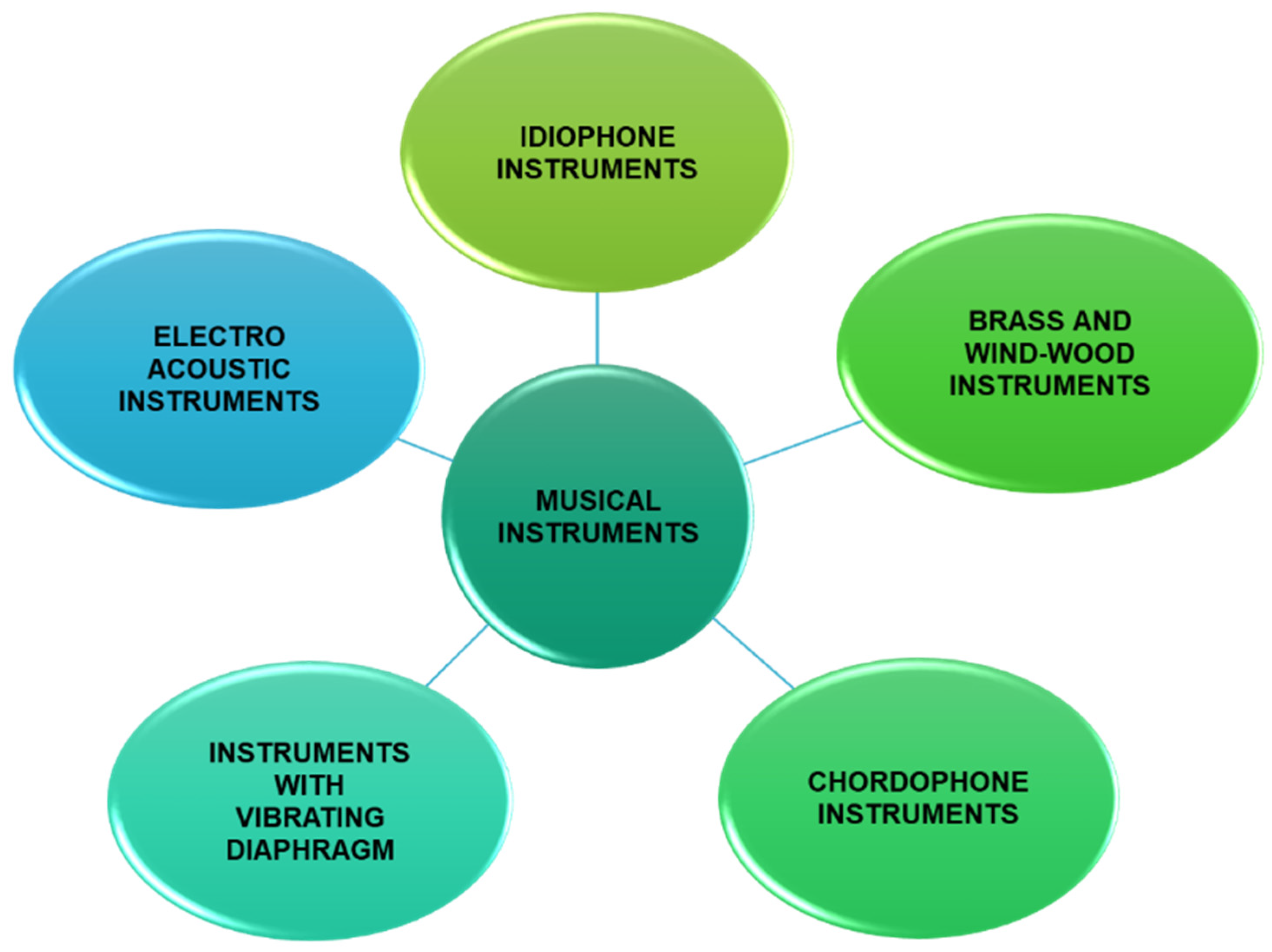
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Experimental Tests
2.2.2. Numerical Simulation of Forced Vibration
2.2.3. Modal Transient Response Analysis
3. Results
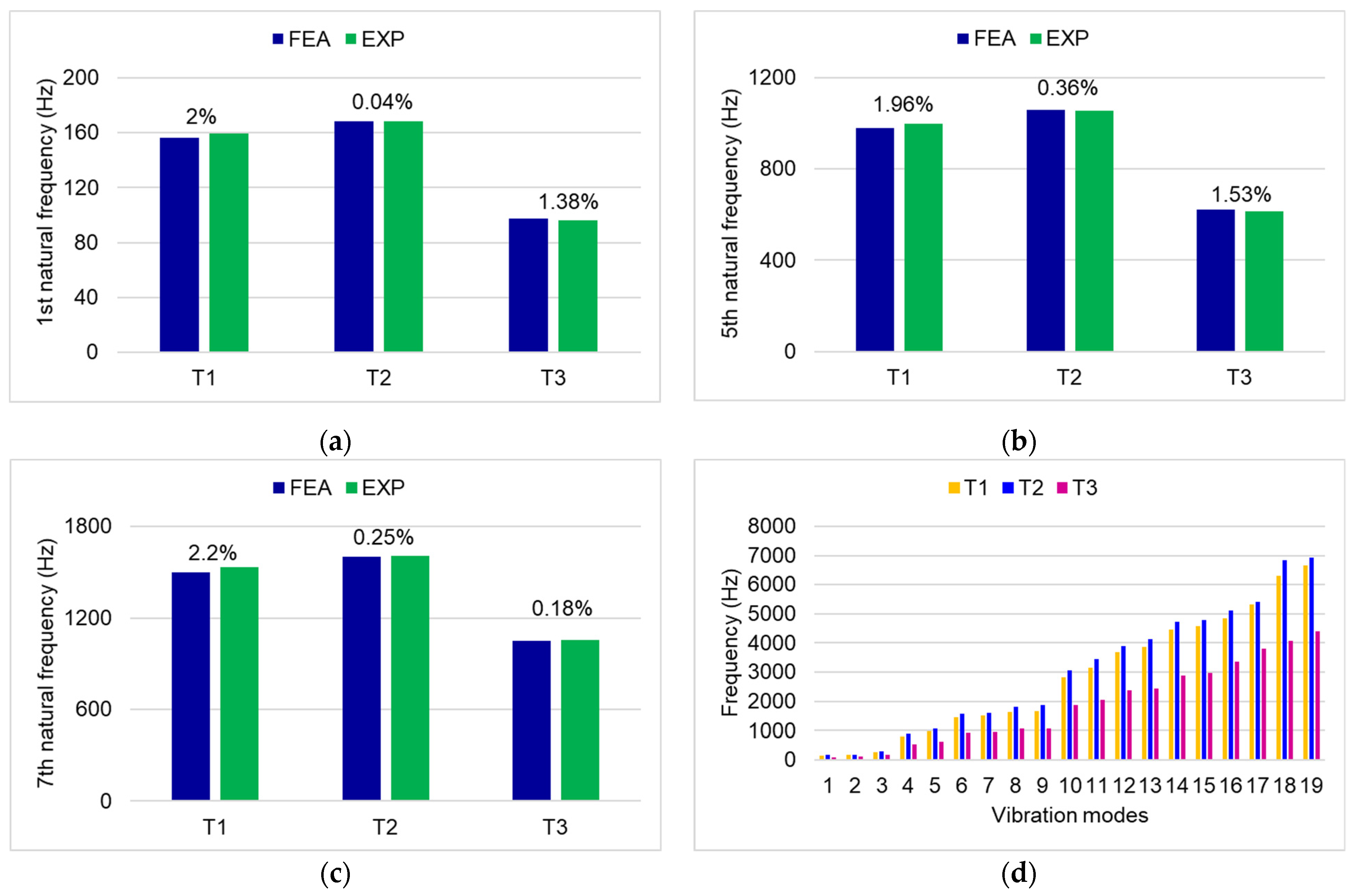
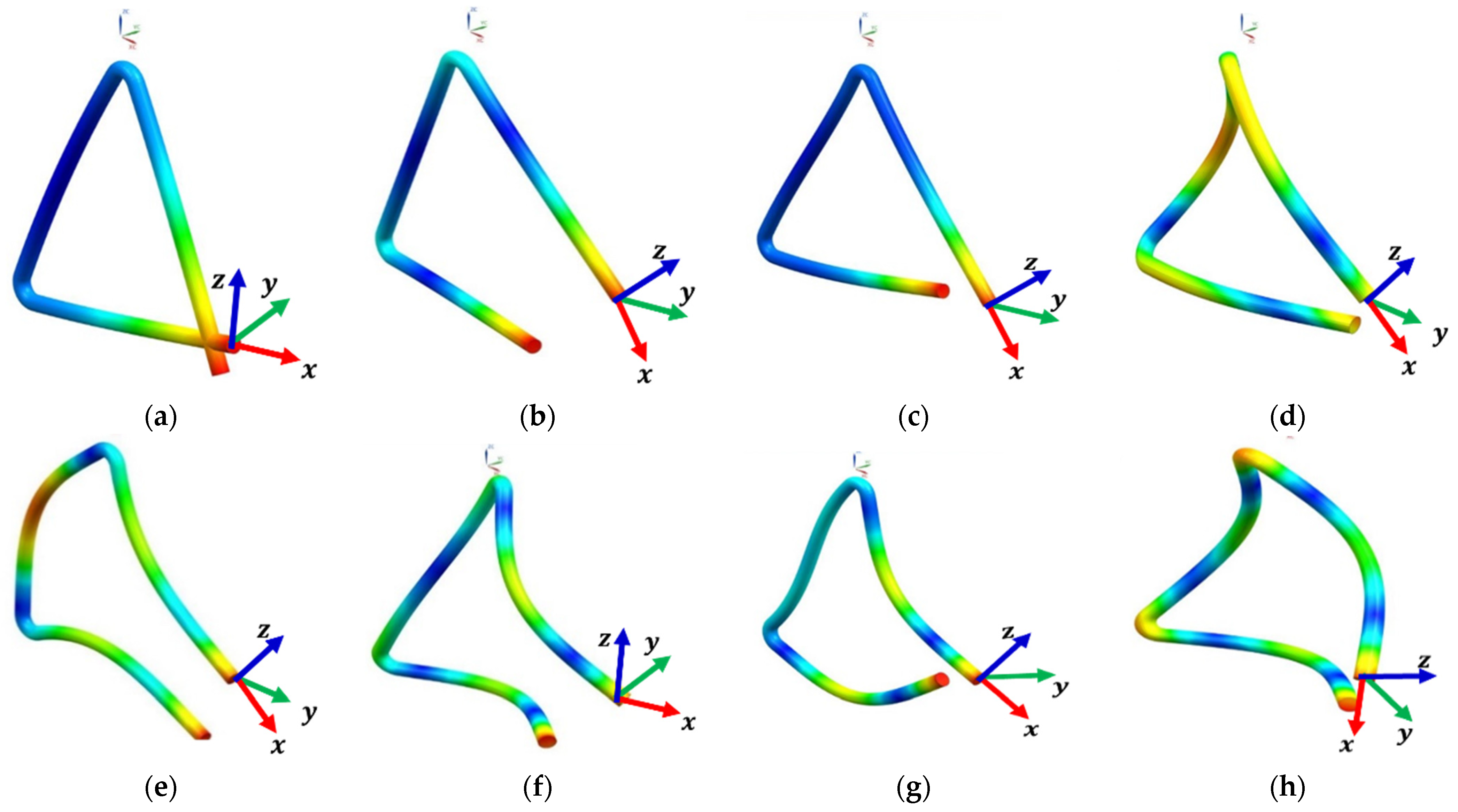
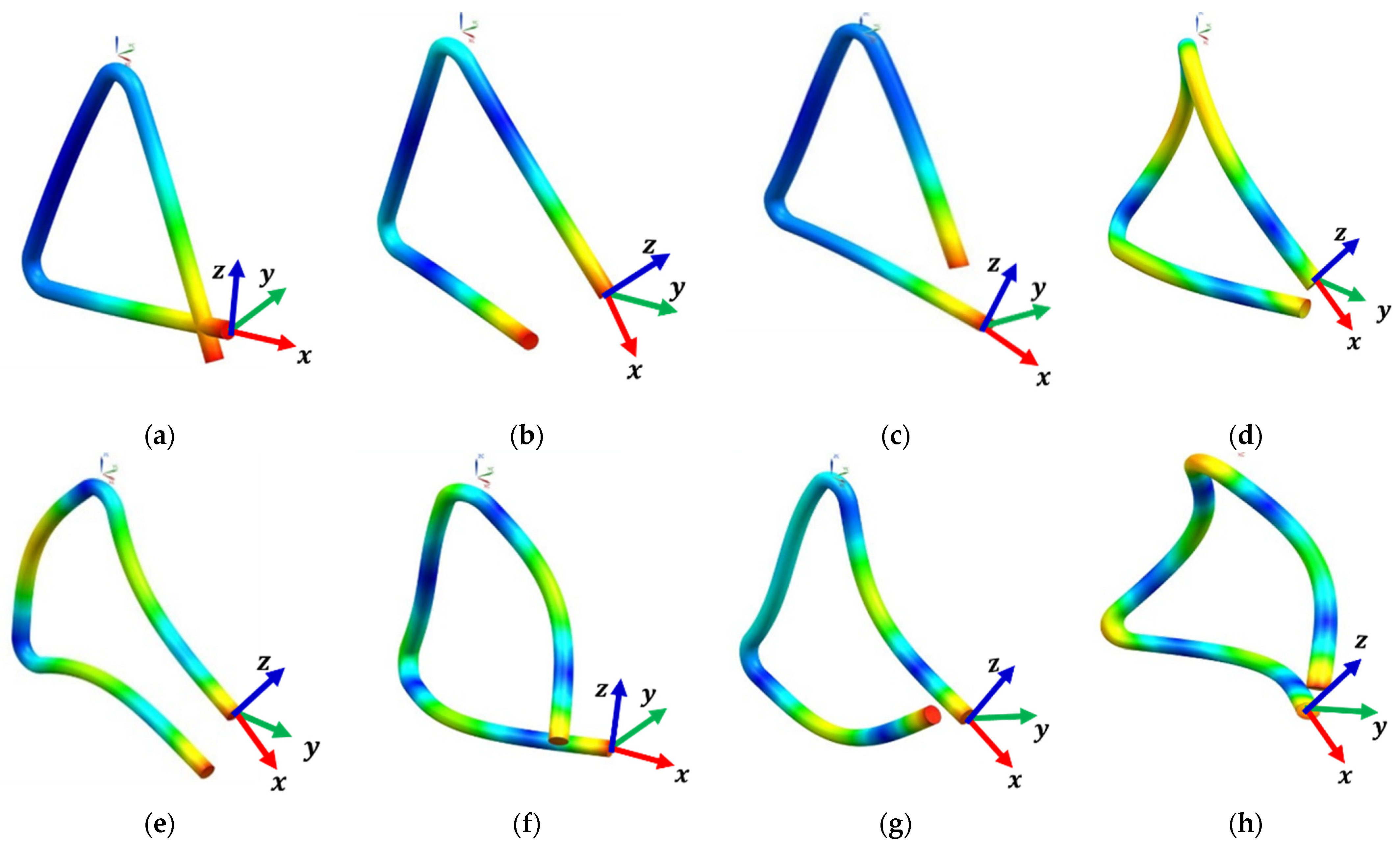
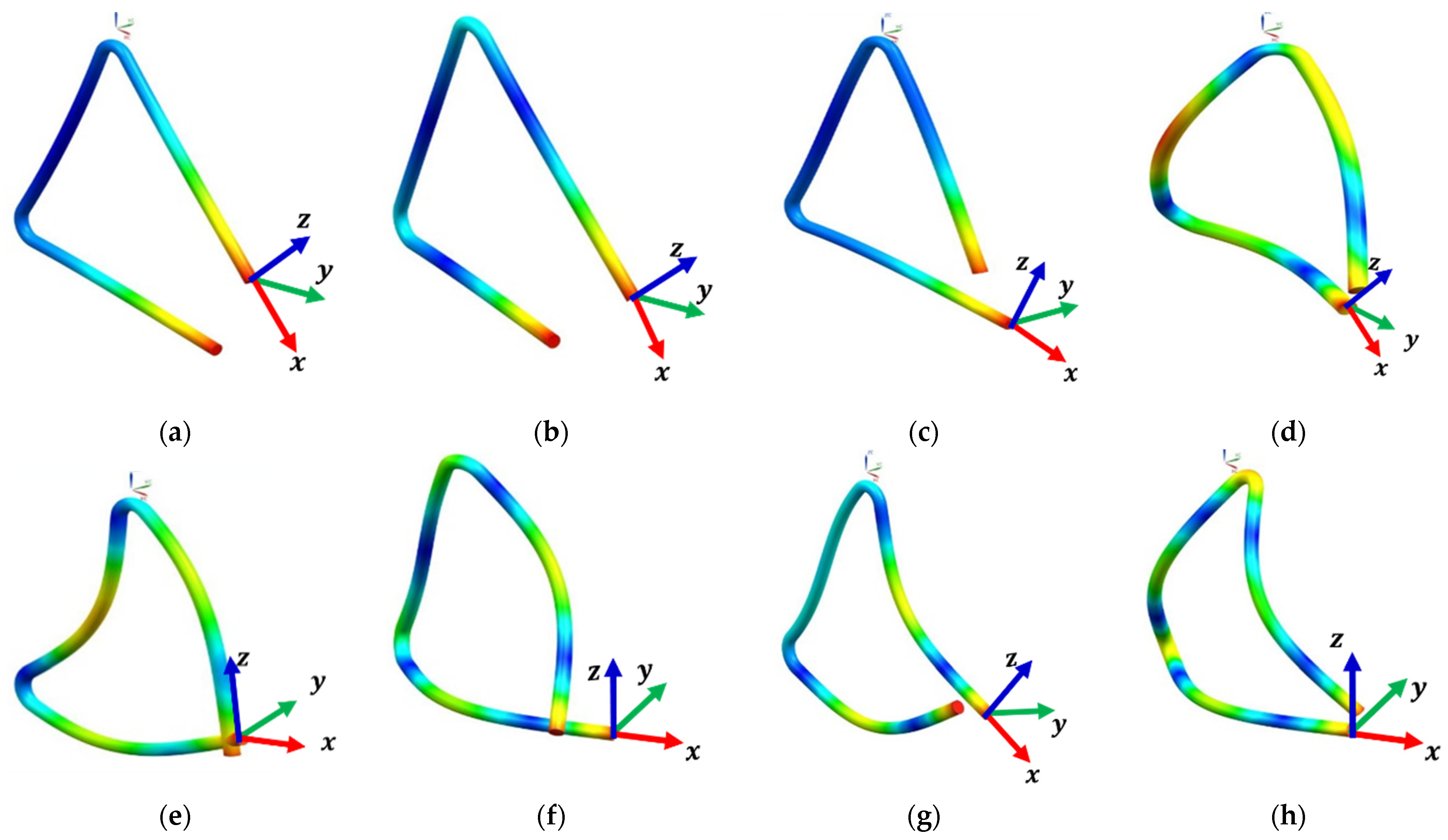
3.1. Comparison between Experimental and Numerical Modal Analysis
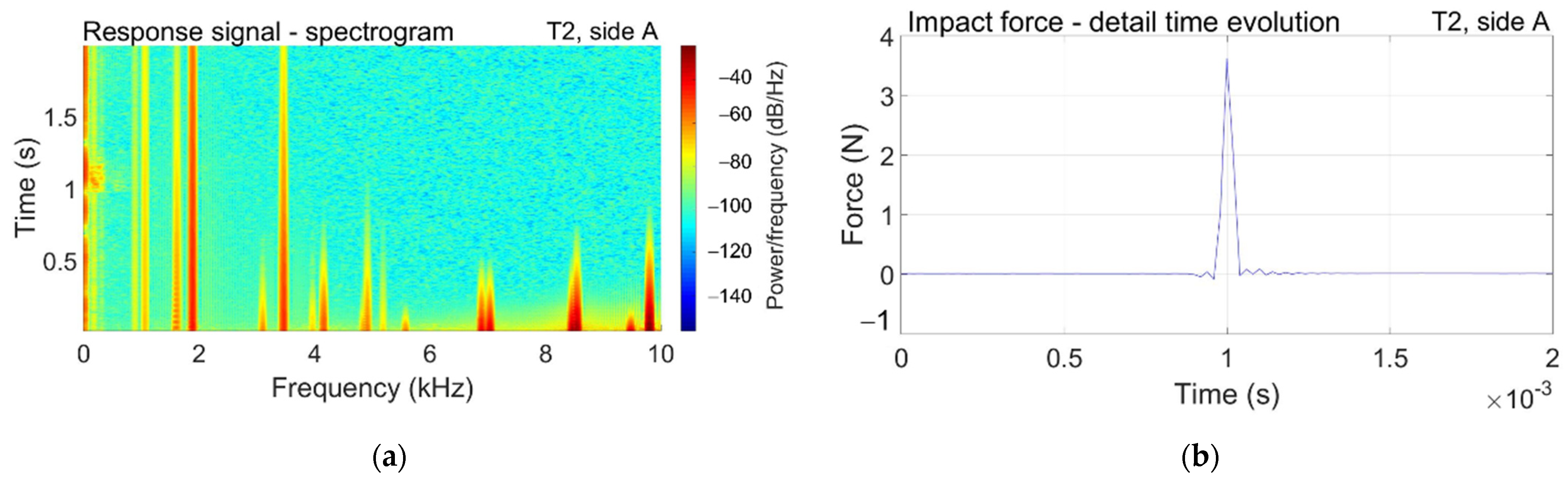
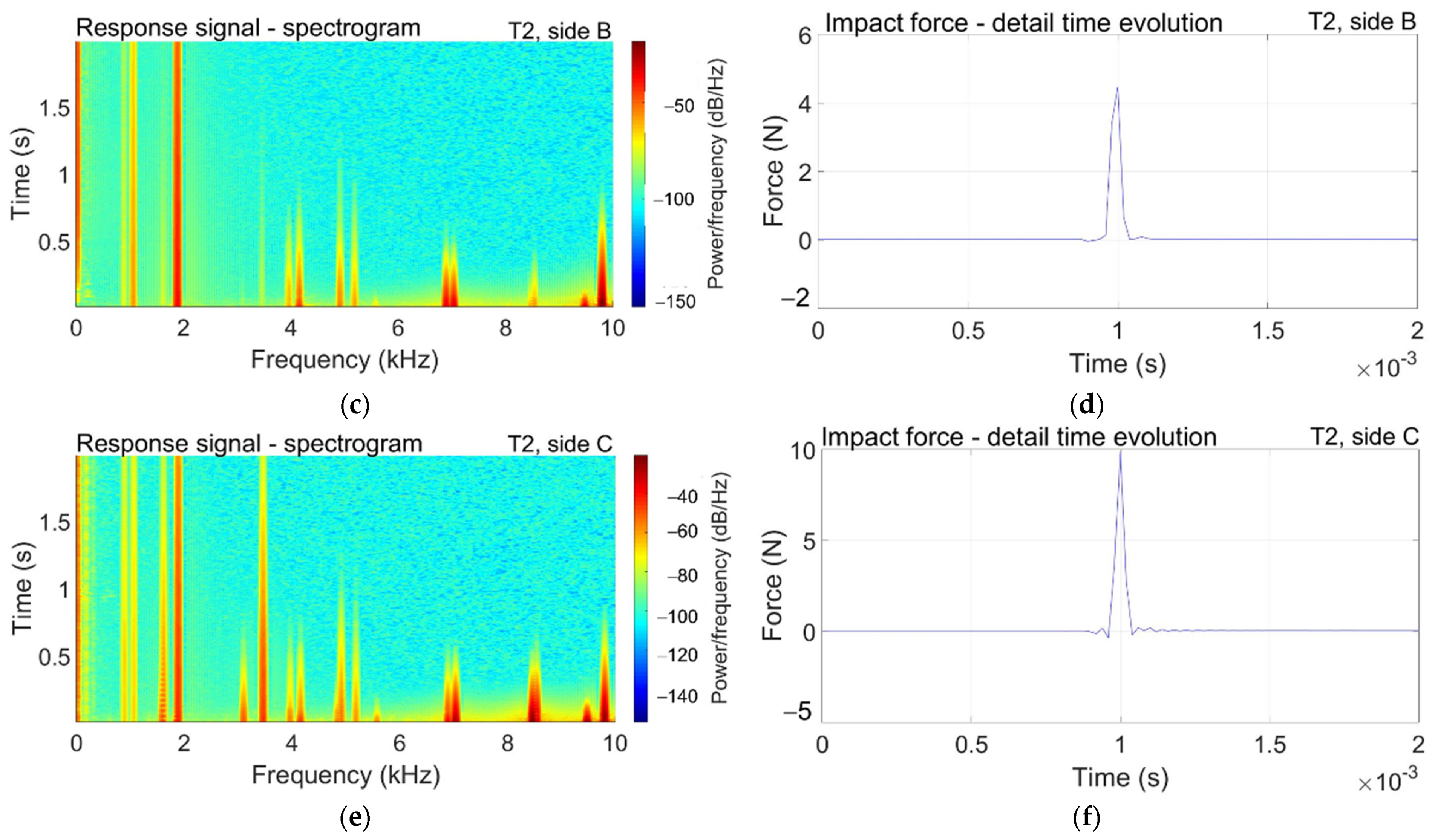
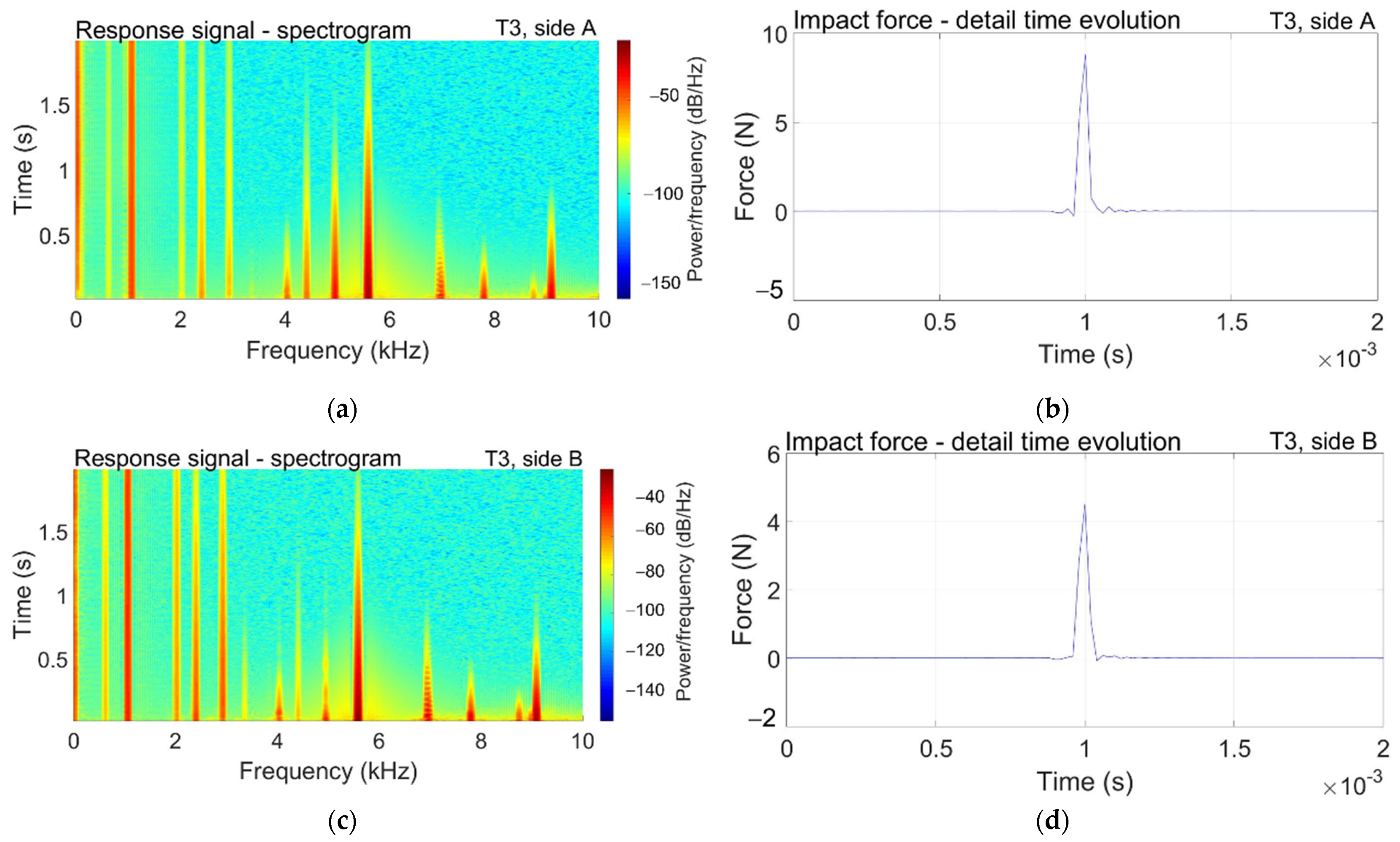
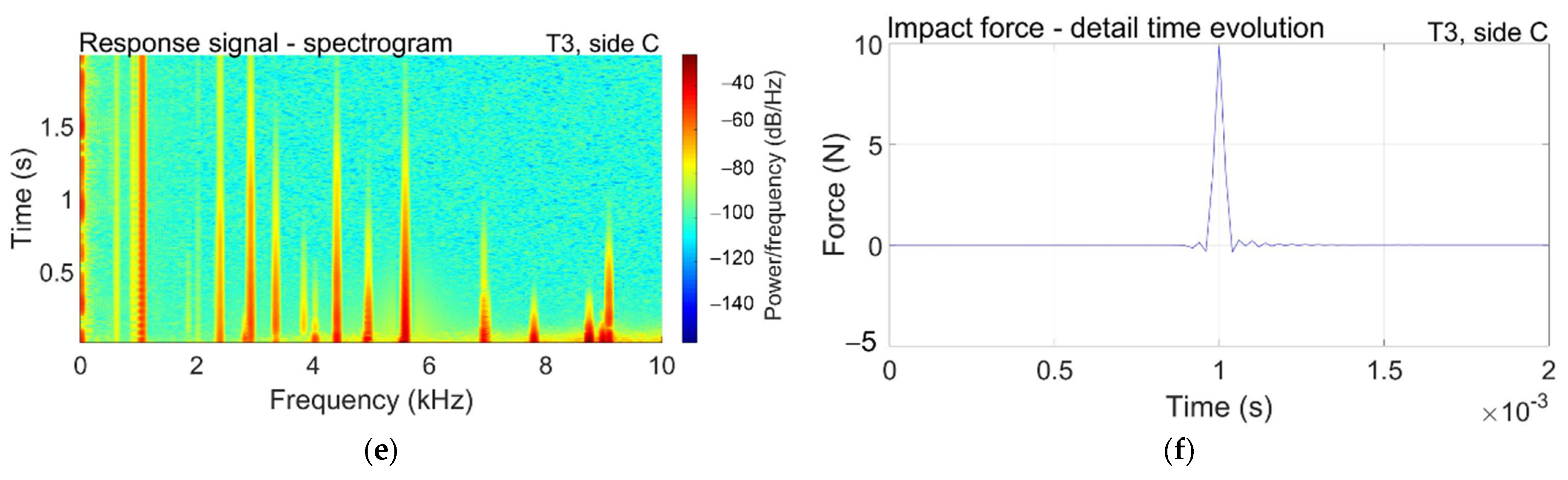
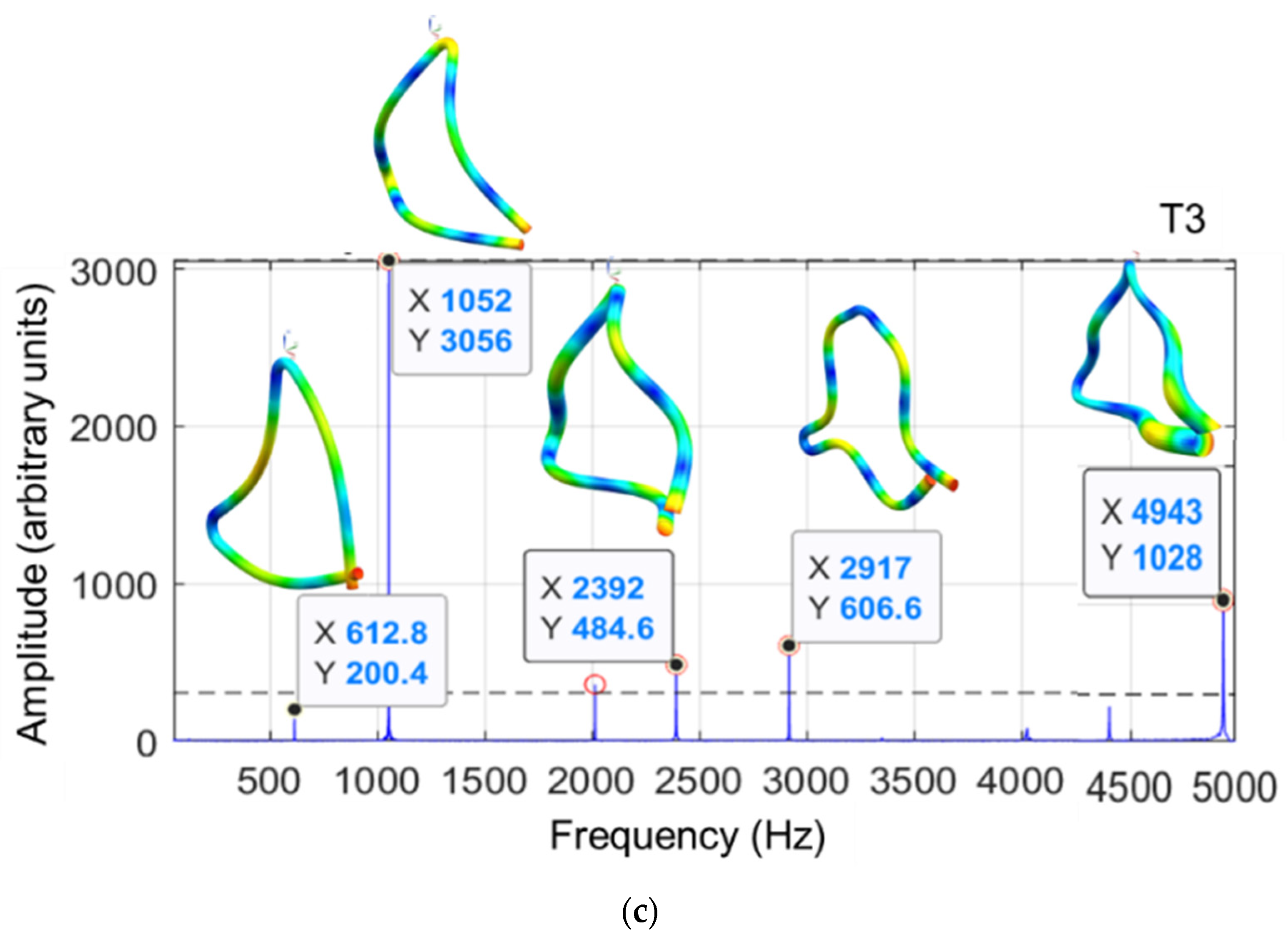
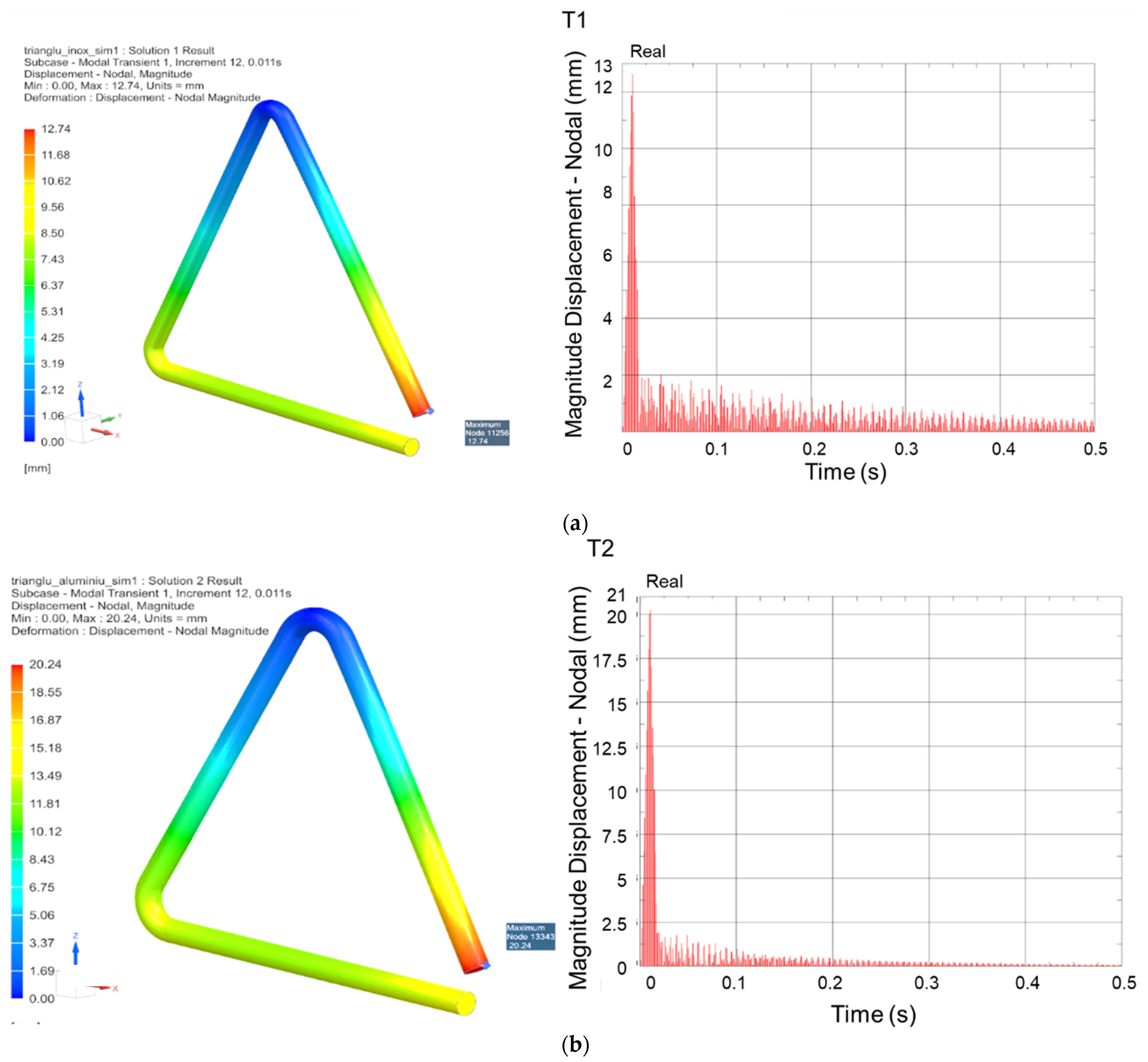
3.2. Modal Transient Response
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peters, G. The Drummer, Man: A Treatise on Percussion; Kemper-Peter Publications: Wilmette, IL, USA, 1975. [Google Scholar]
- Antolli, M.; Ovens, C.; Grieg, E. Peer Gynt Suite No. 1, Op. 46, Teacher Resource Booklet, Tasmanian Symphony Orchestra Pty Ltd. 2019. Available online: https://www.tso.com.au/wp-content/uploads/2019/11/Grieg-Peer-Gynt-Resources-Updated-06112019.pdf (accessed on 2 June 2022).
- Canazza, S.; De Poli, G.; Drioli, C.; Rodà, A.; Vidolin, A. Modeling and Control of Expressiveness in Music Performance. Proc. IEEE 2004, 92, 712–729. [Google Scholar] [CrossRef]
- Clynes, M. Microstructural musical linguistics: Composers’ pulses are liked most by the best musicians. Cognition 1995, 55, 269–310. [Google Scholar] [CrossRef]
- Legge, K.A.; Fletcher, N.H. Non-Linear Mode Coupling in Symmetrically Kinked Bars. J. Sound Vib. 1987, 118, 23–34. [Google Scholar] [CrossRef][Green Version]
- Blades, J. Percussion Instruments and Their History; Faber and Faber: London, UK, 1974. [Google Scholar]
- Bestle, P.; Hanss, M.; Eberhard, P. Experimental and numerical analysis of the musical behavior of triangle instruments. In Proceedings of the 5th European Conference of Computational Mechanics (ECCM V), Barcelona, Spain, 20–25 July 2014; pp. 3104–3114. [Google Scholar]
- Bucur, V. Mechanical characterization of materials for string instruments. In Handbook of Materials for String Musical Instruments; Springer: Berlin/Heidelberg, Germany, 2016; Chapter 3; pp. 93–132. [Google Scholar]
- Gough, C. Chapter 15—Musical Acoustics. In Handbook of Acoustics; Rossing, T.D., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 533–667. [Google Scholar]
- Brant-Smith, A. On playing the triangle. Musical Times 1930, 71, 21–22. [Google Scholar] [CrossRef]
- Wotton, T.S. On playing the triangle. Musical Times 1930, 71, 154. [Google Scholar] [CrossRef]
- Rossing, T.D. Acoustics of percussion instruments. Phys. Teach. 1976, 14, 546–556. [Google Scholar] [CrossRef]
- Bărbuceanu, V. Dictionary of Musical Instruments (Dicționar de Instrumente Musicale–in Romanian Language); Grafoart, B., Ed.; Matei Banica: Bucuresti, Romania, 2014. [Google Scholar]
- Bestle, P.; Hanss, M.; Eberhard, P. Musical Instruments–Sound synthesis of virtual idiophones. J. Sound Vib. 2017, 395, 187–200. [Google Scholar] [CrossRef]
- Dunlop, J.I. Flexural vibrations of the triangle. Acustica 1984, 55, 250–253. [Google Scholar]
- Bucur, V. Handbook of Materials for Percussion Instruments; Springer International Publishing: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Stanciu, M.D.; Trandafir, M.; Dron, G.; Munteanu, M.V.; Bucur, V. Numerical Modal Analysis of Kinked Bars–Triangle Case of Study. In Proceedings of the 9th International Conference on Modern Manufacturing Technologies in Industrial Engineering, online, 23–26 June 2021. [Google Scholar]
- Rossing, T.D.; Fletcher, N.H. Principles of Vibration and Sound; Springer: New York, NY, USA, 2004. [Google Scholar]
- Flynt, W.E. The Construction and Tuning of Vibrating Bars. Mechanical Music Digest. 2009. Available online: https://www.mmdigest.com/Gallery/Tech/XyloBars.html (accessed on 31 May 2022).
- Trandafir, M. Static and Dynamic Analysis of a Kinked Bars with Different Geometric and Structural Parameters—The Triangle Case of Study (in Romanian Language). Master’s Thesis, Transilvania University of Brasov, Brașov, Romania, 2021. [Google Scholar]
- Product Lifecycle Management Software Inc. Basic Dynamic Analysis User’s Guide-SIEMENS PLM 2014 Siemens. Available online: bhttps://docs.plm.automation.siemens.com/data_services/resources/nxnastran/10/help/en_US/tdocExt/pdf/basic_dynamics.pdf (accessed on 28 April 2022).
- Noor, A.K.; Knight, N.F. Nonlinear dynamic analysis of curved beams. Comp. Meths. Appl. Mech. Eng. 1980, 23, 225–251. [Google Scholar] [CrossRef]
- Wan, Z.-Q.; Li, S.-R.; Ma, H.-W. Geometrically nonlinear analysis of functionally graded Timoshenko curved beams with variable curvatures. Adv. Mater. Sci. Eng. 2019, 2019, 6204145. [Google Scholar] [CrossRef]
- Karmvir, T.; Ramakrishna, K. Overview of methods of analysis of beams on elastic foundation. IOSR J. Mech. Civil Eng. 2014, 11, 22–29. [Google Scholar]
- Shahba, A.; Attarnejad, R.; Semnani, S.J. New shape functions for non-uniform curved Timoshenko beam with arbitrarily varying curvature using basic displacement functions. Meccanica 2013, 48, 159–174. [Google Scholar] [CrossRef]





| Type of Triangle | Length of Sides (mm) | Diameter (mm) | Mass (g) | Density (kg/m3) | Materials | ||
|---|---|---|---|---|---|---|---|
| A | B | C | |||||
| T1 | 149 | 161 | 149 | 7.84 | 166.971 | 2708 | Stainless steel |
| T2 | 162 | 170 | 162 | 9.60 | 88.895 | 7818 | Aluminum |
| T3 | 214 | 222.5 | 214 | 9.60 | 118.644 | 7818 | Aluminum |
| Type of Triangle | Elasticity Modulus (MPa) | Density (kg/m3) | Poisson Coefficient | Materials |
|---|---|---|---|---|
| T1 | 184,479 | 7818 | 0.30 | Stainless steel |
| T2 | 68,382 | 2708 | 0.33 | Aluminum |
| T3 | 68,382 | 2708 | 0.33 | Aluminum |
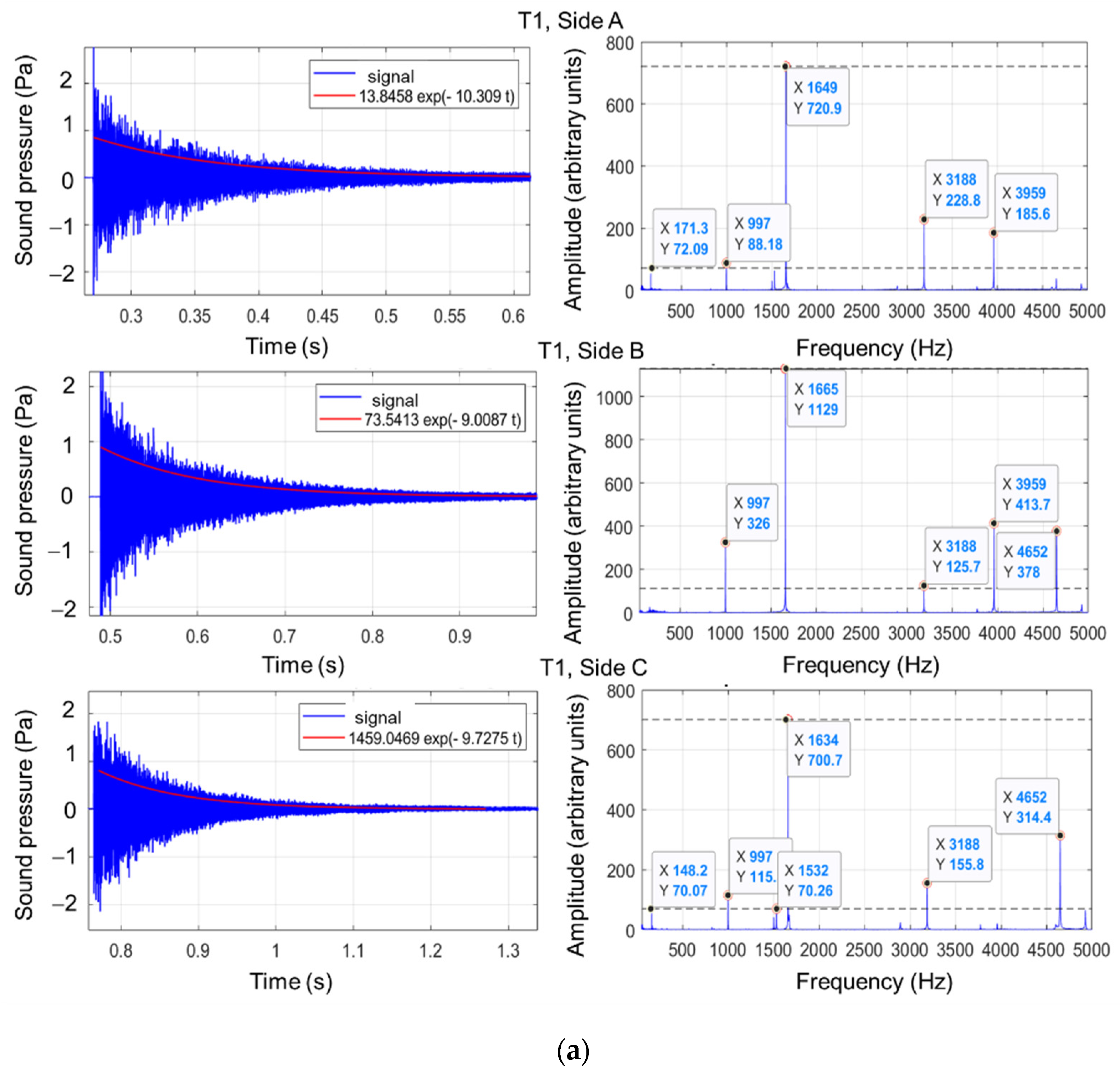
| Type of Triangle | Excited Side | Average Values of Frequency (Hz) | ||||
|---|---|---|---|---|---|---|
| f1 | f2 | f3 | f4 | fAmax | ||
| T1 | A | 159.43 | 997.30 | 1531.33 | - | 1657.10 |
| B | - | 996.97 | - | - | 1657.10 | |
| C | 159.53 | 996.97 | 1531.66 | - | 1657.10 | |
| T2 | A | 168.13 | 878.13 | 1053.00 | 1605.80 | 1876.06 |
| B | - | 878.10 | 1052.90 | 1606.00 | 1876.29 | |
| C | 168.20 | 878.17 | 1054.71 | 1597.66 | 1876.57 | |
| T3 | A | 96.29 | 612.70 | - | 1052.09 | 1052.09 |
| B | - | 612.83 | - | 1052.24 | 1052.24 | |
| C | 96.41 | 612.86 | 899.70 | 1045.47 | 1045.47 | |
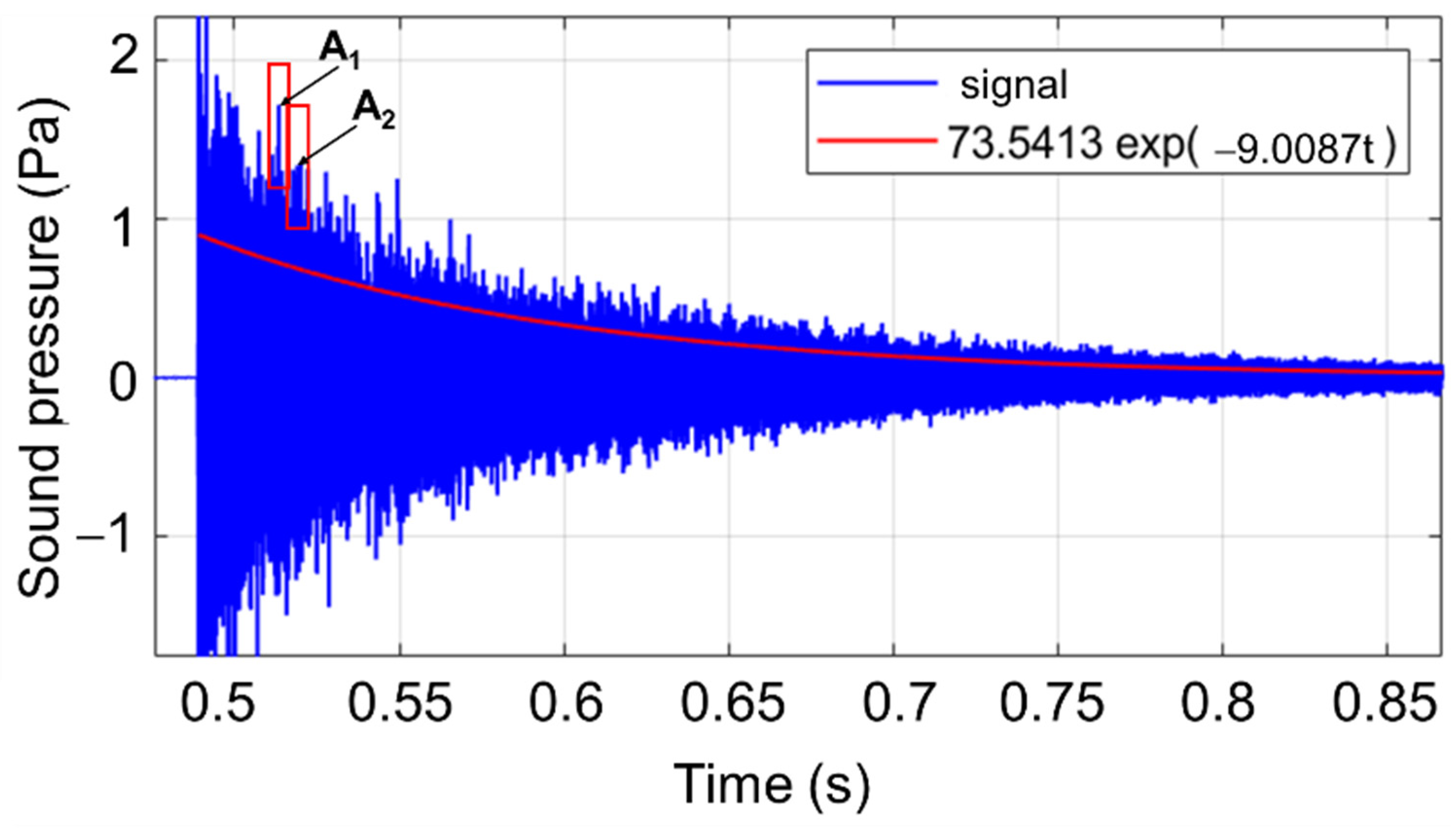
| Type of Triangle | The Amplitude | Damping Factor | Average Value/STDV | |
|---|---|---|---|---|
| A1 | A2 | ξ | ||
| T1 (stainless steel) | 0.5045 | 0.4743 | 0.009824 | 0.0103 0.0005 |
| 0.5810 | 0.5462 | 0.009830 | ||
| 0.3197 | 0.2989 | 0.010707 | ||
| 0.1482 | 0.1384 | 0.010889 | ||
| 0.1384 | 0.1296 | 0.010456 | ||
| T2 (aluminum) | 0.9847 | 0.8704 | 0.019637 | 0.0211 0.0012 |
| 0.8704 | 0.7606 | 0.021461 | ||
| 0.7606 | 0.6601 | 0.022555 | ||
| 0.6601 | 0.5731 | 0.022494 | ||
| 0.5731 | 0.5076 | 0.019316 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanciu, M.D.; Nastac, S.M.; Bucur, V.; Trandafir, M.; Dron, G.; Nauncef, A.M. Dynamic Analysis of the Musical Triangles—Experimental and Numerical Approaches. Appl. Sci. 2022, 12, 6275. https://doi.org/10.3390/app12126275
Stanciu MD, Nastac SM, Bucur V, Trandafir M, Dron G, Nauncef AM. Dynamic Analysis of the Musical Triangles—Experimental and Numerical Approaches. Applied Sciences. 2022; 12(12):6275. https://doi.org/10.3390/app12126275
Chicago/Turabian StyleStanciu, Mariana Domnica, Silviu Marian Nastac, Voichita Bucur, Mihai Trandafir, Gheorghe Dron, and Alina Maria Nauncef. 2022. "Dynamic Analysis of the Musical Triangles—Experimental and Numerical Approaches" Applied Sciences 12, no. 12: 6275. https://doi.org/10.3390/app12126275
APA StyleStanciu, M. D., Nastac, S. M., Bucur, V., Trandafir, M., Dron, G., & Nauncef, A. M. (2022). Dynamic Analysis of the Musical Triangles—Experimental and Numerical Approaches. Applied Sciences, 12(12), 6275. https://doi.org/10.3390/app12126275








