A Graph-Cut-Based Approach to Community Detection in Networks

Abstract

Networks can be used to model various aspects of our lives as well as relations among many real-world entities and objects. To detect a community structure in a network can enhance our understanding of the characteristics, properties, and inner workings of the network. Therefore, there has been significant research on detecting and evaluating community structures in networks. Many fields, including social sciences, biology, engineering, computer science, and applied mathematics, have developed various methods for analyzing and detecting community structures in networks. In this paper, a new community detection algorithm, which repeats the process of dividing a community into two smaller communities by finding a minimum cut, is proposed. The proposed algorithm is applied to some example network data and shows fairly good community detection results with comparable modularity Q values.

1. Introduction

Graphs consisting of vertices and edges can be used to model various aspects of our lives and real-world environments. For example, social media services can model each service subscriber as a vertex and a friend relationship between two individuals as an edge connecting the two corresponding vertices. Another example would be a water supply network; a pipe network connecting many water sources and consumers can be modeled as a graph. The Internet and the world wide web can be modeled as networks as well.

As networks can represent many abstract contexts of our lives, it is a natural desire to try to discover a core structure inherent in them. Partitioning a network via grouping vertices of similar affiliations can help us to grasp the main structure of a given network with a holistic viewpoint. In other words, a community structure of a network can give us a better understanding of its characteristics, properties, and inner workings. An example of community detection of a network is shown in Figure 1.

There has been significant research on detecting and evaluating community structures in networks. Many fields, including social sciences, biology, engineering, computer science, and applied mathematics, have identified their own needs for developing methods to analyze and detect community structures in networks. Graph partitioning problems in graph theory are also closely related to the community detection problem. Many algorithms for community detection and clustering have been proposed so far, and there are a few extensive review papers on them [1,2].

The main contribution of this paper is to propose a new community detection algorithm, which repeats the process of dividing a community into two smaller communities by finding a minimum cut of the community. In order to compute the minimum cut of a community, the betweenness centrality values of vertices are used to choose the source and sink nodes. The modularity criterion is used in a greedy way to determine the local optimal partition among many candidate communities to be cut.

The rest of this paper is organized as follows. Section 2 briefly reviews prior work on community detection methods. Section 3 presents the proposed algorithm, and Section 4 illustrates the results of the algorithm applied to a few example networks. Finally, Section 5 discusses the results and concludes the paper.

2. Prior Works

Uncovering community structures inherent in networks can shed light on many aspects of our world because networks can model various relations and inner workings among entities and objects. Therefore, community detection in networks has received a lot of attention from many fields [2,3,4,5,6,7], and it is rapidly evolving. Scientists and researchers from various fields have accordingly produced a large number of research articles and study results.

The community detection problem has been studied mainly for static networks, but the problem has also been studied for dynamic networks as well as overlapping communities recently [8,9,10,11,12,13,14]. At their initial development phase, community detection algorithms concerned disjoint communities, where each vertex of a network belongs to only one community. However, many real-world networks such as social networks can have overlapping communities, so that a vertex is permitted to belong to several communities at the same time. Even though the problems for dynamic networks or overlapping communities are interesting and worth tackling, this paper limits its scope to methods for disjoint community detection of static networks.

Since it is unrealistic to review all the previously proposed algorithms for community detection, only a few representative algorithms are mentioned in this section. More detailed reviews and studies regarding community detection can be accessed through several extensive review articles and books [2,3,4,5,15,16,17].

Even though many algorithms for community detection have been proposed so far, it seems that there is no single algorithm that can detect communities universally well for many kinds of various networks [18,19]. Therefore, it is believed to be better to have multiple different algorithms and apply suitable one to each particular network. Most algorithms proposed for disjoint community detection of static networks may be classified into three categories: traditional, modularity-based, and dynamic algorithms [2].

Traditional algorithms include hierarchical clustering [1,20,21,22,23,24], Girvan–Newman (GN) algorithms [25,26,27,28] and their variants [29,30,31], spectral clustering [32,33,34,35,36,37,38,39], and graph-partitioning-based algorithms [39,40]. Most of these algorithms are based on clustering, and they have provided basic concepts of community detection for later developments.

Modularity-based algorithms include the Guimera and Amaral algorithm [41], the fast GN algorithm [27], the Clauset algorithm [42], optimization-based algorithms [25,41,43,44,45,46], and genetic algorithms [47,48,49,50,51]. The concept of modularity was introduced by Newman and Girvan [25], and modularity-based algorithms try to optimize the modularity value by finding a good community structure in a network via some heuristics. The concept of modularity is briefly reviewed in Section 3.

Dynamic algorithms include those that are based on spin models, random walk, and synchronization. A random walk can be used for community detection by letting an entity make random moves along the edges of a network [52,53,54,55]. More details on dynamic algorithms can be found in review papers and books [2,3,4,5].

Since many algorithms and methods for community detection have been proposed, the task of evaluating them becomes important as well. To measure the performance of the algorithms and methods, a few standard benchmarks of complex networks with known community structures have been devised. Among these benchmarks, the GN and LFR (Lancichinetti, Fortunato, and Radicchi) benchmarks are frequently used [56,57]. These benchmark networks are synthesized with predetermined community structures, and an algorithm is evaluated by comparing the result of community detection to the known answer, i.e., the predetermined community structure. Besides these synthetic benchmarks, there are some real-world network data that are frequently used to evaluate community detection algorithms. In Section 4, some of these real-world network data are used to illustrate the performance of the algorithm proposed in this paper.

3. Methods

The community detection method proposed in this paper is based on the idea that connections between vertices of the same community tend to be denser than connections between vertices of different communities. Since a minimum cut in graph theory finds as few connections to a cut as possible, applying a minimum cut to a network may give us boundaries between different communities. In other words, a minimum cut might result in a cut-set that contains more inter-connections between communities than intra-connections within communities.

The proposed method of this paper iteratively applies the minimum cut solution to a network to generate a community structure. The method first finds two temporary source and sink nodes that are expected to be of different communities, and computes a minimum cut between the two nodes. As a result of the cut, the network is divided into two groups. Then, the same procedure is applied to each group, and quality measures of the resulting community structures of the entire network are compared to select the better result between the two. The same procedure is repeated until no further refinement of the quality of community structure is obtained. A precise description of the proposed algorithm is presented later in this section.

3.1. Network and Community Structure

To describe the problem and the proposed algorithm precisely, some basic notations are introduced.

Definition 1.

A network is a graph $G=(V,E)$ defined by V and E, where V and E are the set of vertices (nodes) and the set of edges, respectively. An edge is a pair of two vertices. Given a network $G=(V,E)$ and a subset $C\subset V$ of vertices, $E\left(C\right)\subset E$ is a subset of E consisting of all the edges whose endpoints belong to C.

This paper concerns undirected graphs without loops or multiple edges even though the proposed method may be easily extended to the case of directed graphs. Therefore, an edge $e=\{u,v\}\in E$ is a pair of two vertices $u,v\in V$, and the order of the two is not relevant unless it is noted otherwise. We also assume that the graph is connected; every pair of vertices $(u,v)$ of G has a path from u to v. In this paper, networks are used interchangeably with graphs.

Definition 2.

A community structure$C=\{C_1,C_2,\dots ,C_k\}$ of a network $G=(V,E)$ is a partition of V, the set of vertices of G. In other words, ${\cup }_{i=1}^k{C}_i=V$ and $C_i\cap C_j=\varnothing$ for $i,j=1,\dots ,k$ with $i\ne j$. Here, k refers to the number of communities of the community structure C.

With these definitions, the objective of the community detection problem can be stated as finding a good community structure C when a network G is given.

3.2. Minimum Cut

Since the minimum cut in graph theory is employed in the proposed method, a brief review is provided in this section.

Definition 3.

A cut$C=(S,T)$ is a partition of the set of vertices V of a graph $G=(V,E)$ into two subsets S and T. The cut-set of a cut $C=(S,T)$ is the set $\left\{\{u,v\}\in E|u\in S,v\in T\right\}$ of edges that have one endpoint in S and the other endpoint in T. If s and t are specified vertices of the graph G, then an s-t cut is a cut $C=(S,T)$ such that $s\in S$ and $t\in T$.

In this paper, we consider networks whose edges have no weight values assigned, i.e., unweighted and undirected graphs. However, graphs may have edge weights in general, and the weight of a cut in an undirected graph is defined as follows.

Definition 4.

In an unweighted and undirected graph, the size or weight of a cut is defined to be the number of edges that belong to the cut-set of the cut. In a weighted graph, the value or weight of a cut is defined to be the sum of the weights of the edges in the cut-set.

Given the definitions of a cut and the weight of a cut, a minimum cut of a network is defined as follows.

Definition 5.

A minimum cut of an undirected graph is a cut whose weight is not larger than the weight of any other cut.

It is well known in network science that the maximum flow of a flow network from a source vertex s to a sink vertex t is equal to the capacity of a minimum cut that separates the two vertices s and t. This result is called the max-flow min-cut theorem and was introduced by Ford and Fulkerson [58]. The Ford–Fulkerson method can be used to find a minimum cut and a maximum flow, and the Edmonds–Karp algorithm is an implementation of the method that runs in polynomial time [59,60].

Even though the max-flow min-cut theorem deals with a directed graph with capacity values assigned on edges, it is straightforward to extend the theorem to undirected and weighted graphs. Besides the Ford–Fulkerson method, there are other algorithms for finding a minimum cut of undirected edge-weighted graphs such as the Stoer–Wagner algorithm [61,62]. The Stoer–Wagner algorithm has the time complexity of $O\left(\right|V\left|\right|E|+|V{|}^{2}log\left|V\right|)$ [62].

Since the max-flow min-cut theorem is well known and there are many algorithms for finding a minimum cut of undirected graphs, we denote such an algorithm as MINIMUM-CUT without a detailed description of the procedure.

Definition 6.

Given a connected graph $G=(V,E)$, a capacity function c, and source and sink vertices s and t, the procedure MINIMUM-CUT ($G,c,s,t$) is an implementation of a method that finds a minimum cut of the graph G with c, s, and t.

The capacity function c in Definition 6 gives the weight value of each edge of a weighted graph, i.e., a capacity is used interchangeably with a weight in this paper. The MINIMUM-CUT procedure is employed in our proposed algorithm, and more details are described later.

3.3. The Betweenness Centrality

To apply MINIMUM-CUT to a graph, source and sink vertices s and t should be provided as well as the capacity c for each edge. For community detection, the source and sink vertices should be chosen so that the two vertices do not belong to the same community, because the two vertices are cut by MINIMUM-CUT. The betweenness centrality in graph theory is used to select two vertices in our proposed method. In particular, the two vertices of highest betweenness centrality values are chosen as the source and sink vertices in applying MINIMUM-CUT.

In graph theory, betweenness centrality is a measure of the centrality of a vertex in a graph [63]. Roughly speaking, the betweenness centrality of a vertex represents the degree of how many pairs of nodes are connected via the shortest paths passing through the vertex. The betweenness centrality $c_B\left(v\right)$ of a vertex $v\in V$ of a graph $G=(V,E)$ based on shortest paths is defined as the following

$$c_B\left(v\right)=\sum _{s,t\in V}\frac{\sigma (s,t|v)}{\sigma (s,t)},$$

(1)

where $\sigma (s,t)$ is the number of shortest paths from $s\in V$ to $t\in V$, and $\sigma (s,t|v)$ is the number of those paths passing through a vertex v other than s and t [64,65]. If $s=t$, we let $\sigma (s,t)=1$, and if $v\in \{s,t\}$, we let $\sigma (s,t|v)=0$. On unweighted graphs, computing betweenness centrality takes $O\left(\right|V\left|\right|E\left|\right)$ times using Brandes’ algorithm [64].

As briefly mentioned before, the betweenness centrality values for all the vertices are computed to select the source and sink vertices s and t, which are provided as inputs to MINIMUM-CUT. Those two vertices of the highest values are chosen because it is expected that many shortest paths connecting vertices of different communities pass through these two nodes.

3.4. The DIVIDE-INTO-TWO Algorithm

To find a community structure of a given network, the proposed algorithm of this paper iterates by dividing a group of vertices into two smaller groups until a stopping criterion is satisfied. Before the algorithm is described precisely, we present the procedure of dividing a group of vertices into two smaller groups in Algorithm 1, called DIVIDE-INTO-TWO.

Algorithm 1: The DIVIDE-INTO-TWO algorithm.

Input: A connected graph $G=(V,E)$    Output: $C=\{C_1,C_2\}$, a partition of G 1:    procedure DIVIDE-INTO-TWO(G) 2:          if $\left|V\right|\le 1$ then 3:           $C\leftarrow \left\{V\right\}$ 4:          else 5:           Compute betweenness centrality $c_B\left(v\right)$ for all $v\in V$ 6:           $s\leftarrow {arg\; max}_{v\in V}{c}_B\left(v\right)$ 7:           $t\leftarrow {arg\; max}_{v\in V\backslash \left\{s\right\}}{c}_B\left(v\right)$ 8:           $S\leftarrow \left\{v\in V\left|\right\{s,v\}\in E\right\}$ 9:           $T\leftarrow \left\{v\in V\left|\right\{t,v\}\in E\right\}$ 10:         for all $\{u,v\}\in E$ do 11:            $c_{uv}\leftarrow 1$ 12:         end for 13:         for all $v\in S$ do 14:            if $v\notin T\cup \left\{t\right\}$ then 15:               $c_{sv}\leftarrow \infty$ 16:            end if 17:         end for 18:         for all $v\in T$ do 19:            if $v\notin S\cup \left\{s\right\}$ then 20:               $c_{tv}\leftarrow \infty$ 21:            end if 22:         end for 23:         $C\leftarrow$ MINIMUM-CUT$(G,c,s,t)$ 24:           end if 25:   end procedure

After the source s and sink t are selected by the betweenness centrality computation, DIVIDE-INTO-TWO initializes the capacity values of all the edges of the network to be one. Then, it assigns infinity as the capacity to the edges that are connected to the source or sink vertices. This assignment is to prevent the edges connected to s or t from being cut by MINIMUM-CUT. The procedure forms a group of vertices S and T, where vertices of S and T are neighbors of the source and sink nodes, respectively. The capacity value of infinity makes the vertices of groups S or T strongly connected to themselves, which prevents the edges from being cut by MINIMUM-CUT. All the other edges remain with a capacity of one, as initialized.

When assigning infinity as a capacity value to edges, it should be avoided that the source s and sink t are connected by a path whose every edge has infinity as its capacity value. If there is any path connecting the source and sink vertices where all the edges of the path have infinity as capacity, then MINIMUM-CUT cannot find a cut set of finite minimum cut value. To carefully assign infinity as capacity, DIVIDE-INTO-TWO checks whether the other vertex belongs to S or T, as described precisely in Algorithm 1.

Computing the betweenness centralities via Brandes’ algorithm takes $O\left(\right|V\left|\right|E\left|\right)$ time, while the MINIMUM-CUT procedure takes $O\left(\right|V\left|\right|E|+|V{|}^{2}log\left|V\right|)$ time when using the Stoer–Wagner algorithm. The Stoer–Wagner algorithm is one of the fast algorithms for finding a minimum cut from a graph. Considering these time complexities, the DIVIDE-INTO-TWO algorithm has the same time complexity as MINIMUM-CUT. Note that all the other executions of DIVIDE-INTO-TWO except for the two main procedures can be performed in linear time. For example, selecting the source and sink vertices and forming the two sets S and T can be done in linear time. Assigning capacity values to all the edges also takes linear time.

3.5. Modularity: A Quality Measure

In most practical cases, community detection algorithms are applied to a network whose community structure is not known ahead of time. Therefore, it is necessary to have a quality measure to evaluate a community structure derived by a community detection algorithm. In other words, we need a measure to answer the question of how well the found community structure represents the underlying connection characteristics of the network.

Even though a quality measure of community structure is needed, there exists one difficulty in defining such a measure. There is no pre-defined precise answer for the community structure of a given network; two people may have different opinions about the inherent community structure of the same network. It is hard to say that a community structure of a network is strictly better than another community structure of the same network. Examples that illustrate this difficulty are presented in Section 4.

Although it is difficult to find a well-defined and unified quality measure to evaluate a particular division of a given network, some measures have been proposed so far. One of the widely used measures is modularity [25]. The modularity measure is defined as follows.

Definition 7.

Given a network $G=(V,E)$ with a community structure $C=\{C_1,C_2,\dots ,C_k\}$, a $k\times k$ symmetric matrix M is defined, where each element $M_{ij}$ for $i,j=1,\dots ,k$ is the fraction of all edges that connect vertices in community i to vertices in community j. Then, the modularitymeasure Q of the community structure C of the network G is defined by

$$Q(C;G)=TrM-∥M^2∥,$$

(2)

where $∥X∥$ is the sum of the elements of the matrix X.

Note that the row sum $m_i={\sum }_j{M}_{ij}$ of the matrix M represents the fraction of edges that have at least one vertex in community i at its endpoints. If all the pre-existing edges are removed and new edges are randomly placed between vertices while preserving the row sums, the expected fraction of all the new edges that connect vertices in community i and vertices in community j equals $m_i·m_j$. Therefore, the difference between the pre-existing and the expected fraction, $M_{ii}-m_i^2$, may be used as an indication of how strongly the vertices in the community i are connected to each other. In other words, it can measure how densely the vertices in the community i are linked. By adding these differences for all the k communities, the modularity measure can be defined as

$$Q=\sum _{i=1}^k\left(M_{ii}-m_i^2\right),$$

(3)

which is shown to be equal to the right side of Equation (2).

The maximum value that Q can have is $Q=1$, and this value indicates a network with a very strong community structure [25,66]. The modularity Q values for networks with strong community structure usually range from about $0.3$ to $0.7$.

Our proposed algorithm computes the modularity value after each division of the given network via graph cuts, and it determines the next step based on the calculated Q values. In particular, the Q value is used as a stopping criterion to stop iterations of community division. Therefore, the Q values are critical for the algorithm.

3.6. The Proposed Algorithm

The proposed algorithm is a divisive one, so that a given network is divided into groups of vertices in a stepwise manner. The main idea of the algorithm is that a connected network may be partitioned into two subgroups by finding a minimum cut separating the two, which is expected to reveal a good community structure of the given network. After a division of each connected component of a network, the Q value for the resulting community structure is calculated. By comparing the resulting Q value for every connected component, the algorithm selects the best partition and creates two communities out of the selected component. The algorithm iterates this process until no further improvement in the modularity value is observed. The algorithm is named MCCD (Minimum Cut-based Community Detection) and is presented precisely in Algorithm 2.

Algorithm 2: The MCCD algorithm.

Input: A connected graph $G=(V,E)$    Output: $C=\{C_1,\dots ,C_k\}$, a community structure of G 1:    procedure MCCD(G) 2:          $C\leftarrow \left\{V\right\}$ 3:          $Q\leftarrow 0$ 4:          loop 5:             if $\left|C\right|=\left|V\right|$ then 6:                break 7:             end if 8:             for $i\leftarrow 1$ to $\left|C\right|$ do 9:                $\{C_{i1},C_{i2}\}\leftarrow$ DIVIDE-INTO-TWO($C_i$, $E\left(C_i\right)$) 10:               $Q_i\leftarrow Q\left(\{C_1,\dots ,C_{i-1},C_{i1},C_{i2},C_{i+1},\dots ,C_{\left|C\right|}\};G\right)$ 11:            end for 12:            $m\leftarrow {arg\; max}_i{Q}_i$ 13:            if $Q>Q_m$ then 14:               break 15:            end if 16:            $C\leftarrow \{C_1,\dots ,C_{m-1},C_{m1},C_{m2},C_{m+1},\dots ,C_{\left|C\right|}\}$ 17:            $Q\leftarrow Q_m$ 18:        end loop 19:   end procedure

Note that the locally optimal partition $\{C_1,\dots ,C_{m-1},C_{m1},C_{m2},C_{m+1},\dots ,C_{\left|C\right|}\}$, where $m = {arg\; max}_i{Q}_i$, is selected at each iteration of the MCCD algorithm. The iteration repeats until a decrease in the modularity Q value is observed or each vertex has its own community, i.e., the entire network is partitioned into one-vertex communities. As illustrated in Section 4, however, the Q value starts decreasing after only a few iterations for many networks. In other words, many networks are expected to have a community structure consisting of not so many communities.

Even though the MCCD algorithm stops its iteration of dividing each community into two smaller communities when it detects decreasing Q values, it is also possible to continue the iteration until a desired number of communities are obtained, via a slight modification of the algorithm. This modified algorithm is precisely presented in Algorithm 3 and is called k-MCCD. The desired number of communities k, which is given as an input, is assumed to satisfy $1\le k\le \left|V\right|$. As presented in Algorithm 3, k-MCCD stops its iterations when the number of communities reaches the desired number k.

Algorithm 3: The k-MCCD algorithm.

Input: A connected graph $G=(V,E)$ and a desired number of communities k    Output: $C=\{C_1,\dots ,C_k\}$, a community structure of G 1:    procedurek-MCCD(G, k) 2:          $C\leftarrow \left\{V\right\}$ 3:          $Q\leftarrow 0$ 4:          loop 5:             if $\left|C\right|=k$ then 6:                break 7:             end if 8:             for $i\leftarrow 1$ to $\left|C\right|$ do 9:                $\{C_{i1},C_{i2}\}\leftarrow$ DIVIDE-INTO-TWO($C_i$, $E\left(C_i\right)$) 10:               $Q_i\leftarrow Q\left(\{C_1,\dots ,C_{i-1},C_{i1},C_{i2},C_{i+1},\dots ,C_{\left|C\right|}\};G\right)$ 11:            end for 12:            $m\leftarrow {arg\; max}_i{Q}_i$ 13:            $C\leftarrow \{C_1,\dots ,C_{m-1},C_{m1},C_{m2},C_{m+1},\dots ,C_{\left|C\right|}\}$ 14:            $Q\leftarrow Q_m$ 15:        end loop 16:   end procedure

As mentioned previously, the procedure DIVIDE-INTO-TWO has the time complexity of $O\left(\right|V\left|\right|E|+|V{|}^{2}log\left|V\right|)$. Therefore, when MCCD calls DIVIDE-INTO-TWO($C_i$, $E\left(C_i\right)$) for a community $C_i$, it takes $O\left(\right|C_i\left|\right|E\left(C_i\right)|+|C_i{|}^{2}log\left|C_i\right|)$ time. MCCD calls DIVIDE-INTO-TWO for each community $C_i$ during one iteration, so the total computation time summed for every community can be given by

$$\sum _{i=1}^{\left|C\right|}O\left(\right|C_i\left|\right|E\left(C_i\right)|+|C_i{|}^{2}log|C_i\left|\right).$$

(4)

The computation time of Equation (4) satisfies

$$\begin{array}{ccc}\hfill \sum _{i=1}^{\left|C\right|}O\left(\right|C_i\left|\right|E\left(C_i\right)|+|C_i{|}^{2}log|C_i\left|\right)& \le & \sum _{i=1}^{\left|C\right|}O\left(\right|C_i\left|\right|E|+|C_i{|}^{2}log|C_i\left|\right)\hfill \\ & \le & O\left(\right|V\left|\right|E|+|V{|}^{2}log\left|V\right|),\hfill \end{array}$$

where the convexity of a function $f\left(x\right)=yx+x^{2}logx$ for sufficiently large x is used for the second inequality.

Besides DIVIDE-INTO-TWO, another procedure should be accounted for when considering the time complexity of MCCD, which is the computation of the modularity $Q_i$ for each community $C_i$. Assuming that the change in Q is tracked during the iterations, it is known that the time complexity of modularity computation is bounded by $O\left(\right|V|+|E\left|\right)$ [27]. Therefore, the modularity computation does not affect the time complexity of MCCD, because DIVIDE-INTO-TWO takes a longer time. Since MCCD iterates dividing a community into two smaller communities until the stopping criterion is satisfied, in the worst case where the iteration number is equal to $\left|V\right|$, the time complexity of MCCD is given by $O\left(\right|V{|}^2\left|E\right|+|V{|}^{3}log|V\left|\right)$, which is in polynomial time. However, many practical networks are believed to have a small number of communities, which is equal to the total number of iterations of MCCD. Therefore, the time complexity of MCCD may be bounded by $O\left(\right|V\left|\right|E|+|V{|}^{2}log\left|V\right|)$ in those cases.

4. Results

This section describes the results of application of the proposed MCCD algorithm to four different example networks. The first example deals with a very simple network whose community structure is obvious. This example checks the validity of the proposed algorithm; if the algorithm cannot detect the obvious community structure of the simple network, it is useless to consider it any further. After the simple validity check, three more examples are used to show the performance of the MCCD algorithm. These examples are frequently used in the literature on the study of networks, so they can provide an evaluation of the performance of the proposed algorithm.

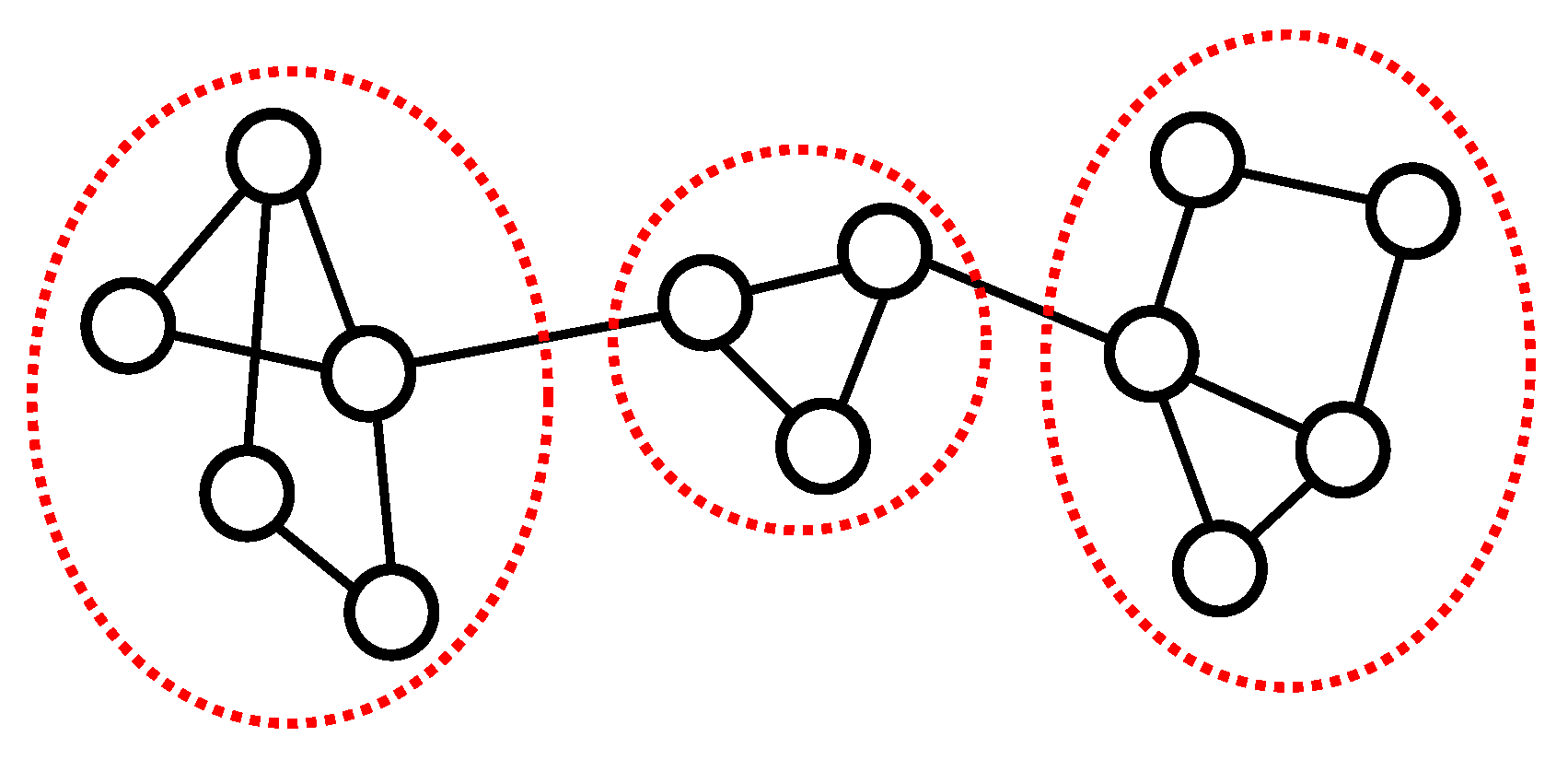
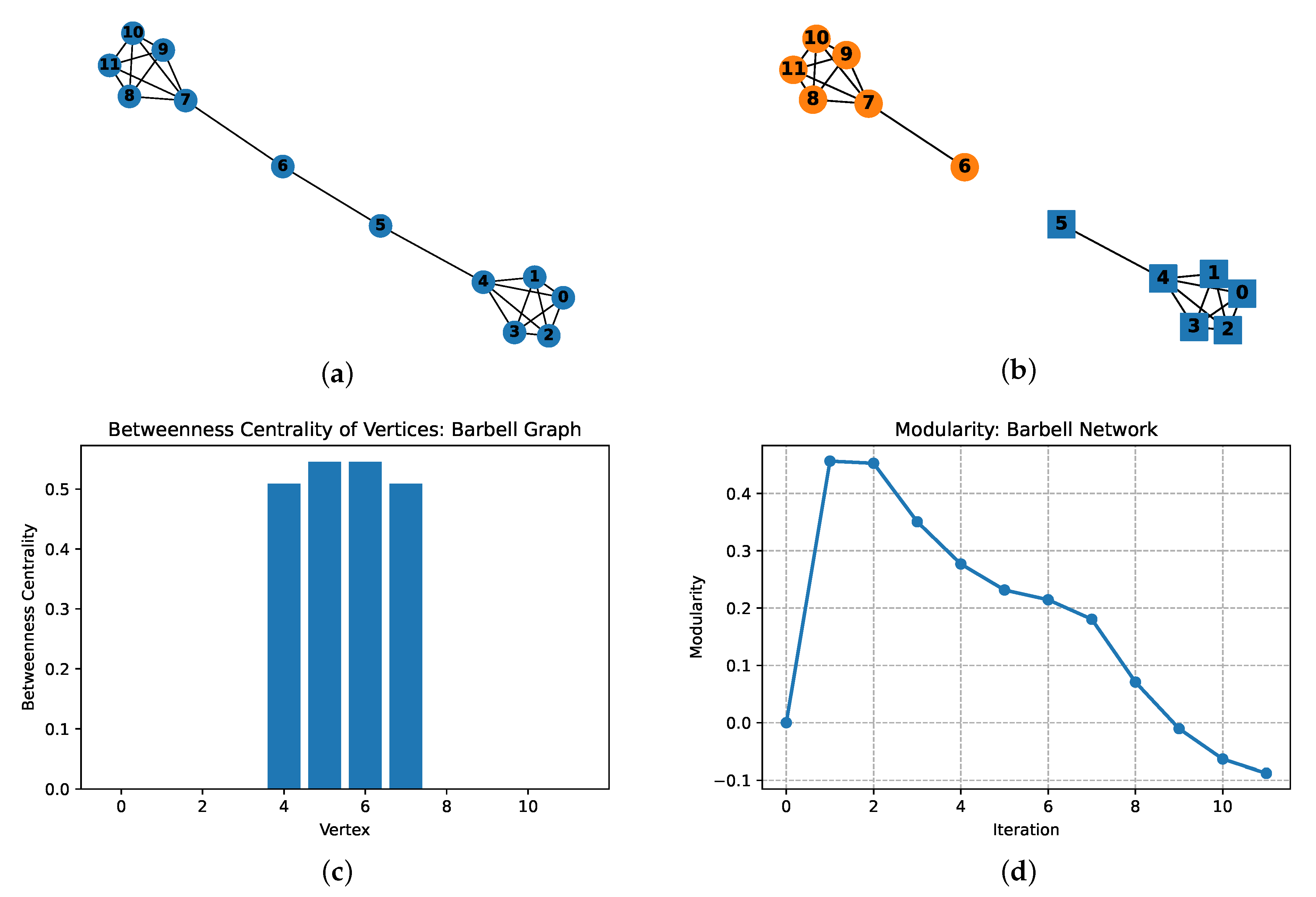
4.1. Example 1: A Simple Network

A very simple network, whose community structure is obvious, is generated as shown in Figure 2a. The network is a slightly generalized version of a graph, usually called an n-barbell graph, and it has two complete subgraphs that are connected by a path [67,68,69]. It is obvious that the network has two communities: $C_1=\{0,1,2,3,4,5\}$ and $C_2=\{6,7,8,9,10,11\}$.

The result of the MCCD algorithm applied to the network is shown in Figure 2b. As expected, the MCCD algorithm detects the two obvious communities, and they are represented as blue rectangles ($C_1$) and orange circles ($C_2$) in the figure. Therefore, the MCCD algorithm works well for the simple barbell graph.

The betweenness centrality value $c_B\left(v\right)$ for all vertices v of the barbell network is shown in Figure 2c. Vertices 5 and 6, which are boundary nodes of each community, have the highest betweenness centrality value because the shortest paths connecting nodes of the network pass through them more than any other nodes. Therefore, the MCCD algorithm selects the two vertices 5 and 6 as the source and sink nodes at the first iteration of the process. The algorithm then succeeds in finding the minimum cut between the two vertices and in detecting the obvious communities $C_1$ and $C_2$.

Note that the MCCD algorithm stops its iteration after the second pass because the modularity score of the second pass, which is about $0.4527$, is lower than that of the first pass, which is about $0.4565$. The modularity value of every iteration is shown in Figure 2d, where the MCCD algorithm is slightly modified to perform its iterations even though the modularity value $Q_m$ of each iteration starts decreasing; the lines 13–15 of MCCD Algorithm 2 are temporarily ignored to repeat the DIVIDE-INTO-TWO procedure until every edge is cut, so that each vertex forms its own community. As can be observed in Figure 2d, the modularity value quickly decreases as MCCD repeats its iteration passes.

4.2. Example 2: Zachary’s Karate Club Network

One of the frequently used real-world network data is Zachary’s karate club network [7]. The karate club network represents social interactions between 34 individuals, who were the members of a karate club at a university. Wayne Zachary obtained the network data by observing social interactions between the members for a period of three years from 1970 to 1972.

Before the study began, the club had employed an instructor (Mr. Hi) for karate lessons. At the beginning of the study, there was a conflict between the instructor and the club president (John A.) over the price of karate lessons. The instructor wished to raise prices while the president wanted to stabilize them. As time passed, there arose a series of factional confrontations, and then the president fired the instructor for attempting to raise lesson prices unilaterally. The supporters of the instructor resigned and formed a new organization headed by the instructor, thus completing the fission of the club.

Figure 3a shows the karate club network, where each vertex represents a member of the club. Vertices 0 and 33 represent the instructor and the president, respectively; the members who belong to the group headed by the instructor after the fission are represented by blue square vertices and the members who belong to the other group are represented by orange circle vertices. An edge of the network is drawn if two individuals were observed to interact outside the normal activities of the club, i.e., if they could be said to be friends outside the club activities.

The result of the proposed MCCD algorithm is shown in Figure 3b. Comparing the result with the data shown in Figure 3a, only one vertex, which is labeled 8, is misclassified by MCCD; vertex 8 joined the organization headed by the instructor after the fission, but the MCCD algorithm predicts that it belongs to the other group. Therefore, it can be said that MCCD works well for the karate club network.

Figure 3c shows the betweenness centrality values $c_B\left(v\right)$ for the vertices of the network. As expected, the instructor and the president nodes have the highest values, so MCCD selects the two vertices as the source and sink nodes at its first iteration. The modularity values after each iteration of MCCD are shown in Figure 3d. The modularity value achieves its maximum value of $0.3715$ after the first iteration, and the values quickly decrease as MCCD iterates its DIVIDE-INTO-TWO procedures.

To model information flow in the karate club, Zachary defined a capacitated network for the club, which includes a capacity matrix C whose entries are interpreted as representing a capacity or value of maximum possible information flow between two members of the club [7]. In other words, each edge of the network has a quantified value representing the strength/weakness of friend relationship between the two end vertices. These capacity values were assigned by analyzing data of social interactions between the club members. Using this capacitated network model, Zachary employed the max-flow min-cut theory and applied the labeling procedure of Ford and Fulkerson [58,70,71]. To apply the algorithm, the vertices 0 and 33 of the network were manually designated as the source and sink nodes.

Zachary obtained the same result as MCCD, which is expected, and explained why vertex 8 is misclassified [7]. One point to note is that, contrary to Zachary’s method, MCCD automatically selects the source and sink nodes and iterates the DIVIDE-INTO-TWO operation to find the best result for community detection.

Many community detection algorithms that have been proposed previously used the karate club network data to verify their performances, and the modularity results of a few well-known algorithms are shown in Table 1. Most algorithms result in higher modularity values than MCCD, but the ground truth of the karate club network has the modularity value of $0.371$ [6]. As described above, MCCD misclassifies only one vertex, so that the modularity value of MCCD is very close to the ground truth. This result illustrates that modularity is not a perfect measure even though it is a very good one.

Table 1. Modularity values for the karate club network of a few well-known community detection algorithms and MCCD: Girvan and Newman (GN) [25]; Newman (FN) [27]; Clauset, Newman, and Moore (CNM) [42]; Duch and Arenas (DA) [72]. Data from [25,27,46,72].

Algorithm	GN	FN	CNM	DA	MCCD
Modularity	0.401	0.381	0.381	0.419	0.372

Table 1. Modularity values for the karate club network of a few well-known community detection algorithms and MCCD: Girvan and Newman (GN) [25]; Newman (FN) [27]; Clauset, Newman, and Moore (CNM) [42]; Duch and Arenas (DA) [72]. Data from [25,27,46,72].

Algorithm	GN	FN	CNM	DA	MCCD
Modularity	0.401	0.381	0.381	0.419	0.372

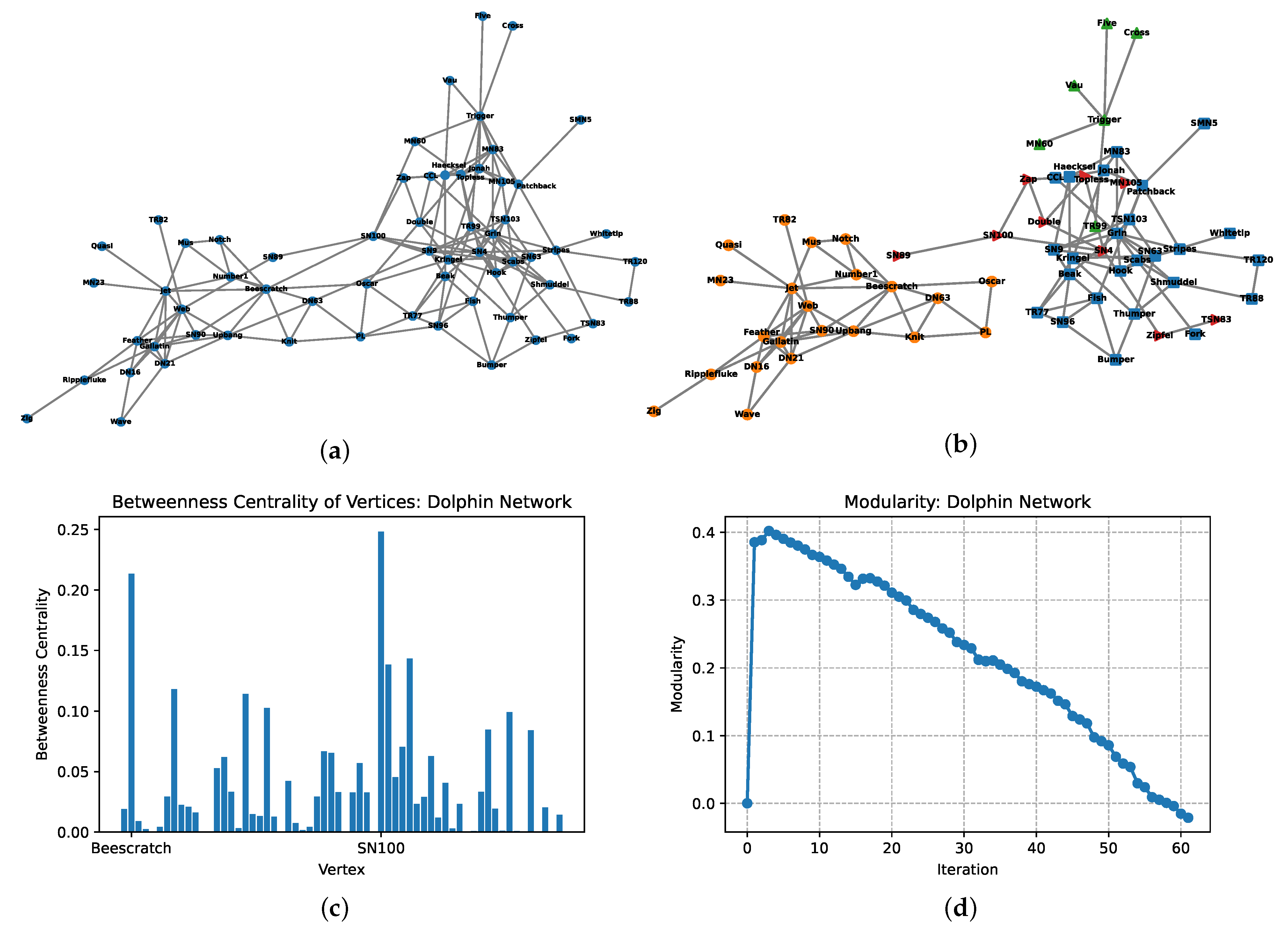
4.3. Example 3: The Social Network of Bottlenose Dolphins

The third example network is the social network of bottlenose dolphins that was studied by Lusseau [73]. Lusseau conducted a study about a social network of bottlenose dolphins residing in the Doubtful Sound, Fiordland, New Zealand, from November 1994 to November 2001. Based on the observations and study, 62 dolphins were formed into a social network, and it is shown in Figure 4a [74].

As can be seen from Figure 4a, the community structure of the dolphin network is not random, but it is not obvious, either. In other words, it seems that there is a weak community structure in the network, and different people may have different opinions on the structure as well as the number of communities. As mentioned before, it is hard to find a universally agreed answer for the community structure of a network, and this example illustrates this difficulty.

Figure 4b shows the result of MCCD application to the network. The modularity value achieved its maximum of $0.4021$ after three iterations; hence, MCCD detects four communities shown in the figure. The betweenness centrality values of the vertices and the modularity values after each iteration are shown in Figure 4c,d, respectively. It turns out that the modularity values of the first few iterations are similar, and this implies that it is hard to tell which structure is best for community detection. Even though MCCD generates the four community structure, structures of slightly different numbers of communities are also plausible. Lusseau presented a sociogram with three groups in his original paper [74]. In fact, the whole network visually seems to have two large groups, where the network is divided into two groups mostly by the gender of dolphins: males and females.

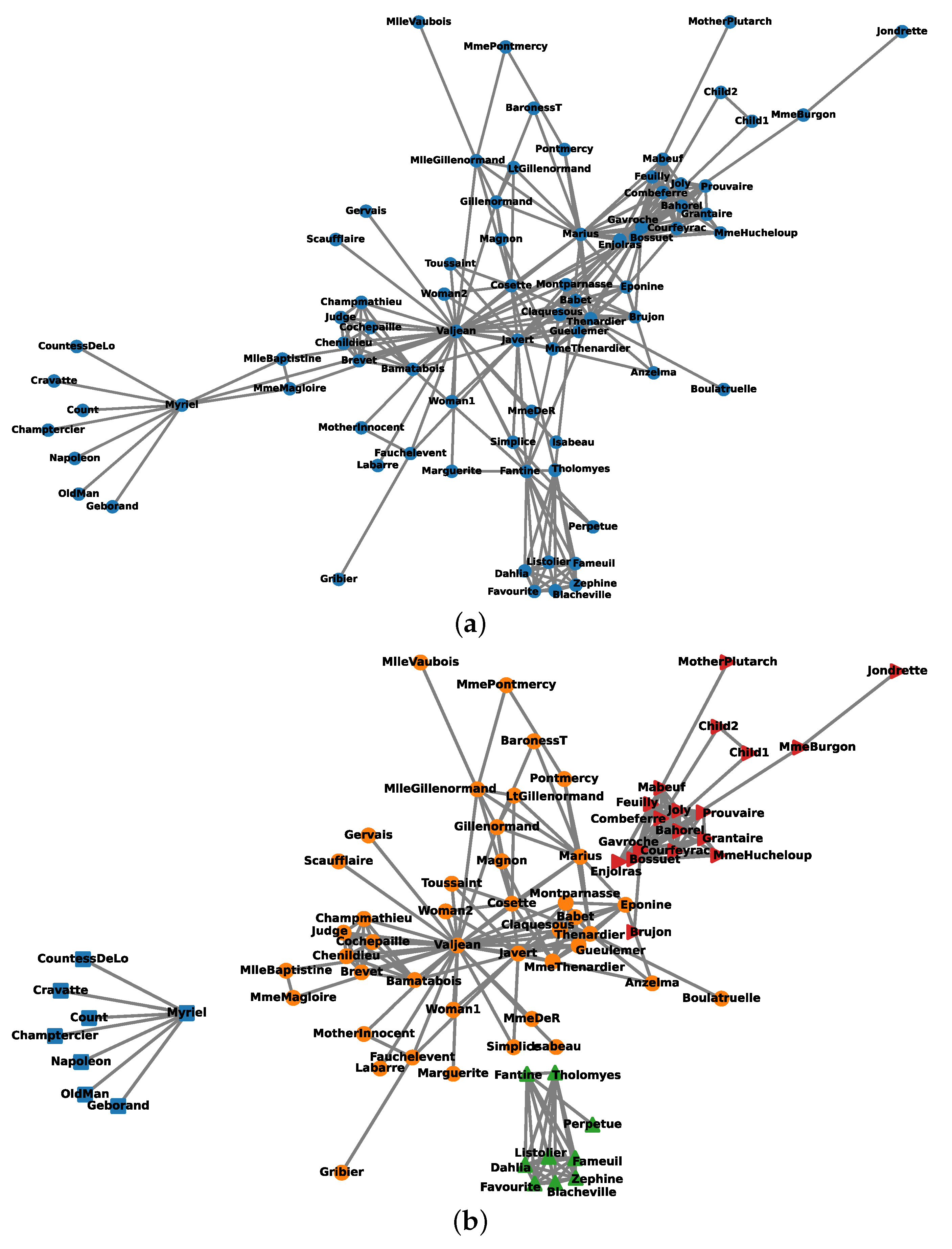
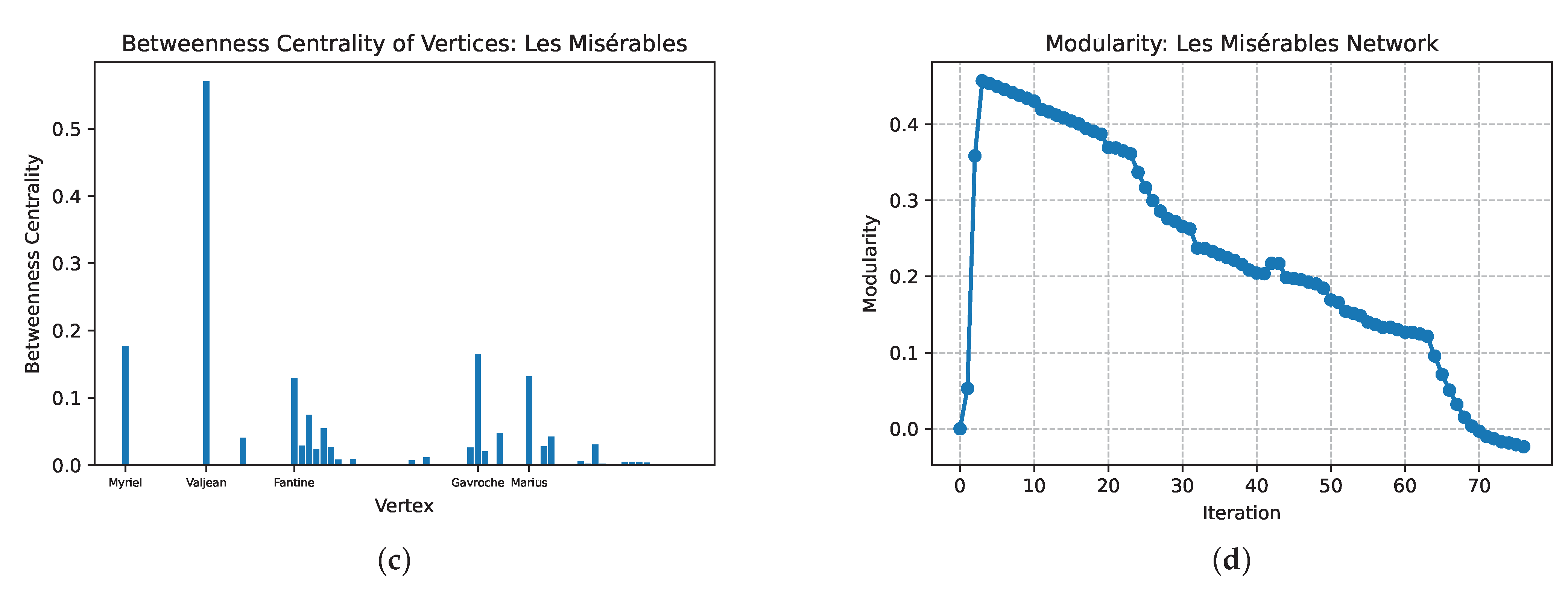
4.4. Example 4: The Characters Network of Les Misérables

Figure 5a shows the network of major characters in Les Misérables, a famous novel written by Victor Hugo. The network data was constructed by considering coappearances of characters in the same chapter of the book [75]. The 77 vertices of the network are major characters, and an edge between two vertices represents coappearance of the corresponding two characters in the same chapter. Even though Knuth assigned a value to each edge by counting the number of coappearances of the two characters, our method does not use the edge attribute values; MCCD uses the network structure only.

The result of MCCD application to the network is shown in Figure 5b. As shown in Figure 5d, the modularity value achieves its maximum of $0.4570$ when the network is partitioned into four communities. As expected, the protagonist Jean Valjean and the police officer Javert form the central positions of the main community. Another community that consists mainly of the members of the Friend of the ABC, the fictional association of revolutionary French republican students, is also detected. Enjolras, the charismatic leader of the association, belongs to this community. Furthermore, two more communities are also detected, and it can be observed that these two are centered by the main characters Myriel and Fantine, respectively.

5. Discussion

In this paper, a new algorithm for community detection was proposed and some experimental results were provided. As previously mentioned, the problem of community detection has its inherent difficulties; there is no exact solution for the problem. People may have different opinions about the community structure of a given network. As seen in Section 4, the networks of bottlenose dolphins and of characters in the novel Les Misérables are complicated, so that there is no universally agreed-upon community structure. Even though the modularity measure Q can provide a criterion to estimate the quality of community structures, it is only an indirect measure, and some may find a lower-scored community structure to be better than a higher-scored one.

Considering that the problem of community detection has no exact solution, the proposed algorithm MCCD shows fairly good results with comparable Q values when applied to the example networks of Section 4. In particular, the algorithm shows satisfactory results for the barbell graph and Zachary’s karate club network. For the more complicated networks in Section 4, it also detects community structures well, which can be visually observed from Figure 4 and Figure 5.

Even though the proposed algorithm showed its feasibility via the example networks of Section 4, further evaluation of the performance of the algorithm by using various benchmarks and larger network data is needed and remains as future work. Frequently used benchmarks such as GN and LFR may be used for the evaluation. For the example networks of Section 4, MCCD takes a few seconds with typical current computers, but the time performance should be carefully investigated with larger networks and benchmarks.

Optimization of the MCCD algorithm implementation is also left as future work. Many procedures called by MCCD may be carefully modified and implemented to reduce computation time. Modifying the algorithm so that it can be applied to detect overlapping community structures may be left as another element of future work. This may not be easy, however, because graph cut methods in general divide vertices without overlapping.