Asymmetric Quantum Multicast Network Coding: Asymmetric Optimal Cloning over Quantum Networks
Abstract
1. Introduction
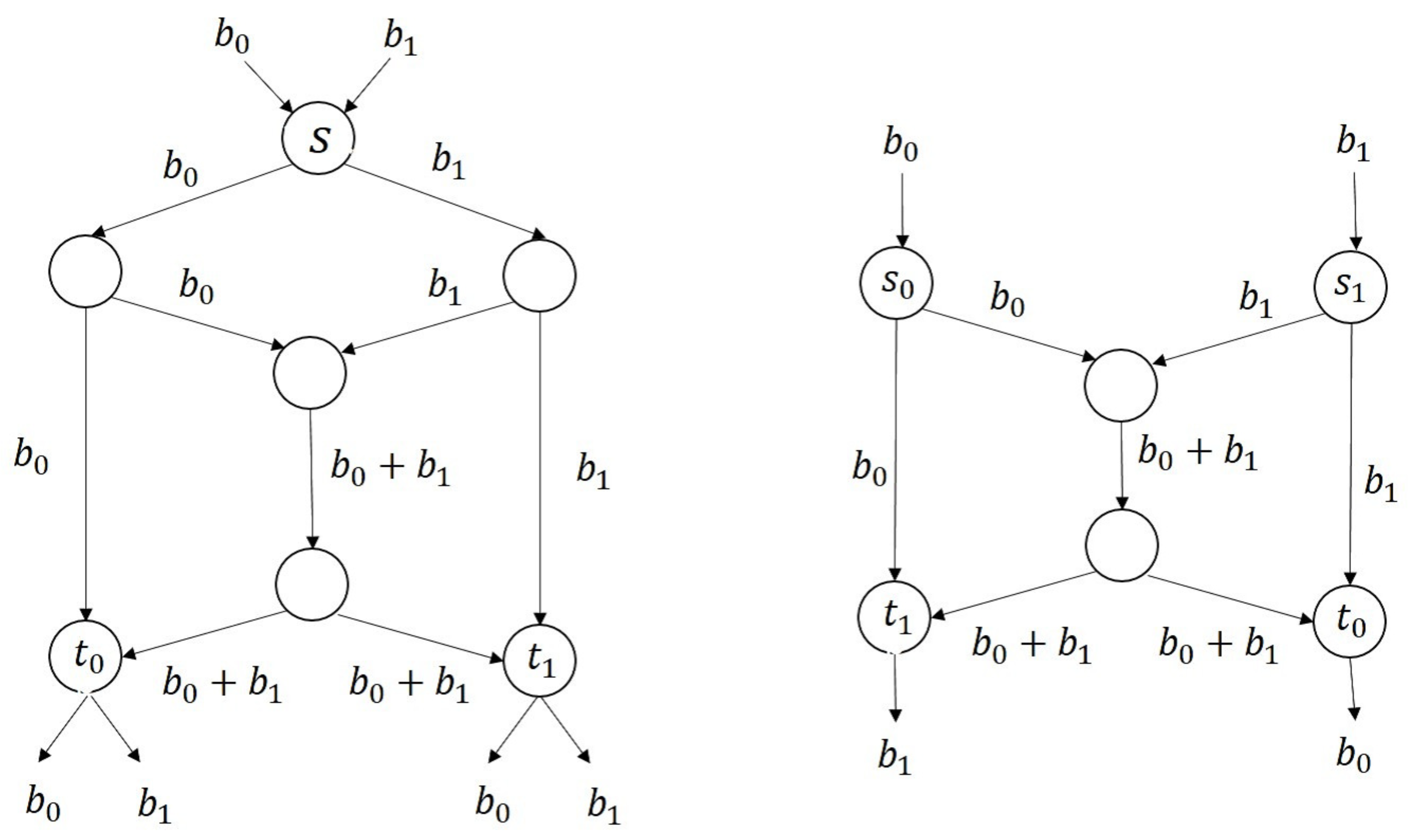
- The noise-free quantum network can be described by an undirected graph G with one source node and two (three) target nodes.
- Each quantum channel on the quantum network can transmit one q-dimensional quantum system in a single session.
- Measurement results (or classical information) can be sent freely from one node to another node on the quantum network.
- A small amount of entanglement that does not scale with q, is shared among the target nodes. The amount of entanglement is at most 2 ebit for two target nodes, and at most ebit for the case of three target nodes.
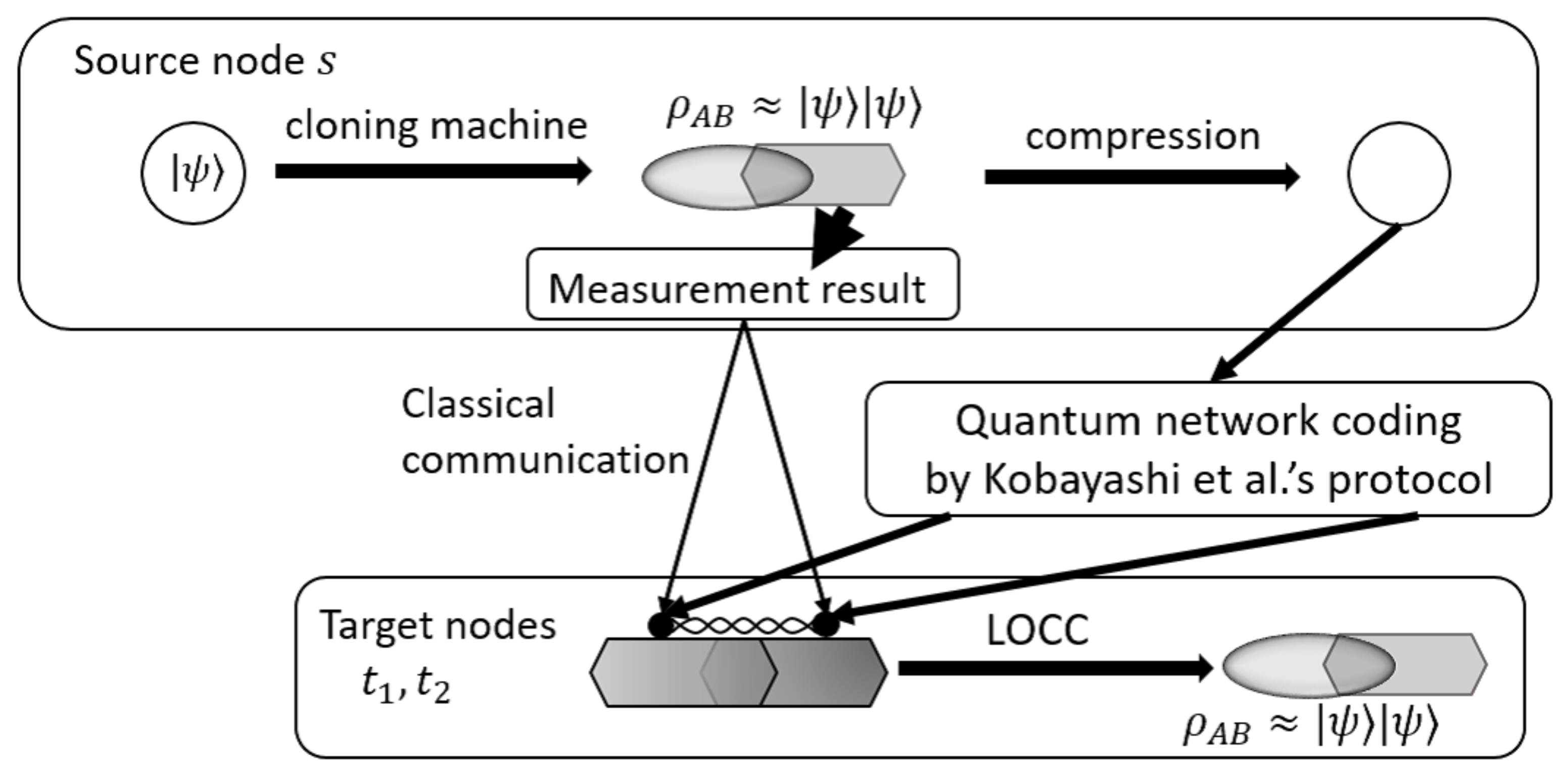
- We create two (three) asymmetric optimal UQCs of an input state with an ancilla system at a source node.
- We measure the ancilla system and send the measurement outcomes to the target nodes.
- We compress the whole ()-dimensional system into a d-dimensional system.
- We transmit the resulting state to two (three) target nodes using Kobayashi et al.’s multicast quantum network coding [44]. As a result, a GHZ-type state is shared among target nodes.
- We reconstruct the asymmetric optimal UQCs of the input state from the GHZ-type state using LOCC with a small amount of entanglement among the target nodes and the measurement outcomes sent from the source node.
2. Materials and Methods
2.1. Optimal Asymmetric Quantum Universal Cloning Machine
2.2. Classical Multicast Network Coding
2.3. Quantum Multicast Network Coding
| Protocol 1 The quantum multicast network coding protocol of Kobayashi et al. |
|
3. Results
3.1. Asymmetric UQC Multicast Protocol
3.1.1. Quantum Multicast Protocol
| Protocol 2 quantum multicast network coding protocol |
|
3.1.2. Proof of Quantum Multicast Protocol
3.2. Optimal Asymmetric Quantum Universal Clones Multicast Protocol
3.2.1. Quantum Multicast Protocol
| Protocol 3 quantum multicast network coding protocol (beginning) |
|
| Protocol 4 Continuation of Protocol 3 for quantum multicast network coding (for ) |
|
| Protocol 5 Continuation of Protocol 3 for quantum multicast network coding (for ) |
|
3.2.2. Proof of Quantum Multicast Protocol
4. Discussion
4.1. Comparison with a Conventional Schemes
4.2. Relation to Quantum Telecloning
4.3. Possibility of the Extension of Our Protocol for More Than 3 Receivers
- Step 1
- A quantum operation possibly including measurements are applied to on s, where the measurement result (if they exist) is sent to .
- Step 2
- The output of the quantum operation, which should be d-dimensional system, is multicasted to the target nodes by the protocol of Kobayashi et al.
- Step 3
- The state defined by Equation (89) is constructed by LOCC with an additional entanglement resource on .
4.4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Preskill, J. Quantum computing in the nisq era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Pednault, E.; Gunnels, J.A.; Nannicini, G.; Horesh, L.; Wisnieff, R. Leveraging secondary storage to simulate deep 54-qubit sycamore circuits. arXiv 2019, arXiv:1910.09534. [Google Scholar]
- Liu, Y.; Liu, X.; Li, F.; Fu, H.; Yang, Y.; Song, J.; Zhao, P.; Wang, Z.; Peng, D.; Chen, H.; et al. Closing the “Quantum Supremacy” Gap: Achieving Real-Time Simulation of a Random Quantum Circuit Using a New Sunway Supercomputer. In Proceedings of the SC ’21: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, St. Louis, MO, USA, 14–19 November 2021; pp. 1–12. [Google Scholar]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum Machine Learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef]
- Havlícĕk, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef]
- Cerezo, M.; Arrasmith, A.; Babbush, R.; Benjamin, S.C.; Endo, S.; Fujii, K.; McClean, J.R.; Mitarai, K.; Yuan, X.; Cincio, L.; et al. Variational quantum algorithms. Nat. Rev. Phys. 2021, 3, 625–644. [Google Scholar]
- Bharti, K.; Cervera-Lierta, A.; Kyaw, T.H.; Haug, T.; Alperin-Lea, S.; Anand, A.; Degroote, M.; Heimonen, H.; Kottmann, J.S.; Menke, T.; et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 2022, 94, 015004. [Google Scholar] [CrossRef]
- Zhou, M.-G.; Cao, X.-Y.; Lu, Y.-S.; Wang, Y.; Bao, Y.; Jia, Z.-Y.; Fu, Y.; Yin, H.-L.; Chen, Z.-B. Experimental Quantum Advantage with Quantum Coupon Collector. Research 2022, 2022, 9798679. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.-H.; Zhou, X.-Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- O’Malley, P.J.J.; Babbush, R.; Kivlichan, I.D.; Romero, J.; McClean, J.R.; Barends, R.; Kelly, J.; Roushan, P.; Tranter, A.; Ding, N.; et al. Scalable Quantum Simulation of Molecular Energies. Phys. Rev. X 2016, 6, 031007. [Google Scholar] [CrossRef]
- Cao, Y.; Romero, J.; Olson, J.P.; Degroote, M.; Johnson, P.D.; Kieferová, M.; Kivlichan, I.D.; Menke, T.; Peropadre, B.; Sawaya, N.P.D.; et al. Quantum Chemistry in the Age of Quantum Computing. Chem. Rev. 2019, 119, 10856–10915. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Boixo, S. Hartree-Fock on a superconducting qubit quantum computer. Science 2020, 369, 1084–1089. [Google Scholar]
- Kawachi, A.; Koshiba, T. Progress in quantum computational cryptography. J. Univ. Comput. Sci. 2006, 12, 691–709. [Google Scholar]
- Broadbent, A.; Fitzsimons, J.; Kashefi, E. Universal blind quantum computation. In Proceedings of the 50th Annual IEEE Symposium on Foundation of Computational Science, Washington, DC, USA, 25–27 October 2009; pp. 517–526. [Google Scholar]
- Morimae, T.; Fujii, K. Blind quantum computation protocol in which alice only makes measurements. Phys. Rev. A 2013, 87, 050301. [Google Scholar] [CrossRef]
- Wiesner, S. Conjugate Coding. SIGACT News 1983, 15, 78–88. [Google Scholar] [CrossRef]
- Aaronson, S. Quantum Copy-Protection and Quantum Money. In Proceedings of the 24th Annual IEEE Conference on Computational Complexity, Paris, France, 15–18 July 2009; pp. 229–242. [Google Scholar]
- Van Mete, R. Quantum Networking; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef]
- Acín, A.; Cirac, J.; Lewenstein, M. Entanglement percolation in quantum networks. Nat. Phys. 2007, 3, 256–259. [Google Scholar] [CrossRef]
- Pirandola, S.; Laurenza, R.; Ottaviani, C.; Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 15043. [Google Scholar] [CrossRef]
- Rigovacca, L.; Kato, G.; Bäuml, S.; Kim, M.S.; Munro, W.J.; Azuma, K. Versatile relative entropy bounds for quantum networks. New J. Phys. 2018, 20, 013033. [Google Scholar] [CrossRef]
- Pirandola, S. End-to-end capacities of a quantum communication network. Commun. Phys. 2019, 2, 51. [Google Scholar] [CrossRef]
- Hahn, F.; Pappa, A.; Eisert, J. Quantum network routing and local complementation. NPJ Quant. Inf. 2019, 5, 76. [Google Scholar] [CrossRef]
- Bäuml, S.; Azuma, K.; Kato, G.; Elkouss, D. Linear programs for entanglement and key distribution in the quantum internet. Commun. Phys. 2020, 3, 55. [Google Scholar] [CrossRef]
- Hahn, F.; Dahlberg, A.; Eisert, J.; Pappa, A. Limitations of nearest-neighbour quantum networks. arXiv 2022, arXiv:2202.10886. [Google Scholar]
- Flamini, F.; Spagnolo, N.; Sciarrino, F. Photonic quantum information processing: A review. Rep. Prog. Phys. 2018, 82, 016001. [Google Scholar] [CrossRef]
- Pompili, M.; Hermans, L.N.; Baier, S.; Beukers, H.K.C.; Humphreysr, P.C.; Schouten, R.N.; Vermeulen, R.F.; Tiggelman, M.J.; dos Santos Martins, L.; Dirkse, B.; et al. Realization of a multinode quantum network of remote solid-state qubits. Science 2021, 372, 259–264. [Google Scholar] [CrossRef]
- Briegel, H.-J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Phys. Rev. Lett. 1998, 81, 5932. [Google Scholar] [CrossRef]
- Duan, L.-M.; Lukin, M.D.; Cirac, J.I.; Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 2001, 414, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Tanenbaum, A.S.; Feamster, N.; Wetherall, D.J. Computer Networks, 6th ed.; Pearson: London, UK, 2021. [Google Scholar]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Ho, T.; Lun, D.S. Network Coding: An Introduction; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Yeung, R.W. Information Theory and Network Coding; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ahlswede, R.; Cai, N.; Li, S.-Y.R.; Yeung, R.W. Network information flow. IEEE Trans. Inf. Theor. 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Hayashi, M.; Iwama, K.; Nishimura, H.; Raymond, R.; Yamashita, S. Quantum Network Coding. In Proceedings of the STACS 2007 SE-52, Aachen, Germany, 22–24 February 2007; Lecture Notes in Computer Science. Thomas, W., Weil, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4393, pp. 610–621. [Google Scholar]
- Hayashi, M. Prior entanglement between senders enables perfect quantum network coding with modification. Phys. Rev. A 2007, 76, 40301. [Google Scholar] [CrossRef]
- Shi, Y.; Soljanin, E. On multicast in quantum networks. In Proceedings of the 40th Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 22–24 March 2006; pp. 871–876. [Google Scholar]
- Kobayashi, H.; Le Gall, F.; Nishimura, H.; Rötteler, M. General Scheme for Perfect Quantum Network Coding with Free Classical Communication. In Proceedings of the ICALP 2009: Automata, Languages and Programming, Rhodes, Greece, 5–12 July 2009; Lecture Notes in Computer Science. Albers, S., Marchetti-Spaccamela, A., Matias, Y., Nikoletseas, S., Thomas, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5555, pp. 622–633. [Google Scholar]
- Kobayashi, H.; Le Gall, F.; Nishimura, H.; Rötteler, M. Perfect quantum network communication protocol based on classical network coding. In Proceedings of the 2010 IEEE International Symposium on Information Theory (ISIT), Austin, TX, USA, 13–18 June 2010; pp. 2686–2690. [Google Scholar]
- Leung, D.; Oppenheim, J.; Winter, A. Quantum Network Communication; The Butterfly and Beyond. IEEE Trans. Inf. Theory 2010, 56, 3478–3490. [Google Scholar] [CrossRef]
- Kobayashi, H.; Le Gall, F.; Nishimura, H.; Rotteler, M. Constructing quantum network coding schemes from classical nonlinear protocols. In Proceedings of the 2011 IEEE International Symposium on Information Theory (ISIT), St. Petersburg, Russia, 31 July–5 August 2011; pp. 109–113. [Google Scholar]
- Jain, A.; Franceschetti, M.; Meyer, D.A. On quantum network coding. J. Math. Phys. 2011, 52, 032201. [Google Scholar] [CrossRef]
- Owari, M.; Kato, G.; Murao, M. Multicast Quantum Network Coding on the Butterfly Network. JP2013-201654A, 3 October 2013. (In Japanese). [Google Scholar]
- Kato, G.; Owari, M.; Murao, M. Multicast Quantum Network Coding. JP2014-192875A, 6 October 2014. (In Japanese). [Google Scholar]
- Kato, G.; Owari, M.; Murao, M. Multicast Quantum Network Coding. JP2015-220621A, 7 December 2015. (In Japanese). [Google Scholar]
- Li, J.; Chen, X.-B.; Xu, G.; Yang, Y.-X.; Li, Z.-P. Perfect Quantum Network Coding Independent of Classical Network Solutions. IEEE Commun. Lett. 2015, 19, 115–118. [Google Scholar] [CrossRef]
- Xu, G.; Chen, X.-B.; Li, J.; Wang, C.; Yang, Y.-X.; Li, Z. Network coding for quantum cooperative multicast. Quant. Inf. Process. 2015, 14, 4297–4322. [Google Scholar] [CrossRef]
- Epping, M.; Kampermann, H.; Bruß, D. Quantum Router with Network Coding. New J. Phys. 2006, 18, 103052. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; Sun, X.; Li, Z.; Yang, Y. Quantum network coding for multi-unicast problem based on 2D and 3D cluster states. Sci. China Inf. Sci. 2016, 59, 042301. [Google Scholar] [CrossRef]
- Li, D.D.; Gao, F.; Qin, S.J.; Wen, Q.-Y. Perfect quantum multiple-unicast network coding protocol. Quant. Inf. Process. 2018, 17, 13. [Google Scholar] [CrossRef]
- Pan, X.-B.; Xu, G.; Li, Z.-P.; Chen, X.-B.; Yang, Y.-X. Quantum network coding without loss of information. Quant. Inf. Process. 2021, 20, 65. [Google Scholar] [CrossRef]
- Pan, X.-B.; Chen, X.-B.; Xu, F.; Dou, Z.; Li, Z.-P.; Yang, Y.-X. Quantum multicast communication over the butterfly network. Chin. Phys. B 2022, 31, 010305. [Google Scholar] [CrossRef]
- Owari, M.; Kato, G.; Hayashi, M. Secure Quantum Network Coding on Butterfly Network. Quant. Sci. Technol. 2017, 3, 014001. [Google Scholar] [CrossRef]
- Kato, G.; Owari, M.; Hayashi, M. Single-Shot Secure Quantum Network Coding for General Multiple Unicast Network With Free One-Way Public Communication. IEEE Trans. Inf. Theor. 2021, 67, 4564–4587. [Google Scholar] [CrossRef]
- Song, S.; Hayashi, M. Quantum Network Code for Multiple-Unicast Network with Quantum Invertible Linear Operations. In Proceedings of the 13th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2018), Sydney, Australia, 16–18 July 2018. [Google Scholar]
- Song, S.; Hayashi, M. Secure Quantum Network Code without Classical Communication. IEEE Trans. Inf. Theor. 2020, 66, 1178–1192. [Google Scholar] [CrossRef]
- Shang, T.; Zhang, Y.; Liu, R.; Liu, J. Quantum network coding reducing decoherence effect. Quant. Inf. Process. 2021, 20, 267. [Google Scholar] [CrossRef]
- Satoh, T.; Ishizaki, K.; Nagayama, S.; Van Meter, R. Analysis of Quantum Network Coding for Realistic Repeater Networks. Phys. Rev. A 2016, 93, 032302. [Google Scholar] [CrossRef]
- Matsuo, T.; Satoh, T.; Nagayama, S.; Van Meter, R. Analysis of Measurement-based Quantum Network Coding over Repeater Networks under Noisy Conditions. Phys. Rev. A 2018, 97, 062328. [Google Scholar] [CrossRef]
- Akibue, S.; Murao, M. Network coding for distributed quantum computation over cluster and butterfly networks. IEEE Trans. Inf. Theor. 2016, 62, 6620–6637. [Google Scholar] [CrossRef]
- Lu, H.; Li, Z.-D.; Yin, X.-F.; Zhang, R.; Fang, X.-X.; Li, L.; Liu, N.-L.; Xu, F.; Chen, Y.-A.; Pan, J.-W. Experimental Quantum Network Coding. NPJ Quant. Inf. 2019, 5, 1–5. [Google Scholar] [CrossRef]
- Pathumsoot, P.; Matsuo, T.; Satoh, T.; Hajdušek, M.; Suwanna, S.; Van Meter, R. Modeling of measurement-based quantum network coding on a superconducting quantum processor. Phys. Rev. A 2020, 101, 052301. [Google Scholar] [CrossRef]
- Traskov, D.; Ratnakar, N.; Lun, D.S.; Koetter, R.; Medard, M. Network Coding for Multiple Unicasts: An Approach based on Linear Optimization. Proceedings the of 2006 IEEE International Symposium on Information Theory (ISIT2006), Washington, DC, USA, 9–14 July 2006; pp. 1758–1762. [Google Scholar]
- Wootters, W.K.; Zurek, W.H. A single quantum cannot be clone. Nature 1982, 299, 802–833. [Google Scholar] [CrossRef]
- Scarani, V.; Iblisdir, S.; Gison, N. Quantum cloning. Rev. Mod. Phys. 2005, 77, 1225–1256. [Google Scholar] [CrossRef]
- Fan, H.; Wang, Y.-N.; Jing, L.; Yue, J.-D.; Shi, H.-D.; Zhang, Y.-L.; Mu, L.-Z. Quantum cloning machines and the applications. Phys. Rep. 2014, 544, 241–322. [Google Scholar] [CrossRef]
- Buzek, V.; Hillery, M. Quantum copying: Beyond the no-cloning theorem. Phys. Rev. A 1996, 54, 1844. [Google Scholar] [CrossRef]
- Gisin, N.; Massar, S. Optimal Quantum Cloning Machines. Phys. Rev. Lett. 1997, 79, 2153. [Google Scholar] [CrossRef]
- Werner, R.F. Optimal cloning of pure states. Phys. Rev. A 1998, 58, 1827. [Google Scholar] [CrossRef]
- Niu, C.-S.; Griffiths, R.B. Optimal copying of one quantum bit. Phys. Rev. A 1998, 58, 4377. [Google Scholar] [CrossRef]
- Cerf, N.J. Asymmetric quantum cloning machines. Acta. Phys. Slov. 1998, 48, 115. [Google Scholar]
- Buzek, V.; Hillery, M.; Bednik, R. Controlling the flow of information in quantum cloners: Asymmetric cloning. Acta Phys. Slov. 1998, 48, 177–184. [Google Scholar]
- Cerf, N.J. Asymmetric quantum cloning in any dimension. J. Mod. Opt. 2000, 47, 187–209. [Google Scholar] [CrossRef]
- Fiurasek, J.; Filip, R.; Cerf, N.J. Highly asymmetric quantum cloning in arbitrary dimension. Quant. Inform. Comp. 2005, 5, 583. [Google Scholar]
- Iblisdir, S.; Acín, A.; Cerf, N.J.; Filip, R.; Fiurášek, J.; Gisin, N. Multipartite asymmetric quantum cloning. Phys. Rev. A 2005, 72, 042328. [Google Scholar] [CrossRef]
- Key, A.; Kaszlikowski, D.; Ramanathan, R. Optimal Cloning and Singlet Monogamy. Phys. Rev. Lett. 2009, 103, 050501. [Google Scholar] [CrossRef]
- Ren, X.-J.; Xiang, Y.; Fan, H. Optimal asymmetric 1→4 quantum cloning in arbitrary dimension. Eur. Phys. J. D 2011, 65, 621–625. [Google Scholar] [CrossRef]
- Ćwikliński, P.; Horodecki, M.; Studziński, M. Region of fidelities for 1→N universal qubit quantum cloner. Phys. Lett. A 2012, 376, 2178–2187. [Google Scholar] [CrossRef][Green Version]
- Key, A.; Ramanathan, R.; Kaszlikowski, D. Optimal Asymmetric Quantum Cloning. Quant. Inf. Comput. 2013, 13, 880. [Google Scholar]
- Xiao, X.; Yao, Y.; Zhou, L.M.; Wang, X. Distribution of quantum Fisher information in asymmetric cloning machines. Sci. Rep. 2014, 4, 7361. [Google Scholar] [CrossRef] [PubMed]
- Lamas-Linares, A.; Simon, C.; Howell, J.C.; Bouwmeester, D. Experimental Quantum Cloning of Single Photons. Science 2002, 296, 712. [Google Scholar] [CrossRef]
- Irvine, W.T.M.; Linares, A.L.; de Dood, M.J.A.; Bouwmeester, D. Optimal Quantum Cloning on a Beam Splitter. Phys. Rev. Lett. 2004, 92, 047902. [Google Scholar] [CrossRef] [PubMed]
- Andersen, U.L.; Josse, V.; Leuchs, G. Unconditional Quantum Cloning of Coherent States with Linear Optics. Phys. Rev. Lett. 2005, 94, 240503. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, A.-N.; Zhou, X.-Q.; Chen, Y.-A.; Lu, C.-Y.; Karlsson, A.; Pan, J.-W. Experimental Realization of Optimal Asymmetric Cloning and Telecloning via Partial Teleportation. Phys. Rev. Lett. 2005, 95, 030502. [Google Scholar] [CrossRef]
- Sabuncu, M.; Leuchs, G.; Andersen, U.L. Experimental continuous-variable cloning of partial quantum information. Phys. Rev. A 2008, 78, 052312. [Google Scholar] [CrossRef]
- Nagali, E.; Sansoni, L.; Sciarrino, F.; De Martini, F.; Marrucci, L.; Piccirillo, B.; Karimi, E.; Santamato, E. Optimal quantum cloning of orbital angular momentum photon qubits through Hong–Ou–Mandel coalescence. Nat. Photon. 2009, 3, 720–723. [Google Scholar] [CrossRef]
- Bechmann-Pasquinucci, H.; Gisin, N. Incoherent and coherent eavesdropping in the six-state protocol of quantum cryptography. Phys. Rev. A 1999, 59, 4238. [Google Scholar] [CrossRef]
- Bruß, D.; Macchiavello, C. Optimal Eavesdropping in Cryptography with Three-Dimensional Quantum States. Phys. Rev. Lett. 2002, 88, 127901. [Google Scholar] [CrossRef]
- Cerf, N.J.; Bourennane, M.; Karlsson, A.; Gisin, N. Security of Quantum Key Distribution Using d-Level Systems. Phys. Rev. Lett. 2002, 88, 127902. [Google Scholar] [CrossRef]
- Acin, A.; Gisin, N.; Scarani, V. Coherent pulse implementations of quantum cryptography protocols resistant to photon number splitting attacks. Phys. Rev. A 2004, 69, 012309. [Google Scholar] [CrossRef]
- Xiong, Z.-X.; Shi, H.-D.; Wang, Y.-N.; Jing, L.; Lei, J.; Mu, L.-Z.; Fan, H. General quantum key distribution in higher dimension. Phys. Rev. A. 2012, 85, 012334. [Google Scholar] [CrossRef]
- Sharma, U.K.; Chakrabarty, I.; Shukla, M.K. Broadcasting quantum coherence via cloning. Phys. Rev. A 2017, 96, 052319. [Google Scholar] [CrossRef]
- Kato, G.; Murao, M. Owari, Multicast quantum network coding as optimal cloning over a quantum network. 2022; in preparation. [Google Scholar]
- Ghiu, I. Asymmetric quantum telecloning of d-level systems and broadcasting of entanglement to different locations using the “many-to-many” communication protocol. Phys. Rev. A 2003, 67, 012323. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Y.-X. Asymmetric quantum telecloning of multiqubit states. Quant. Inf. Comp. 2007, 7, 716–729. [Google Scholar]
- Hayashi, M. Group Representation for Quantum Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen Channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Murao, M.; Jonathan, D.; Plenio, M.B.; Vedral, V. Quantum telecloning and multiparticle entanglement. Phys. Rev. A 1999, 59, 156–161. [Google Scholar] [CrossRef]
- Murao, M.; Plenio, M.B.; Vedral, V. Quantum-information distribution via entanglement. Phys. Rev. A 2000, 61, 032311. [Google Scholar] [CrossRef]
- Dür, W.; Cirac, J.I. Multiparty teleportation. J. Mod. Opt. 2000, 47, 247–255. [Google Scholar] [CrossRef]
- Fu, Y.; Yin, H.-L.; Chen, T.-Y.; Chen, Z.-B. Long-Distance Measurement-Device-Independent Multiparty Quantum Communication. Phys. Rev. Lett. 2015, 114, 090501. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirota, Y.; Owari, M. Asymmetric Quantum Multicast Network Coding: Asymmetric Optimal Cloning over Quantum Networks. Appl. Sci. 2022, 12, 6163. https://doi.org/10.3390/app12126163
Hirota Y, Owari M. Asymmetric Quantum Multicast Network Coding: Asymmetric Optimal Cloning over Quantum Networks. Applied Sciences. 2022; 12(12):6163. https://doi.org/10.3390/app12126163
Chicago/Turabian StyleHirota, Yuichi, and Masaki Owari. 2022. "Asymmetric Quantum Multicast Network Coding: Asymmetric Optimal Cloning over Quantum Networks" Applied Sciences 12, no. 12: 6163. https://doi.org/10.3390/app12126163
APA StyleHirota, Y., & Owari, M. (2022). Asymmetric Quantum Multicast Network Coding: Asymmetric Optimal Cloning over Quantum Networks. Applied Sciences, 12(12), 6163. https://doi.org/10.3390/app12126163





