Prediction Method of Water Absorption of Soft Rock Considering the Influence of Composition, Porosity, and Solute Quantitatively
Abstract
:1. Introduction
2. Materials and Methods
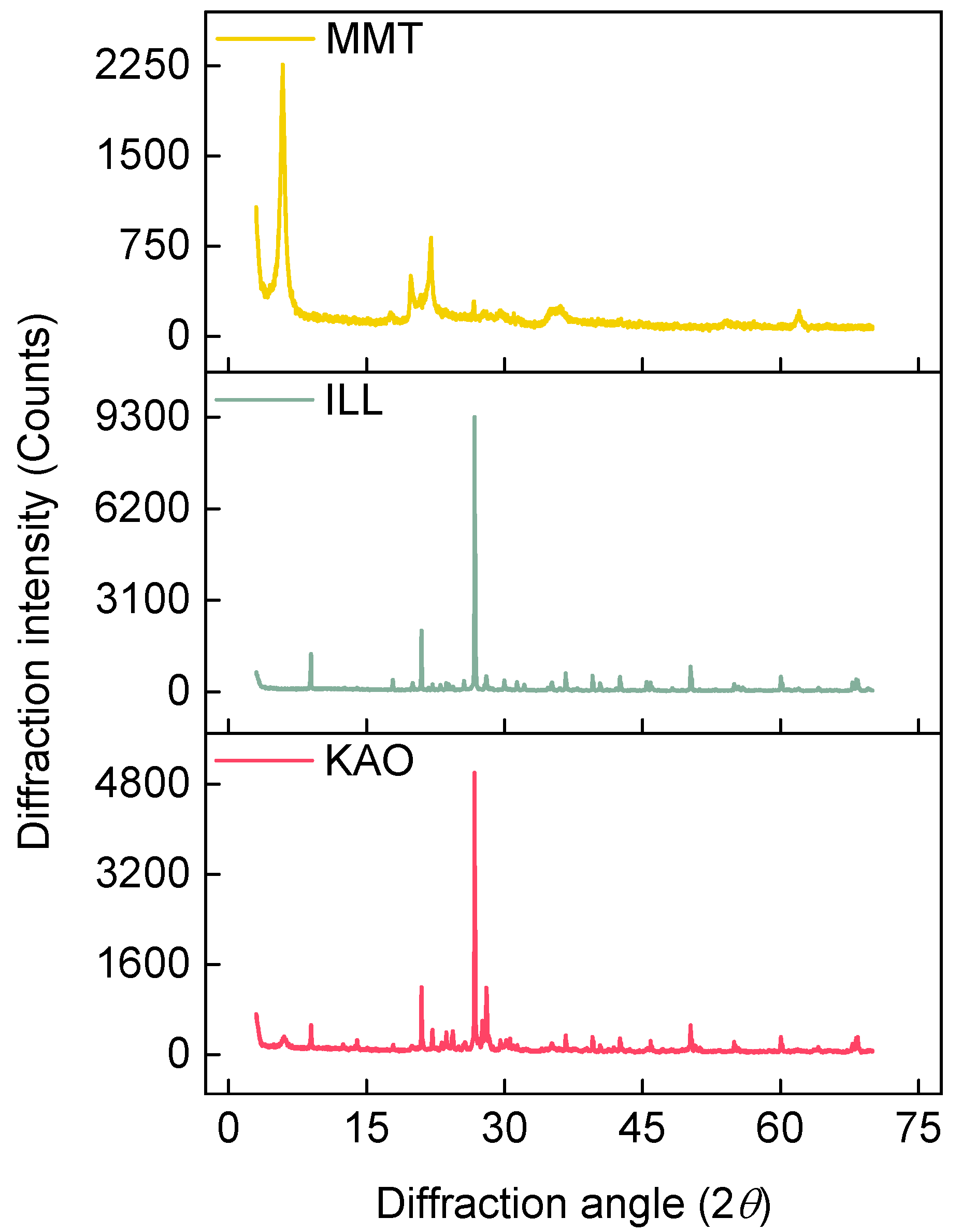
2.1. Test Materials
2.2. Test Methods
3. Results and Discussion
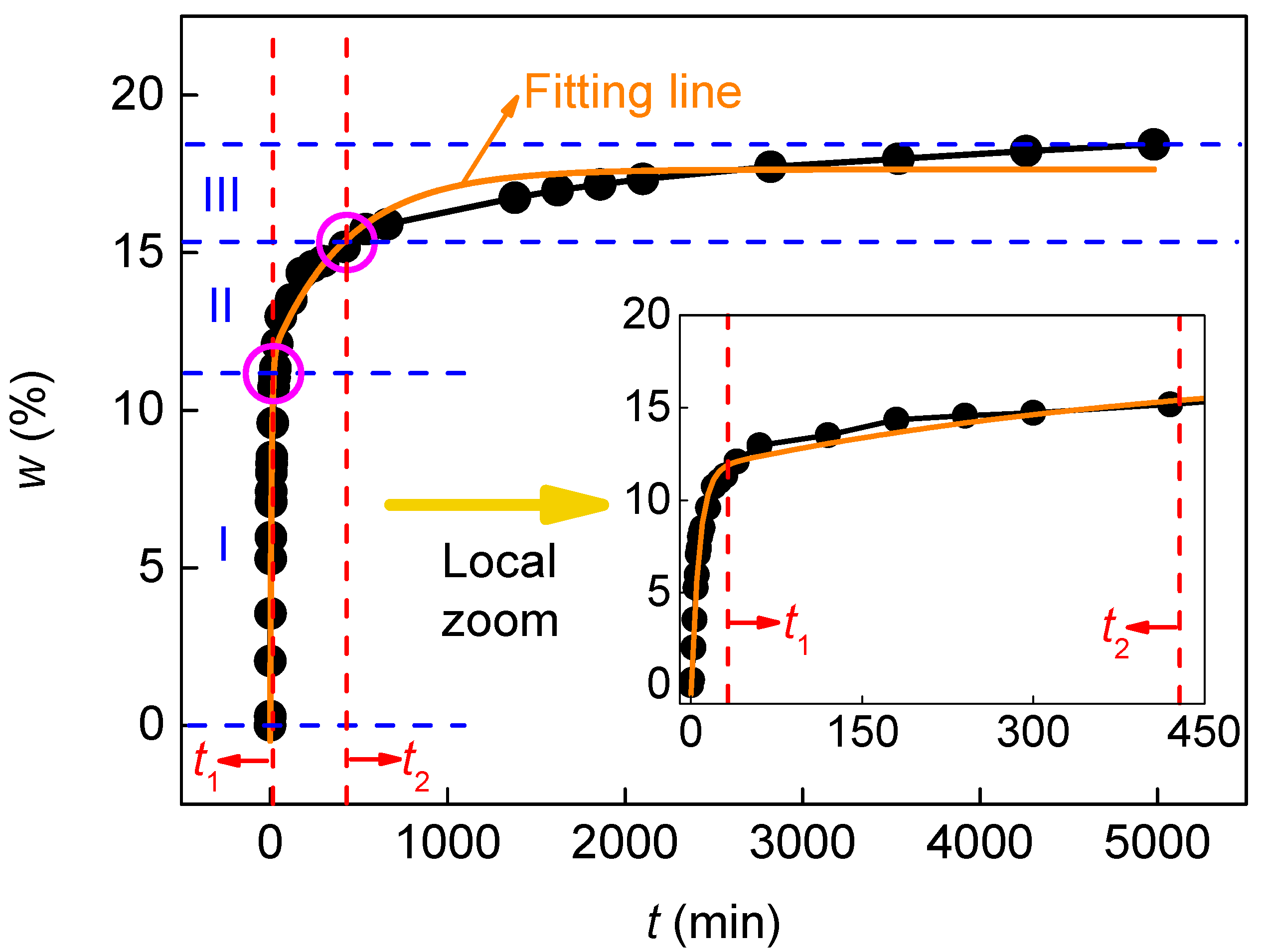
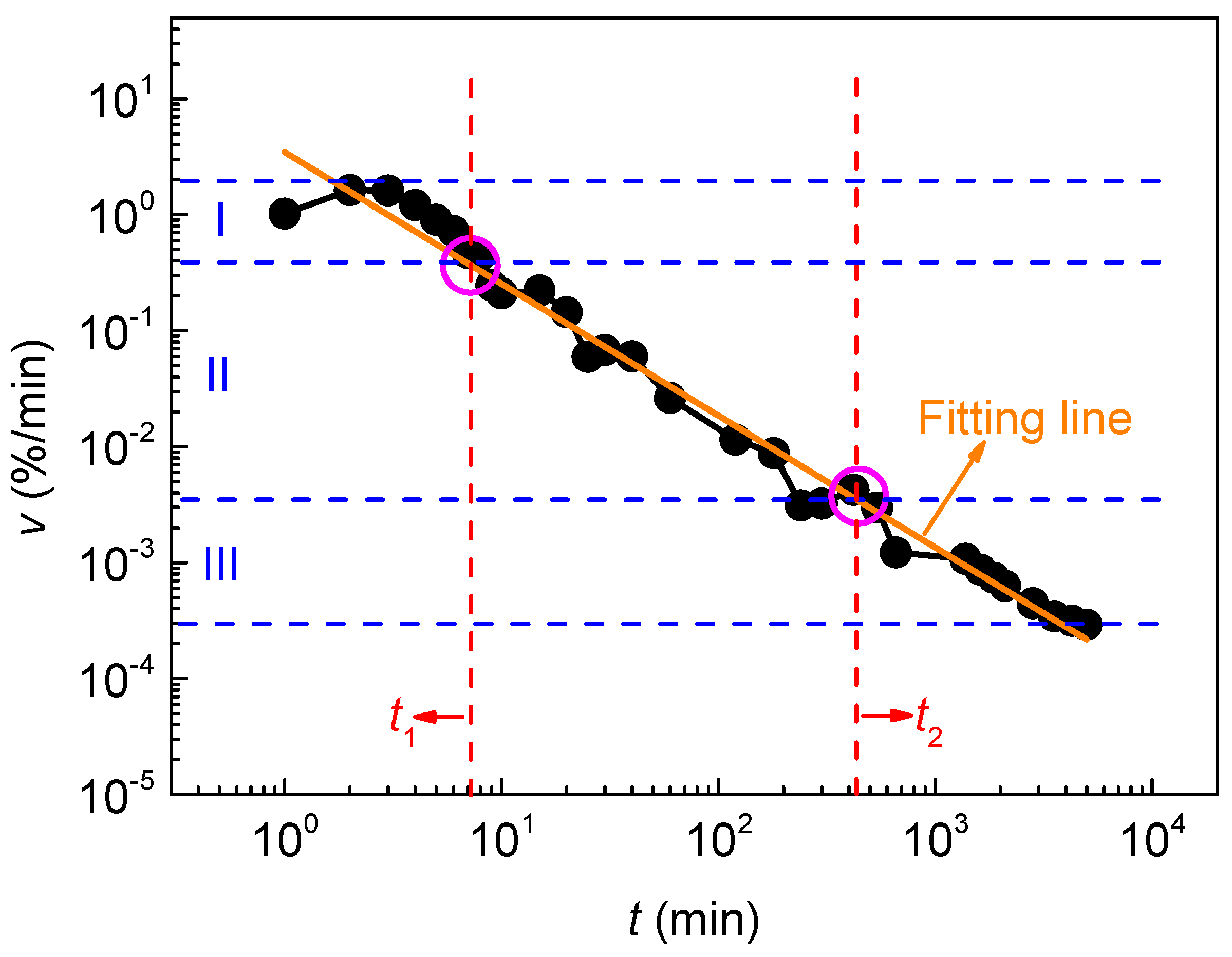
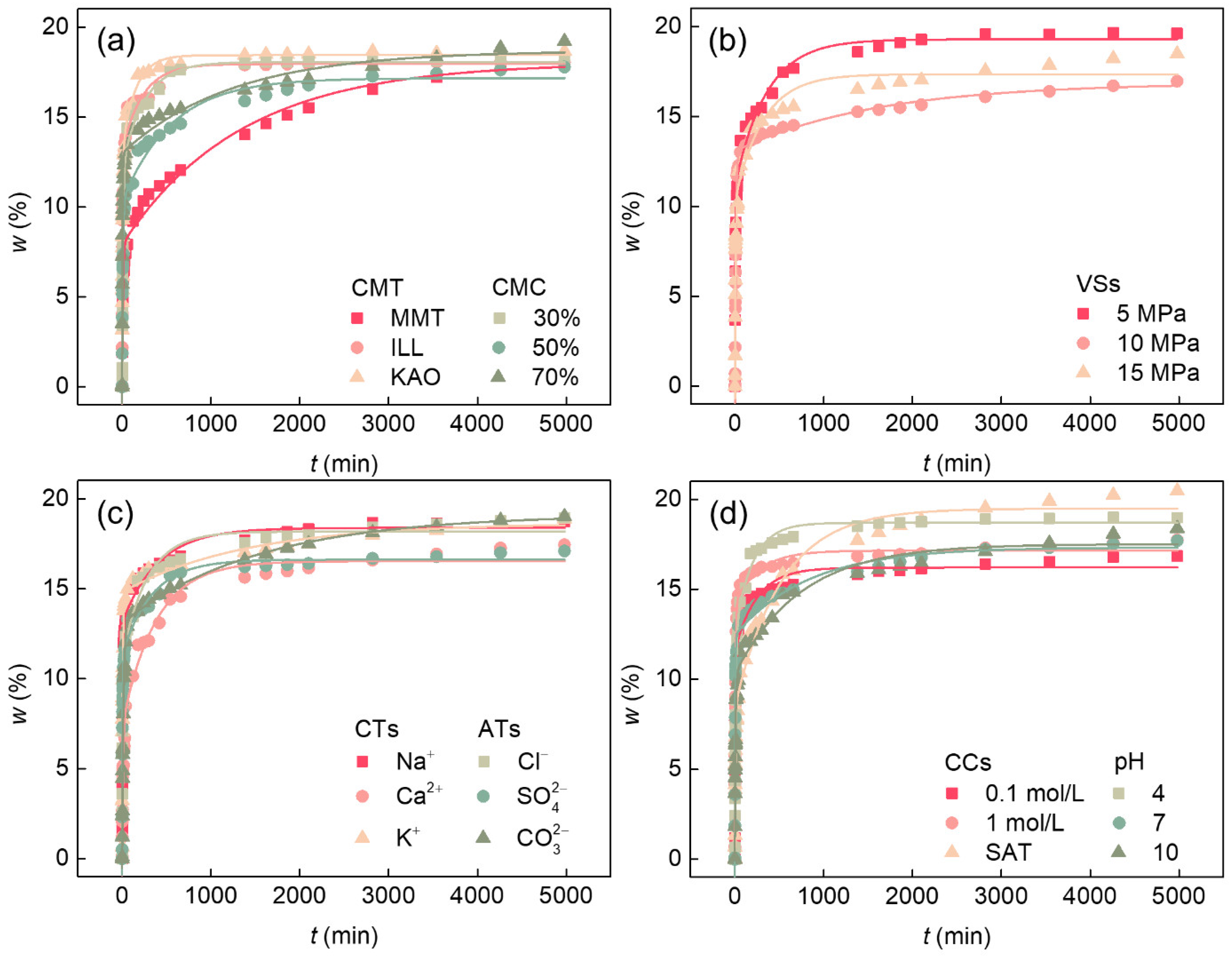
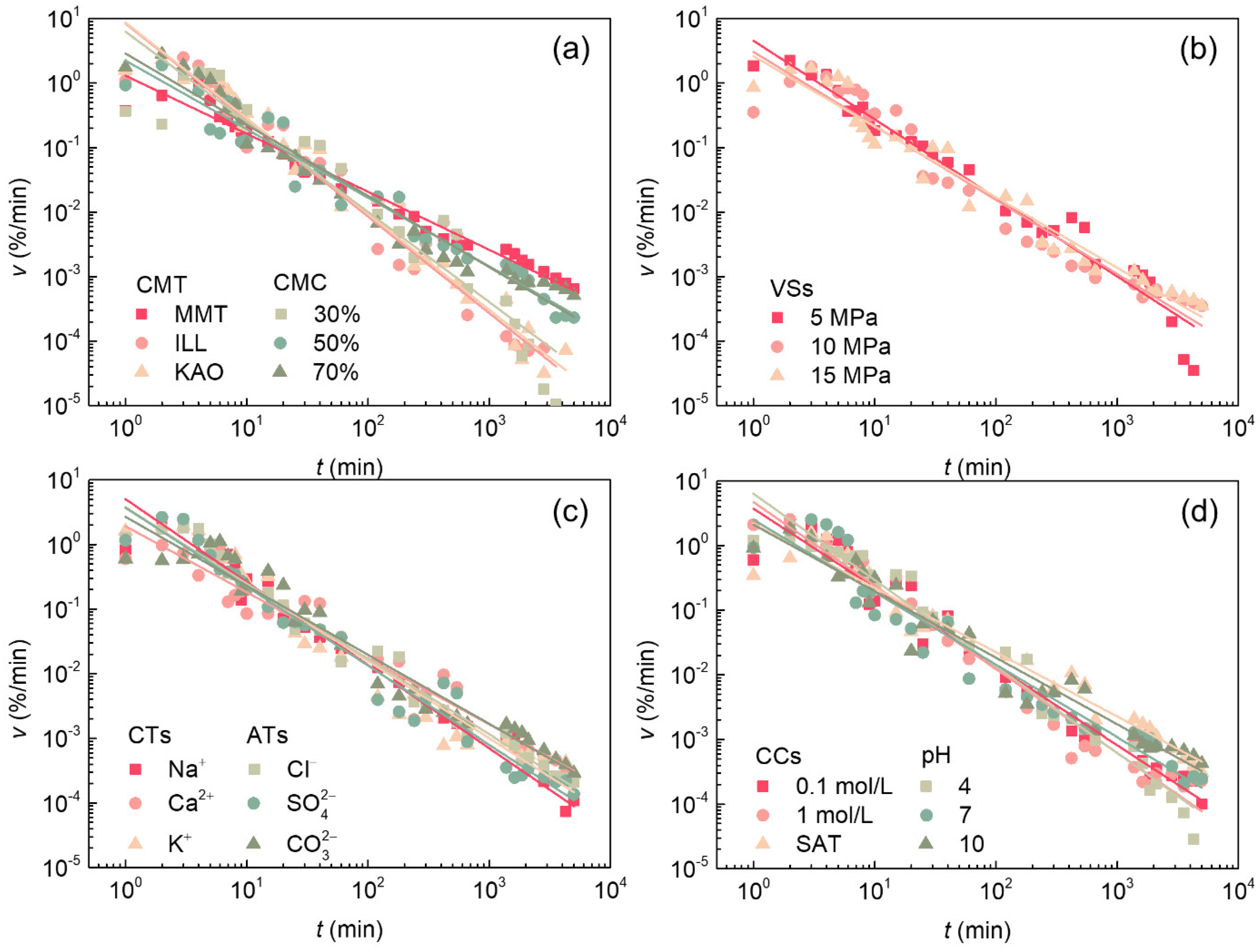
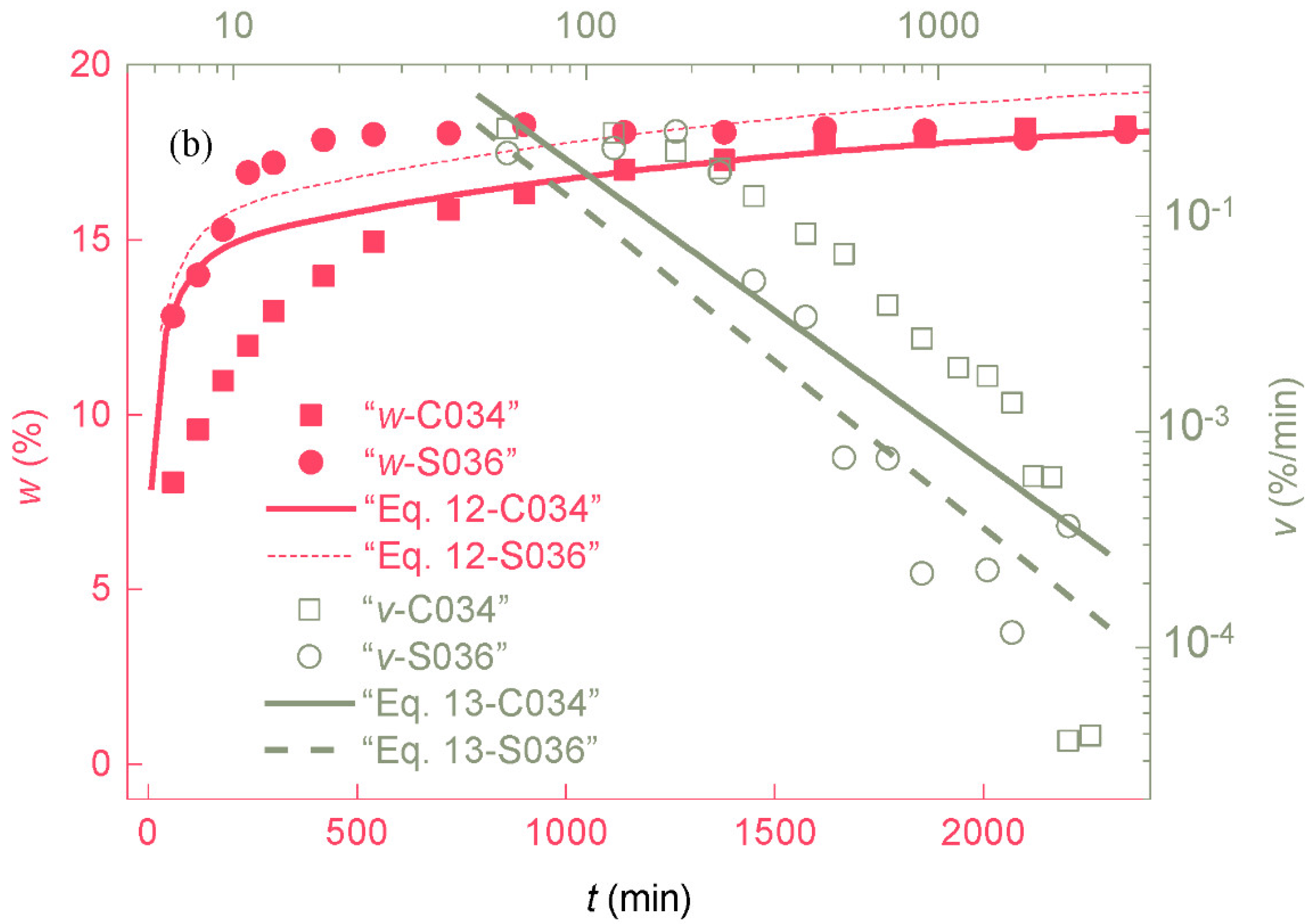
3.1. Change in Water Absorption with Time
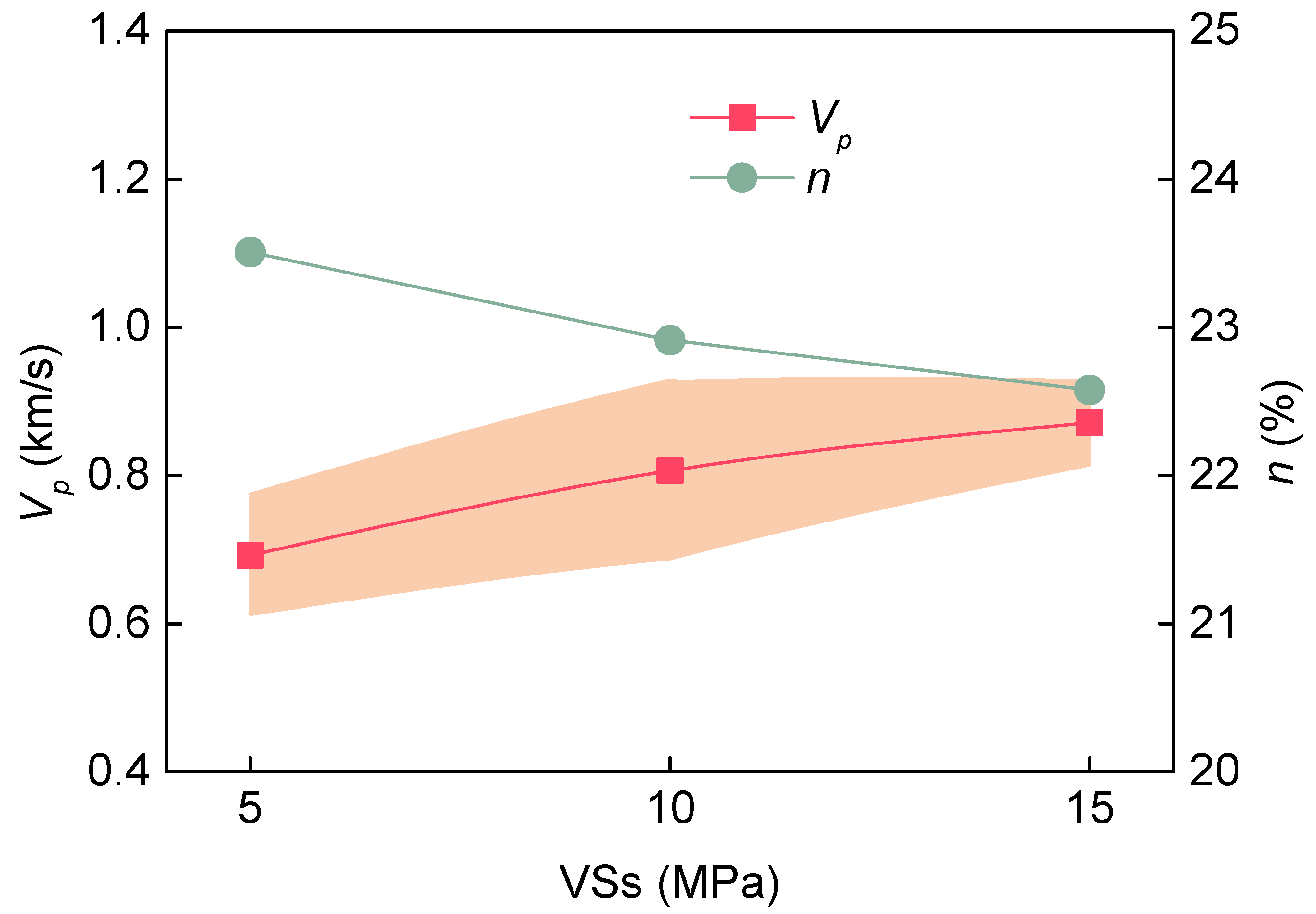
3.2. Influence of Various Factors on the Water Absorption Process of Soft Rock
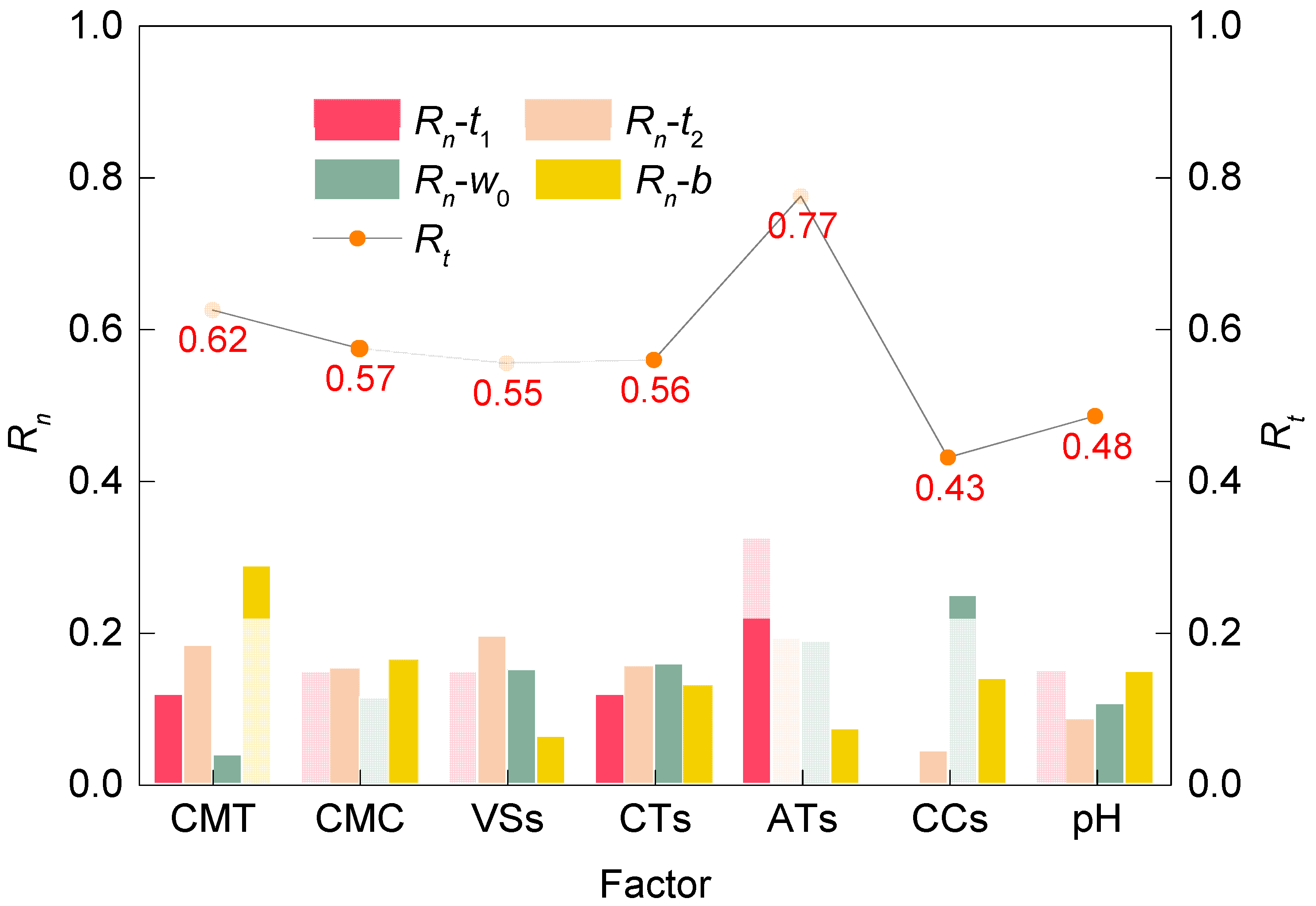
3.3. Quantification of the Degree of Influence of Each Factor
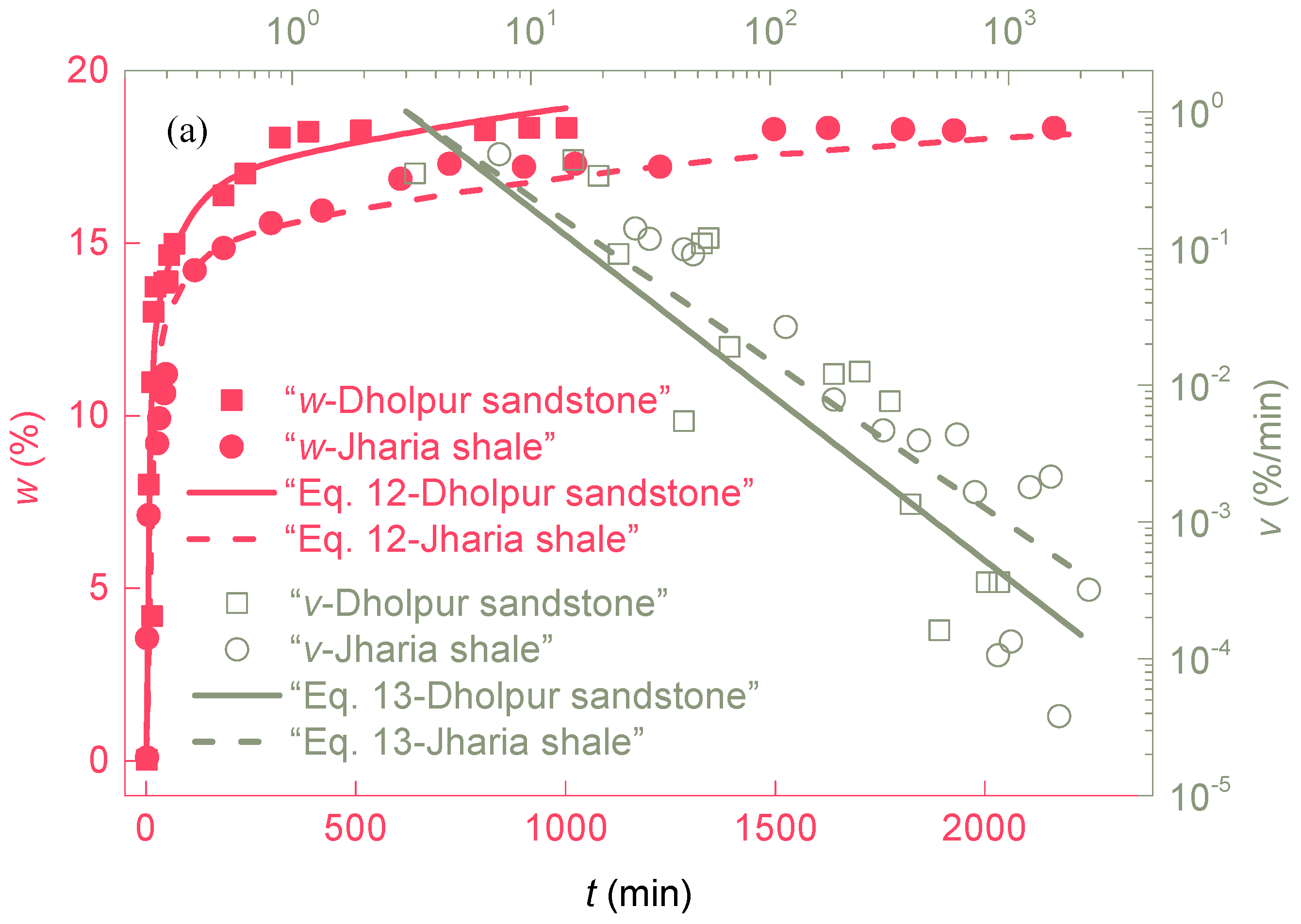
3.4. Water Absorption Prediction Model of Soft Rock
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.L.; Wang, P.G.; Zhao, M.; Du, X.L.; Zhao, X. Seismic structure-water-sediment-rock interaction model and its application to immersed tunnel analysis under obliquely incident earthquake. Tunn. Undergr. Space Technol. 2021, 109, 103758. [Google Scholar] [CrossRef]
- Li, Y.T.; Zhang, B.; Shi, L.; Ye, Y.W. Dynamic Variation Characteristics of Seawater Intrusion in Underground Water-Sealed Oil Storage Cavern under Island Tidal Environment. Water 2019, 11, 130. [Google Scholar] [CrossRef] [Green Version]
- Zangiabadi, B.; Gomari, S.R. Systematic Evaluation of Rock Mechanical Behavior of Chalk Reservoirs in the Presence of a Variety of Water Compositions. Int. J. Geomech. 2017, 17, 04017040. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, J.A.; Mortimore, R.N.; Stone, K.J.; Busby, J.P. Sea saltwater weakening of chalk and the impact on cliff instability. Geomorphology 2013, 191, 14–22. [Google Scholar] [CrossRef] [Green Version]
- Zaid, M.; Sadique, M.R.; Samanta, M. Effect of unconfined compressive strength of rock on dynamic response of shallow unlined tunnel. SN Appl. Sci. 2020, 2, 2131. [Google Scholar] [CrossRef]
- Mishra, S.; Zaid, M.; Rao, K.S.; Gupta, N.K. FEA of Urban Rock Tunnels Under Impact Loading at Targeted Velocity. Geotech. Geol. Eng. 2022, 40, 1693–1711. [Google Scholar] [CrossRef]
- Zaid, M.; Mishra, S. Numerical Analysis of Shallow Tunnels Under Static Loading: A Finite Element Approach. Geotech. Geol. Eng. 2021, 39, 2581–2607. [Google Scholar] [CrossRef]
- Zaid, M.; Sadique, M.R.; Alam, M.M. Blast Resistant Analysis of Rock Tunnel Using Abaqus: Effect of Weathering. Geotech. Geol. Eng. 2022, 40, 809–832. [Google Scholar] [CrossRef]
- Sadique, M.R.; Zaid, M.; Alam, M.M. Rock Tunnel Performance Under Blast Loading Through Finite Element Analysis. Geotech. Geol. Eng. 2022, 40, 35–56. [Google Scholar] [CrossRef]
- Zaid, M.; Sadique, M.R. A Simple Approximate Simulation Using Coupled Eulerian–Lagrangian (CEL) Simulation in Investigating Effects of Internal Blast in Rock Tunnel. Indian Geotech. J. 2021, 51, 1038–1055. [Google Scholar] [CrossRef]
- Zaid, M.; Sadique, R. Numerical modelling of internal blast loading on a rock tunnel. Adv. Comput. Des. 2020, 5, 417–443. [Google Scholar]
- Zaid, M.; Shah, I.A. Numerical Analysis of Himalayan Rock Tunnels under Static and Blast Loading. Geotech. Geol. Eng. 2021, 39, 5063–5083. [Google Scholar] [CrossRef]
- Deng, H.F.; Zhou, M.L.; Li, J.L.; Sun, X.S.; Huang, Y.L. Creep degradation mechanism by water-rock interaction in the red-layer soft rock. Arab. J. Geosci. 2016, 9, 601. [Google Scholar] [CrossRef]
- Russell, T.; Pham, D.; Neishaboor, M.T.; Badalyan, A.; Behr, A.; Genolet, L.; Kowollik, P.; Zeinijahromi, A.; Bedrikovetsky, P. Effects of kaolinite in rocks on fines migration. J. Nat. Gas Sci. Eng. 2017, 45, 243–255. [Google Scholar] [CrossRef]
- Shi, P.X.; Zhang, D.L.; Pan, J.L.; Liu, W. Geological Investigation and Tunnel Excavation Aspects of the Weakness Zones of Xiang’an Subsea Tunnels in China. Rock Mech. Rock Eng. 2016, 49, 4853–4867. [Google Scholar] [CrossRef]
- Nilsen, B. Characteristics of Water Ingress in Norwegian Subsea Tunnels. Rock Mech. Rock Eng. 2014, 47, 933–945. [Google Scholar] [CrossRef]
- Liu, Z.; He, X.F.; Fan, J.; Zhou, C.Y. Study on the Softening Mechanism and Control of Red-Bed Soft Rock under Seawater Conditions. J. Mar. Sci. Eng. 2019, 7, 235. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.L.; Wang, L.G.; Sun, X.K.; Wang, J. Experimental study of the influence of water and temperature on the mechanical behavior of mudstone and sandstone. Bull. Eng. Geol. Environ. 2017, 76, 645–660. [Google Scholar] [CrossRef]
- Verstrynge, E.; Adriaens, R.; Elsen, J.; van Balen, K. Multi-scale analysis on the influence of moisture on the mechanical behavior of ferruginous sandstone. Constr. Build. Mater. 2014, 54, 78–90. [Google Scholar] [CrossRef]
- Tinnacher, R.M.; Holmboe, M.; Tournassat, C.; Bourg, I.C.; Davis, J.A. Ion adsorption and diffusion in smectite: Molecular, pore, and continuum scale views. Geochim. Cosmochim. Acta 2016, 177, 130–149. [Google Scholar] [CrossRef] [Green Version]
- Manaka, M.; Takeda, M. An experimental examination of the effect of the salt type on the chemo-osmotic, diffusive, and hydraulic parameters of Wakkanai mudstones. J. Hydrol. 2018, 564, 1058–1073. [Google Scholar] [CrossRef]
- Chai, Z.Y.; Kang, T.H.; Feng, G.R. Effect of aqueous solution chemistry on the swelling of clayey rock. Appl. Clay Sci. 2014, 93–94, 12–16. [Google Scholar] [CrossRef]
- Binal, A. Prediction of mechanical properties of non-welded and moderately welded ignimbrite using physical properties, ultrasonic pulse velocity, and point load index tests. Q. J. Eng. Geol. Hydrogeol. 2009, 42, 107–122. [Google Scholar] [CrossRef]
- Wang, L.; Bornert, M.; Héripré, E.; Chanchole, S.; Pouya, A.; Halphen, B. Microscale insight into the influence of humidity on the mechanical behavior of mudstones. J. Geophys. Res. Solid Earth 2015, 120, 3173–3186. [Google Scholar] [CrossRef]
- Tertre, E.; Savoye, S.; Hubert, F.; Pret, D.; Dabat, T.; Ferrage, E. Diffusion of Water through the Dual-Porosity Swelling Clay Mineral Vermiculite. Environ. Sci. Technol. 2018, 52, 1899–1907. [Google Scholar] [CrossRef]
- Simonyan, A.V.; Dultz, S.; Behrens, H. Diffusive transport of water in porous fresh to altered mid-ocean ridge basalts. Chem. Geol. 2012, 306, 63–77. [Google Scholar] [CrossRef]
- Yagiz, S. P-wave velocity test for assessment of geotechnical properties of some rock materials. Bull. Mater. Sci. 2011, 34, 947–953. [Google Scholar] [CrossRef]
- Fabricius, I.L.; Gommesen, L.; Krogsboll, A.; Olsen, D. Chalk porosity and sonic velocity versus burial depth: Influence of fluid pressure, hydrocarbons, and mineralogy. AAPG Bull. 2008, 92, 201–223. [Google Scholar] [CrossRef]
- Gonzalez, J.; Saldana, M.; Arzua, J. Analytical Model for Predicting the UCS from P-Wave Velocity, Density, and Porosity on Saturated Limestone. Appl. Sci. 2019, 9, 5265. [Google Scholar] [CrossRef] [Green Version]
- Pavicic, I.; Brisevac, Z.; Vrbaski, A.; Grgasovic, T.; Duic, Z.; Sijak, D.; Dragicevic, I. Geometric and Fractal Characterization of Pore Systems in the Upper Triassic Dolomites Based on Image Processing Techniques (Example from Zumberak Mts, NW Croatia). Sustainability 2021, 13, 7668. [Google Scholar] [CrossRef]
- Briševac, Z.; Kujundžić, T. Models to estimate the Brazilian indirect tensile strength of limestone in saturated state. Min.-Geol.-Pet. Eng. Bull. 2016, 31, 59–67. [Google Scholar] [CrossRef]
- Brisevac, Z.; Kujundzic, T.; Macenic, M. Estimation of Uniaxial Compressive and Tensile Strength of Rock Material from Gypsum Deposits in the Knin Area. Teh. Vjesn. 2017, 24, 855–861. [Google Scholar] [CrossRef] [Green Version]
- Feng, D.; Wu, K.; Wang, X.; Li, J.; Shi, J.; Zhang, Y.; Qi, P.; Li, X. Analytical investigations the effect of temperature and pressure on spontaneous countercurrent imbibition in unsaturated porous media. Energ Fuel 2019, 33, 8544–8556. [Google Scholar] [CrossRef]
- Erguler, Z.A.; Ulusay, R. Water-induced variations in mechanical properties of clay-bearing rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 355–370. [Google Scholar] [CrossRef]
- Rahromostaqim, M.; Sahimi, M. Molecular Dynamics Simulation of Hydration and Swelling of Mixed-Layer Clays. J. Phys. Chem. C 2018, 122, 14631–14639. [Google Scholar] [CrossRef]
- Rahromostaqim, M.; Sahimi, M. Molecular Dynamics Simulation of Hydration and Swelling of Mixed Layer Clays in the Presence of Carbon Dioxide. J. Phys. Chem. C 2019, 123, 4243–4255. [Google Scholar] [CrossRef]
- Feng, D.; Li, X.F.; Wang, X.Z.; Li, J.; Sun, F.R.; Sun, Z.; Zhang, T.; Li, P.H.; Chen, Y.; Zhang, X. Water adsorption and its impact on the pore structure characteristics of shale clay. Appl. Clay Sci. 2018, 155, 126–138. [Google Scholar] [CrossRef]
- Millero, F.J.; Feistel, R.; Wright, D.G.; McDougall, T.J. The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale. Deep Sea Res. Part I 2008, 55, 50–72. [Google Scholar] [CrossRef]
- Wei, G.J.; Wang, Z.B.; Ke, T.; Liu, Y.; Deng, W.F.; Chen, X.F.; Xu, J.F.; Zeng, T.; Xie, L.H. Decadal variability in seawater pH in the West Pacific: Evidence from coral delta B-11 records. J. Geophys. Res. Oceans 2015, 120, 7166–7181. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.N.; Hu, H.X.; Li, X.C.; Fang, Z.M. Interplay of Montmorillonite-H2O-scCO(2) System between Mechanical Behavior and Adsorption: Molecular Dynamics. J. Phys. Chem. C 2015, 119, 21959–21968. [Google Scholar] [CrossRef]
- Zhao, L.; Ward, C.R.; French, D.; Graham, I.T.; Dai, S.F.; Yang, C.; Xie, P.P.; Zhang, S.Y. Origin of a kaolinite-NH4-illite-pyrophyllite-chlorite assemblage in a marine-influenced anthracite and associated strata from the Jincheng Coalfield, Qinshui Basin, Northern China. Int. J. Coal Geol. 2018, 185, 61–78. [Google Scholar] [CrossRef]
- Cui, G.; Zhou, C.; Liu, Z.; Xia, C.; Zhang, L. The synthesis of soft rocks based on physical and mechanical properties of red mudstone. Int. J. Rock Mech. Min. Sci. 2022, 151, 105037. [Google Scholar] [CrossRef]
- Deng, L.N.; Feng, B.; Zhang, Y. An optimization method for multi-objective and multi-factor designing of a ceramic slurry: Combining orthogonal experimental design with artificial neural networks. Ceram. Int. 2018, 44, 15918–15923. [Google Scholar] [CrossRef]
- Bal, H.; Jannot, Y.; Quenette, N.; Chenu, A.; Gaye, S. Water content dependence of the porosity, density and thermal capacity of laterite based bricks with millet waste additive. Constr. Build. Mater. 2012, 31, 144–150. [Google Scholar] [CrossRef]
- Bataee, M.; Irawan, S. Porosity and Permeability Alteration around Wellbore during Injection Process. Int. J. Géoméch. 2018, 18, 04017145. [Google Scholar] [CrossRef]
- He, M.; Sun, X.; Zhao, J. Advances in interaction mechanism of water (gas) on clay minerals in China. Int. J. Min. Sci. Technol. 2014, 24, 727–735. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Maruvanchery, V.; Liu, G. Water effects on rock strength and stiffness degradation. Acta Geotech. 2016, 11, 713–737. [Google Scholar] [CrossRef]
- Zhang, Q.; Jia, W.; Fan, X.; Liang, Y.; Yang, Y. A review of the shale wellbore stability mechanism based on mechanical–chemical coupling theories. Petroleum 2015, 1, 91–96. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.P.; Liu, L.M.; Zhang, F.T.; Cao, J.Z. Development and application of new composite grouting material for sealing groundwater inflow and reinforcing wall rock in deep mine. Sci. Rep. 2018, 8, 5642. [Google Scholar] [CrossRef]
- Roy, D.G.; Singh, T.N.; Kodikara, J.; Das, R. Effect of Water Saturation on the Fracture and Mechanical Properties of Sedimentary Rocks. Rock Mech. Rock Eng. 2017, 50, 2585–2600. [Google Scholar] [CrossRef]
- Gao, J.; Yu, Q.C. Effect of Water Saturation on Pressure-Dependent Permeability of Carboniferous Shale of the Qaidam Basin, China. Transp. Porous Media 2018, 123, 147–172. [Google Scholar] [CrossRef]
- Zhu, Z.; Dou, J.; Wang, H. An entropic model for the rock water absorption process. Stoch. Environ. Res. Risk Assess. 2020, 34, 1871–1886. [Google Scholar] [CrossRef]


| Exp. | CMT | CMC (wt%) | VSs (MPa) | CTs | ATs | CCs (mol/L) | pH |
|---|---|---|---|---|---|---|---|
| 1 | MMT | 30 | 5 | Na+ | Cl− | 0.1 | 4 |
| 2 | MMT | 50 | 10 | Ca2+ | SO42− | 1.0 | 7 |
| 3 | MMT | 70 | 15 | K+ | CO32− | SAT | 10 |
| 4 | ILL | 30 | 5 | Ca2+ | SO42− | SAT | 10 |
| 5 | ILL | 50 | 10 | K+ | CO32− | 0.1 | 4 |
| 6 | ILL | 70 | 15 | Na+ | Cl− | 1.0 | 7 |
| 7 | KAO | 30 | 10 | Na+ | CO32− | 1.0 | 10 |
| 8 | KAO | 50 | 15 | Ca2+ | Cl− | SAT | 4 |
| 9 | KAO | 70 | 5 | K+ | SO42− | 0.1 | 7 |
| 10 | MMT | 30 | 15 | K+ | SO42− | 1.0 | 4 |
| 11 | MMT | 50 | 5 | Na+ | CO32− | SAT | 7 |
| 12 | MMT | 70 | 10 | Ca2+ | Cl− | 0.1 | 10 |
| 13 | ILL | 30 | 10 | K+ | Cl− | SAT | 7 |
| 14 | ILL | 50 | 15 | Na+ | SO42− | 0.1 | 10 |
| 15 | ILL | 70 | 5 | Ca2+ | CO32− | 1.0 | 4 |
| 16 | KAO | 30 | 15 | Ca2+ | CO32− | 0.1 | 7 |
| 17 | KAO | 50 | 5 | K+ | Cl− | 1.0 | 10 |
| 18 | KAO | 70 | 10 | Na+ | SO42− | SAT | 4 |
| Factor | Level | Equation (3) | Equation (4) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| t1 | t2 | A1 | A2 | w0 | a | b | ||||
| CMT | MMT | 10 | 1338 | −10 | −8 | 18.0 | 0.990 | 0.12 | −0.90 | 0.969 |
| ILL | 6 | 229 | −14 | −5 | 17.9 | 0.985 | 0.93 | −1.50 | 0.945 | |
| KAO | 7 | 152 | −14 | −5 | 18.4 | 0.995 | 0.94 | −1.48 | 0.964 | |
| CMC | 30% | 10 | 252 | −13 | −6 | 18.1 | 0.991 | 0.80 | −1.40 | 0.909 |
| 50% | 8 | 556 | −10 | −7 | 17.2 | 0.987 | 0.35 | −1.06 | 0.959 | |
| 70% | 5 | 1237 | −14 | −6 | 18.7 | 0.985 | 0.46 | −1.10 | 0.959 | |
| VSs | 5 MPa | 5 | 352 | −12 | −8 | 19.3 | 0.990 | 0.66 | −1.22 | 0.965 |
| 10 MPa | 10 | 1584 | −14 | −4 | 16.9 | 0.994 | 0.48 | −1.15 | 0.944 | |
| 15 MPa | 6 | 316 | −11 | −7 | 17.3 | 0.984 | 0.42 | −1.09 | 0.960 | |
| CTs | Na+ | 6 | 408 | −14 | −5 | 18.4 | 0.991 | 0.70 | −1.29 | 0.939 |
| Ca2+ | 10 | 378 | −9 | −7 | 16.5 | 0.987 | 0.28 | −1.02 | 0.952 | |
| K+ | 7 | 1379 | −15 | −4 | 18.6 | 0.992 | 0.58 | −1.19 | 0.953 | |
| ATs | Cl− | 5 | 286 | −12 | −7 | 18.2 | 0.990 | 0.56 | −1.17 | 0.980 |
| SO42− | 4 | 336 | −12 | −5 | 16.6 | 0.985 | 0.57 | −1.22 | 0.969 | |
| CO32− | 15 | 1534 | −14 | −6 | 19.1 | 0.997 | 0.43 | −1.07 | 0.954 | |
| CCs | 0.1 mol/L | 7 | 248 | −12 | −5 | 16.2 | 0.986 | 0.57 | −1.22 | 0.966 |
| 1 mol/L | 7 | 277 | −14 | −3 | 17.1 | 0.992 | 0.67 | −1.29 | 0.974 | |
| SAT | 7 | 526 | −11 | −9 | 19.5 | 0.989 | 0.34 | −1.00 | 0.955 | |
| pH | 4 | 10 | 199 | −13 | −6 | 18.7 | 0.996 | 0.81 | −1.34 | 0.970 |
| 7 | 5 | 823 | −14 | −5 | 17.3 | 0.975 | 0.40 | −1.12 | 0.941 | |
| 10 | 9 | 744 | −10 | −7 | 17.5 | 0.990 | 0.33 | −1.03 | 0.957 | |
| Factor | t1 | t2 | w0 | b | ||||
|---|---|---|---|---|---|---|---|---|
| R | PDI | R | PDI | R | PDI | R | PDI | |
| CMT | 4 | 5 | 1186 | 3 | 0.5 | 7 | 0.60 | 1 |
| CMC | 5 | 2 | 985 | 5 | 1.5 | 5 | 0.34 | 2 |
| VSs | 5 | 2 | 1268 | 1 | 2.0 | 4 | 0.13 | 7 |
| CTs | 4 | 5 | 1001 | 4 | 2.1 | 3 | 0.27 | 5 |
| ATs | 11 | 1 | 1248 | 2 | 2.5 | 2 | 0.15 | 6 |
| CCs | 0 | 7 | 278 | 7 | 3.3 | 1 | 0.29 | 4 |
| pH | 5 | 2 | 545 | 6 | 1.4 | 6 | 0.31 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, G.; Zhou, C.; Liu, Z. Prediction Method of Water Absorption of Soft Rock Considering the Influence of Composition, Porosity, and Solute Quantitatively. Appl. Sci. 2022, 12, 5938. https://doi.org/10.3390/app12125938
Cui G, Zhou C, Liu Z. Prediction Method of Water Absorption of Soft Rock Considering the Influence of Composition, Porosity, and Solute Quantitatively. Applied Sciences. 2022; 12(12):5938. https://doi.org/10.3390/app12125938
Chicago/Turabian StyleCui, Guangjun, Cuiying Zhou, and Zhen Liu. 2022. "Prediction Method of Water Absorption of Soft Rock Considering the Influence of Composition, Porosity, and Solute Quantitatively" Applied Sciences 12, no. 12: 5938. https://doi.org/10.3390/app12125938
APA StyleCui, G., Zhou, C., & Liu, Z. (2022). Prediction Method of Water Absorption of Soft Rock Considering the Influence of Composition, Porosity, and Solute Quantitatively. Applied Sciences, 12(12), 5938. https://doi.org/10.3390/app12125938






