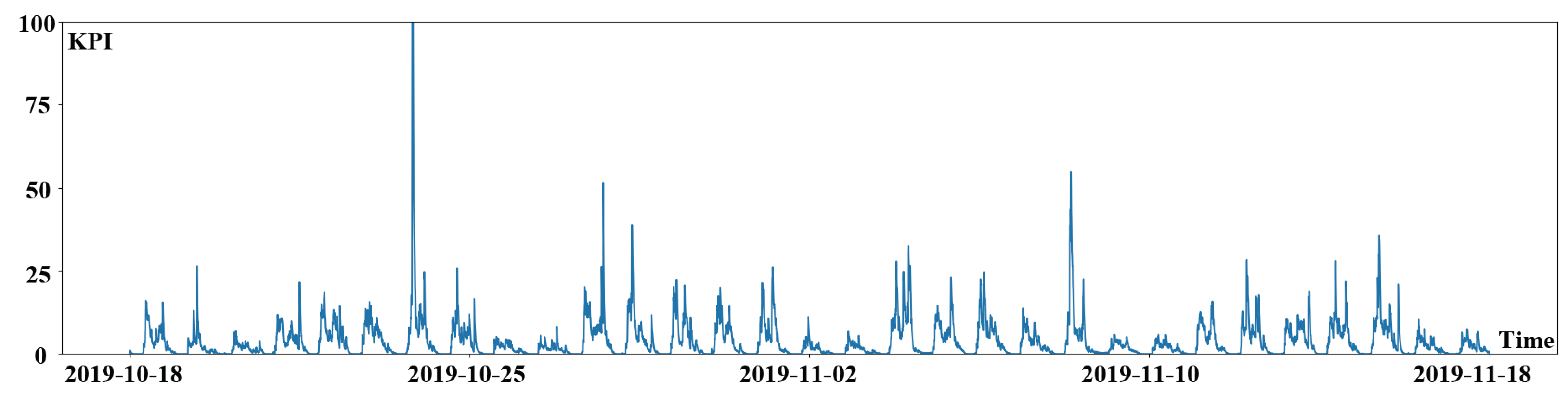
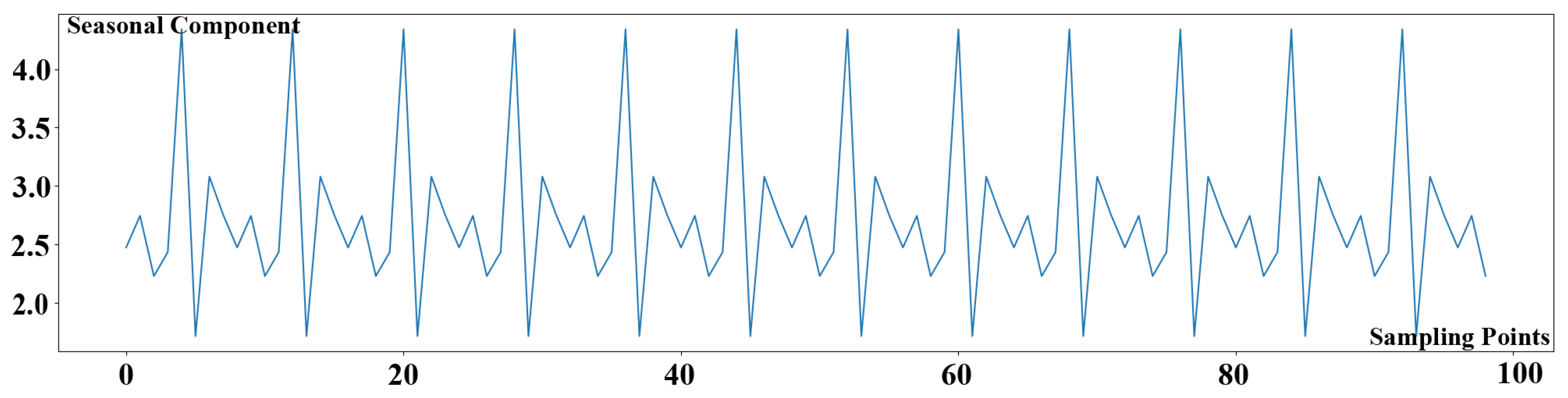
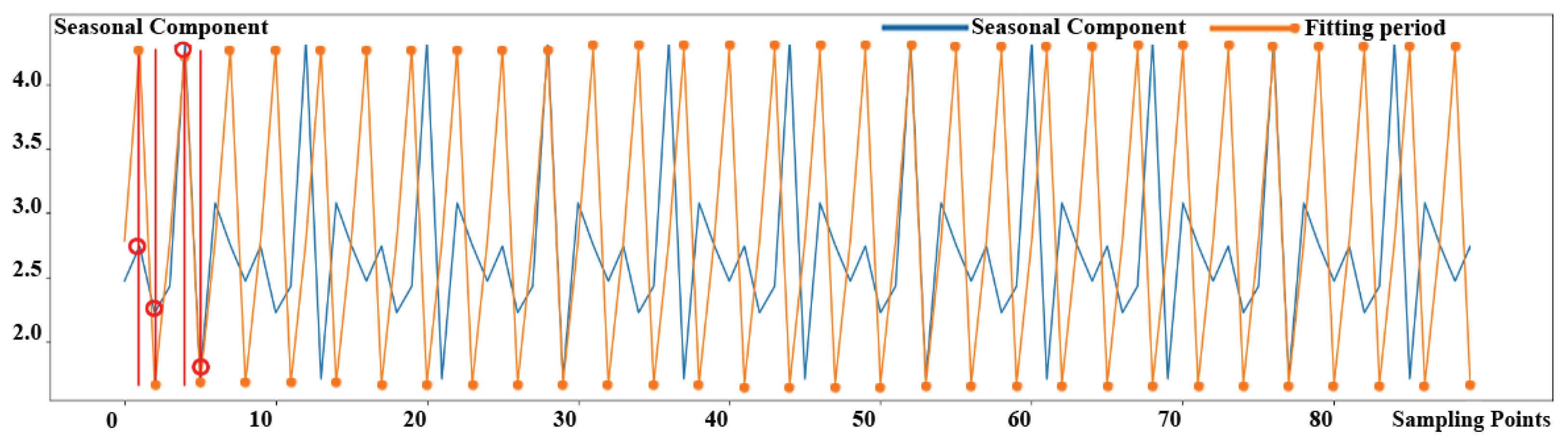
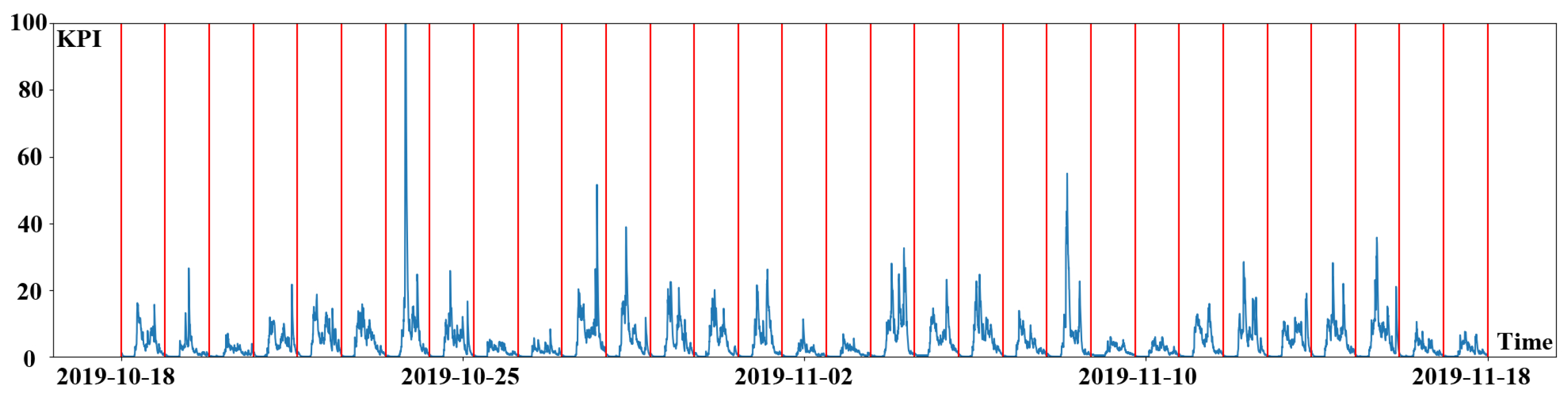
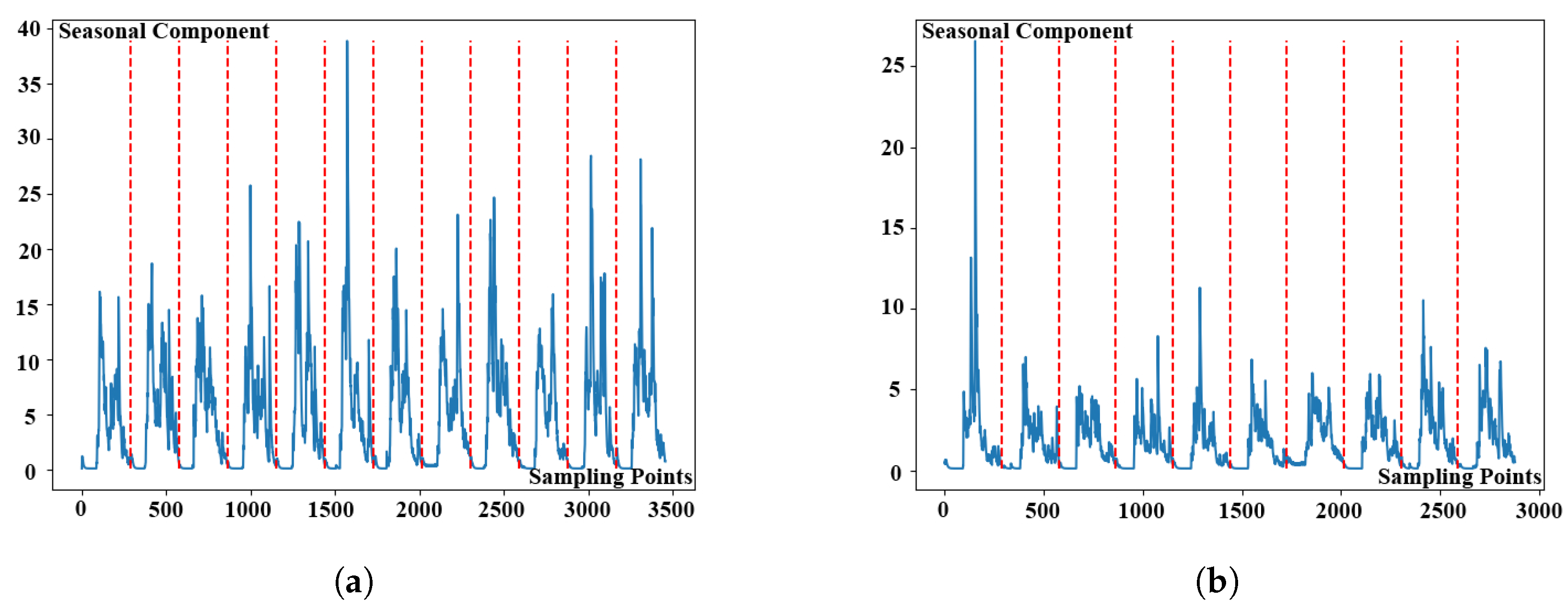
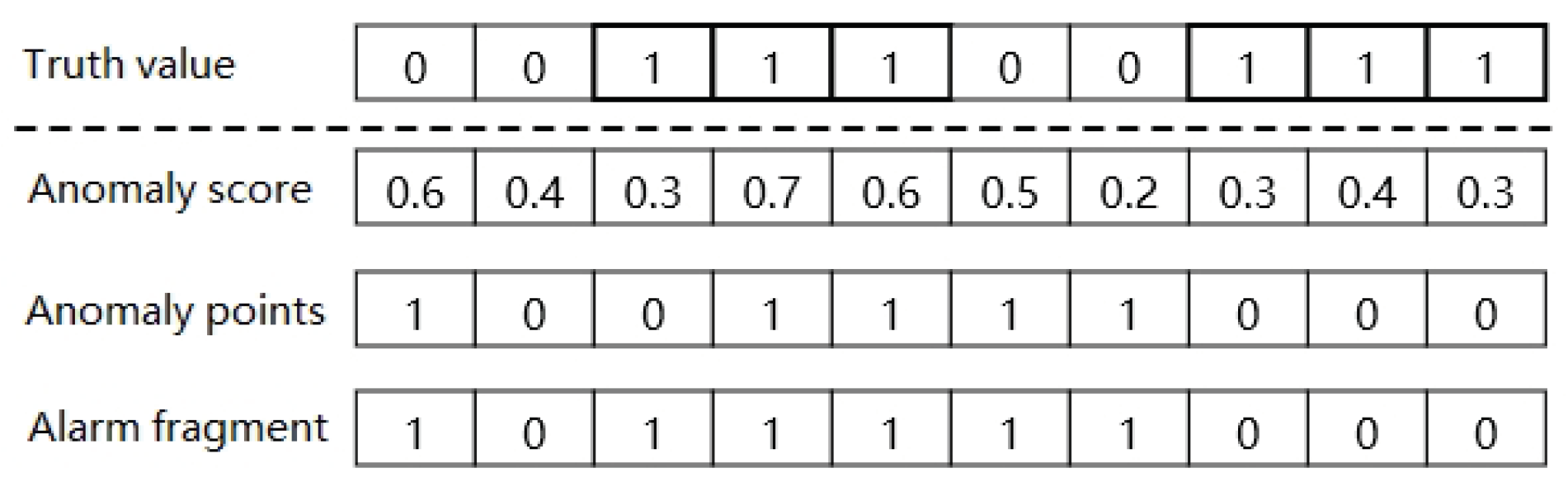
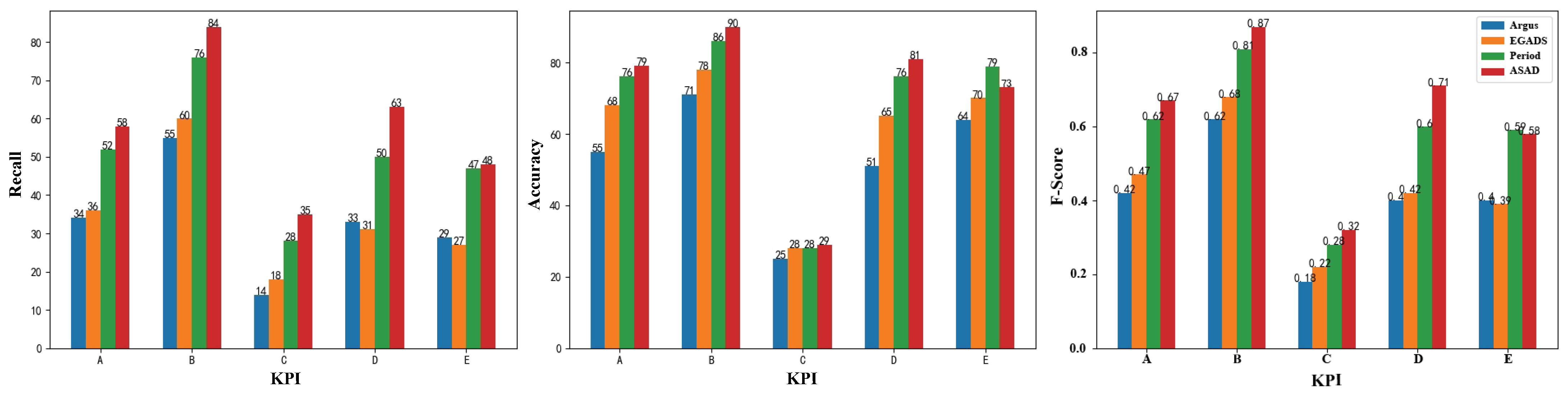
After determining the seasonal length, the original KPI time series data could be split into many sub-sequences. The segmented KPI sequence data is shown in
Figure 5. KPI time series data is denoted by the blue line in the picture, whereas segmentation is represented by the red line. The following content is the procedure for clustering sub-sequences. To begin, calculate the distance between the KPI time series data sub-sequences by using a new lightweight distance measurement algorithm. Then cluster the sub-sequences by using DBSCAN clustering technique.
3.2.1. Lightweight Distance Measurement Algorithm
The choice of distance measurement algorithm has an important influence on the clustering algorithm [
28]. In the previous literature, researchers have presented a variety of distance measurement algorithms, such as Move-Split-Merge [
29], Spade [
30],
norm [
31] and so on. Wang [
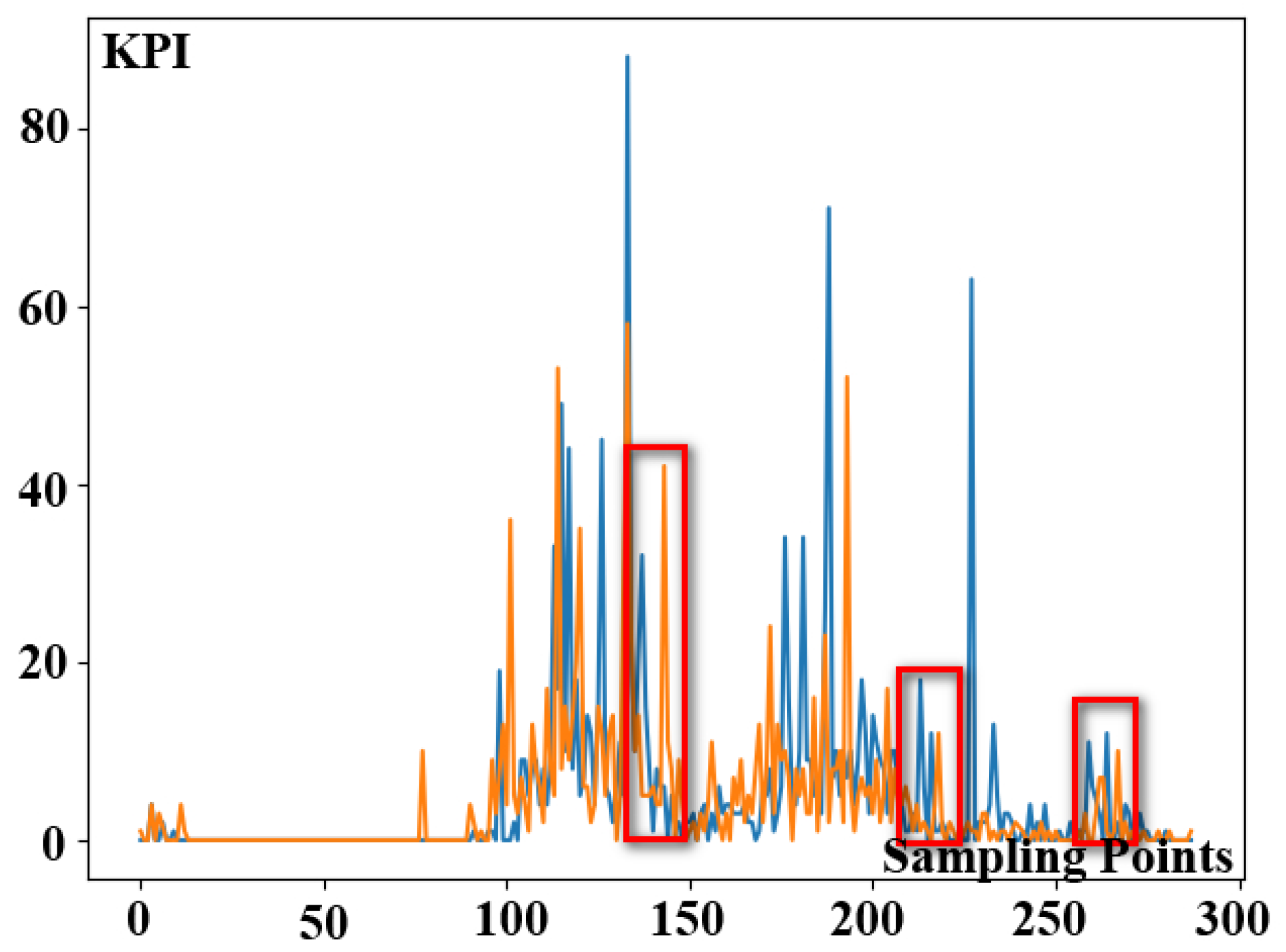
32] evaluated nine distance measurement algorithms and corresponding derivative algorithms. Therefore, they discovered that Euclidean distance is more accurate than other distance measurement algorithms, and that DTW outperforms them. There is a significant variance in the direct use of Euclidean distance for distance measurement due to the offset of the KPI time series data. The offset phenomenon of KPI time series data is shown in
Figure 6. In the picture, we use two color lines to represent two separated dates of KPI time series data. Furthermore, the peak values in the two pieces of KPI time series data shown in red rectangles are not perfectly aligned in time, indicating the offset phenomena of KPI time series data. DTW can handle the offset of KPI time series data, but the computation time will be very long because a large number of short sample intervals exist in intricate KPI time series data. Therefore, it is not appropriate to use the DTW algorithm directly under intricate KPI profiles.
To reduce time consumption of the clustering algorithm [
33], we propose a lightweight distance measurement algorithm in
ASAD to quantify the distance between KPI time series data sub-sequences. It can reduce the consuming time by extracting the primary information from a piece of KPI time series data and then utilizing the DTW method to estimate the distance. In short, there are three phases in this algorithm. Firstly, divide time series data into a set of data blocks. Secondly, modify each data block by using the discrete cosine transform, and the most important information is gathered in the upper left corner. Finally, extract the most significant data using a quantitative approach and matrix division. Following the above steps, we can extract the essential information and mask the offset of some KPI time series data to compress the sequence length.
The specific algorithm flow is as follows. At first, divide the data by one window size (
n) for a given period of time series data. For example
, for the observed data of
, divide
Y into
matrices. If the last matrix has less than
elements, fill it with 0. After completing the previous step, the data in each window can form a matrix
,
i = 1, 2, 3...,
,
can be expressed as
Then, the discrete cosine transform is performed on the divided data block
.
where
U is a discrete cosine variable matrix.
In our method, the discrete cosine variable matrix can be expressed as
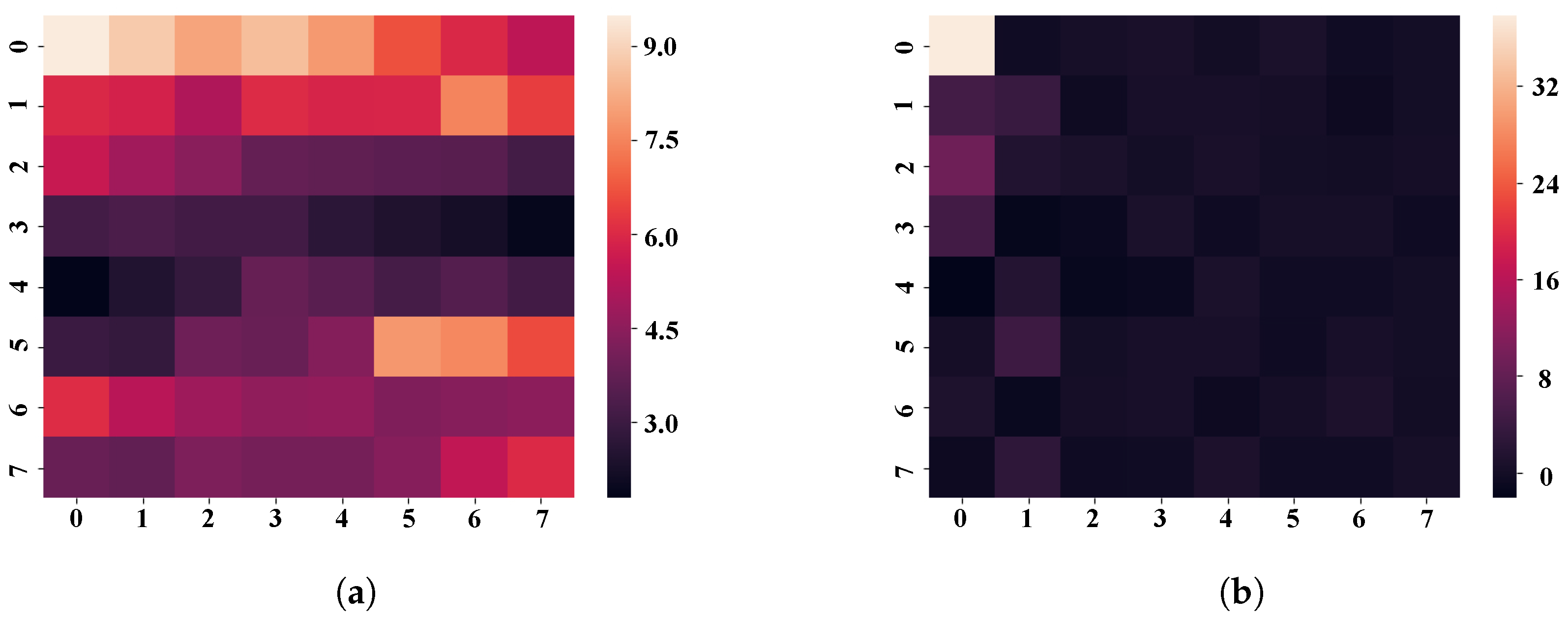
Taking one of the matrices as an example, the data aggregation effect of
is shown in
Figure 7. The color closest to white in the heat map represents a bigger absolute value of the data, whereas the color closest to black suggests a smaller absolute value of the data. The thermal data distribution of the original matrix is shown in
Figure 7a. It can be seen that the original matrix’s data distribution is not concentrated, and the four corners of the matrix have more data. The thermal distribution of the data after the discrete cosine transform is shown in
Figure 7b. Discrete cosine transform can express a finite time series sequence of KPI data in terms of a sum of cosine functions oscillating at different frequencies. The use of cosine rather than sine functions is critical for compression, since it turns out that fewer cosine functions are needed to approximate a typical signal, whereas for differential equations the cosines express a particular choice of boundary conditions. According to observations, the larger data in the updated matrix is predominantly dispersed in the upper left, while the absolute values of data scattered in other places are close to zero. As a result, the major data information in the matrix converges in the upper-left corner.
After the discrete cosine transform, quantify and divide the matrix, then determine the eigenvalues. The matrix
D’s quantization matrx
Q is as follows.
where
is rounding function and
Z is the standard quantization matrix for discrete cosine transform [
34].
For the matrix
Q, it can be divided into four small matrices.
Because the matrix
Q is generated by converging the principal information of the matrix
D to the top-left corner, it can be seen that the matrix
keeps the main data information and the matrix
barely retains it in the figure. The highest values of the matrices
and
surpass the minimum value of the matrix
, indicating that the matrices
and
maintain the secondary information of the data. As a result, the matrix
Q is represented as when the matrices
and
include the secondary information of the data.
where we calculate the eigenvalues of the matrices
,
and
, sort them in descending order to form an array as the principal information extracted from
.
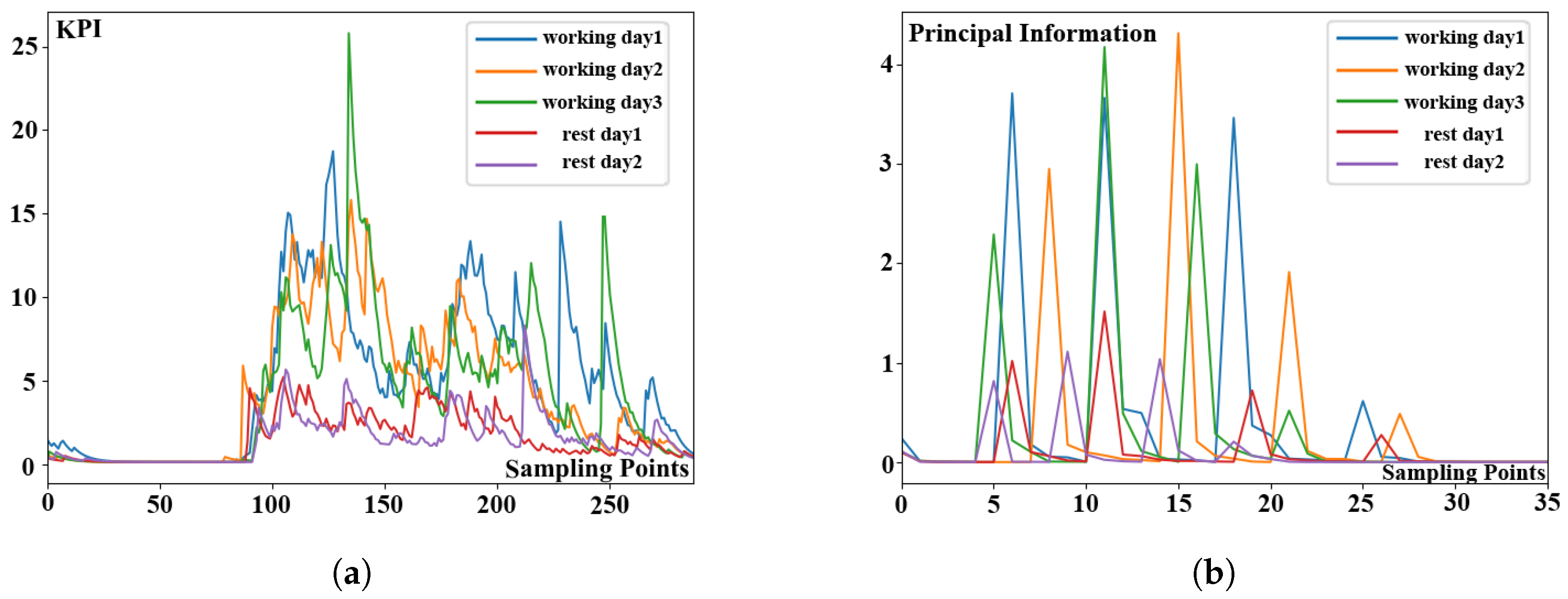
The comparison charts before and after extracting principal information of KPI time series data sub-sequences are shown in
Figure 8. The KPI time series data sub-sequences segmented by day are shown in
Figure 8a. The five different color sub-sequences in the figure represent different working days and rest days. Each of sub-sequences contains 288 observations. According to experimental results, KPI profiles of these three sub-sequences representing the working days are more similar. Similarly, the profiles of other two sub-sequences representing rest days are more similar. The KPI time series data sub-sequences after extracting the principal information are shown in
Figure 8b. Five sub-sequences with various colors reflect distinct working days and rest days in the diagram. Each sub-sequence concludes 36 observations once the principal information has been extracted. Based on experimental observations, the analytical results are as follows. It can be seen that the data length of sub-sequences can be compressed by 87.5% without compromising profile similarity. Then, we use the classical DTW algorithm to calculate the distance between different sub-sequences because of the short length of extracted KPI time series data. As a result, we can say that our lightweight distance measurement algorithm is useful for reducing the clustering time consumption by extracting principal information from origin KPI time series data.
3.2.2. DBSCAN Clustering Algorithm
The second step in ASAD is an unsupervised learning technique to cluster the sub-sequences. When the samples are not labeled, it may divide the data into various clusters. The clustering process is based on calculating the distance between the data points. According to previous studies, there are two main clustering algorithms available for ASAD. K-means and DBSCAN are two of the most widely used clustering methods. The k-means algorithm is a traditional clustering algorithm that requires the number of groups to be specified. On the contrary, DBSCAN clustering algorithm does not need to determine the number of clustering centers. DBSCAN can cluster KPI time series data automatically based on the density of data points by setting the minimum number of clustering points and the clustering distance radius, rather than the number of clusters.
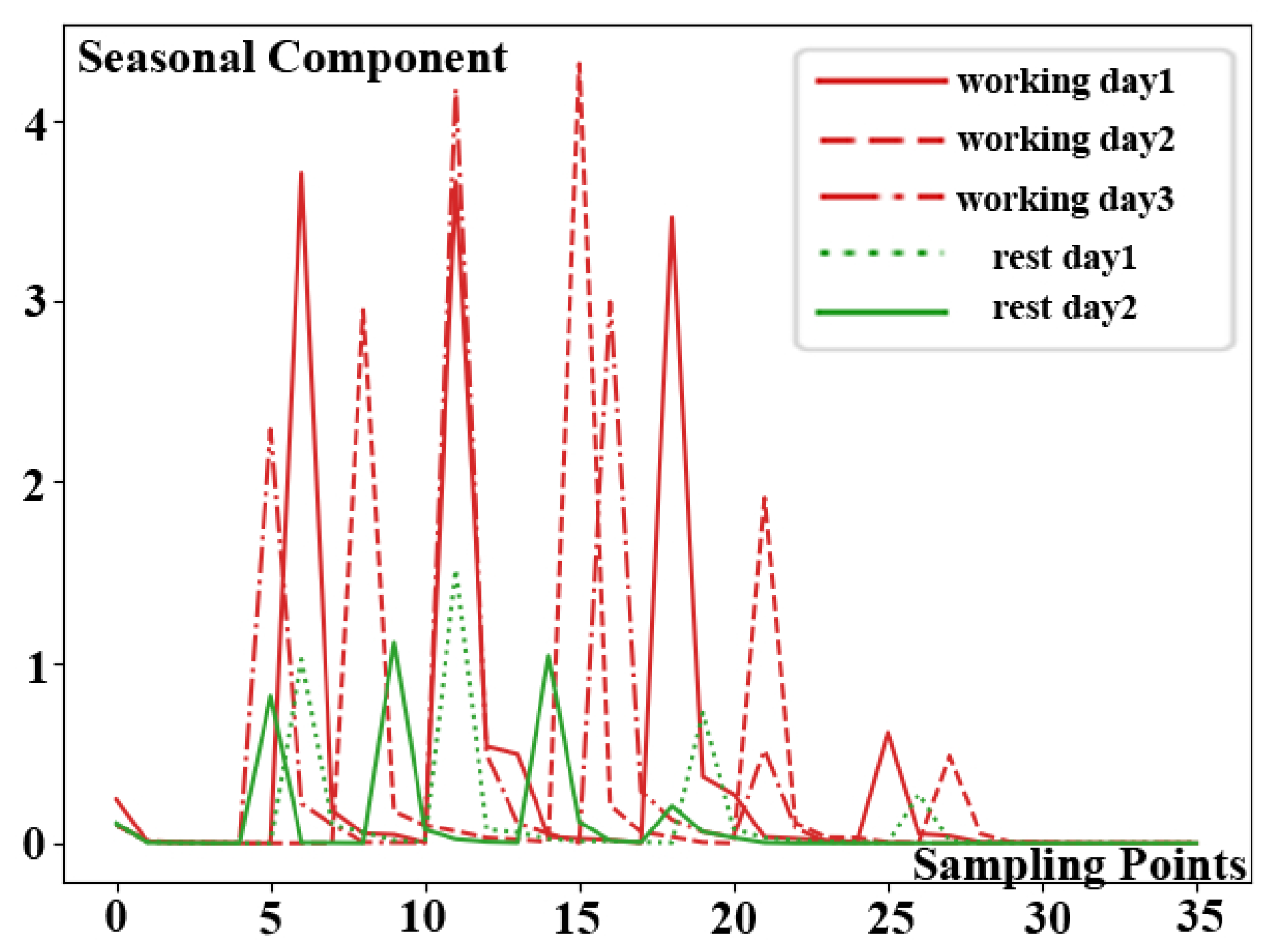
The result of DBSCAN clustering algorithm is shown in
Figure 9. Five separate KPI time series data sub-sequences are shown in the figure by five different lines with varied patterns. Moreover, they are divided into two groups after being calculated using the DBSCAN clustering technique, which are denoted by red and green respectively. The working day mode is represented by the red KPI time series data sub-sequences, while the rest day mode is represented by the green KPI time series data sub-sequences. According to the experimental results, the similar KPI profiles among three sub-sequences in red belong to one category, while similar profiles between the two sub-sequences in green belong to another category. Meanwhile, it is worth noting that the clustering results corroborate the observations.