Fiber Model Considering the Local Instability Effect and Its Application to the Seismic Analysis of Eccentrically Compressed Steel Piers
Abstract
:1. Introduction
2. FE Model of Steel Piers
2.1. Structural Form and Parameters of Steel Piers
2.2. Hybrid-Element Model
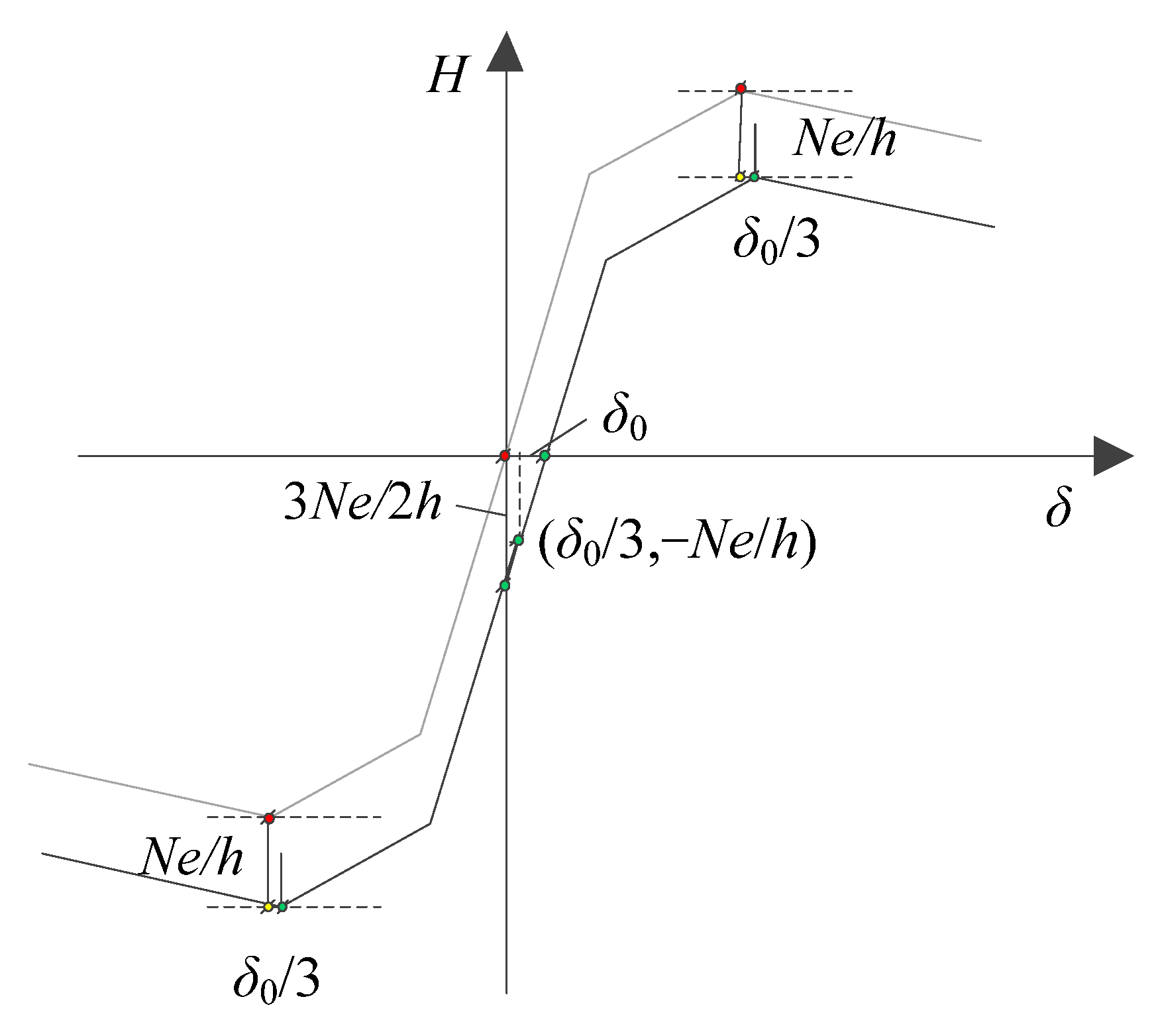
3. Review of the Improved Fiber Model
4. Calculation and Discussion for Eccentrically Compressed Steel Piers
4.1. In-Plane Pseudo-Static Analysis
4.2. Out-of-Plane Pseudo-Static Analysis
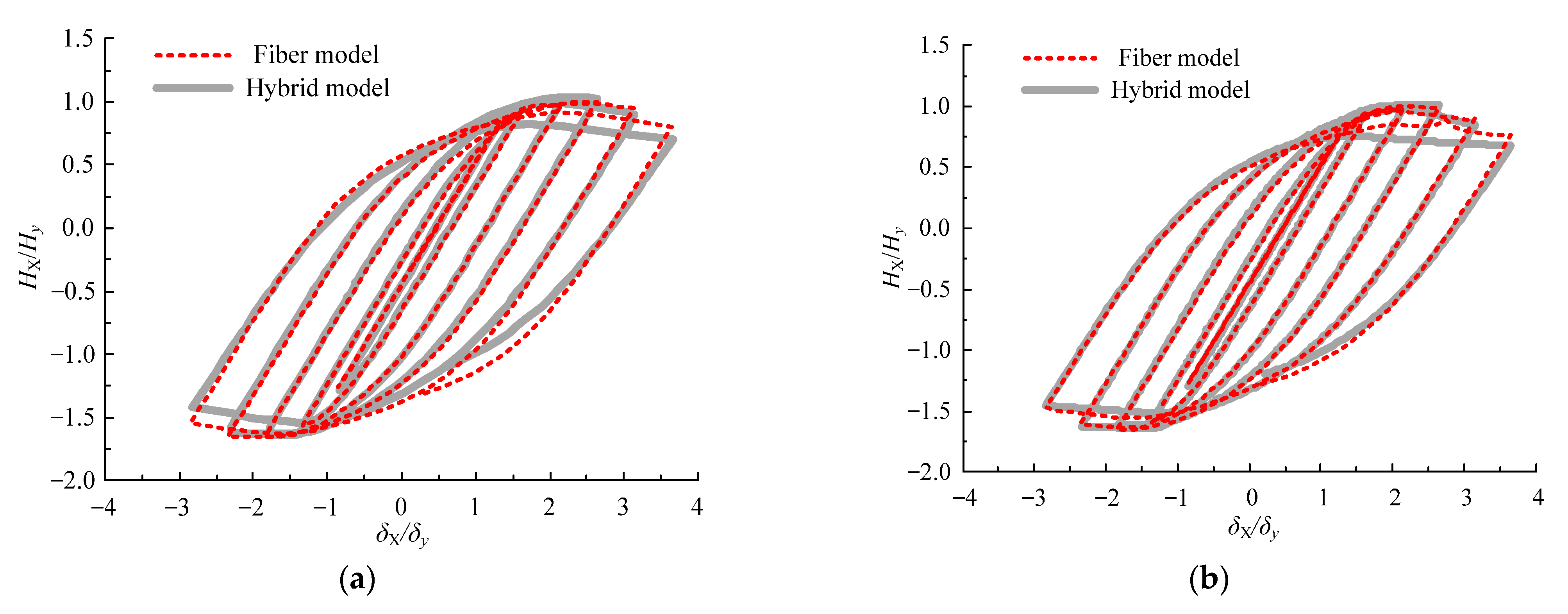
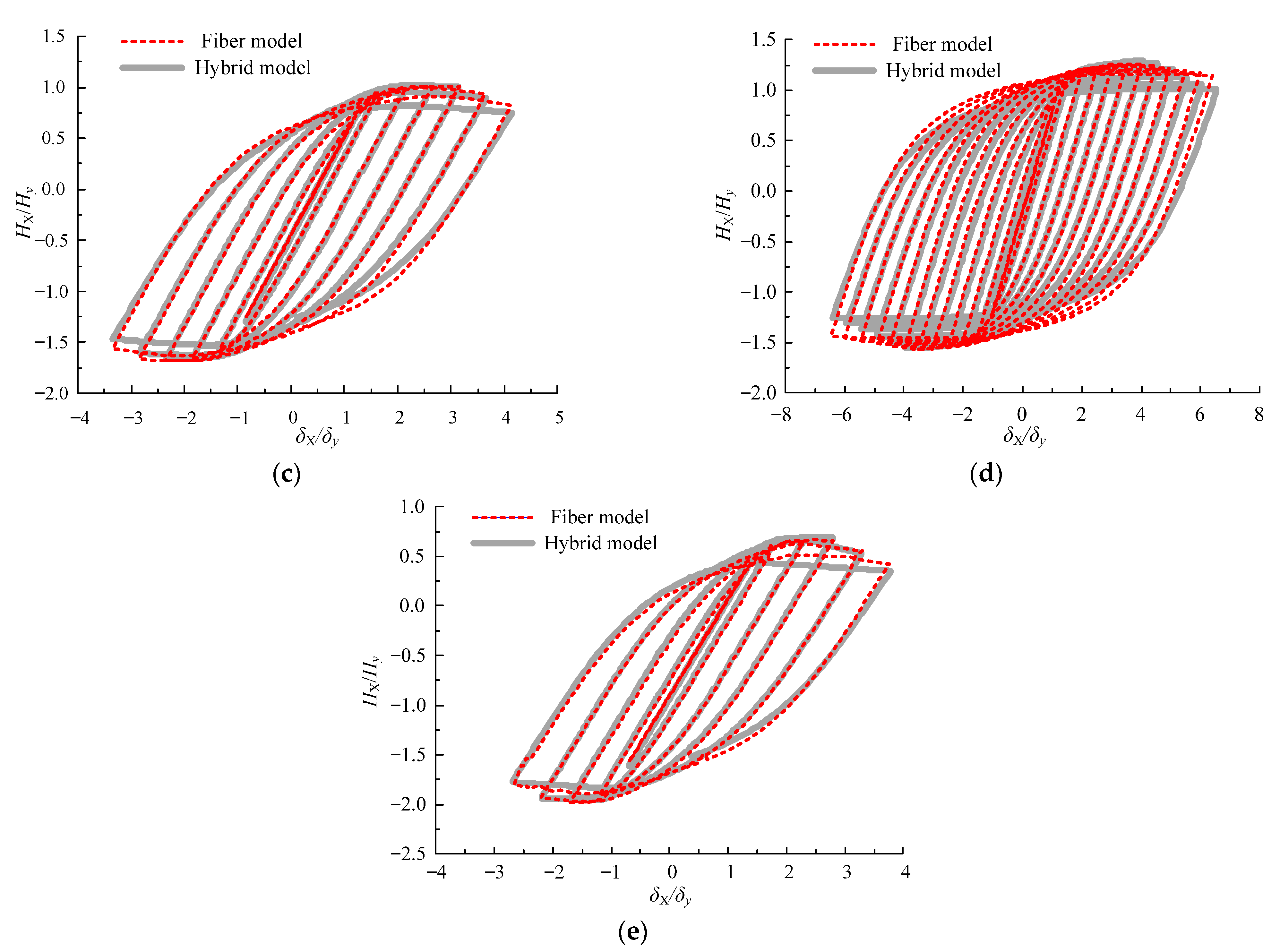
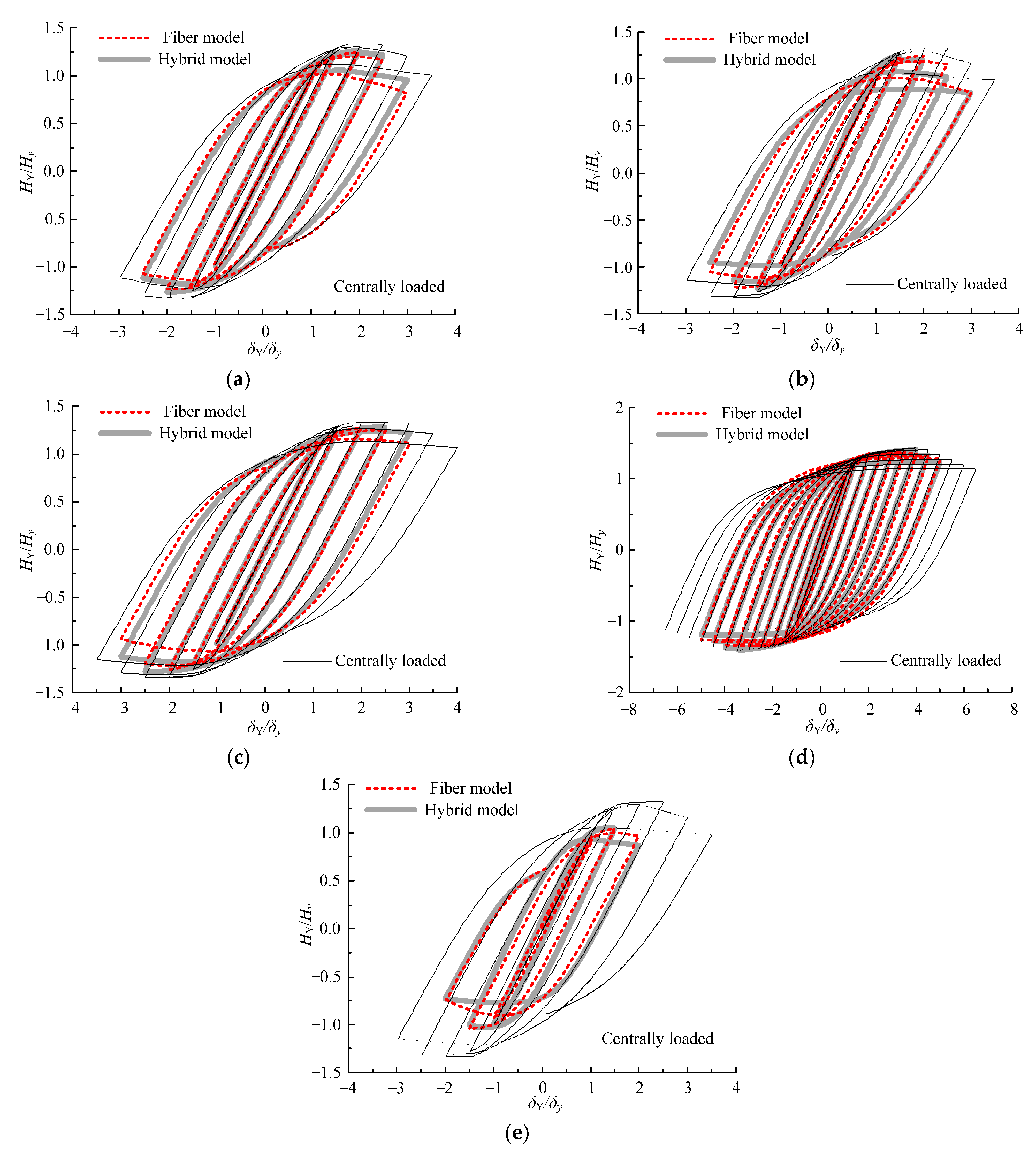
4.3. Seismic Response Analysis
5. Conclusions and Discussion
- (1)
- The hysteretic curves in the in-plane direction of the eccentrically compressed steel piers can be obtained by translating those of the centrally compressed piers. The improved fiber model can accurately simulate the hysteretic performance of the structures in the in-plane direction;
- (2)
- The bearing capacity and ductility of the eccentrically compressed steel piers in the out-of-plane direction are lower than those of the centrally compressed piers. The improved fiber model can also accurately calculate the structural hysteretic performance in the out-of-plane direction;
- (3)
- By taking five piers as examples, the improved fiber model was used to analyze the horizontal bidirectional seismic response of the eccentrically compressed steel piers. The results show that this kind of beam-based model can obtain accurate seismic response analysis results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watanabe, E.; Sugiura, K.; Nagata, K.; Kitane, Y. Performances and damages to steel structures during the 1995 Hyogoken-Nanbu earthquake. Eng. Struct. 1998, 20, 282–290. [Google Scholar] [CrossRef]
- Usami, T. Guidelines for Seismic and Damage Control Design of Steel Bridges; Gihodo Shuppan Co., Ltd.: Tokyo, Japan, 2007. [Google Scholar]
- Ge, H.; Gao, S.; Usami, T.; Matsumura, T. Numerical Study on Cyclic Elasto-plastic Behavior of Steel Bridge Piers of Pipe-Sections without Stiffeners. Doboku Gakkai Ronbunshu 1997, 1997, 181–190. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Usami, T.; Ge, H.B. Ductility evaluation procedure for thin-walled steel structures. J. Struct. Eng. 2000, 126, 1312–1319. [Google Scholar] [CrossRef]
- Watanabe, E.; Sugiura, K.; Oyawa, W.O. Effects of multi-directional displacement paths on the cyclic behaviour of rectangular hollow steel columns. Doboku Gakkai Ronbunshu 2000, 2000, 79–95. [Google Scholar] [CrossRef] [Green Version]
- Goto, Y.; Jiang, K.; Obata, M. Hysteretic behavior of thin-walled circular steel columns under cyclic biaxial loading. Doboku Gakkai Ronbunshu 2005, 2005, 181–198. [Google Scholar] [CrossRef] [Green Version]
- Goto, Y.; Jiang, K.; Obata, M. Hysteretic behavior of thin-walled stiffened rectangular steel columns under cyclic bi-directional loading. Doboku Gakkai Ronbunshuu A 2007, 63, 122–141. [Google Scholar] [CrossRef] [Green Version]
- Goto, Y.; Koyama, R.; Fujii, Y.; Obata, M. Ultimate state of thin-walled stiffened rectangular steel columns under bi-directional seismic excitations. Doboku Gakkai Ronbunshuu A 2009, 65, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Dang, J.; Nakamura, T.; Aoki, T.; Suzuki, M. Bi-directional loading hybrid test of square section steel piers. J. Struct. Eng. A 2010, 56A, 367–380. [Google Scholar]
- Usami, T.; Gao, S.B.; Ge, H.B. Stiffened steel box columns. Part 2: Ductility evaluation. Earthq. Eng. Struct. Dyn. 2000, 29, 1707–1722. [Google Scholar] [CrossRef]
- Chen, S.X.; Xie, X.; Zhuge, H.Q. Hysteretic model for steel piers considering the local buckling of steel plates. Eng. Struct. 2019, 183, 303–318. [Google Scholar] [CrossRef]
- Zheng, Y.; Usami, T.; Ge, H.B. Ductility of thin-walled steel box stub-columns. J. Struct. Eng. 2000, 126, 1304–1311. [Google Scholar] [CrossRef]
- Kulkarni, N.; Sakai, A.; Tsuboi, H. Displacement based seismic verification method for thin-walled circular steel columns subjected to bi-directional cyclic loading. Eng. Struct. 2009, 31, 2779–2786. [Google Scholar] [CrossRef]
- Dang, J.; Yuan, H.H.; Igarashi, A.; Aoki, T. Curve-approximated hysteresis model for steel bridge columns. J. Struct. Eng. 2014, 140, 04014058. [Google Scholar] [CrossRef]
- Suzuki, M.; Usami, T.; Terada, M.; Itoth, T.; Saizuka, K. Hysteresis models for steel bridge piers and their application to elasto-plastic seismic response analysis. Doboku Gakkai Ronbunshu 1996, 1996, 191–204. [Google Scholar] [CrossRef] [Green Version]
- Kolwankar, S.; Kanvinde, A.; Kenawy, M.; Lignos, D.; Kunnath, S. Simulating cyclic local buckling–induced softening in steel beam-columns using a nonlocal material model in displacement-based fiber elements. J. Struct. Eng. 2020, 146, 04019174. [Google Scholar] [CrossRef]
- Kazuhiko, K.; Tran-Tuan, N.; Bruce, F.M. Structural collapse correlative analysis using phenomenon logical fiber hinge elements to simulate two-directional column deteriorations. Earthq. Eng. Struct. Dyn. 2016, 45, 1581–1601. [Google Scholar]
- Zhuge, H.; Xie, X. Hysteresis Model for Fiber Elements in Effective Damaged Zone of Square-Section Steel Piers Considering Local Instability Effect of Steel Plates. J. Struct. Eng. 2020, 146, 04020156. [Google Scholar] [CrossRef]
- Zhuge, H.Q.; Xie, X.; Li, S.L.; Wang, J.D. Seismic performance test and practical calculation method of thin-walled square-section steel piers under horizontal bi-directional seismic excitations. China Civ. Eng. J. 2020, 53, 74–85. [Google Scholar]
- Li, H.F.; Luo, Y.F. Experimental and numerical study on cyclic behavior of eccentrically-compressed steel box columns. Thin-Walled Struct. 2015, 96, 269–285. [Google Scholar] [CrossRef]
- Li, H.F.; Lv, K.D.; Cui, R.S. Seismic behaviour of eccentrically compressed steel-box bridge-pier columns with embedded energy-dissipating shell plates. Bull. Earthq. Eng. 2020, 18, 3401–3432. [Google Scholar] [CrossRef]
- Luo, W.W.; Li, H.F.; Cao, B.A. Seismic performance of eccentrically-compressed steel pier under multi-directional earthquake loads. Earthq. Eng. Eng. Vib. 2021, 20, 771–789. [Google Scholar]
- Gao, S.B.; Usami, T.; Ge, H.B. Eccentrically loaded steel columns under cyclic in-plane loading. J. Struct. Eng. 2000, 126, 964–973. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Usami, T.; Kasai, A. Inelastic seismic response analysis of eccentrically loaded steel bridge piers. Doboku Gakkai Ronbunshu 2000, 2000, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Goto, Y.; Li, X.S.; Yamaguchi, E. Ultimate behavior and design of inverted L-shaped bridge piers under longitudinally applied seismic force. Doboku Gakkai Ronbunshu 2001, 2001, 313–330. [Google Scholar] [CrossRef] [Green Version]
- Aoki, T.; Suzuki, S.; Watanabe, S.; Suzuki, M.; Usami, T.; Ge, H.B. Experimental study on strength and deformation capacity of inverted L-shaped steel bridge piers subjected to out-of-plane cyclic loading. Doboku Gakkai Ronbunshu 2003, 2003, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Ge, H.B.; Watanabe, S.; Usami, T.; Aoki, T. Analytical study on strength and deformation capacity of inverted L-shaped steel bridge piers subjected to out-of-plane cyclic loading. Doboku Gakkai Ronbunshu 2003, 2003, 207–218. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.B.; Usami, T.; Ge, H.B. Eccentrically loaded steel columns under cyclic out-of-plane loading. J. Struct. Eng. 2000, 126, 974–981. [Google Scholar] [CrossRef]
- Japan Road Association. Specifications for Highway Bridges; Part V: Seismic Design; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2017. [Google Scholar]
- Ministry of Transport, PRC. Specifications for Design of Highway Steel Bridge; JTG D64-2015; China Communications Press: Beijing, China, 2015. [Google Scholar]
- Chen, W.F.; Duan, L. Bridge Engineering Handbook, 2nd ed.; Seismic Design; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gao, S.B.; Ge, H.B. Applicable range of steel constitutive models under cyclic load. China J. Highw. Transp. 2008, 21, 69–75. [Google Scholar]
- Shen, C.; Mizuno, E.; Usami, T. A generalized two-surface model for structural steels under cyclic loading. Doboku Gakkai Ronbunshu 1993, 1993, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Mamaghani, I.; Mizuno, E.; Usami, T. Cyclic behavior of structural steel, II: Theory. J. Eng. Mech. 1995, 121, 1165–1172. [Google Scholar] [CrossRef]
- Wang, T.; Xie, X.; Shen, C.; Tang, Z.Z. Effect of hysteretic models on elasto-plastic seismic performance evaluation of a steel arch bridge. Eqrthq. Struct. 2016, 10, 1089–1109. [Google Scholar] [CrossRef]
- Zhuge, H.Q.; Xie, X.; Tang, Z.Z. Lengths of damaged zones of steel piers under bidirectional horizontal earthquake components. China J. Highw. Transp. 2019, 32, 79–90. [Google Scholar]
- JMA (Japan Meteorological Agency). Type 95 Seismic Signatures; JMA, CD-ROM: Tokyo, Japan, 2004. [Google Scholar]

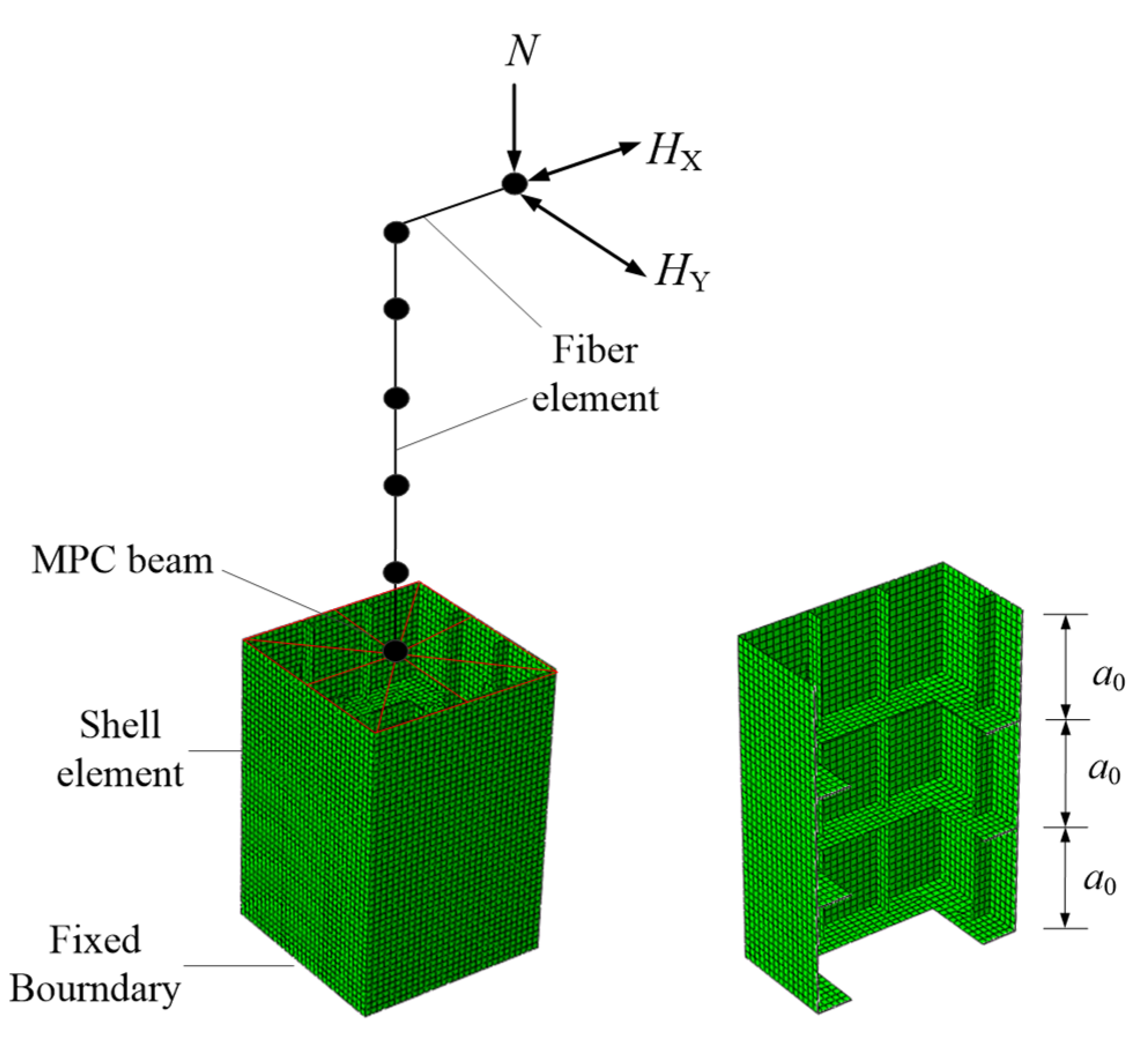
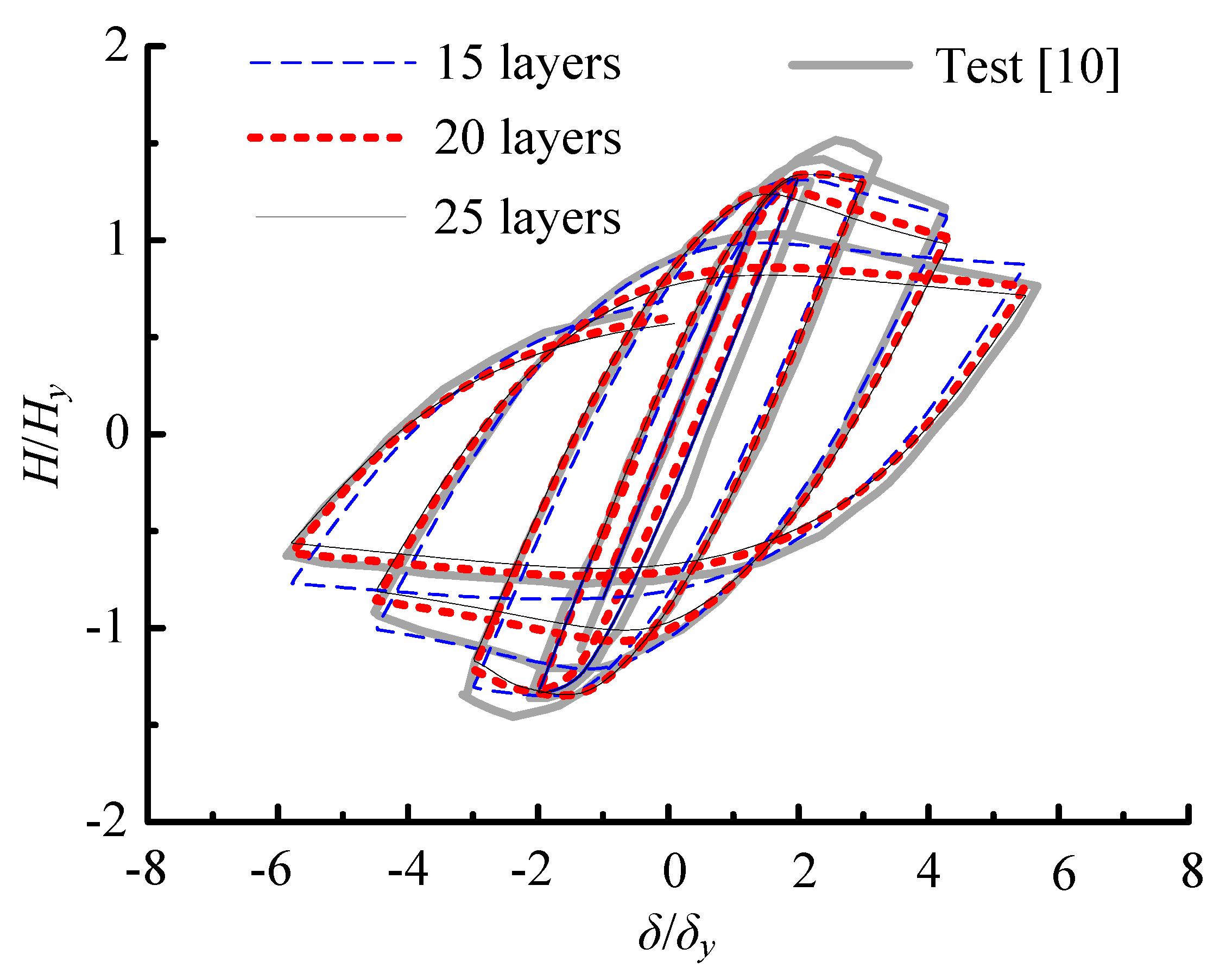
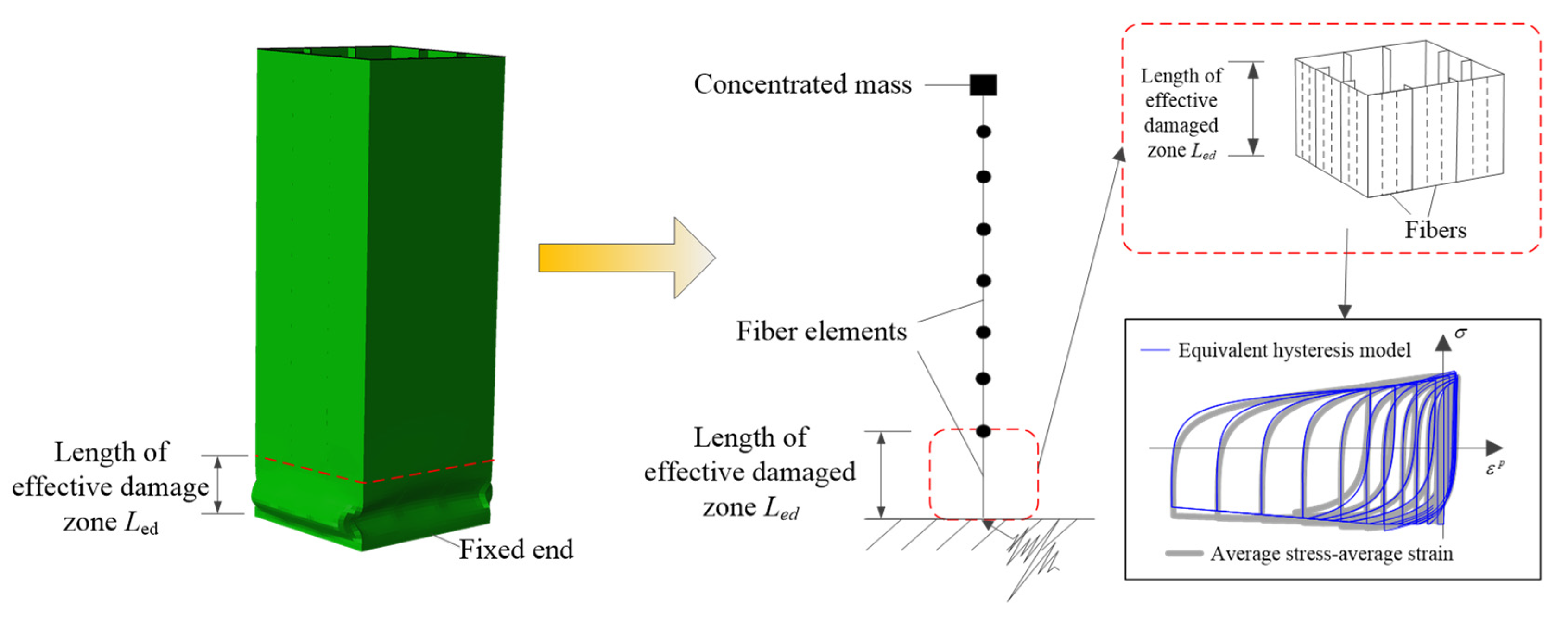
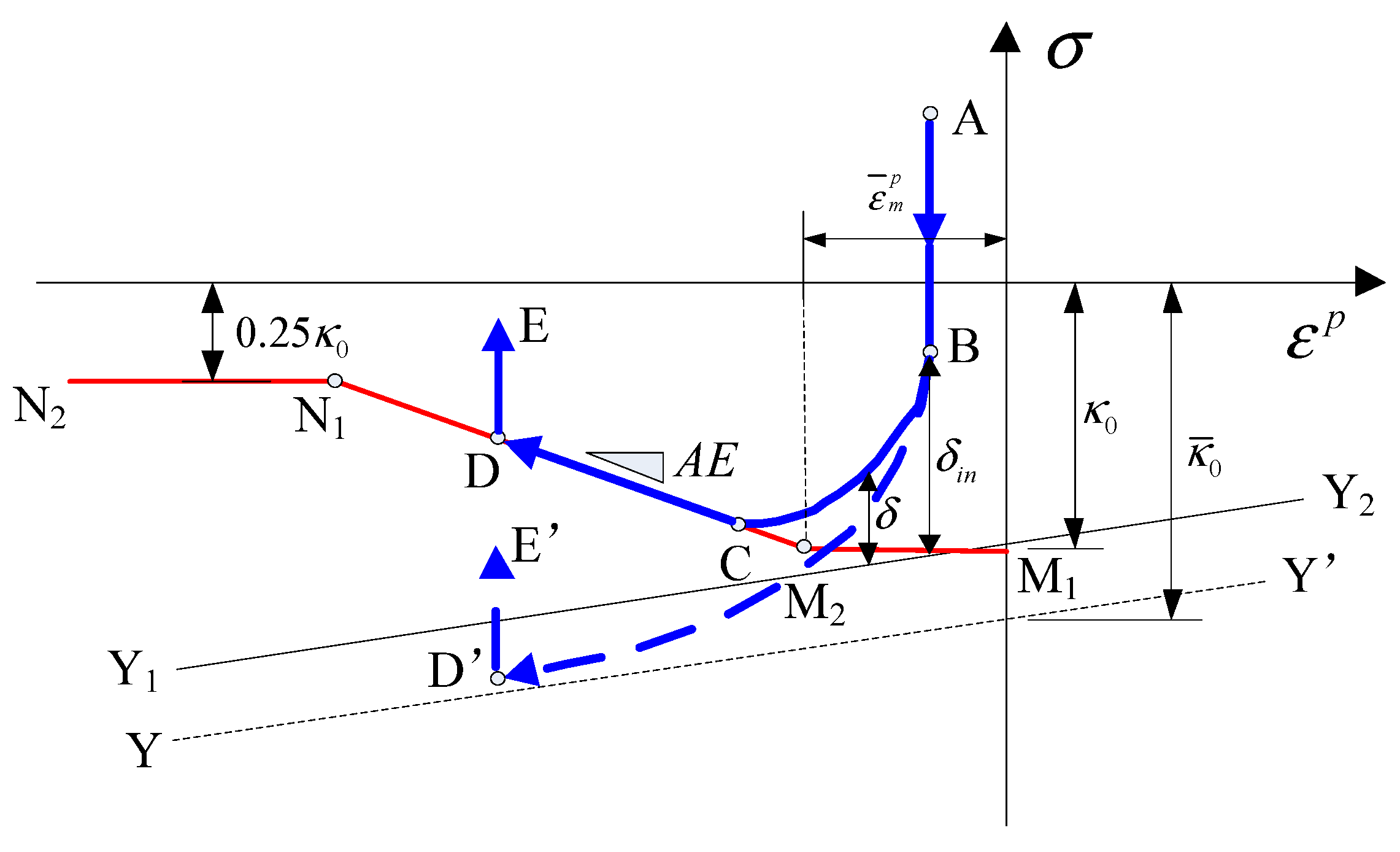



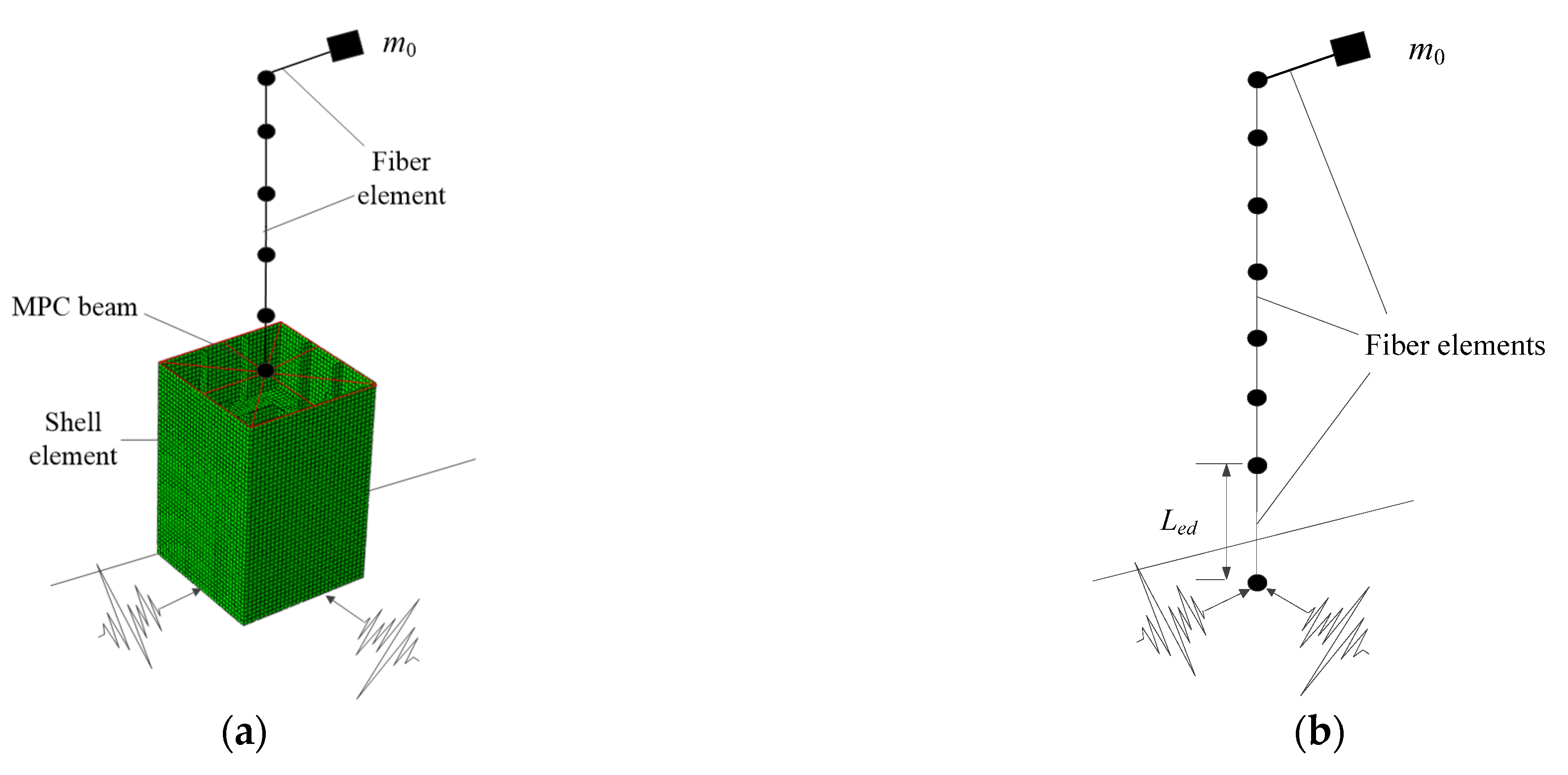
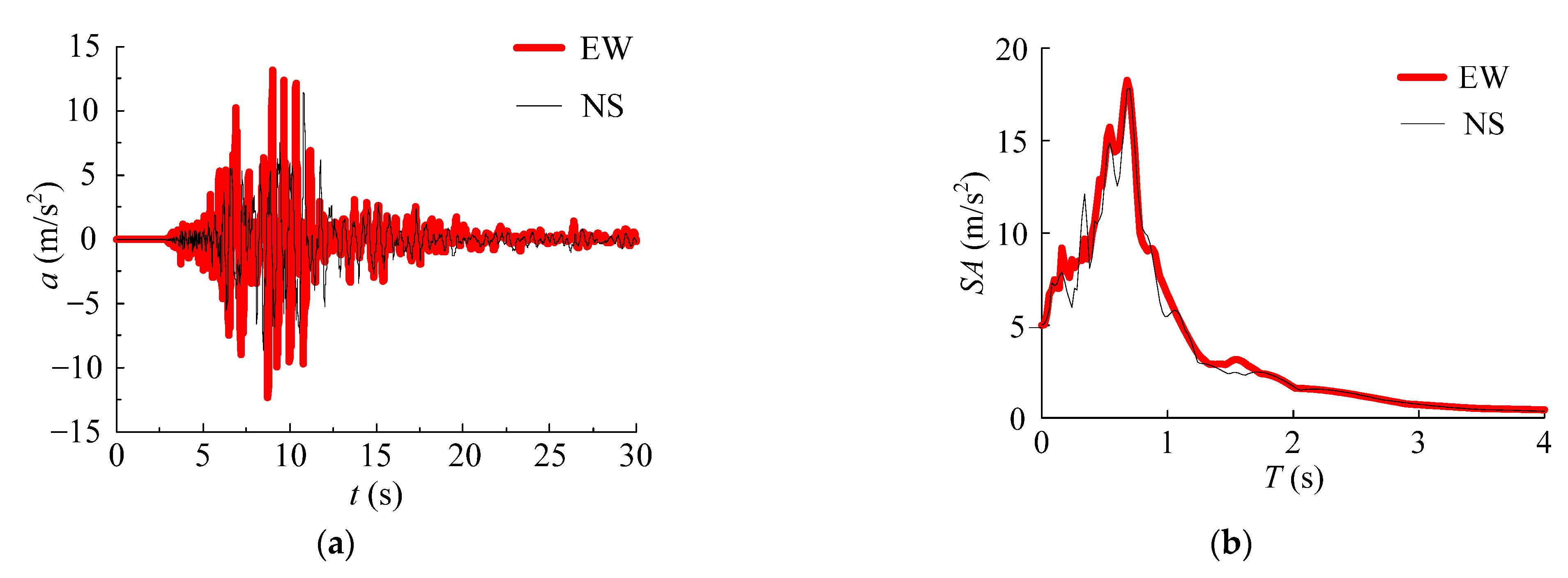
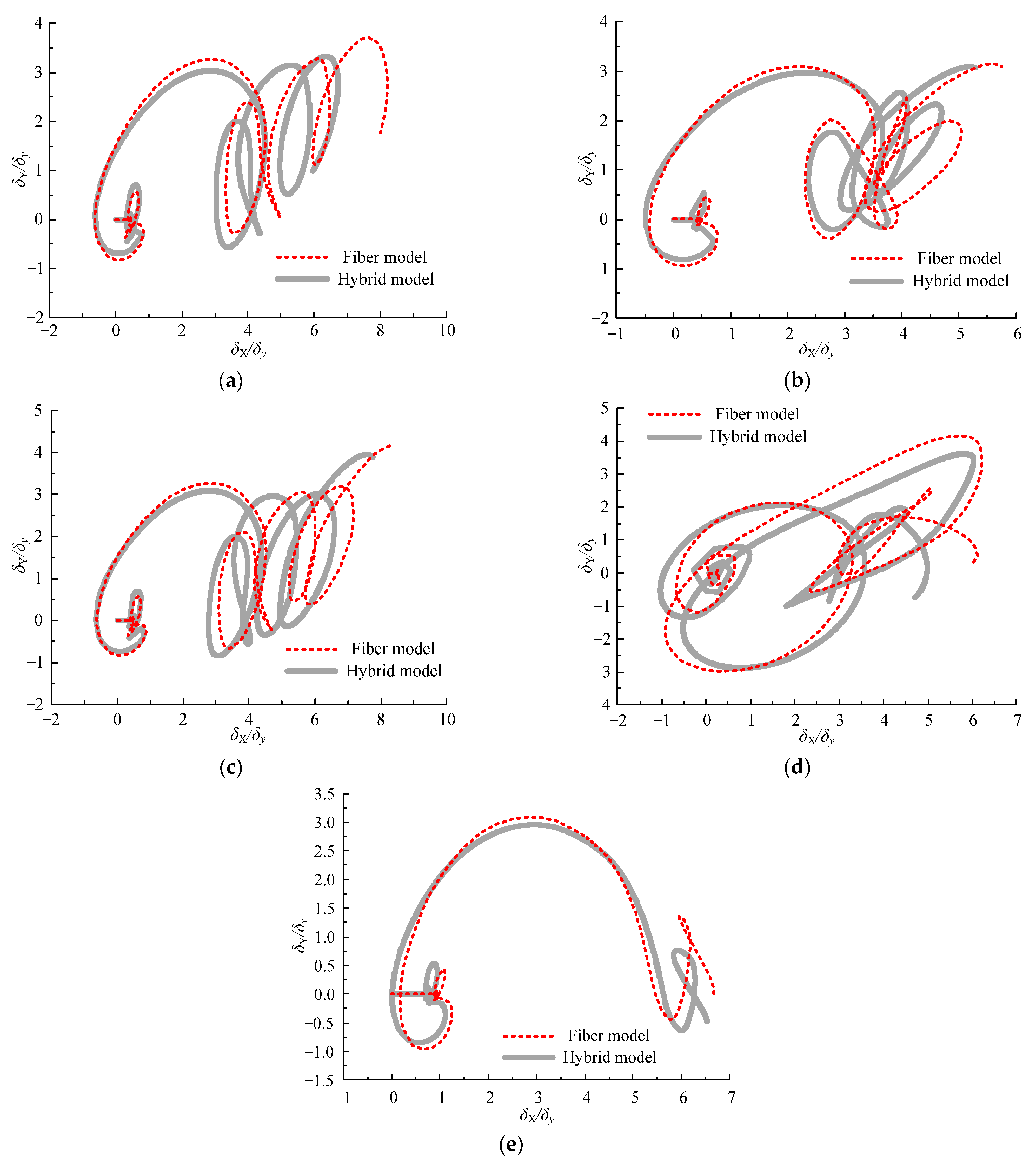
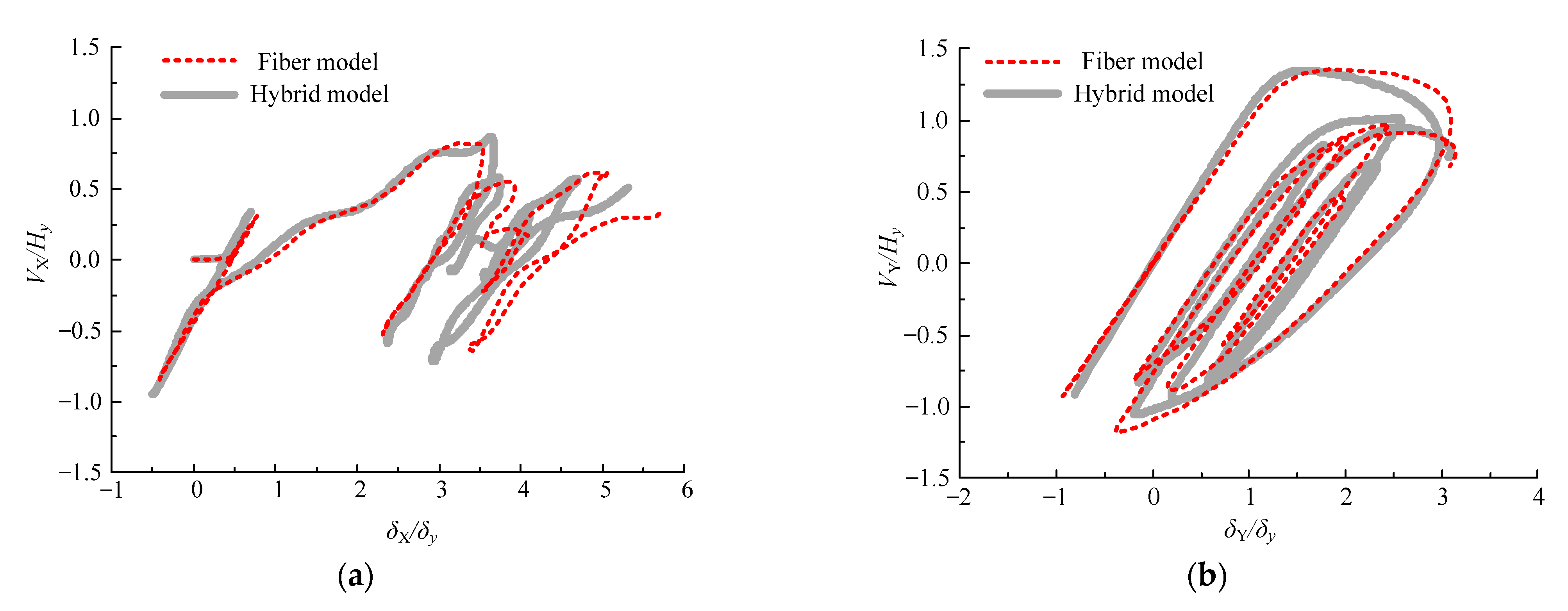

| No. | Pier | B0 (m) | RR | Rf | λ | α | γ/γ* | N/Ny | e/h |
|---|---|---|---|---|---|---|---|---|---|
| 1 | b2 | 1.023 | 0.3924 | 0.3924 | 0.3924 | 0.5 | 1.0 | 0.15 | 0.1 |
| 2 | b3 | 1.344 | 0.5155 | 0.3104 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.1 |
| 3 | b4 | 1.023 | 0.3924 | 0.3924 | 0.3945 | 0.7 | 1.0 | 0.15 | 0.1 |
| 4 | b5 | 1.023 | 0.3924 | 0.2355 | 0.2255 | 0.5 | 3.0 | 0.15 | 0.1 |
| 5 | b6 | 1.023 | 0.3924 | 0.3924 | 0.3945 | 1.0 | 1.0 | 0.15 | 0.1 |
| 6 | b7 | 1.023 | 0.3924 | 0.2295 | 0.3945 | 1.0 | 3.0 | 0.15 | 0.1 |
| 7 | b8 | 1.023 | 0.3924 | 0.2355 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.1 |
| 8 | b9−10 | 1.023 | 0.3924 | 0.2332 | 0.3945 | 0.7 | 3.0 | 0.1 | 0.1 |
| 9 | b9−15 | 1.023 | 0.3924 | 0.2332 | 0.3945 | 0.7 | 3.0 | 0.15 | 0.1 |
| 10 | b9−20 | 1.023 | 0.3924 | 0.2332 | 0.3945 | 0.7 | 3.0 | 0.2 | 0.1 |
| 11 | b9−30 | 1.023 | 0.3924 | 0.2332 | 0.3945 | 0.7 | 3.0 | 0.3 | 0.1 |
| 12 | b10 | 1.023 | 0.3924 | 0.2355 | 0.3039 | 0.5 | 3.0 | 0.15 | 0.1 |
| 13 | b11−10 | 1.023 | 0.3924 | 0.2332 | 0.225 | 0.7 | 3.0 | 0.1 | 0.1 |
| 14 | b11−15 | 1.023 | 0.3924 | 0.2332 | 0.225 | 0.7 | 3.0 | 0.15 | 0.1 |
| 15 | b11−20 | 1.023 | 0.3924 | 0.2332 | 0.225 | 0.7 | 3.0 | 0.2 | 0.1 |
| 16 | b11−30 | 1.023 | 0.3924 | 0.2332 | 0.225 | 0.7 | 3.0 | 0.3 | 0.1 |
| 17 | b13−10 | 1.023 | 0.3924 | 0.2332 | 0.3079 | 0.7 | 3.0 | 0.1 | 0.1 |
| 18 | b13−15 | 1.023 | 0.3924 | 0.2332 | 0.3079 | 0.7 | 3.0 | 0.15 | 0.1 |
| 19 | b13−20 | 1.023 | 0.3924 | 0.2332 | 0.3079 | 0.7 | 3.0 | 0.2 | 0.1 |
| 20 | b13−30 | 1.023 | 0.3924 | 0.2332 | 0.3079 | 0.7 | 3.0 | 0.3 | 0.1 |
| 21 | b14 | 1.023 | 0.3924 | 0.2295 | 0.2254 | 1.0 | 3.0 | 0.15 | 0.1 |
| 22 | b15 | 1.023 | 0.3924 | 0.2295 | 0.3071 | 1.0 | 3.0 | 0.15 | 0.1 |
| 23 | b16 | 1.344 | 0.5155 | 0.3071 | 0.3945 | 0.7 | 3.0 | 0.15 | 0.1 |
| 24 | b18 | 1.344 | 0.5155 | 0.3051 | 0.3945 | 1.0 | 3.0 | 0.15 | 0.1 |
| 25 | b20 | 1.184 | 0.4542 | 0.2730 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.1 |
| 26 | b21 | 1.184 | 0.4542 | 0.2708 | 0.3945 | 0.7 | 3.0 | 0.15 | 0.1 |
| 27 | b22 | 1.184 | 0.4542 | 0.2668 | 0.3945 | 1.0 | 3.0 | 0.15 | 0.1 |
| 28 | b3−b | 1.344 | 0.3924 | 0.2373 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.1 |
| 29 | b3−c | 1.023 | 0.5155 | 0.3104 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.1 |
| 30 | b7−b | 1.344 | 0.3924 | 0.2332 | 0.3945 | 1.0 | 3.0 | 0.15 | 0.1 |
| 31 | b7−c | 1.023 | 0.5155 | 0.3062 | 0.3945 | 1.0 | 3.0 | 0.15 | 0.1 |
| 32 | b9−b | 1.344 | 0.3924 | 0.2332 | 0.3945 | 0.7 | 3.0 | 0.15 | 0.1 |
| 33 | b9−c | 1.023 | 0.5155 | 0.3071 | 0.3945 | 0.7 | 3.0 | 0.15 | 0.1 |
| 34 | b2−b | 1.023 | 0.3924 | 0.3924 | 0.3924 | 0.5 | 1.0 | 0.15 | 0.2 |
| 35 | b2−c | 1.023 | 0.3924 | 0.3924 | 0.3924 | 0.5 | 1.0 | 0.15 | 0.3 |
| 36 | b3−d | 1.344 | 0.5155 | 0.3104 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.2 |
| 37 | b3−e | 1.344 | 0.5155 | 0.3104 | 0.3945 | 0.5 | 3.0 | 0.15 | 0.3 |
| 38 | b4−b | 1.023 | 0.3924 | 0.3924 | 0.3945 | 0.7 | 1.0 | 0.15 | 0.2 |
| 39 | b4−c | 1.023 | 0.3924 | 0.3924 | 0.3945 | 0.7 | 1.0 | 0.15 | 0.3 |
| M | ω (MPa−1) | σu (MPa) | ||||
|---|---|---|---|---|---|---|
| 4.47 | 0.0153 | −0.142 | 1.43 | 0.0161 | 412.2 | 636.4 |
| ζ | e | f (GPa) | a | b | c | α |
| 307.4 | 470.0 | 0.53 | −0.358 | 21.4 | 1.03 | 0.343 |
| σy/MPa | σu/MPa | E/GPa | μ |
|---|---|---|---|
| 379 | 629 | 206 | 0.3 |
| RR | λ | N/Ny | γ/γ* | α |
|---|---|---|---|---|
| 0.560 | 0.26 | 0.125 | 0.9 | 1.0 |
| Pier | Model | Elastic Stiffness | Hm | δm | δ80 | Total Hysteretic Energy |
|---|---|---|---|---|---|---|
| b2 | Fiber model | 0.966 | 0.998 | 2.65 | 3.65 | 21.36 |
| Hybrid model | 0.987 | 1.019 | 2.65 | 3.26 | 20.97 | |
| b3 | Fiber model | 0.967 | 0.997 | 2.65 | 3.60 | 21.38 |
| Hybrid model | 0.989 | 1.014 | 2.65 | 3.21 | 20.31 | |
| b4 | Fiber model | 0.962 | 1.009 | 2.65 | 4.15 | 32.11 |
| Hybrid model | 0.981 | 1.019 | 2.65 | 4.02 | 30.29 | |
| b13−10 | Fiber model | 0.997 | 1.256 | 4.15 | 7.05 | 135.87 |
| Hybrid model | 0.969 | 1.288 | 4.15 | 6.24 | 123.29 | |
| b3−d | Fiber model | 0.968 | 0.666 | 2.80 | 5.51 | 21.32 |
| Hybrid model | 0.989 | 0.699 | 2.80 | 5.45 | 20.29 |
| Pier | Model | Elastic Stiffness | Hm | δm | δ80 | Total Hysteretic Energy |
|---|---|---|---|---|---|---|
| b2 | Fiber model | 0.967 | 1.248 | 2.00 | 2.708 | 24.89 |
| Hybrid model | 0.997 | 1.263 | 2.00 | 2.852 | 24.57 | |
| b3 | Fiber model | 0.967 | 1.243 | 2.00 | 2.695 | 25.21 |
| Hybrid model | 1.099 | 1.241 | 2.00 | 2.510 | 23.66 | |
| b4 | Fiber model | 0.962 | 1.259 | 2.50 | 3.21 | 31.62 |
| Hybrid model | 0.983 | 1.276 | 2.50 | 2.64 | 30.69 | |
| b13−10 | Fiber model | 0.968 | 1.362 | 3.50 | 5.15 | 98.89 |
| Hybrid model | 0.997 | 1.410 | 4.00 | 4.93 | 96.26 | |
| b3−d | Fiber model | 0.973 | 1.042 | 1.50 | 1.77 | 10.86 |
| Hybrid model | 1.103 | 1.026 | 1.50 | 1.78 | 10.62 |
| Pier | Model | δm | δr | f | ||
|---|---|---|---|---|---|---|
| X | Y | X | Y | |||
| b2 | Fiber model | 8.234 | 3.699 | 8.125 | 2.395 | 1.452 |
| Hybrid model | 6.722 | 3.328 | 6.043 | 1.987 | 1.473 | |
| b3 | Fiber model | 5.762 | 3.148 | 4.483 | 1.254 | 1.341 |
| Hybrid model | 5.293 | 3.093 | 3.991 | 1.152 | 1.350 | |
| b4 | Fiber model | 8.345 | 4.181 | 5.870 | 1.791 | 1.457 |
| Hybrid model | 7.868 | 3.946 | 5.778 | 1.716 | 1.468 | |
| b13−10 | Fiber model | 6.219 | 4.168 | 3.852 | 0.0180 | 2.553 |
| Hybrid model | 6.024 | 3.614 | 3.774 | 0.0108 | 2.560 | |
| b3−d | Fiber model | 6.742 | 3.094 | 6.445 | 0.520 | 1.310 |
| Hybrid model | 6.532 | 2.957 | 6.347 | 0.106 | 1.316 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuge, H.; Zheng, X.; Song, F.; Tang, Z. Fiber Model Considering the Local Instability Effect and Its Application to the Seismic Analysis of Eccentrically Compressed Steel Piers. Appl. Sci. 2022, 12, 5838. https://doi.org/10.3390/app12125838
Zhuge H, Zheng X, Song F, Tang Z. Fiber Model Considering the Local Instability Effect and Its Application to the Seismic Analysis of Eccentrically Compressed Steel Piers. Applied Sciences. 2022; 12(12):5838. https://doi.org/10.3390/app12125838
Chicago/Turabian StyleZhuge, Hanqing, Xianglong Zheng, Fangyuan Song, and Zhanzhan Tang. 2022. "Fiber Model Considering the Local Instability Effect and Its Application to the Seismic Analysis of Eccentrically Compressed Steel Piers" Applied Sciences 12, no. 12: 5838. https://doi.org/10.3390/app12125838







