Finite-Time Consensus Tracking Control for Speed Sensorless Multi-Motor Systems
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
2.1. Graph Theory
2.2. Lemmas
2.3. Problem Description
3. Finite-Time Convergent Observer Design
4. Finite-Time Consensus Tracking Protocol Design
5. Simulations
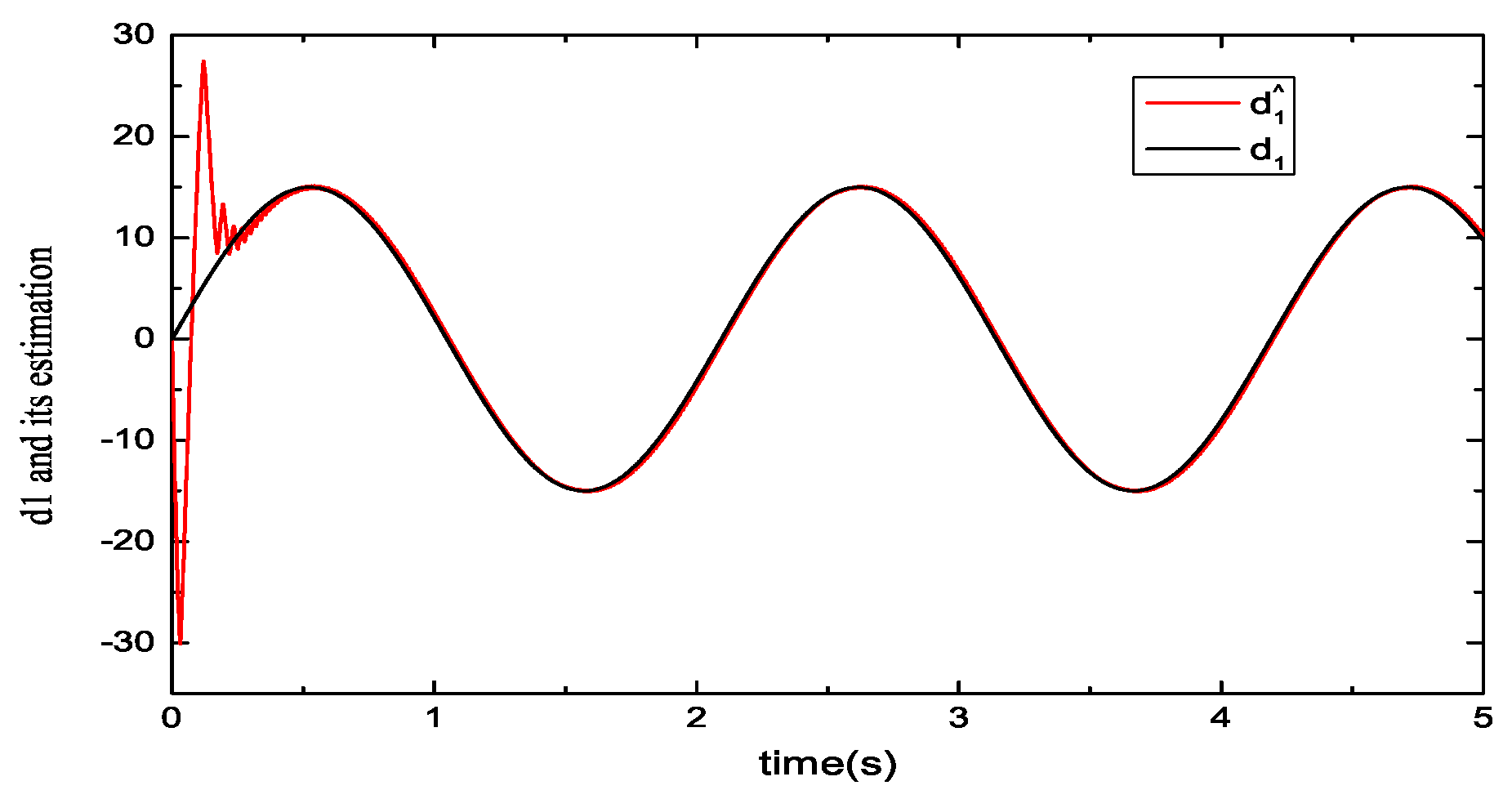
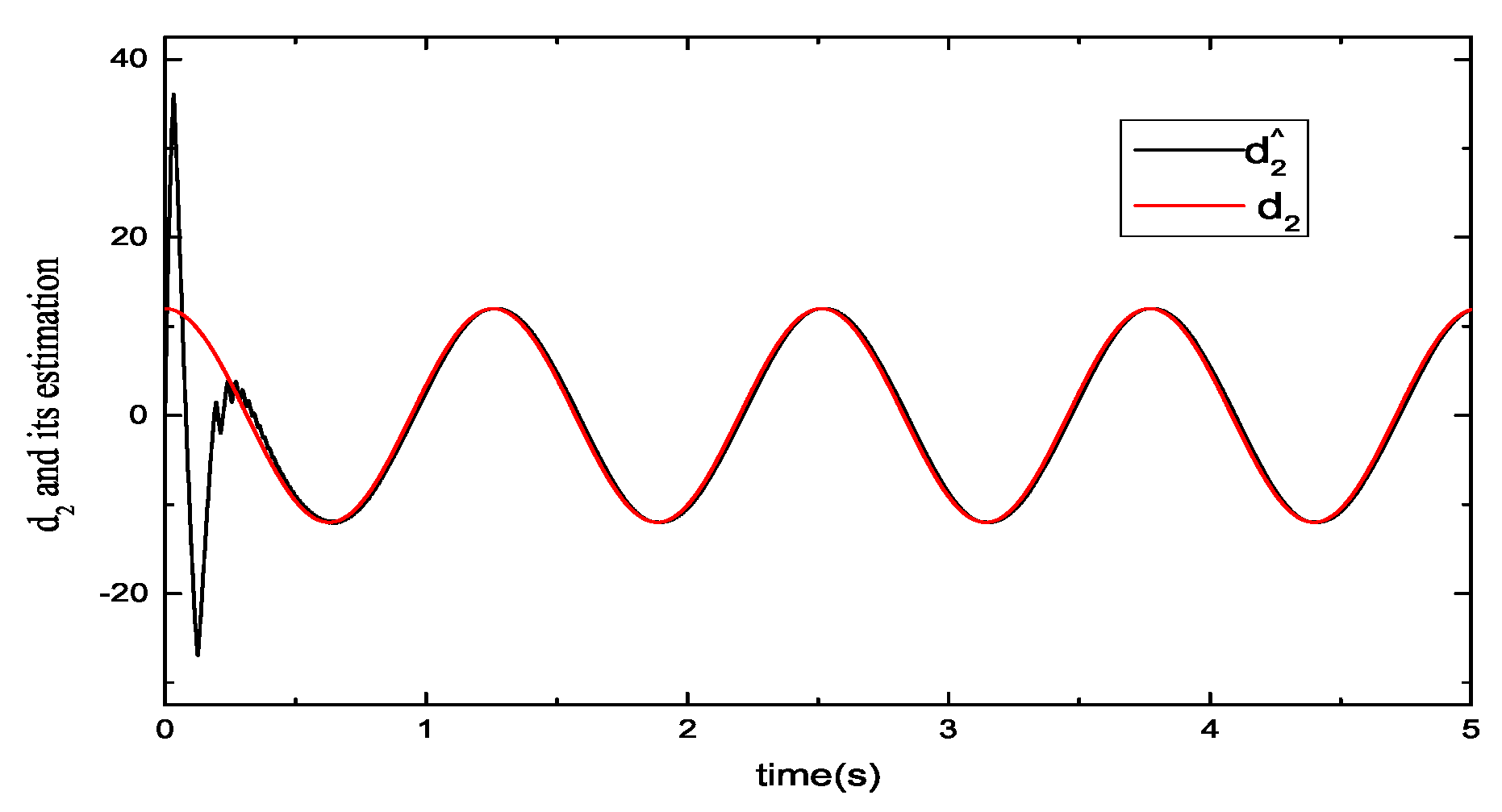
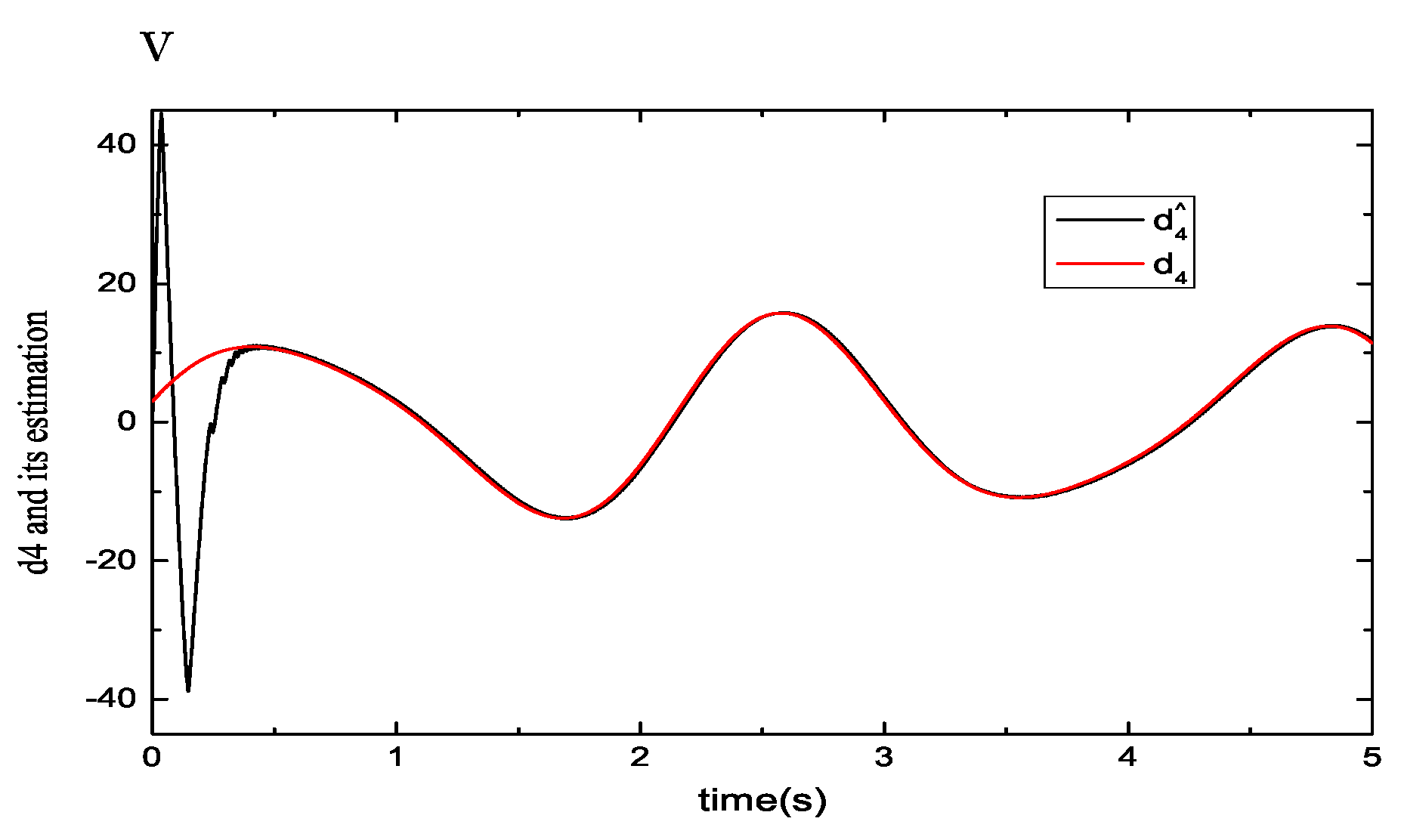
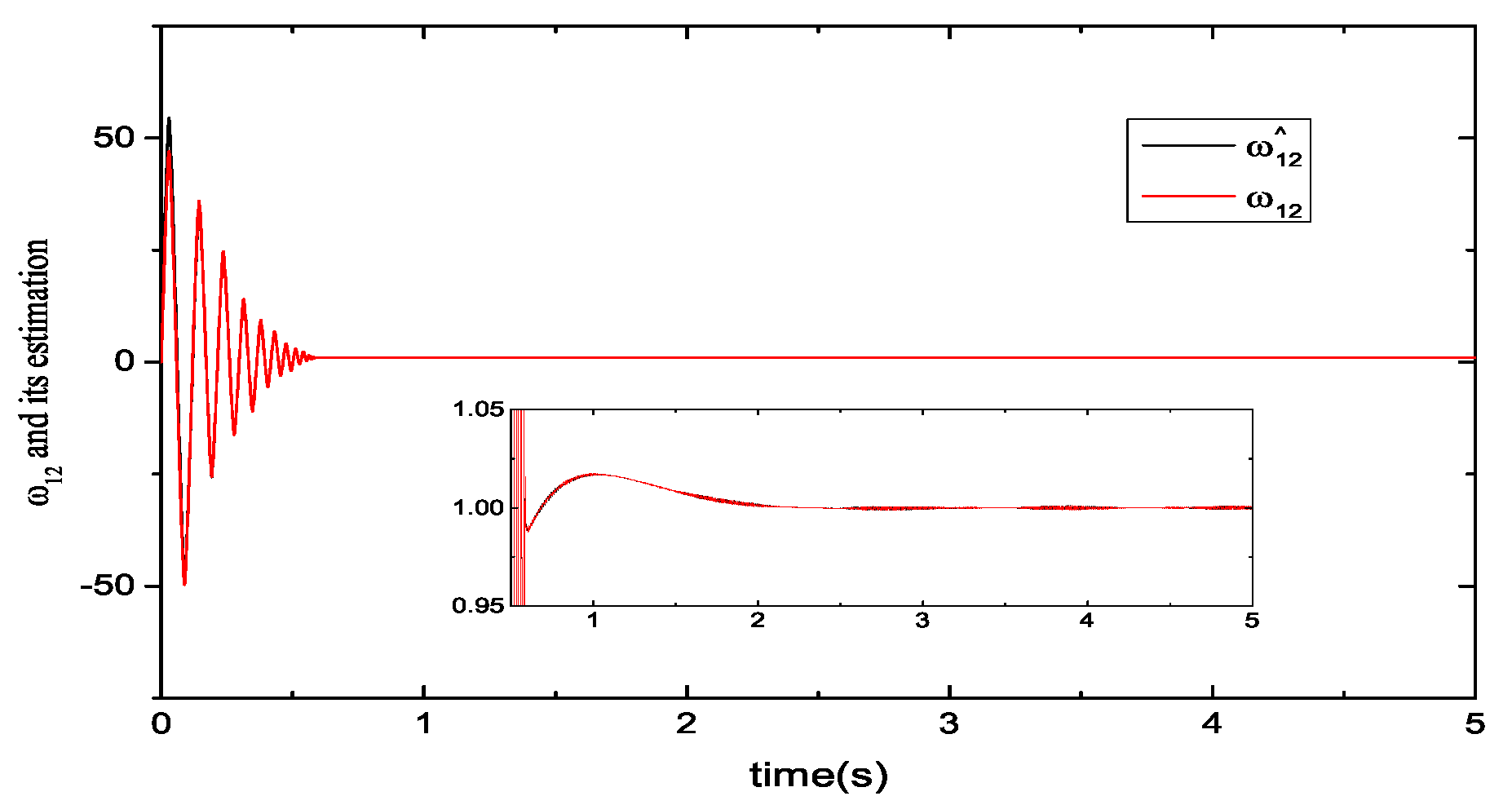
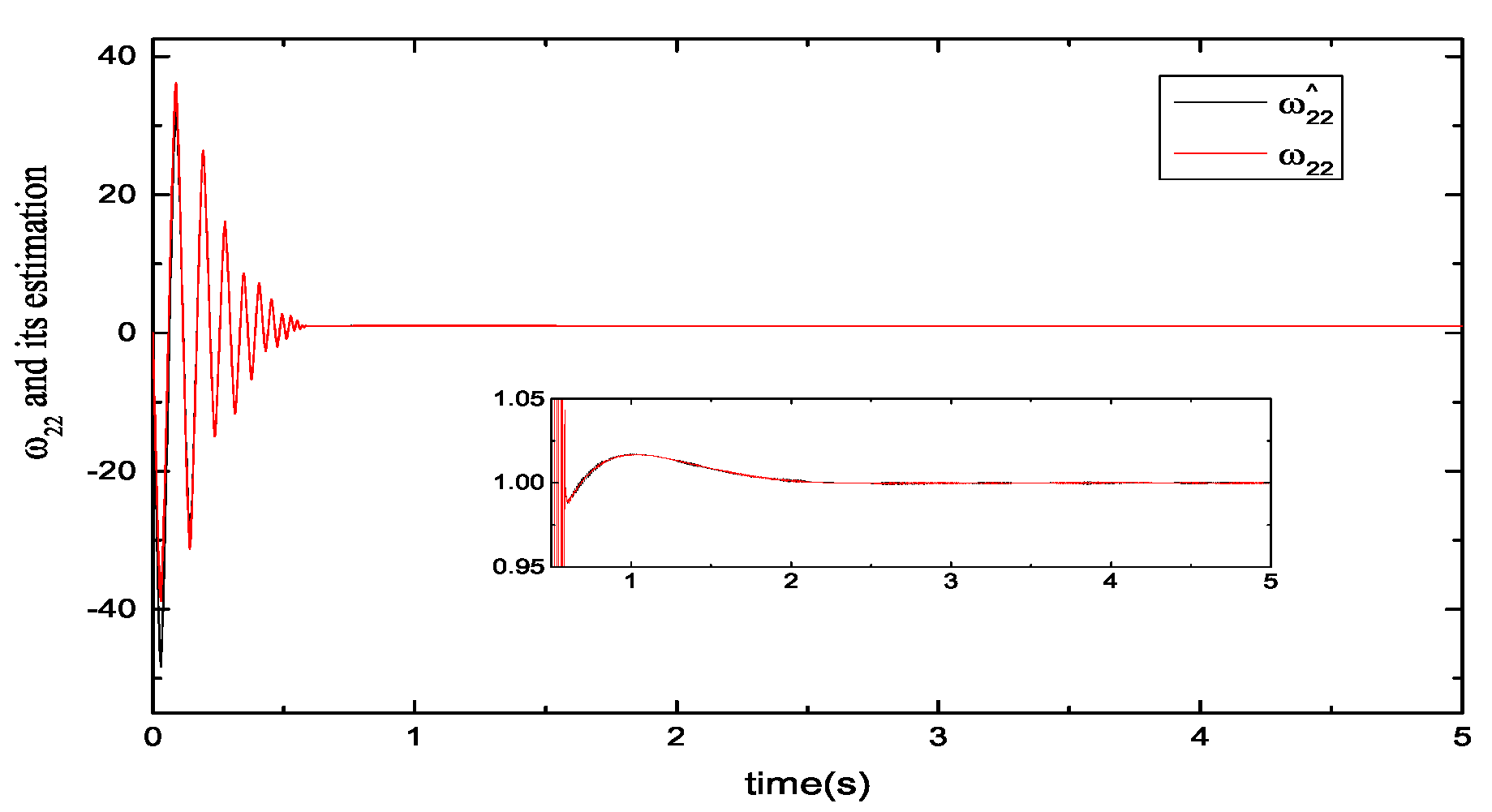
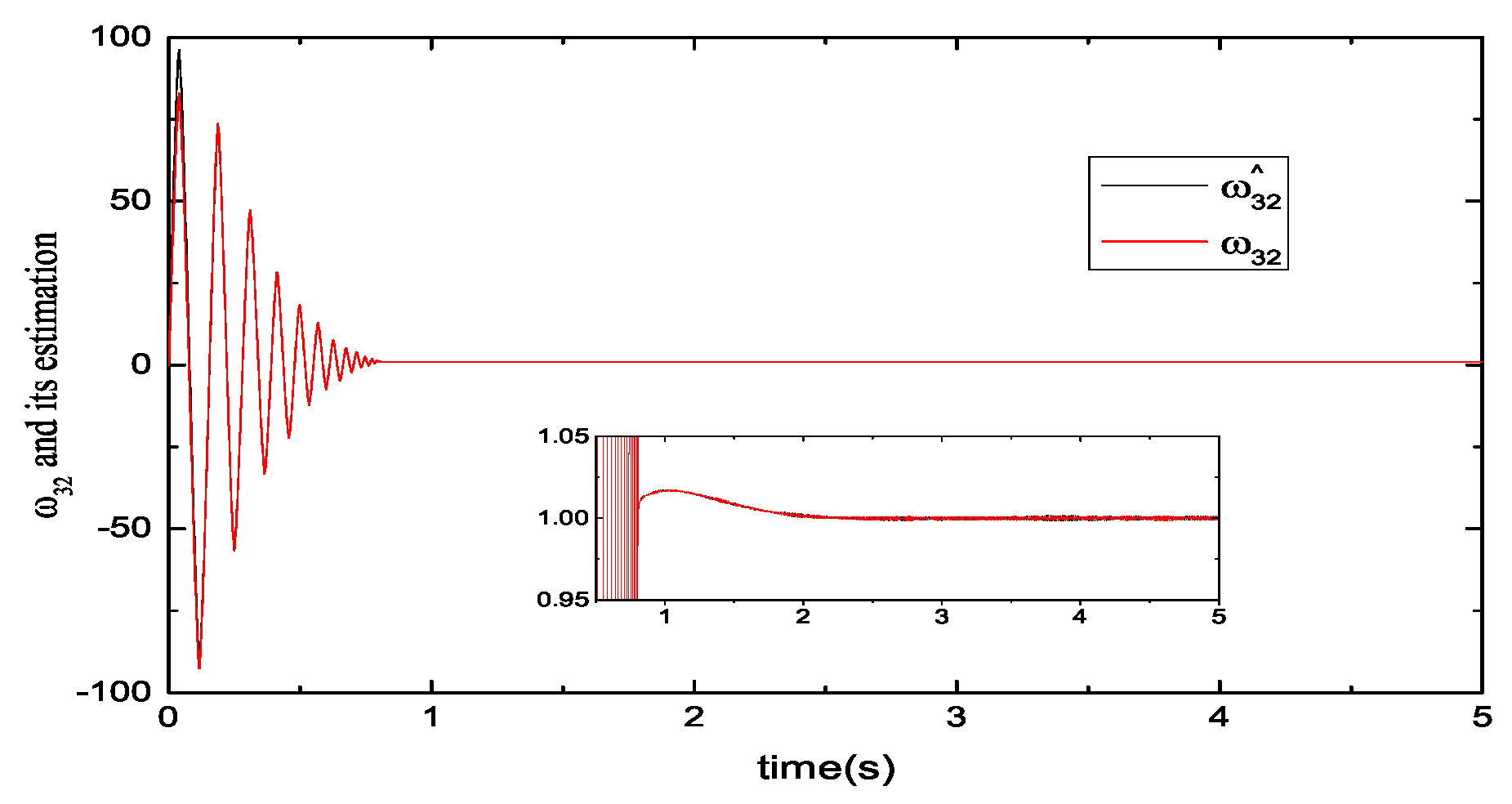
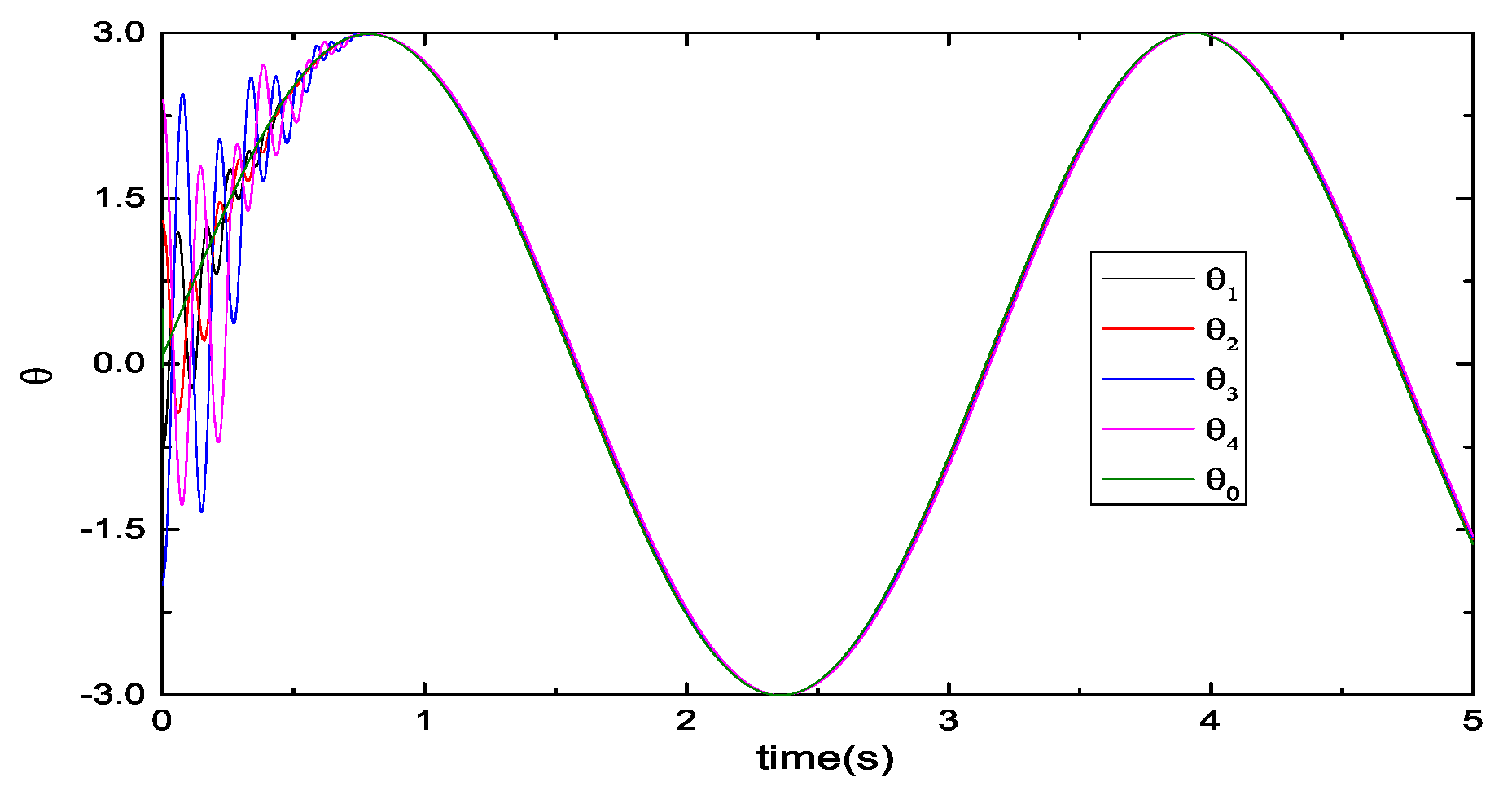
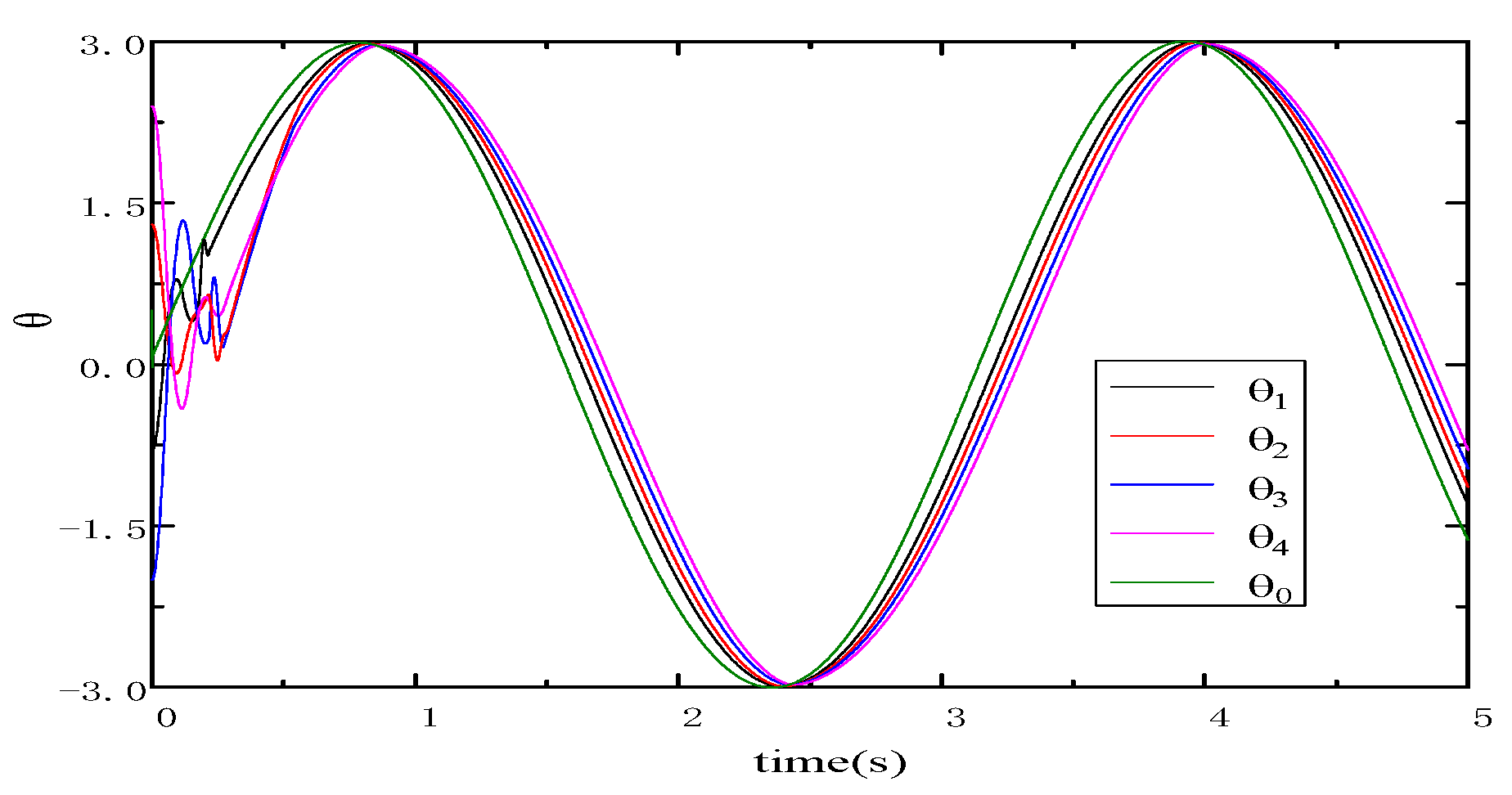
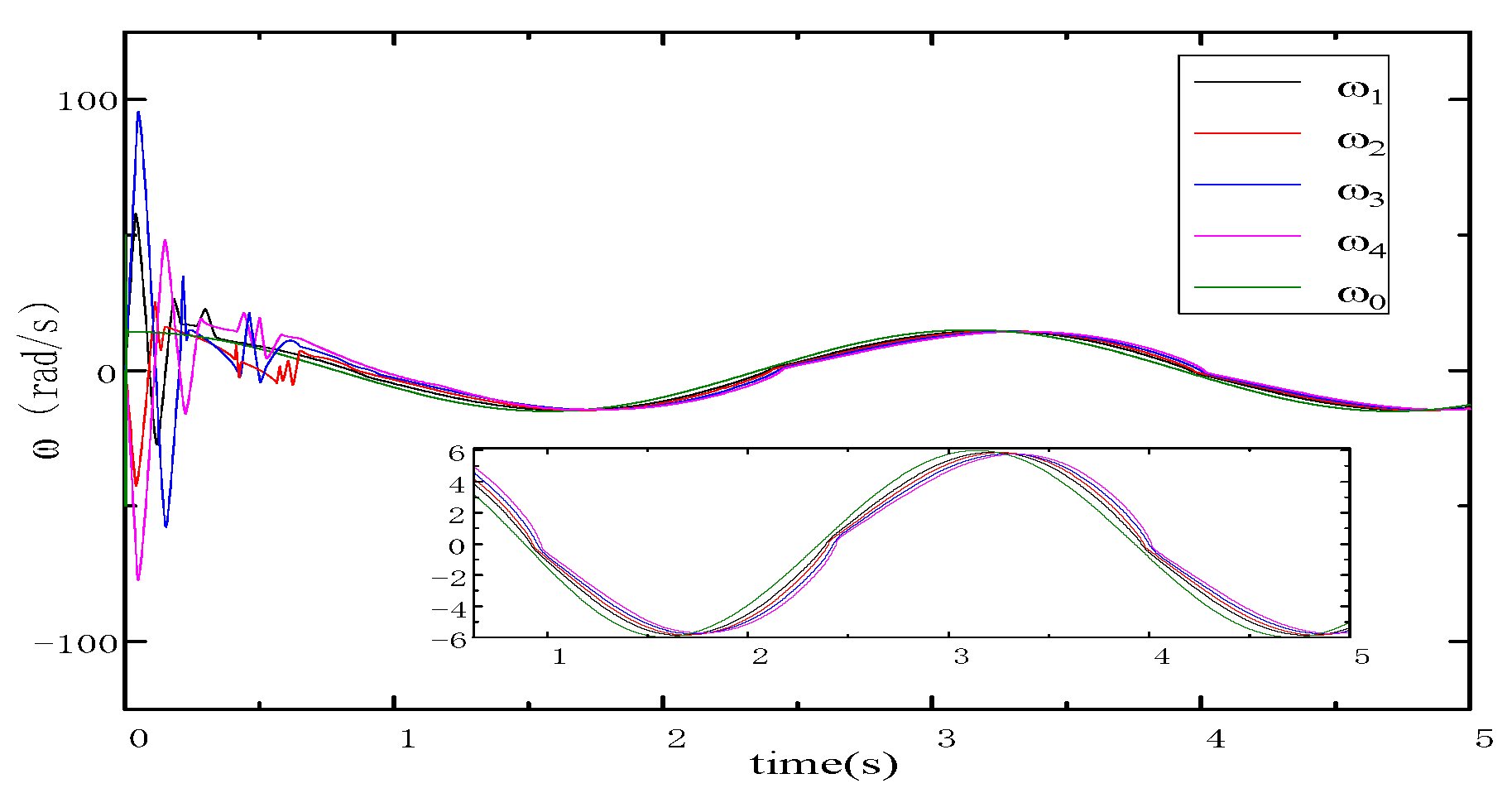
5.1. Performance Evaluations of Observers
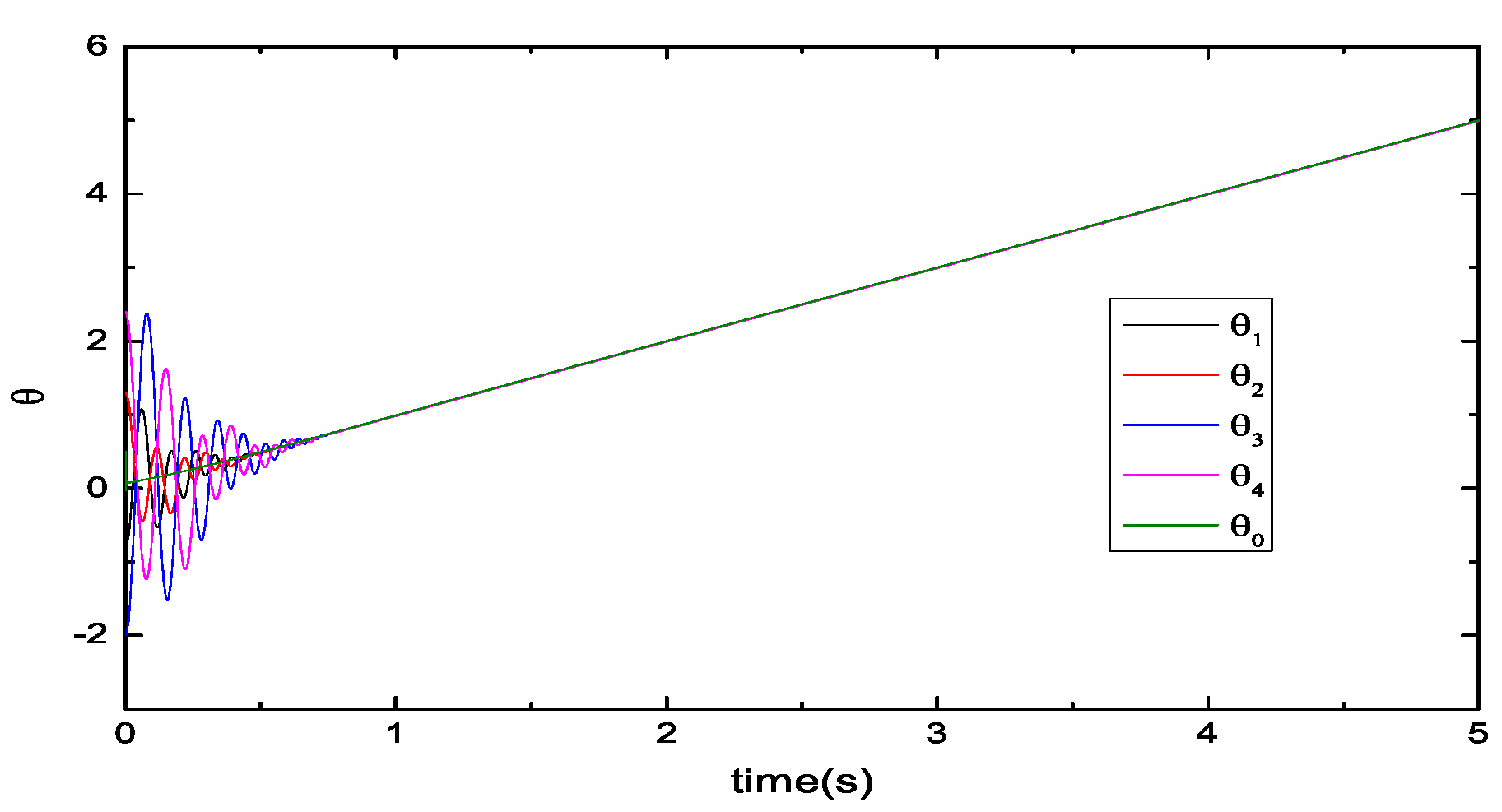
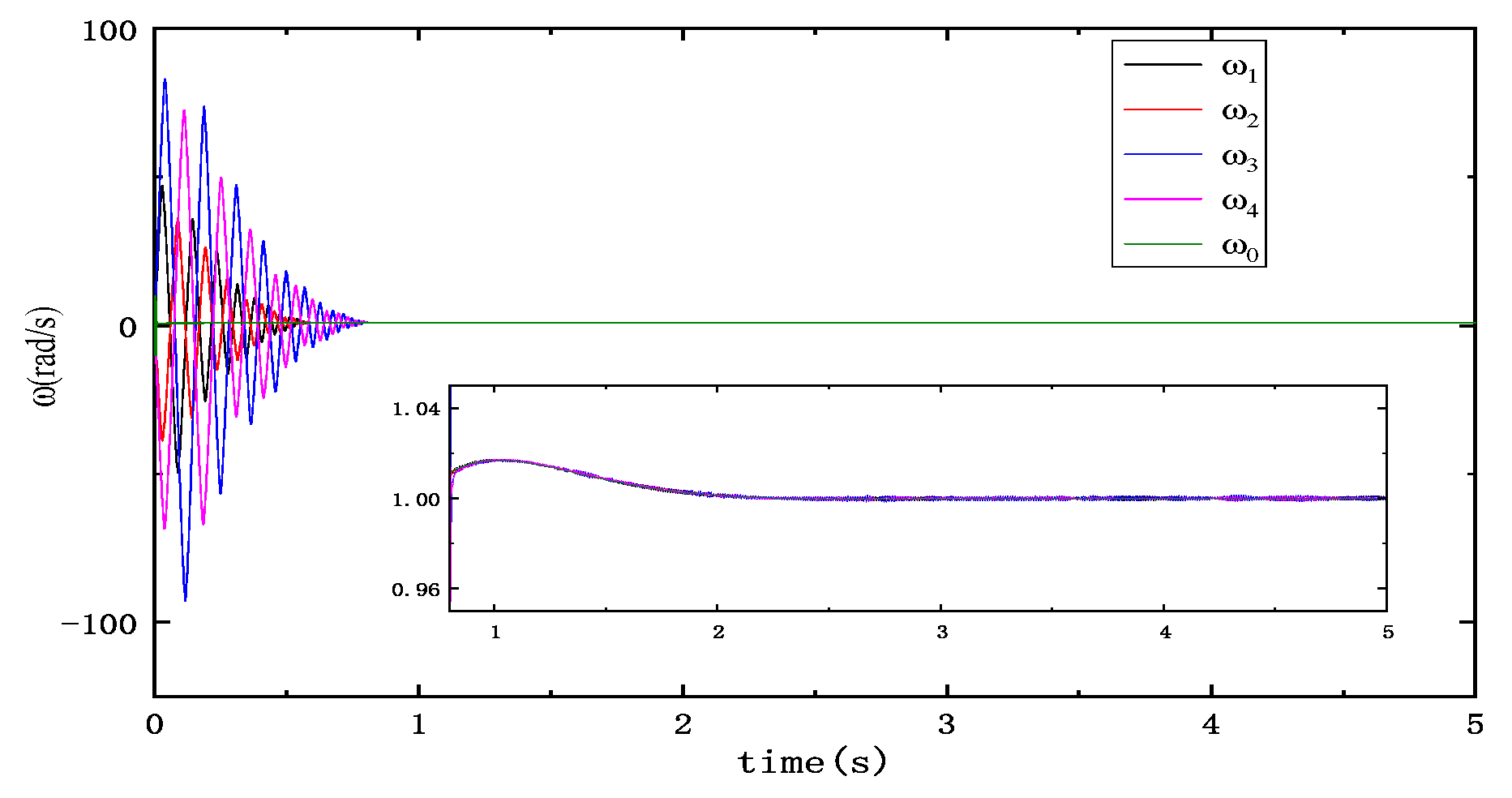
5.2. Performance Evaluations of the Consensus Control Protocol
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M.; Ren, X.; Chen, Q. Robust tracking and distributed synchronization control of a multi-motor servomechanism with H-infinity performance. ISA Trans. 2018, 72, 147–160. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Ren, X.; Lv, Y. Predictor-Based Tracking and Synchronization Control for Multi-Motor Drive Servo Systems. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; Volume 1, pp. 539–544. [Google Scholar]
- Canese, L.; Cardarilli, G.C.; Nunzio, L.D.; Fazzolari, R.; Giardino, D.; Re, M.; Spanò, S. Multi-Agent Reinforcement Learning: A Review of Challenges and Applications. Appl. Sci. 2021, 11, 4948. [Google Scholar] [CrossRef]
- Fang, P.; Wang, Y.; Hou, Y.; Wu, Y.F. Synchronous Control of Multi-Motor Coupled with Pendulum in a Vibration System. IEEE Access 2020, 8, 51964–51975. [Google Scholar] [CrossRef]
- Masroor, S.; Peng, C. Agent-based consensus on speed in the network-coupled DC motors. Neural Comput. Appl. 2016, 30, 1647–1659. [Google Scholar] [CrossRef]
- Amornwongpeeti, S.; Ekpanyapong, M.; Chayopitak, N.; Monteiro, J. A single chip FPGA-based cross-coupling multi-motor drive system. IEICE Electron. Express 2015, 12, 383–389. [Google Scholar] [CrossRef][Green Version]
- Chen, B.; Ding, J. Adaptive Model-Free Coupling Controller Design for Multi-Axis Motion Systems. Appl. Sci. 2020, 10, 3592. [Google Scholar] [CrossRef]
- He, J.; Ding, J.; Zhang, C.; Mao, S.; Liu, J.; Hu, J.; Ma, Z. Research on Multi-axis Servo Synergic Control System Based on Sliding Mode Variable Structure. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Voluem 1, pp. 6908–6915. [Google Scholar]
- Koren, Y. Cross-Coupled Biaxial Computer Control for Manufacturing Systems. J. Dyn. Syst. Meas. Control.-Trans. Asme 1980, 102, 265–272. [Google Scholar] [CrossRef]
- Shuang, B.; Zhu, Z.Q.; Wu, X. Improved Cross-coupling Effect Compensation Method for Sensorless Control of IPMSM with High Frequency Voltage Injection. IEEE Trans. Energy Convers. 2022, 37, 347–358. [Google Scholar] [CrossRef]
- Zhu, C.; Tu, Q.; Jiang, C. A Cross Coupling Control Strategy for Dual-Motor Speed Synchronous System Based on Second Order Global Fast Terminal Sliding Mode Control. IEEE Access 2020, 8, 217967–217976. [Google Scholar] [CrossRef]
- Chen, W.; Liang, J.; Shi, T. Speed Synchronous Control of Multiple Permanent Magnet Synchronous Motors Based on an Improved Cross-Coupling Structure. Energies 2018, 11, 282. [Google Scholar] [CrossRef]
- Li, L.; Sun, L.; Zhang, S. Mean deviation coupling synchronous control for multiple motors via second-order adaptive sliding mode control. ISA Trans. 2016, 62, 222–235. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Liu, H.; Geng, Q.; Xia, C. Improved relative coupling control structure for multi-motor speed synchronous driving system. Iet Electr. Power Appl. 2016, 10, 451–457. [Google Scholar] [CrossRef]
- Štil, V.J.; Varga, T.; Benšić, T.; Barukčić, M. A Survey of Fuzzy Algorithms Used in Multi-Motor Systems Control. Electronics 2020, 9, 1788. [Google Scholar] [CrossRef]
- Li, L.; Sun, L.; Zhang, S.; Yang, Q. Speed tracking and synchronization of multiple motors using ring coupling control and adaptive sliding mode control. ISA Trans. 2015, 58, 635–649. [Google Scholar] [CrossRef]
- Yu, S.; Long, X. Finite-time consensus for second-order multi-agent systems with disturbances by integral sliding mode. Automatica 2015, 54, 158–165. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, Z.; Yang, S.X.; He, J. Total-Amount Synchronous Control Based on Terminal Sliding-Mode Control. IEEE Access 2017, 5, 5436–5444. [Google Scholar] [CrossRef]
- Koren, Y. Distributed finite-time tracking of multiple non-identical second-order nonlinear systems with settling time estimation. Automatic 2016, 64, 86–93. [Google Scholar]
- Amornwongpeeti, S.; Ekpanyapong, M.; Chayopitak, N.; Monteiro, J. Finite-time consensus for second-order multi-agent systems with saturated control protocols. IET Control Theory Appl. 2015, 9, 312–319. [Google Scholar]
- Ma, X.; Sun, F.; Li, H.; He, B. Neural-network-based integral sliding-mode tracking control of second-order multi-agent systems with unmatched disturbances and completely unknown dynamics. Int. J. Control Autom. Syst. 2017, 15, 1925–1935. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, H.; He, J.; Xu, C. Consensus tracking for multi-motor system via observer based variable structure approach. J. Frankl. Inst. 2015, 352, 3366–3377. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, Z.; Liu, J.; He, J.; Wu, H.; Li, P. Consensus-based total-amount cooperative tracking control for multi-motor locomotive traction system. J. Frankl. Inst. 2019, 356, 819–834. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, H.; Liu, B.; He, J.; Li, B. Hybrid Structure Based Tracking and Consensus for Multiple Motors. Math. Probl. Eng. 2014, 2, 1–9. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, C.; Duan, G. Distributed and Truncated Reduced-Order Observer Based Output Feedback Consensus of Multi-Agent Systems. IEEE Trans. Autom. Control 2014, 59, 2264–2270. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Li, S. Finite-Time Output Consensus of Higher-Order Multiagent Systems With Mismatched Disturbances and Unknown State Elements. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2571–2581. [Google Scholar] [CrossRef]
- Chen, W.-H.; Ding, K.; Lu, X. Disturbance-observer-based control design for a class of uncertain systems with intermittent measurement. J. Frankl. Inst. 2017, 354, 5266–5279. [Google Scholar] [CrossRef]
- Chen, W.-H.; Cheng, L.; Lu, X. Observer-based feedback stabilization of Lipschitz nonlinear systems in the presence of asynchronous sampling and scheduling protocols. Nonlinear Anal. Hybrid Syst. 2019, 33, 282–299. [Google Scholar] [CrossRef]
- Chen, W.-H.; He, H.; Lu, X.; Deng, X. Impulsive observer-based design for state estimation of a class of nonlinear singularly perturbed systems with discrete measurements. Nonlinear Anal. Hybrid Syst. 2021, 41, 101–117. [Google Scholar] [CrossRef]
- Chen, S.; Liu, G.; Zhu, L. Sensorless Control Strategy of a 315 kW High-Speed BLDC Motor Based on a Speed-Independent Flux Linkage Function. IEEE Trans. Ind. Electron. 2017, 64, 8607–8617. [Google Scholar] [CrossRef]
- Jakobsen, U.; Lu, K.; Rasmussen, P.O.; Lee, D.; Ahn, J. Sensorless Control of Low-Cost Single-Phase Hybrid Switched Reluctance Motor Drive. IEEE Trans. Ind. Appl. 2015, 51, 2381–2387. [Google Scholar] [CrossRef]
- Xiao, D.; Nalakath, S.; Filho, S.R.; Fang, G.; Dong, A. Universal Full-Speed Sensorless Control Scheme for Interior Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2021, 36, 4723–4737. [Google Scholar] [CrossRef]
- Chen, J.; Huang, J.; Sun, Y. Resistances and Speed Estimation in Sensorless Induction Motor Drives Using a Model with Known Regressors. IEEE Trans. Ind. Electron. 2019, 66, 2659–2667. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, R.; Rind, S.J.; Zeng, P.; Jiang, L. Speed sensorless nonlinear adaptive control of induction motor using combined speed and perturbation observer. Control Eng. Pract. 2022, 1, 105–119. [Google Scholar] [CrossRef]
- Abadi, A.S.S.; Hosseinabadi, P.A.; Mekhilef, S. Fuzzy Adaptive Fixed-time Sliding Mode Control with State Observer for A Class of High-order Mismatched Uncertain Systems. Int. J. Control Autom. Syst. 2020, 3, 1–17. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Krstić, M.; Wen, C. Adaptive finite time coordinated consensus for high-order multi-agent systems: Adjustable fraction power feedback approach. Inf. Sci. 2016, 372, 392–406. [Google Scholar] [CrossRef]
- Mo, S.; Chen, W.; Lu, X. Distributed hybrid secondary control strategy for DC microgrid group based on multi-agent system. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; Volume 1, pp. 109–114. [Google Scholar]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications; Springer: Berlin/Heidelberg, Germany, 1980; Volume 146. [Google Scholar]
- Aung, W.P. Analysis on Modeling and Simulink of DC Motor and its Driving System Used for Wheeled Mobile Robot. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2007, 1, 1141–1148. [Google Scholar]




| Motor | (kg · m2) | (mv/rad/s) | Initial Value (0) (Rad) | ||
|---|---|---|---|---|---|
| 0 | 0.2 | 0.025 | 0.12 | 0.006 | 0.5 |
| 1 | 0.6 | 0.035 | 0.24 | 0.012 | −0.8 |
| 2 | 0.5 | 0.03 | 0.24 | 0.009 | 1.3 |
| 3 | 0.7 | 0.06 | 0.25 | 0.018 | −2.1 |
| 4 | 0.8 | 0.04 | 0.3 | 0.02 | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Mo, S.; Zhou, H.; Qin, T.; Zhong, Y. Finite-Time Consensus Tracking Control for Speed Sensorless Multi-Motor Systems. Appl. Sci. 2022, 12, 5518. https://doi.org/10.3390/app12115518
Zhang B, Mo S, Zhou H, Qin T, Zhong Y. Finite-Time Consensus Tracking Control for Speed Sensorless Multi-Motor Systems. Applied Sciences. 2022; 12(11):5518. https://doi.org/10.3390/app12115518
Chicago/Turabian StyleZhang, Bolun, Shuangye Mo, Hao Zhou, Tong Qin, and Yong Zhong. 2022. "Finite-Time Consensus Tracking Control for Speed Sensorless Multi-Motor Systems" Applied Sciences 12, no. 11: 5518. https://doi.org/10.3390/app12115518
APA StyleZhang, B., Mo, S., Zhou, H., Qin, T., & Zhong, Y. (2022). Finite-Time Consensus Tracking Control for Speed Sensorless Multi-Motor Systems. Applied Sciences, 12(11), 5518. https://doi.org/10.3390/app12115518






