Settlements and Subgrade Reactions of Surface Raft Foundations Subjected to Vertically Uniform Load
Abstract
:1. Introduction
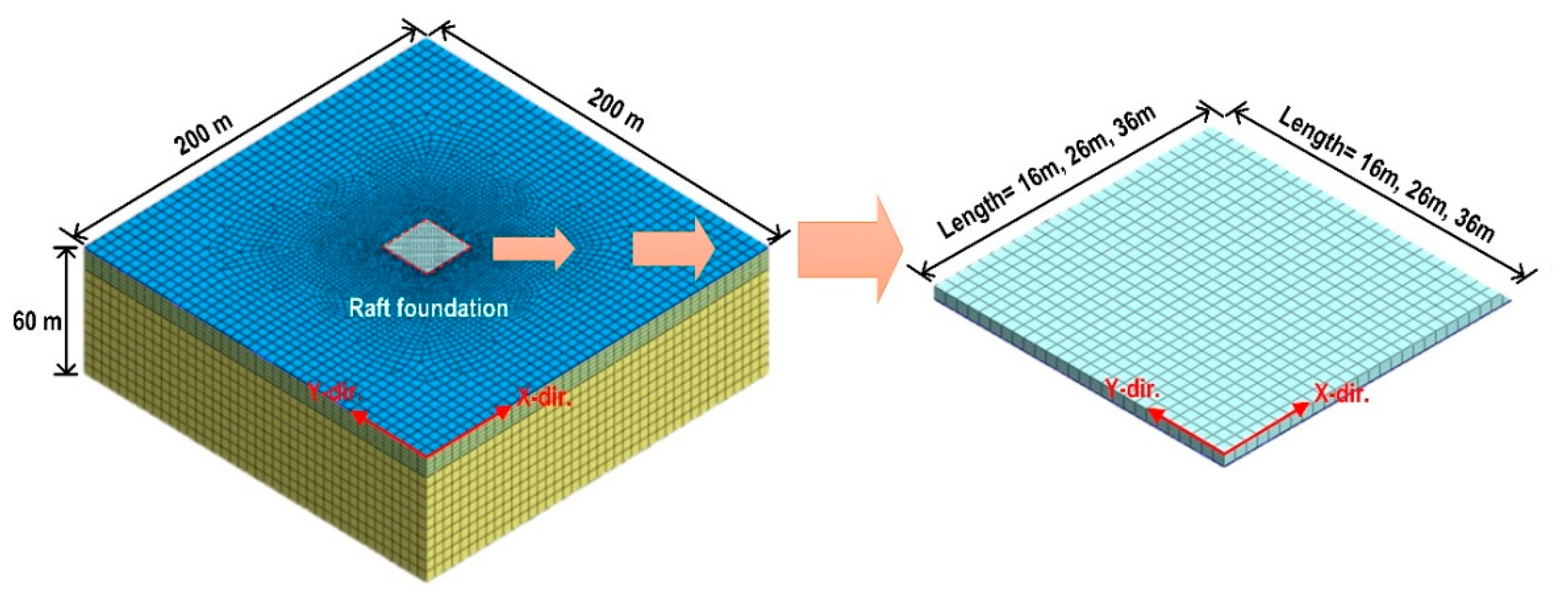
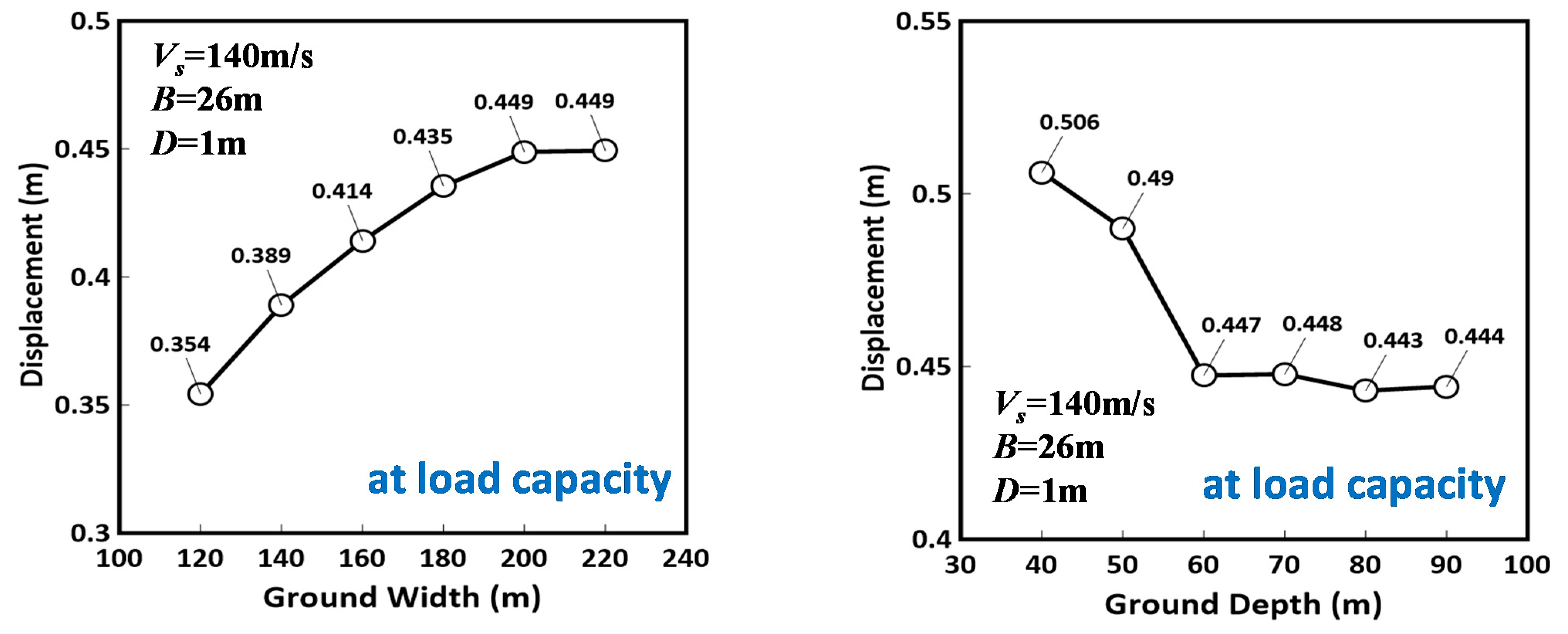
2. Numerical Modeling
3. Observations and Discussions
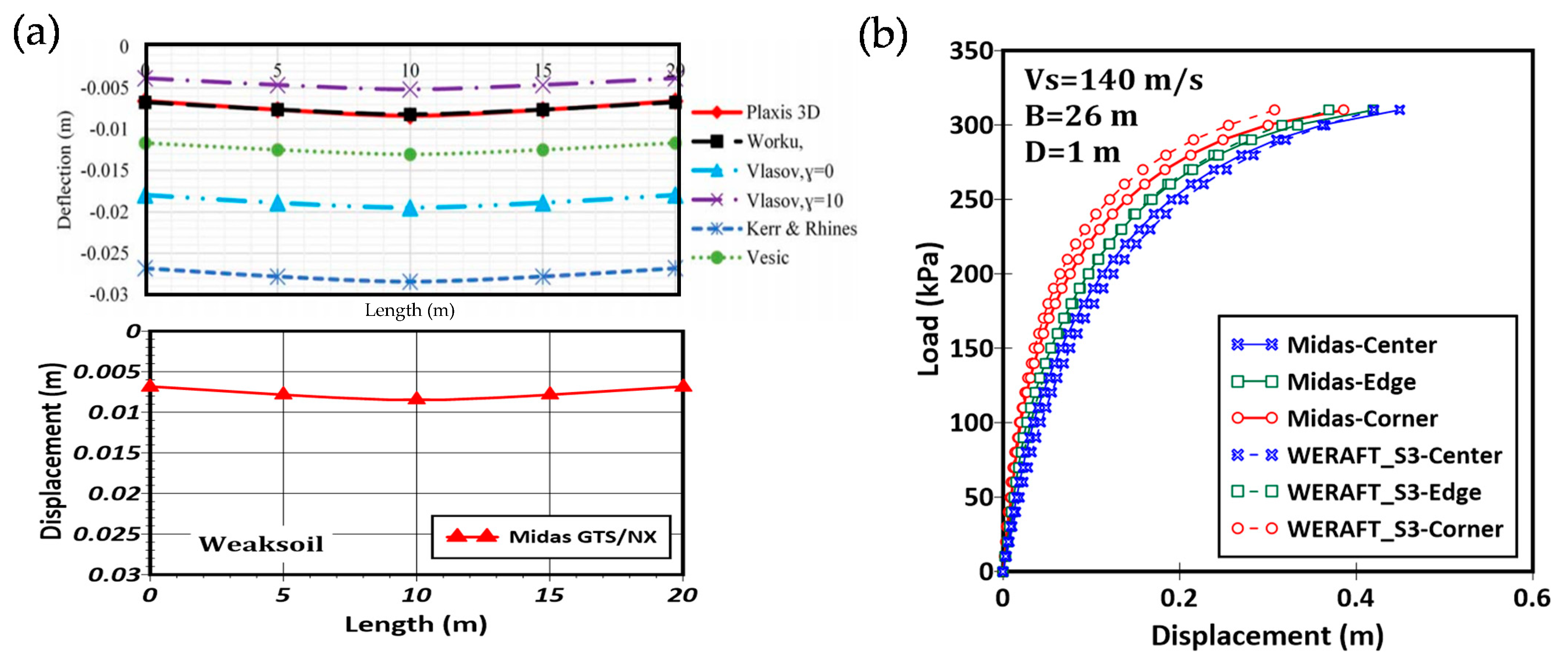
3.1. Foundation Settlements
3.2. Contact Pressures of Soils
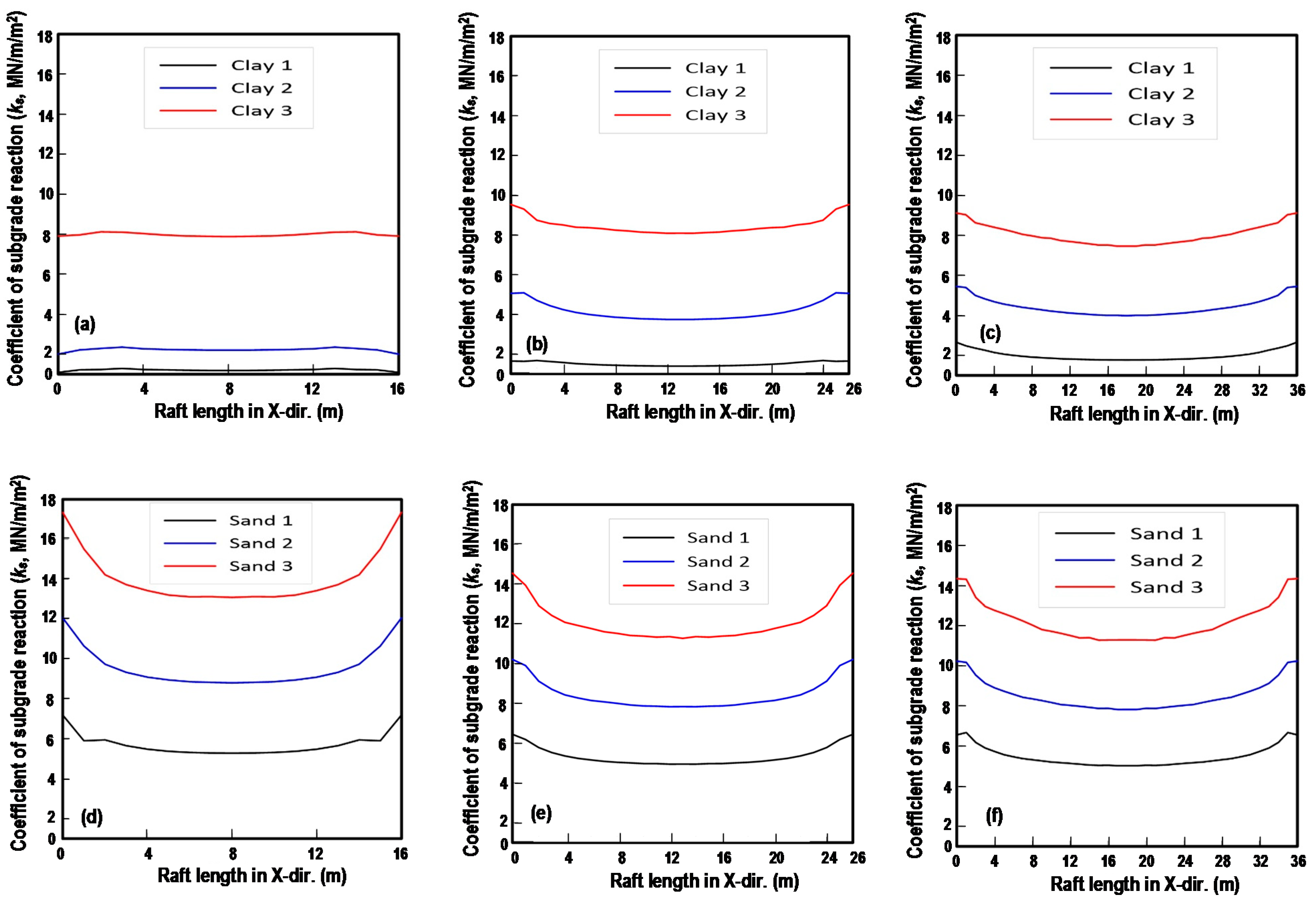
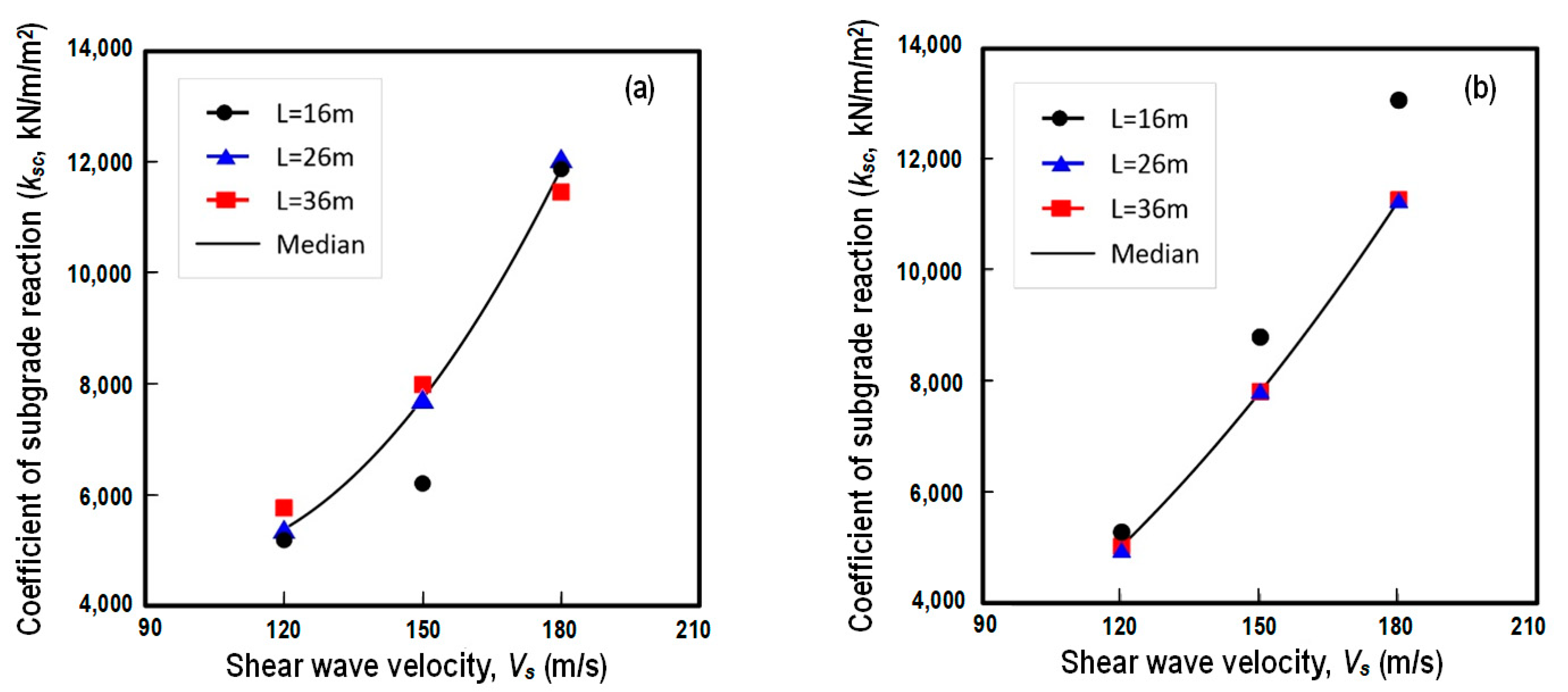
3.3. Coefficient of Subgrade Reaction (ks)
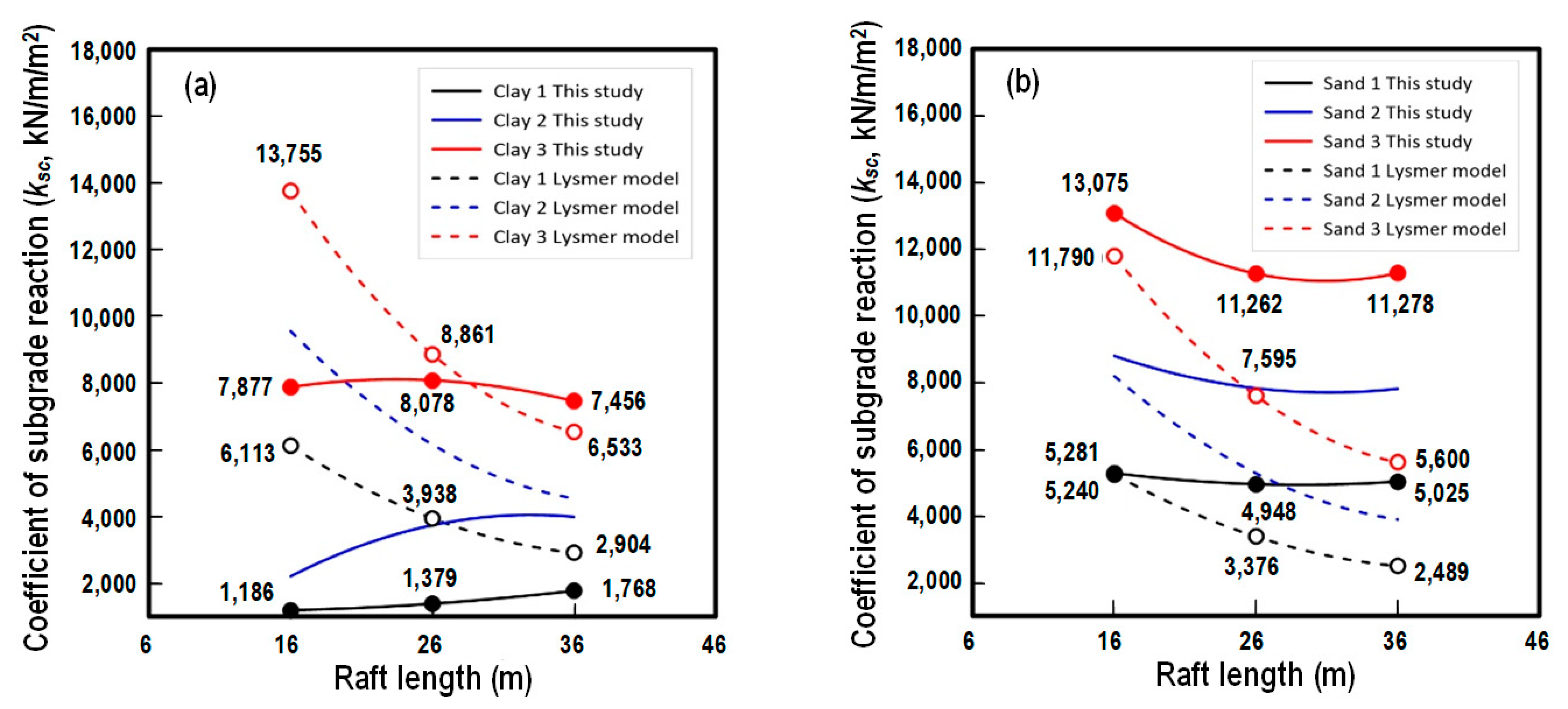
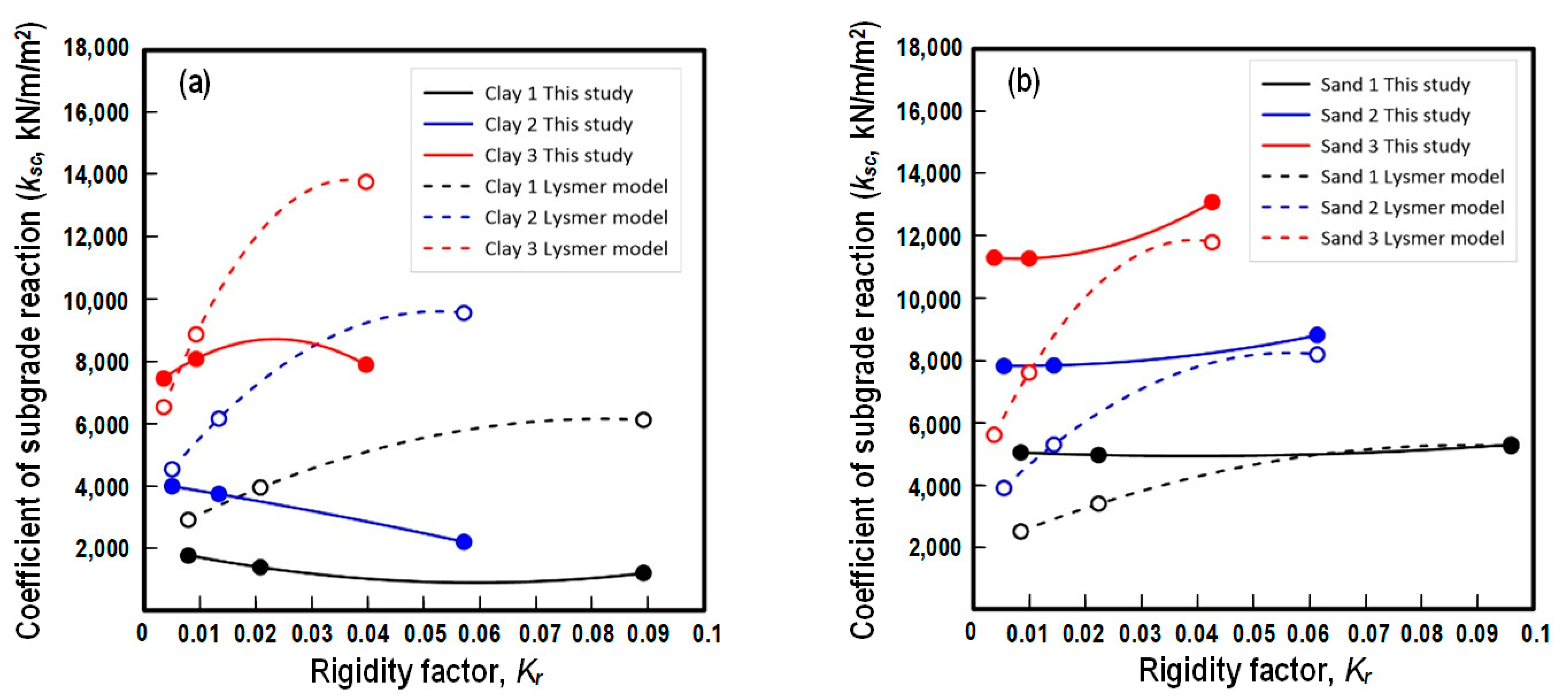
3.4. Comparisons to Lysmer’s Analog Spring Model
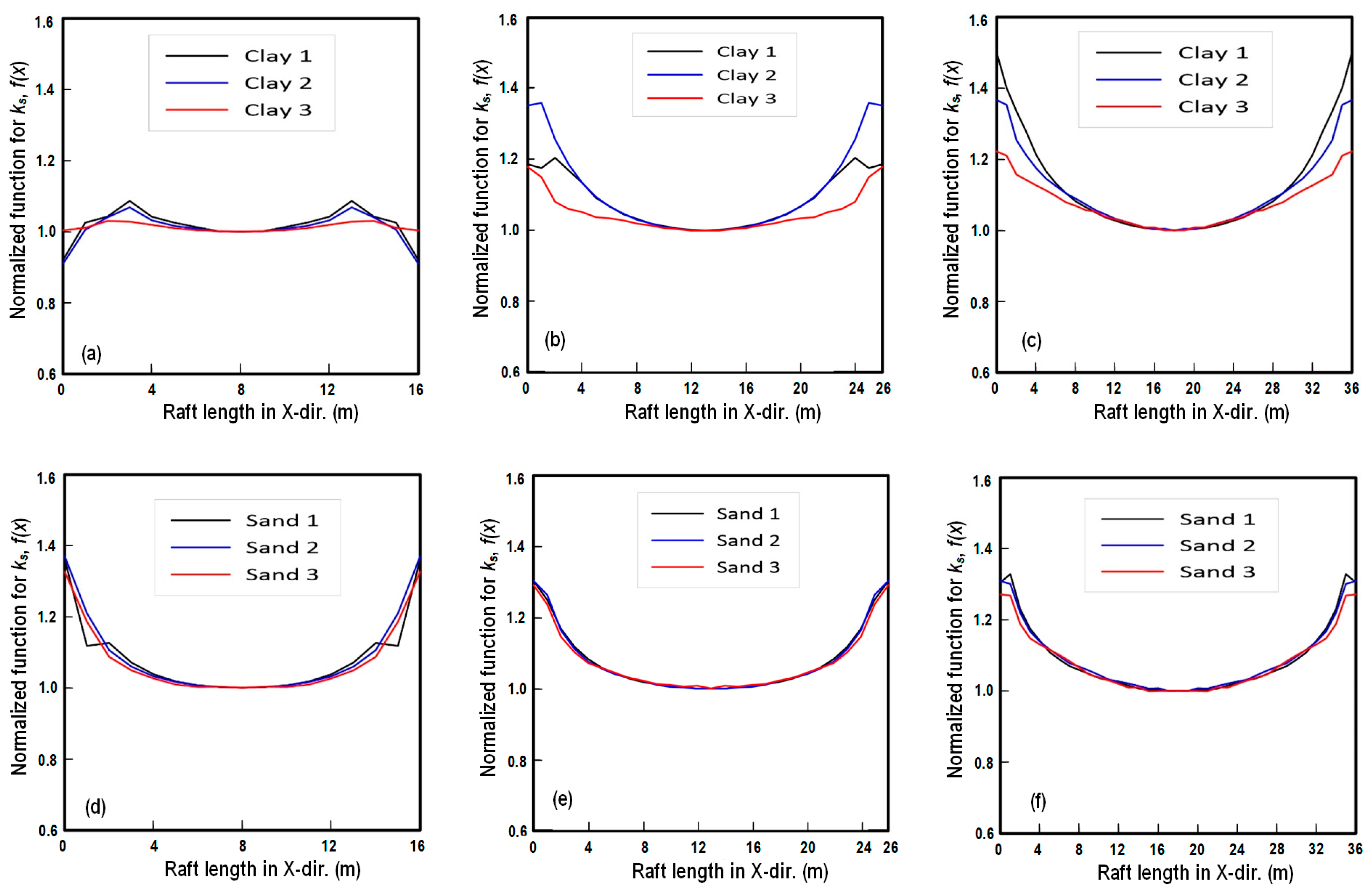
3.5. Modeling of ks
4. Concluding Remarks
- (1)
- For the raft foundation models simulated in this study, the rigidity of the foundation Kr was calculated following the Egyptian code. The values of Kr were in the range of 0.005–0.1, indicating that the foundations were semi-rigid. The maximum foundation settlements were found at the center of the foundation models. The foundation settlements decreased with increases in soil stiffness.
- (2)
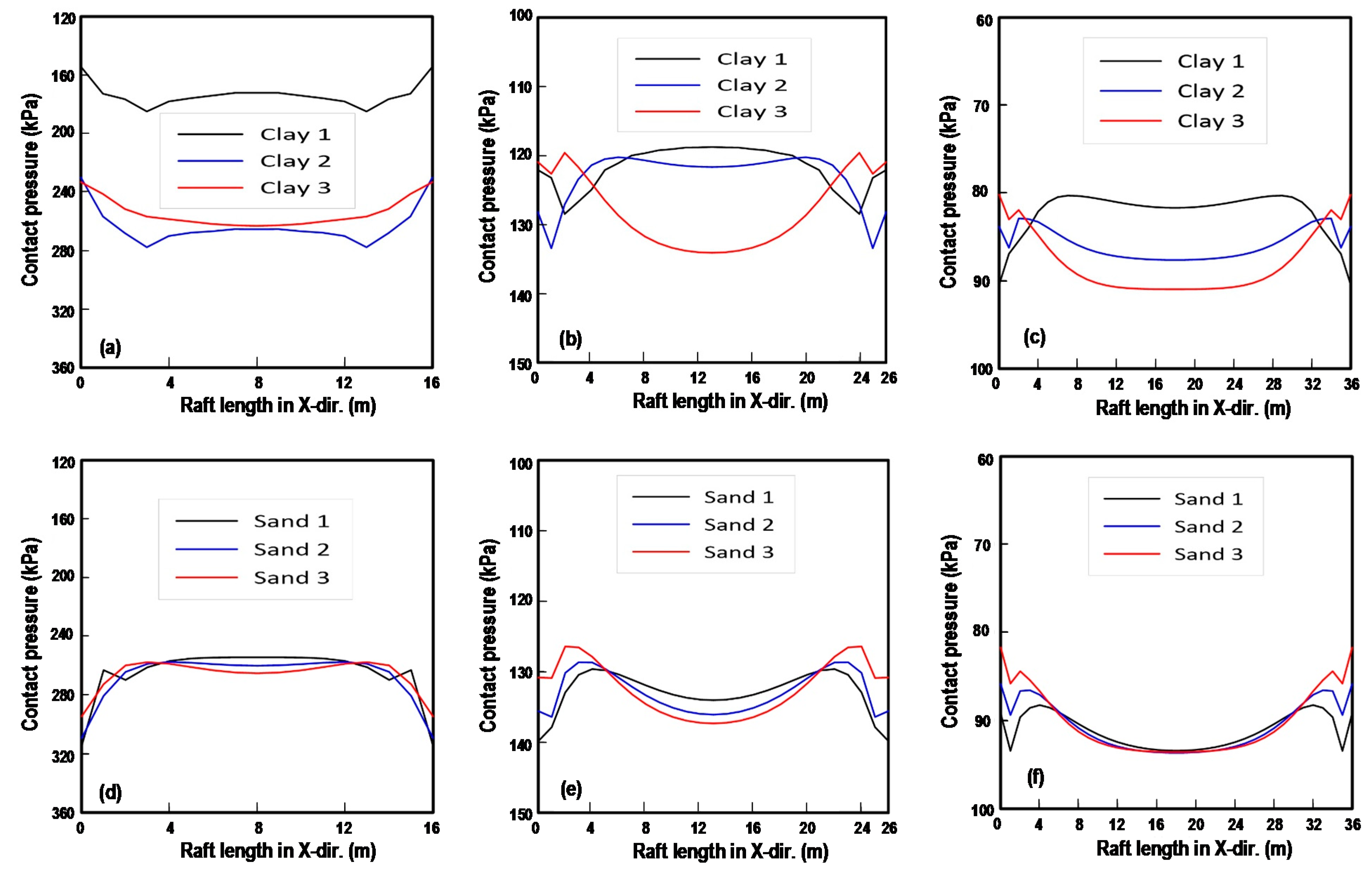
- The contact pressure distribution was significantly affected by the rigidity factor of the foundation and the soil stiffness. For the rafts with L = 16 m in clay, the contact pressure was relatively consistent. For the raft with L ≥ 26 m in very soft clay, the contact pressure was found to be low at the center and high at the edges. As the clays became stiffer, a higher contact pressure was then noted at the center. For the foundation with L = 16 m in sandy soil, the contact pressure was independent of soil stiffness and was low at the center. For the foundation with L ≥ 26 m in sandy soil, high contact pressure was observed at the center. This pattern was more prominent in soil with higher soil stiffness. Owing to the discontinuity of the structure geometry, sudden changes in contact pressures near to the edges were observed in all cases; however, it was negligible for high soil stiffness.
- (3)
- Unlike the distributions of contact pressure, the distributions of coefficients of subgrade reactions of the soils under the raft were found to be more consistent. They will be generally lower at the center and become higher at the edge. For the smallest rafts in clay, the coefficients of subgrade reaction would be slightly varied under the foundation.
- (4)
- The coefficient of subgrade reactions ks is suggested by mathematic function. The value of ks can be determined by multiplying the reference value ksc at the center of the foundation with a 2D polynomial function. For raft foundations in sand, the functions are only dependent on foundation dimensions. For raft foundations in clay, the functions are dependent on both soil stiffness and foundation dimension.
- (5)
- With the presumed design loads, the coefficient of subgrade reaction ksc at the center of foundations was found to be 1186~1768 kN/m/m2, 2201~3983 kN/m/m2, and 7456~8078 kN/m/m2 for Clay 1, Clay 2, and Clay 3, respectively. Similarly, for Sand 1, Sand 2, and Sand 3, the value of ksc was found to be 4948~5281 kN/m/m2, 7808~8793 kN/m/m2, and 11,262~13,075 kN/m/m2, respectively. It is noted that the value of ksc will be affected by foundation dimensions.
- (6)
- It should be noted that the actual stiffness of sand in the field could be much higher than the values obtained in this study. Much higher values of ksc for sand should be expected in actual applications. In spite of the possible influence of ksc, the suggested functions are applicable to sand because the influence of soil stiffness was found to be trivial to the proposed functions in sand.
- (7)
- For raft foundations in clay, if Lysmer’s analog spring model is used, it will generally overestimate the value of ks. For raft foundations in sand, Lysmer’s model will underestimate the value of ks, especially for foundations with low rigidity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ACI Committee 336. Suggested analysis and design procedures for combined footings and mats. Struct. J. 1988, 86, 304–324. [Google Scholar]
- DIN 4018; Berechnung der Sohldruckverteilung unter Flächengründungen Einschl. DIN-Normenausschuss Bauwesen (NABau): Berlin, Germany, 1974.
- IS 2950; Code of Practice for Design and Construction of Raft Foundations: Part 1. Bureau of Indian Standards: Delhi, India, 1981.
- Milovic, D. Stresses and Displacements for Shallow Foundations; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Brown, P.T. Numerical Analyses of Uniformly Loaded Circular Rafts on Deep Elastic Foundations. Geotechnique 1969, 19, 399–404. [Google Scholar] [CrossRef]
- Pantelidis, L.; Gravanis, E. Elastic Settlement Analysis of Rigid Rectangular Footings on Sands and Clays. Geosciences 2020, 10, 491. [Google Scholar] [CrossRef]
- El Gendy, M. An analysis for determination of foundation rigidity. In Proceedings of the 8th International Colloquium on Structural and Geotechnical Engineering, Ain Shams University, Cairo, Egypt, 15–17 December 1998. [Google Scholar]
- ECP 196; A Egyptian Code for Soil Mechanics-Design and Construction of Foundations: Part 3. The Housing and Building Research Center (HBRC): Cairo, Egypt, 1995.
- Barden, L. Distribution of Contact Pressure Under Foundations. Geotechnique 1962, 12, 181–198. [Google Scholar] [CrossRef]
- Dash, S.K.; Saikia, R.; Nimbalkar, S. Contact pressure distribution on subgrade soil underlying geocell reinforced foundation Beds. Front. Built Environ. 2019, 5, 137. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Salim, N.M.; Alwan, K.K. Contact pressure distribution under circular shallow foundation subjected to vertical and rocking vibration modes. J. Build. Eng. 2019, 26, 100908. [Google Scholar] [CrossRef]
- Kumar, A.; Choudhury, D.; Katzenbach, R. Effect of Earthquake on Combined Pile–Raft Foundation. Int. J. Geomech. 2016, 16, 04016013. [Google Scholar] [CrossRef]
- Roy, J.; Kumar, A.; Choudhury, D. Pseudostatic approach to analyze combined pile-raft foundation. Int. J. Geomech. 2020, 20, 06020028. [Google Scholar] [CrossRef]
- Pasternak, P.L. On a New Method of an Elastic Foundation by Means of Two Foundation Constants; Gosstroiizdat: Moscow, Russia, 1954. [Google Scholar]
- Vlasov, V.N.; Leont’ev, N.N. Beams, Plates and Shells on Elastic Foundations; Israel Program for Scientific Translations: Jerusalem, Israel, 1960. [Google Scholar]
- Kerr, A.D.; Rhines, W.J. A Further Study of Elastic Foundation Models; Rep. S-67-1; New York University School of Engineering and Science: Bronx, NY, USA, 1967. [Google Scholar]
- Ozgan, K.; Daloglu, A.T. Effect of transverse shear strains on plates resting on elastic foundation using modified Vlasov model. Thin-Walled Struct. 2008, 46, 1236–1250. [Google Scholar] [CrossRef]
- Worku, A. Development of a calibrated Pasternak foundation model for practical use. Int. J. Geotech. Eng. 2014, 8, 26–33. [Google Scholar] [CrossRef]
- Jeong, S.; Park, J.; Hong, M.; Lee, J. Variability of subgrade reaction modulus on flexible mat foundation. Geomech. Eng. 2017, 13, 757–774. [Google Scholar]
- Liao, S.S.C. Estimating the coefficient of subgrade reaction for plane strain conditions. Proc. Inst. Civ. Eng.-Geotech. Eng. 1995, 113, 166–181. [Google Scholar] [CrossRef]
- Loukidis, D.; Tamiolakis, G.-P. Spatial distribution of Winkler spring stiffness for rectangular mat foundation analysis. Eng. Struct. 2017, 153, 443–459. [Google Scholar] [CrossRef]
- Worku, A.; Seid, T. Application of a robust subgrade model in the analysis of plates on an elastic foundation. Int. J. Geomech. 2020, 20, 04020192. [Google Scholar] [CrossRef]
- Chang, D.W.; Hung, M.H.; Jeong, S.S. Modified Lysmer’s Analog model for two dimensional mat settlements under vertically uniform load. Geomech. Eng. 2021, 25, 221–231. [Google Scholar]
- Poulos, H.G. Pile-raft foundation: Design and applications. Geotechnique 2001, 51, 95–113. [Google Scholar] [CrossRef] [Green Version]
- Poulos, H.G. The Design of Foundations for High-rise Buildings. Proc. Inst. Civ. Eng. 2010, 163, 27–32. [Google Scholar] [CrossRef]
- Katzenbach, R.; Leppla, S.; Choudhury, D. Foundation Systems for High-Rise Structures; CRC Press: Boca Raton, FL, USA, 2016; pp. 154–196. [Google Scholar]
- Shehata, H.F.; EI-Zahaby, K.M. New trends in foundation design using the finite element analysis method. In Proceedings of the 4th Geo-China International Conference, Jinan, China, 25–27 July 2016. [Google Scholar]
- Dickenson, S.E. Dynamic Response of Soft and Deep Cohesive Soils during the Loma Prieta Earthquake of October 17, 1989. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Ashford, S.A.; Jakrapiyanun, W.; Lukkunaprasit, P. Amplification of earthquake ground motion in Bangkok. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Hatanaka, M.; Uchida, A. Empirical correlation between penetration resistance and internal friction angle of sandy soils. Soil Found. 1996, 36, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ministry of the Inderior. Seismic Design Code for Buildings; Construction and Planning Agency, Ministry of the Interior: Taipei, Taiwan, 2011. (In Chinese)
- Midas. Midas GTS NX User Manual; Midas Ltd., Co.: Tokyo, Japan, 2017. [Google Scholar]
- Chang, D.-W.; Lien, H.-W.; Wang, T. Finite difference analysis of vertically loaded raft foundation based on the plate theory with boundary concern. J. GeoEngineering 2018, 13, 135–147. [Google Scholar]
- Chang, D.-W.; Lien, H.-W.; Hu, G.-Y.; Chuang, Y.-A. Developing a three dimensional finite-difference analysis for piled raft foundation settlements under vertical loads. In Proceedings of the 4th International Conference on Deep Foundations, Santa Cruz, Bolivia, 23–24 May 2019. [Google Scholar]
- Ryltenius, A. FEM Modeling of Piled Raft Foundations in Two and Three Dimensions. Master’s Thesis, Lund University, Lund, Sweden, 2011. [Google Scholar]
- Vu, A.; Pham, D.; Nguyen, Y.; He, Y. 3D finite element analysis on behaviour of piled raft foundations. Appl. Mech. Mater. 2014, 580–583, 3–8. [Google Scholar] [CrossRef]


| Parameters | Value | |
|---|---|---|
| Soils | Shear wave velocity, Vs (m/s) | 120, 150, 180 |
| Unit weight, γs (kN/m3) | 20 | |
| Poisson’s ratio, | 0.4 for clays, 0.3 for sands | |
| Calculated Young’s modulus, E (MPa), where E = 2G ), G = Vs2ρs, ρs is the mass density of soil = γs/g, g = 9.81 m/s2 | 82, 128, 185 for clays 76, 119, 171 for sands | |
| Calculated strength parameters Vs = 23 su0.475 (Refs. [28,29]) φ′ = 3.5(N)0.5 + 22 (Ref. [30]) and Vs = 80(N)0.33 (Ref. [31]), where N is SPT-N value | The undrained shear strengths, Su for clays = 32, 52, 76 kPa The drained internal friction angles, for sands = 28°, 31°, 34° | |
| Foundation | Length, L (m) (L = B) | 16, 26, 36 |
| Width, B (m) (B = L) | 16, 26, 36 | |
| Thickness, d (m) | 1 | |
| Unit weight, γ (kN/m3) | 24 | |
| Poisson’s ratio | 0.13 | |
| Young’s modulus, Eb (GPa) | 30 | |
| Applied Load | Uniform load with intensity, q (kPa) | 264, 100, and 52 for raft with dimensions of 16 m, 26 m, and 36 m |
| Size (L = B) | The Relative Stiffness of a Raft Foundation (Kr) | |||||
|---|---|---|---|---|---|---|
| Clay 1 | Clay 2 | Clay 3 | Sand 1 | Sand 2 | Sand 3 | |
| 16 m | 0.0891 | 0.0570 | 0.0396 | 0.0959 | 0.0614 | 0.0426 |
| 26 m | 0.0207 | 0.0133 | 0.0092 | 0.0224 | 0.0143 | 0.0099 |
| 36 m | 0.0078 | 0.0050 | 0.0035 | 0.0084 | 0.0054 | 0.0037 |
| Size (L = B) | The Coefficients of Subgrade Reactions at the Center of the Foundation (ksc) | |||||
|---|---|---|---|---|---|---|
| Clay 1 | Clay 2 | Clay 3 | Sand 1 | Sand 2 | Sand 3 | |
| 16 m | 1186 | 2201 | 7877 | 5281 | 8793 | 13,075 |
| 26 m | 1379 | 3732 | 8078 | 4948 | 7824 | 11,262 |
| 36 m | 1768 | 3983 | 7456 | 5025 | 7808 | 11,278 |
| Soil | ksc (Units in kN/m/m2) | Vs (Units in m/s) |
|---|---|---|
| Clay | ksc = 0.9956(Vs)2 − 190.378Vs + 9888.4 | 120 ≤ Vs ≤ 180 |
| Sand | ksc = 0.3721(Vs)2 − 7.6883Vs + 588.467 |
| L | f(x) Where 0 ≤ x ≤ L/2 (Unit of x: m) | |||
|---|---|---|---|---|
| Sand 1~Sand 3 | Clay 1 | Clay 2 | Clay 3 | |
| 16 m | 0.00534x2 + 0.9662, r2 = 0.954 | −0.0001x4 + 0.00555x2+ 0.9924, r2 = 0.967 | −0.000096x4 + 0.0049x2+ 0.9905, r2 = 0.979 | −0.000026x4 + 0.00167x2+ 0.9992, r2 = 0.938 |
| 26 m | 0.00172x2 + 0.9758, r2 = 0.963 | 0.00131x2 + 1.0054, r2 = 0.962 | 0.002255x2 + 0.9788, r2 = 0.983 | 0.000944x2 + 0.992, r2 = 0.955 |
| 36 m | 0.00091x2 + 0.9883, r2 = 0.978 | 0.0014x2 + 0.9709, r2 = 0.978 | 0.00108x2 + 0.9897, r2 = 0.985 | 0.00065x2 + 1.0037, r2 = 0.995 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, D.-W.; Lu, C.-W.; Tu, Y.-J.; Cheng, S.-H. Settlements and Subgrade Reactions of Surface Raft Foundations Subjected to Vertically Uniform Load. Appl. Sci. 2022, 12, 5484. https://doi.org/10.3390/app12115484
Chang D-W, Lu C-W, Tu Y-J, Cheng S-H. Settlements and Subgrade Reactions of Surface Raft Foundations Subjected to Vertically Uniform Load. Applied Sciences. 2022; 12(11):5484. https://doi.org/10.3390/app12115484
Chicago/Turabian StyleChang, Der-Wen, Chih-Wei Lu, Yu-Jhang Tu, and Shih-Hao Cheng. 2022. "Settlements and Subgrade Reactions of Surface Raft Foundations Subjected to Vertically Uniform Load" Applied Sciences 12, no. 11: 5484. https://doi.org/10.3390/app12115484
APA StyleChang, D.-W., Lu, C.-W., Tu, Y.-J., & Cheng, S.-H. (2022). Settlements and Subgrade Reactions of Surface Raft Foundations Subjected to Vertically Uniform Load. Applied Sciences, 12(11), 5484. https://doi.org/10.3390/app12115484






