An Effect of Radiation and MHD Newtonian Fluid over a Stretching/Shrinking Sheet with CNTs and Mass Transpiration

Abstract

The invention of carbon nanotubes (CNT) has a wide range of industrial and medical applications. The notion of boundary layer flow is used in medicine, particularly in nanomedicine, and the use of magnetic fields is used to treat cancer tumour growth. The governing PDEs are altered into ODEs with the help of suitable transformations. The mass transfer of a chemically reactive species and the flow of MHD over a stretching plate subjected to an inclined magnetic field are investigated, and analytical solutions for velocity in terms of exponential function and temperature field in terms of incomplete Gamma function are obtained using the Laplace transformation. We investigate the variation of physically important parameters with varying suction, magnetic field, and slip using the analytical results. The differences in velocity and temperature profiles are explored in relation to a number of physical parameters. MWCNT nanofluids have higher effective velocities than the SWCNT deferred nanofluids, and this might assist in industrial applications and medical benefits. Earlier research tells us that carbon nanotubes are likely quicker than nanoparticles at achieving the same tumour instance. As a result, in the presence of CNTs or nanoparticles, the magnetic field can also act as a source. We found that SWCNTs nanofluids are better nanofluids than MWCNTs nanofluids.

1. Introduction

Iigima [1] introduced the concept of carbon nanotubes during the emergency of the 1990s. The utilization of SWCNTs and MWCNTs in engineering and medicinal fields increases their direct influence on increasing the thermal conductivity of the base fluid. Since heat transfer fluids are used in power generation, microelectronics, cooling, chemical processing, refrigeration, air conditioning, and the collection of various fulfilments, they have low thermal conductivity. It is necessary to enhance their effective thermal conductivity to develop the heat transfer rate. In the first advanced study by Choi [2], Enhancement of Heat Transfer in a Two-Dimensional Enclosure Using Nanofluids Due to Buoyancy was studied by Khanafer et al. [3]. Xue et al. [4] are investigating the thermodynamic conductivity of carbon nanotube-based composites in their research work. For boundary-layer flow of a nanofluid past a stretched sheet, new exact solutions have been developed by Ebaid et al. [5]. Meyer et al. [6] studied the transitional flow regime of smooth tubes and the effects of multi-walled carbon nanotubes on single-phase heat transfer and pressure drop characteristics. The peristaltic flow of nanofluids in an asymmetric channel is affected by the velocity second slip boundary condition; a precise solution was revealed by Ebaid et al. [7]. Many researchers [8] have examined the flow and heat transfer of the regular nano fluids and the carbon nanotubes that delay nano fluids. As an example, Hamad et al. [9] studied the natural convection flow of a nano fluid across a linearly stretched sheet in the presence of a magnetic field. In the presence of a magnetic field, Ebaid and Sharif [10] investigated and obtained a new analytical solution. Fazle et al. [11] investigated unsteady flow with velocity, temperature, and slips to arrive at a numerical solution. Siddheshwar et al. [12] study Newtonian fluid flow caused by a superliner stretched sheet. Siddheshwar et al. [13] employed the concept of perturbation to develop a new analytical solution strategy for both Newtonian and non-Newtonian fluid flows due to a linear stretching sheet and found the analytical solution for velocity and stream function. Mahabaleshwar et al. [14] used the differential transform approach to solve the problem of axisymmetric flow over an extending sheet in the presence of slip, which does not have a precise analytical solution. Radiation and MHD on Non-Newtonian fluid flow across a stretching/shrinking sheet with mass transpiration are investigated by Sneha et al. [15]. Vishalakshi et al. [16], describe a magnetohydrodynamics fluid flow across a stretching/shrinking sheet with slips and mass transpiration. Anusha et al. [17] also presented their work on magnetohydrodynamics flow over a stretching/shrinking plate with mass transpiration.

Nazir et al. [18,19] investigated fluid mechanics associated with electrically conducting fluids alongside an electromagnetic field, which has huge industrial applications. MHDs have various applications, which are dependent on their extensive utilization in industry and are used at the mechanical level. The involvement of tri-hybrid nanoparticles was incorporated into the pseudo-plastic model to enhance the heat transfer rate, and the transport problem of thermal energy and solute mechanisms was modelled considering the heat generation/absorption and the chemical reaction [20,21]. In medical fulfilment, the significance of the magnetic field in addition to the nanoparticles/CNTs was investigated to treat cancerous cells. In such medical implementation, the nanoparticles/CNTs are inserted into the blood vessels nearest to the tumour, along with placing the magnet close to the tumour. In addition to an exact analytical solution of the heat equations obtained by using Laplace transfer, the impact of different types of CNTs on the magnetic fields was also addressed.

Many papers employ the Laplace transformation to obtain an analytical solution for the flow and heat transfer of CNTs and nanofluids when various factors are present. Saleh et al. [22] explored the medical application, focusing on the therapy of cancer tumour in convective conditions, and provided numerical results. The precise features of the Laplace transformation are described by Bhullar et al. [23].

The goal of this study is to investigate the effects of CNT magnetic field flow caused by a stretched plate in the presence of Navier’s slip. Then, using the Laplace transformation, derive the analytic solution for the velocity profile and concentration field. By using the gamma function, an exact analytical solution can be acquired for both the temperature distribution and the velocity. The variety of different parameters is in detail discussed and gives rise to many graphs.

2. Materials and Methods

The incompressible Newtonian CNT flow due to a linearly stretched semi-infinite plate embedded in MHD with mass transpiration is investigated, with Navier’s slip taken into account. The flow is in the x-direction, with the y-axis perpendicular to it (see Figure 1), and a homogeneous magnetic field of intensity is supplied along it. The equations of conservation of mass and momentum are described as follows.

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}={\upsilon }_{nf}\frac{{\partial }^{2}u}{\partial y^2}-\frac{{\sigma }_{nf}{B}_0^2{\sin }^2(\tau )u}{{\rho }_{nf}},$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{{\kappa }_{nf}}{{(\rho C_P)}_{nf}}\frac{{\partial }^{2}T}{\partial y^2}-\frac{1}{{(\rho C_p)}_{nf}}\frac{\partial q_r}{\partial y},$$

(3)

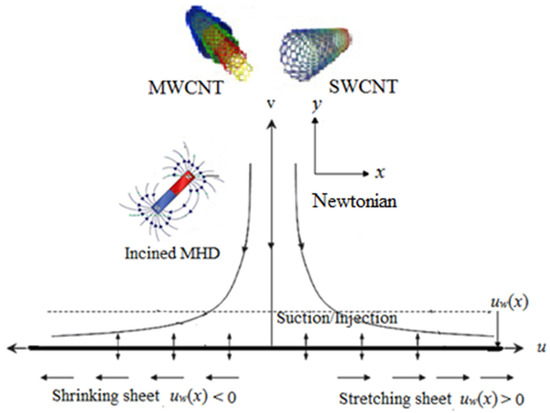
Figure 1. Physical model of the stretching/shrinking surface.

The boundary conditions are Saleh et al. [22].

$$\begin{array}{l}u(x,0)=dax+A\frac{\partial u}{\partial y},v(x,0)=V_c,u(x,\infty )\to 0,\\ \theta (0)=0, \theta (0)=1+\xi {\theta }^{\prime }(0) \end{array}\}.$$

(4)

where A is the first order slip parameter.

We now introduce the similarity variable.

$$\begin{array}{l}\psi =\sqrt{a{\upsilon }_f}xf\left(\eta \right),\eta =\sqrt{\frac{a}{{\upsilon }_f}}y,\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_{\omega }-T_{\infty }}\\ u=\frac{\partial \psi }{\partial y}=ax{f}^{\prime }\left(\eta \right),v=-\frac{\partial \psi }{\partial x}=-a{f}^{\prime }\left(\eta \right).\end{array}\}.$$

(5)

where ${\upsilon }_{nf}$ is the effective kinematic viscosity, ${\kappa }_{nf}$ is the thermal conductivity, T is temperature, and ${({\rho }_{cp})}_{nf}$ is the heat capacity, $\eta$ is the similarity variables, and $\psi$ is the stream function defines as follows [24].

$$\begin{array}{l}{\rho }_{nf}= \left(1-\varphi \right){\rho }_f+\varphi {\rho }_{CNT}, {\nu }_{nf} = \frac{{\mu }_{nf}}{{\rho }_{nf}},\\ {\left(\rho c_p\right)}_{nf} = \left(1-\varphi \right){\left(\rho c_p\right)}_f+\varphi {\left(\rho c_p\right)}_{CNT}, {\alpha }_{nf} = \frac{{\kappa }_{nf}}{{\left(\rho c_p\right)}_{nf}},\\ \frac{{\kappa }_{nf}}{{\kappa }_f} = \frac{1-\varphi +2\varphi \frac{{\kappa }_{CNT}}{{\kappa }_{CNT}-{\kappa }_f}\log \frac{{\kappa }_{CNT}+{\kappa }_f}{2{\kappa }_f}}{1-\varphi +2\varphi \frac{{\kappa }_f}{{\kappa }_{CNT}-{\kappa }_f}\log \frac{{\kappa }_{CNT}+{\kappa }_f}{2{\kappa }_f}},\\ \frac{{\sigma }_{nf}}{{\sigma }_f} = 1+\frac{3\varphi \left(\frac{{\sigma }_{CNT}}{{\sigma }_f}-1\right)}{\frac{{\sigma }_{CNT}}{{\sigma }_f}-2-\left(\frac{{\sigma }_{CNT}}{{\sigma }_f}-1\right)\varphi }.\end{array}\}$$

(6)

where ${\rho }_{nf}$ the density of the Nano fluid is, $\varphi$ is the solid volume fraction of the Nano fluid, and ${\sigma }_{nf}$ is the electrical conductivity of the Nano fluid.

Rosseland [25] approximation and Radiative heat flux $q_r$ is simplified as follows using Mahabaleshwar et al. [26,27,28]:

$$q_r=-\frac{4{\sigma }^{*}}{3k^{*}}\frac{\partial T^4}{\partial y},$$

(7)

where ${\sigma }^{*}$ is the Stefan–Boltzmann constant and absorption coefficient is $k^{*}$, $q_r$ is the radioactive flux. Expanding $T^4$ in a Taylor expression we obtain.

$$T^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4.$$

(8)

By using Equations (7) and (8) in (3), reduce to

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{{\kappa }_{nf}}{{({\rho }_{cp})}_{nf}}\left(1+\frac{16{\sigma }^{*}{T}_{\infty }^3}{3k^{*}{\kappa }_{nf}}\right)\frac{{\partial }^{2}T}{\partial y^2},$$

(9)

With the introduction of the stream function the continuity Equation (1) is satisfied, and the momentum Equations (2) and (3) transform into

$$f^{‴}+\alpha \left[f{f}^{″}-{f^{\prime }}^2\right]-\gamma {\sin }^2(\tau )f^{\prime }=0,$$

(10)

$$\tau \left(1+N_r\right){\theta }^{″}+f{\theta }^{\prime }=0.$$

(11)

where $\alpha ={(1-\varphi )}^{2.5}\left((1-\varphi )+\varphi \left(\frac{{\rho }_s}{{\rho }_f}\right)\right)$, and $\gamma =M{\left(1-\varphi \right)}^{2.5}$.

The boundary conditions are transformed into following equations:

$$f^{\prime }\left(\eta \right)=d+\lambda f^{″}\left(\eta \right),f\left(\eta \right)=V_c,\theta \left(\eta \right)=1+\xi {\theta }^{\prime }\left(\eta \right) \mathrm{at} \eta \to 0$$

(12a)

$$f^{\prime }\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0 \mathrm{as} \eta \to \infty$$

(12b)

Here, $Vc=v_w{(v_{f}a)}^{\frac{1}{2}}$ is the suction and injection, $Pr=\frac{v_f}{{\alpha }_f}$ is the Prandtl number, d is the stretching and shrinking parameter and magnetic field is $M=\frac{{\sigma }_{nf}{B}_0^2}{a{\rho }_f}$.

2.1. Analysis Solution

Now we obtain the solution of Equation (11) in the form of

$$f(\eta )=V_c+\frac{(1-e^{-\beta \eta })}{\beta (1+\lambda \beta )},$$

(13)

The unknown $\lambda$ can be deduced from the equation as follows:

$$\lambda {\beta }^3+(1-\alpha V_c\lambda ){\beta }^2-(\alpha V_c+\gamma \lambda {\sin }^2(\tau ))\beta -(\alpha +\gamma {\sin }^2(\tau ))=0$$

(14)

The local skin friction coefficient can also be calculated as follows:

$$f_{\eta \eta }\left(0\right)=\frac{-\beta }{(1+\lambda \beta )}.$$

(15)

2.2. Solution for Heat Transfer

Now, when we substitute Equation (13) in Equation (11), we obtain Sneha et al.’s [15]

$$\tau (1+Nr){\theta }^{"}+\left(V_c+\frac{(1-e^{-\beta \eta })}{\beta (1+\lambda \beta )}\right){\theta }^{\prime }=0$$

(16)

where

$$\tau =\frac{1}{\mathrm{Pr}}\times \left(\frac{k_{nf}}{k_f}\right)\times \left[{\frac{1}{(1-\varphi ){(\rho C_p)}_f+\varphi (\rho C_p)}}_{CNT}\right],$$

(17)

Next, we study the solution of the temperature in terms of the generalized incomplete gamma function by using Laplace transformation.

By introducing the new variable $t=e^{-\beta \eta }$ we obtain

$$(1+Nr)t{\theta }^{″}(t)+(m-nt){\theta }^{\prime }(t)=0$$

(18)

where

$$m=(1+N_r)-\frac{V_c}{\tau \beta }-\frac{1}{\tau {\beta }^2}, n=\frac{-1}{\tau {\beta }^2(1+\lambda \beta )},$$

(19)

Now we apply Laplace transform to both sides of Equation (18) we obtain

$$s(n-(1+Nr)s){\mathsf{\Theta }}^{\prime }(s)+(n+(m-2(1+Nr)s)\mathsf{\Theta }(s)=0,$$

(20)

Here, $\mathsf{\Theta }(s)$ is the LT of $\theta (t)$, i.e., $\mathsf{\Theta }(s) =L\left\{\theta \left(t\right)\right\}.$ The closing equation changed into accomplished the usage of the primary transformed boundary condition $\theta (0)=0$, now integrate Equation (20), we obtain

$$\mathsf{\Theta }(s)=\frac{c}{s{\left(s-\frac{n}{1+Nr}\right)}^{\left(1-\frac{m}{1+Nr}\right)}}$$

(21)

where c is integration constant. We apply the inverse Laplace transform $L^{-1}$ to Equation (21), with a restriction on m which is $m<1$, resulting in

$$\theta (t)=c L^{-1}\left[\frac{1}{s}\right]*L^{-1}\left[\frac{1}{{\left(s-\frac{n}{1+Nr}\right)}^{\left(1-\frac{m}{1+Nr}\right)}}\right], =\frac{c*e^{\left(\frac{n}{1+Nr}\right)t}{t}^{\frac{-m}{1+Nr}}}{\Gamma \left(1-\frac{m}{1+Nr}\right)}.$$

(22)

where * indicates the convolution property represented by

$$L^{-1}\left\{\psi (s).\mathsf{\Phi }(s)\right\}=\psi (s)*\varphi (t)={\displaystyle \underset{0}{\overset{t}{\int }}\psi (\mu ).\varphi (t-\mu )d\mu }$$

(23)

$$\begin{array}{l}\theta (t)=\frac{c}{\Gamma \left(1-\frac{m}{1+Nr}\right)}{\displaystyle {\int }_o^t{\mu }^{\frac{-m}{1+Nr}}{e}^{\frac{n\mu }{1+Nr}}d\mu ,}\\ =\frac{c}{\Gamma \left(1-\frac{m}{1+Nr}\right)}{\left(\frac{-1}{n}\right)}^{1-\frac{m}{1+Nr}}{\displaystyle {\int }_0^{-nt}{\sigma }^{\frac{-m}{1+Nr}}}{e}^{\frac{-\sigma }{1+Nr}}d\sigma , \sigma =-n\mu ,\\ \theta (t)=\frac{c}{\Gamma \left(1-\frac{m}{1+Nr}\right)}{\left(\frac{-1}{n}\right)}^{1-\frac{m}{1+Nr}}\Gamma \left(1-\frac{m}{1+Nr},0,-nt\right),\end{array}$$

(24)

By introducing the B. Cs $\theta \left(t\right) = 1+\xi {\theta }^{\prime }\left(1\right),$ the value of c is given as

$$\begin{array}{c}c=\frac{1}{\Gamma \left(1-\frac{m}{1+Nr}\right)}{\left(\frac{-1}{n}\right)}^{1-\frac{m}{1+Nr}}\Gamma \left(1-\frac{m}{1+Nr},0,\frac{-n}{1+Nr}\right)\\ -\xi {\left(-n\right)}^{1-\frac{-n}{1+Nr}}{e}^{\frac{-n}{1+Nr}}\end{array}$$

(25)

Hence, exact form of $\theta (t)$ is given as follows

$$\theta \left(t\right)=\frac{\Gamma \left(1-\frac{m}{1+Nr},0,\frac{-n}{1+Nr}t\right)}{\Gamma \left(1-\frac{m}{1+Nr},0,\frac{-n}{1+Nr}\right)-\xi {(-n)}^{1-\frac{m}{1+Nr}}{e}^{\frac{-n}{1+Nr}}}$$

(26)

In respect of $\eta$, we have

$$\theta \left(t\right)=\frac{\Gamma \left(1-\frac{m}{1+Nr},0,\frac{-n}{1+Nr}{e}^{-\beta \eta }\right)}{\Gamma \left(1-\frac{m}{1+Nr},0,\frac{-n}{1+Nr}\right)-\xi {(-n)}^{1-\frac{m}{1+Nr}}{e}^{\frac{-n}{1+Nr}}}$$

(27)

2.3. Validation

The temperature behaviour of the present problem is verified with the closed-form analytical solution proposed by Crane (1970). Furthermore, in the absence of radiation and viscous dissipation, the results of the problem for heat sink yield the results of the analogous isothermal problem for species concentration with first-order chemical reaction. Additionally, the velocity behaviour when $\mathsf{\Lambda }=1 \mathrm{and} \mathsf{\varphi }=0$ results are converted into the form of results of Sneha et al. [15]. In Sneha et al. [15], work is given in terms of parameter $\alpha$. The following Table 1 shows related works by other authors and finding existing results.

Table 1. Expression for $\alpha$ various physical parameters.

Authors	Fluids	$\mathbf{Value} \mathbf{of} \mathit{\alpha }$
Siddheshwar et al. [13]	Non-Newtonian	$\alpha = \sqrt{\frac{1+M}{\left(1-k_1\right)}}$
Siddheshwar et al. [12]	Non-Newtonian	$\lambda {\alpha }^3 +\left(1-Re k_1\right){\alpha }^2-\lambda \alpha -\left(1+Re\right)=0$
Saleh et al. [22]	Newtonian	$\begin{array}{l}\delta {\beta }^4-\left(\lambda +\delta \alpha V_c\right){\beta }^3-\left(1-\alpha \lambda V_c+\gamma \delta \right){\beta }^2\\ +\left(\lambda \gamma + \alpha V_c\right)\beta +\left(\alpha + \gamma \right)= 0,\end{array}$
Sneha et al. [15]	Non-Newtonian	$f(\eta ) = a+b\left(exp\left(-\alpha \eta \right)\right),$ $a = V_c-\frac{1}{\alpha \left({\chi }_1{\alpha }^2-{\chi }_2\alpha -d\right)}, b = \frac{1}{\alpha \left({\chi }_1{\alpha }^2-{\chi }_2\alpha -d\right)}$ $\begin{array}{l}{\chi }_1{\alpha }^4-\left({\chi }_2+\delta {\chi }_1 V_c\right){\alpha }^3-\left(1-\delta {\chi }_1 V_c+\omega Q Si{n}^2(\tau ) {\chi }_1\right){\alpha }^2\\ +\left({\chi }_2 \omega Q Si{n}^2(\tau )+ \delta V_c\right)\alpha +\left(\delta +\omega Q Si{n}^2(\tau )\right)= 0,\end{array}$
Present work	Newtonian	$\begin{array}{l}f(\eta )=v_c+\frac{(1-e^{-\beta \eta })}{\beta (1+\lambda \beta )},\\ \lambda {\beta }^3+(1-\alpha v_c\lambda ){\beta }^2-(\alpha v_c+\gamma \lambda {\sin }^2(\tau ))\beta \\ -(\alpha +\gamma {\sin }^2(\tau ))=0\end{array}$

3. Results

The effects of a magnetic field, mass transpiration, and Navier’s slip on the flow of incompressible viscous fluid with CNT are examined. Using the appropriate similarity transformations for velocity and temperature, the system of PDEs is transformed into a system of nonlinear ODEs with constant coefficients. The analytical solution for the velocity profile is then obtained in exponential form, whereas the analytical solution for the concentration field was produced via the Laplace transformation in terms of an incomplete gamma function. Different graphs for the CNT are used to assess the consequences of the problem. The advantages of adopting MHD for its applications in industry and medicine are discussed, as well as a model of MHD nanofluid flow over a stretching/shrinking surface.

Figure 2 depicts the variation in transverse velocity with different values of M for the suction case and keeping all other parameters constant as shown in the figure. Demonstrating that the transverse velocity decreases as M increases on the stretching surface, MWCNT nanofluids have higher effective velocities than the SWCNT-deferred nanofluids, and this might assist in industrial applications and medical benefits.

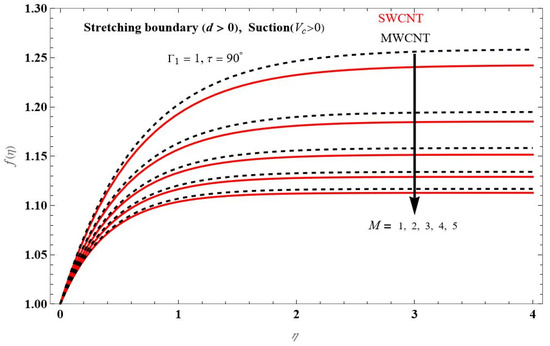
Figure 2. The impact of transvers velocity profile for changing M at $\Gamma =1,v_c=1,\lambda =1,\tau ={90}^{\circ }$, $\xi =0.01$.

Earlier research tells us that carbon nanotubes are likely quicker than nanoparticles in achieving the same tumour instance. As a result, in the presence of CNTs or nanoparticles, the magnetic field can also act as a source. We notice that the SWCNT Nanofluids are better nanofluids than the MWCNT Nanofluids. We study from these final results that the usage of CNTs in most cancerous therapies can be more useful than all sorts of nanoparticles.

Figure 3 portrays the variation in axial velocity with different values of M for the suction case and keeping all other parameters are constant as shown in the figure. It is helpful that in the stretching surface, the transverse velocity decreases as M increases. Due to the development of the Lorenz force, the velocity boundary layer will decrease as the magnetic field increases. For both circumstances, transverse velocity increases fast at first and then remains constant after a certain value of $\eta$, whereas axial velocity falls exponentially at first and then reaches zero after a certain value of $\eta$. Figure 4 shows the impact of the $\phi$ on the axial velocity for stretching/shrinking sheet. From this figure, it is clear show that velocity increases with increasing the value of the $\phi$ parameter and also tells us that MWCNTs nano fluids are of higher velocities than the SWCNTs nano fluid velocity.

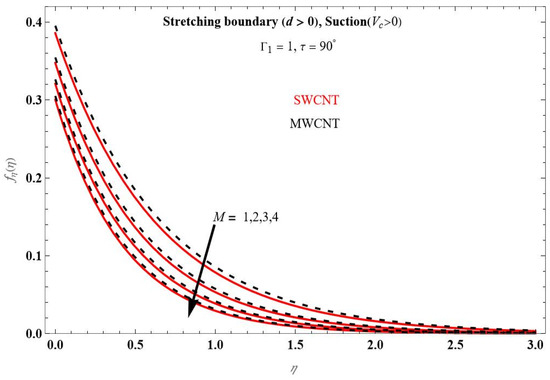
Figure 3. The impact of axial velocity profile for changing M at $\Gamma =1, v_c=1, \lambda =1, \tau ={90}^{\circ }$, $\xi =0.01$.

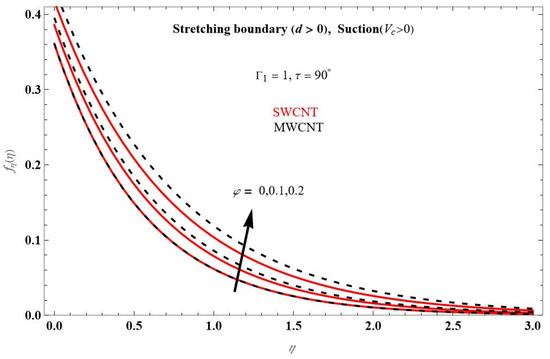
Figure 4. The impact of axial velocity profile for changing $\phi$ at $=M=v_c=\lambda =1, \tau ={90}^{\circ },$ $\xi =0.01$.

For axial velocity, the similar result is illustrated in Figure 5. The velocity boundary layer decreases as the $\lambda$ increases. The axial velocity does not have to be positive because the transverse velocity is always positive. The CNTs may be quicker than nanoparticles in achieving the same tumour site. As a result, in the presence of CNTs or nanoparticles, the magnetic field can also act as a source. We notice that SWCNTs are better nanofluids than the MWCNTs. We can deduct from these results that the usage of CNTs in most cancerous therapies can be more effective than all sorts of nano particles. This is over an excessive temperature for nanofluids, which is dependent on temperature.

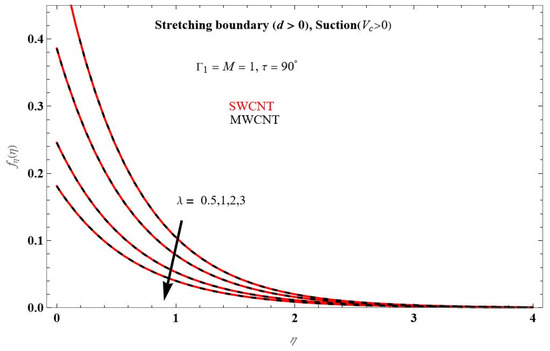
Figure 5. The impact of axial velocity profile for changing $\lambda$ at $=M=v_c=1, \tau ={90}^{\circ },$ $\xi =0.01$.

Figure 6 depicts the variation in temperature profile with different values of M for the suction case, respectively, and keeping all other parameters constant, as shown in the figure. Illuminating that in the stretching surface, the temperature profile rises as M increases. The temperature profile for CNT-water nanofluids increases somewhat as the rotation parameter M is rises, as seen in Figure 6.

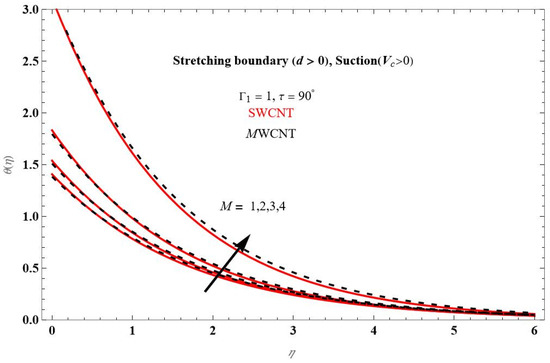
Figure 6. Temperature profile for different values of M at $\lambda =1, \xi =0.01, \varphi =1, \Gamma =1, v_c=1$.

Figure 7 shows that as the nanoparticle volume fraction $\phi$ grows, the temperature profile $\theta (\eta )$ raises. This is because, in comparison to the base fluid water, both nanoparticles have lower specific heat and higher thermal conductivity, resulting in a rising temperature profile $\theta (\eta )$.

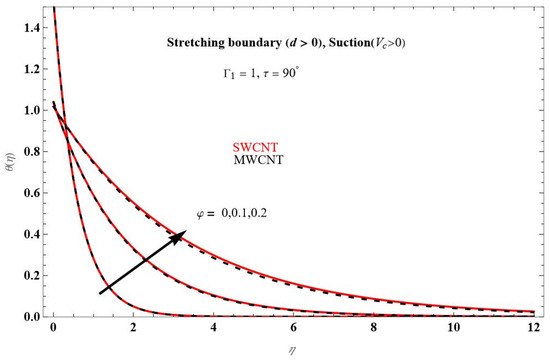
Figure 7. The temperature profile for different values of $\phi$ at $\lambda =M=\Gamma =v_c=1$.

Figure 8 depicts the $\lambda$ on temperature profile $\theta (\eta )$ via $\eta$ for stretching/shrinking surface. When the boundary layer increases $\lambda$ also increases. Finally, Figure 9 depicts the variation in temperature profile with different values of $\xi$ for the suction case, respectively, and keeping all other parameters are constant as shown in the figure. Illuminating that in the stretching surface, the transverse velocity rises as $\xi$ increases. It gives the result that the boundary layer will increase with the increase in different values of $\xi$.

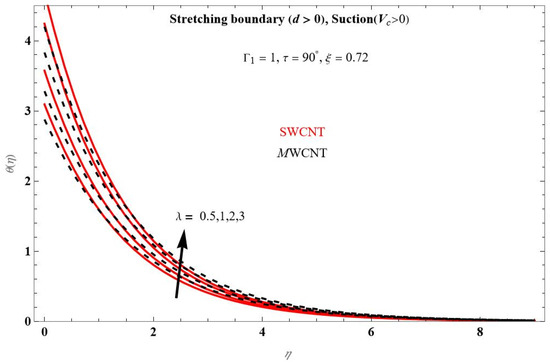
Figure 8. The temperature profile for different values of $\lambda$ at $M=\Gamma =v_c=1, \phi =0.1$.

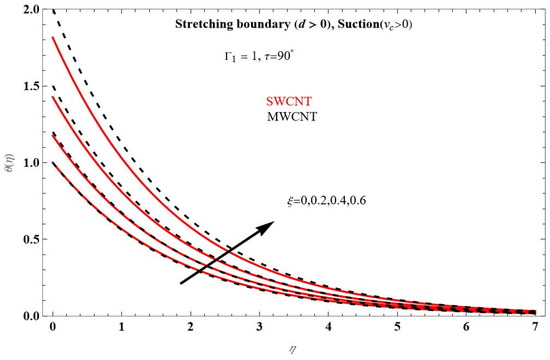
Figure 9. Temperature profile for different values of $\xi$ at $M=\Gamma =v_c=\lambda =1, \phi =0.1$.

In addition to that, MWCNT-Nano fluids are of a more effective temperature than the SWCNT-Nano fluids. Figure 10 depicts the variation in temperature profile $\theta (\eta )$ with different values of $\xi$ for the suction case. Here, we are comparing the $\phi =0.0$ and $\phi =0.1$. When increasing $\xi$, the boundary layer also increases.

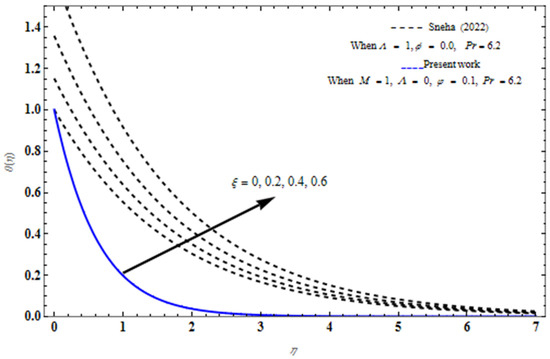
Figure 10. Temperature profile for different values of $\xi$ at $M=\Gamma =v_c=\lambda =1, \phi =0.1$.

4. Conclusions

The flow and heat transfer properties of CNTs are described by a series of nonlinear equations. The mathematical model’s systematic presentation emphasizes the importance of convective heat conditions in CNT and nanofluid flow and heat transmission. Furthermore, the best analytical technique given in this study is used to determine suction and injection. WMCNT suspended nanofluids have evolved faster velocities than SWCNT suspended nanofluids, indicating that they may be beneficial in a few applications. Primary research has shown that MWCNT nano particles can reach the tumour faster than SWCNT nano particles in the treatment of disorder. The effect of suspended SWCNTs and MWCNT Nano fluids’ transvers velocity, axial velocity, and temperature profile is dependent on solid volume fraction in this result. The MWCNT nano fluids outperform the SWCNT nano fluids in all cases of the graphs.

• Transverse velocity decreases as magnetic field enhances.
• Various parameter increases as axial velocity decreases.
• The value of M, Γ, λ and φ increases as the temperature profile also increases.