Selection of Production Reliability Indicators for Project Simulation Model
Abstract
:1. Introduction
2. Literature Background
2.1. Modeling Project Manufacturing Processes
- Project initiation: The need for special services or products has arisen. The main specification is settled and discussed in financial and other terms, such as agreed time frames.
- Project planning: A more detailed analysis is performed in terms of production: activities, dependencies are revealed, resources are estimated, initial risk assessment is performed.
- Execution: Value creation occurs in this stage: the provision of the services or product manufacturing. In this phase, all the activities are monitored and compared to the plan, and where needs and workflows are carried out.
- Closure: This stage is for the evaluation of positive and negative impacts of the project execution. Drawing conclusions are crucial and these can support later projects.
- A small change in the activity times can induce a change in the list of bottleneck activities (critical activities).
- It ignores the stochastic feature of the production; the model uses deterministic values for human resources and raw materials.
- It does not provide the possibility of risk management.
- It does not take the resource allocation into account.
- It only deals with time indicator, it excludes financial calculations.
- PERT uses the result of the CPM method.
- Authors argue that beta is the best distribution for time estimations.
2.2. Reliability Indicators and Risk Analysis
- (1)
- Faultlessness: these indicators are created in order to examine the smooth operation of the production system. These are usually time-bounded/calculated ratio: failure rate, mean operation time, probability of failure, probability of faultless operation and mean time between failure.
- (2)
- Reparability: it includes all the indicators which are calculated when a job breaks down and needs to be repaired. These indicators are usually time-bounded or a calculated ratio: mean repair time, mean downtime, recovery intensity, probability of recovery, mean time to repair.
- (3)
- Durability: this category reflects on the durability of the jobs, such as: mean operation time, mean lifespan, q-percent operation.
- (4)
- Storability: this category stands for the storability of the product. This is also an important factor for the customer, as it also has an effect on the perception of quality: mean storage life, percentage of storage time.
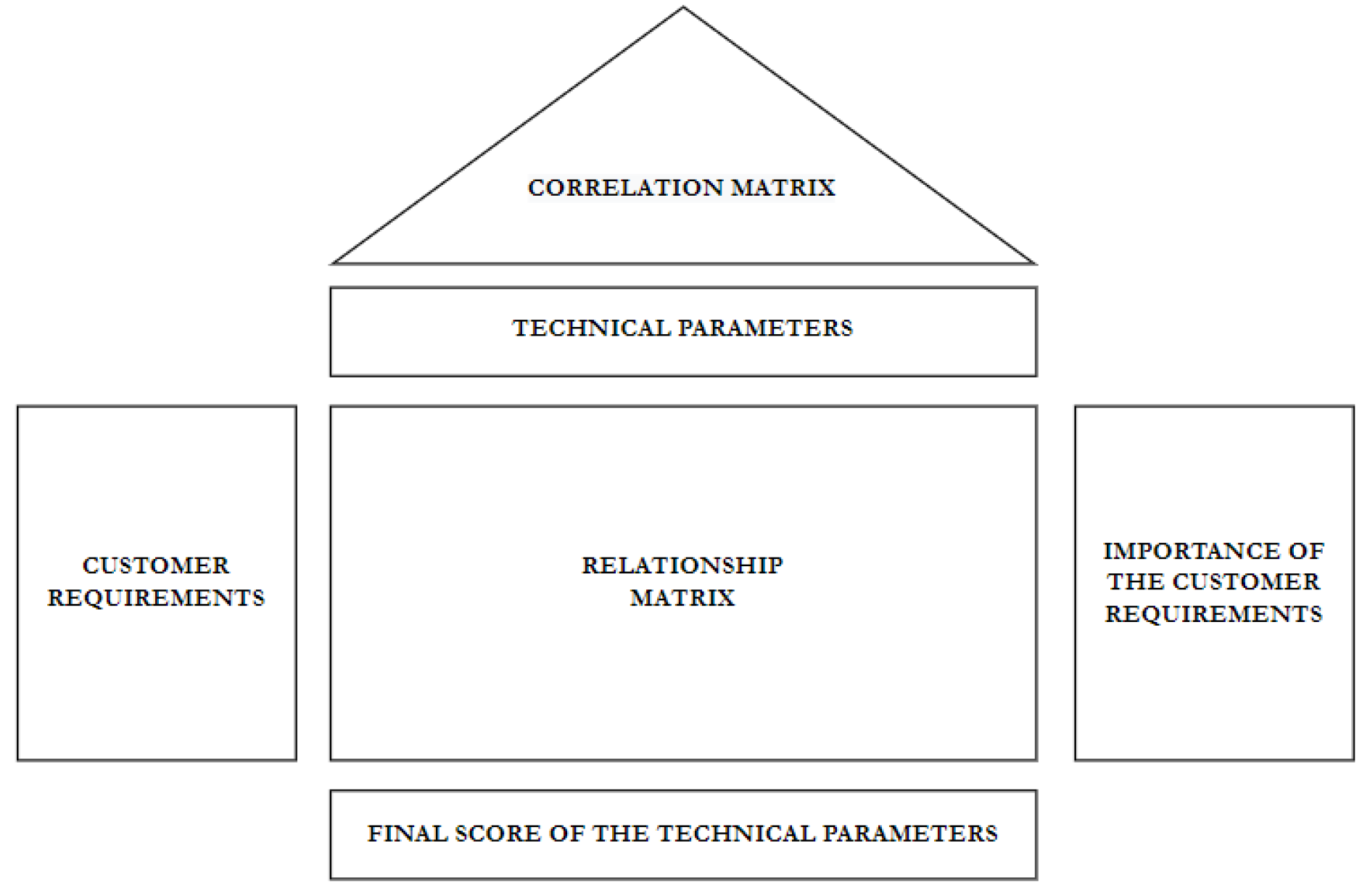
2.3. Quality Function Deployment (QFD)
3. Materials and Methods
3.1. Research Goal, Hypotheses
3.2. Operationalization, Steps of the Process
4. Results
4.1. Meta-Analysis
AND
(reliability OR uncertainty OR stochastic)
AND
(simulation OR analysis)
4.2. Results of the Quality Function Deployment
- Time-based (CR1): A crucial part of production scheduling is the time. The time consequences of probable problems should be implemented in the model.
- Measurable (CR2): All the included indicators should be described quantitatively.
- Correlation among failures (CR3): When a model is created, the dependency among problems should be described to examine domino-effect.
- Frequency (CR4): A frequency of a certain problem can be given or calculated.
- Critical Path change (CR5): In the case of time increase, total process time and critical path should be evaluated.
- Integration to production scheduling method (CR6): A certain component, indicator or parameter only helps the decision-maker when it is logically built in the model.
- The speed of calculation (CR7): The execution of a stochastic model should take as little time as it is possible. The calculation speed depends on the complexity of the indicator built in the simulation.
4.3. Implementation of the Selected Indicators to a Process Simulation Model
- Based on experimental data or professional estimation, an exact value can be assigned to trigger the failure in the activity. This is done by accumulating total process times and examining the value by mod operator.
- The other approach is providing information about the failure in cycle format. This can be very useful when a production process is described in network format (e.g., CPM) and stochastic methodology is applied. The stochastic CPM can also be applied when a high volume production is modeled and the activities should wait for the end of the process. A decision-maker can have an estimate about how frequently a certain failure repeats itself, e.g., every 5th run is affected by that particular problem.
| Algorithm 1 ReliabilitySimulation. | |
| 1: | seti to 1, |
| 2: | setsetShift to 2, // 2 shifts per day |
| 3: | setsetMinutes to 480, // 8 h in a shift |
| 4: | settotalProcessTime to 0, |
| 5: | setcumulatedTPT to 0, |
| 6: | setnrDays to 0, |
| 7: | setnrShifts to 0, |
| 8: | setactivityDuration, //array |
| 9: | setproblemList //problemCount, activityAffected, MTBFCycle, meanDownTime |
| 10: | fori to n |
| 11: | randomizeactivityDuration |
| 12: | for each problem n |
| 13: | if i % problemList[MTBFCycle] == 0 then |
| 14: | activityDuration[n] = activityDuration[n] + problemList[meanDownTime] |
| 15: | end if |
| 16: | else activityDuration[n] = activityDuration[n] |
| 17: | end for |
| 18: | solvetotalProcessTime → min! |
| 19: | createsensitivityReport |
| 20: | cumulatedTPT = cumulatedTPT + totalProcessTime, |
| 21: | nrDays = cumulatedTPT / (setShift ∗ setMinutes) |
| 22: | nrShifts = cumulatedTPT / setMinutes |
| 23: | copyi, activityDuration, totalProcessTime, cumulatedTPT, sensitivityReport, nrDays, |
| nrShifts | |
| 24: | end for |
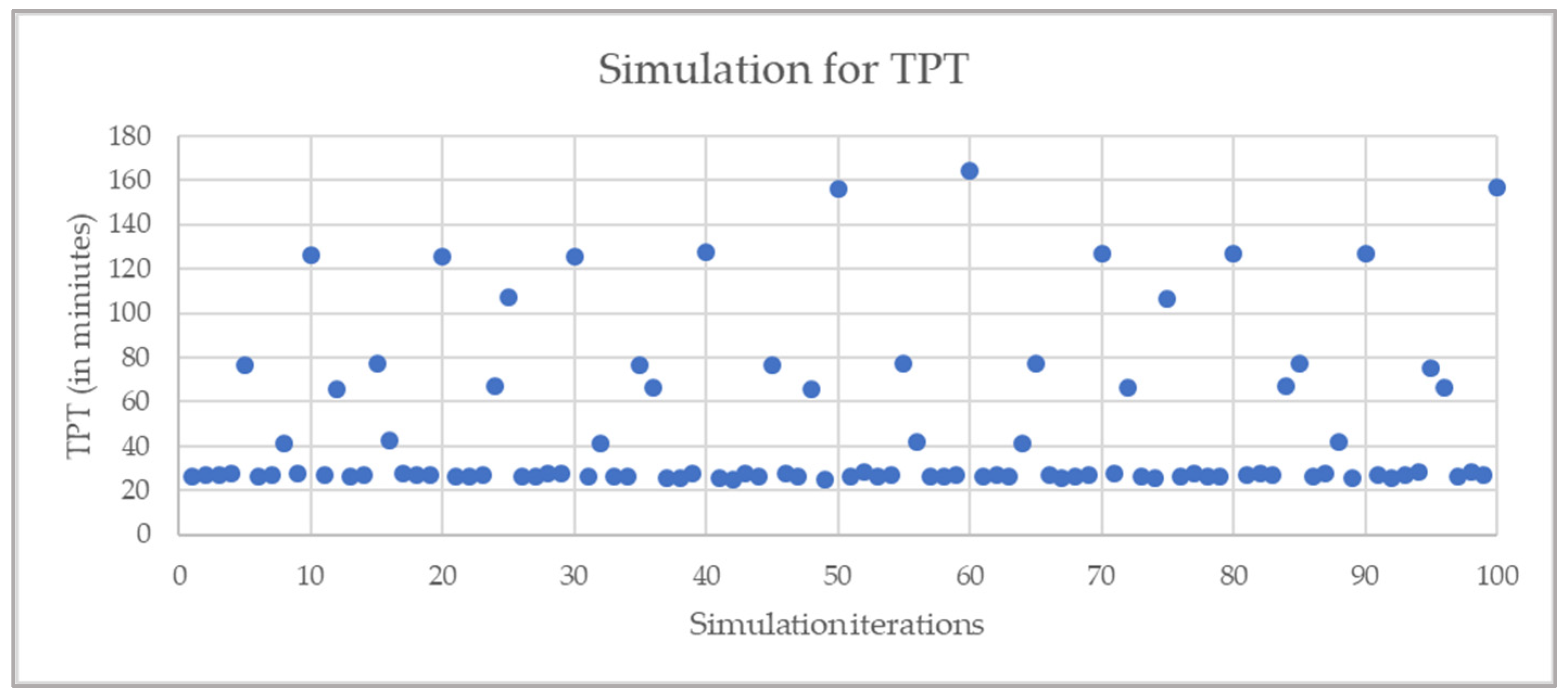
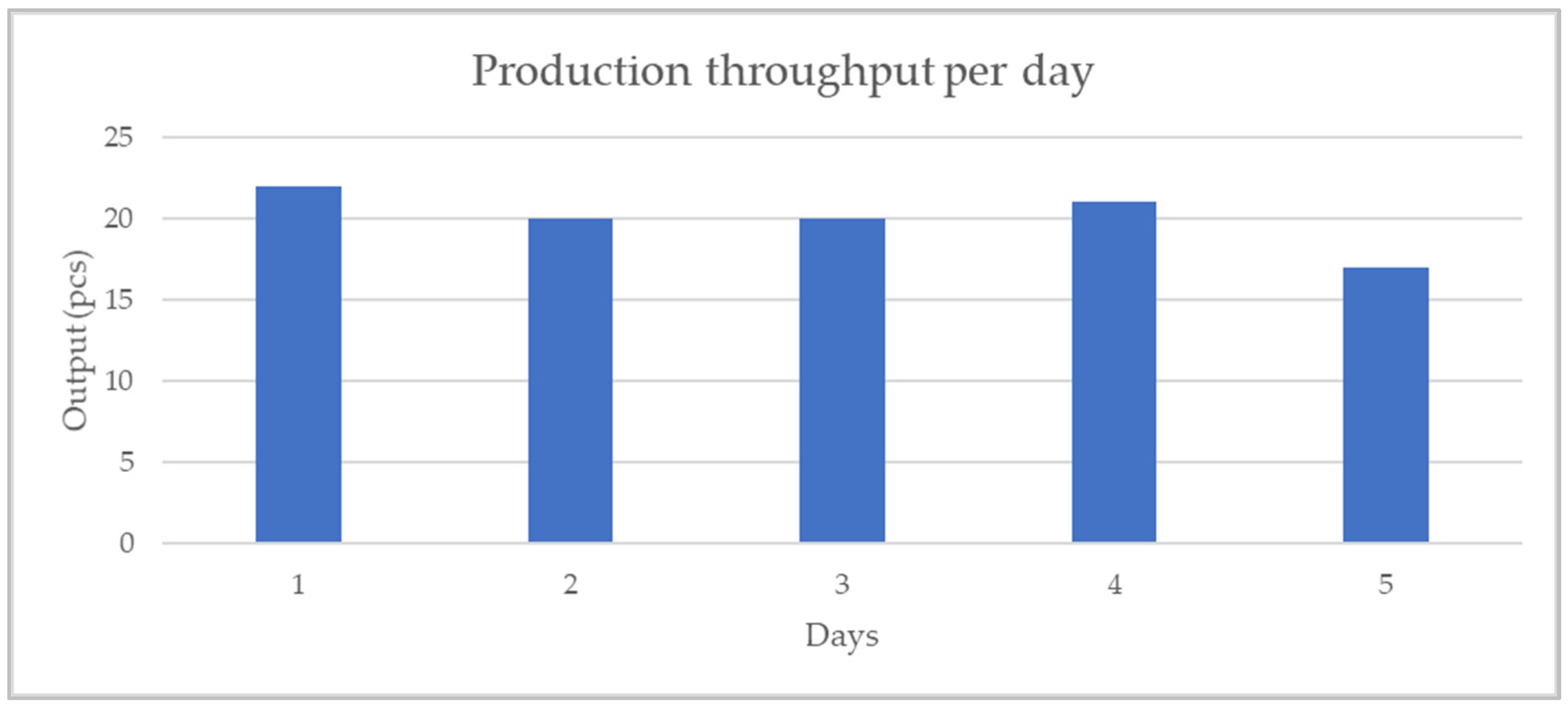
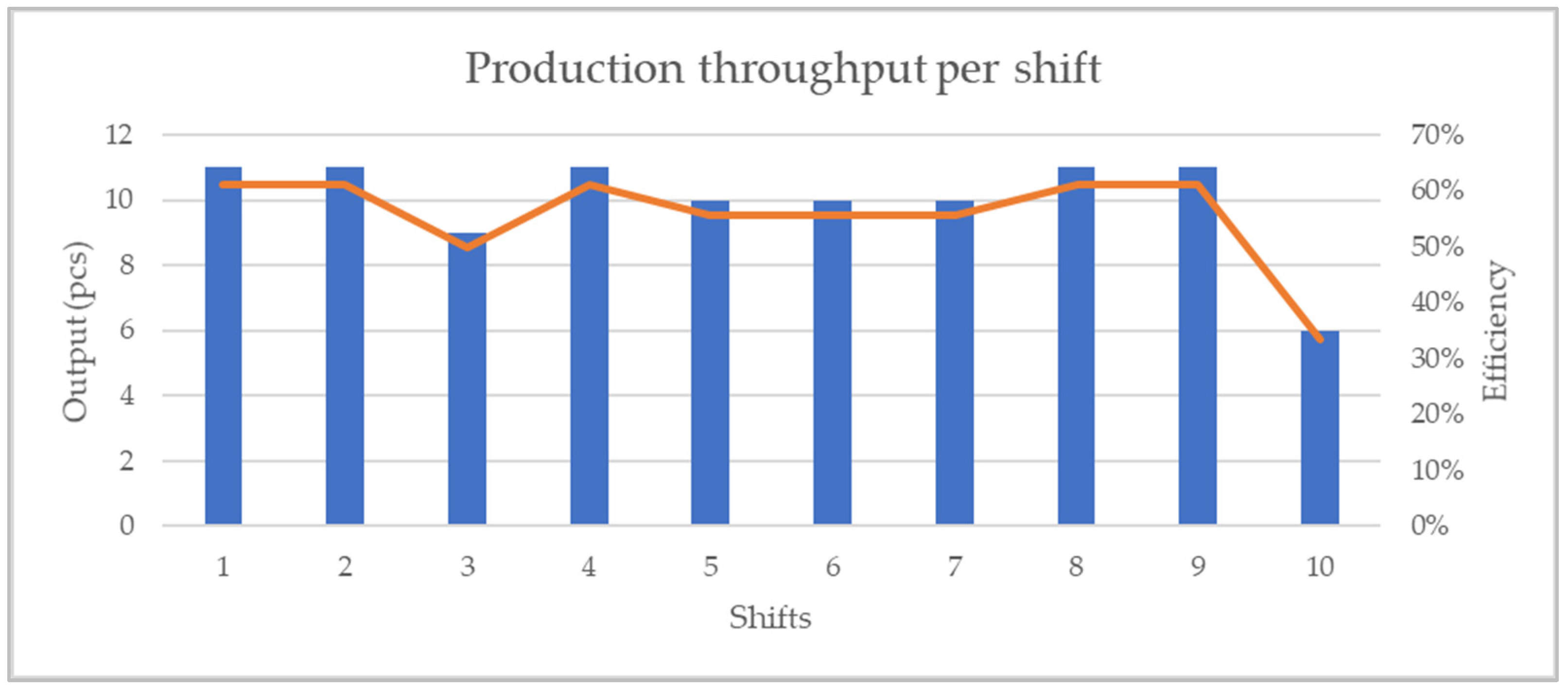
4.4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Espinoza Pérez, A.T.; Rossit, D.A.; Tohmé, F.; Vásquez, Ó.C. Mass customized/personalized manufacturing in industry 4.0 and blockchain: Research challenges, main problems, and the design of an information architecture. Inf. Fusion 2022, 79, 44–57. [Google Scholar] [CrossRef]
- Project Management Institute. A Guide to the Project Management Body of Knowledge: (PMBOK® Guide), 6th ed.; Project Management Institute: Newtown Square, PA, USA, 2017. [Google Scholar]
- Ragsdale, C.T. Spreadsheet Modeling & Decision Analysis: A Practical Introduction to Business Analytics; Cengage Learning: Stamford, CT, USA, 2021. [Google Scholar]
- Wayne, W.L. Operations Research: Applications and Algorithms; Duxbury Press: Belmont, CA, USA, 2004. [Google Scholar]
- Temesi, J.; Varró, Z. Operációkutatás; Akadémiai Kiadó: Budapest, Hungary, 2014. [Google Scholar]
- Pusztai, L.; Kocsi, B.; Budai, I. Making engineering projects more thoughtful with the use of fuzzy value-based project planning. Pollack Period. 2019, 14, 25–34. [Google Scholar] [CrossRef]
- Kövesi, J.; Erdei, J. Minőség És Megbízhatóság a Menedzsmentben; Typotex: Budapest, Hungary, 2011. [Google Scholar]
- Ferreira, S.; Silva, F.J.G.; Casais, R.B.; Pereira, M.T.; Ferreira, L.P. KPI development and obsolescence management in industrial maintenance. Procedia Manuf. 2019, 38, 1427–1435. [Google Scholar] [CrossRef]
- Korayem, M.H.; Iravani, A. Improvement of 3P and 6R mechanical robots reliability and quality applying FMEA and QFD approaches. Robot. Comput.-Integr. Manuf. 2008, 24, 472–487. [Google Scholar] [CrossRef]
- Abusalem, O.; Bertalan, N.; Kocsi, B. Implementing quantitative techniques to improve decision making in construction projects: A case study. Pollack Period. 2019, 14, 223–234. [Google Scholar] [CrossRef]
- Kocsi, B.; Matonya, M.M.; Pusztai, L.P.; Budai, I. Real-time decision-support system for high-mix low-volume production scheduling in industry 4.0. Processes 2020, 8, 912. [Google Scholar] [CrossRef]
- Lux, A.; Mawo De Bikond, J.; Etienne, A.; Quillerou-Grivot, E. FMEA and consideration of real work situations for safer design of production systems. Int. J. Occup. Saf. Ergon. 2016, 22, 557–564. [Google Scholar] [CrossRef]
- Adedigba, S.A.; Oloruntobi, O.; Khan, F.; Butt, S. Data-driven dynamic risk analysis of offshore drilling operations. J. Pet. Sci. Eng. 2018, 165, 444–452. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y. Failure risk analysis of pipelines using data-driven machine learning algorithms. Struct. Saf. 2021, 89, 102047. [Google Scholar] [CrossRef]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. Customer-oriented product design using an integrated neutrosophic AHP & DEMATEL & QFD methodology. Appl. Soft Comput. 2022, 118, 108445. [Google Scholar] [CrossRef]
- Rampal, A.; Mehra, A.; Singh, R.; Yadav, A.; Nath, K.; Chauhan, A.S. Kano and QFD analyses for autonomous electric car: Design for enhancing customer contentment. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Hashim, A.M.; Dawal, S.Z.M. Kano model and QFD integration approach for ergonomic design improvement. Procedia-Soc. Behav. Sci. 2012, 57, 22–32. [Google Scholar] [CrossRef] [Green Version]
- Chan, L.-K.; Wu, M.-L. Quality function deployment: A literature review. Eur. J. Oper. Res. 2002, 143, 463–497. [Google Scholar] [CrossRef]
- de Oliveira, L.M.V.; Santos, H.F.D.; de Almeida, M.R.; Costa, J.A.F. Quality function deployment and analytic hierarchy process: A literature review of their joint application. Concurr. Eng. 2020, 28, 239–251. [Google Scholar] [CrossRef]
- Ho, W. Integrated analytic hierarchy process and its applications—A literature review. Eur. J. Oper. Res. 2008, 186, 211–228. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy process: Decision making in complex environments. In Quantitative Assessment in Arms Control; Springer: Berlin/Heidelberg, Germany, 1984; pp. 285–308. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef] [Green Version]
- Maceika, A.; Bugajev, A.; Šostak, O.R.; Vilutienė, T. Decision tree and AHP methods application for projects assessment: A case study. Sustainability 2021, 13, 5502. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Aggarwal, U.; Charles, V. An integrated AHP-DEA multi-objective optimization model for sustainable transportation in mining industry. Resour. Policy 2018, 74, 101180. [Google Scholar] [CrossRef]
- Li, H.; Díaz, H.; Guedes Soares, C. A failure analysis of floating offshore wind turbines using AHP-FMEA methodology. Ocean. Eng. 2021, 234, 109261. [Google Scholar] [CrossRef]
- Sarraf, R.; McGuire, M.P. Integration and comparison of multi-criteria decision making methods in safe route planner. Expert Syst. Appl. 2020, 154, 113399. [Google Scholar] [CrossRef]
- Díaz, H.; Loughney, S.; Wang, J.; Guedes Soares, C. Comparison of multicriteria analysis techniques for decision making on floating offshore wind farms site selection. Ocean Eng. 2022, 248, 110751. [Google Scholar] [CrossRef]
- Huerta, J.R.; Silva, R.S.; De Tomi, G.; Ayres da Silva, A.L.M. A dynamic simulation approach to support operational decision-making in underground mining. Simul. Model. Pract. Theory 2022, 115, 102458. [Google Scholar] [CrossRef]
- Friederich, J.; Lazarova-Molnar, S. Towards data-driven reliability modeling for cyber-physical production systems. Procedia Comput. Sci. 2021, 184, 589–596. [Google Scholar] [CrossRef]
- Chen, X.; An, Y.; Zhang, Z.; Li, Y. An approximate nondominated sorting genetic algorithm to integrate optimization of production scheduling and accurate maintenance based on reliability intervals. J. Manuf. Syst. 2020, 54, 227–241. [Google Scholar] [CrossRef]
- O’Brien, E.M.; Baily, S.A.; Birnbaum, E.R.; Chapman, C.; Espinoza, E.A.; Faucett, J.A.; Hill, J.O.; John, K.D.; Marroquin, P.S.; McCrady, R.C.; et al. Novel design and diagnostics improvements for increased production capacity and improved reliability at the los alamos isotope production facility. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectromet. Detect. Assoc. Equip. 2020, 956, 163316. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Jaber, M.Y. Economic production quantity model with learning in production, quality, reliability and energy efficiency. Comput. Ind. Eng. 2019, 129, 502–511. [Google Scholar] [CrossRef]
- Görkemli, L.; Kapan Ulusoy, S. Fuzzy bayesian reliability and availability analysis of production systems. Comput. Ind. Eng. 2010, 59, 690–696. [Google Scholar] [CrossRef]
- Kumar, N.S.H.; Manjunath, C.; John, R.P.; Chand, R.P.; Madhusudhana, S.; Venkatesha, B.K. Reliability, availability and maintainability study of 6.5 cubic meters shovel and 60 tone dumper in a surface limestone mine. Mater. Today Proc. 2022, 54, 199–204. [Google Scholar] [CrossRef]
- Li, Y.; Coolen, F.P.A.; Zhu, C. A practical reliability design method considering the compound weight and load-sharing. Int. J. Approx. Reason. 2020, 127, 17–32. [Google Scholar] [CrossRef]
- Harmon, V.L.; Wolfrum, E.; Knoshaug, E.P.; Davis, R.; Laurens, L.M.L.; Pienkos, P.T.; McGowen, J. Reliability metrics and their management implications for open pond algae cultivation. Algal Res. 2021, 55, 102249. [Google Scholar] [CrossRef]
- He, Y.; Zhang, H.; Wang, P.; Huang, Y.; Chen, Z.; Zhang, Y. Engineering application research on reliability prediction of the combined DC-DC power supply. Microelectron. Reliab. 2021, 118, 114059. [Google Scholar] [CrossRef]
- Alavian, P.; Eun, Y.; Liu, K.; Meerkov, S.M.; Zhang, L. The (α, β)-precise estimates of MTBF and MTTR: Definition, calculation, and observation time. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1469–1477. [Google Scholar] [CrossRef]
- Leite, M.; Costa, M.A.; Alves, T.; Infante, V.; Andrade, A.R. Reliability and availability assessment of railway locomotive bogies under correlated failures. Eng. Fail. Anal. 2022, 135, 106104. [Google Scholar] [CrossRef]
- Dubový, D.; Famfulík, J.; Richtář, M. Determination of operational reliability of firefighting special vehicles. Transp. Res. Procedia 2021, 55, 126–132. [Google Scholar] [CrossRef]
- Kavyashree, N.; Supriya, M.C.; Lokesh, M.R. Site reliability engineering for IOS mobile application in small-medium scale industries. Glob. Transit. Proc. 2021, 2, 137–144. [Google Scholar] [CrossRef]
- Jayaswal, K.; Palwalia, D.K. Role of reliability assessment in si-based non-isolated DC-DC power electronic converters. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Yasseri, S. Subsea technologies selection using analytic hierarchy process. Underw. Technol. 2012, 30, 151–164. [Google Scholar] [CrossRef]
- Belton, V. A comparison of the analytic hierarchy process and a simple multi-attribute value function. Eur. J. Oper. Res. 1986, 26, 7–21. [Google Scholar] [CrossRef]
- Coles, S.; Rowley, J. Spreadsheet modelling for management decision making. Ind. Manag. Data Syst. 1996, 96, 17–23. [Google Scholar] [CrossRef]

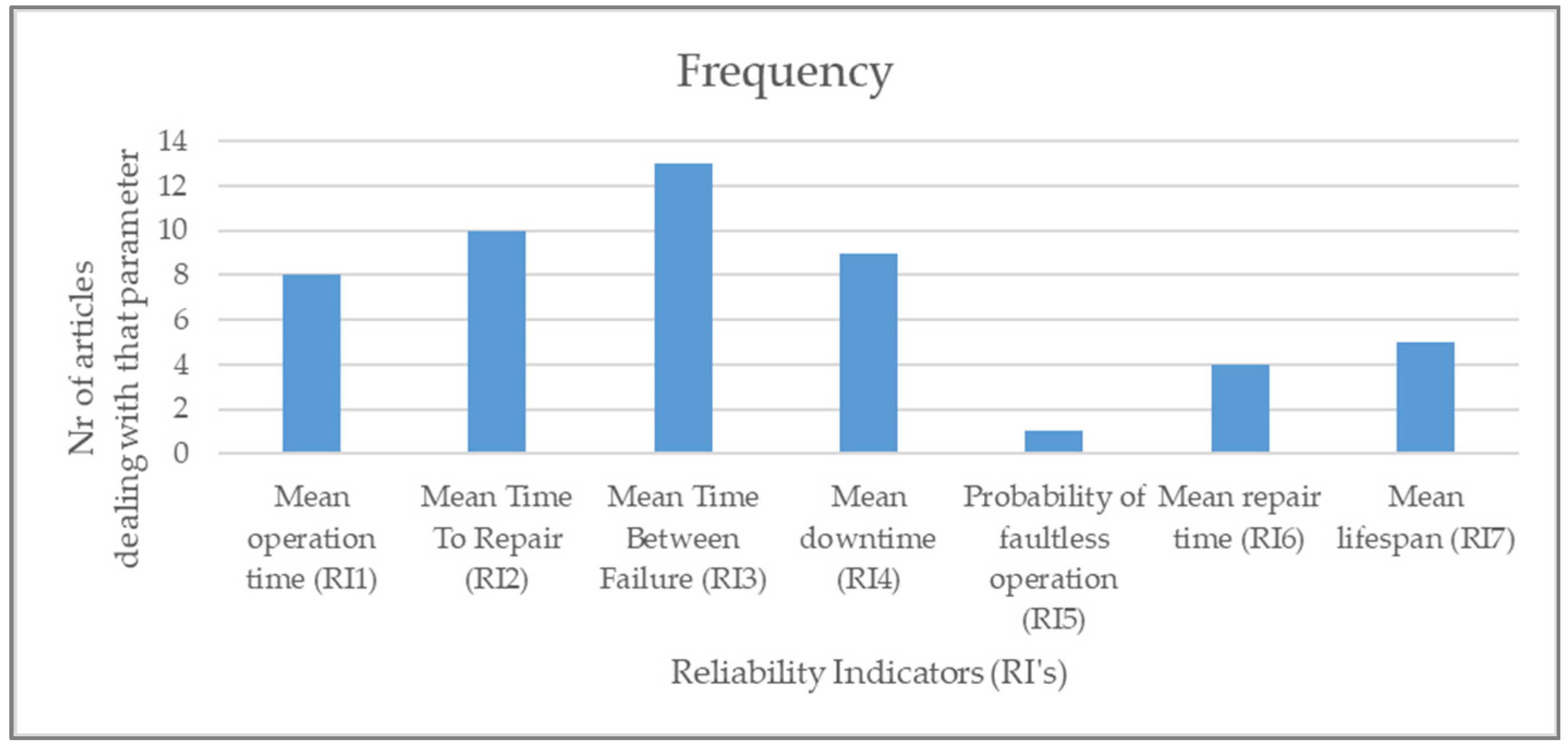

| Article | Mean Operation Time (RI1) | Mean Time to Repair (RI2) | Mean Time between Failure (RI3) | Mean Downtime (RI4) | Probability of Faultless Operation (RI5) | Mean Repair Time (RI6) | Mean Lifespan (RI7) |
|---|---|---|---|---|---|---|---|
| [29] | M | M | M | - | - | - | - |
| [30] | M | M | M | - | - | M | - |
| [31] | M | - | - | M | - | - | - |
| [32] | - | - | - | - | - | - | M |
| [33] | - | - | M | M | - | - | M |
| [34] | - | M | M | M | - | M | - |
| [35] | - | M | M | M | - | - | - |
| [36] | M | M | M | M | - | - | M |
| [37] | - | M * | M | M | - | - | - |
| [38] | - | - | M | - | M | - | - |
| [39] | - | M | M | M | - | - | - |
| [40] | M | M | M | M | - | M | M |
| [41] | M | M | M | M | - | - | M |
| [42] | M | M | M | - | - | M | - |
| [43] | M | M | M | - | - | - | - |
| Criteria | CR1 | CR2 | CR3 | CR4 | CR5 | CR6 | CR7 | Importance |
|---|---|---|---|---|---|---|---|---|
| CR1 | 0.241 | 0.199 | 0.200 | 0.462 | 0.272 | 0.227 | 0.176 | 0.254 |
| CR2 | 0.241 | 0.199 | 0.200 | 0.103 | 0.136 | 0.227 | 0.176 | 0.183 |
| CR3 | 0.048 | 0.040 | 0.040 | 0.051 | 0.019 | 0.045 | 0.059 | 0.043 |
| CR4 | 0.027 | 0.099 | 0.040 | 0.051 | 0.136 | 0.045 | 0.118 | 0.074 |
| CR5 | 0.121 | 0.199 | 0.280 | 0.051 | 0.136 | 0.114 | 0.294 | 0.171 |
| CR6 | 0.241 | 0.199 | 0.200 | 0.256 | 0.272 | 0.227 | 0.118 | 0.216 |
| CR7 | 0.080 | 0.066 | 0.040 | 0.026 | 0.027 | 0.114 | 0.059 | 0.059 |
| Sum | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Methods | RI 1 | RI 2 | RI 3 | RI 4 | RI 5 | RI 6 | RI 7 | Importance | |
|---|---|---|---|---|---|---|---|---|---|
| Reqs. | |||||||||
| CR1 | 9 | 9 | 9 | 9 | 0 | 9 | 0 | 0.254 | |
| CR2 | 9 | 9 | 9 | 9 | 3 | 3 | 3 | 0.183 | |
| CR3 | 3 | 3 | 3 | 1 | 3 | 3 | 1 | 0.043 | |
| CR4 | 1 | 3 | 9 | 9 | 9 | 3 | 9 | 0.074 | |
| CR5 | 1 | 3 | 9 | 9 | 3 | 3 | 9 | 0.171 | |
| CR6 | 3 | 9 | 9 | 3 | 9 | 3 | 3 | 0.216 | |
| CR7 | 3 | 1 | 3 | 3 | 3 | 1 | 3 | 0.059 | |
| Abs. Weight | 5.13 | 6.80 | 8.39 | 7.00 | 3.98 | 4.41 | 3.62 | ||
| Activity | Between Nodes | Minimum Value | Maximum Value | |
|---|---|---|---|---|
| A | X1–X2 | 75 | 85 | β (2;2) |
| B | X1–X3 | 60 | 65 | β (2;2) |
| C | X2–X3 | 30 | 33 | β (2;2) |
| D | X2–X4 | 50 | 70 | β (2;2) |
| E | X3–X4 | 30 | 40 | β (2;2) |
| F | X4–X5 | 80 | 96 | β (2;2) |
| G | X5–X6 | 30 | 33 | β (2;2) |
| Problem | Activity Affected | MTBF Cycle | Downtime (Repair + Waiting) |
|---|---|---|---|
| 1 | A | 5 | 50 |
| 2 | B | 8 | 20 |
| 3 | C | 12 | 30 |
| 4 | D | 12 | 40 |
| 5 | E | 25 | 30 |
| 6 | F | 10 | 50 |
| Critical Path Name | Critical Path | Contribution |
|---|---|---|
| A | A-C-E-F-G | 73% (73/100) |
| B | A-D-F-G | 21% (21/100) |
| C | B-E-F-G | 6% (6/100) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pusztai, L.P.; Nagy, L.; Budai, I. Selection of Production Reliability Indicators for Project Simulation Model. Appl. Sci. 2022, 12, 5012. https://doi.org/10.3390/app12105012
Pusztai LP, Nagy L, Budai I. Selection of Production Reliability Indicators for Project Simulation Model. Applied Sciences. 2022; 12(10):5012. https://doi.org/10.3390/app12105012
Chicago/Turabian StylePusztai, László Péter, Lajos Nagy, and István Budai. 2022. "Selection of Production Reliability Indicators for Project Simulation Model" Applied Sciences 12, no. 10: 5012. https://doi.org/10.3390/app12105012
APA StylePusztai, L. P., Nagy, L., & Budai, I. (2022). Selection of Production Reliability Indicators for Project Simulation Model. Applied Sciences, 12(10), 5012. https://doi.org/10.3390/app12105012







