Numerical Simulation of the Force Acting on the Riser by Two Internal Solitary Waves
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Design and Data Collection
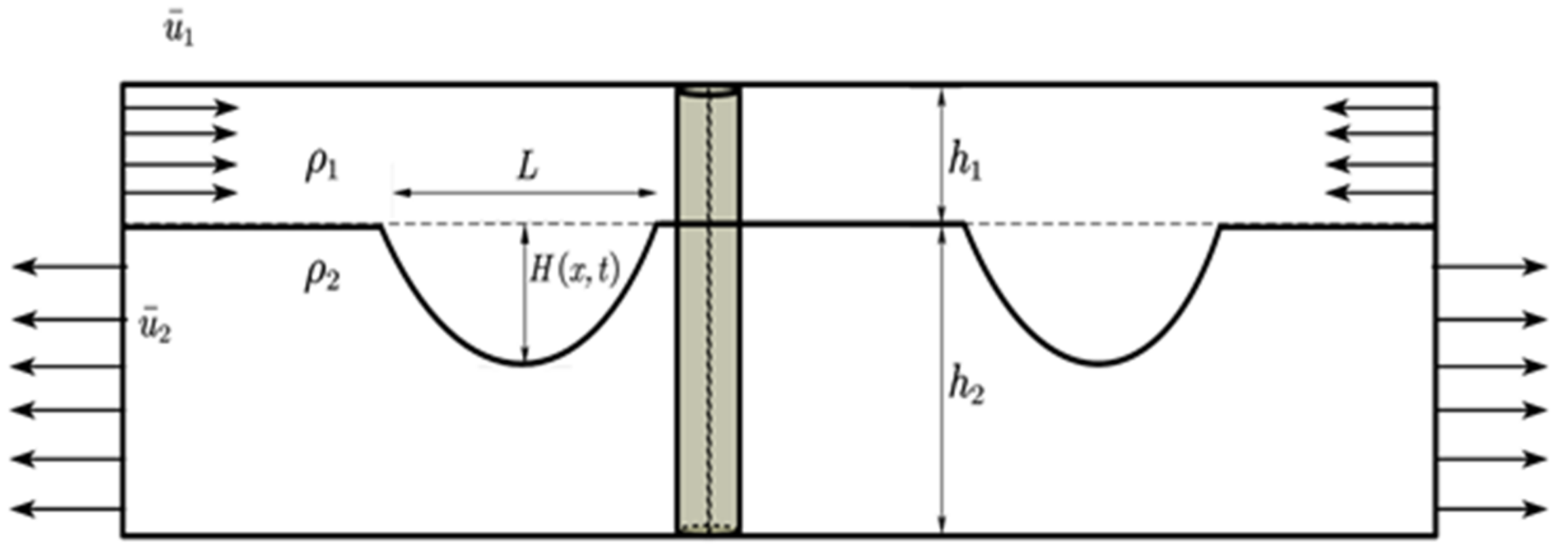
2.2. Geometric Model and Mesh Parameters
2.3. Mathematical Models
2.3.1. Governing Equation
2.3.2. Internal Isolated Wave Theory
2.3.3. Turbulence Method and Liquid Level Capture
- αi = 0 represents that the grid element has no phase i at all;
- αi = 1 represents that the grid cell is filled by phase I;
- 0 < αi < 1 represents that the grid element has an interphase interface.
2.3.4. Numerical Methods and Boundary Condition
2.3.5. Model Validation
2.3.6. Numerical Methods and Boundary Condition
3. Results
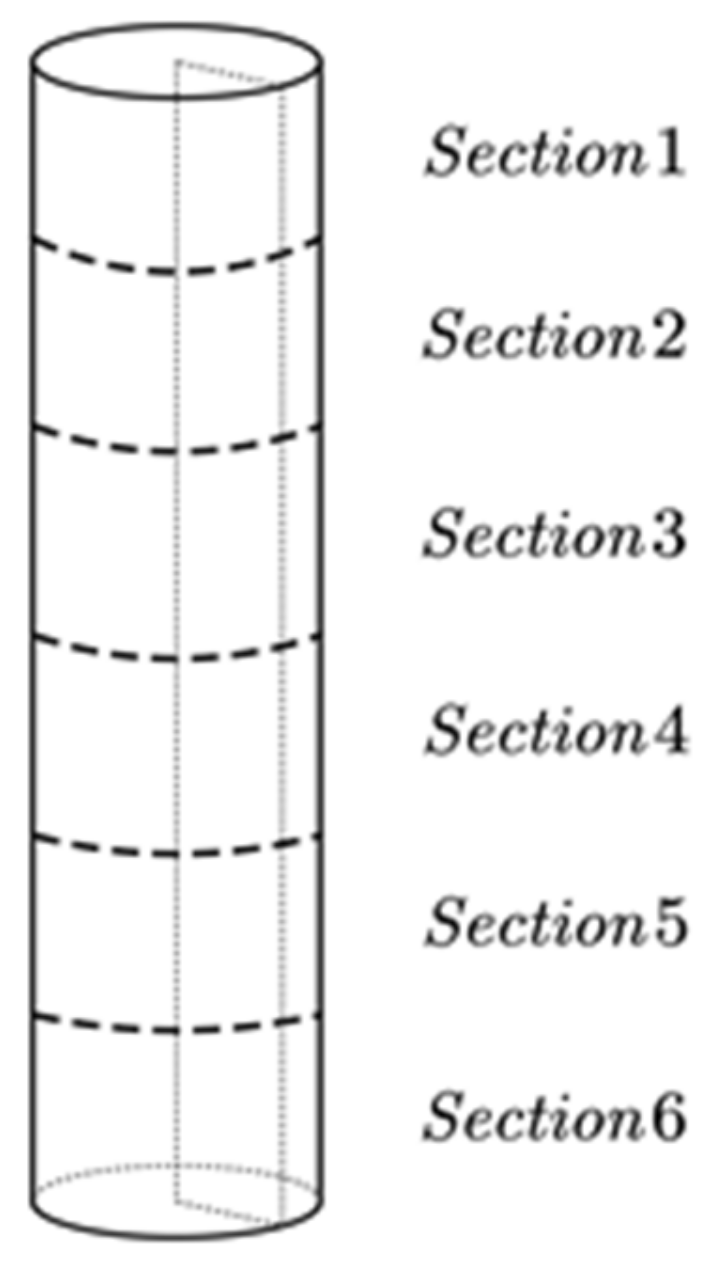
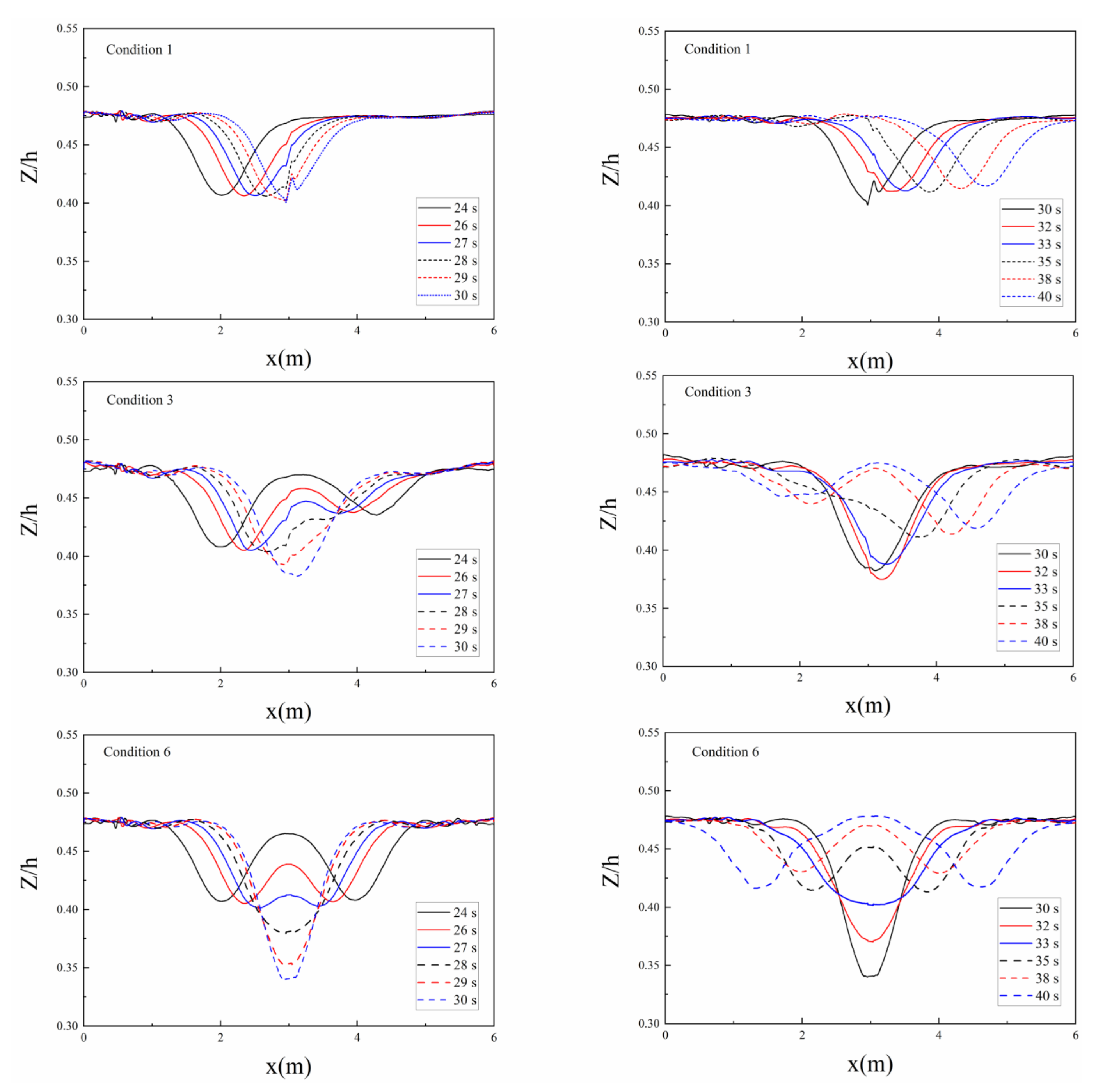
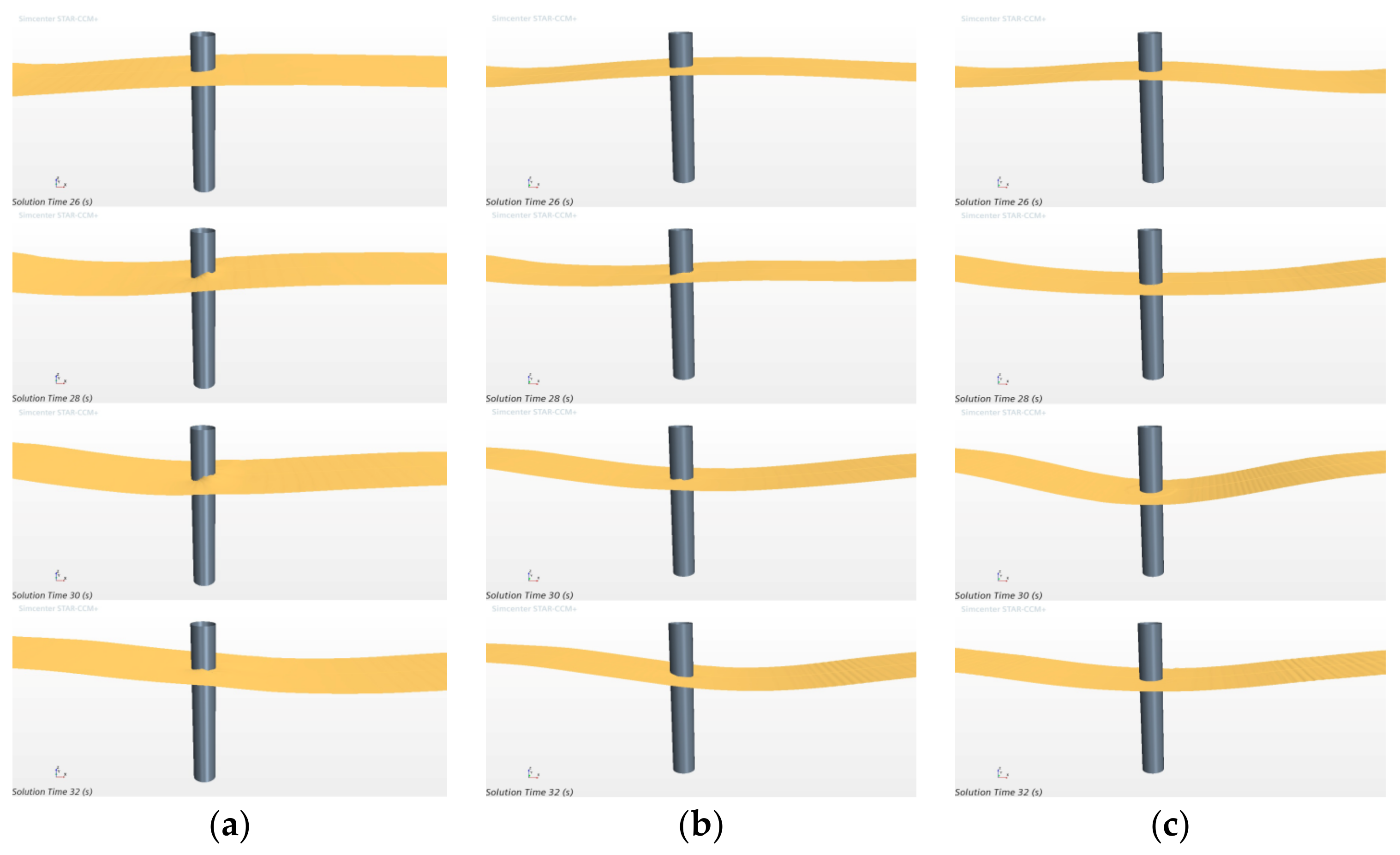
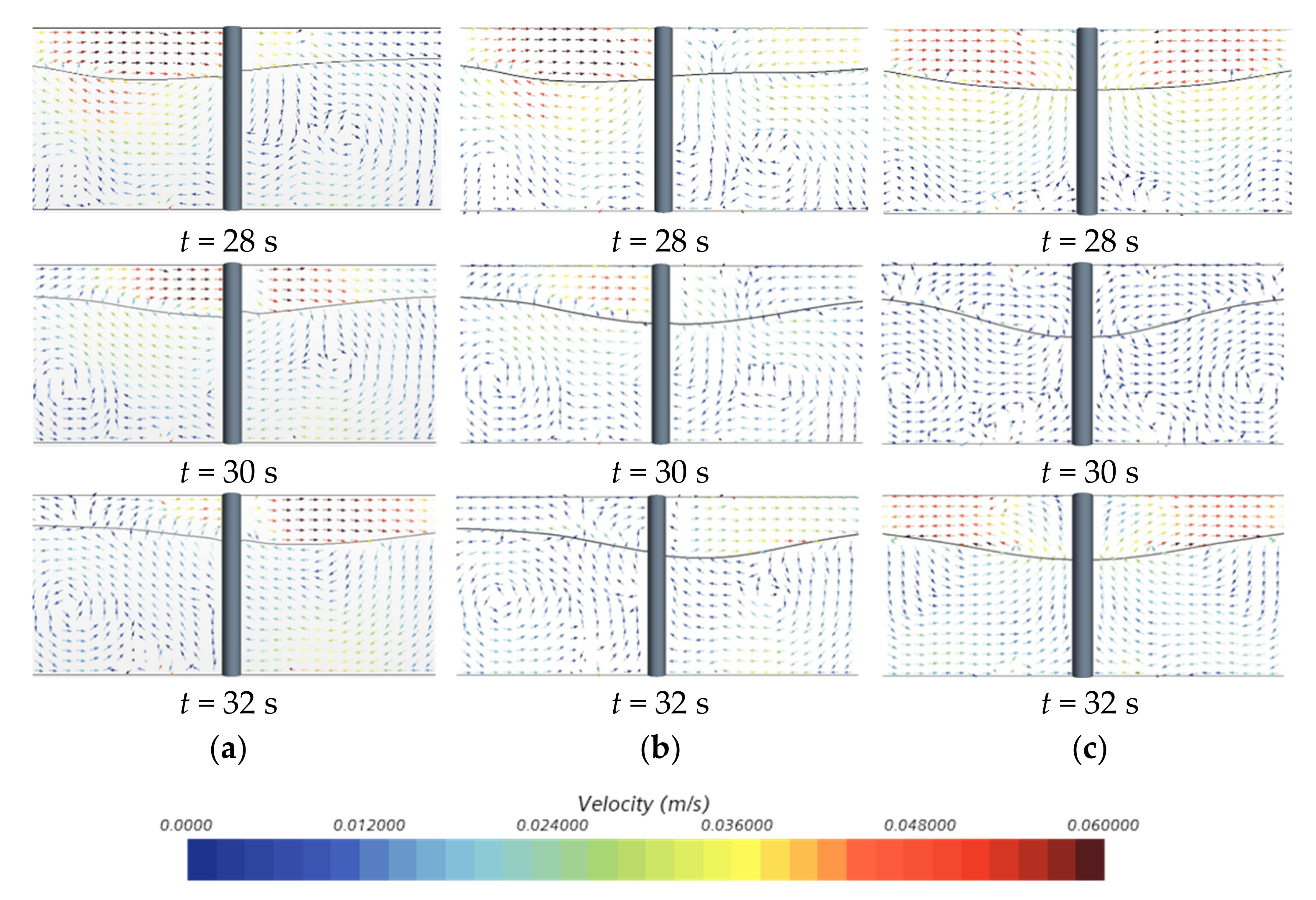
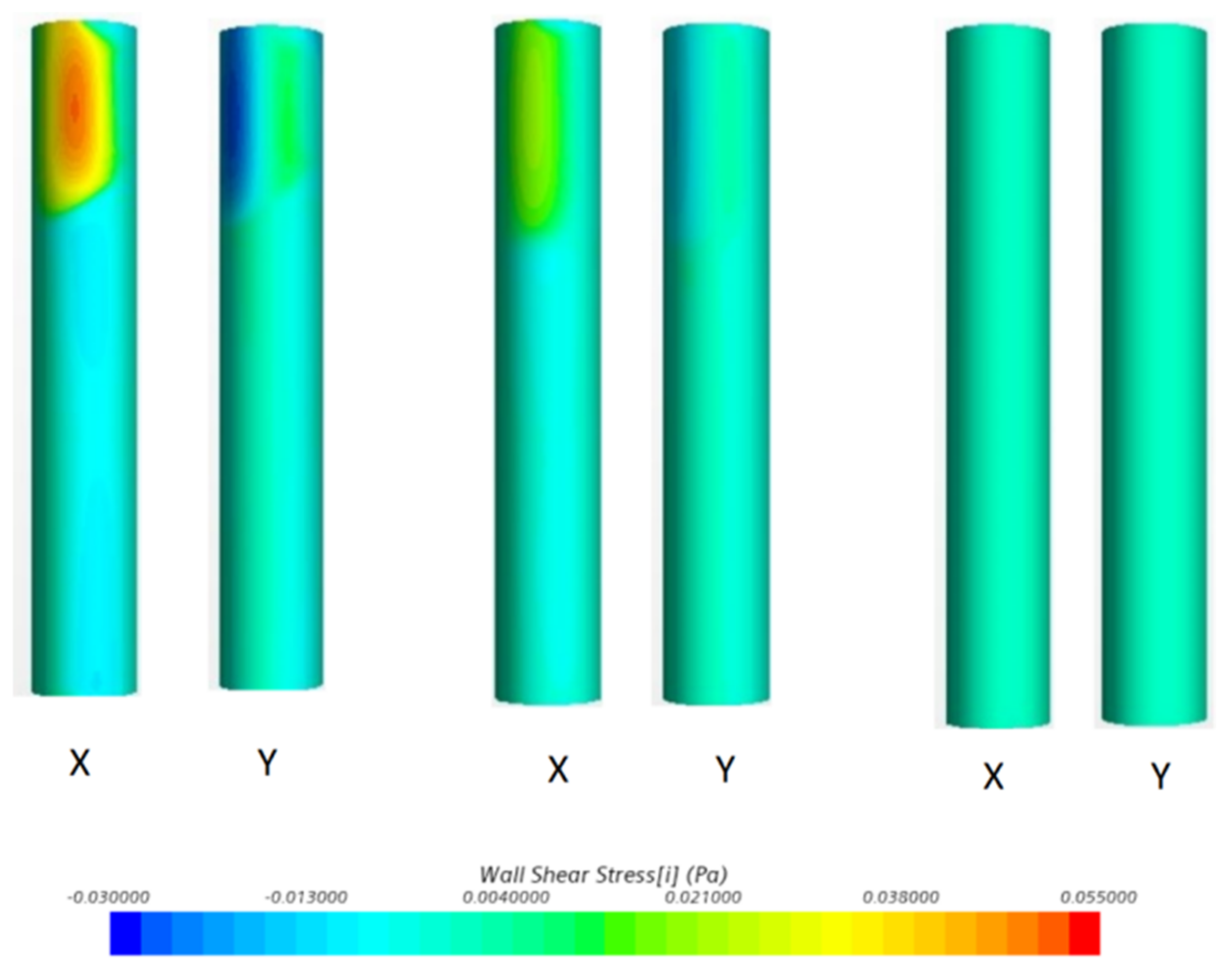
3.1. Flow Field Analysis
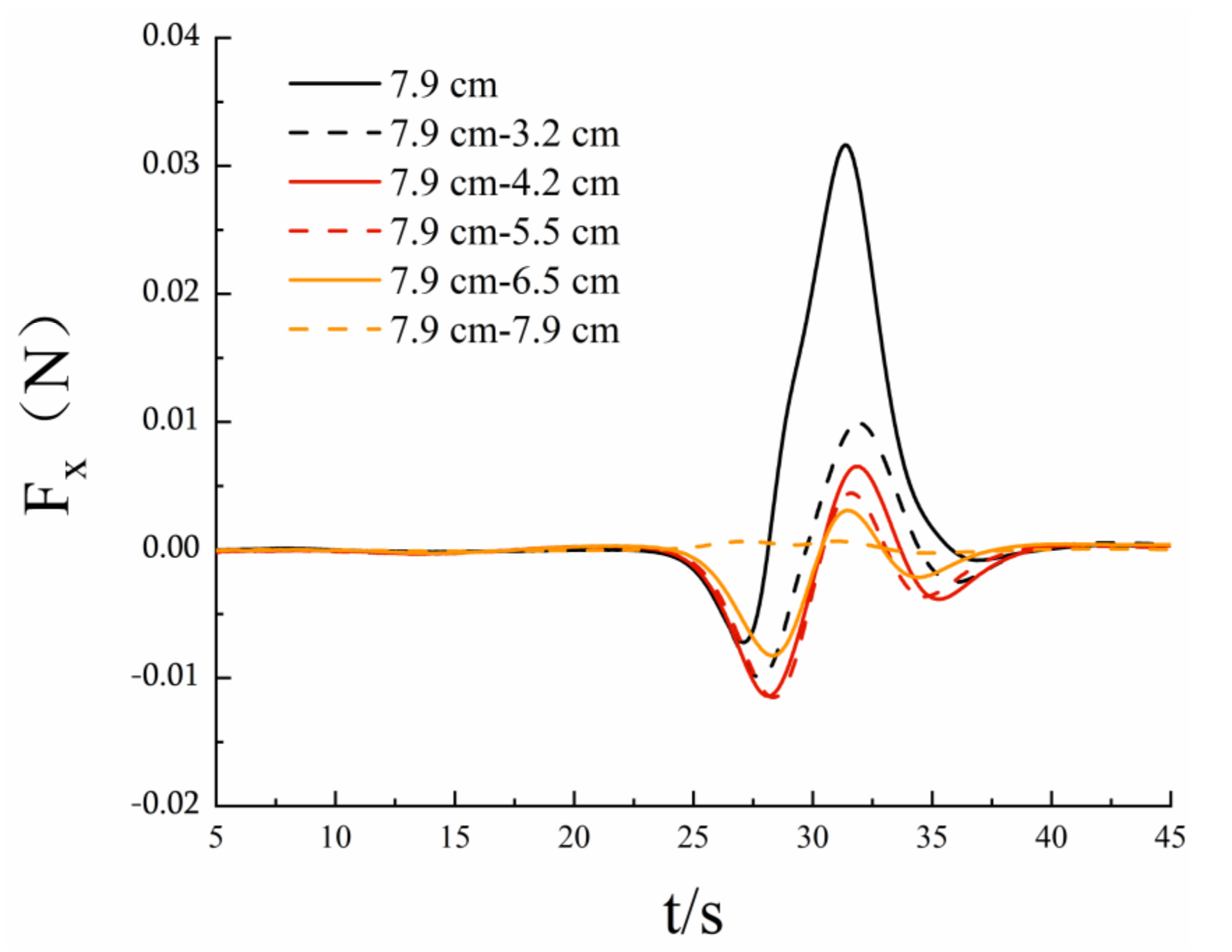
3.2. Riser Force Analysis
4. Discussion
- Unlike a single internal solitary wave, after the two internal solitary waves collide at the riser, they gradually fuse. When they finally fuse into a single wave, their amplitude reaches the maximum and is slightly less than the sum of the amplitudes of the two waves. At that point, the velocity of the flow field around the riser reaches a minimum. When the two waves act together, the change in the wave surface tends to be gentle. When the amplitude difference between the two sides is less than a certain degree, the wave surface will not deform;
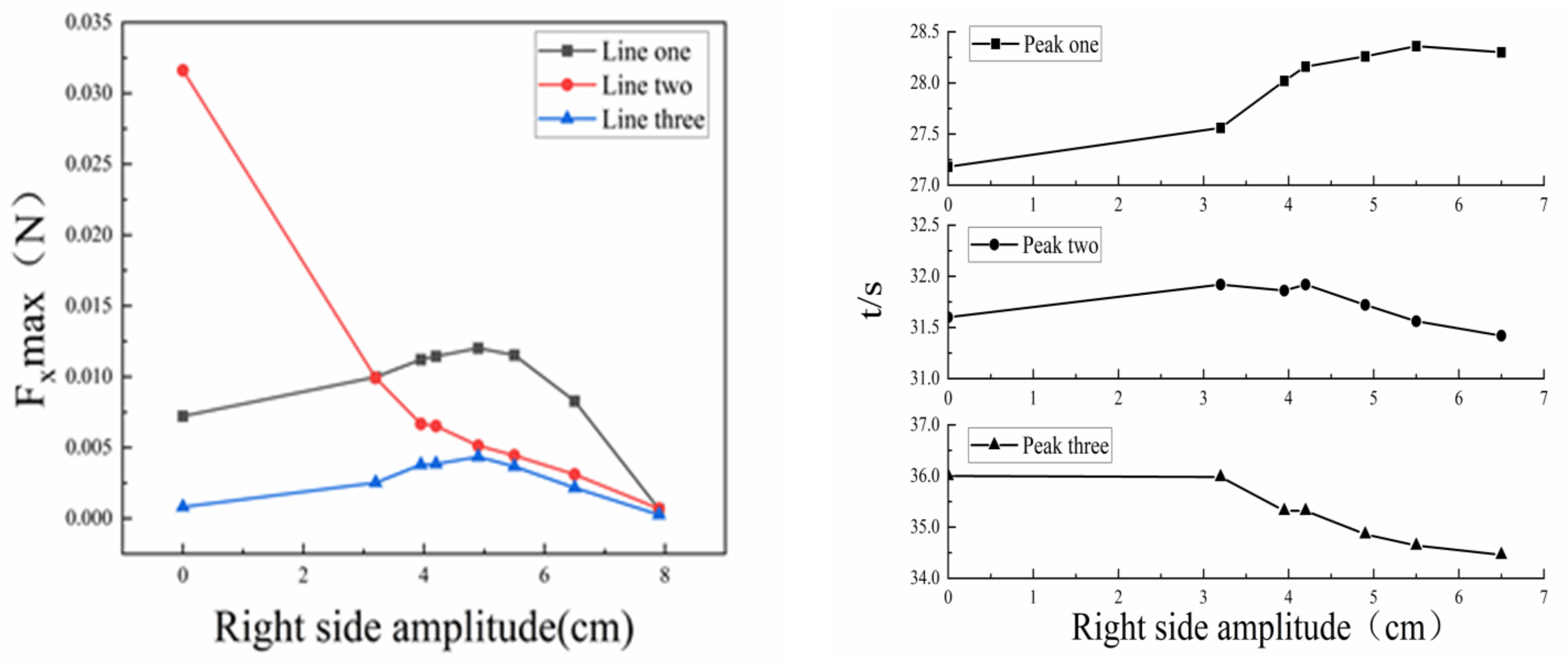
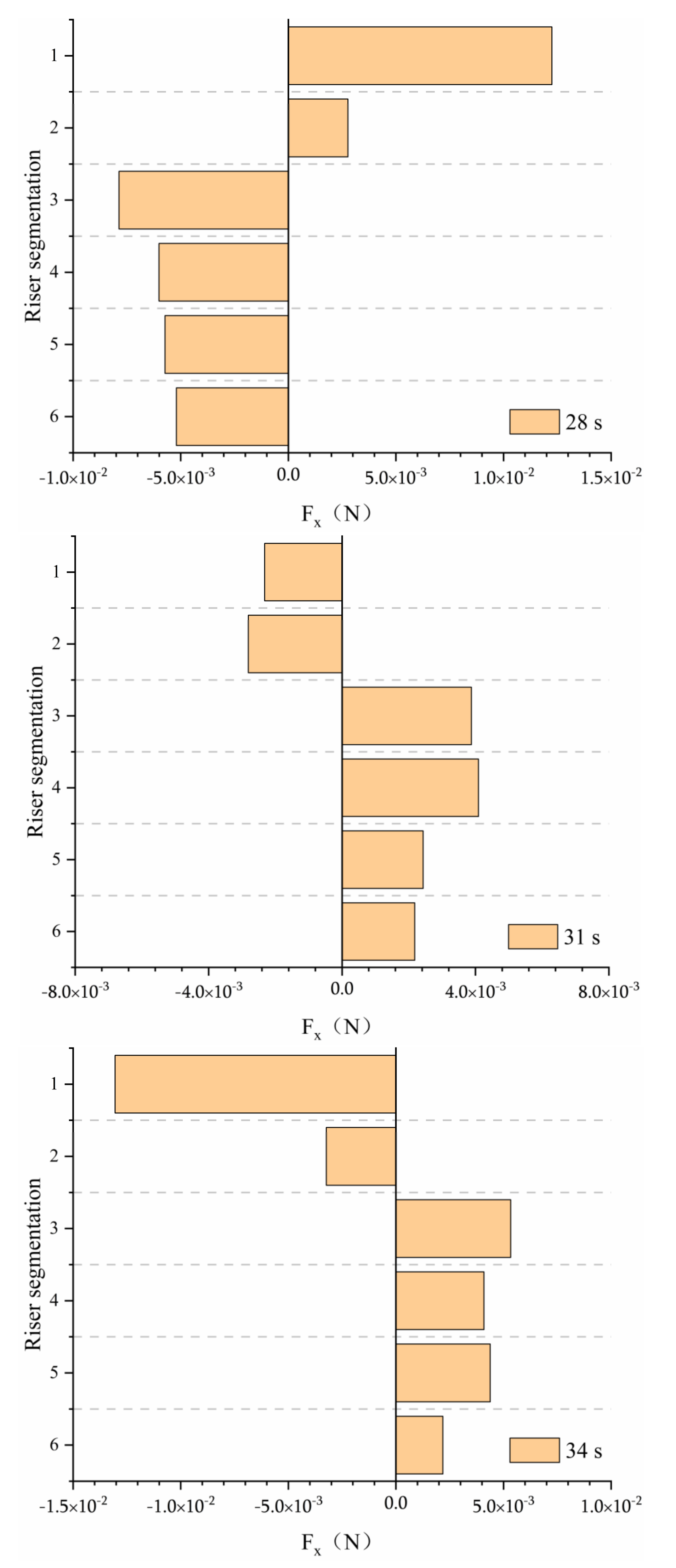
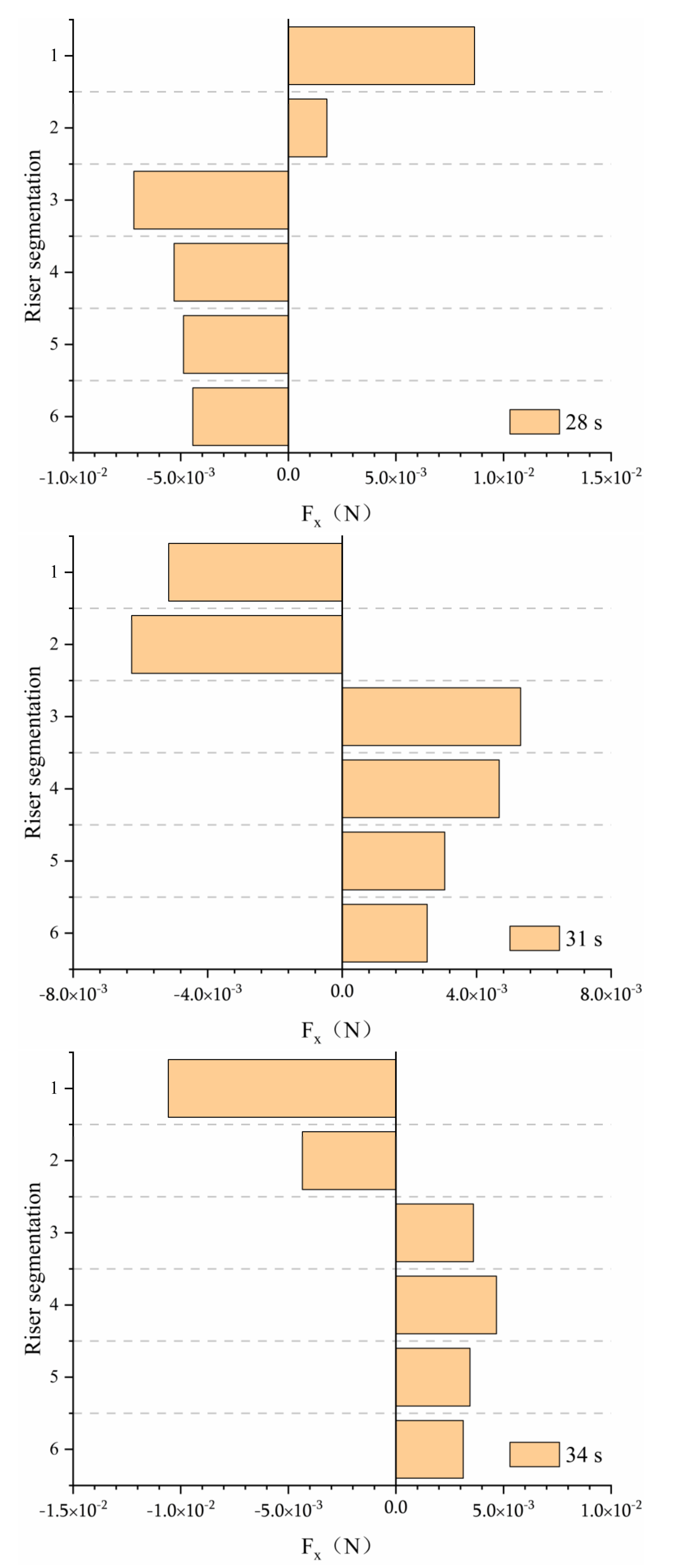
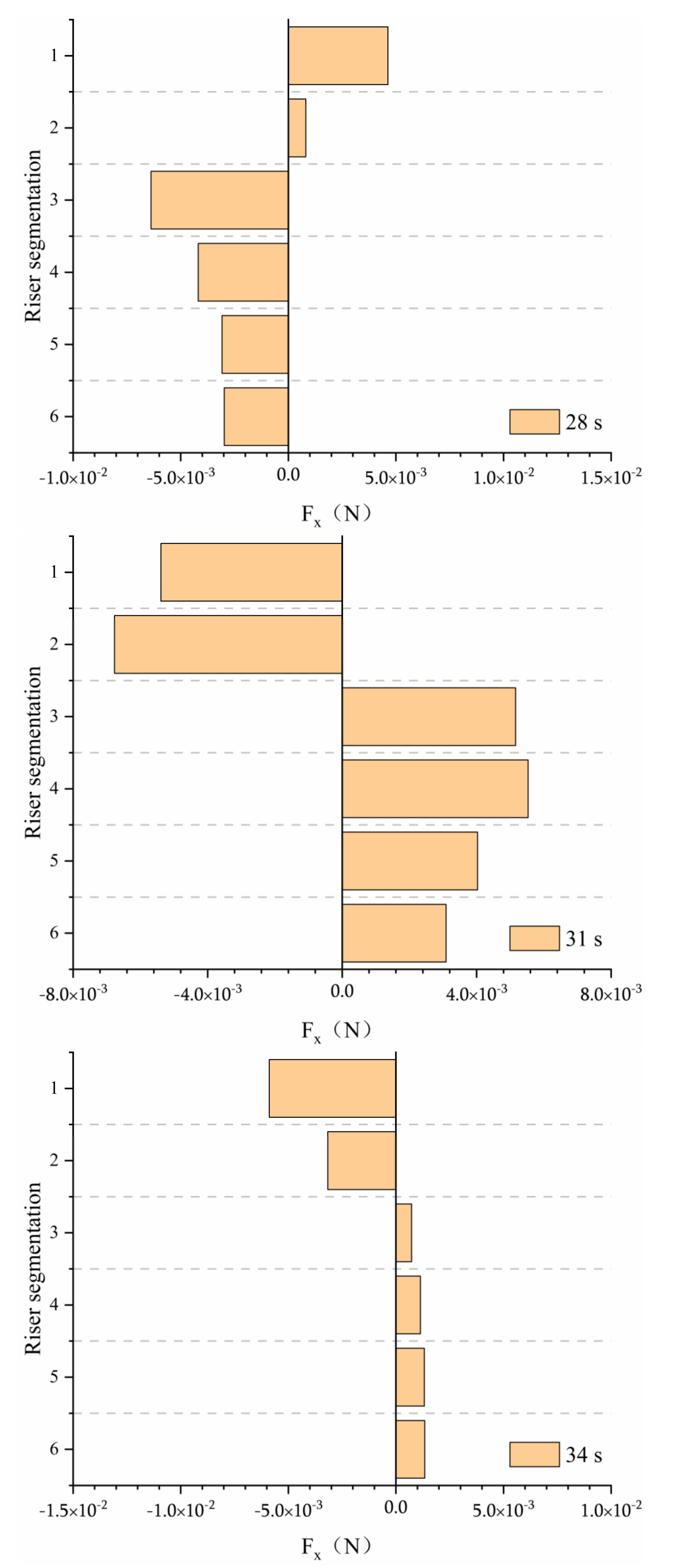
- The force on the riser in the horizontal and vertical directions is more significant than that in the z direction, and the sectional force on the riser in the upper fluid area is greater. Overall, with the continuous reduction in the difference in amplitude, the stress direction, extreme value, and occurrence time of the extreme value in the horizontal and vertical directions will change. The overall force of the riser under the joint action of two waves is less than that under the condition of a single wave, and when the amplitude difference of waves on both sides is large, the riser will be subjected to an additional section of X negative force with small amplitude after being subjected to X positive force;
- As the amplitude difference between the two sides decreases, the amplitude and time of the positive X force on the riser decreases; the X negative force first increases and then decreases, and the duration of the negative force increases. The horizontal force of the riser section changes before and after the collision and separation of two waves. At the same time, the force amplitude of the riser section is affected by the amplitude difference. When a stable single wave is generated in the flow field, the amplitude difference on both sides has a negative correlation with the horizontal force of the riser section; Before and after single wave fusion and separation, the amplitude difference between the two sides is positively correlated with the horizontal force of the riser section.
5. Conclusions
6. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aguilar, D.A.; Sutherland, B.R.; Muraki, D.J. Laboratory generation of internal waves from sinusoidal topography. Deep Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 96–115. [Google Scholar] [CrossRef]
- Ramp, S.R.; Tang, T.Y.; Duda, T.F.; Lynch, J.F.; Liu, A.K.; Chiu, C.S.; Yang, Y.J. Internal solitons in the northeastern South China Sea—Part I: Sources and deep water propagation. IEEE J. Ocean. Eng. 2004, 29, 1157–1181. [Google Scholar] [CrossRef]
- Lam, F.-P.A.; Maas, L.R.M. Internal wave focusing revisited; a reanalysis and new theoretical links. Fluid Dyn. Res. 2008, 40, 95–122. [Google Scholar] [CrossRef]
- Petrusevich, V.Y.; Dmitrenko, I.A.; Kozlov, I.E.; Kirillov, S.A.; Kuzyk, Z.Z.A.; Komarov, A.S.; Ehn, J.K. Tidally-generated internal waves in Southeast Hudson Bay. Cont. Shelf Res. 2018, 167, 65–76. [Google Scholar] [CrossRef]
- Rayson, M.D.; Ivey, G.N.; Jones, N.L.; Fringer, O.B. Resolving high-frequency internal waves generated at an isolated coral atoll using an unstructured grid ocean model. Ocean Model. 2018, 122, 67–84. [Google Scholar] [CrossRef]
- Held, P.; Schrottke, K.; Bartholomä, A. Generation and evolution of high-frequency internal waves in the Ems estuary, Germany. J. Sea Res. 2013, 78, 25–35. [Google Scholar] [CrossRef]
- Álvarez, Ó.; Izquierdo, A.; González, C.J.; Bruno, M.; Mañanes, R. Some considerations about non-hydrostatic vs. hydrostatic simulation of short-period internal waves. A case study: The Strait of Gibraltar. Cont. Shelf Res. 2019, 181, 174–186. [Google Scholar] [CrossRef]
- Jensen, T.G.; Magalhães, J.; Wijesekera, H.W.; Buijsman, M.; Helber, R.; Richman, J. Numerical modelling of tidally generated internal wave radiation from the Andaman Sea into the Bay of Bengal. Deep Sea Res. Part II Top. Stud. Oceanogr. 2020, 172, 104710. [Google Scholar] [CrossRef]
- Marchenko, A.V.; Morozov, E.G.; Kozlov, I.E.; Frey, D.I. High-amplitude internal waves southeast of Spitsbergen. Cont. Shelf Res. 2021, 227, 104523. [Google Scholar] [CrossRef]
- Sato, M.; Klymak, J.M.; Kunze, E.; Dewey, R.; Dower, J.F. Turbulence and internal waves in Patricia Bay, Saanich Inlet, British Columbia. Cont. Shelf Res. 2014, 85, 153–167. [Google Scholar] [CrossRef]
- Davies, A.M.; Xing, J. Modelling processes influencing wind-induced internal wave generation and propagation. Cont. Shelf Res. 2004, 24, 2245–2271. [Google Scholar] [CrossRef]
- Carter, G.S.; Gregg, M.C.; Lien, R.-C. Internal waves, solitary-like waves, and mixing on the Monterey Bay shelf. Cont. Shelf Res. 2005, 25, 1499–1520. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Smith, G.B.; Bowles, J.H.; Rhea, W.J. Infrared imagery of ‘breaking’ internal waves. Cont. Shelf Res. 2008, 28, 485–490. [Google Scholar] [CrossRef]
- Posada-Bedoya, A.; Gómez-Giraldo, A.; Román-Botero, R. Decoupled basin-scale internal waves in a continuously stratified two-basin tropical Andean reservoir. Limnologica 2021, 93, 125931. [Google Scholar] [CrossRef]
- Wang, B.-J.; Redekopp, L.G. Long internal waves in shear flows: Topographic resonance and wave-induced global instability. Dyn. Atmos. Ocean. 2001, 33, 263–302. [Google Scholar] [CrossRef]
- Chioua, J.; Bruno, M.; Vázquez, A.; Reyes, M.; Gomiz, J.J.; Mañanes, R.; Álvarez, O.; González, C.; López, L.; Gómez-Enri, J. Internal waves in the Strait of Gibraltar and their role in the vertical mixing processes within the Bay of Algeciras. Estuar. Coast. Shelf Sci. 2013, 126, 70–86. [Google Scholar] [CrossRef] [Green Version]
- Lamb, K.G.; Lien, R.-C.; Diamessis, P.J. Internal Solitary Waves and Mixing. In Encyclopedia of Ocean Sciences, 3rd ed.; Cochran, J.K., Bokuniewicz, H.J., Yager, P.L., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 533–541. [Google Scholar]
- Boegman, L. Currents in Stratified Water Bodies: Internal Waves. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Bodnár, T.; Fraunié, P. Numerical simulation of three-dimensional lee waves behind an isolated hill. Appl. Math. Model. 2020, 78, 648–664. [Google Scholar] [CrossRef]
- Liu, G.J.; Li, H.Y.; Qiu, Z.Z.; Leng, D.X.; Li, Z.X.; Li, W.H. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Eng. 2020, 195, 17. [Google Scholar] [CrossRef]
- Zan, X.X.; Lin, Z.H. On the applicability of Morison equation to force estimation induced by internal solitary wave on circular cylinder. Ocean Eng. 2020, 198, 6. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.L.; Zhu, H.; Tang, H.W.; Wei, G. A Numerical Study of the Forces on Two Tandem Cylinders Exerted by Internal Solitary Waves. Math. Probl. Eng. 2016, 2016, 15. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.H.; Hwang, R.R.; Hsieh, C.M. Numerical study on the transformation of an internal solitary wave propagating across a vertical cylinder. Appl. Ocean Res. 2020, 95, 19. [Google Scholar] [CrossRef]
- Lu, H.; Xie, J.; Xu, J.; Chen, Z.; Liu, T.; Cai, S. Force and torque exerted by internal solitary waves in background parabolic current on cylindrical tendon leg by numerical simulation. Ocean Eng. 2016, 114, 250–258. [Google Scholar] [CrossRef]
- Gong, Y.; Song, H.; Zhao, Z.; Guan, Y.; Kuang, Y. On the vertical structure of internal solitary waves in the northeastern South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2021, 173, 103550. [Google Scholar] [CrossRef]
- Xie, H.; Xiong, X.; Chen, L. Calculation of the Maximal Force Exerted by Internal Solitary Waves on Piles in Slope Area of the Northern South China Sea. Adv. Mar. Sci. 2019, 37, 171–186. [Google Scholar]
- Hu, Y.; Zou l Xinyu, M.; Sun, Z.; Wang, A.; Sun, T. Numerical Simulation for the Evolution of Internal Solitary Waves Propagating over Slope Topography. J. Mar. Sci. Eng. 2021, 9, 1224. [Google Scholar] [CrossRef]
- Nakayama, K.; Sato, T.; Shimizu, K.; Boegman, L. Classification of internal solitary wave breaking over a slope. Phys. Rev. Fluids 2019, 4, 014801. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Chen, Z.; Xie, J.; Deng, X.; Lv, H. The effect of a seasonal stratification variation on the load exerted by internal solitary waves on a cylindrical pile. Acta Oceanol. Sin. 2014, 33, 21–26. [Google Scholar] [CrossRef]
- Ding, W.; Ai, C.; Jin, S.; Lin, J. Numerical investigation of an internal solitary wave interaction with horizontal cylinders. Ocean Eng. 2020, 208, 107430. [Google Scholar] [CrossRef]
- Jiang, C.; Liu, X.; Yao, Y.; Deng, B. Numerical investigation of solitary wave interaction with a row of vertical slotted piles on a sloping beach. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 530–541. [Google Scholar] [CrossRef]
- Wang, F.; Sun, R.; Wang, C.; Fu, Q.; Li, P.; Guo, H. Experimental study on flow field induced by internal solitary wave and load characteristics on pile sections at different depth. Ocean Eng. 2019, 188, 106292. [Google Scholar] [CrossRef]
- Canpolat, C.; Sahin, B. Influence of single rectangular groove on the flow past a circular cylinder. Int. J. Heat Fluid Flow 2017, 64, 79–88. [Google Scholar] [CrossRef]
- Canpolat, C. Characteristics of flow past a circular cylinder with a rectangular groove. Flow Meas. Instrum. 2015, 45, 233–246. [Google Scholar] [CrossRef]
- Huang, W.; You, Y.; Wang, X.; Hu, T. Internal solitary wave loads experiments and its theoretical model for a cylindrical structure. Chin. J. Theor. Appl. Mech. 2013, 45, 716–728. [Google Scholar]
- Wang, X.; Zhou, J.-F.; Wang, Z.; You, Y.-X. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean Eng. 2018, 150, 298–308. [Google Scholar] [CrossRef]
- Song, Z.J.; Teng, B.; Gou, Y.; Lu, L.; Shi, Z.M.; Xiao, Y.; Qu, Y. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses. Appl. Ocean Res. 2011, 33, 120–129. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, J.; Jia, H.; Gu, B. A numerical model for Internal wave popagation in continuously stratified ocean. Chin. J. Theor. Appl. Mech. 2012, 44, 896–903. [Google Scholar]
- Tian, Z.; Jia, Y.; Du, Q.; Zhang, S.; Guo, X.; Tian, W.; Zhang, M.; Song, L. Shearing stress of shoaling internal solitary waves over the slope. Ocean Eng. 2021, 241, 110046. [Google Scholar] [CrossRef]
- Wang, L.L.; Xu, J.; Wang, Y.; Wei, G.; Lin, C.; Zhu, H. Reduction of internal-solitary-wave-induced forces on a circular cylinder with a splitter plate. J. Fluids Struct. 2018, 83, 119–132. [Google Scholar] [CrossRef]
- Zhi, C.; Wang, H.; Chen, K.; You, Y. Theoretical and experimental investigation on strongly nonlinear internal solitary waves moving over slope-shelf topography. Ocean Eng. 2021, 223, 108645. [Google Scholar] [CrossRef]
- Zou, P.X.; Bricker, J.D.; Uijttewaal, W.S.J. The impacts of internal solitary waves on a submerged floating tunnel. Ocean Eng. 2021, 238, 109762. [Google Scholar] [CrossRef]
- Zou, L.; Yu, Y.; Sun, Z.; Zhang, J.M.; Li, Z.H.; Yu, Z.B.; Destech Publications, Inc. CFD Simulation of Internal Solitary Wave Using the Volume-of-fluid Method within OpenFOAM. In International Conference on Mathematics Modelling and Simulation Technologies and Applications; Destech Publications, Inc.: Lancaster, PA, USA, 2017; Volume 215, pp. 53–58. [Google Scholar]
- Wang, F.; Xiao, W.; Yao, Y.; Liu, Q.; Li, C. An Analytical Procedure to Predict Transverse Vibration Response of Jack-Up Riser under the Random Wave Load. Shock Vib. 2020, 2020, 5072989. [Google Scholar] [CrossRef]
- Chang, S.B.; Chun, W.D.; Jeongsun, J.E.E.; Park, W.-G. Subchannelflow in 2×2 Rrod bundle with using STAR-CCM+ commercal CODESTAR-CCM+. Korean Soc. Comput. Fluids Eng. 2018, 23, 45–51. [Google Scholar] [CrossRef]
- Al-Zoubi, A.; Beilke, R.; Korchagova, V.N.; Kraposhin, M.V.; Strizhak, S.V. Comparison of the Performance of Open-Source and Commercial CFD Packages for Simulating Supersonic Compressible Jet Flows. In Proceedings of the 2018 Ivannikov Memorial Workshop (IVMEM 2018), Yerevan, Armenia, 3–4 May 2018. [Google Scholar]
- Wang, T.; Wang, H.; Tang, G. Benchmarking the Star-CCM plus Compressible Flow Solver by Simulating Typical Compressible Flow Problems: A Case Study and Comparison. In Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems, Pt III; Springer: Singapore, 2016. [Google Scholar]
- Lin, P.Z.; Liu, P.L.F. Internal wave-maker for Navier-Stokes equations models. J. Waterw. Port Coast. Ocean Eng. Asce 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Sheng, L.; Wang, Y.; You, Y.; Zhang, X. Investigation on propagation and evolution models for internal solitary waves in a two layer fluid system of finite depth. Chin. J. Hydrodynomics 2016, 31, 659–672. [Google Scholar]
- Cui, J.; Dong, S.; Wang, Z. Study on applicability of internal solitary wave theories by theoretical and numerical method. Appl. Ocean. Res. 2021, 111, 102629. [Google Scholar] [CrossRef]
- Rodi, W. Experience with two-layer models combining the k-epsilon model with a one-equation model near the wall. In Proceedings of the 29th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. [Google Scholar]
- Choi, W.; Camassa, R. Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 1999, 396, 1–36. [Google Scholar] [CrossRef]
- Wang, F.; Guo, H.-Y.; Li, X.-M.; Meng, F.-S. Experimental Study on Ocean Internal Wave Force on Vertical Cylinders in Different Depths. China Ocean Eng. 2016, 30, 459–468. [Google Scholar] [CrossRef]

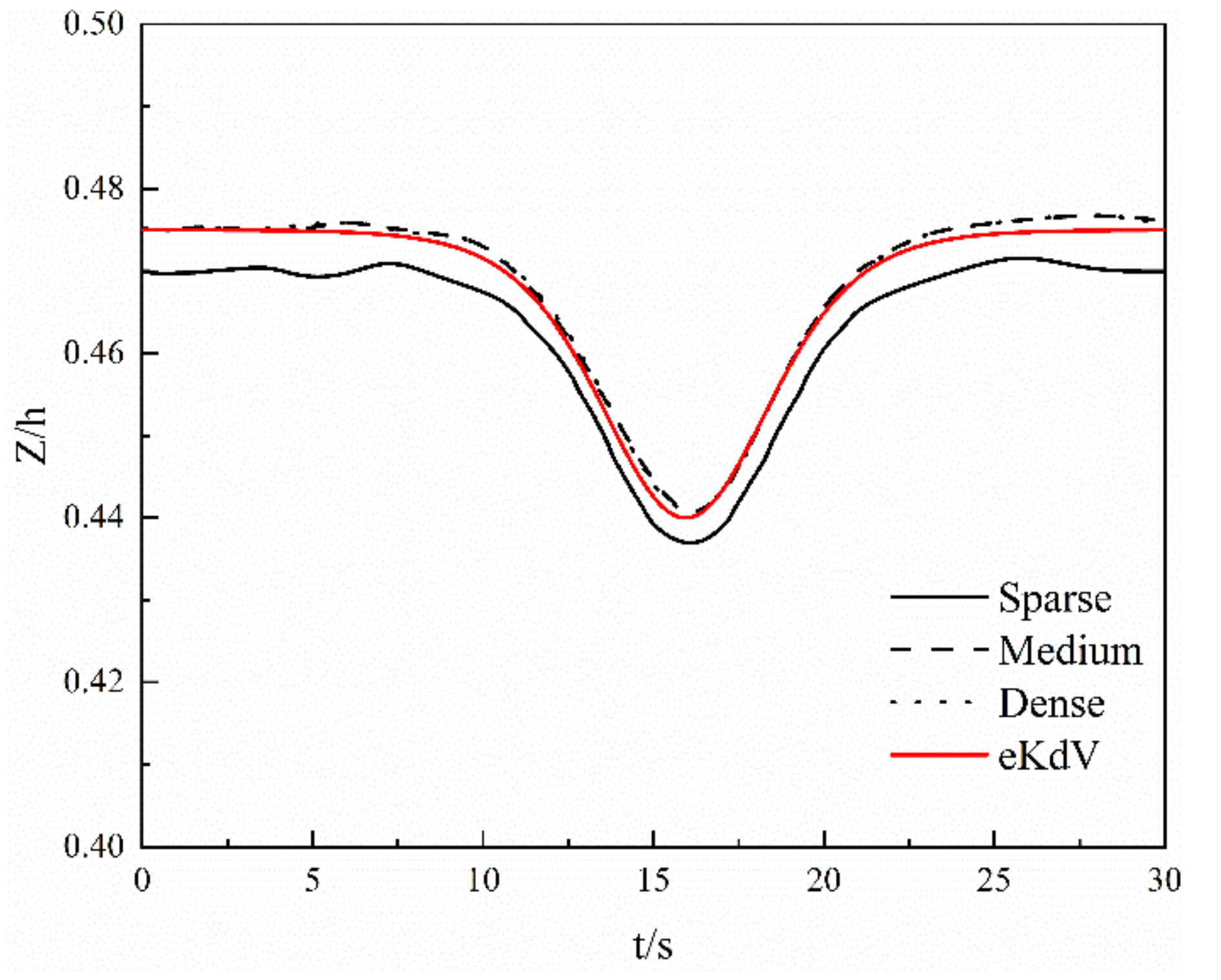

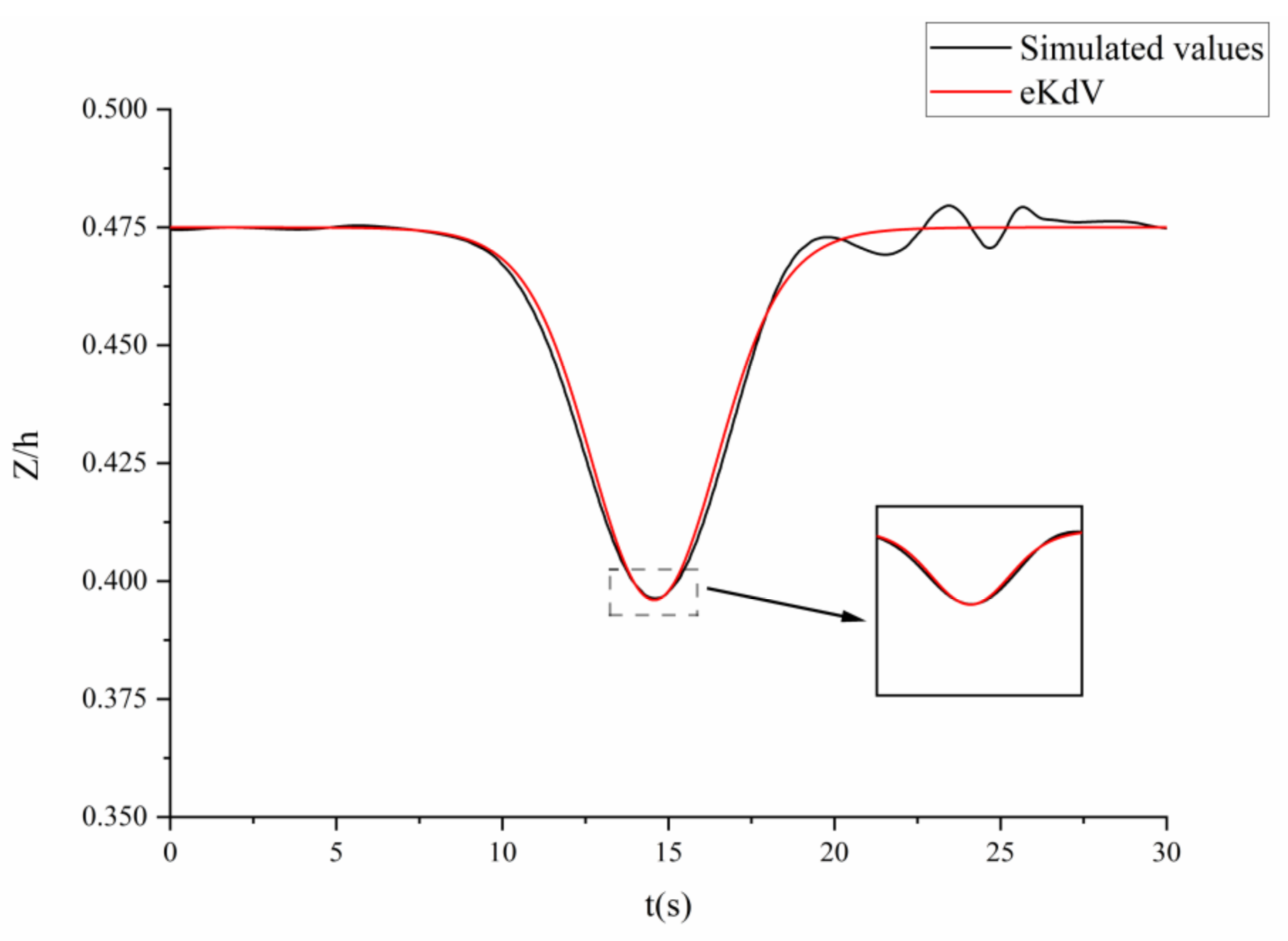


| Mesh | Δx (m) | Δy (m) | Δz (m) | N |
|---|---|---|---|---|
| Sparse | 0.0075 | 0.01 | 0.0075 | 1,019,752 |
| Medium | 0.005 | 0.01 | 0.005 | 3,171,556 |
| Dense | 0.0025 | 0.01 | 0.005 | 6,109,244 |
| Working Condition | Left Amplitude, η0 (cm) | Right Amplitude, η0 (cm) |
|---|---|---|
| 1 | 7.9 | None |
| 2 | 7.9 | 3.2 |
| 3 | 7.9 | 4.2 |
| 4 | 7.9 | 5.5 |
| 5 | 7.9 | 6.5 |
| 6 | 7.9 | 7.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Wang, F.; Lin, J.; Li, D. Numerical Simulation of the Force Acting on the Riser by Two Internal Solitary Waves. Appl. Sci. 2022, 12, 4873. https://doi.org/10.3390/app12104873
Yu W, Wang F, Lin J, Li D. Numerical Simulation of the Force Acting on the Riser by Two Internal Solitary Waves. Applied Sciences. 2022; 12(10):4873. https://doi.org/10.3390/app12104873
Chicago/Turabian StyleYu, Wen, Fenggang Wang, Jianguo Lin, and Dong Li. 2022. "Numerical Simulation of the Force Acting on the Riser by Two Internal Solitary Waves" Applied Sciences 12, no. 10: 4873. https://doi.org/10.3390/app12104873
APA StyleYu, W., Wang, F., Lin, J., & Li, D. (2022). Numerical Simulation of the Force Acting on the Riser by Two Internal Solitary Waves. Applied Sciences, 12(10), 4873. https://doi.org/10.3390/app12104873






