1. Introduction
Road tunnels, as part of an infrastructure system, are extremely important for the transport of goods and people. To provide the social and economic benefits for which a tunnel is designed and built, it should be kept open to traffic as much as possible. However, the functionality of a road tunnel might be temporarily compromised by a traffic accident or fire occurring within the structure. The consequent non-availability for the passage of traffic flow through the tunnel, which can be caused by the aforementioned incidental event, might also require a great deal of time and effort to normalize the situation. Therefore, the recovery process of the operating conditions of the road tunnel after a disruption of traffic flow, as well as the possible presence of alternative itineraries in the nearby road network, is nowadays becoming a crucial issue for community interests at different levels.
Road tunnels, and more commonly a transportation network containing them, that show an adaptive response to a disruptive event are generally described as resilient. However, it is worth pointing out how there is not a shared concept of resilience in different research disciplines, and consequently various definitions can be found in current literature. With specific reference to the case of a transportation system, resilience might, for example, be defined as reported in Freckleton et al. [
1]: “
the ability of the system to maintain its demonstrated level of service or to restore itself to that level of service in a
specified timeframe”. Resilience, however, should not be confused with the vulnerability of a transportation system that, instead, represents its susceptibility to a given event without considering the recovery process.
Resilience analyses involve the use of certain specific metrics. Since the resilience of a transportation infrastructure is more especially related to its functionality, traffic-related resilience metrics expressed in terms of traffic flow properties should be used. In this respect, a discussion on some available metrics in the field of transportation networks can be found, for example, in Faturechi and Miller-Hooks [
2], and Sun et al. [
3]. However, given that the disruption of functionality of the transportation system caused by an event (e.g., a collision or fire in a tunnel) might significantly increase the travel time of vehicles, the delay time (i.e., the excess time in the transportation facility) can be an appropriate traffic parameter related to resilience. The congestion index due to an event (i.e., the ratio of delay time to acceptable travel time) can also be a measure related to resilience.
Resilience may also be treated in terms of the adaptive or restorative capacity. The adaptive capacity is the ability of the transportation system to gradually adapt itself to a disruption. For example, in the case of a twin-tube road tunnel, if a disruption leads to the functionality loss of a one-way tube having two or more lanes, the transportation infrastructure may still recover the functionality by using the remaining undisrupted lane, or in the event of the complete closure of the tube by reorganizing the traffic flow using the adjacent tube for bi-directional traffic (adaptive capacity). If the tunnel operating team restores the disrupted one-way tunnel tube by means of specific activities, this corresponds to the restorative capacity. In addition, the availability of an alternative itinerary in the nearby road network, which might be used when the aforementioned one-way tube is completely blocked due to an incident, may be helpful to represent the resilience of a transportation system (e.g., in terms of the travel time after the disruptive event and the following functionality recovery).
The resilience analysis of a transportation system can be conducted through qualitative or quantitative methods. The former approach provides only a descriptive assessment of the resilience of an infrastructure (e.g., low, medium, and high resilience). Therefore, it does not appear to be suitable for computing the resilience of more complex systems such as a transportation network. On the contrary, quantitative methods are more appropriate. Quantitative resilience analyses are often carried out by using analytical or simulation models. However, traffic simulation models, by identifying the vulnerable components of a transport system and comparing different scenarios, appear to be better since they may represent a more useful tool for supporting the decisions made by road and/or tunnel management agencies.
There are various studies, which by using traffic simulation models, have investigated the resilience of a transportation network from different perspectives. However, as far as the authors of the present paper are aware, the resilience of road tunnels, as a part of a transportation network, has been scarcely studied. In particular, it has not been sufficiently investigated in relation to different possible strategies for containing the delay time, after the occurrence of a traffic accident or fire in a tunnel and its following functionality recovery. This represents a gap of knowledge that the present paper will attempt to fill.
Given the limited body of research dedicated to road tunnel resilience, the goal of our paper is: (i) to perform a traffic macro-simulation model to investigate the issue in greater detail; (ii) to identify a more appropriate strategy for containing the delay time in order to improve tunnel resilience. In this respect, an existing twin-tube motorway tunnel has been investigated.
In the light of the above considerations, it is to be stressed that the paper is primary concerned with delay time-resilience relations during an incidental event occurring in a tube of a twin-tube motorway tunnel. Its scope is to describe the concept of resilience for road tunnels and to give additional points of view on certain relevant aspects, as well as to recommend more appropriate recovery strategies in order to improve the tunnel resilience, which is based on the methodology developed and the knowledge of findings achieved. In addition, it allows to collect further information on this topic for the management of the tunnel as a system.
The manuscript is organized as follows: the next section contains a literature review concerning studies on the resilience of transportation networks. Then, a traffic simulation model is developed and implemented. Subsequently, the results are presented and discussed by comparing different scenarios, and a proposal is presented to improve the resilience of the tunnel investigated. Finally, comments for practical applications, conclusions, and further developments of the research are made.
2. Literature Review
Over the last few years, several studies have been carried out to evaluate the resilience of a transportation network.
Knoop et al. [
4], for example, by using traffic flow simulation models, investigated the robustness of a road network (i.e., the ability to deal with variations in traffic demand without excessive increases in travel times) in the event of closure of a link. A morning peak period, and four different scenarios, were simulated and the delay time was chosen as the main performance indicator. The authors found that to accurately assess the robustness of a network due to a disruptive event, the spillback phenomenon (i.e., congestion propagation to upstream links) should be also modeled. This study also showed the positive influence of information that makes drivers adapt their routes, as well as the major reduction of network performance when a motorway is blocked.
Omer et al. [
5] proposed a framework to assess the resilience of a road network connecting Manhattan to other regions after hypothetical disruptions involving the reduction of the link capacities. The resilience metric used in this study was related to the ratio of total network travel time before and after the disruption. They concluded that a vulnerability reduction may be obtained by means of the re-routing of traffic to other links of the network, and that the adaptive capacity might be improved through using parallel systems such as ferries.
Constantinos et al. [
6] proposed a framework to develop accident scenarios and traffic re-routing strategies based on the use of variable message signs (VMS). The analysis was carried out during a morning peak period, and the travel time was chosen as the main performance indicator. The findings of the case study indicated that predictive VMS is effective in diverting significant numbers of vehicles along routes, with a consequent reduction in delays.
Freckleton et al. [
7], after having reported certain definitions of resilience applied in different fields of research (i.e., engineering, psychology, sociology, and economics), proposed a methodology that when applied showed how specific weaknesses may be identified within a transportation network. According to these authors, the methodology might provide the means to prioritize transportation infrastructure projects in order to increase network resilience.
Liao et al. [
8], by means of simulation techniques, investigated the effectiveness of different management strategies in order to alleviate traffic congestion in the case of a possible traffic accident occurring within a specified tunnel. These strategies included: access control (ramp metering), lane control (shoulder lane is open to increase capacity), route guidance via VMS. The results showed that the ramp control provided the best benefits in terms of the reduction of queue length. Alternative itineraries were found to be characterized by considerable travel time.
Faturechi and Miller-Hooks [
2] provided a literature review concerning the transportation system performance metrics in the case of potential disastrous events. The studies are identified and grouped from different perspectives.
Reggiani et al. [
9] focused on the concept of resilience and vulnerability in transportation studies. They underlined the importance of the linkage between these concepts and the connectivity in transportation networks.
D’Lima and Medda [
10] proposed a measure of resilience based on the concept that a system is more or less resilient depending on the speed (i.e., rapidity) with which the system recovers from a disruptive event.
Kaviani et al. [
11] presented an approach to find the optimal location along a regional road network of road guidance devices useful for diverting traffic following a disruptive event such as a natural disaster. The results showed that communicating road closures through guidance devices (e.g., VMS or ITS) decreases the travel time (i.e., increases resilience) of the network.
Sun et al. [
3] provided a literature review of different metrics for the resilience assessment. Discussions concerning uncertainties, interdependencies, and validations due to a general scarcity of data are also made. Additionally, they stressed that the functionality of the transportation system can be improved by increasing the network connectivity (e.g., a greater number of interconnections between two nodes means a higher redundancy of the transportation network).
Amini et al. [
12] proposed a methodology able to demonstrate the effectiveness of re-routing as a real-time traffic management measure on the resilience of an urban road network when a link is closed due to an incident. They found that when 15% of the vehicles are re-routed, gridlock is avoided, thus enhancing the resilience of the network.
Xu et al. [
13] dealt with transportation network redundancy, which is another important concept in characterizing resilience. In particular, they introduced two measures (i.e., travel alternative diversity, and network spare capacity) to characterize the redundancy of a transportation system in the case of a disruptive event, such as an earthquake or a severe traffic accident. By performing two numerical examples, the authors demonstrated the necessity both of introducing new routes and increasing the capacity of existing links to improve network redundancy.
Sohouenou and Neves [
14] focused both on the ability of a network to sustain the consequences of a disruption (i.e., resistance) and quickly recover its performance (i.e., rapidity). By modeling both these concepts to characterize the resilience and to identify an optimal choice, they showed for a specific case how some recovery strategies can reduce the disruption consequences.
Abudayyeh et al. [
15] developed a method to optimize traffic signal settings in an urban road network in order to improve the resilience during the occurrence of disruptive events. Several blockage scenarios involving various combinations of capacity reduction and duration of the blockage were simulated. The optimization of the traffic signals was found to minimize both network travel time and carbon dioxide emissions.
Khetwal et al. [
16] developed a stochastic simulation model in order to quantitatively assess the functionality loss and resilience of a tunnel subjected to random events (e.g., traffic accidents or fires) or planned events (e.g., operation and maintenance of the tunnel). A functionality metric dependent on traffic capacity loss and its duration was used.
Zhao [
17] set up a genetic algorithm for optimizing a highway network after a natural disaster or accident that led to the failure of a certain number of road sections. The resilience metrics used were expressed in terms of both the shortest time for road repair and the least loss of road network performance. The functionality of the road network was assumed to be restored by means of external recovery measures, such as the intervention of engineering repair teams.
Bindzaret et al. [
18] evaluated the functional changes in the organization of a transportation network concerning the transition to one-way roads vs two-way traffic.
PIARC [
19] reported the state-of-the-art on road tunnel resilience with applications of some case studies.
The above chronological literature review, even if it is not exhaustive due to a great number of studies on resilience in different disciplines of research, is sufficient to show how many scientific articles focused prevalently on both different metrics to evaluate transportation network resilience and the concepts for its characterization in the event of disruptions. They also consider different recovery strategies. However, the resilience of road tunnels, as a part of a transportation network, appears to have been investigated to a lesser degree. Moreover, the aforementioned studies have been carried out in countries where the transportation infrastructure geometry, the traffic characteristics, and the driving behavior differ from those in Italy.
Therefore, given this lacuna, the contribution to research of our paper is to provide insights on certain relevant aspects of tunnel resilience and to disseminate further information on this topic for the management of road tunnels.
Traffic accidents occurring in Italian road tunnels have been prevalently studied in Caliendo and Guida [
20], and Caliendo et al. [
21,
22,
23,
24], while the consequences of fires in tunnels are investigated in Caliendo et al. [
25,
26,
27,
28,
29,
30,
31], Caliendo and De Guglielmo [
32,
33,
34,
35], and Caliendo and Genovese [
36]. Applications of traffic simulation models in order to assess the functionality of road infrastructures and/or intersections can also be found in Caliendo and Guida [
37], Caliendo and De Guglielmo [
38], Caliendo [
39], and Astarita et al. [
40]. However, it is to be pointed out how the cited Italian studies do not address the issue of resilience.
As a result, there are sufficient reasons to motivate our study that, by developing and calibrating a traffic simulation model to evaluate the delay time, intends to investigate the effectiveness of a set of recovery strategies to improve the resilience of twin-tube motorway tunnels in the case of a traffic accident or fire occurring within a tube.
3. Materials and Methods
3.1. Description of the Tunnel and the Corresponding Road Network
An existing twin-tube tunnel located along an Italian motorway was investigated. Each tube is characterized by two lanes and unidirectional traffic in ordinary conditions of functionality, and with a length of 850 m. It has a horseshoe-shaped cross-section of 55.2 m
2, with a maximum height of 6.8 m and a total width of 9.5 m (i.e., two lanes of 3.5 m, and two sidewalks). Each tube is straight, and flat without an emergency lane.
Figure 1 shows the cross-section of the investigated twin-tube motorway tunnel.
Figure 1 also indicates the occurrence of a disruptive event (i.e., a traffic crash or fire) within the tube which is characterized by the transit traffic towards the north direction (namely, the north tube).
The occurrence of an incident within the aforementioned tube was assumed to lead to different possible scenarios causing the partial or complete closure of the tube, with consequences (i.e., delay times) affecting the vehicular transit both on the motorway as well as on the nearby road network connected by means of the motorway junctions.
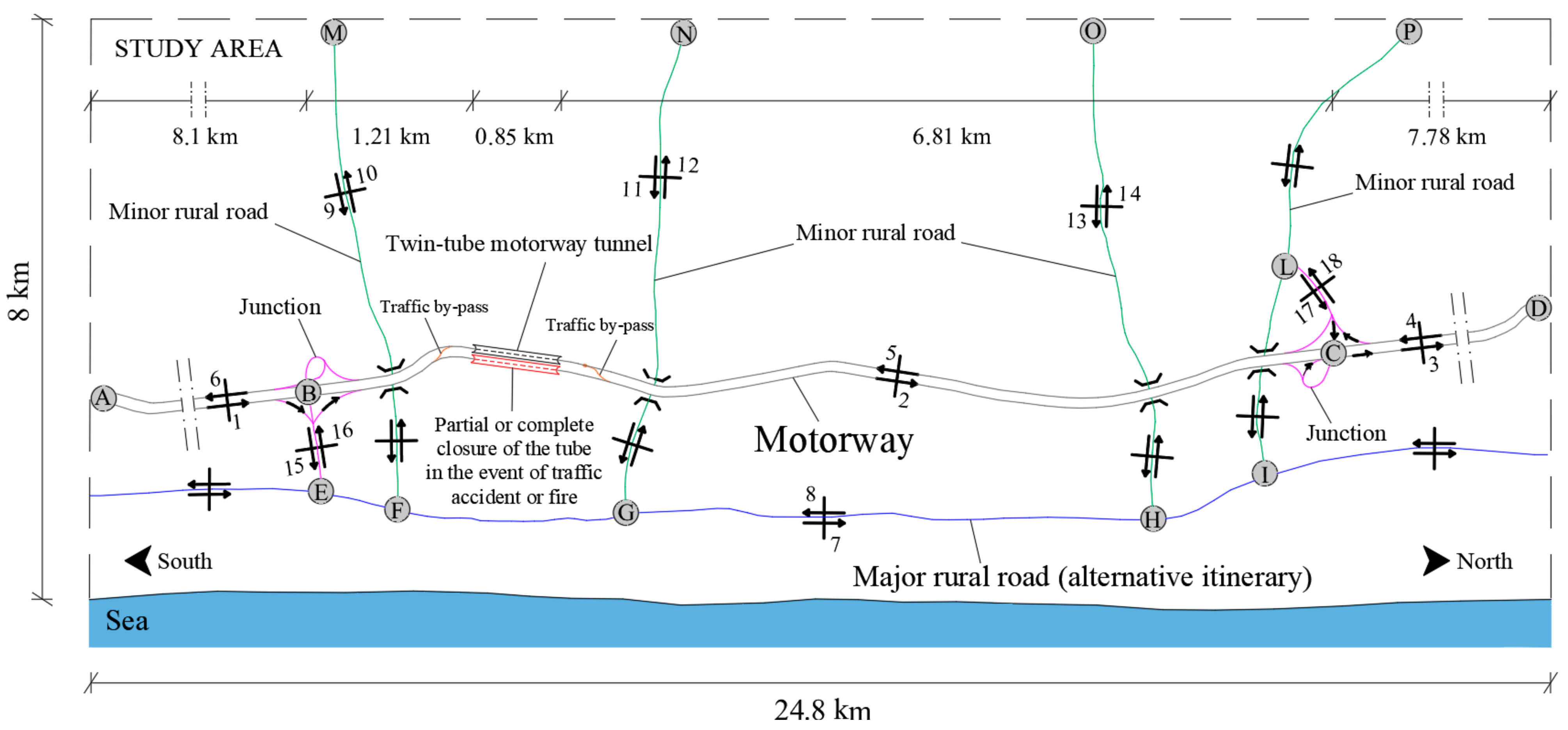
Several preliminary macro-simulations were performed in order to define an appropriate area of study (i.e., a portion of the road network within which the major effects on traffic due to an incident occurred in the mentioned tunnel tube might be confined). In this respect, we found that the consequences on traffic caused by the disruptive event affected an area of about 25 km long and 8 km wide, which is schematically represented in
Figure 2.
In particular,
Figure 2 shows: (i) the motorway section containing the investigated twin-tube tunnel; (ii) the tunnel tube that might be interested by a disruptive event (e.g., a crash or fire in the tube characterized in ordinary conditions by unidirectional traffic towards the north direction (i.e., from the Nodes A to D)); (iii) the undisruptive tube (i.e., the tube characterized in normal operating conditions by unidirectional traffic towards the south direction (i.e., from the Nodes D to A)); (iv) the major rural road, which is characterized by bi-directional traffic (i.e., E–I road section), that might be used due to the presence of the two motorway junctions (i.e., B and C) as an alternative itinerary in the case of the complete closure of the north tube of the tunnel (e.g., by using the links B–E and C–L–I); (v) several minor rural roads (i.e., F–M, G–N, H–O, I–L, and L–P) characterized by bi-directional traffic that are connected by means of certain intersections with the aforementioned major rural road (i.e., F, G, H, and I intersections); (vi) two traffic by-passes at the twin-tube tunnel portals that can be used in order to reorganize the traffic flow (e.g., by utilizing the adjacent tube for bi-directional traffic in the event of the complete closure of the other tube (i.e., the north tube in our case)); (vii) the sea that delimits the study area to the east.
3.2. Speed Limits
Table 1 reports the speed limits foreseen by the Italian Highway Code for both passenger cars and heavy goods vehicles (HGVs) for each type of road segment of the transportation network investigated.
3.3. Scenarios Investigated
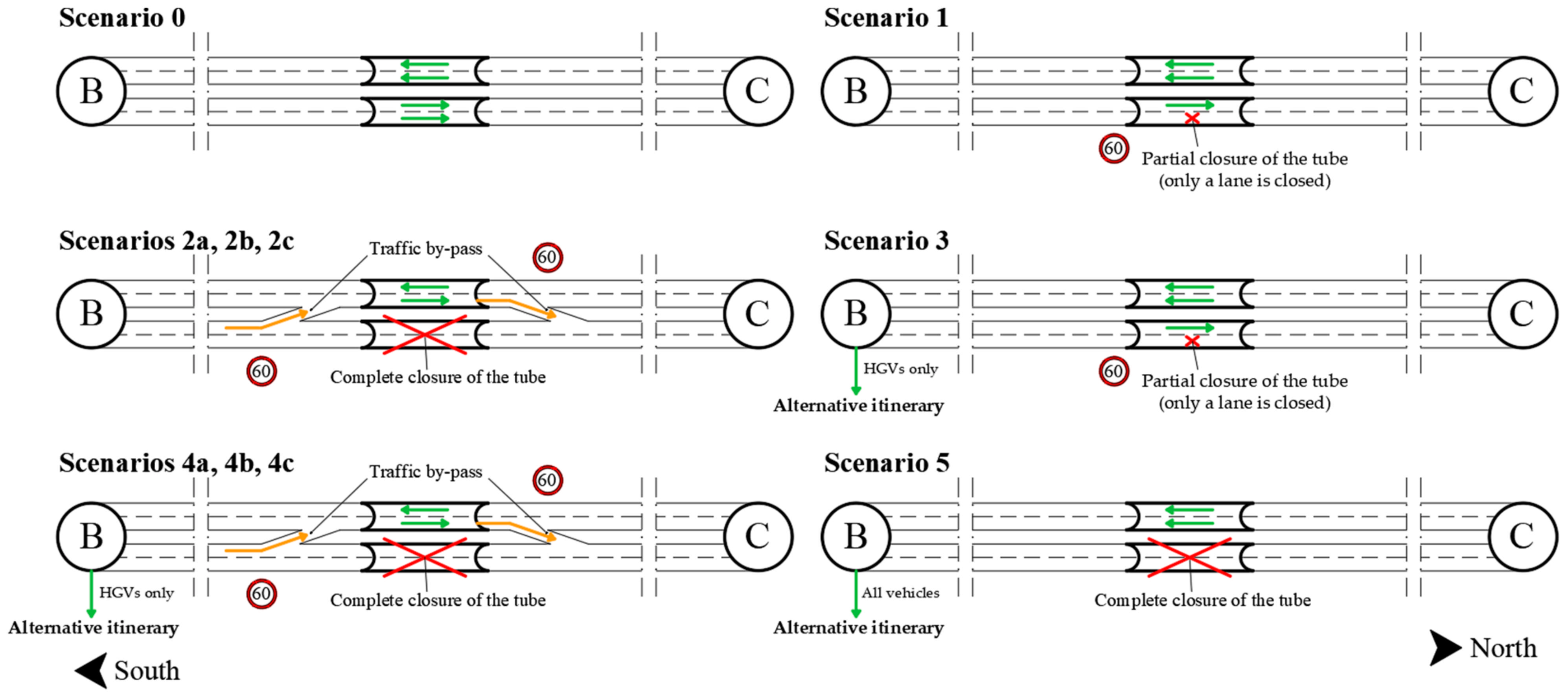
The disruptive event was assumed to be due to a traffic accident or fire occurring within the north tube (reported in red in
Figure 2). In order to investigate the worst effects on the traffic, the incidental event was assumed to occur at a peak hour in the morning (i.e., at the beginning of 7:00 a.m.). The duration of the partial or complete blockage of the mentioned north tube was assumed to be equal respectively to 1 h, 2 h, or 3 h (i.e., from 7:00 to 8:00 a.m., from 7:00 to 9:00 a.m., or from 7:00 to 10:00 a.m.).
Figure 3 shows the scenarios investigated: (i) Scenario 0 corresponds to the ordinary functionality of each tunnel tube without any disruptive event (i.e., unidirectional traffic transit on the two lanes of each tube, both for the north and south direction, respectively); (ii) Scenario 1 represents the partial closure of the tube interested by a traffic accident or fire (i.e., only one lane is closed, while the remaining lane continues to be used for unidirectional traffic towards the north direction), the speed limit imposed at the entrance portal is in this case equal to 60 km/h; (iii) Scenario 2 corresponds to the complete closure of the aforementioned north tube (i.e., both lanes are closed) with the reorganization of the traffic flow by using the adjacent tube for bi-directional traffic, in this respect different hypotheses were made about the intervention time of the emergency service team to open the two traffic by-passes at the tunnel portals from the start of the incidental event (i.e., 10 min (Scenario 2a), 20 min (Scenario 2b), and 30 min (Scenario 2c)), the speed limits imposed at the two portals are 60 km/h; (iv) Scenario 3 is similar to Scenario 1, however it also involves the use of the alternative itinerary for heavy goods vehicles (HGVs) only traveling on the motorway section towards the partially blocked north tube, in this scenario includes the activation of the variable message signs (VMS) located before the Motorway Junction B in order to suggest the alternative route to HGVs only; (v) Scenario 4 is similar to Scenario 2, however it also involves the use of the mentioned alternative itinerary for HGVs only (i.e., Scenarios 4a, 4b, and 4c) traveling on the motorway section towards the completely blocked north tube, obviously through the activation of the mentioned VMS; (vi) finally, Scenario 5 regards the complete closure of the north tube affected by the incidental event, in which the alternative itinerary is used by all the vehicles (i.e., both passenger cars and HGVs) of the motorway section traveling towards the completely blocked north tube.
3.4. Hourly Traffic Volume (VHP)
In keeping with the aforementioned analysis period of the scenarios investigated, we computed from the traffic database of road management agencies, the traffic flows expressed in terms of hourly volumes transiting through the cross-sections (i.e., traffic streams) both in terms of peak hours and off-peak hours in the morning for all the roads reported in
Figure 2 (i.e., motorway, motorway junctions, major and minor rural roads). However, for the two peak hours in the morning (i.e., 7:00–8:00 a.m., and 8:00–9:00 a.m.) we assumed approximately the same high hourly traffic volume, while the traffic flow in the off-peak hour (i.e., 9:00–10:00 a.m.) was found to be significantly less than that of the two mentioned peak hours.
Table 2 reports the results obtained.
The road management agencies also provided the percentage of heavy vehicles (i.e., HGVs and buses), which was about the same for the two peak hours and one off-peak hour, namely: 25% for the motorway, 2.5% for both the major and minor rural roads, and 20% for the motorway junctions.
The capacity per lane of each road segment was estimated according to the
Highway Capacity Manual [
41] by considering similar roads. In particular, the capacity of a single lane for the unidirectional traffic carriageway was assumed to be equal to 2400 vehicles/h (i.e., in our case each carriageway of the motorway under normal conditions of functionality), while the capacity per lane when a carriageway is used for bi-directional traffic (e.g., the carriageway of the adjacent tube when the other tube is completely closed, or the major and minor roads of
Figure 2) was assumed to be equal to 1600 vehicles/h. For the motorway junctions, given that we have unidirectional carriageways in proximity of the motorway that become bi-directional near the alternative route, we assumed an average traffic capacity per lane equal to 2000 vehicles/h.
3.5. Resilience Metrics
The functionality of both the motorway section containing the north tube investigated and the nearby road network (i.e., including the motorway section, the motorway junctions, the major and minor rural roads of
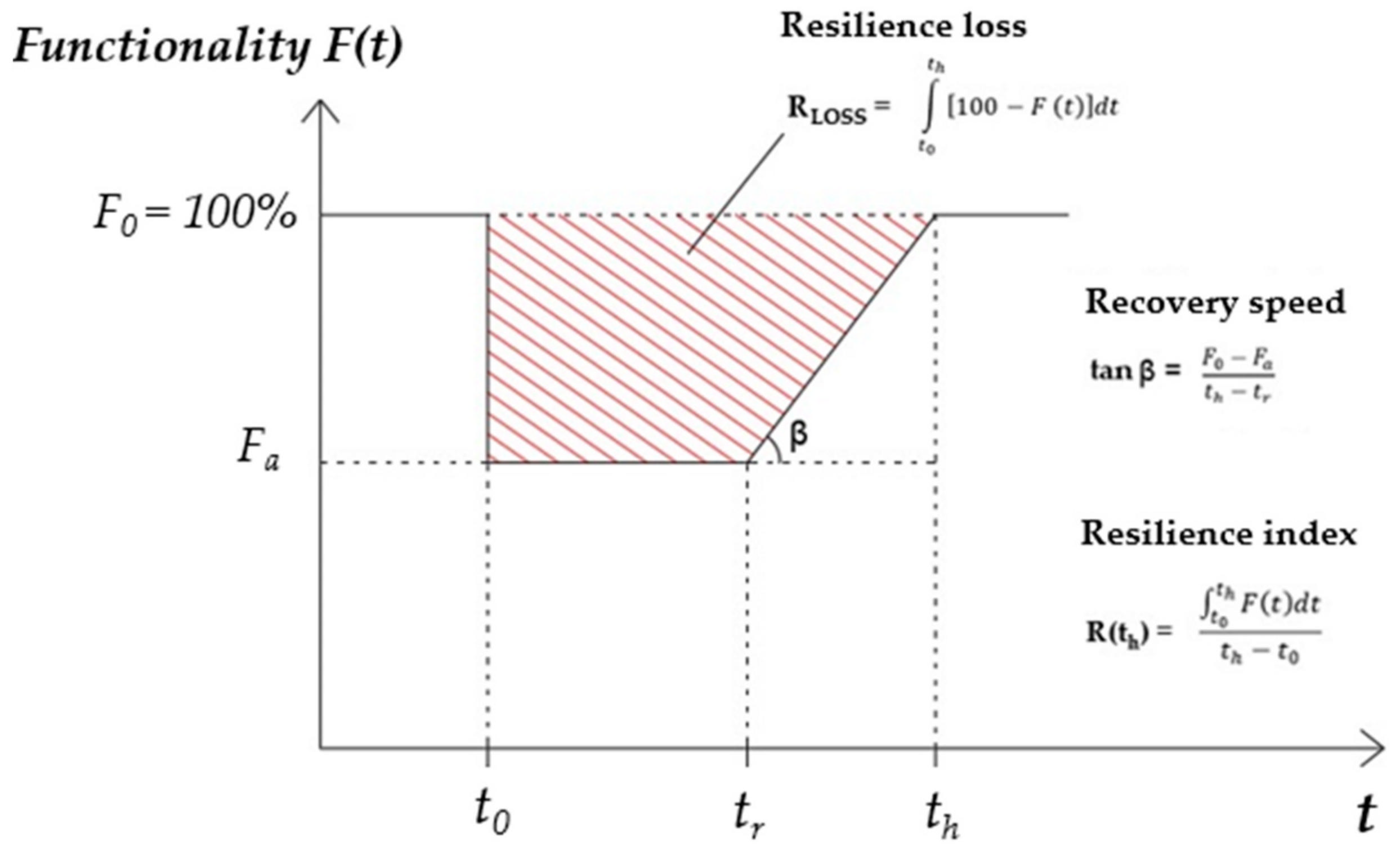
Figure 2) was expressed in terms of the delay time. The adopted resilience metrics are: (i) resilience loss; (ii) recovery speed; (iii) and resilience index. In this respect, we found in our case that the functionality recovery curve may be schematically represented by the geometric form of a resilience trapezoid (see the subsequent Paragraph 5.2.2. for more details). The resilience trapezoid schematically shown in
Figure 4 consists of four edges: the first edge showing 100% of the functionality level, the second edge representing the decrease of the functionality level at the time instant
t0 (i.e., when an incidental event occurs), the third edge showing the time during which the reduction of functionality remains constant (
tr–
t0), the fourth edge representing the recovery of functionality in the time (
th–
tr), and its corresponding slope is the recovery speed.
3.6. Research Framework
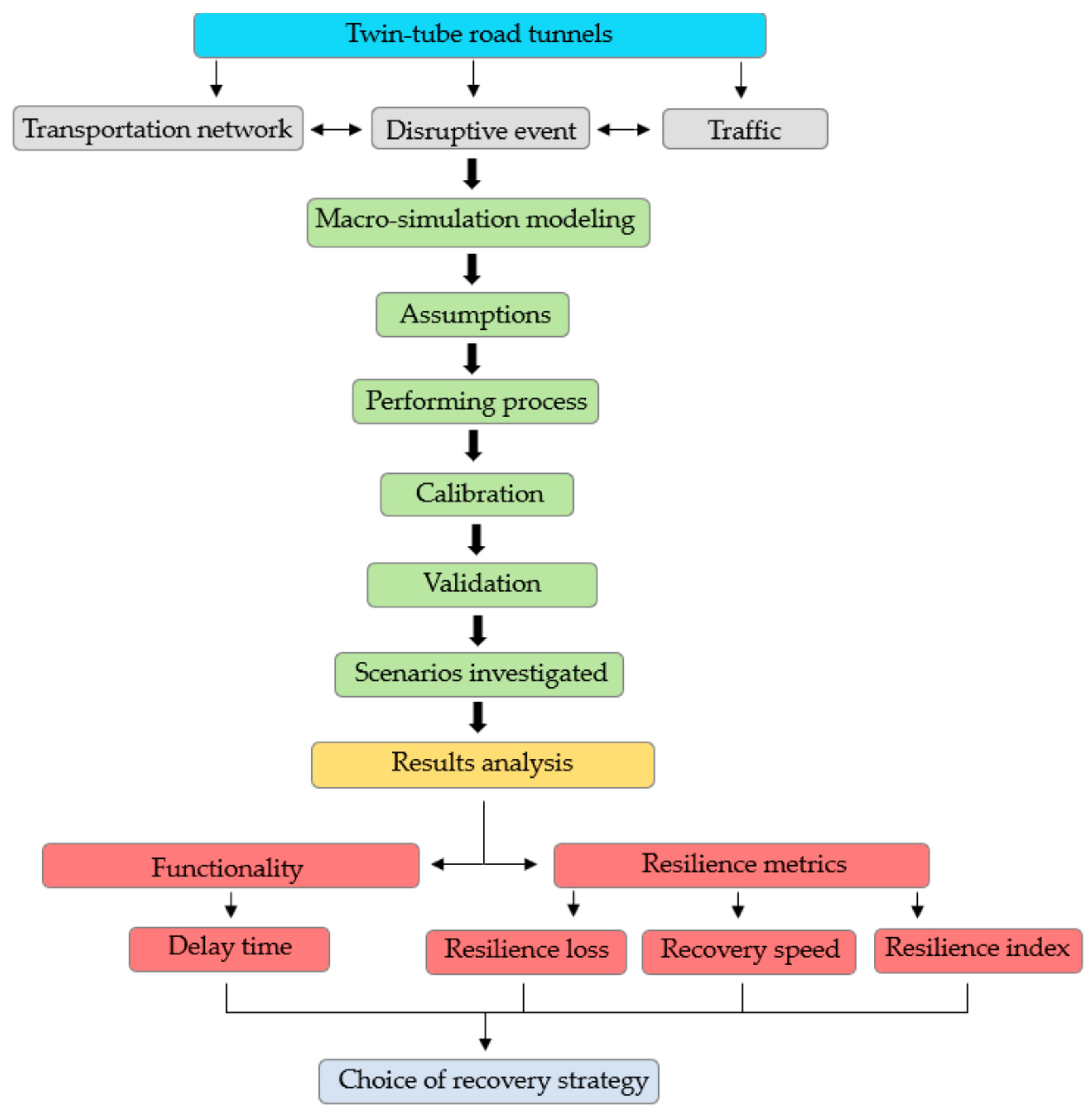
The present paper is set in the field of research on the resilience of road tunnels in the case of incidental events occurring within the structure, but it extends the state-of-the-art by developing a traffic simulation model to quantitatively assess the effectiveness of different strategies to recover the functionality level of the transportation infrastructure. Therefore, this research aims to serve, given the lack of knowledge on tunnel resilience, as a potential reference for the tunnel management agencies in the event of a traffic accident or fire within the tunnel, and to increase our experience in the study of road networks.
The methodology applied is briefly described in
Figure 5.
4. Traffic Simulation Modeling
4.1. Assumptions
The macro-simulation software known as PTV Visum 17 version [
42], which has been widely used to analyze relatively large transportation networks, was applied.
Given that the partial or complete closure of the tube affected by the incident was assumed to be equal to a maximum of 3 h (i.e., from 7:00 a.m. to 10:00 a.m.), the simulations were carried out by considering an analysis period of seven hours (i.e., from 6:00 a.m. to 1:00 p.m.). Namely one hour before the disruptive event in order to simulate that the transportation network had already charged before the occurrence of the incident, and an extra-time of three hours after the end of the partial or complete closure of the north tube in order to continue the investigation of the effects on traffic flow subsequently to the recovery process.
4.2. Performing Process
The main steps to perform the PTV Visum macro-simulation software were: (i) defining the road network geometry (i.e., nodes, arcs, and turning maneuvers); (ii) identifying the speed limit for each vehicle category; (iii) defining the capacity of each road segment of the transport network; (iv) specifying the traffic assignment procedure; (v) defining the simulation time interval.
The road network geometry (see
Figure 2) was imported into PTV Visum as a shapefile, and through the graphic interface contained in the code, the speed limit of passenger cars and HGVs, as well as the capacity, were defined for each road segment of the investigated system. The traffic demand was modeled by specifying the hourly traffic volume of passenger cars and HGVs going from a point of origin to one of destination.
The traffic assignment procedure can be static or dynamic. The former considers both the demand and transport supply constant over time; whereas they might be assumed time-dependent using dynamic traffic assignment procedures. The latter, in fact, considers the traffic flow as a continuous fluid for which specific variables such as the traffic flow, vehicle speed, and density, can be defined at each point of space and time. In this way, it is possible to model not only the variability of traffic demand (e.g., peak traffic flow) but also that of the transport supply (e.g., the closure of a lane and/or a link), so that specific dynamic phenomena that characterize a congested network, as well as the delay time and the formation of the queue can be considered, too. In the present paper, the dynamic user equilibrium (DUE) traffic assignment procedure, integrated into PTV Visum, was more especially implemented to have several potentialities with respect to the following aspects: (i) simulation of congested network in which over-saturation conditions occur for several hours; (ii) simulation of transportation network with congestion effects resulting in different route choices; (iii) simulation of the effects of accidents and their management (for more details see PTV Visum 17 User’s Manual [
42]).
With reference to the simulation time interval, according to the PTV Visum 17 User’s Manual, it should be included in the range of 5 and 15 min. In this study, we set a simulation time interval equal to 5 min: this means that the code provides the output (i.e., average vehicles’ speed and traffic flow) every 5 min of simulation for each road segment.
The proposed macro-simulation model was then resolved, and the results are shown in the subsequent paragraphs.
However, it is to be stressed that the convergence criterion adopted in simulation foresees the runs to be stopped when the difference in the results between two consecutive runs is less than 5%. In this regard, 10 runs were found to be sufficient in our case.
4.3. Calibration
The calibration process was performed in order to test the capability of the developed model to reproduce the observed traffic values provided by the road management agencies. In particular, the model accuracy was evaluated by comparing the simulated traffic volumes with those measured in the field.
The differences between the traffic generated in the simulation and measured ones were within the statistical tolerance levels. Specifically, the GEH statistic was used in this paper in order to validate the calibration process:
where M is the simulated hourly traffic volume, and C is the measured hourly traffic volume. By using this methodology in each road section during both peak hours and off-peak hours, the GEH value was found to be less than the recommended threshold of 5, thus demonstrating a good agreement between the simulated and measured traffic data.
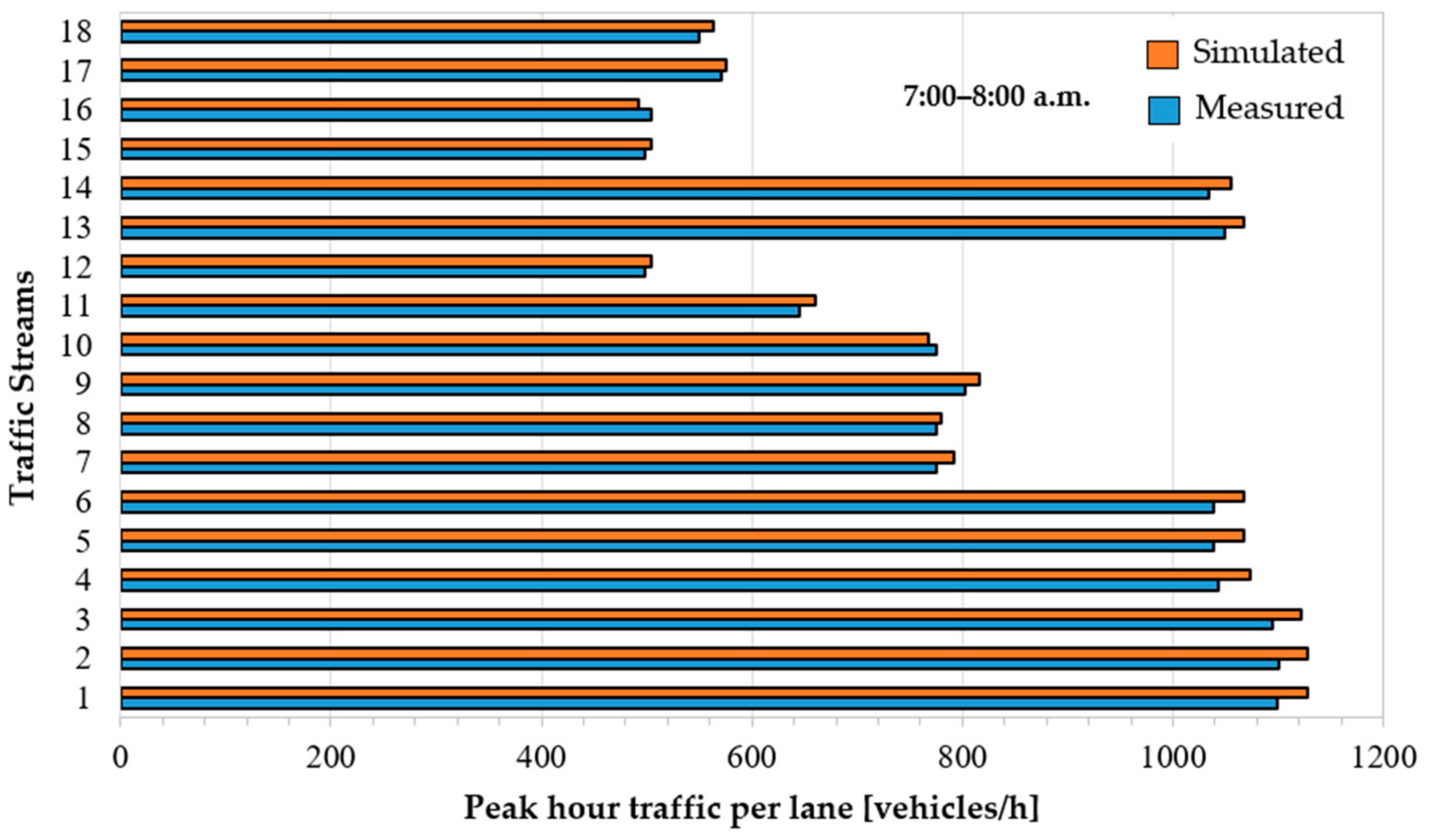
Figure 6 shows, for example, the comparison between the simulated and measured peak traffic volumes per lane in the morning from 7:00 a.m. to 8:00 a.m. The graphic comparison also confirms the high level of conformity between the simulated and observed traffic volumes. Therefore, the authors are confident that macro-simulation modeling performed in this paper is able to accurately reproduce the actual traffic conditions.
It is to be stressed that the aforementioned level of conformity was also found for the second peak hour, as well as for the remaining off-peak hours. However, the findings are not reported here.
4.4. Validation
The PTV Visum code was preliminarily validated through a comparison with the queue length measured by the motorway management agency after a real frontal collision between a heavy vehicle and a car occurred within the north tube.
The traffic accident occurred at 7:30 a.m., leading to the complete closure of the north tube. After 30 min from the incident (i.e., 8:00 a.m.), the motorway management agency imposed all vehicles to exit the motorway at Junction B of
Figure 2, which is located before the entrance portal of the tube blocked. The measured queue length upstream of the mentioned Junction B was found to be equal to 2 km and 4 km at 8:30 a.m. and 9:15 a.m., respectively. Finally, at 9:30 a.m., one lane of the tube was opened and at 11:00 a.m. the traffic queue ended.
The aforementioned event was simulated by using the PTV Visum, and by assuming that a passenger car and HGV in the queue occupy a space of 7 m and 14 m (default values in PTV Visum), respectively. Under these hypotheses, the queue length upstream of the mentioned motorway junction was computed to be in simulation equal to 2.1 km at 8:30 a.m., and 4.2 km at 9:15 a.m.; finally, the simulated traffic queue ended at 11:10 a.m. Therefore, there was a good level of conformity between the measured and simulated values of the queue (i.e., an error of no more than 5%).
5. Results Analysis
5.1. Simulation Results for Scenario 0
Table 3 shows the simulation results of the average speed and consequently of the average travel time under ordinary functionality of each tunnel tube without any disruptive event (i.e., Scenario 0), relating to the road segments of the transport network investigated. The average travel time is calculated as the ratio of each road segment length to the corresponding average speed, this last one is an output of the code. The first part of
Table 3 reports the results related to the road segments characterized by unidirectional traffic (i.e., those of the motorway), whereas the second part of
Table 3 refers to the road segments affected by bi-directional traffic (e.g., the major and minor rural roads) and motorway junctions.
From
Table 3, it is possible to observe that all the average travel speeds are below the speed limits for each type of road as defined in the
Table 1. Moreover, under ordinary functionality of each tunnel tube without any disruptive event, the average travel time spent by vehicles using the motorway section to go from the Nodes A to D (i.e., motorway section length equal to 24.754 km, and average speed of 118.69 km/h) was found to be equal to 12.514 min. With reference to the potential alternative itinerary (i.e., the major rural road, segment E-I) characterized by a length of 7.80 km, it can be noted how in an ordinary situation the average travel speed is 69.50 km/h, and the average travel time is of 6.734 min.
5.2. Simulation Results for Scenarios 1–5
Given that the partial or complete closure of the tunnel tube affected by an incident (i.e., the tube characterized in ordinary situations by unidirectional traffic towards the north direction) was assumed to happen in the morning between the 7:00 a.m. and 10:00 a.m., it is to be recorded that we investigated in the simulations the effects on traffic flow due to the duration of a disruptive event occurring in the north tube of 1, 2, and 3 h, respectively (i.e., from 7:00 to 8:00 a.m. (1 h), from 7:00 to 9:00 a.m. (2 h), and from 7:00 to 10:00 a.m. (3 h)). With reference to these durations of disruption,
Table 4,
Table 5 and
Table 6 show the average speed, the average travel time, and the delay time (i.e., the difference between the travel time with and without disruptive event) for the aforementioned cases: Scenario 1 (i.e., partial closure of the north tube); Scenarios 2a, 2b, and 2c (i.e., complete closure of the north tube with the use of the adjacent tube for bi-directional traffic under the hypotheses that the traffic by-pass is opened after 10, 20, and 30 min from the start of the incident, respectively); Scenario 3 (i.e., similar to the Scenario 1, but with the use of the alternative itinerary for HGVs only); Scenarios 4a, 4b, and 4c (i.e., similar to Scenario 2, but with the use of the alternative itinerary for HGVs only); Scenario 5 (i.e., complete closure of the north tube, but with the use of the alternative itinerary for all vehicles (i.e., both passenger cars and HGVs)).
5.2.1. Delay Time
By comparing
Table 4,
Table 5 and
Table 6, it can be noted that the delay time increases with the duration of the partial or complete closure of the north tube interested by a traffic accident or fire (i.e., passing from 1 to 2 and 3 h, respectively).
Moreover, as expected, smaller delay times were found with the partial closure of the tube (i.e., Scenario 1) in contrast with the complete one.
In the case of the complete closure of the tube, the delay time on the motorway (i.e., corresponding to the traffic flow from the Nodes A to D) is computed to be smaller when the traffic by-pass is opened—by the emergency service team in order to allow for the use of the adjacent tube for bi-directional traffic—within a time of 10 min from the start of the incident (i.e., Scenario 2a in contrast with Scenarios 2b, and 2c). Obviously, the use of the adjacent tube for bi-directional traffic led to an increase in the average travel time on the motorway for traffic flow towards the south direction (i.e., from the Nodes D to A).
From
Table 4,
Table 5 and
Table 6, it is also possible to observe that when the alternative itinerary is activated for HGVs only, both in the case of the partial (i.e., Scenario 3) and complete closure (i.e., Scenarios 4a, 4b, and 4c) of the north tube, minor delay times are computed when compared to those of the corresponding scenarios previously mentioned (i.e., respectively 1, 2a, 2b, and 2c). In this respect, however, it is to be said that this reduction of the delay time on the motorway is related to passenger cars only.
The worst scenario, however, was found to be under the following hypotheses: (i) complete closure of the north tube; (ii) the adjacent tube is not used for bi-directional traffic but it continues to be characterized only by the traffic flow towards the south direction; (iii) all the traffic flow towards the north direction (i.e., both passengers cars and HGVs) is redirected to the alternative itinerary which is formed by the set of the following bi-directional road segments: B–E, E–F, F–G, G–H, H–I, I–L, and L–C of
Figure 2. By including in our analysis also the two motorway sections upstream and downstream of the mentioned alternative route (i.e., the unidirectional motorway Sections A–B and C–D of
Figure 2) we computed in simulation very high values of the delay time due to the reaching of congested traffic conditions. In particular, with reference to the total length of the road section investigated (i.e., itinerary: A–B–E–I–L–C–D of
Figure 2) connecting the Nodes A to D of length equal to 27.349 km, the delay time was found to be equal to about 14, 25, and 31 min for a closure time of the north tube equal to 1, 2, and 3 h, respectively. The corresponding average travel speed was found to be respectively of 61, 44, and 37 km/h.
5.2.2. Resilience Loss
The level of functionality of the system during the time period in which the north tube is partially or completely closed was computed as the ratio between the average travel time required to reach a given destination from a specific origin before and after the occurrence of the disruptive event (obviously in absence of the incidental event in the north tube, the functionality level is assumed to be equal to 100%). In particular, our analysis is related to the average travel time of traffic flow towards the north direction (i.e., from the Nodes A to D). As an example, given that under ordinary conditions of functionality of the north tube, the average travel time of traffic flow from the Nodes A to D is 12.514 min (i.e., Scenario 0, A–D motorway section of
Table 3) and the corresponding average travel time of Scenario 1 is 14.233 min when the duration of interruption is 1 h (see
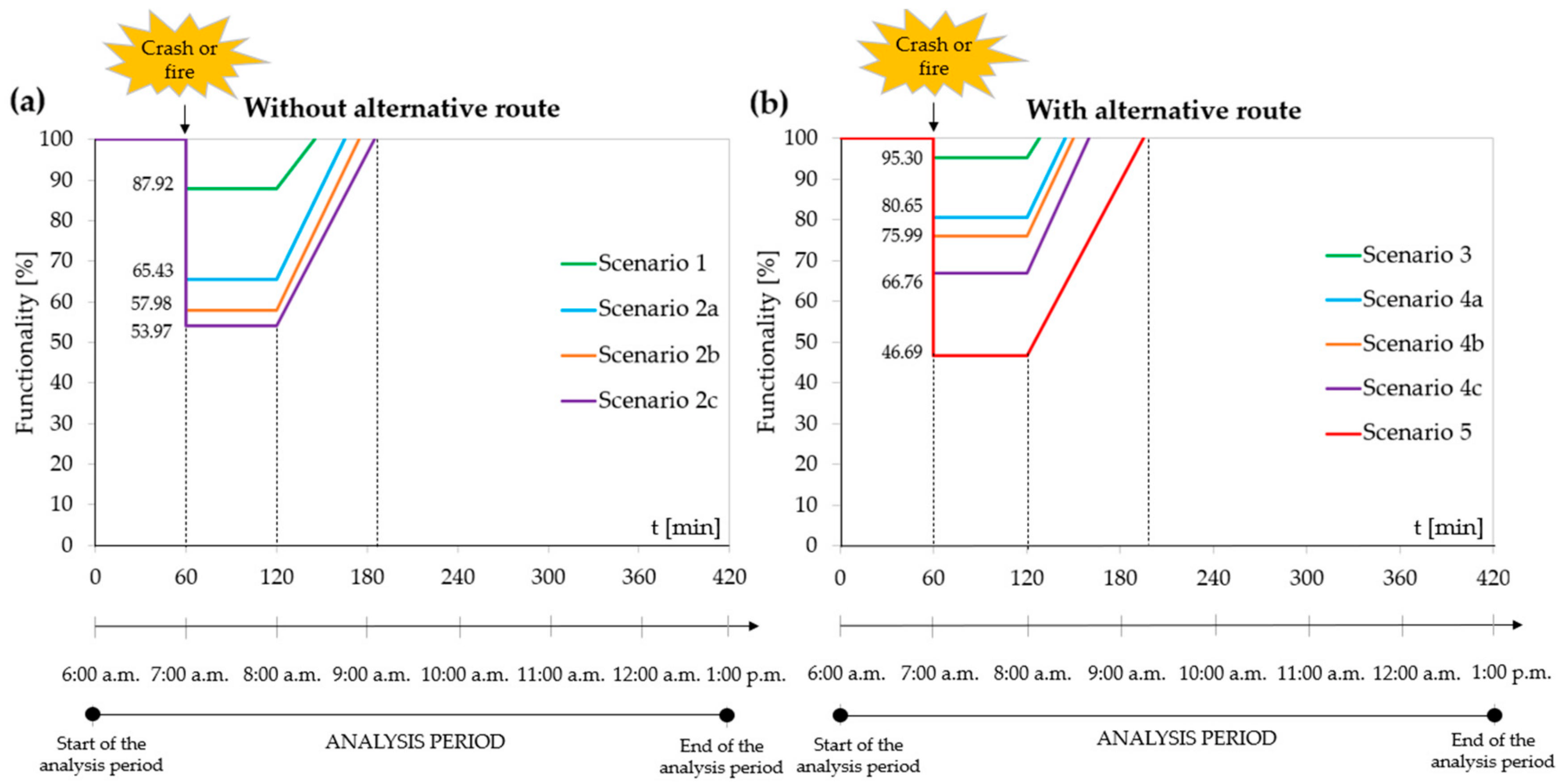
Table 4), we computed that the functionality level in the event of the partial closure of the north tube is reduced to: 100 × 12.514/14.233 = 87.92%; while in the case of the complete closure of the north tunnel for 1 h of disruption the functionality level is reduced to: 100 × 12.514/19.125 = 65.43% (i.e., Scenario 2a); 100 × 12.514/21.582 = 57.98% (i.e., Scenario 2b); 100 × 12.514/23.185 = 53.97% (i.e., Scenario 2c). Obviously, we computed the reduction of the functionality level for all the remaining scenarios investigated in a similar way. It is to be stressed that higher values of the mentioned percentage indicate greater reductions of the functionality level (i.e., a lower resistance (or a lower robustness) of the road network in the event of a disruptive event).
By reporting in the y-axis, the values of these reductions of the functionality level expressed in terms of percent, and in the x-axis the time of analysis (i.e., from 6:00 a.m. to 1:00 p.m.)—as well as the time instant t0 when the incident occurs in the north tube (i.e., 7:00 a.m., or in other terms 60 min from the start of analysis period), the time instant tr when the system starts the recovery process (i.e., 60 (1 h), 120 (2 h), and 180 (3 h) min from t0, or in other terms respectively 120, 180, and 240 min from the start of the analysis period), and the time instant th when the system is again fully functional—we build the functionality recovery curves F(%)—t.
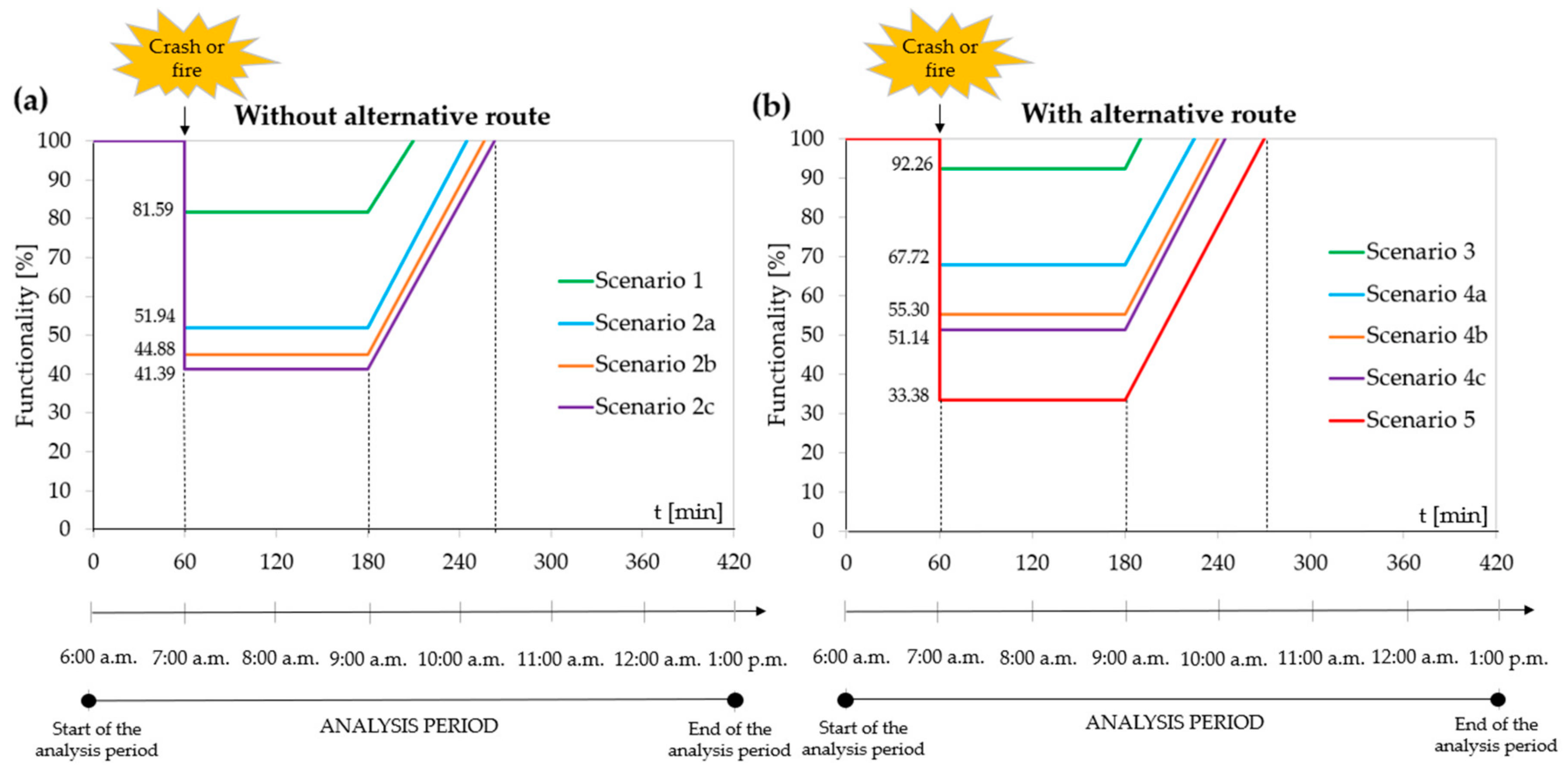
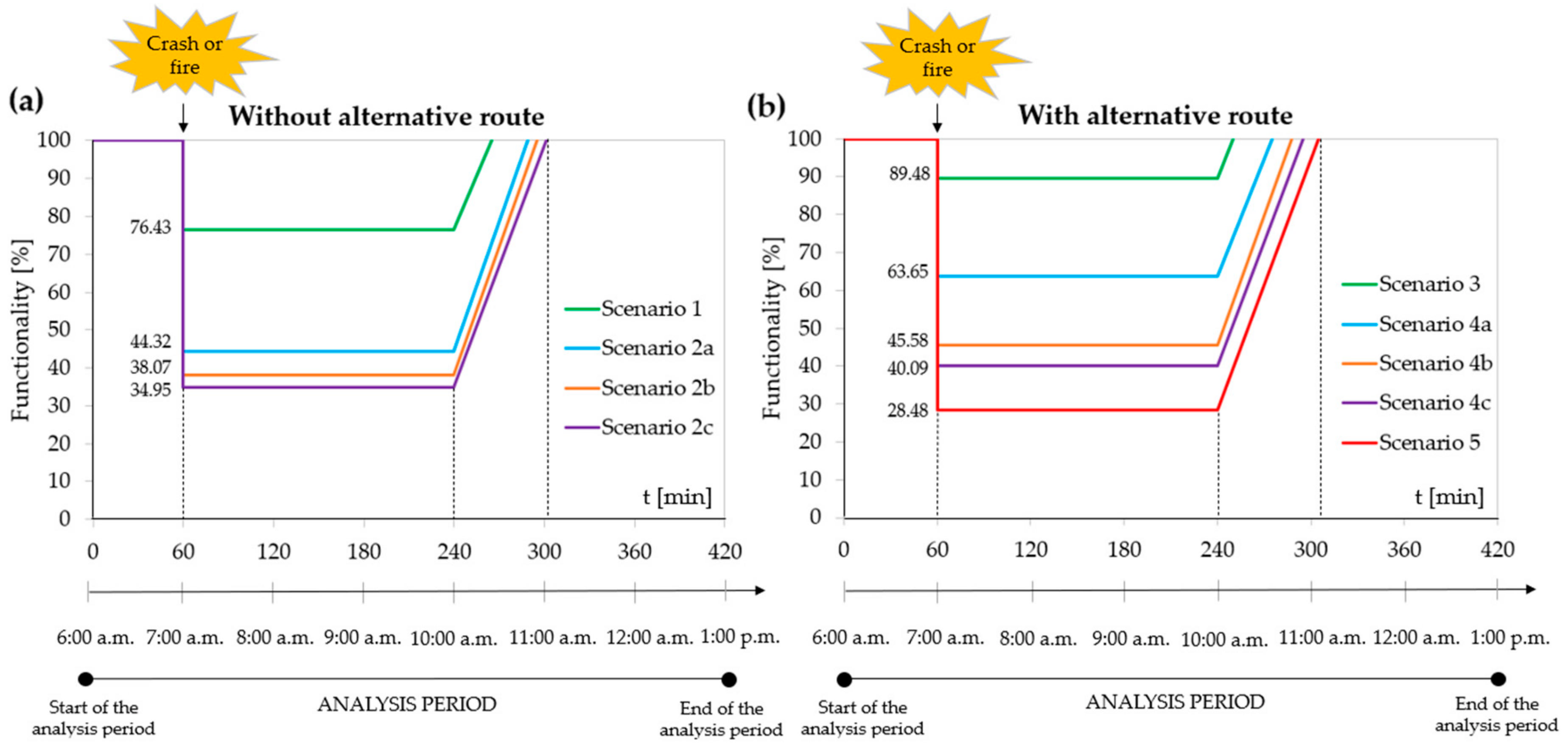
Figure 7,
Figure 8 and
Figure 9 show the aforementioned functionality recovery curves for the scenarios investigated in the case of the partial or complete closure of the north tube for a duration of the disruptive event 1, 2, or 3 h, respectively. The resilience loss (
) is given, in our case by the extension of the area of the trapezium (i.e., a small extension area means a high-resilience scenario, a large extension area indicates a low-resilience scenario, and a medium extension area represents an intermediate resilience scenario). By comparing
Figure 7,
Figure 8 and
Figure 9, it can be noted that the resilience loss increases with the duration of the partial or complete closure of the north tube.
Smaller resilience losses were found with the partial closure of the tube (i.e., Scenario 1) in contrast with the complete one.
In the event of the complete closure of the north tube, the resilience loss that is related to the traffic flow on the motorway from the Nodes A to D was computed to be smaller when the traffic by-pass is opened within a time of 10 min from the start of the incident (i.e., Scenario 2a against the Scenarios 2b, and 2c).
From
Figure 7,
Figure 8 and
Figure 9, it can also be noted that when the alternative itinerary is activated for HGVs only, both in the case of the partial (i.e., Scenario 3) and complete closures (i.e., Scenarios 4a, 4b, and 4c) of the north tube, minor resilience losses are computed when compared to those of the corresponding scenarios (i.e., respectively 1, 2a, 2b, and 2c) with reference to the motorway section from A to B and passenger cars only.
Greater resilience losses were found when the north tube is completely closed and all the traffic flows (i.e., both passenger cars and HGVs) are redirected to the alternative itinerary of
Figure 2. It is to be noted that the resilience losses found are coherent with the aforementioned delay times.
5.2.3. Recovery Speed
Figure 7,
Figure 8 and
Figure 9, show also that the recovery speed (i.e.,
) for a given duration of the disruptive event in the north tube (i.e., 1 h, 2 h, or 3 h) is more or less the same for all the scenarios investigated. In fact, the set of computed lines never meet in the period of time t
h–t
r.
5.2.4. Resilience Index
Resilience index () tries to represent the resilience through a parameter, the value of which varies between 0 and 1. It is widely used in current literature for resilience analyses of transport infrastructures. A high resilience index indicates a low resilience loss (i.e., a resilience index equal to one corresponds to a zero-resilience loss).
Figure 10a,b shows the resilience index computed for the scenarios investigated without and with the use of the alternative itinerary. In particular, it can be noted how the resilience index decreases with the duration of the partial or complete closure of the north tube (i.e., from 1 h to 2 h, and 3 h, respectively). Higher resilience indexes were found with the partial closure of the tube (i.e., Scenario 1) in contrast with the complete one. In the event of the complete closure of the north tube, the resilience index is higher when the traffic by-pass is opened within a time of 10 min from the start of the incident (i.e., Scenario 2a against Scenarios 2b, and 2c). By comparing
Figure 10a,b, it can also be noted how when the alternative itinerary is activated for HGVs only, both in the case of the partial (i.e., Scenario 3) and complete closures (i.e., Scenarios 4a, 4b, and 4c) of the north tube, higher resilience indexes are found in contrast with those of the corresponding scenarios (i.e., respectively 1, 2a, 2b, and 2c) for passenger cars only. Lower resilience indexes were found when the north tube is completely closed and all the traffic flows (i.e., both passenger cars and HGVs) are redirected to the aforementioned alternative itinerary. In other words, the results of the resilience index confirm our previous comments on the resilience loss in all the cases investigated.
6. Conclusions and Discussion for Future Investigations
This study was mainly motivated by the need to develop a traffic simulation model to quantitatively assess the resilience of transportation infrastructures containing a twin-tube motorway tunnel in the event of traffic accidents or fires occurring in a tube, as well as to identify a more appropriate strategy for reducing delay times.
The occurrence of the disruptive event was assumed to lead to different possible scenarios including the partial or complete closure of a tube, with consequences (i.e., delay times) affecting the vehicular transit on both the motorway and the corresponding road network connected by means of the motorway junctions. In the light of these considerations, the present paper was not limited to the study of the tube in which the accident occurred but extended the analysis to a relatively large portion of the road network affected by the disruptive event. On this basis, the PTV Visum macro-simulation software, which has been widely used to analyze relatively large transportation networks, was applied. After performing several preliminary macro-simulations in order to define the study area, we found that the main effects on traffic due to an incident occurred in the mentioned tunnel tube are confined within an area of about 25 km long and 8 km wide.
The functionality of the road system, in the case of an incident occurring in the tube characterized by traffic flow towards the north direction, was assumed to be recovered by using the remaining undisrupted lane (only one lane is closed) in the case of the partial closure of the tube or reorganizing the traffic flow by utilizing the adjacent tube for bi-directional traffic in the event of the complete closure. In the latter case, different hypotheses were made about the intervention time of the emergency service team to open the traffic by-passes at the tunnel portals from the start of the incidental event (i.e., 10, 20, and 30 min). The effect of an alternative itinerary individualized in the corresponding open road network was also examined.
The level of functionality of the system during the time period in which the north tube is partially or completely closed was computed as the ratio between the average travel time required to reach a given destination from a specific origin before and after the occurrence of the disruptive event. The resilience metrics were assumed to be resilience loss, recovery speed, and resilience index.
The results showed that: (i) the best scenario was found to be with the partial closure of the tube in contrast with the complete one; (ii) in order to contain the resilience loss due to the complete closure of the tube disrupted, the traffic by-pass before the entrance portal of the closed tube should be open in a very short time by the tunnel management team to allow for the quick use of the adjacent tube for bi-directional traffic; (iii) an additional improvement with reference exclusively to passenger cars might be obtained by suggesting the use of an alternative itinerary for heavy good vehicles (HGVs) only, through the activation of variable message signs located at a sufficient distance from the motorway junction before the entrance portal; (iv) an alternative itinerary used by all the vehicles (i.e., both passenger cars and HGVs) was instead found to be characterized by excessive resilience loss, then it would not be advisable.
The recovery speed, for a given duration of the disruptive event in the tube, was found to be more or less the same in all the cases investigated.
The resilience index was found to confirm the aforementioned results of the resilience loss in all the scenarios examined.
The findings obtained might be useful as a decision-making support tool aimed at improving the resilience of twin-tube tunnels.
Although this study can represent an advancement in the field of research on the resilience of road tunnels in the case of incidental events occurring in the structure, it is worth mentioning that the randomness of the factors that play a role might also cause some uncertainties in the resilience analysis. Therefore, studies based on uncertainties in resilience analysis should be carried out. Moreover, it is to be said that a disruption in a motorway tunnel belonging to a road network might also propagate to the other transport systems. This means that the interdependency among different transport systems should also be taken into account.
In the light of the above considerations, our knowledge needs to be completed with future research in order to make further progress in the field of transport systems resilience.