Space-Time Effect Prediction of Blasting Vibration Based on Intelligent Automatic Blasting Vibration Monitoring System
Abstract
:1. Introduction and Related Works
2. Construction of Intelligent Automatic Blasting Vibration Monitoring System
2.1. Configuration of the Data Acquisition Device
2.2. Neural Network Model Based on the Fuzzy-Rough Set
- (1)
- The fuzzification of excavated and unexcavated rock’s integrity
- (2)
- The fuzzification of the relative position between the measuring point and the face
- (3)
- The fuzzification of the relative height of building floors
2.3. Development of Intelligent Data Analysis and Prediction Software
2.4. The Effectiveness of the Intelligent Automatic Blasting Vibration Monitoring System
3. Results and Discussions
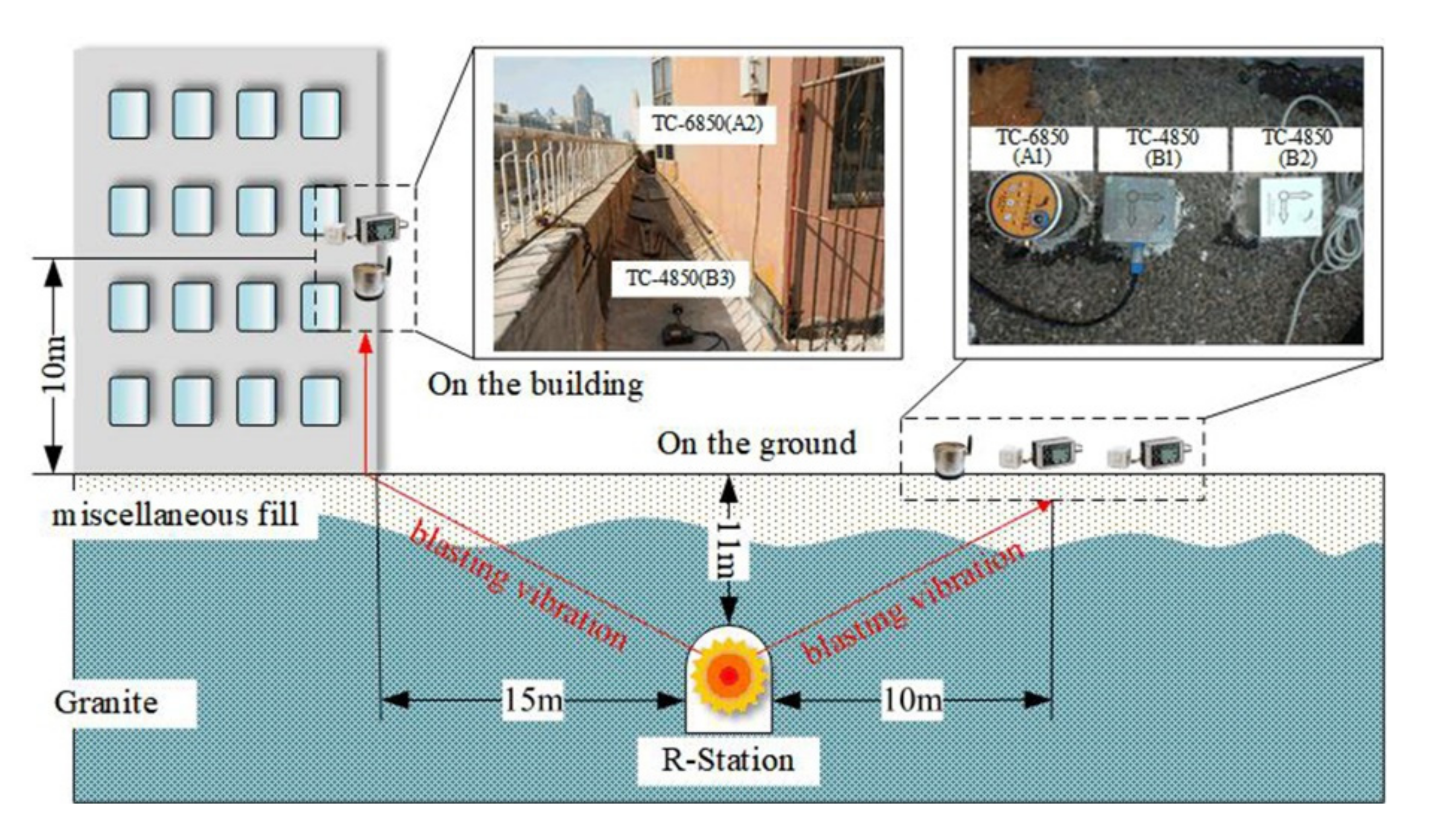
3.1. Arrangement of Data Acquisition Device
- Step 1. Adjacent to the area of the foundation pit, the upper part is a mixed soil layer, the middle section is a soft rock formation, and the lower part is a hard rock formation. Sensors are placed on the surrounding rock in the foundation pit near the blasting point. A sensor is set every 5 m on the surrounding rock wall.
- Step 2. The ground near the palm surface is blasted, and four sensors are arranged on the ground in front of and behind the blasting palm with the same distance between each sensor.
- Step 3. High-rise building area, from −2 to 20 floors, each floor is equipped with a sensor, each measuring point is placed on the load-bearing wall of the room, each floor is set at the same location, and each sensor is kept on the same straight line.
3.2. Analysis of Monitoring Results of Near Foundation Pit
3.3. Analysis of Monitoring Results of the Hollow Effect
3.4. Analysis of Monitoring Results of High-Rise Buildings
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agrawa, H.; Mishra, A.K. Modified scaled distance regression analysis approach for prediction of blast-induced ground vibration in multi-hole blasting. J. Rock Mech. Geotech. Eng. 2019, 11, 202–207. [Google Scholar] [CrossRef]
- Jayasinghe, B.; Zhao, Z.; Chee, A.G.T.; Zhou, H.; Gui, Y. Attenuation of rock blasting induced ground vibration in rock-soil interface. J. Rock Mech. Geotech. Eng. 2019, 11, 770–778. [Google Scholar] [CrossRef]
- Chu, H.; Yang, X.; Li, S.; Liang, W. Experimental study on the blasting-vibration safety standard for young concrete based on the damage accumulation effect. Constr. Build. Mater. 2019, 217, 20–27. [Google Scholar] [CrossRef]
- Gou, Y.; Shi, X.; Qiu, X.; Zhou, J.; Chen, H.; Huo, X. Propagation Characteristics of Blast-Induced Vibration in Parallel Jointed Rock Mass. Int. J. Géoméch. 2019, 19, 04019025. [Google Scholar] [CrossRef]
- Sheykhi, H.; Bagherpour, R.; Ghasemi, E.; Kalhori, H. Forecasting ground vibration due to rock blasting: A hybrid intelligent approach using support vector regression and fuzzy C-means clustering. Eng. Comput. 2017, 34, 357–365. [Google Scholar] [CrossRef]
- Ongen, T.; Karakus, D.; Konak, G.; Onur, A.H. Assessment of blast-induced vibration using various estimation models. J. Afr. Earth Sci. 2018, 145, 267–273. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Jin, X.-G. Prediction of peak velocity of blasting vibration based on artificial neural network optimized by dimensionality reduction of FA-MIV. Math. Probl. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Shahri, A.A.; Asheghi, R. Optimized developed artificial neural network based models to predict the blast induced ground vibration. Innov. Infrastruct. Solut. 2018, 3, 34. [Google Scholar] [CrossRef]
- Li, A.; Fang, Q.; Zhang, D.; Luo, J.; Hong, X. Blast vibration of a large-span high-speed railway tunnel based on microseismic monitoring. Smart Struct. Syst. 2018, 21, 561–569. [Google Scholar] [CrossRef]
- Xue, X. Neuro-fuzzy based approach for prediction of blast-induced ground vibration. Appl. Acoust. 2019, 152, 73–78. [Google Scholar] [CrossRef]
- Kostić, S.; Perc, M.; Vasović, N.; Trajković, S. Predictions of experimentally observed stochastic ground vibrations induced by blasting. PLoS ONE 2013, 8, e0082056. [Google Scholar] [CrossRef]
- Taheri, K.; Hasanipanah, M.; Golzar, S.B.; Majid, M.Z.A. A hybrid artificial bee colony algorithm-artificial neural network for forecasting the blast-produced ground vibration. Eng. Comput. 2017, 33, 689–700. [Google Scholar] [CrossRef]
- Yang, N.-H.; Xue, L.; Lin, S.-X. Remote monitoring system for blasting vibration and its application. Eng. Blasting 2012, 18, 71–74. (In Chinese) [Google Scholar]
- Zhu, M.; Wei, P.-G.; Zhang, J.-G.; Si, X.-D. Research on Automatic Monitoring System of Blast Vibration Based on TC-6850 and Its Application. In Proceedings of the Blasting Engineering Technology Exchange (Engineering Society of China Railway Society: China Railway Society), Beijing, China, 29 August 2018; pp. 262–272. [Google Scholar]
- Muhammad, W.; Hart, G.R.; Nartowt, B.; Farrell, J.J.; Johung, K.; Liang, Y.; Deng, J. Pancreatic Cancer Prediction Through an Artificial Neural Network. Front. Artif. Intell. 2019, 2. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Li, W.; Wang, Y. Robust Learning Control for Shipborne Manipulator with Fuzzy Neural Network. Front. Neurorobotics 2019, 13. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.-C.; Wu, L.; Yuan, Q.; Ma, C.-Y. Blasting Vibration Prediction based on Rough Set-Fuzzy Neural Network Method. Blasting 2016, 33, 127–131. (In Chinese) [Google Scholar]
- Wang, Z.; Wen, G.-G.; Qiu, X.-L. Stock Prediction Research Based on Rough Set and Dynamic Fuzzy Neural Network. Comput. Digit. Eng. 2020, 48, 517–522. (In Chinese) [Google Scholar]
- Homer, E.R.; Hensley, D.M.; Rosenbrock, C.W.; Nguyen, A.H.; Hart, G.L.W. Machine-Learning Informed Representations for Grain Boundary Structures. Front. Mater. 2019, 6. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.-X.; Zhang, Y.-H. Research on vibration velocity responses of surface building under the condition of blasting excavation in tunnel. Earthq. Eng. Eng. Vib. 2010, 30, 112–119. (In Chinese) [Google Scholar]
- Li, H.-T.; Shu, D.-Q.; Lu, W.-B.; Zhu, C.-Y. Response characteristics of a structure to different frequency components in blasting vibration energy. J. Vib. Shock. 2010, 29, 154–158. (In Chinese) [Google Scholar]
- Ma, H.; Zhong, M.; Li, X.; Xie, Q.; Zhou, Y.; Yin, Q. Experimental and Numerical Simulation Study on the Shock and Vibration Effect of OD1422-X80 Mainline Natural Gas Pipeline Explosion. Shock. Vib. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Shi, X.-Z.; Lin, D.-N.; Chen, S.-S. Blasting-vibration-induced damage prediction by rough set-based fuzzy-neural network. Explos. Shock. Waves 2009, 29, 401–407. (In Chinese) [Google Scholar]
- Shi, X.-Z.; Xue, J.-G.; Chen, S.-S. A fuzzy neural network prediction model based on rough set for characteristic variables of blasting vibration. J. Vib. Shock. 2009, 28, 73–76+213. (In Chinese) [Google Scholar]
- Liu, D.; Lu, W.; Liu, Y.; Chen, M.; Yan, P.; Sun, P. Analysis of the Main Factors Influencing the Dominant Frequency of Blast Vibration. Shock. Vib. 2019, 2019, 1–17. [Google Scholar] [CrossRef]
- Liu, T.; Huang, Y.-L.; Lei, G. Analysis of the Optimum Support Dismantling Scheme for Shallow Bored Subway Stations in a Soil-Rock Compound Stratum. Mod. Tunn. Technol. 2015, 52, 131–137. (In Chinese) [Google Scholar]
- Zhang, G.-C.; Liu, T. Monitoring and analysis of deformation of foundation pits in strata with rock-soil combination. Chin. J. Geotech. Eng. 2010, 32, 550–553. (In Chinese) [Google Scholar] [CrossRef]
- Monjezi, M.; Baghestani, M.; Faradonbeh, R.S.; Saghand, M.P.; Armaghani, D.J. Modification and prediction of blast-induced ground vibrations based on both empirical and computational techniques. Eng. Comput. 2016, 32, 717–728. [Google Scholar] [CrossRef]
- Huo, R.; Li, S.; Song, Z.; Fujii, Y.; Lei, S.; Mao, J.; Tian, S.; Miao, Z. Analysis of vibration response law of multi-story building under tunnel blasting loads. Adv. Civ. Eng. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Gu, W.; Wang, Z.; Liu, J.; Xu, J.; Liu, X.; Cao, T. Water-Depth-Based Prediction Formula for the Blasting Vibration Velocity of Lighthouse Caused by Underwater Drilling Blasting. Shock. Vib. 2017, 2017, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Song, K.-I.; Oh, T.-M.; Cho, G.-C. Precutting of tunnel perimeter for reducing blasting-induced vibration and damaged zone—numerical analysis. KSCE J. Civ. Eng. 2014, 18, 1165–1175. [Google Scholar] [CrossRef]
- Xie, L.; Lu, W.; Gu, J.; Wang, G. Excavation Method of Reducing Blasting Vibration in Complicated Geological Conditions. Shock. Vib. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Yu, L. Safety influence of blasting vibration on multistory building. J. Railw. Eng. Soc. 2015, 32, 86–89. [Google Scholar]












| Parameter | Technical Description |
|---|---|
| Number of channels | X/Y/Z |
| Frequency | 5–300 Hz |
| Range (speed) | 0–25 cm/s |
| Range (acceleration) | ±16 g |
| Sample rate | 6.4 KSps |
| Sample time | 1/2/5/10/15 s |
| Storage capacity | 1 GB |
| Measurement accuracy | 0.1 cm/s, 0.02 g |
| Short-message warning | Support |
| System error | <5% |
| Working time | >72 H |
| Stand-by time | >240 H |
| Battery capacity | 6400 mAH |
| Operating temperature | −20 °C to +70 °C |
| Guideline of Attribute (Units) | Description of Decision | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| a(kg) | <30 | 30~50 | >50 |
| b(kg) | <200 | 200~300 | >300 |
| c(m) | <20 | ≥20 | |
| d(m) | <10 | 10~20 | >20 |
| e(m) | <0.5 | ≥0.5 | |
| f(ms) | <0.5 | 0.5~0.7 | >0.7 |
| g | <0.5 | 0.5~0.7 | >0.7 |
| h | 0~180 | >180 | |
| i(m) | <0.3 | 0.3~0.8 | >0.8 |
| X(cm/s) | <0.5 | 0.5~1 | >1 |
| Y(cm/s) | <0.5 | 0.5~1 | >1 |
| Z(cm/s) | <0.5 | 0.5~1 | >1 |
| F(Hz) | <100 | 100~200 | >200 |
| Location | Nci | X | Y | Z | F |
|---|---|---|---|---|---|
| R-Station | a | 35/100 | 15/100 | 22/100 | 32/100 |
| b | 23/100 | 21/100 | 15/100 | 31/100 | |
| c | 26/100 | 12/100 | 16/100 | 19/100 | |
| d | 3/100 | 18/100 | 25/100 | 21/100 | |
| e | 15/100 | 12/100 | 19/100 | 6/100 | |
| f | 2/100 | 5/100 | 2/100 | 1/100 | |
| g | 1/100 | 2/100 | 3/100 | 2/100 | |
| h | 3/100 | 7/100 | 15/100 | 4/100 | |
| i | 15/100 | 10/100 | 34/100 | 23/100 | |
| Y-Station | a | 32/100 | 12/100 | 19/100 | 29/100 |
| b | 20/100 | 18/100 | 13/100 | 23/100 | |
| c | 21/100 | 17/100 | 11/100 | 24/100 | |
| d | 15/100 | 18/100 | 25/100 | 21/100 | |
| e | 15/100 | 12/100 | 19/100 | 6/100 | |
| f | 12/100 | 18/100 | 16/100 | 21/100 | |
| g | 25/100 | 29/100 | 32/100 | 25/100 | |
| h | 10/100 | 2/100 | 8/100 | 13/100 | |
| i | 0/100 | 0/100 | 0/100 | 0/100 | |
| H-Station | a | 35/100 | 15/100 | 22/100 | 32/100 |
| b | 23/100 | 21/100 | 15/100 | 31/100 | |
| c | 26/100 | 12/100 | 16/100 | 19/100 | |
| d | 3/100 | 18/100 | 25/100 | 21/100 | |
| e | 15/100 | 12/100 | 19/100 | 6/100 | |
| f | 4/100 | 9/100 | 1/100 | 0/100 | |
| g | 5/100 | 6/100 | 9/100 | 1/100 | |
| h | 21/100 | 15/100 | 18/100 | 28/100 | |
| i | 0/100 | 0/100 | 0/100 | 0/100 |
| Item | TC-4850 | TC-6850 |
|---|---|---|
| Shape | Square | Cylindrical |
| Size | 168 mm × 99 mm × 64 mm | D = 81 mm, H = 80 mm |
| Weight | 1 kg | 0.56 kg |
| Integration | Separate sensor and host | Combined sensor and host |
| Working temperature | −10~75 °C | −20~75 °C |
| Sealing, waterproof and dustproof | Poor | Good |
| Data transmission | USB | WIFI/4G/3G |
| Power | Lithium battery | Lithium battery/Solar energy |
| Operation | Wired | Wireless |
| Data acquisition | Manual | Automatic |
| Data output | PC | PC & Mobile phone |
| Parameters output | Velocity | Velocity & Acceleration |
| Data viewing | Paper report | Network data platform |
| Sensor Number | Origin of the Age | Geotechnical Name | Layer Thickness/m |
|---|---|---|---|
| J1 | Q4ml | Plain fill | 1.85 |
| J2 | Q4ml | Miscellaneous fill | 2.11 |
| J3 | γ53 | Strongly weathered granite | 5.44 |
| J4 | γ53 | Middle weathered granite | 3.69 |
| J5 | γ53 | Slightly weathered granite | 7.15 |
| J6 | γπ53 | Slightly weathered granite porphyry | 4.76/excavated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; He, G.; Dong, S.; Zhao, S.; Shi, L.; Liu, X.; Zhang, B.; Qi, N.; Deng, S.; Zhang, J. Space-Time Effect Prediction of Blasting Vibration Based on Intelligent Automatic Blasting Vibration Monitoring System. Appl. Sci. 2022, 12, 12. https://doi.org/10.3390/app12010012
Chen F, He G, Dong S, Zhao S, Shi L, Liu X, Zhang B, Qi N, Deng S, Zhang J. Space-Time Effect Prediction of Blasting Vibration Based on Intelligent Automatic Blasting Vibration Monitoring System. Applied Sciences. 2022; 12(1):12. https://doi.org/10.3390/app12010012
Chicago/Turabian StyleChen, Fan, Gengsheng He, Shun Dong, Shunjun Zhao, Lin Shi, Xian Liu, Baichuan Zhang, Ning Qi, Shenggui Deng, and Jin Zhang. 2022. "Space-Time Effect Prediction of Blasting Vibration Based on Intelligent Automatic Blasting Vibration Monitoring System" Applied Sciences 12, no. 1: 12. https://doi.org/10.3390/app12010012
APA StyleChen, F., He, G., Dong, S., Zhao, S., Shi, L., Liu, X., Zhang, B., Qi, N., Deng, S., & Zhang, J. (2022). Space-Time Effect Prediction of Blasting Vibration Based on Intelligent Automatic Blasting Vibration Monitoring System. Applied Sciences, 12(1), 12. https://doi.org/10.3390/app12010012





