Influence of Soil Heterogeneity on the Contact Problems in Geotechnical Engineering
Abstract
1. Introduction
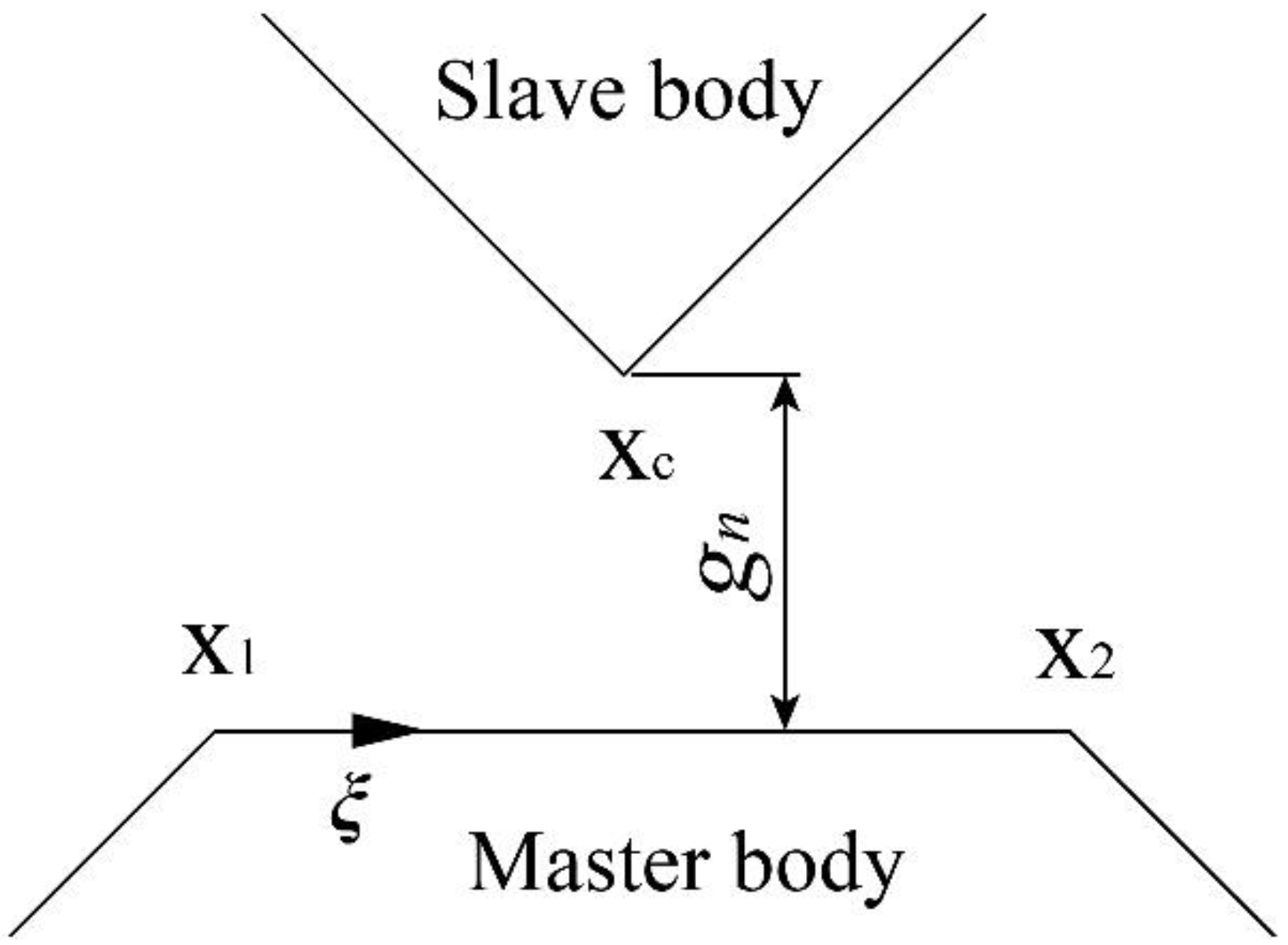
2. Implementation of the Penalty Method in the FEM
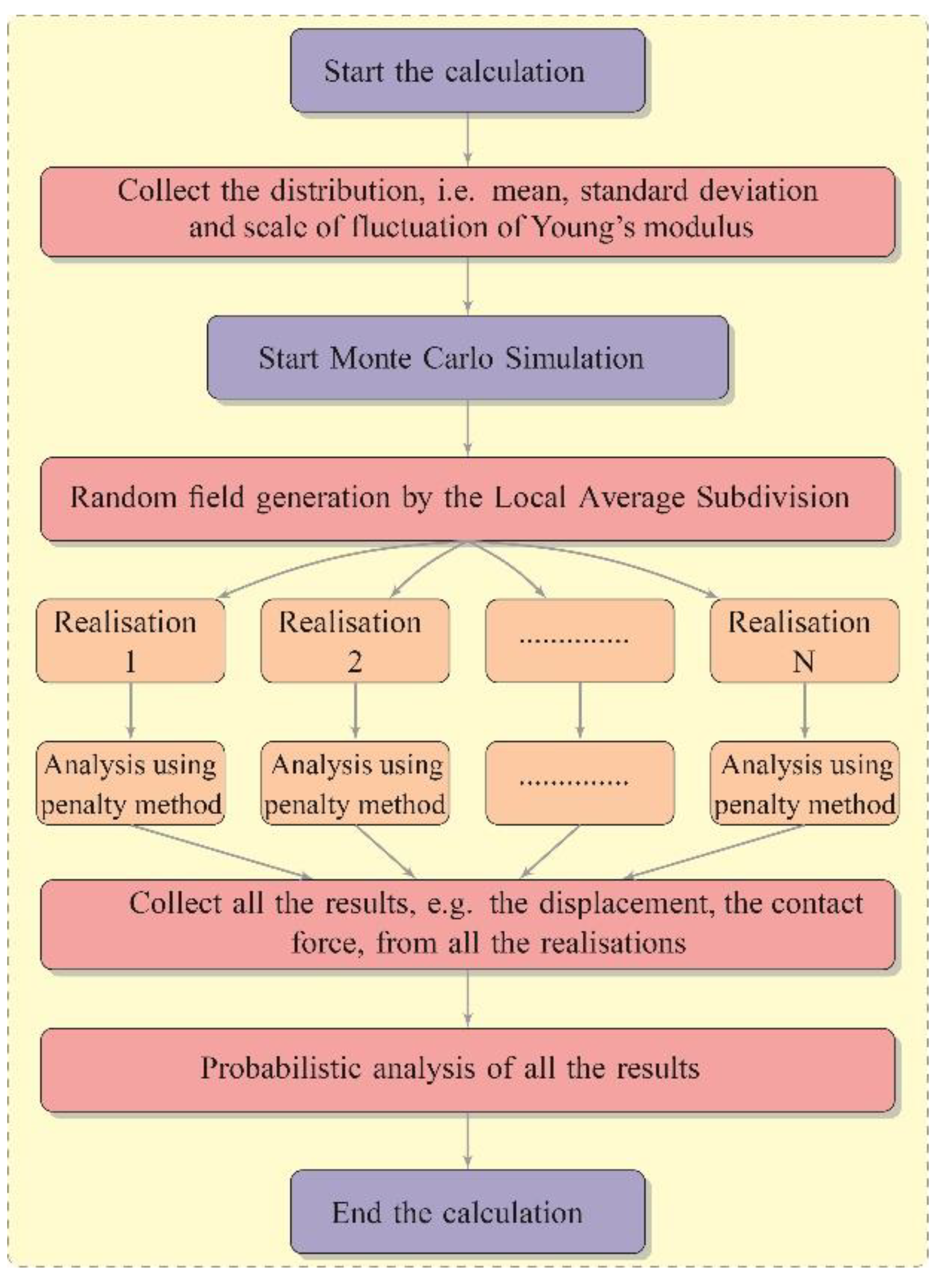
3. Radom Field Generation
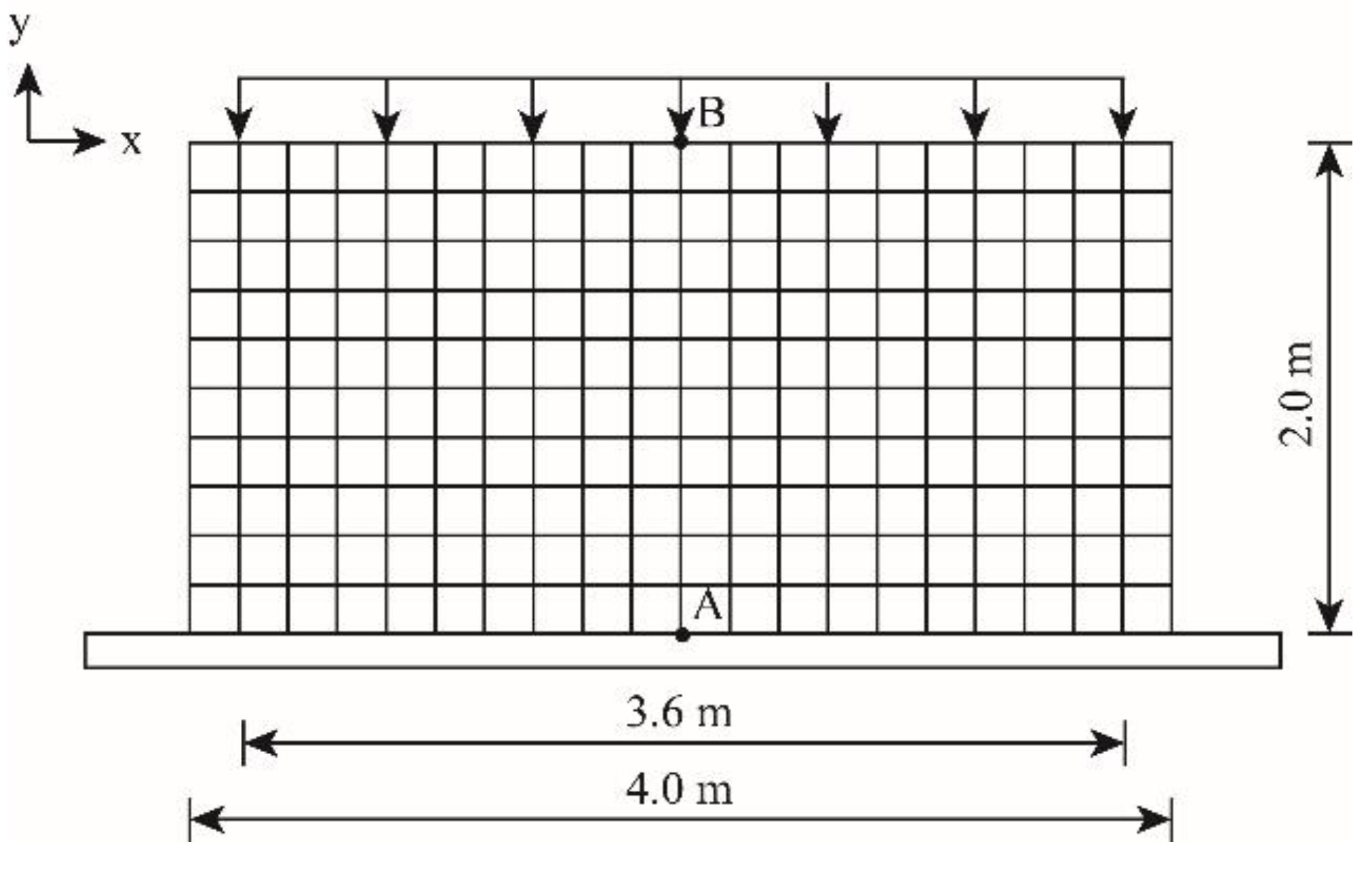
4. Illustrative Example
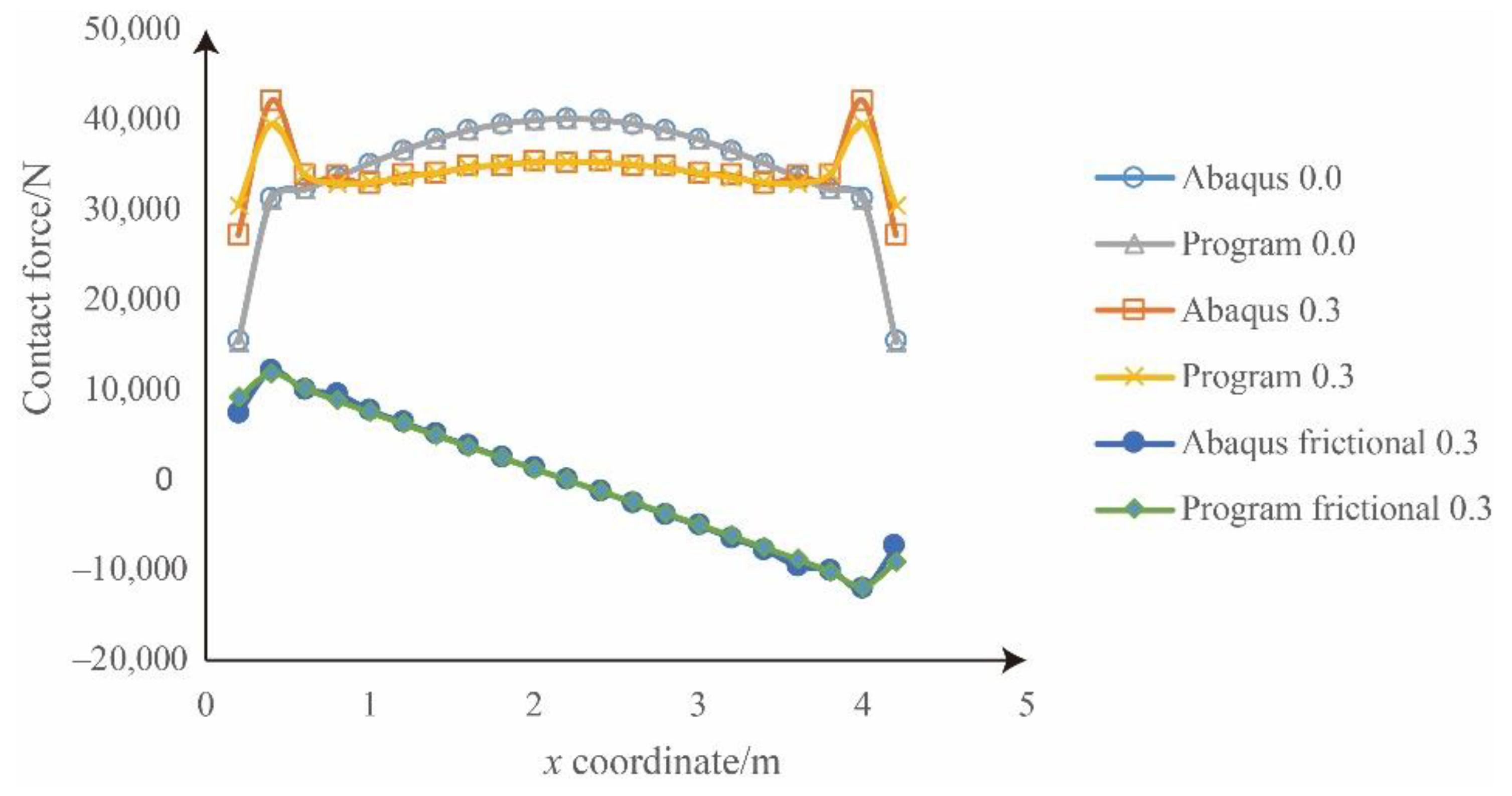
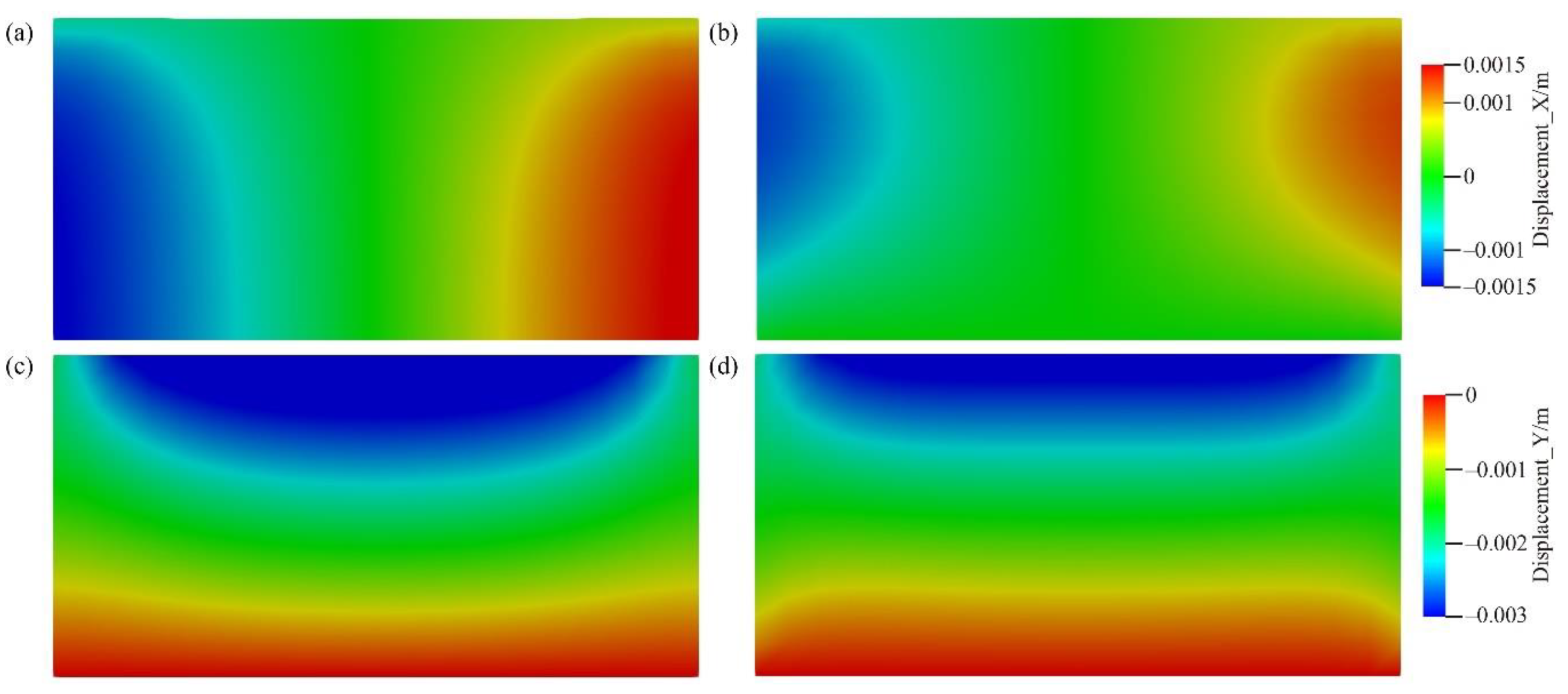
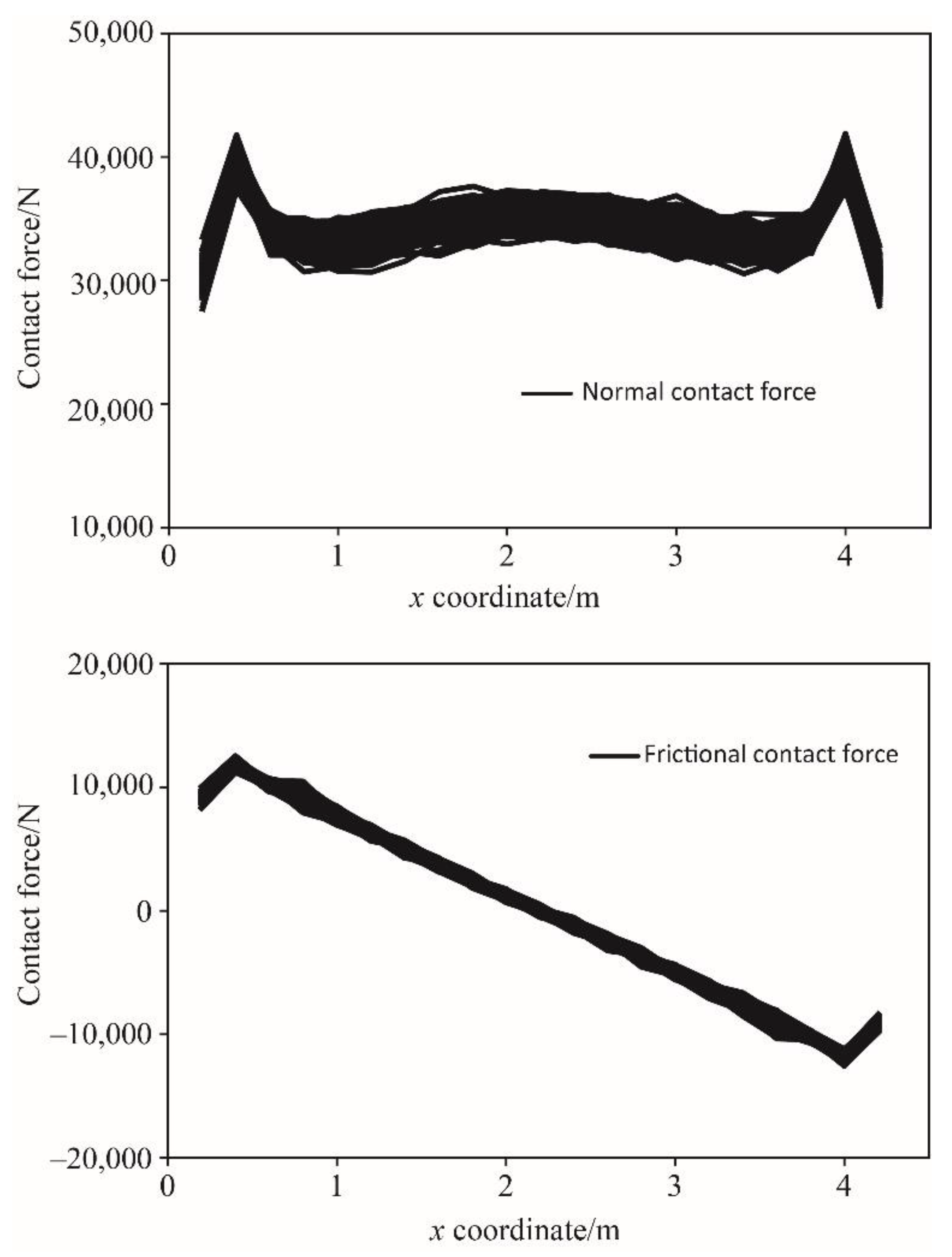
4.1. Validation of the Numerical Results
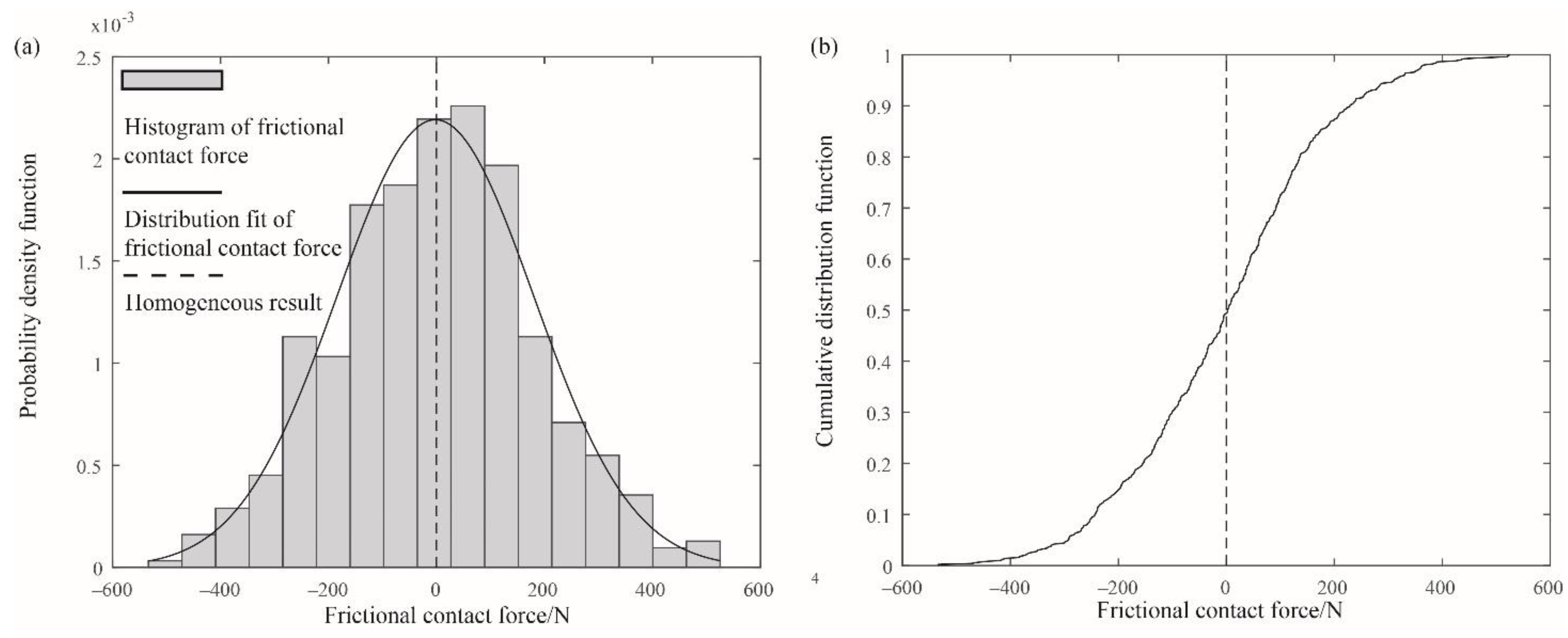
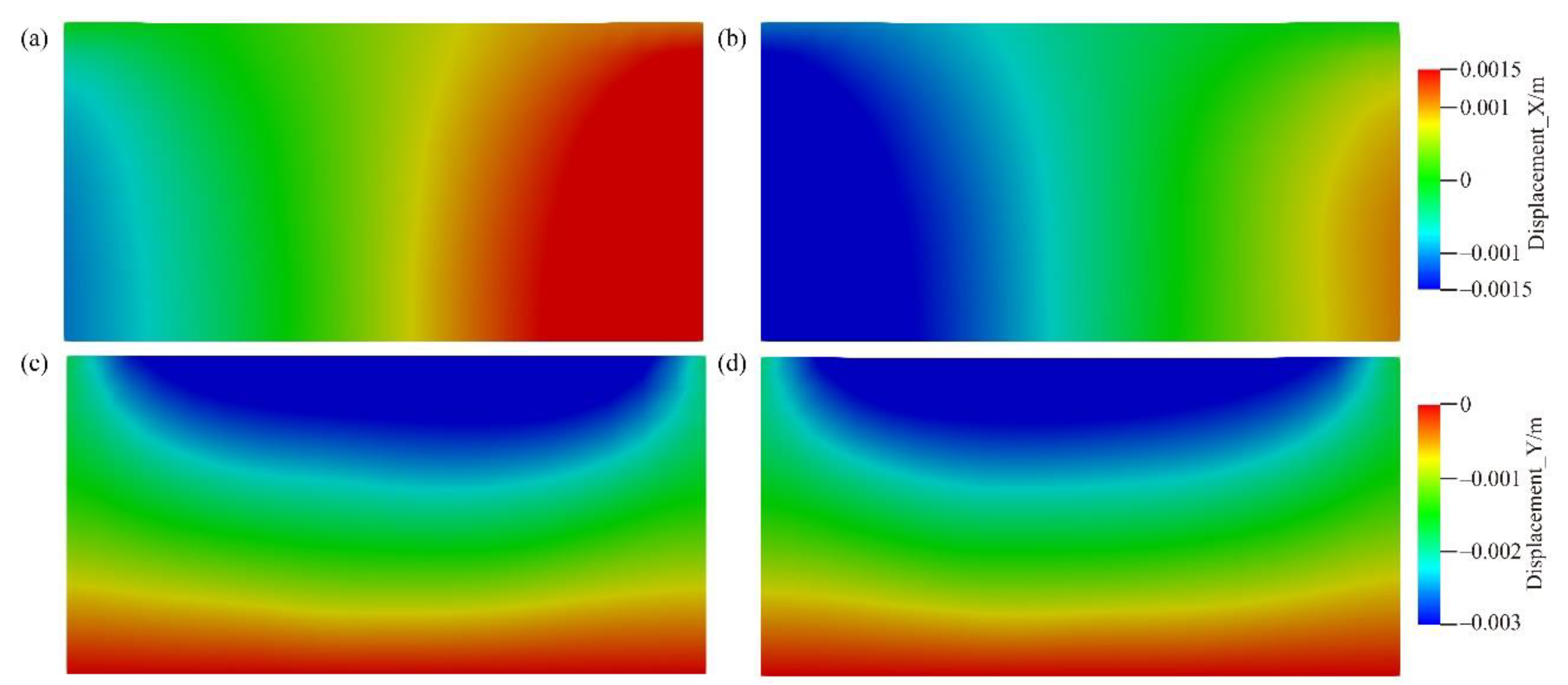
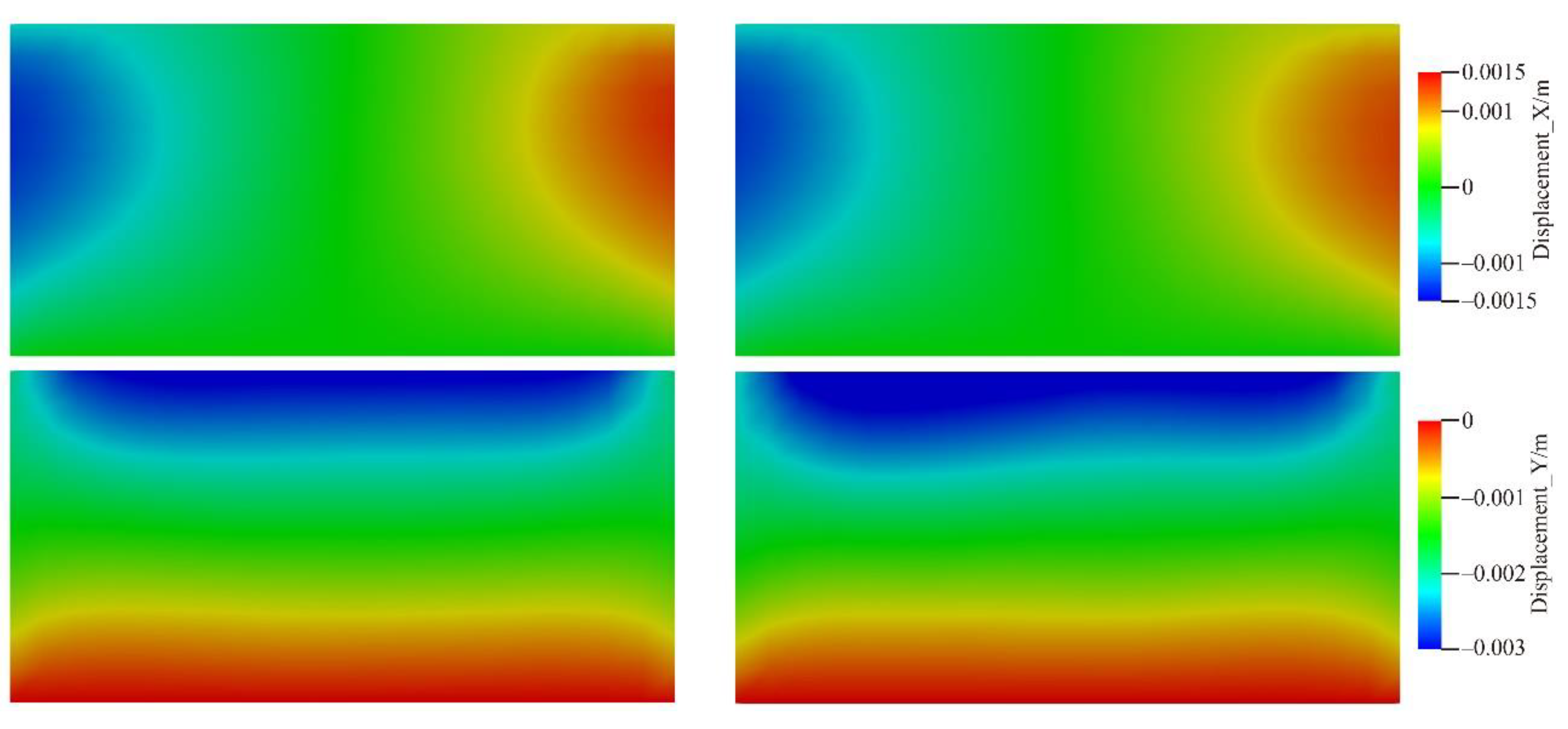
4.2. Comparison between the Homogeneous Case and Heterogeneous Case
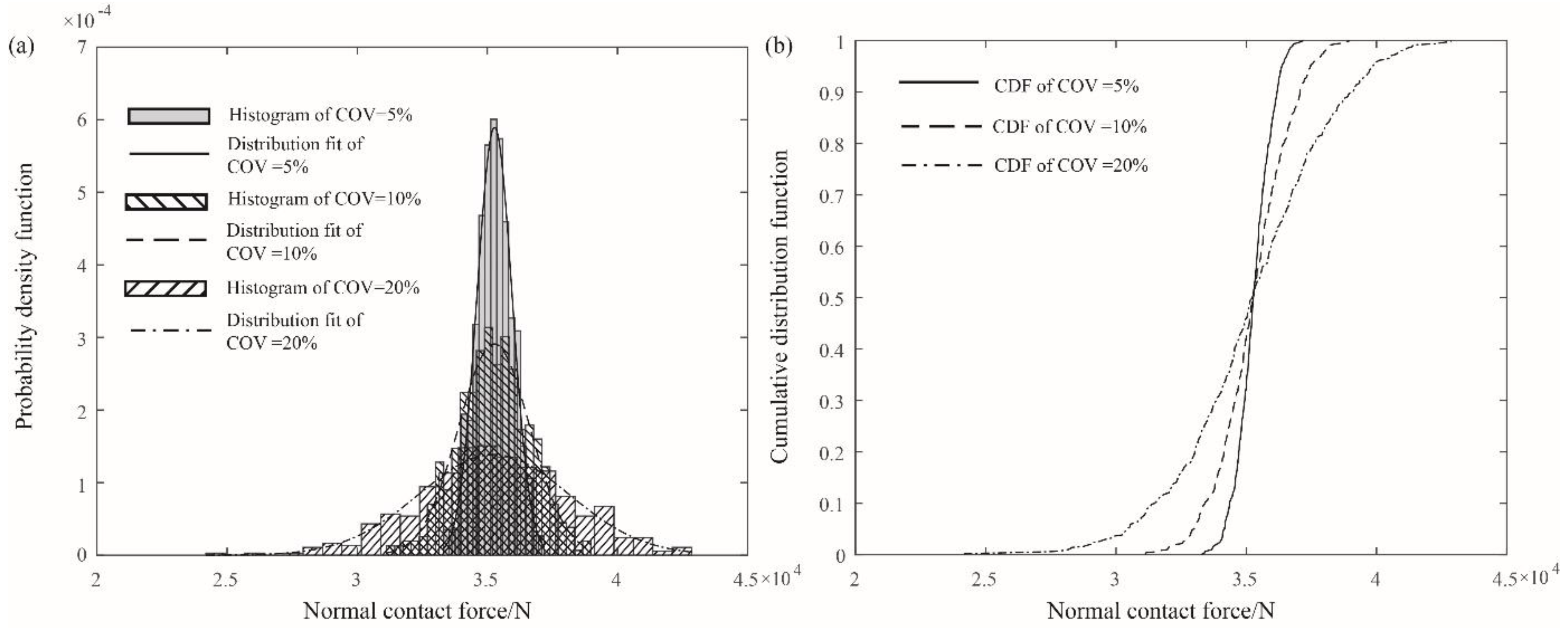
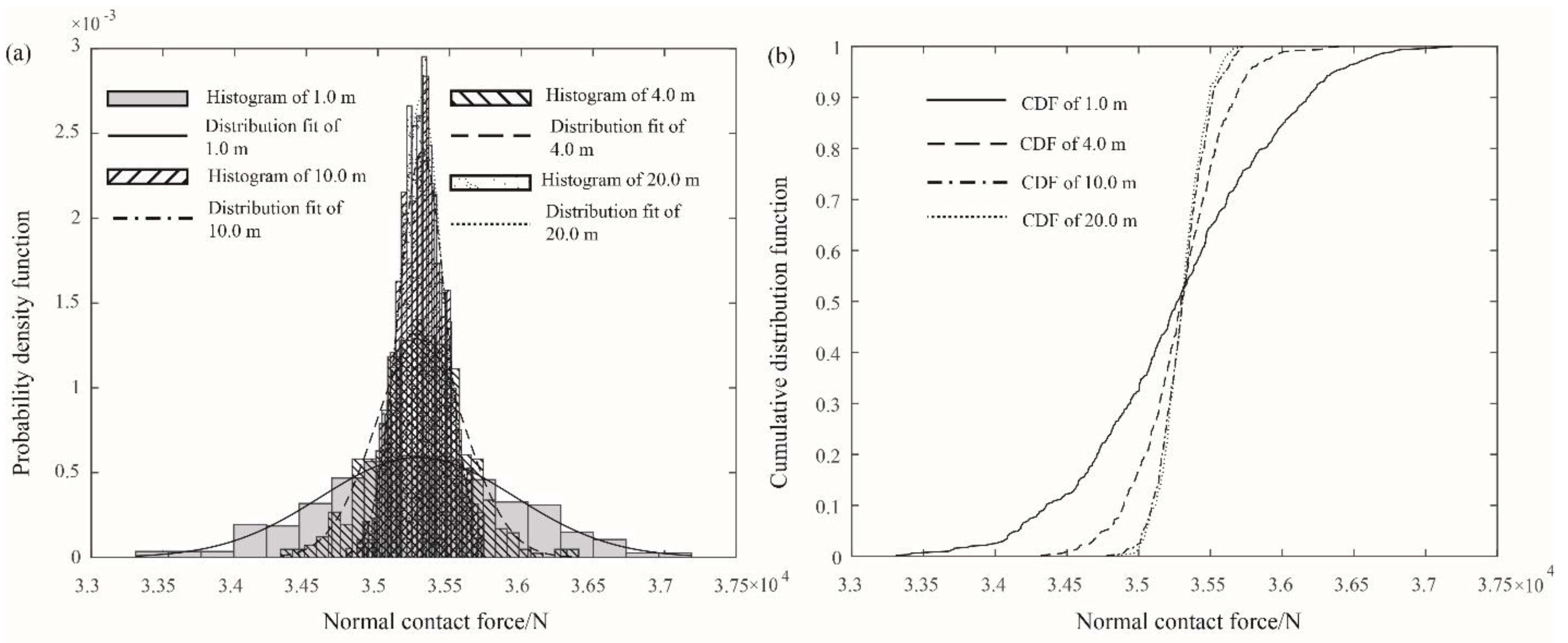
4.3. Influence of the Statistics of Young’s Modulus on the Contact Force
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDF | cumulative distribution function |
| COV | coefficient of variation |
| FEM | finite element method |
| LAS | local average subdivision |
| probability density function |
References
- Zhang, B.Y.; Wang, J.G.; Shi, R. Time-dependent deformation in high concrete-faced rock-fill dam and separation between concrete face slab and cushion layer. Comput. Geotech. 2004, 31, 559–573. [Google Scholar] [CrossRef]
- Liu, S.H.; Wang, L.J.; Wang, Z.J.; Bauer, E. Numerical stress-deformation analysis of cut-off wall in clay-core rockfill dam on thick overburden. Water Sci. Eng. 2016, 9, 219–226. [Google Scholar] [CrossRef]
- Youakim, S.A.S.; El-Metewally, S.E.E.; Chen, W.F. Nonlinear analysis of tunnels in clayey/sandy soil with a concrete lining. Eng. Struct. 2000, 22, 707–722. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar] [CrossRef]
- Desai, C.S.; Zaman, M.M.; Lightner, J.G.; Siriwardane, H.J. Thin-layer element for interfaces and joints. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 19–43. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Taylor, R.L.; Sackman, J.L.; Curnier, A.; Kanoknukulchai, W. A finite element method for a class of contact-impact problems. Comput. Methods Appl. Mech. Eng. 1976, 8, 249–276. [Google Scholar] [CrossRef]
- Papadopoulos, P.; Solberg, J.M. A Lagrange multiplier method for the finite element solution of frictionless contact problems. Math. Comput. Model. 1998, 28, 373–384. [Google Scholar] [CrossRef]
- Oysu, C.; Fenner, R.T. Coupled FEM-BEM for elastoplastic contact problems using Lagrange multipliers. Appl. Math. Model. 2006, 30, 231–247. [Google Scholar] [CrossRef]
- Hansbo, P.; Rashid, A.; Salomonsson, K. Least-squares stabilized augmented Lagrangian multiplier method for elastic contact. Finite Elem. Anal. Des. 2016, 116, 32–37. [Google Scholar] [CrossRef]
- White, D.J.; Enderby, L.R. Finite-element stress analysis of a non-linear problem: A connecting-road eye loaded by means of a pin. J. Strain Anal. 1970, 5, 41–48. [Google Scholar] [CrossRef]
- Babuska, I. The finite element method with penalty. Math. Comput. 1973, 27, 221–228. [Google Scholar] [CrossRef]
- Hird, C.C.; Kwok, C.M. Finite element studies of interface behaviour in reinforced embankments of soft ground. Comput. Geotech. 1989, 8, 111–131. [Google Scholar] [CrossRef]
- Sharma, K.G.; Desai, C.S. Analysis and implementation of thin-layer element for interfaces and joints. J. Eng. Mech. 1992, 118, 2442–2462. [Google Scholar] [CrossRef]
- Qian, X.X.; Yuan, H.N.; Li, Q.M.; Zhang, B.Y. Comparative study on interface elements, thin-layer elements, and contact analysis methods in the analysis of high concrete-faced rockfill dams. J. Appl. Math. 2013, 2013, 320890. [Google Scholar] [CrossRef]
- Weyler, R.; Oliver, J.; Sain, T.; Cante, J.C. On the contact domain method: A comparison of penalty and lagrange multiplier implementations. Comput. Methods Appl. Mech. Eng. 2012, 205–208, 68–82. [Google Scholar] [CrossRef]
- Zeng, M.H.; Wu, Z.M.; Wang, Y.J. A stochastic model considering heterogeneity and crack propagation in concrete. Constr. Build. Mater. 2020, 254, 119289. [Google Scholar] [CrossRef]
- Amato, F.; Moscato, V.; Picariello, A.; Sperlí, G. Diffusion algorithms in multimedia social networks: A preliminary model. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Sydney, Australia, 31 July–3 August 2017; pp. 844–851. [Google Scholar]
- Fenton, G.A.; Griffiths, D.V. Bearing capacity prediction of spatially random c−ϕ soil. Can. Geotech. J. 2003, 40, 54–65. [Google Scholar] [CrossRef]
- Cho, S.E.; Park, H.C. Effect of spatial variability of cross-correlated soil properties on bearing capacity of strip footing. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 1–26. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Seepage beneath water retaining structures founded on spatially random soil. Géotechnique 1993, 43, 577–587. [Google Scholar] [CrossRef]
- Liu, K.; Vardon, P.J.; Hicks, M.A. Sequential reduction of slope stability uncertainty based on temporal hydraulic measurements via the ensemble Kalman filter. Comput. Geotech. 2017, 95, 147–161. [Google Scholar] [CrossRef]
- Yetbarek, E.; Kumar, S.; Ojha, R. Effects of soil heterogeneity on subsurface water movement in agricultural fields: A numerical study. J. Hydrol. 2020, 590, 125420. [Google Scholar] [CrossRef]
- Hicks, M.A.; Li, Y. Influence of length effect on embankment slope reliability in 3D. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 891–915. [Google Scholar]
- ElGhoraiby, M.A.; Manzari, M.T. The effects of base motion variability and soil heterogeneity on lateral spreading of mildly sloping ground. Soil Dyn. Earthq. Eng. 2020, 135, 106185. [Google Scholar] [CrossRef]
- Fenton, G.A. Error evaluation of three random-field generators. J. Eng. Mech. 1994, 120, 2478–2497. [Google Scholar] [CrossRef]
- Kim, N.H. Introduction to Nonlinear Finite Element Analysis; Springer: New York, NY, USA, 2015. [Google Scholar]
- Fenton, G.A.; Vanmarcke, E.H. Simulation of random fields via local average subdivision. J. Eng. Mech. 1990, 116, 1733–1749. [Google Scholar] [CrossRef]
- Samy, K. Stochastic Analysis with Finite Elements in Geotechnical Engineering; University of Manchester: Manchester, UK, 2003. [Google Scholar]
- Spencer, W.A. Parallel Stochastic and Finite Element Modelling of Clay Slope Stability in 3D; University of Manchester: Manchester, UK, 2007. [Google Scholar]


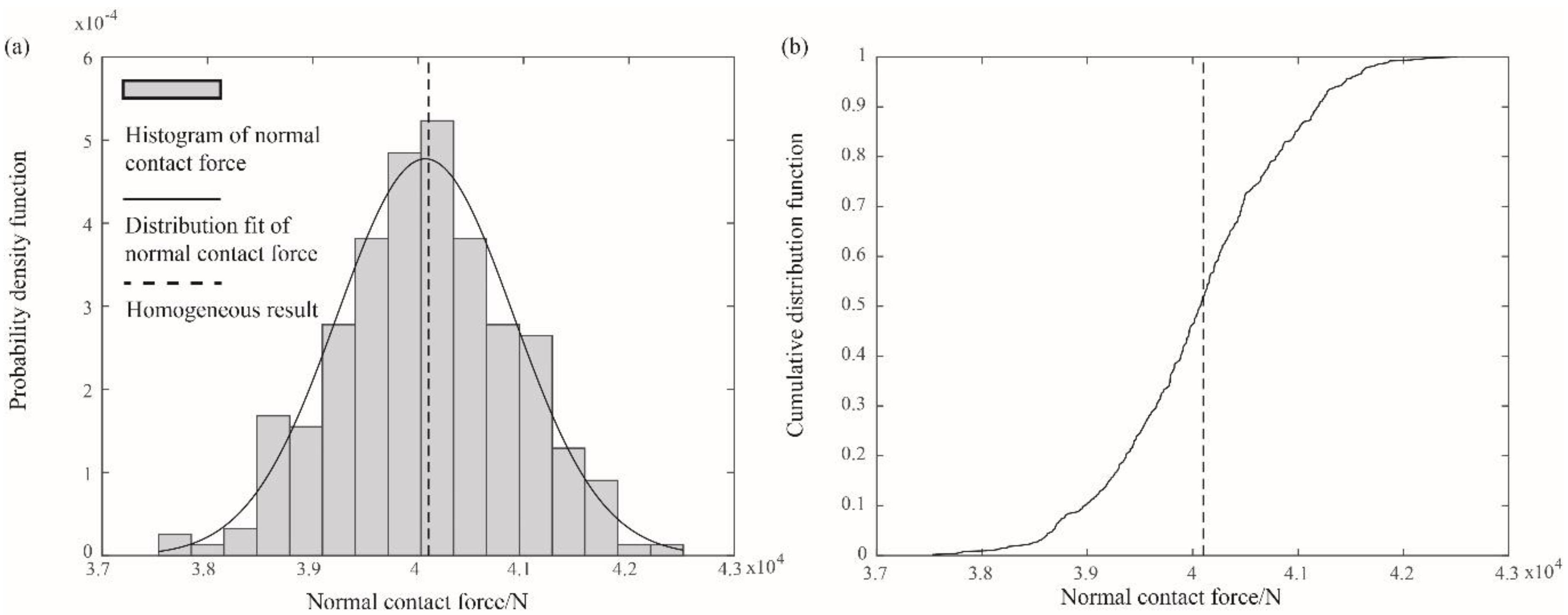
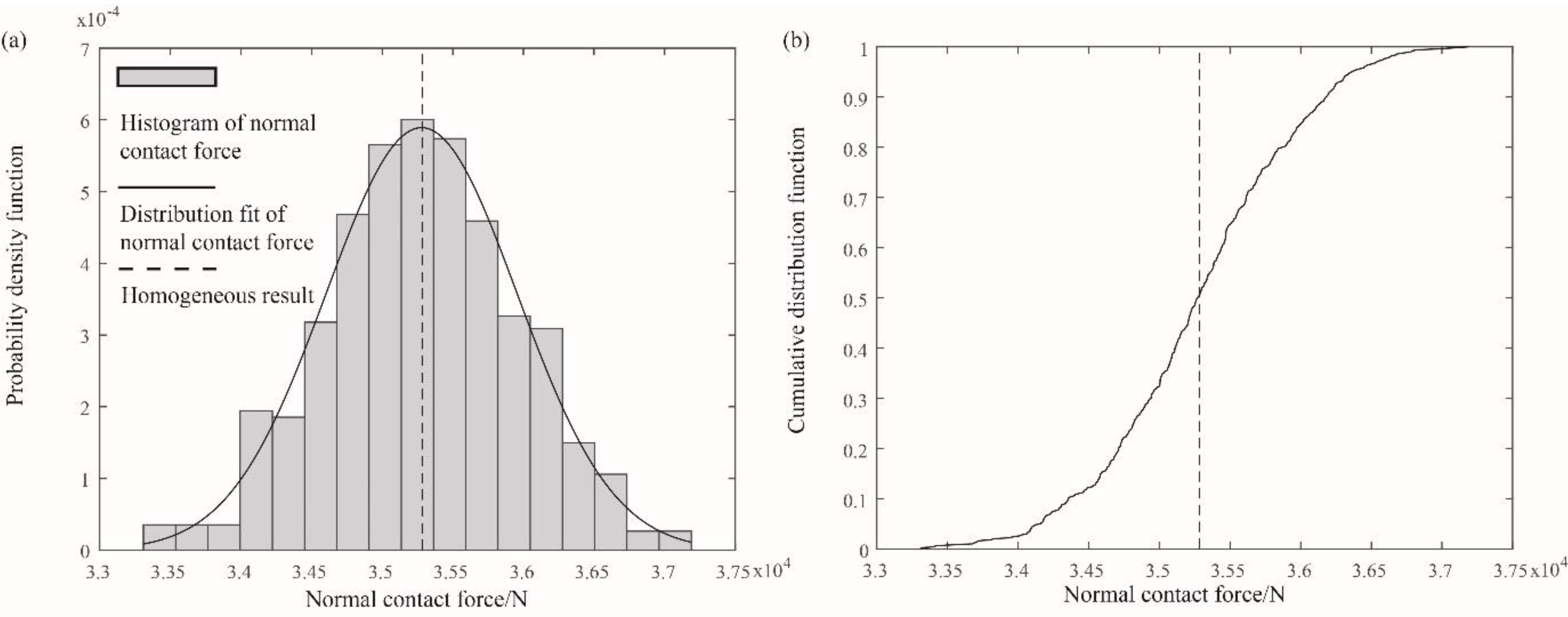


| Horizontal Scale of Fluctuation (m) | Mean of the Normal Contact Force (N) | Standard Deviation of the Normal Contact Force (N) |
|---|---|---|
| 1.0 | 35,279 | 677.2 |
| 4.0 | 35,292 | 310.8 |
| 10.0 | 35,308 | 166.8 |
| 20.0 | 35,304 | 147.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, H.; Liu, K. Influence of Soil Heterogeneity on the Contact Problems in Geotechnical Engineering. Appl. Sci. 2021, 11, 4240. https://doi.org/10.3390/app11094240
Gu H, Liu K. Influence of Soil Heterogeneity on the Contact Problems in Geotechnical Engineering. Applied Sciences. 2021; 11(9):4240. https://doi.org/10.3390/app11094240
Chicago/Turabian StyleGu, Hao, and Kang Liu. 2021. "Influence of Soil Heterogeneity on the Contact Problems in Geotechnical Engineering" Applied Sciences 11, no. 9: 4240. https://doi.org/10.3390/app11094240
APA StyleGu, H., & Liu, K. (2021). Influence of Soil Heterogeneity on the Contact Problems in Geotechnical Engineering. Applied Sciences, 11(9), 4240. https://doi.org/10.3390/app11094240







