Aerodynamic Characteristics of Coupled Twin Circular Bridge Hangers with Near Wake Interference
Abstract
1. Introduction
2. Experimental Apparatus
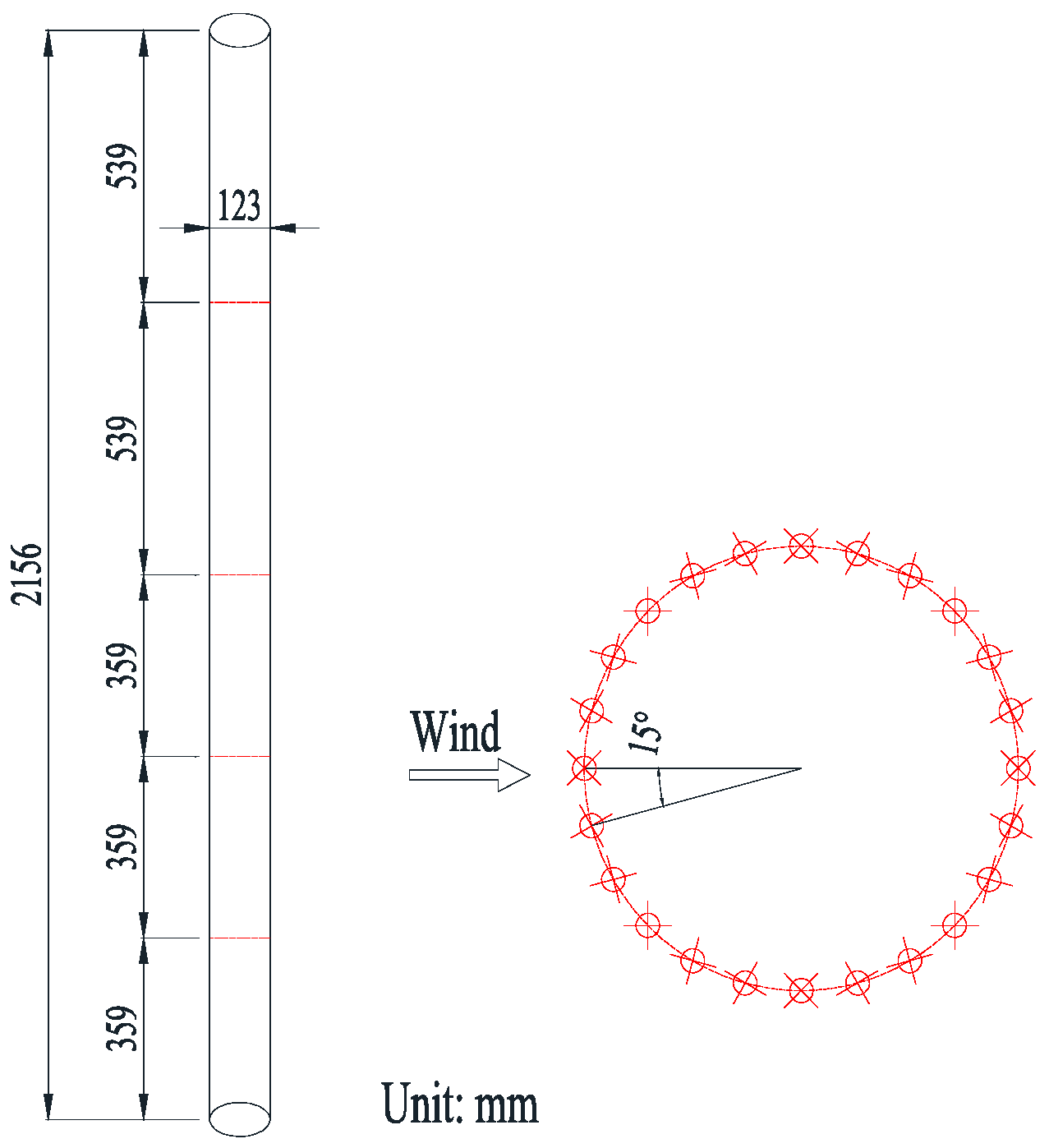
2.1. Description of Stationary Model
2.2. Data Processing Method
3. Results and Discussion
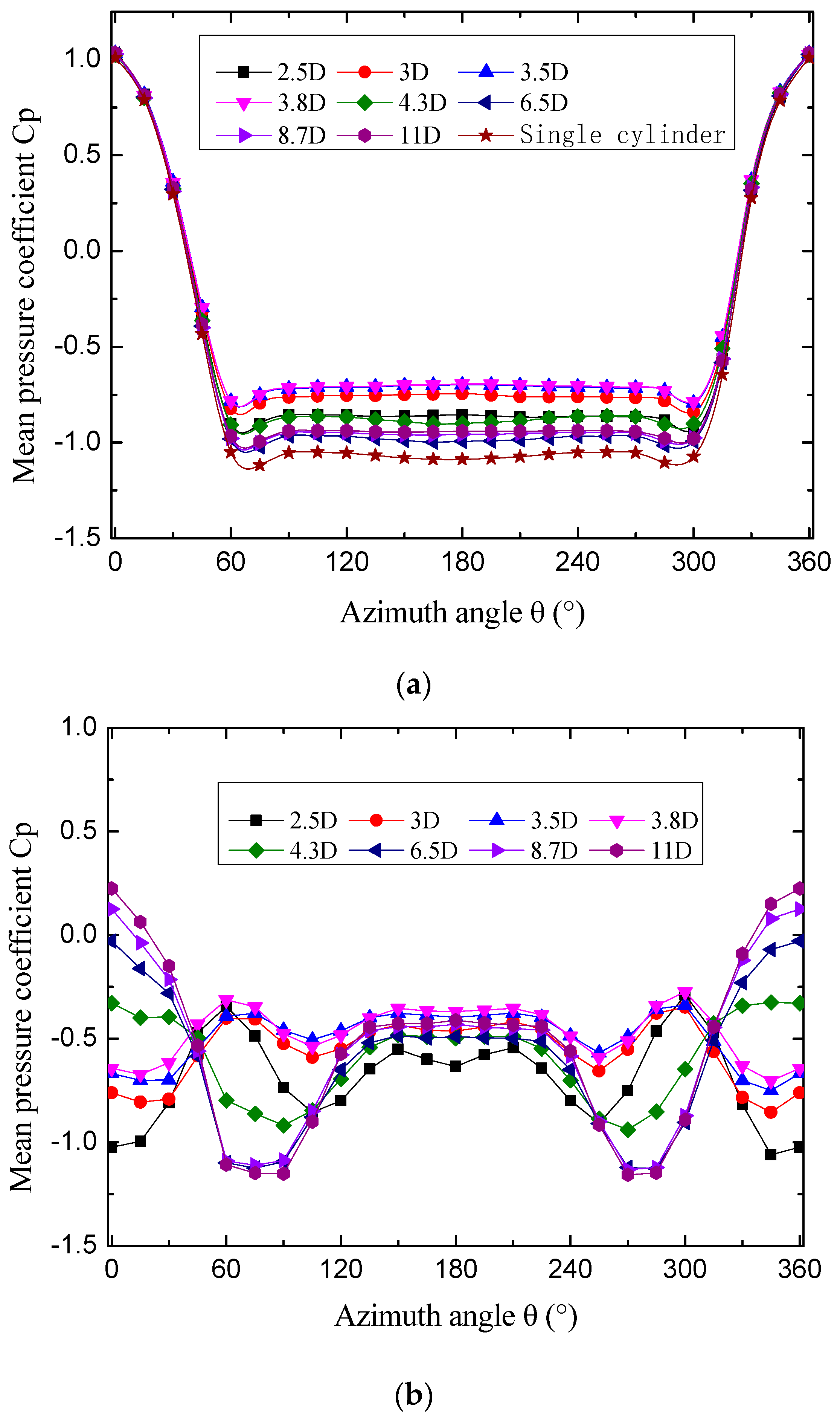
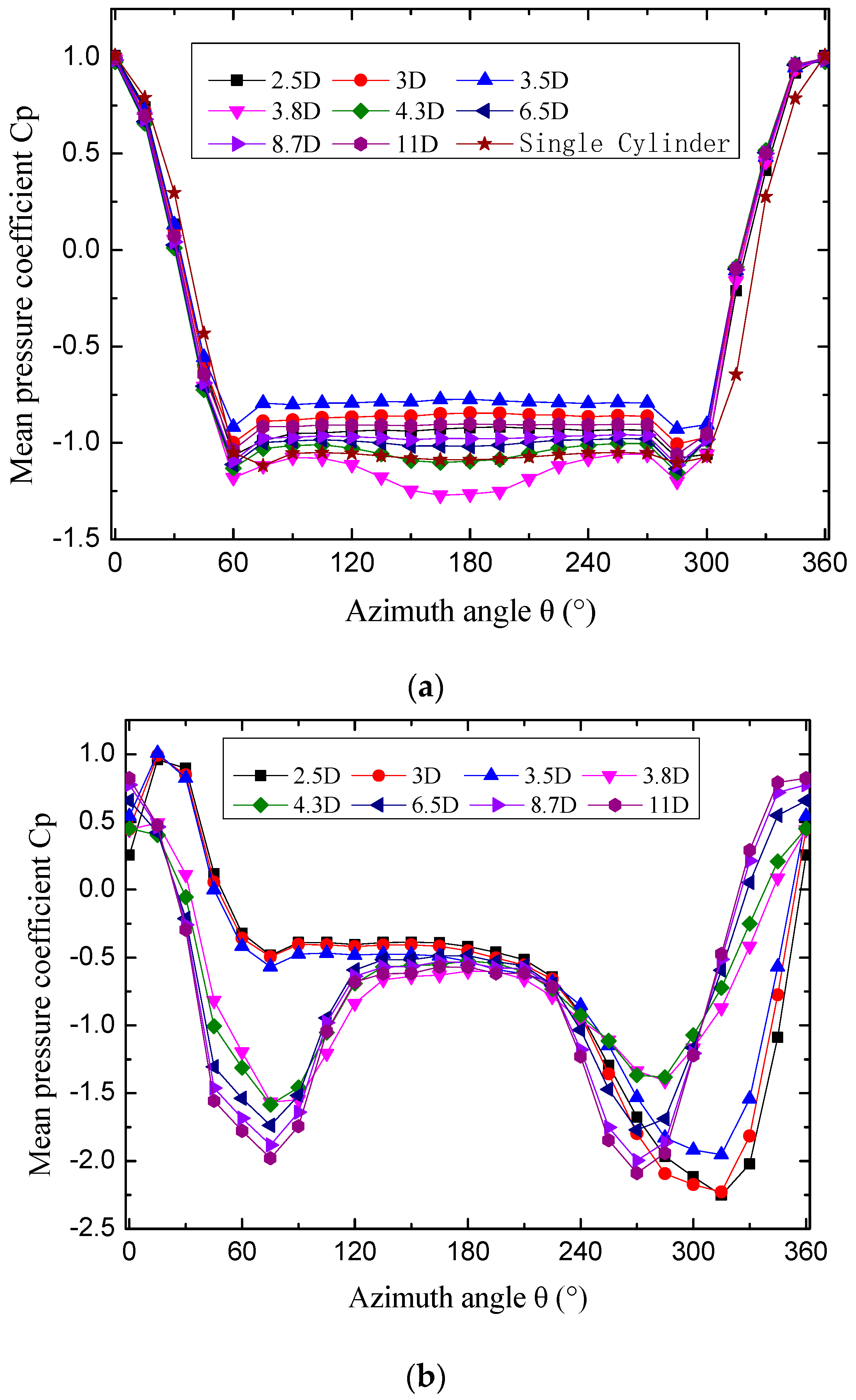
3.1. Time–Mean Pressure
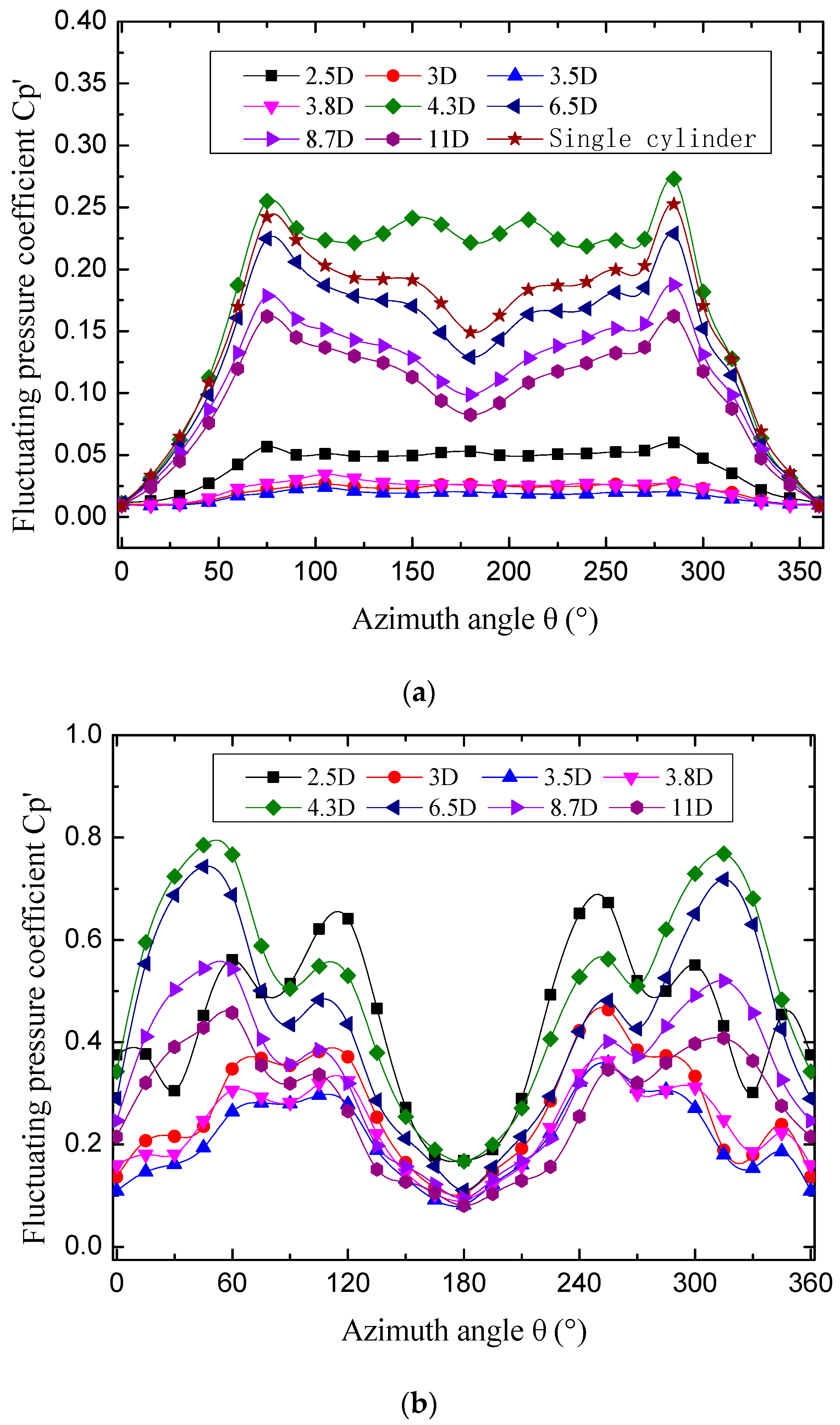
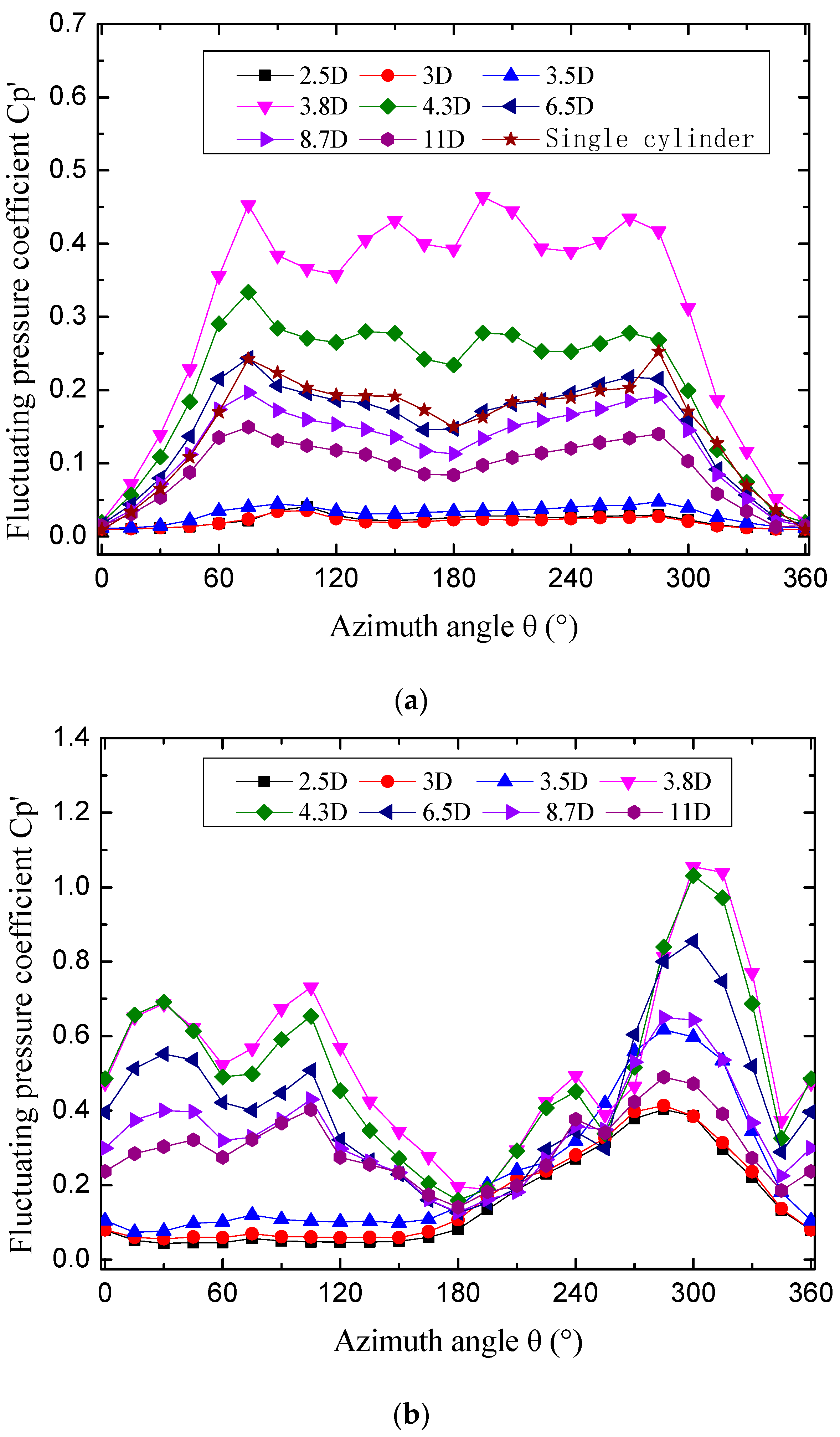
3.2. Fluctuating Pressure
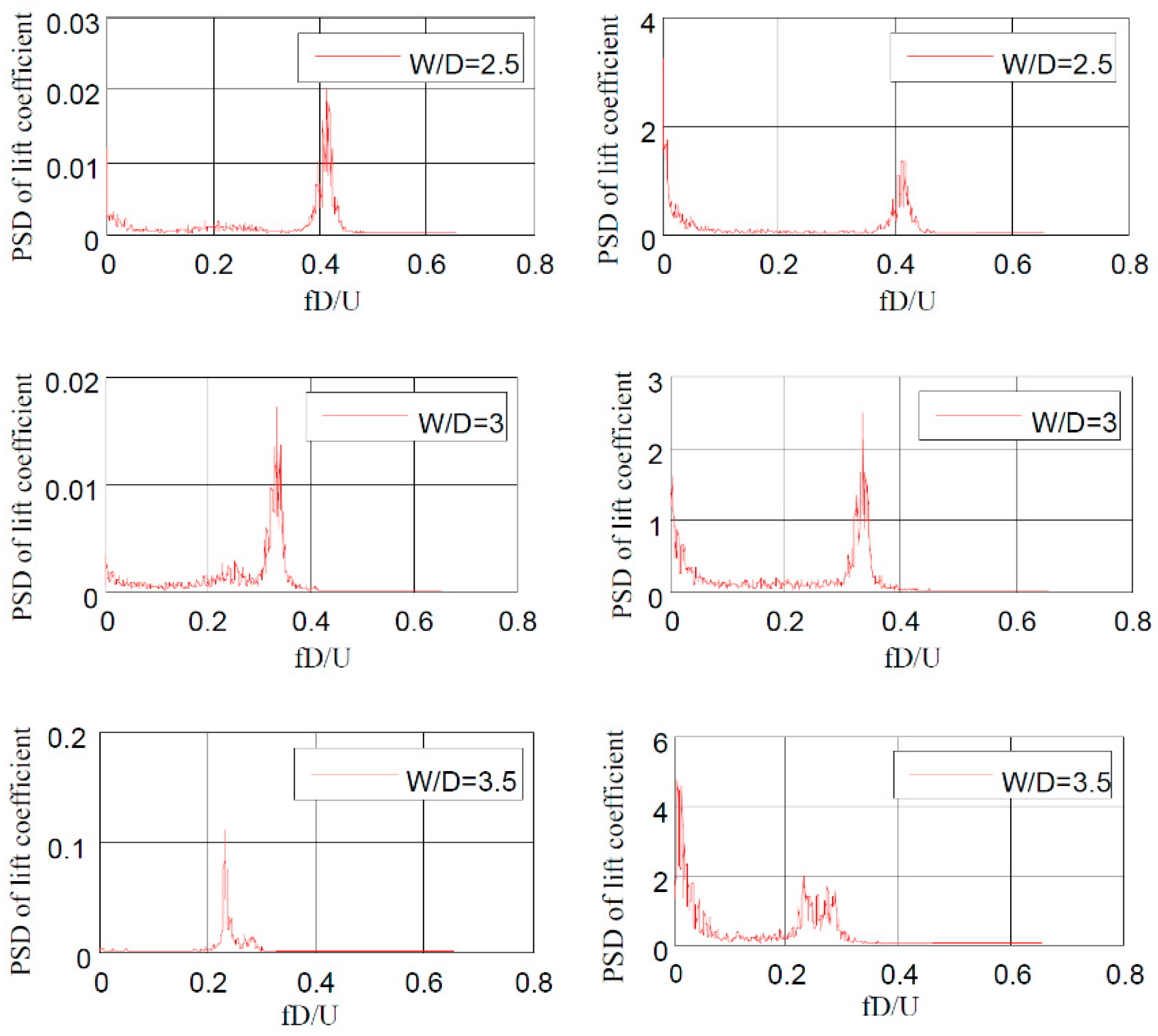
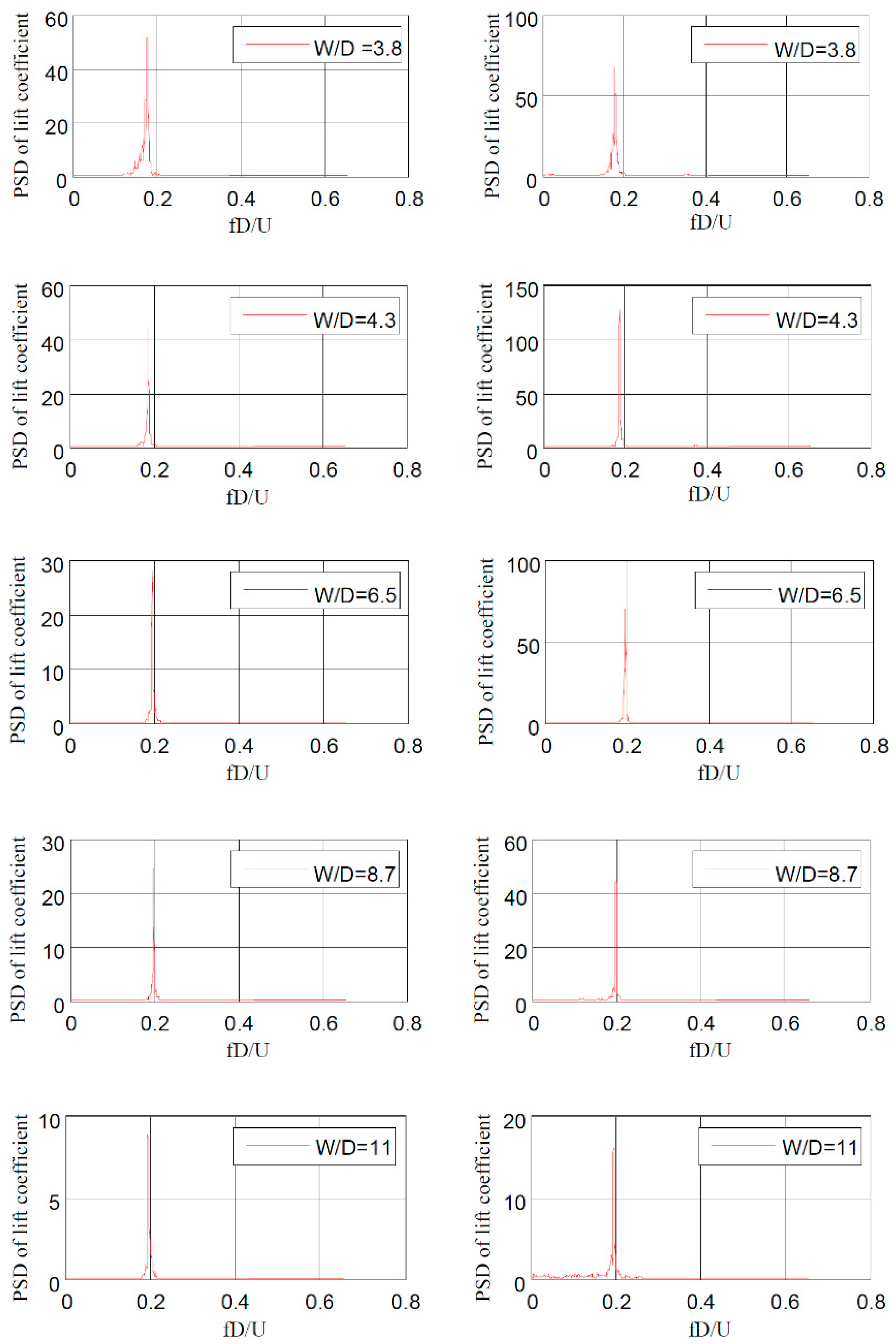
3.3. Spectral Analysis
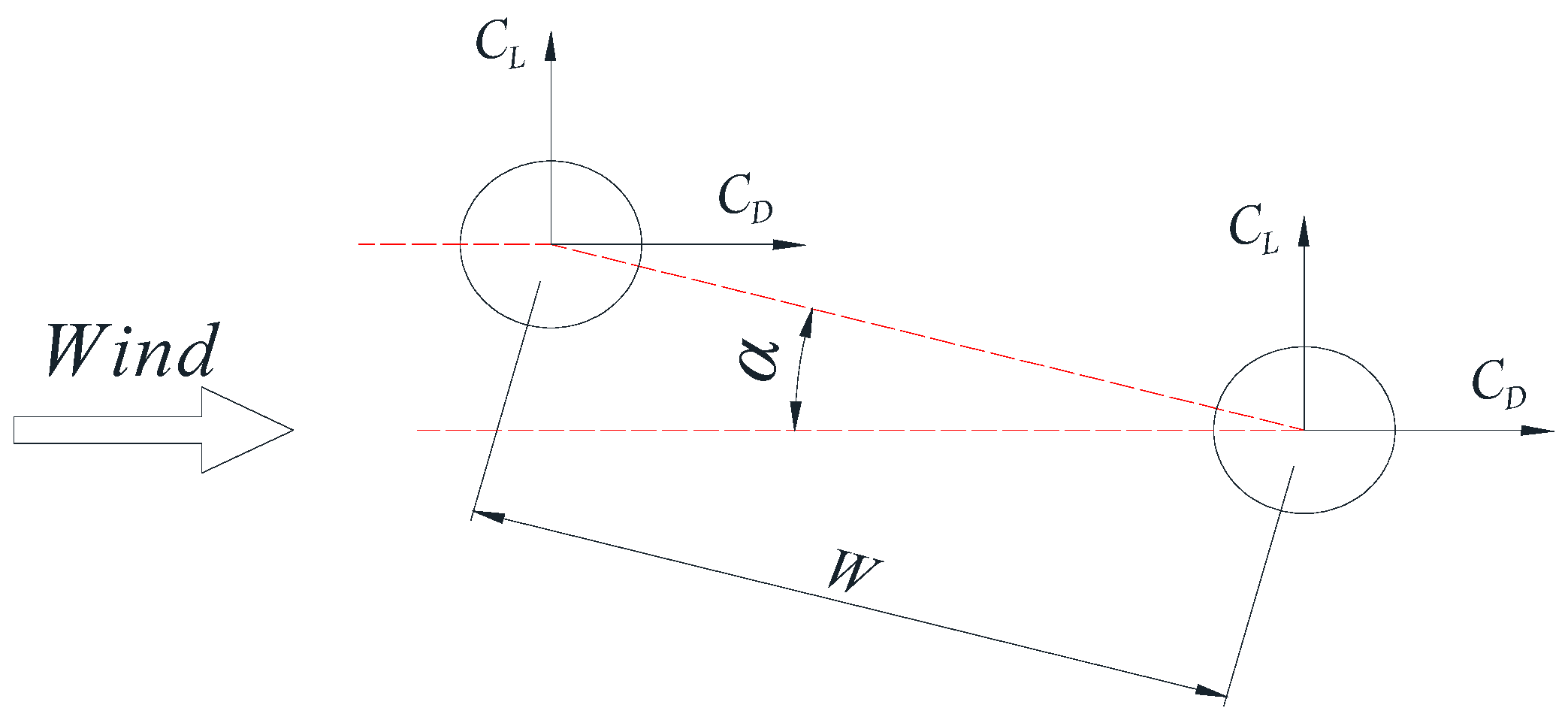
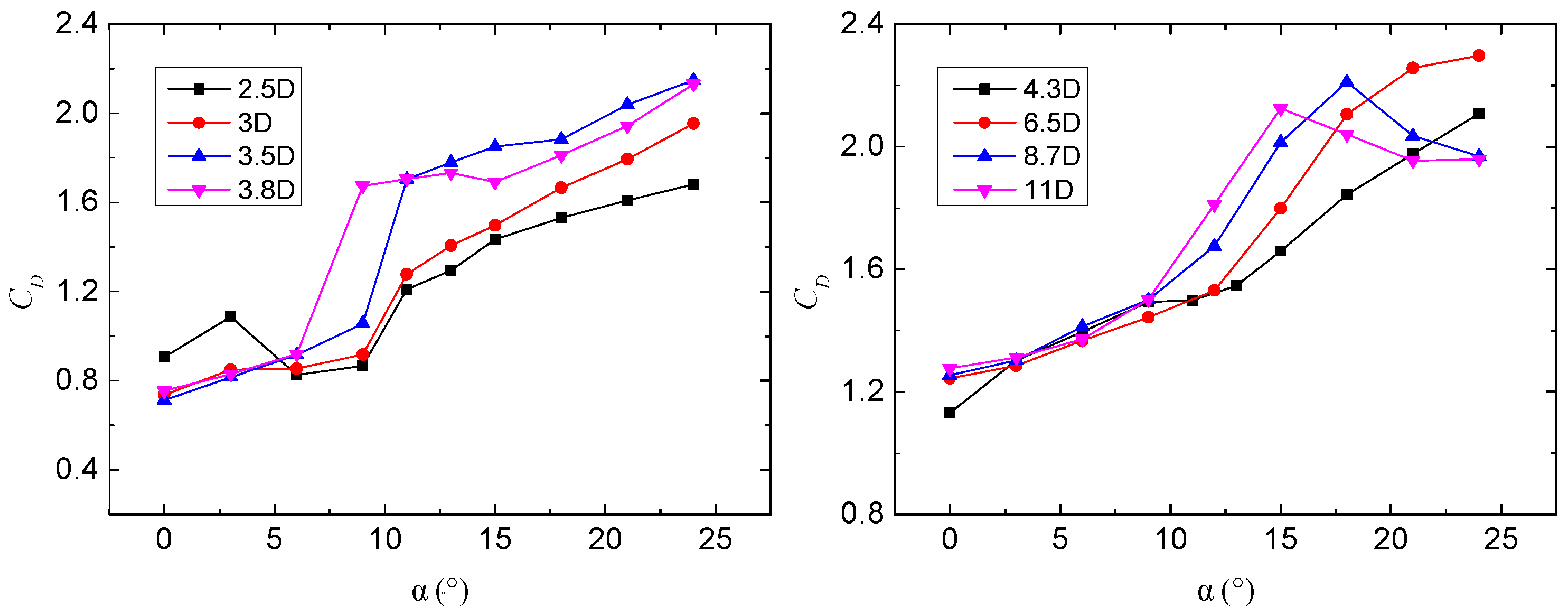
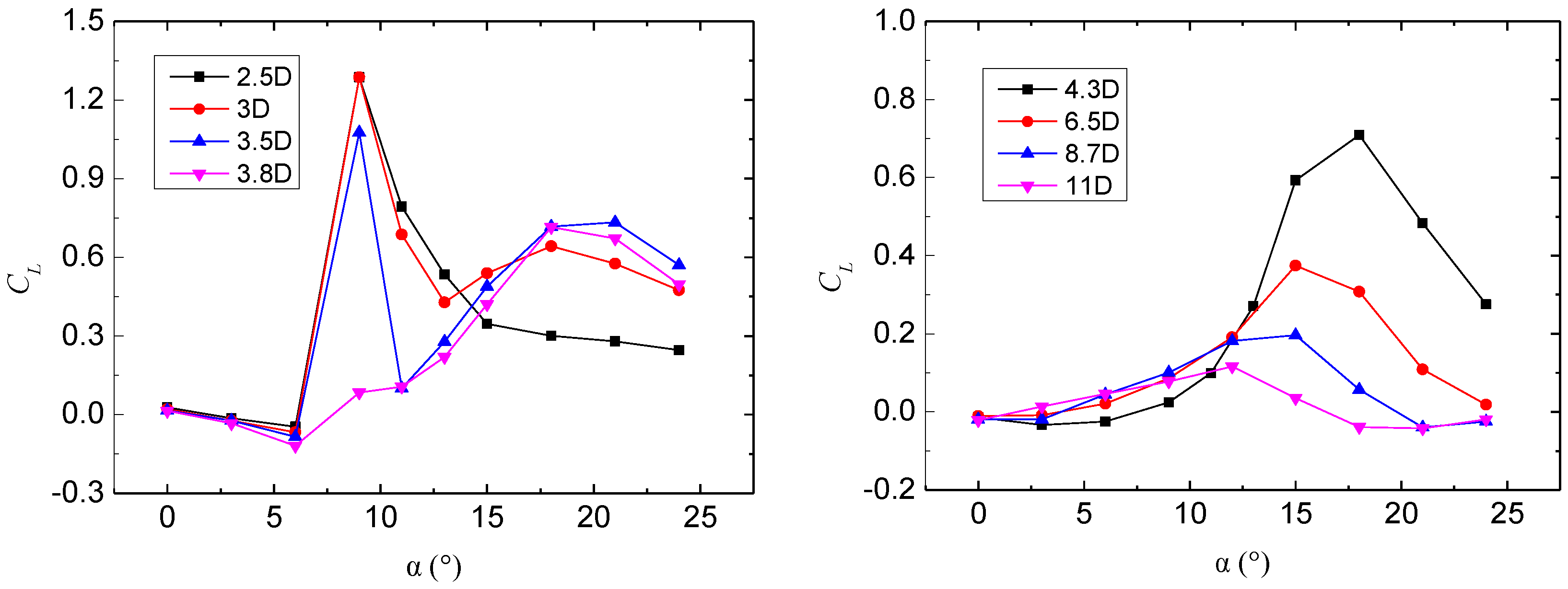
3.4. Aerodynamic Forces
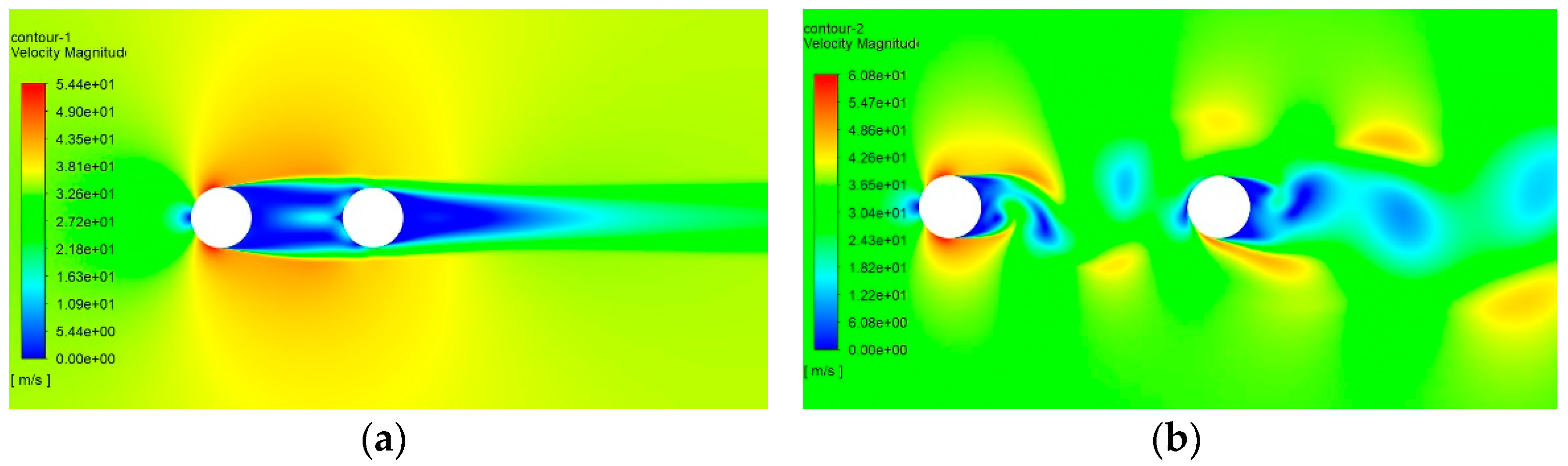
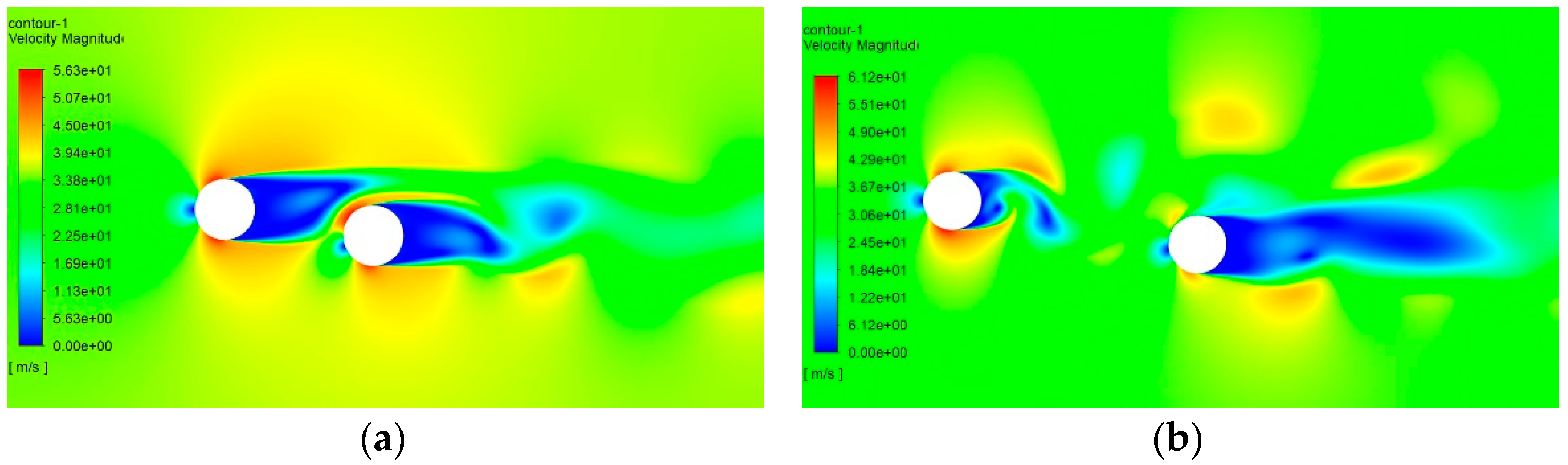
4. Flow Visualization
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| y+ | Number of Mesh | CD | CL | St |
|---|---|---|---|---|
| y+ < 10 | 4.2 × 104 | 1.40 | 0.00 | 0.22 |
| y+ < 3 | 7.6 × 104 | 1.13 | 0.00 | 0.20 |
| y+ < 1.5 | 1.1 × 105 | 0.95 | 0.00 | 0.21 |
| y+ < 0.8 | 1.4 × 105 | 0.94 | 0.00 | 0.21 |
References
- Gimsing, N.J.; Georgakis, C.T. Cable Supported Bridges: Concept and Design; John Wiley Sons: Chichester, UK, 2011. [Google Scholar]
- Katsuchi, H.; Jones, N.P.; Scanlan, R.H.; Akiyama, H. Multi-mode flutter and buffeting analysis of the Akashi-Kaikyo bridge. J. Wind Eng. Ind. Aerodyn. 1998, 77, 431–441. [Google Scholar] [CrossRef]
- Larsen, A. Aerodynamic aspects of the final design of the 1624 m suspension bridge across the Great Belt. J. Wind Eng. Ind. Aerodyn. 1993, 48, 261–285. [Google Scholar] [CrossRef]
- Hua, X.G.; Chen, Z.Q.; Lei, X.; Wen, Q.; Niu, H.W. Monitoring and control of wind-induced vibrations of hanger ropes of a suspension bridge. Smart Struct. Syst. 2019, 31, 683–693. [Google Scholar]
- Wardlaw, R.L.; Cooper, K.R.; Ko, R.G.; Watts, J.A. Wind tunnel and analytical investigations into the aeroelastic behaviors of bundle conductors. IEEE Trans. Power Appar. Syst. 1975, 94, 642–653. [Google Scholar] [CrossRef]
- Wardlaw, R.L. Interference and Proximity Effects in Wind-Excited Vibrations of Structures; Springer: Wien, Germany, 1994. [Google Scholar]
- Paidoussis, M.; Price, S.; de Langre, E. Fluid-Structure Interactions: Cross-Flow-Induced Instabilities; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- An, Y.H.; Wang, C.Q.; Li, S.L.; Wang, D.W. Galloping of steepled main cables in long-span suspension bridges during construction. Wind Struct. 2016, 23, 595–613. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Review of flow interference between two circular cylinders various arrangements. J. Fluids Eng. 1977, 99, 618–633. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow induced oscillations of two interfering circular cylinders. J. Fluids Eng. 1985, 99, 618–633. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. Flow around Circular Cylinders, Vol. 1. Fundamentals; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Matsumoto, M.; Shiraishi, N.; Shirato, H. Aerodynamic instabilities of twin circular cylinders. J. Wind Eng. Ind. Aerodyn. 1990, 33, 91–100. [Google Scholar] [CrossRef]
- Li, S.L.; An, Y.H.; Wang, C.Q.; Wang, D.W. Experimental and numerical studies on galloping of the flat-topped main cables for the long span suspension bridge during construction. J. Wind Eng. Ind. Aerodyn. 2017, 163, 24–32. [Google Scholar] [CrossRef]
- Zhou, Y.; Alam, M.M. Wake of two interacting circular cylinders: A review. Int. J. Heat Fluid Flow 2016, 62, 510–537. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibrations; Van Nostrand Reinhold: New York, NY, USA, 1990. [Google Scholar]
- Zdravkovich, M.M. Flow around Circular Cylinders, Vol. 2. Applications; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Kim, B.; Tse, K.T.; Yoshida, A.; Chen, Z.S.; Phuc, P.V.; Park, H.S. Investigation of flow visualization around linked tall buildings with circular sections. Build. Environ. 2019, 153, 60–76. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.T.; Tamura, Y. POD analysis for aerodynamic characteristics of tall linked buildings. J. Wind Eng. Ind. Aerodyn. 2018, 181, 126–140. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.T.; Yoshida, A.; Tamura, Y.; Chen, Z.S. Statistical analysis of wind-induced pressure fields and PIV measurements on two buildings. J. Wind Eng. Ind. Aerodyn. 2019, 188, 161–174. [Google Scholar] [CrossRef]
- Zhao, M.; Yan, G.R. Numerical simulation of vortex-induced vibration of two circular cylinders of different diameters at low Reynolds number. Phys. Fluids 2013, 25, 083601. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.K. Wake galloping phenomena between two parallel/unparallel Cylinders. Wind Struct. 2014, 18, 511–528. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Liu, M.G.; Liu, Z.W. Experimental study on aerodynamic interference of tandem cables based on aeroelastic model. J. Vib. Shock 2008, 27, 7–11. [Google Scholar]
- Tokoro, S.; Homatsu, H.; Nakasu, M.; Mizuguchi, K.; Kasuga, A. A study on wake-galloping employing full aeroelastic twin cable model. J. Wind Eng. Ind. Aerodyn. 2010, 88, 247–261. [Google Scholar] [CrossRef]
- Takeguchi, M.; Fukunaga, S. Aerodynamic stabilization for wake-induced vibration in parallel hanger ropes of the Akashi Kaikyo Bridge. Wind Eng. JAWE 2012, 37, 300–306. [Google Scholar] [CrossRef][Green Version]
- Zhao, M. Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by side arrangements at a low Reynolds number of 150. Phys. Fluids 2013, 25, 123601. [Google Scholar] [CrossRef]
- Kim, S.; Alam, M.M.; Sakamoto, H.; Zhou, Y. Flow-induced vibrations of two circular cylinders in tandem arrangement. Part1: Characteristics of vibration. J. Wind Eng. Ind. Aerodyn. 2009, 97, 304–311. [Google Scholar] [CrossRef]
- Sun, T.F.; Gu, Z.F.; He, D.X.; Zhang, L.L. Fluctuating Pressure on Two Circular Cylinders at High Reynolds Numbers. J. Wind Eng. Ind. Aerodyn. 1992, 41, 577–588. [Google Scholar] [CrossRef]
- Wen, Q.; Hua, X.G.; Lei, X.; Chen, Z.Q.; Niu, H.W. Experimental study of wake-induced instability of coupled parallel hanger ropes for suspension bridges. Eng. Struct. 2018, 167, 175–187. [Google Scholar] [CrossRef]
- De Wang, J.S.; Fan, D.; Lin, K. A review on flow-induced vibration of offshore circular cylinders. J. Hydrodyn. 2020, 32, 415–440. [Google Scholar] [CrossRef]
- Lin, K.; Fan, D.; Wang, J. Dynamic response and hydrodynamic coefficients of a cylinder oscillating in crossflow with an upstream wake interference. Ocean Eng. 2020, 209, 107520. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. The effects of interference between circular cylinders in cross flow. J. Fluids Eng. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Cigada, A.; Diana, G.; Falco, M.; Fossati, F.; Manenti, A. Vortex shedding and wake-induced vibrations in single and bundle cables. J. Wind Eng. Ind. Aerodyn. 1997, 72, 253–263. [Google Scholar] [CrossRef]
- Mederios, E.B.; Zdravkovich, M.M. Interference-induced oscillation of two un- equal cylinders. J. Wind Eng. Ind. Aerodyn. 1992, 41, 753–762. [Google Scholar] [CrossRef]
- Alam, M.M.; Moriya, M.; Takai, K.; Sakamoto, H. Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number. J. Wind Eng. Ind. Aerodyn. 2003, 91, 139–154. [Google Scholar] [CrossRef]
- Alam, M.M.; Sakamoto, H.; Zhou, Y. Effect of a T-shaped plate on reduction in fluid forces acting on two tandem circular cylinders in a cross-flow. J. Wind Eng. Ind. Aerodyn. 2006, 94, 525–551. [Google Scholar] [CrossRef]
- Sumner, D.; Price, S.J.; Païdoussis, M.P. Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 2000, 411, 263–303. [Google Scholar] [CrossRef]
- Ribeiro, J.D. Effects of surface roughness on the two-dimensional flow past circular cylinders II: Fluctuating forces and pressures. J. Wind Eng. Ind. Aerodyn. 1991, 37, 311–326. [Google Scholar] [CrossRef]
- Mizushima, J.; Suehiro, N. Instability and transition of flow past two tandem circular cylinders. Phys. Fluids 2005, 17, 104107. [Google Scholar] [CrossRef]
- Acampora, A.; Macdonald, J.H.G.; Georgakis, C.T.; Nikitas, N. Identification of aeroelastic forces and static drag coefficients of a twin cable bridge stay from full-scale ambient vibration measurements. J. Wind Eng. Ind. Aerodyn. 2014, 124, 90–98. [Google Scholar] [CrossRef]
- Hu, G.; Tse, K.T.; Kwok, K.C.S.; Chen, Z.S. Pressure measurements on inclined square prisms. J. Wind Eng. Ind. Aerodyn. 2015, 142, 232–245. [Google Scholar] [CrossRef]
- Zu, G.B.; Lam, K.M. Across-wind excitation mechanism for interference of twin tall buildings in staggered arrangement. J. Wind Eng. Ind. Aerodyn. 2018, 177, 167–185. [Google Scholar] [CrossRef]
- Batham, J.P. Pressure Distributions on Circular Cylinders at Critical Reynolds Numbers. J. Fluid Mech. 1973, 57, 209–228. [Google Scholar] [CrossRef]
- Wang, Y.T.; Yan, Z.M.; Wang, H.M. Numerical simulation of low-Reynolds number flows past two tandem cylinders of different diameters. Water Sci. Eng. 2013, 6, 433–445. [Google Scholar]
- Assi, G.R.S.; Bearman, P.W.; Meneghini, J.R. On the wake-induced vibration of tandem circular cylinders: The vortex interaction excitation mechanism. J. Fluids Mech. 2010, 661, 365–401. [Google Scholar] [CrossRef]
- Igarashi, T. Characteristics of the flow around two circular cylinders arranged in tandem. Bull. JSME 1981, 24, 323–331. [Google Scholar] [CrossRef]
- Arie, M.; Kiya, M.; Moriya, M.; Mori, H. Pressure Fluctuations on the Surface of Two Circular Cylinders in Tandem Arrangement. J. Fluids Eng. 1983, 105, 161–166. [Google Scholar] [CrossRef]
- Gu, Z.F.; Sun, T. On interference between two circular cylinders in staggered arrangement at high subcritical Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 1999, 80, 287–309. [Google Scholar] [CrossRef]
- Gu, Z.F.; Sun, T.F.; He, D.X.; Zhang, L.L. Two circular cylinders in high-turbulence flow at supercritical Reynolds number. J. Wind Eng. Ind. Aerodyn. 1993, 49, 379–388. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.T. POD analysis of aerodynamic correlations and wind-induced responses of two tall linked buildings. Eng. Struct. 2018, 176, 369–384. [Google Scholar] [CrossRef]
- Schewe, G. On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 1983, 133, 265–285. [Google Scholar] [CrossRef]
- Wang, C.Q.; Hua, X.G.; Huang, Z.W.; Tang, Y.; Chen, Z.Q. Post-critical behavior of galloping for main cables of suspension bridges in construction phases. J. Fluids Struct. 2021, 101, 103205. [Google Scholar] [CrossRef]
- Tutar, M.; Holdø, A.E. Computational modeling of flow around a circular cylinder in sub-critical flow regime with various turbulence models. Int. J. Numer. Methods Fluids 2001, 35, 763–784. [Google Scholar] [CrossRef]
- Cantwell, B.; Coles, D. An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 1983, 139, 321–374. [Google Scholar] [CrossRef]
- Orlando, M. Wind-induced interference effects on two adjacent cooling towers. Eng. Struct. 2001, 23, 979–992. [Google Scholar] [CrossRef]
- Gu, M.; Huang, P.; Tao, L.; Zhou, X.Y.; Fan, Z. Experimental study on wind loading on a complicated group-tower. J. Fluids Struct. 2010, 26, 1142–1154. [Google Scholar]
- Xu, F.Y.; Yu, H.Y.; Zhang, M.J.; Han, Y. Experimental study on aerodynamic characteristics of a large-diameter ice-accreted cylin-der without icicles. J. Wind Eng. Ind. Aerodyn. 2021, 208, 104453. [Google Scholar] [CrossRef]


| Reynolds Number | Case | CD | CL | St |
|---|---|---|---|---|
| 1.08 × 105 | Present experiment | 1.14 | 0.02 | 0.20 |
| 1.08 × 105 | Present numerical simulation | 0.92 | 0.00 | 0.21 |
| 1.10 × 105 | Experiment of Schewe [50] | 1.10 | - | 0.20 |
| 1.40 × 105 | Experiment of Cantwell [53] | 1.24 | - | 0.18 |
| 1.40 × 105 | Numerical simulation of Tutar and Holdø [52] | 1.40 | - | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Hua, X.; Huang, Z.; Wen, Q. Aerodynamic Characteristics of Coupled Twin Circular Bridge Hangers with Near Wake Interference. Appl. Sci. 2021, 11, 4189. https://doi.org/10.3390/app11094189
Wang C, Hua X, Huang Z, Wen Q. Aerodynamic Characteristics of Coupled Twin Circular Bridge Hangers with Near Wake Interference. Applied Sciences. 2021; 11(9):4189. https://doi.org/10.3390/app11094189
Chicago/Turabian StyleWang, Chaoqun, Xugang Hua, Zhiwen Huang, and Qing Wen. 2021. "Aerodynamic Characteristics of Coupled Twin Circular Bridge Hangers with Near Wake Interference" Applied Sciences 11, no. 9: 4189. https://doi.org/10.3390/app11094189
APA StyleWang, C., Hua, X., Huang, Z., & Wen, Q. (2021). Aerodynamic Characteristics of Coupled Twin Circular Bridge Hangers with Near Wake Interference. Applied Sciences, 11(9), 4189. https://doi.org/10.3390/app11094189






