This section presents the materials and methods considered.
Section 2.1 presents the cervical cell databases, Herlev and CRIC, used for lesion classification.
Section 2.2 exhibits how the features were extracted and analyzes the correlation between the handcrafted and biological nuclei features.
Section 2.3 presents the classification groups of each database used in the experiments.
Section 2.4 shows the oversampling techniques analyzed in the experiments.
Section 2.5 points out the classifier methods used. Finally,
Section 2.6 shows the hierarchical classification structure proposed for nuclei classification.
2.1. Database
This work deals with two databases of cervical cells: (i) Herlev, well known and used in the literature, and (ii) CRIC, a new database with nucleus and cell segmentation results in smear images.
The Herlev database [
13] (
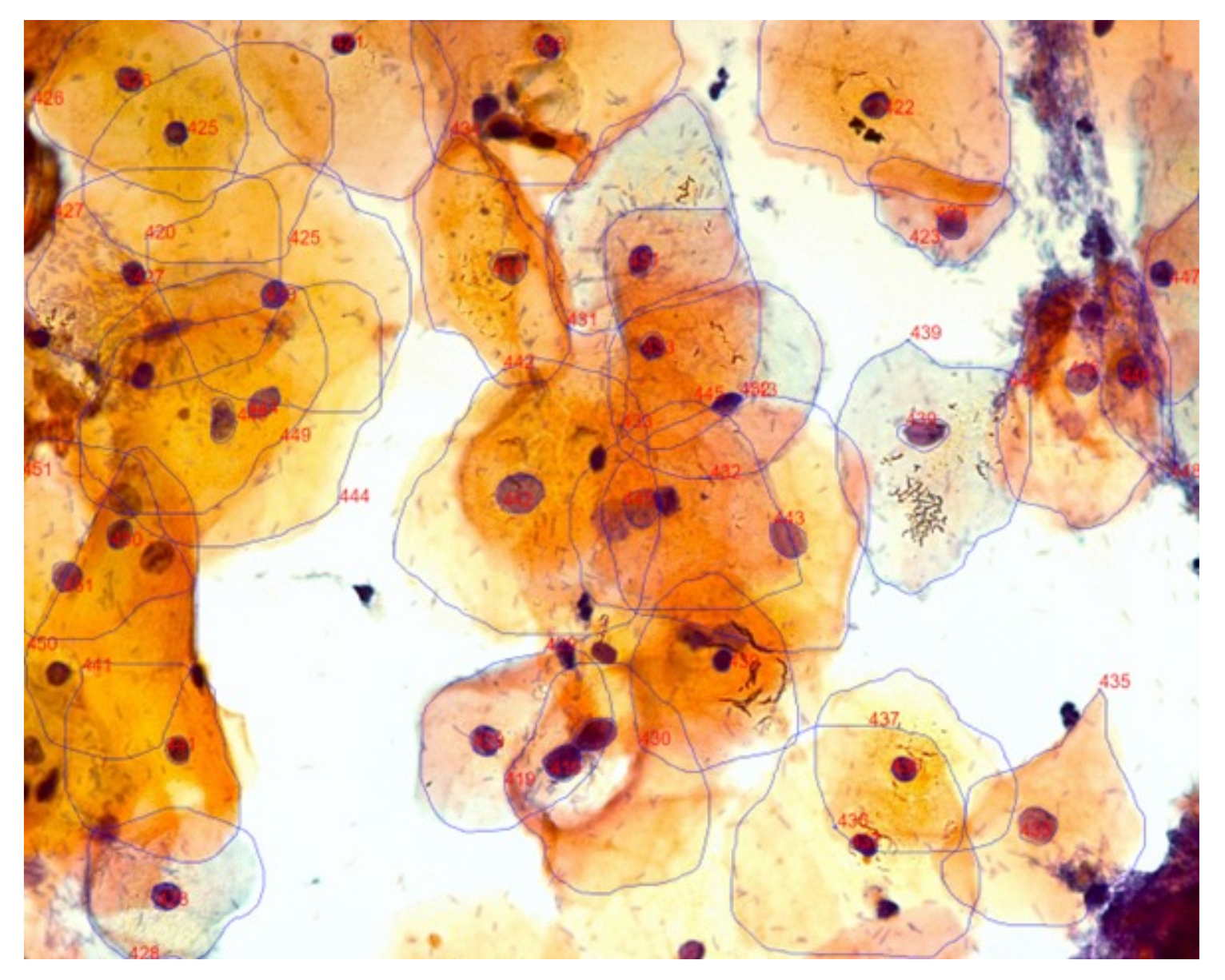
http://mde-lab.aegean.gr/index.php/downloads (accessed on 24 January 2021)) is collected at the Department of Pathology of Herlev University Hospital and the Department of Automation at the Technical University of Denmark. It consists of 917 single cervical cell images, divided into seven classes: superficial squamous epithelial; intermediate squamous epithelial; columnar epithelial; mild, moderate, and severe squamous non-keratinizing dysplasia; and squamous cell carcinoma in situ intermediate. All images also have a label of their regions, nuclei, and cytoplasm.
Figure 1 shows a Herlev example image (a) and its label (b).
The CRIC Searchable Image Database (
https://database.cric.com.br/ (accessed on 24 March 2021)) comprises cervical cell images and it is being developed by the Center for Recognition and Inspection of Cells (CRIC) and aims to support the Pap smear analysis. It covers cervical cells of conventional cytology, based on the standardized and most-used worldwide nomenclature in the diagnosis area, the Bethesda System nomenclature.
Currently, the CRIC database is divided into two collections: one containing only the marking of the cell’s center (classification) and another containing the segmentation of the cell’s nucleus and cytoplasm. In both cases, each cell also has its classification. Only the segmentation collection will be used in this work since the nucleus region’s delimitation will be important for the methodology used. There are 400 images obtained from Pap smears, with 3233 segmentations.
Figure 2 presents an example of a segmentation image.
Table 1 shows each database division, indicating the nuclei’s categories and classifications. The number of nuclei in each class is also shown.
In 1941, George N. Papanicolaou created the first classification system for normal and abnormal cells (class I, II, III, IV, and V). The second system was created by James Reagan in 1953, separating the abnormal cells into mild, moderate, severe dysplasias, and carcinoma in situ. In 1967, Ralph Richart proposed the division into CIN I, CIN II, and CIN III (Cervical Intraepithelial Neoplasia). To standardize the terminologies, in 1988, the ”Bethesda System” was developed and approved by the National Cancer Institute in the USA; the system underwent reviews in 1991, 2001, and 2014. With this new nomenclature system, the current terms for the classification of abnormal squamous cells are ASC-US, LSIL, ASC-H, HSIL, SC [
33,
34].
Herlev’s database uses the second classification system developed in 1953, while the CRIC base uses the most current classification system, the Bethesda System. In this sense, comparing the terminologies, mild dysplasia corresponds to LSIL, and moderate, severe dysplasia and carcinoma in situ corresponds to HSIL. Therefore, Herlev does not include the classifications of classes ASC-US, ASC-H, and SC used in the laboratory routine today.
Our proposal uses information from the segmented nucleus to perform the classification of cells.
2.2. Biological versus Computational Features
As mentioned before, during the screening examination in a cytology laboratory, the cytopathologist manually analyzes optical images of cervical cells. Visual analysis is related to human interpretation of cervical smears, and even with many detailed procedures and routines, it is susceptible to errors of interpretation.
During the analysis, the cytopathologist assesses the variation in the smear cells’ cytomorphological features. Some examples of this variation are the increase in the nucleus/cytoplasm ratio, the nuclear membrane irregularity, the nucleus hyperchromasia, and the chromatin granularity. All of them provide guidance on reporting of cytologic findings in cervical cytology in agreement with the Bethesda System [
4,
34].
Errors related to diagnostic interpretation happen when the cytopathologist either recognizes altered cells, but wrongly classifies them, or does not recognize them at all. Both situations may be attributed to the lack of experience of the professional, variation in the appearance of cytomorphological features, or workload, which affects the subjectivity of the process [
35,
36,
37].
Our proposal extracts and evaluates morphological and texture characteristics related to the cell nucleus, correlated to the Bethesda System’s visual interpretation. The computational results can guide the cell classification systems and assist the lesion diagnosis and interpretation, diminishing error results.
The methodology starts with a feature extraction of each nucleus segmented in the database. The following algorithms were employed: Region Props, Haralick’s features, Local Binary Patterns (LBP), Threshold Adjacency Statistics (TAS), Zernike moments, and Gray Level Co-occurrence Matrix (GLCM). All were implemented in Python, in which Region Props and GLCM are from the scikit-image package [
38], and the others are from the Mahotas package [
39]. Unlike Di Ruberto et al. [
32], we also include morphological and other texture features.
First, Region Props [
40,
41,
42,
43] was used to extract the values of the morphological features of nuclei, such as (a) circularity; (b) minimum, mean, and maximum intensities; (c) area; (d) bounding box, filled, and convex hull image areas; (e) perimeter; (f) Euler number; (g) extent; (h) minor and major axis; (i) eccentricity; and (j) solidity.
Next, Haralick’s texture features [
44] were extracted. These features are: (a) angular second moment; (b) contrast; (c) correlation; (d) variance; (e) inverse difference moment; (f) sum average; (g) sum entropy; (h) entropy; (i) difference variance; (j) difference entropy; (k) measure of correlation 1; (l) measure of correlation 2.
The Local Binary Patterns (LBP) [
45], a set of texture features, were also extracted. The advantage of these features is that they are insensitive to orientation and lighting.
The Threshold Adjancency Statistics (TAS) [
46] features were also considered in the classification. They are used to differentiate images of distinct subcellular localization quickly and with high accuracy.
The Zernike moment [
47] features were extracted and considered in the proposed methodology because they measure how the mass is distributed in the region. Finally, the Gray Level Co-occurrence Matrices [
44] are texture features extracted that consider the pixels’ spatial relation.
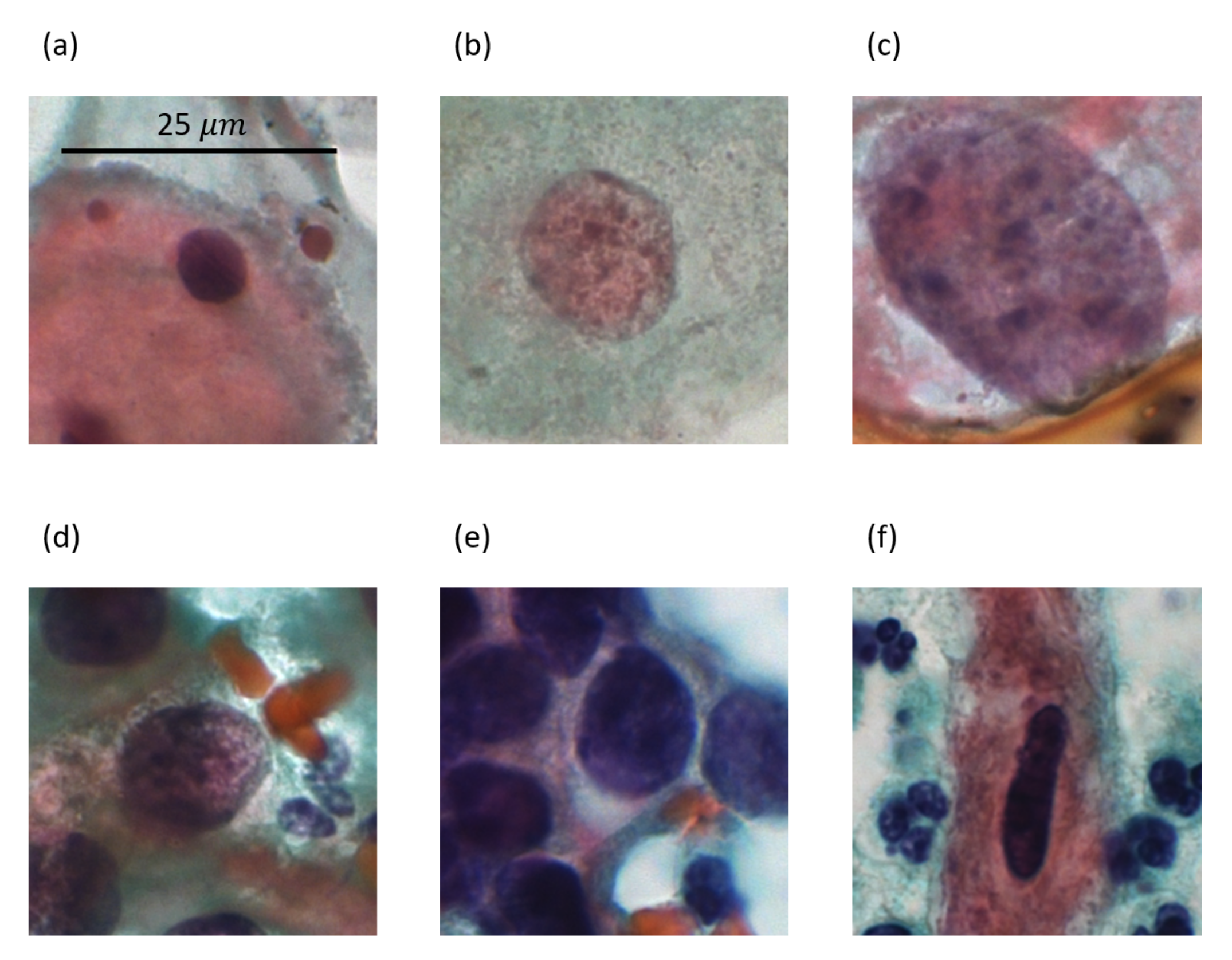
Figure 3 shows a sample image for each type of lesion present in the CRIC database, and
Table 2 presents some feature values extracted from the images in
Figure 3. These features are area, eccentricity (eccent.), circularity (circ.), maximum intensity (max. int.), and contrast.
We extracted features inspired by the ones that a cytopathologist would use to perform the classification, manually. Morphological features such as area, perimeter, extent, and eccentricity are important because they are related to the nuclear size, which characterizes one of the fundamental biological criteria for differentiating abnormal cells from normal ones. For example, ASC-US interpretation requires that the cells in question demonstrate nuclei approximately 2.5 to 3 times the area of the nucleus of a normal intermediate squamous cell (approximately 35 μm
) or twice the size of a squamous metaplastic cell nucleus (approximately 50 μm
). The cells interpreted as ASC-H are the size of metaplastic cells with nuclei that are up 2.5 times larger than normal. Nuclear enlargement more than three times the area of normal intermediate nuclei characterizes LSIL. HSIL often contains relatively small basal-type cells with nuclear augmentation. The characteristic cells of carcinoma (SC) vary markedly in the area but usually show karyomegaly.
Table 2 shows that the area feature has a behavior as observed by cytopathologists, in which the normal cell has the smallest area value and there is an increase in the value according to its lesion.
Another biologically relevant feature is the nuclear membrane shape, as abnormal cells have different degrees of irregularity. ASC-US shows minimal variation in the nuclear shape, while LSIL presents a contour of nuclear membrane ranging from smooth to very irregular with notches. ASC-H and HSIL show irregular nuclear contour, with anisokaryosis of HSIL being more pronounced. Carcinoma cells may show very marked nuclear pleomorphism (bizarre forms). As a whole, abnormal cells may have multinucleation, or variations in the circular shape of a normal cell’s nucleus. This work considered morphological features related to these characteristics (nuclear contour and multinucleation), such as circularity, eccentricity, and minor and major axis.
Table 2 shows eccentricity and circularity values that provide examples of features used in this work to measure the nuclear membrane’s shape as they would typically be analyzed by cytopathologists. The eccentricity measures the nuclei irregularity, while the circularity value represents how circular the nuclei are. Analyzing the images in
Figure 3, the less circular nucleus is the SC, and it has the smallest value for the feature (0.462). Simultaneously, the most irregular nucleus is also the SC, and it has the biggest eccentricity value (0.952).
Nuclear hyperchromasia and irregular chromatin distribution are essential biological characteristics for categorizing cells as abnormal. These characteristics also assist in differentiation among ASC-US, LSIL, ASC-H, and HSIL. Moreover, the morphological features directly related to these characteristics are minimum, mean, and maximum intensities, solidity, contrast, mass distribution in the region (Zernike moments), and a set of texture features such as Local Binary Patterns, Haralick features, and Gray Level Co-occurrence Matrices.
Table 2 shows the maximum intensity and the contrast (Haralick feature) values. With attributes of intensity (minimum, maximum, and medium) and texture, it is possible to estimate the chromatin distribution analyzed by the cytopathologist in the manual analysis.
A total of 232 attributes of the cervical cell nuclei were extracted and considered in this work. A quick analysis of the attribute selection indicated that all attributes used brought benefits to the classification task; thus, all of them were used in our proposal for the nuclei classification.
2.4. Oversampling
In classification problems, a database is imbalanced when the difference between the amount of data of classes is large [
49]. Classification algorithms are often sensitive to imbalance, which means that they tend to value classes with more data and ignore classes with fewer data [
50,
51]. It is possible to observe in
Table 1 that the databases considered in this work are not balanced, so balancing techniques were analyzed.
The first used technique is the Synthetic Minority Oversampling Technique (SMOTE) [
52], which creates artificial sample data based on neighboring interpolation to oversample the minority class. This technique considers the k-nearest neighbors for each sample
of the minority class and creates a synthetic sample
as follows:
In Equation (
1),
corresponds to a random value of the
k neighbors of
and
is a random number in the interval [0,1]. The new sample datum
is a point on the edge that connects
and
.
Another technique was the Borderline-SMOTE [
53]. The difference between the Borderline-SMOTE and the original SMOTE is that the Borderline-SMOTE only oversamples the borderline examples of the minority class, while SMOTE oversamples through all the examples from the minority class.
Finally, the third technique studied is SVM SMOTE. This technique differs from the others because it uses the support vectors to generate a Support Vector Machine (SVM) classifier to approximate the class boundaries.
All these three techniques were implemented in Python using the imbalanced-learn package [
54], and their results were compared according to accuracy.
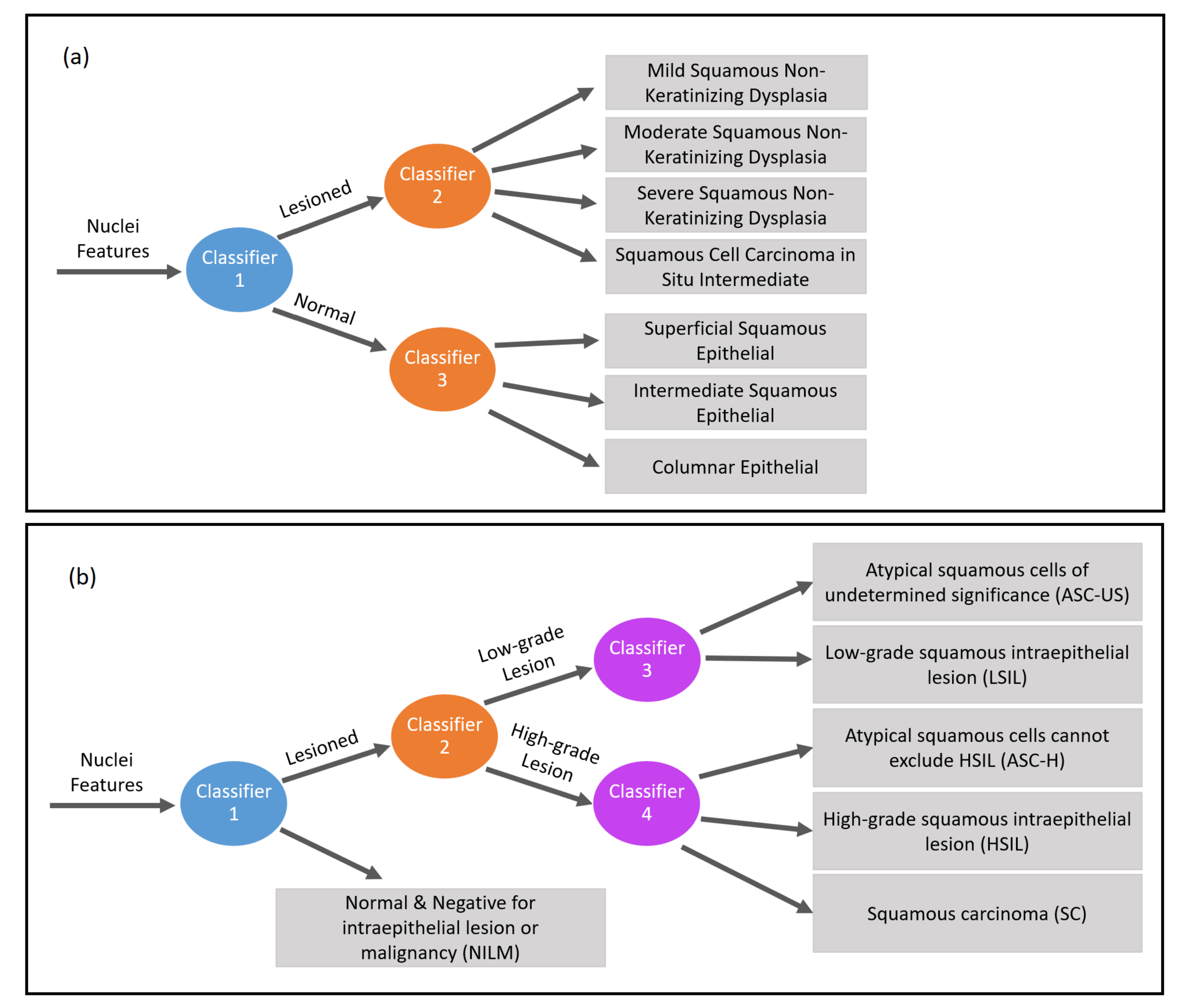
2.6. Hierarchical Classification
Some classification problems present hierarchical relations between classes, indicating that it is possible to divide the problem into sub-problems of less complexity that, when combined, reach the classification expected by the whole problem. These problems are known as hierarchical classification problems.
Here, we address a hierarchical classification problem because it can be reduced into a normal and abnormal classification followed by deeper classifications to discover the nuclei type.
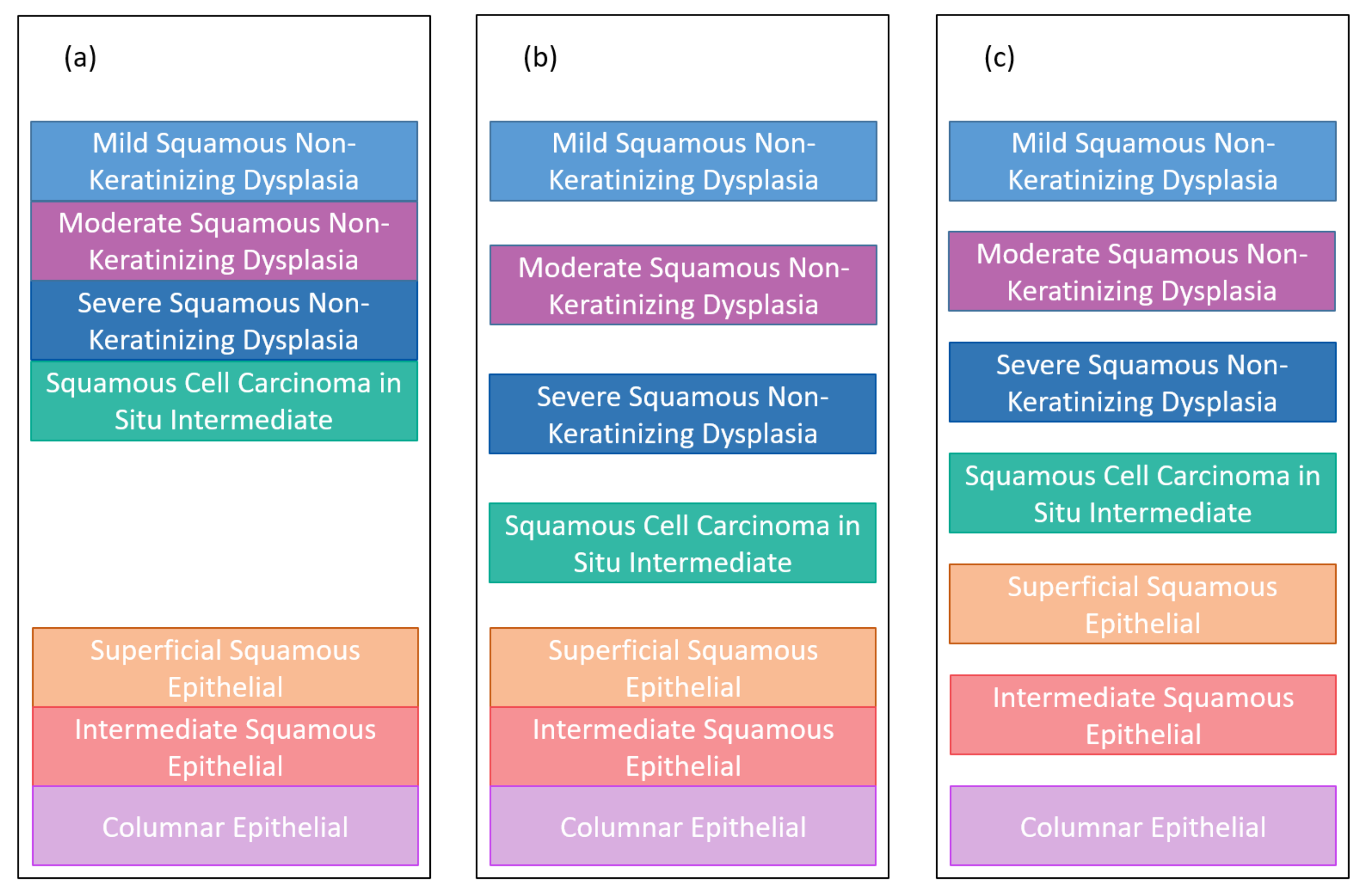
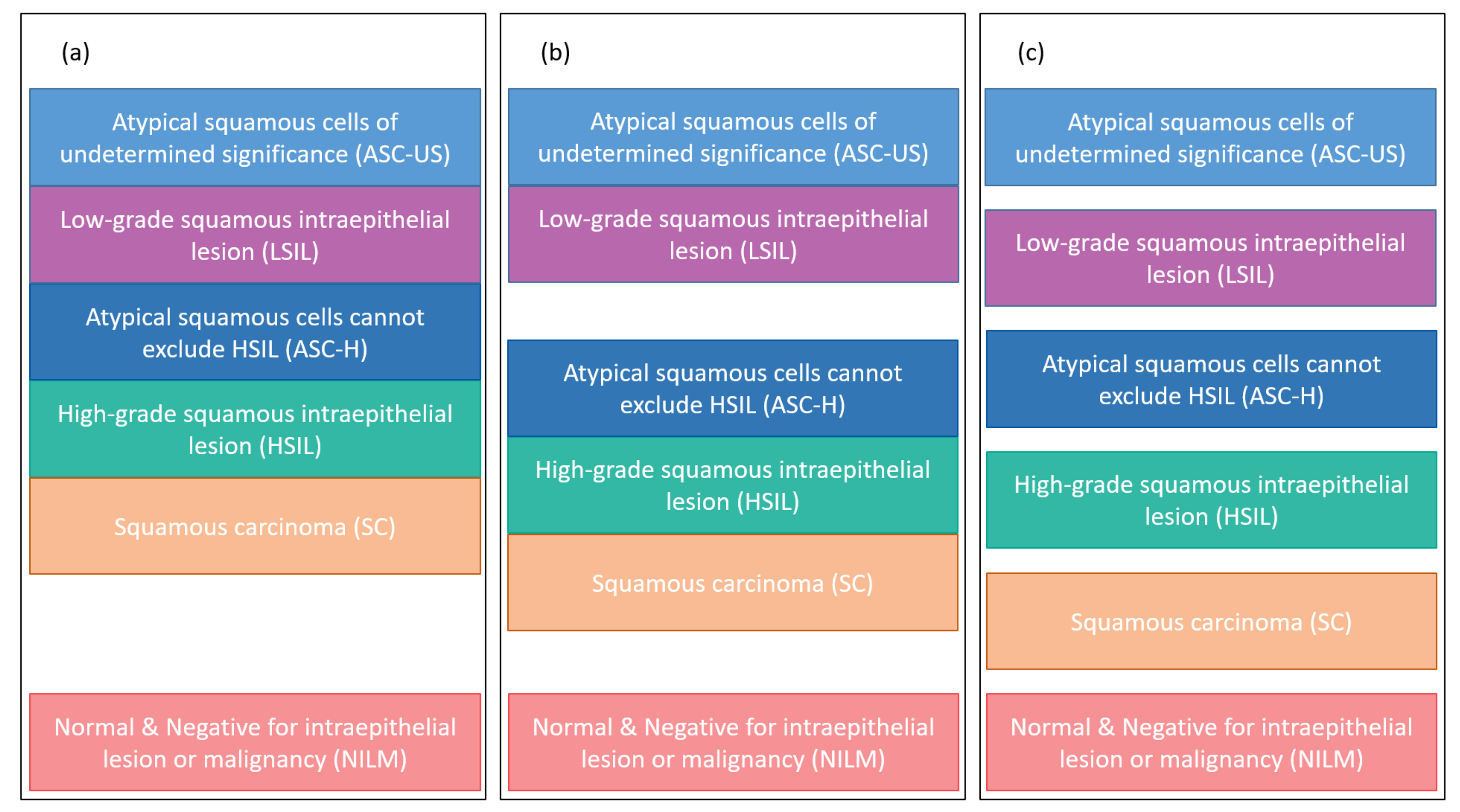
Figure 6 presents the hierarchical classification proposed in this work to classify nuclei features.
Figure 6a shows the hierarchical classification of Herlev nuclei, while
Figure 6b shows the hierarchical classification of CRIC nuclei.
Considering the Herlev data (
Figure 6a), the data can be classified first (with classifier 1 in blue) between normal and abnormal and, subsequently, the lesion can be classified (with classifier 2 in orange) into four other classes (mild squamous non-keratinizing dysplasia, moderate squamous non-keratinizing dysplasia, severe squamous non-keratinizing dysplasia, and squamous cell carcinoma in situ intermediate), and the normal ones can be classified (with classifier 3 in orange) into another three classes (superficial squamous epithelial, intermediate squamous epithelial, columnar epithelial). Therefore, the 2-class classification requires only classifier 1. In turn, the 5-class classification requires classifiers 1 and 2, while the 7-class classification requires the three classifiers.
Considering the CRIC database data (
Figure 6b), the data can be classified (with classifier 1 in blue) into normal and abnormal. The lesion can be classified (with classifier 2 in orange) into low-grade lesion and high-grade lesion, which are then classified (with classifiers 3 and 4 in purple) according to their lesion’s type. Thereby, the 2-class classification applies classifier 1; the 3-class, classifiers 1 and 2; and the 6-class, the four classifiers.