Integrated Optical Phased Arrays for Beam Forming and Steering
Abstract
1. Introduction
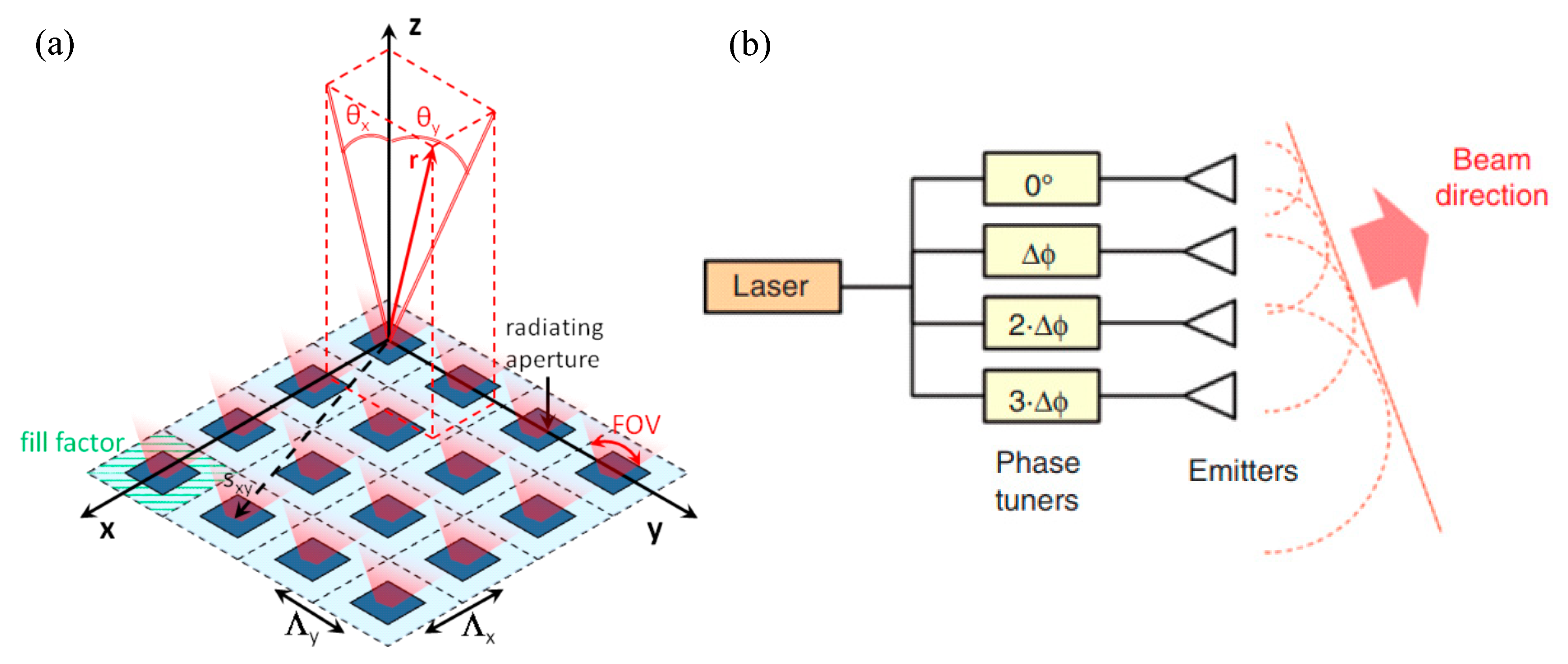
2. Principles
2.1. Fraunhofer Diffraction Model
2.2. Multi-Slit Diffraction Model
2.3. Beam Steering Based on WGAs
2.3.1. 2D Steering Based on Phase Differences
2.3.2. Steering Based on Phase Differences & Wavelengths
2.3.3. 2D Steering Based on Optical Switches at a Fixed Wavelength
2.3.4. 2D Steering Completely Based on Wavelengths
2.4. Transmitters and Receivers
3. Building Blocks
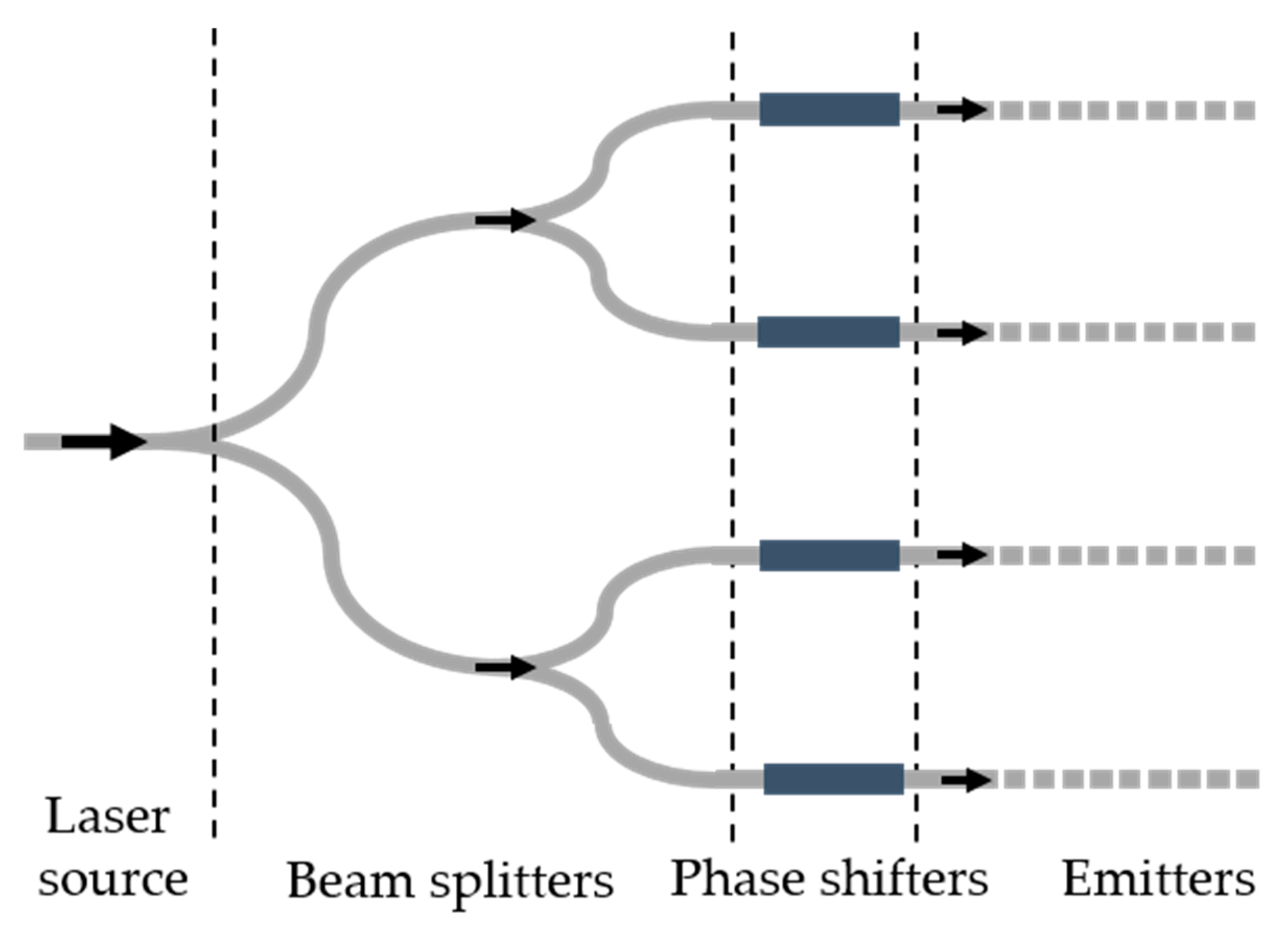
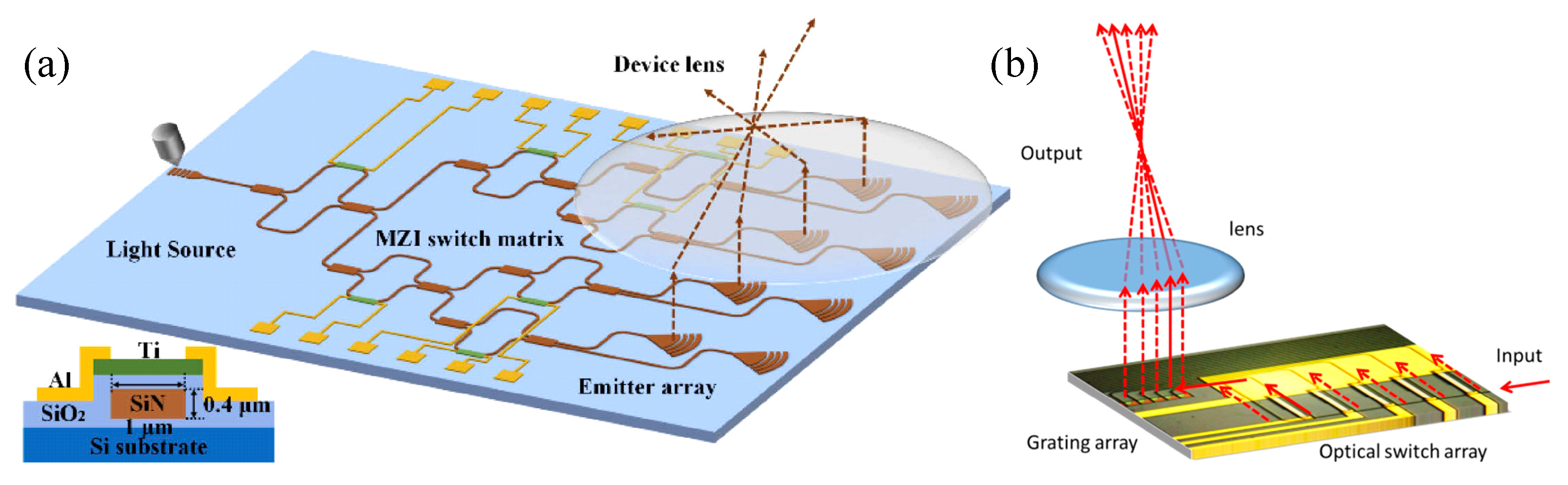
3.1. Laser Sources
3.2. Beam Splitters
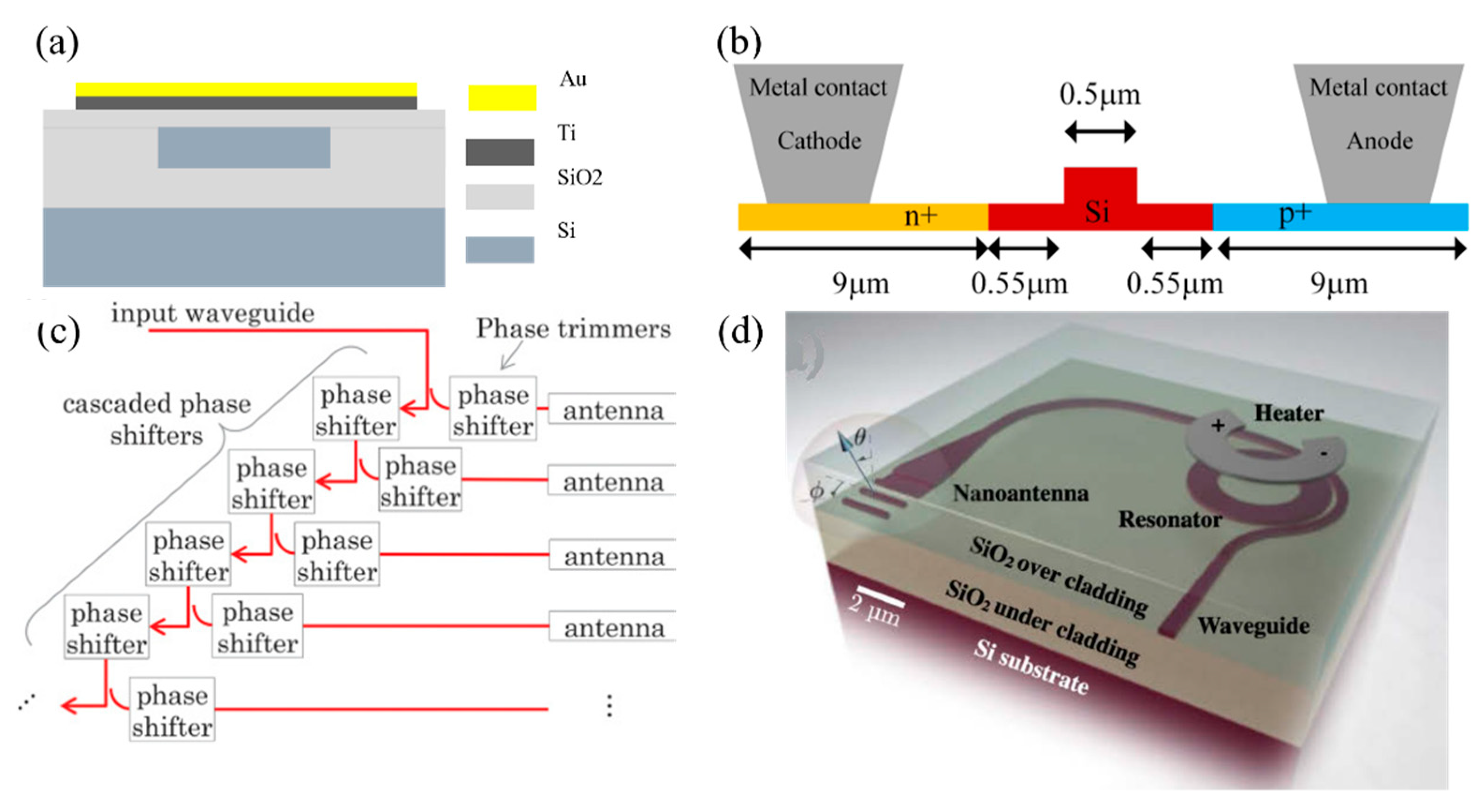
3.3. Phase Shifters
3.4. Emitters
4. Configurations
4.1. EF OPAs
4.2. WGA-Based OPAs
4.3. Other OPAs
5. Material Platforms
5.1. Si Photonics Platforms
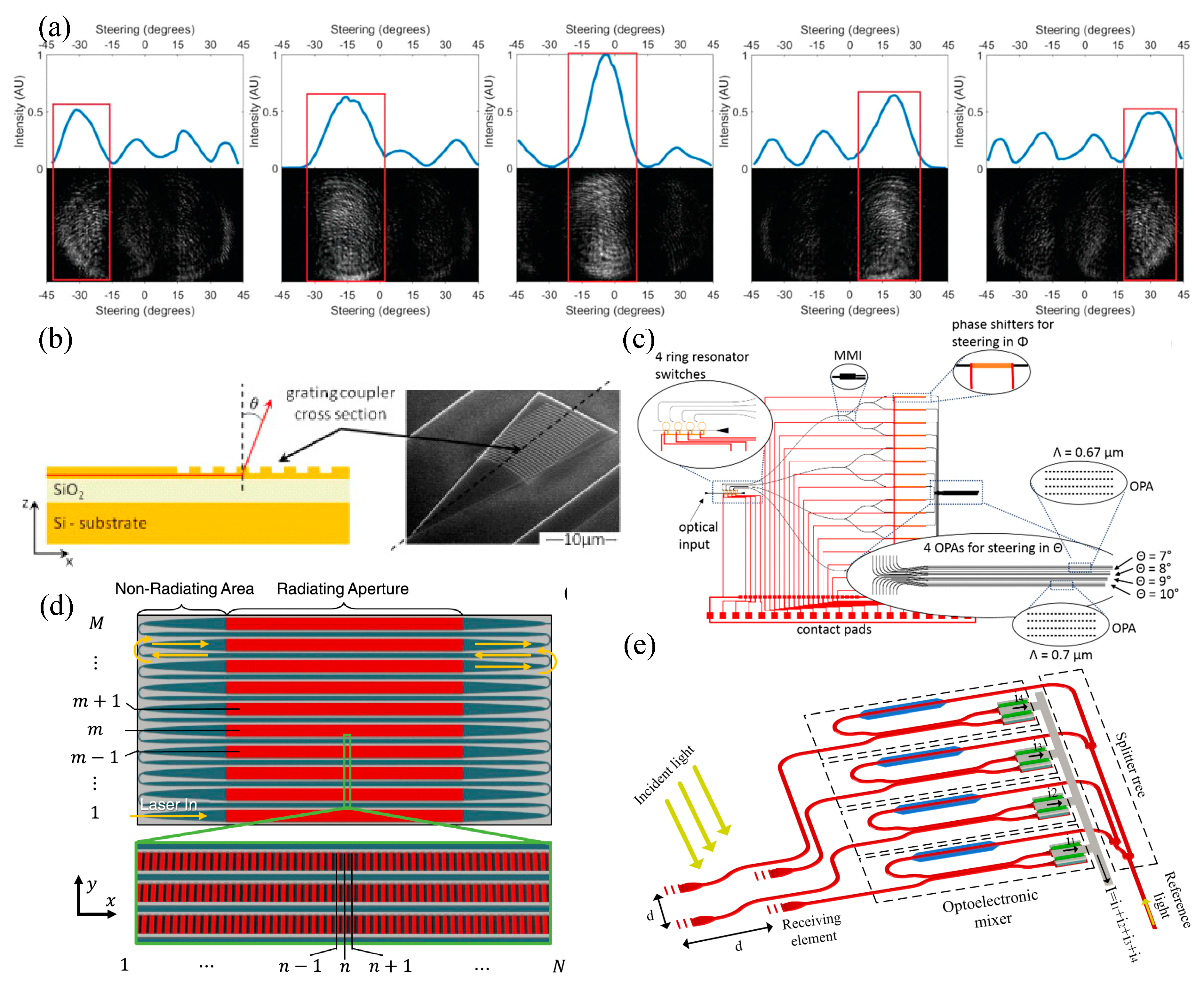
5.1.1. OPAs Based on the Si Platform
5.1.2. OPAs Based on the Si3N4 Platform
5.1.3. OPAs Based on the Si/Si3N4 Platform
5.1.4. OPAs Based on the Ge/Si3N4 Platform
5.2. III-V Platforms
5.3. III-V/Si Hybrid Platforms
6. Wavelengths
7. Performances
7.1. Crosstalk and Suppression
7.2. FOV, Beamwidth, and Sidelobe Suppression
7.3. Modulation Speed
7.4. Power Consumption
7.5. Scalability
7.6. Calibration
8. Applications & Potential Alternatives
8.1. Applications
8.1.1. OPAs for Free-Space Communications
8.1.2. OPAs for LiDAR
8.1.3. OPAs for Imaging
8.1.4. OPAs for Biological Sensing
8.1.5. OPAs for Special Beam Generation
8.2. Potential Alternatives
9. Outlook
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wight, D.R.; Heaton, J.M.; Hughes, B.T.; Birbeck, J.C.H.; Hilton, K.P.; Taylor, D.J. Novel phased array optical scanning device implemented using GaAs/AlGaAs technology. Appl. Phys. Lett. 1991, 59, 899–901. [Google Scholar] [CrossRef]
- Webb, G.W.; Vernon, W.; Sanchez, M.S.; Rose, S.C.; Angello, S. Optically controlled millimeter wave antenna. In Proceedings of the International Topical Meeting on Microwave Photonics, Melbourne, Australia, 17–19 November 1999; p. 275. [Google Scholar]
- Webb, G.W.; Vernon, W.; Sanchez, M.S.; Rose, S.C.; Angello, S. Novel photonically controlled antenna for MMW communications. In Proceedings of the International Topical Meeting on Microwave Photonics, Oxford, UK, 11–13 September 2000; p. 176. [Google Scholar]
- Igor, V.M.; Oleg, V.M. The brief elementary basics of antenna arrays. In Basic Principles of Fresnel Antenna Arrays, 1st ed.; Springer: Berlin, Germany, 2008; pp. 1–12. [Google Scholar]
- Xiao, F.; Hu, W.; Xu, A. Optical phased-array beam steering controlled by wavelength. Appl. Opt. 2005, 44, 5429–5433. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, A.; Kwong, D.; Zhao, Y.; Chen, Y.; Crnogorac, F.; Fabian, R.; Pease, W.; Chen, R.T. Unequally spaced waveguide arrays for silicon nanomembrane-based efficient large angle optical beam steering. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1439–1446. [Google Scholar] [CrossRef]
- Acoleyen, K.V.; Bogaerts, W.; Jágerská, J.; Thomas, N.L.; Houdré, R.; Baets, R. Off-chip beam steering with a one-dimensional optical phased array on silicon-on-insulator. Opt. Lett. 2009, 34, 1477–1479. [Google Scholar] [CrossRef]
- Acoleyen, K.V.; Rogier, H.; Baets, R. Two-dimensional optical phased array antenna on silicon-on-insulator. Opt. Express 2010, 18, 13655–13660. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Zhang, Y.; Chen, R.T. 1 × 12 Unequally spaced waveguide array for actively tuned optical phased array on a silicon nanomembrane. Appl. Phys. Lett. 2011, 99, 051104–051106. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-scale nanophotonic phased array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-range LiDAR and free-space data communication with high-performance optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 7700108. [Google Scholar] [CrossRef]
- Hutchison, D.N.; Sun, J.; Doylend, J.K.; Kumar, R.; Heck, J.; Kim, W.; Phare, C.T.; Feshali, A.; Rong, H. High-resolution aliasing-free optical beam steering. Optica 2016, 3, 887–890. [Google Scholar] [CrossRef]
- Acoleyen, K.V. Nanophotonic Beam Steering Elements Using Silicon Technology for Wireless Optical Applications. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2012. [Google Scholar]
- Kim, T.; Bhargava, P.; Poulton, C.V.; Notaros, J.; Yaacobi, A.; Timurdogan, E.; Baiocco, C.; Fahrenkopf, N.; Kruger, S.; Ngai, T.; et al. A single-chip optical phased array in a wafer-scale silicon photonics/CMOS 3D-integration platform. IEEE J. Solid-State Circuits 2019, 54, 3061–3074. [Google Scholar] [CrossRef]
- Chang, Y.C.; Miller, S.A.; Phare, C.T.; Shin, M.C.; Zadka, M.; Roberts, S.P.; Stern, B.; Ji, X.; Mohanty, A.; Gordillo, O.A.J.; et al. Scalable low-power silicon photonic platform for all-solid-state beam steering. In Proceedings of the Micro- and Nanotechnology Sensors, Systems, and Applications XI, Baltimore, MD, USA, 13 May 2019; SPIE: Bellingham, WA, USA, 2019; Volume 10982. [Google Scholar]
- Chung, S.W.; Abediasl, H.; Hashemi, H. A monolithically integrated large-scale optical phased array in silicon-on-insulator CMOS. IEEE J. Solid-State Circuits 2018, 53, 275–296. [Google Scholar] [CrossRef]
- Poulton, C.V.; Yaacobi, A.; Cole, D.B.; Byrd, M.J.; Raval, M.; Vermeulen, D.; Watts, M.R. Coherent solid-state LiDAR with silicon photonic optical phased arrays. Opt. Lett. 2017, 42, 4091–4094. [Google Scholar] [CrossRef]
- Heck, M. Highly integrated optical phased arrays, photonic integrated circuits for optical beam shaping and beam steering. Nanophotonics 2017, 6, 93–107. [Google Scholar] [CrossRef]
- Luo, X. Engineering Optics 2.0, a Revolution in Optical Theories, Materials, Devices and Systems, 1st ed.; Springer: Singapore, 2019; p. 647. [Google Scholar]
- Meyer, R. Optical beam steering using a multichannel lithium tantalate crystal. Appl. Opt. 1972, 11, 613–616. [Google Scholar] [CrossRef]
- Shang, X.; Tan, J.; Willekens, O.; De Smet, J.; Joshi, P.; Cuypers, D.; Islamaj, E.; Beeckman, J.; Neyts, K.; Vervaeke, M.; et al. Electrically controllable liquid crystal component for efficient light steering. IEEE Photonics J. 2015, 7, 2600113. [Google Scholar] [CrossRef]
- Gou, F.; Peng, F.; Ru, Q.; Lee, Y.; Chen, H.; He, Z.; Zhan, T.; Vodopyanov, K.L.; Wu, S. Mid-wave infrared beam steering based on high-efficiency liquid crystal diffractive waveplates. Opt. Express 2017, 25, 22404–22410. [Google Scholar] [CrossRef]
- Xiao, F.; Kong, L. Optical multi-beam forming method based on a liquid crystal optical phased array. Appl. Opt. 2017, 56, 9854–9861. [Google Scholar] [CrossRef]
- Wu, L.; Wang, X.; He, X.; Huang, Z.; Huang, X.; Xiong, C. Arbitrary multiple beam forming by two cascaded liquid crystal optical phased arrays. Opt. Express 2018, 26, 17066–17077. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S. Liquid crystal beam steering devices, principles, recent advances, and future developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef]
- Yousefzadeh, C.; Van Rynbach, A.; Bos, P.J. Design of a large aperture, tunable, Pancharatnam phase beam steering device. Opt. Express 2020, 28, 991–1001. [Google Scholar] [CrossRef]
- Guo, H.; Li, J.; Wang, X.; Shang, J. Research review on the development of liquid crystal optical phased array device on the application of free space laser communication. In Proceedings of the 9th International symposium on Advanced Optical Manufacturing and Testing Technologies: Meta-Surface-Wave and Planar Optics, Chengdu, China, 26–29 June 2018; Pu, M., Ma, X., Li, X., Hong, M., Wang, C., Luo, X., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 10841. [Google Scholar]
- Zhang, X.; Koppal, S.J.; Zhang, R.; Zhou, L.; Butler, E.; Xie, H. Wide-angle structured light with a scanning MEMS mirror in liquid. Opt. Express 2016, 24, 3479–3487. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, G.; Zhang, X.; Kwon, K.; Blanche, P.; Triesault, N.; Yu, K.; Wu, M.C. 2D broadband beamsteering with large-scale MEMS optical phased array. Optica 2019, 6, 557–562. [Google Scholar] [CrossRef]
- Herranz, C.E.; Thomas, N.L.; Gylfason, K.B. Low-power optical beam steering by microelectromechanical waveguide gratings. Opt. Lett. 2019, 44, 855–858. [Google Scholar] [CrossRef]
- Wang, D.; Watkins, C.; Xie, H. MEMS mirrors for LiDAR: A review. Micromachines 2020, 11, 456. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.R.; Montoya, J.; Kansky, J.E.; Redmond, S.M.; Turner, G.W.; Rubio, A.S. High speed, high power one-dimensional beam steering from a 6-element optical phased array. Opt. Express 2012, 20, 17311–17318. [Google Scholar] [CrossRef] [PubMed]
- Carlson, N.W.; Evans, G.A.; Amantea, R.; Palfrey, S.L.; Hammer, J.M.; Lurie, M.; Carr, L.A.; Hawrylo, F.Z.; James, E.A.; Kaiser, C.J.; et al. Electronic beam steering in monolithic grating surface-emitting diode laser arrays. Appl. Phys. Lett. 1988, 53, 2275–2277. [Google Scholar] [CrossRef]
- Takeuchi, G.; Terada, Y.; Takeuchi, M.; Abe, H.; Ito, H.; Baba, T. Thermally controlled Si photonic crystal slow light waveguide beam steering device. Opt. Express 2018, 26, 11529–11537. [Google Scholar] [CrossRef] [PubMed]
- Acoleyen, K.V.; Komorowska, K.; Bogaerts, W.; Baets, R. One-dimensional off-chip beam steering and shaping using optical phased arrays on silicon-on-insulator. J. Lightwave Technol. 2011, 29, 3500–3505. [Google Scholar] [CrossRef]
- Yang, B.; Chen, H.; Yang, S.; Chen, M. A design method of optical phased array with insufficient phase tuning range. IEEE Photonics J. 2020, 12, 6600409. [Google Scholar] [CrossRef]
- Zeng, Y.; Qu, S.; Wu, J. Polarization-division and spatial-division shared-aperture nanopatch antenna arrays for wide-angle optical beam scanning. Opt. Express 2020, 28, 12805–12826. [Google Scholar] [CrossRef]
- Li, S.Q.; Xu, X.; Veetil, R.M.; Valuckas, V.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science 2019, 364, 1087–1090. [Google Scholar] [CrossRef]
- Abdelsalam, M.; Mahmoud, A.M.; Swillam, M.A. Polarization independent dielectric metasurface for infrared beam steering applications. Sci. Rep. 2019, 9, 10824. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Covey, J.; Zhang, Y.; Xu, X.; Subbaraman, H.; Chen, R.T. On-chip silicon optical phased array for two-dimensional beam steering. Opt. Lett. 2014, 39, 941–944. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.C.; Mohanty, A.; Watson, K.; Bhatt, G.R.; Phare, C.T.; Miller, S.A.; Zadka, M.; Lee, B.S.; Ji, X.; Datta, I.; et al. Chip-scale blue light phased array. Opt. Lett. 2020, 45, 1934–1937. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.; Komljenovic, T.; Huang, J.; Davenport, M.L.; Bowers, J.E. Dense III-V/Si phase-shifter based optical phased array. arXiv 2019, arXiv:1904.01104. [Google Scholar]
- Fatemi, R.; Abiri, B.; Khachaturian, A.; Hajimiri, A. High sensitivity active flat optics optical phased array receiver with a two-dimensional aperture. Opt. Express 2018, 26, 29983–29999. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, Z.; Lv, J.; Peng, C.; Hu, W. Fast beam steering enabled by a chip-scale optical phased array with 8 × 8 elements. Opt. Commun. 2020, 461, 125267. [Google Scholar] [CrossRef]
- Fatemi, R.; Khachaturian, A.; Hajimiri, A. A nonuniform sparse 2-D large-FOV optical phased array with a low-power PWM drive. IEEE J. Solid State Circuits 2019, 54, 1200–1215. [Google Scholar] [CrossRef]
- Hulme, J.C.; Doylend, J.K.; Heck, M.; Peters, J.D.; Davenport, M.L.; Bovington, J.T.; Coldren, L.A.; Bowers, J.E. Fully integrated hybrid silicon free-space beam steering source with 32 channel phased array. In Proceedings of the Smart Photonic and Optoelectronic Integrated Circuits XVI, San Francisco, CA, USA, 8 March 2014; Eldada, L.A., Lee, E., He, S., Eds.; SPIE: Bellingham, WA, USA, 2014; p. 898907. [Google Scholar]
- Guan, B.; Scott, R.P.; Qin, C.; Fontaine, N.K.; Su, T.; Ferrari, C.; Cappuzzo, M.; Klemens, F.; Keller, B.; Earnshaw, M.; et al. Free-space coherent optical communication with orbital angular, momentum multiplexing/demultiplexing using a hybrid 3D photonic integrated circuit. Opt. Express 2014, 22, 145–156. [Google Scholar] [CrossRef]
- Rabinovich, W.S.; Goetza, P.G.; Pruessnera, M.; Mahon, R.; Ferraroa, M.S.; Parka, D.; Fleeta, E.; Prenger, M.J. Free space optical communication link using a silicon photonic optical phased array. In Proceedings of the Free-Space Laser Communication and Atmospheric Propagation XXVII, San Francisco, CA, USA, 16 March 2015; Hemmati, H., Boroson, D.M., Eds.; SPIE: Bellingham, WA, USA, 2015; p. 93540B. [Google Scholar]
- Wang, K.; Yuan, Z.; Wong, E.; Alameh, K.; Li, H.; Sithamparanathan, K.; Skafidas, E. Experimental demonstration of indoor infrared optical wireless communications with a silicon photonic integrated circuit. J. Lightwave Technol. 2019, 37, 619–626. [Google Scholar] [CrossRef]
- Poulton, C.V.; Vermeulen, D.; Hosseini, E.; Timurdogan, E.; Su, Z.; Moss, B.; Watts, M.R. Lens-free chip-to-chip free-space laser communication link with a silicon photonics optical phased array. In Proceedings of the Frontiers in Optics 2017/Silicon Photonics II, Washington, DC, USA, 18–21 September 2017; p. FW5A.3. [Google Scholar]
- Rhee, H.W.; You, J.B.; Yoon, H.; Han, K.; Kim, M.; Lee, B.G.; Kim, S.C.; Park, H.H. 32 Gbps data transmission with 2D beam-steering using a silicon optical phased array. IEEE Photonics Technol. Lett. 2020, 32, 803–806. [Google Scholar] [CrossRef]
- Aflatouni, F.; Abiri, B.; Rekhi, A.; Hajimiri, A. Nanophotonic projection system. Opt. Express 2015, 23, 21012–21022. [Google Scholar] [CrossRef] [PubMed]
- Raval, M.; Yaacobi, A.; Watts, M.R. Integrated visible light phased array system for autostereoscopic image projection. Opt. Lett. 2018, 43, 3678–3681. [Google Scholar] [CrossRef] [PubMed]
- Kohno, Y.; Komatsu, K.; Tang, R.; Ozeki, Y.; Nakano, Y.; Tanemuray, T. Ghost imaging using a large-scale silicon photonic phased array chip. Opt. Express 2019, 27, 3817–3823. [Google Scholar] [CrossRef]
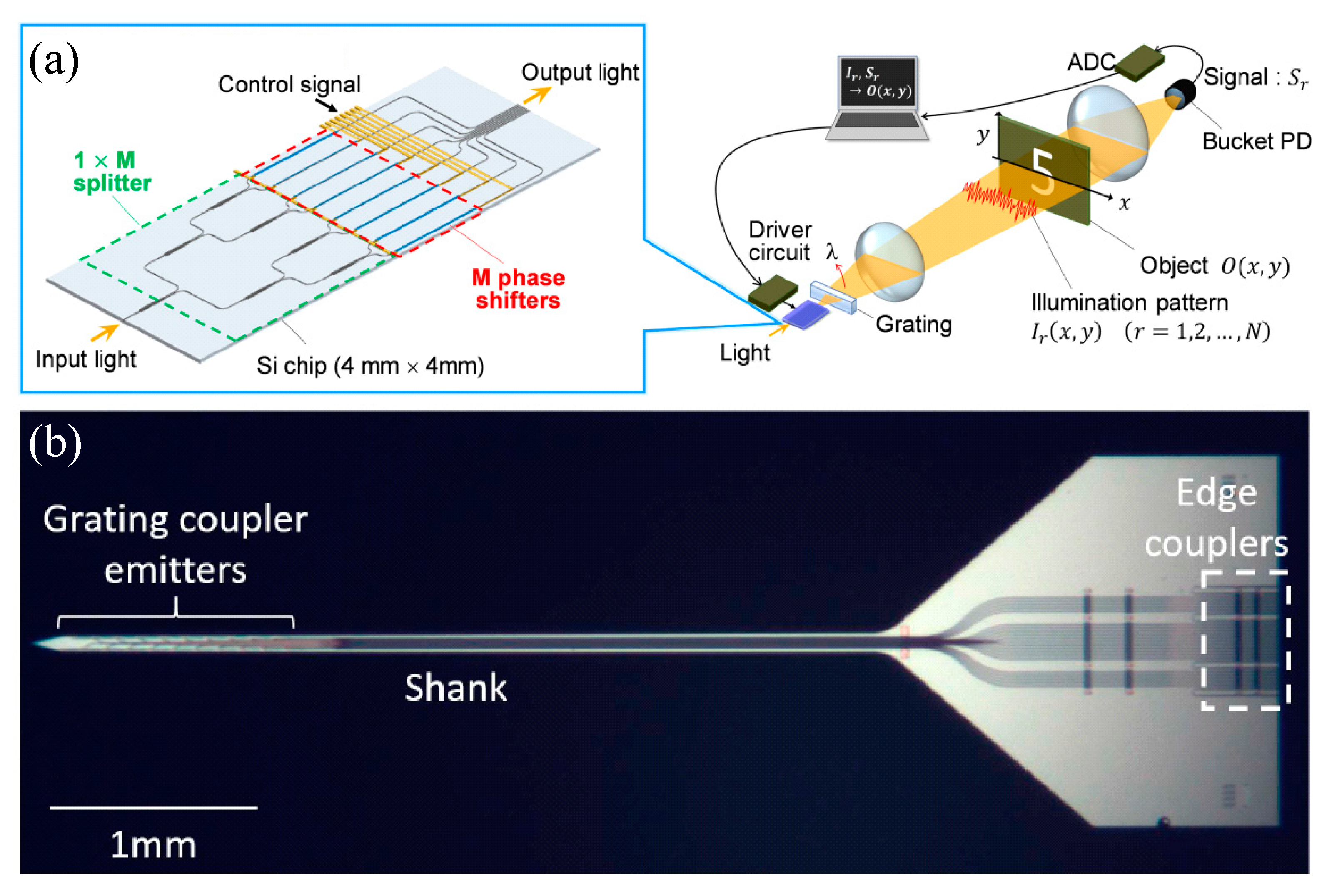
- Sacher, W.D.; Luo, X.; Yang, Y.; Chen, F.; Lordello, T.; Mak, J.C.; Liu, X.; Hu, T.; Xue, T.; Lo, P.G.; et al. Visible-light silicon nitride waveguide devices and implantable neurophotonic probes on thinned 200 mm silicon wafers. Opt. Express 2019, 27, 37400–37418. [Google Scholar] [CrossRef]
- Mohanty, A.; Li, Q.; Tadayon, M.A.; Roberts, S.P.; Bhatt, G.R.; Shim, E.; Ji, X.; Cardenas, J.; Miller, S.A.; Kepecs, A.; et al. Reconfigurable nanophotonic silicon probes for sub-millisecond deep-brain optical stimulation. Nat. Biomed. Eng. 2020, 4, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1996; pp. 74–75. [Google Scholar]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Su, Z.; Hosseini, E.S.; Cole, D.B.; Watts, M.R. Large-scale silicon photonic circuits for optical phased arrays. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 8201115. [Google Scholar]
- Xu, W.; Zhou, L.; Lu, L.; Chen, J. Aliasing-free optical phased array beam-steering with a plateau envelope. Opt. Express 2019, 27, 3354–3368. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, W.; Xia, J.; Huang, Q. Optical phased array antenna with wide steering range using grating array superlattices. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering, Shanghai, China, 24 July 2018; Yu, Y., Zuo, C., Qian, K., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 108272U. [Google Scholar]
- Kossey, M.R.; Rizk, C.; Foster, A.C. End-fire silicon optical phased array with half-wavelength spacing. APL Photonics 2018, 3, 011301. [Google Scholar] [CrossRef]
- Tyler, N.A.; Fowler, D.; Malhouitre, S.; Garcia, S.; Grosse, P.; Rabaud, W.; Szelag, B. SiN integrated optical phased arrays for two-dimensional beam steering at a single near-infrared wavelength. Opt. Express 2019, 27, 5851–5858. [Google Scholar] [CrossRef]
- Dostart, N.; Zhang, B.; Khilo, A.; Brand, M.; Qubaisi, K.A.; Onural, D.; Feldkhun, D.; Wagner, K.H.; Popović, M.A. Serpentine optical phased arrays for scalable integrated photonic lidar beam steering. Optica 2020, 7, 726–733. [Google Scholar] [CrossRef]
- Kim, S.H.; You, J.B.; Ha, Y.G.; Kang, G.; Lee, D.S.; Yoon, H.; Yoo, D.E.; Lee, D.W.; Yu, K.; Youn, C.H.; et al. Thermo-optic control of the longitudinal radiation angle in a silicon-based optical phased array. Opt. Lett. 2019, 44, 411–414. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Raval, M.; Su, Z.; Li, N.; Timurdogan, E.; Coolbaugh, D.; Vermeulen, D.; Watts, M.R. Large-scale silicon nitride nanophotonic phased arrays at infrared and visible wavelengths. Opt. Lett. 2017, 42, 21–24. [Google Scholar] [CrossRef] [PubMed]
- Shang, K.; Qin, C.; Zhang, Y.; Liu, G.; Xiao, X.; Feng, S.; Yoo, S.B. Uniform emission, constant wavevector silicon grating surface emitter for beam steering with ultra-sharp instantaneous field-of-view. Opt. Express 2017, 25, 19655–19661. [Google Scholar] [CrossRef] [PubMed]
- Acoleyen, K.V.; Bogaerts, W.; Baets, R. Two-dimensional dispersive off-chip beam scanner fabricated on silicon-on-insulator. IEEE Photonics Technol. Lett. 2011, 23, 1270–1272. [Google Scholar] [CrossRef]
- Du, Z.; Hu, C.; Cao, G.; Lin, H.; Jia, B.; Yang, S.; Chen, M.; Chen, H. Integrated wavelength beam emitter on silicon for two-dimensional optical scanning. IEEE Photonics J. 2019, 11, 6603710. [Google Scholar] [CrossRef]
- Abiri, B.; Fatemi, R.; Hajimiri, A. A 1-D heterodyne lens-free optical phased array camera with reference phase shifting. IEEE Photonics J. 2018, 10, 6601712. [Google Scholar] [CrossRef]
- Kang, G.; Kim, S.H.; You, J.B.; Lee, D.S.; Yoon, H.; Ha, Y.G.; Kim, J.H.; Yoo, D.E.; Lee, D.W.; Youn, C.H.; et al. Silicon-based optical phased array using electro-optic p-i-n phase shifters. IEEE Photonics Technol. Lett. 2019, 31, 1685–1688. [Google Scholar] [CrossRef]
- Im, C.S.; Bhandari, B.; Lee, K.P.; Kim, S.M.; Oh, M.C.; Lee, S.S. Silicon nitride optical phased array based on a grating antenna enabling wavelength-tuned beam steering. Opt. Express 2020, 28, 3270–3279. [Google Scholar] [CrossRef]
- Prost, M.; Ling, Y.C.; Cakmakyapan, S.; Zhang, Y.; Zhang, K.; Hu, J.; Zhang, Y.; Yoo, S.B. Solid-state MWIR beam steering using optical phased array on germanium-silicon photonic platform. IEEE Photonics J. 2019, 11, 6603909. [Google Scholar] [CrossRef]
- Yepez, P.A.K.; Scholz, U.; Zimmermann, A. Temperature dependence of the steering angles of a silicon photonic optical phased array. IEEE Photonics J. 2020, 12, 6800813. [Google Scholar] [CrossRef]
- Ashtiani, F.; Aflatouni, F. N × N optical phased array with 2N phase shifters. Opt. Express 2019, 27, 27183–27190. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liang, L.; Chen, Y.; Jia, P.; Qin, L.; Liu, Y.; Ning, Y.; Wang, L. Improved performance of optical phased arrays assisted by transparent graphene nanoheaters and air trenches. RSC Adv. 2018, 8, 8442–8449. [Google Scholar] [CrossRef]
- Marchetti, R.; Lacava, C.; Carroll, L.; Gradkowski, K.; Minzioni, P. Coupling strategies for silicon photonics integrated chips. Photonics Res. 2019, 7, 201–239. [Google Scholar] [CrossRef]
- Notaros, J.; Li, N.; Poulton, C.V.; Su, Z.; Byrd, M.J.; Magden, E.S.; Watts, M.R. CMOS-compatible optical phased arrays with monolithically-integrated erbium lasers. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018; p. STu4B.2. [Google Scholar]
- Notaros, J.; Li, N.; Poulton, C.V.; Su, Z.; Byrd, M.J.; Magden, E.S.; Timurdogan, E.; Baiocco, C.; Fahrenkopf, N.M.; Watts, M.R. CMOS-compatible optical phased array powered by a monolithically-integrated erbium laser. J. Lightwave Technol. 2019, 37, 5982–5987. [Google Scholar] [CrossRef]
- Guo, W.; Binetti, P.R.A.; Althouse, C.; Masanovic, M.L.; Ambrosius, H.P.M.M.; Johansson, L.A.; Coldren, L.A. Two-dimensional optical beam steering with InP-based photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 6100212. [Google Scholar]
- Guo, W.; Binetti, P.; Althouse, C.; Ambrosius, H.; Johansson, L.A.; Coldren, L.A. InP photonic integrated circuit for 2d optical beam steering. In Proceedings of the Information Optoelectronics, Nanofabrication and Testing 2012, Wuhan, China, 1–2 November 2012. [Google Scholar]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Davenport, M.L.; Coldren, L.A.; Bowers, J.E. Hybrid III/V silicon photonic source with integrated 1D free-space beam steering. Opt. Lett. 2012, 37, 4257–4259. [Google Scholar] [CrossRef]
- Hulme, J.C.; Doylend, J.K.; Heck, M.J.R.; Peters, J.D.; Davenport, M.L.; Bovington, J.T.; Coldren, L.A.; Bowers, J.E. Fully integrated hybrid silicon two dimensional beam scanner. Opt. Express 2015, 23, 5861–5874. [Google Scholar] [CrossRef]
- Bowers, J.E.; Huang, D.; Jung, D.; Norman, J.; Tran, M.A.; Wan, Y.; Xie, W.; Zhang, Z. Realities and challenges of III-V/Si integration technologies. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Diego, CA, USA, 13–18 May 2019; p. Tu3E.1. [Google Scholar]
- Gao, Y.; Lo, J.C.; Lee, S.; Patel, R.; Zhu, L.; Nee, J.; Tsou, D.; Carney, R.; Sun, J. High-power, narrow-linewidth, miniaturized silicon photonic tunable laser with accurate frequency control. J. Lightwave Technol. 2020, 38, 265–271. [Google Scholar] [CrossRef]
- Bowers, J.E.; Xie, W. High-performance III-V/Si phase shifter arrays for beam steering. In Proceedings of the 2019 IEEE Photonics Society Summer Topical Meeting Series (SUM), Ft. Lauderdale, FL, USA, 8–10 July 2019. [Google Scholar]
- Abedias, H.; Hashemi, H. Monolithic optical phased array transceiver in a stand SOI CMOS process. Opt. Express 2015, 23, 6509–6519. [Google Scholar] [CrossRef]
- Sun, J.; Hosseini, E.; Yaacobi, A.; Cole, D.B.; Leake, G.; Coolbaugh, D.; Watts, M.R. Two-dimensional apodized silicon photonic phased arrays. Opt. Lett. 2014, 39, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Luo, G.; Xu, Y.; Li, Y.; Su, Y.; Ma, J.; Wang, R.; Yang, Z.; Zhou, X.; Zhang, Y.; et al. Design and fabrication of a SiN-Si dual-layer optical phased array chip. Photonics Res. 2020, 8, 912–919. [Google Scholar] [CrossRef]
- Marinins, A.; Dwivedi, S.P.; Kjellman, J.Ø.; Kerman, S.; David, T.; Figeys, B.; Jansen, R.; Tezcan, D.S.; Rottenberg, X.; Soussan, P. Silicon photonics co-integrated with silicon nitride for optical phased arrays. Jpn. J. Appl. Phys. 2020, 59, SGGE02. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, Y.C.; Zhang, K.; Gentry, C.; Sadighi, D.; Whaley, G.; Colosimo, J.; Suni, P.; Yoo, S.B. Sub-wavelength-pitch silicon-photonic optical phased array for large field-of-regard coherent optical beam steering. Opt. Express 2019, 27, 1929–1940. [Google Scholar] [CrossRef]
- Foster, A.C.; Kossey, M.; Farlane, N.M.; Rizk, C.; Kott, T.; Osiander, R.; Mosavi, N. Chip-scale optical phased arrays for inter-spacecraft communications. In Proceedings of the Micro- and Nanotechnology Sensors, Systems, and Applications XI, Baltimore, MD, USA, 13 May 2019; George, T., Islam, M.S., Eds.; SPIE: Bellingham, WA, USA, 2019; p. 109820H. [Google Scholar]
- Hashemi, H. Large-scale monolithic optical phased arrays. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019. [Google Scholar]
- Zhu, S.; Hu, T.; Li, Y.; Xu, Z.; Zhong, Q.; Dong, Y.; Singh, N. CMOS-compatible integrated silicon nitride optical phase array for electrically tunable off-chip laser beam steering. In Proceedings of the 2019 Electron Devices Technology and Manufacturing Conference (EDTM), Singapore, 12–15 March 2019. [Google Scholar]
- Phare, C.T.; Shin, M.C.; Miller, S.A.; Stern, B.; Lipson, M. Silicon optical phased array with high-efficiency beam formation over 180 degree field of view. arXiv 2018, arXiv:1802.04624. [Google Scholar]
- Sabouri, S.; Jamshidi, K. Design considerations of silicon nitride optical phased array for visible light. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 8300707. [Google Scholar] [CrossRef]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Coldren, L.A.; Bowers, J.E. Two-dimensional free-space beam steering with an optical phased array on silicon-on-insulator. Opt. Express 2011, 19, 21595–21604. [Google Scholar] [CrossRef]
- Hirano, Y.; Miyamoto, Y.; Miura, M.; Motoyama, Y.; Machida, K.; Yamada, T.; Otomo, A.; Kikuchi, H. High-speed optical-beam scanning by an optical phased array using electro-optic polymer waveguides. IEEE Photonics J. 2020, 12, 6600807. [Google Scholar] [CrossRef]
- Kim, S.M.; Park, T.H.; Im, C.S.; Lee, S.S.; Kim, T.; Oh, M.C. Temporal response of polymer waveguide beam scanner with thermo-optic phase-modulator array. Opt. Express 2020, 28, 3768–3778. [Google Scholar] [CrossRef]
- Yaacobi, A.; Sun, J.; Moresco, M.; Leake, G.; Coolbaugh, D.; Watts, M.R. Integrated phased array for wide-angle beam steering. Opt. Lett. 2014, 39, 4575–4578. [Google Scholar] [CrossRef]
- Larocque, H.; Ranzani, L.; Leatham, J.; Tate, J.; Niechayev, A.; Yengst, T.; Komljenovic, T.; Fodran, C.; Smith, D.; Soltani, M. Beam steering with ultracompact and low-power silicon resonator phase shifters. Opt. Express 2019, 27, 34639–34654. [Google Scholar] [CrossRef]
- Zhang, R.; He, Y.; Zhang, Y.; An, S.; Zhu, Q.; Li, X.; Su, Y. Ultracompact and low-power-consumption silicon thermo-optic switch for high-speed data. Nanophotonics 2020, 10, 937–945. [Google Scholar] [CrossRef]
- Prost, M.; Ling, Y.C.; Cakmakyapan, S.; Zhang, Y.; Zhang, K.; Hu, J.; Zhang, Y.; Yoo, S.B. MWIR solid-state optical phased array beam steering using germanium-silicon photonic platform. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 3–7 March 2019; p. M4E.3. [Google Scholar]
- Miller, S.A.; Chang, Y.C.; Phare, C.T.; Shin, M.C.; Zadka, M.; Roberts, S.P.; Stern, B.; Ji, X.; Mohanty, A.; Gordillo, O.A.J.; et al. Large-scale optical phased array using a low-power multi-pass silicon photonic platform. Optica 2020, 7, 3–6. [Google Scholar] [CrossRef]
- Miller, S.A.; Phare, C.T.; Chang, Y.C.; Ji, X.; Gordillo, O.A.J.; Mohanty, A.; Roberts, S.P.; Shin, M.C.; Stern, B.; Zadka, M.; et al. 512-element actively steered silicon phased array for low power LIDAR. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Ansari, A.; Chandrasekhar, S.; Winzer, P.; Lončar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef] [PubMed]
- Poulton, C.V.; Yaacobi, A.; Su, Z.; Byrd, M.J.; Watts, M.R. Optical phased array with small spot size, high steering range and grouped cascaded phase shifters. In Proceedings of the Advanced Photonics (IPR, NOMA, Sensors, Networks, SPPCom, SOF), Vancouver, Canada, 18–20 July 2016; p. IW1B.2. [Google Scholar]
- Zhuang, D.; Zhang, L.; Han, X.; Li, Y.; Li, Y.; Liu, X.; Gao, F.; Song, J. Omnidirectional beam steering using aperiodic optical phased array with high error margin. Opt. Express 2018, 26, 19154. [Google Scholar] [CrossRef] [PubMed]
- Raval, M.; Poulton, C.V.; Watts, M.R. Unidirectional waveguide grating antennas with uniform emission for optical phased arrays. Opt. Lett. 2017, 42, 2563–2566. [Google Scholar] [CrossRef] [PubMed]
- Zadka, M.; Chang, Y.; Mohanty, A.; Phare, C.T.; Roberts, S.P.; Lipson, M. On-chip platform for a phased array with minimal beam divergence and wide field-of-view. Opt. Express 2018, 26, 2528–2534. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Luo, G.; Yu, H.; Li, Y.; Wang, M.; Zhou, X.; Chen, W.; Zhang, Y.; Pan, J. Improving the performance of optical antenna for optical phased arrays through high-contrast grating structure on SOI substrate. Opt. Express 2019, 27, 2703–2712. [Google Scholar] [CrossRef] [PubMed]
- Guan, B.; Qin, C.; Scott, R.P.; Ercan, B.; Fontaine, N.K.; Su, T.; Yoo, S.B. Hybrid 3D photonic integrated circuit for optical phased array beam steering. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 10–15 May 2015. [Google Scholar]
- Wu, D.; Yi, Y.; Zhang, Y. High-efficiency end-fire 3D optical phased array based on a multi-layer Si3N4/SiO2 platform. Appl. Opt. 2020, 59, 2489–2497. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, Z.; Wang, L.; Xiong, B.; Sun, C.; Wang, J.; Li, H.; Han, Y.; Luo, Y. A single-chip multi-beam steering optical phased array: Design rules and simulations. Opt. Express 2021, 29, 7049–7059. [Google Scholar] [CrossRef]
- Komljenovic, T.; Helkey, R.; Coldren, L.; Bowers, J.E. Sparse aperiodic arrays for optical beam forming and LIDAR. Opt. Express 2017, 25, 2511–2528. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Zeng, Y.; Wang, W.; Cai, Y.; Tu, Z.; Yue, W.; Wang, X.; Fang, Q.; Yu, M. Dual-layer waveguide grating antenna with high directionality for optical phased arrays. Appl. Opt. 2019, 58, 5807–5811. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.; Meng, D.; Desai, S.; Song, S.; Chew, S.X.; Li, L.; Yi, X. Optimization of optical phased array antenna with grating array superlattice. In Proceedings of the 17th International Conference on Optical Communications and Networks (ICOCN), Zhuhai, China, 14 February 2019; SPIE: Bellingham, WA, USA, 2019; Volume 1104831. [Google Scholar]
- Wang, P.; Luo, G.; Li, Y.; Yang, W.; Yu, H.; Zhou, X.; Zhang, Y.; Pan, J. Large scanning range optical phased array with a compact and simple optical antenna. Microelectron. Eng. 2020, 224, 111237. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Y.; Li, C.; Zhang, L. Bidirectional wide-angle waveguide grating antennas for optical phased arrays. To be submitted.
- Sacher, W.D.; Huang, Y.; Lo, G.Q.; Poon, J.K. Multilayer silicon nitride-on-silicon integrated photonic platforms and devices. J. Lightwave Technol. 2015, 33, 901–910. [Google Scholar] [CrossRef]
- Tsuchizawa, T.; Yamada, K.; Fukuda, H.; Watanabe, T.; Takahashi, J.; Takahashi, M.; Shoji, T.; Tamechika, E.; Itabashi, S.; Morita, H. Microphotonics devices based on silicon microfabrication technology. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 232–240. [Google Scholar] [CrossRef]
- Jalali, B.; Fathpour, S. Silicon photonics. J. Lightwave Technol. 2006, 24, 4600–4615. [Google Scholar] [CrossRef]
- Lim, A.E.; Song, J.; Fang, Q.; Li, C.; Tu, X.; Duan, N.; Chen, K.K.; Tern, R.P.; Liow, T.Y. Review of silicon photonics foundry efforts. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 8300112. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, X.; Zhang, W.; Wang, G.; Feng, N.; Zhao, W. Compact optical phased array using a serial grating antenna design. arXiv 2019, arXiv:1903.04573. [Google Scholar]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 2010, 4, 495–497. [Google Scholar] [CrossRef]
- Baets, R.; Subramanian, A.Z.; Clemmen, S.; Kuyken, B.; Bienstman, P.; Thomas, N.L.; Roelkens, G.; Thourhout, D.V.; Helin, P.; Severi, S. Silicon Photonics: Silicon nitride versus silicon-on-insulator. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–24 March 2016; p. Th3J.1. [Google Scholar]
- Xie, W.; Komljenovic, T.; Huang, J.; Tran, M.; Davenport, M.; Torres, A.; Pintus, P.; Bowers, J. Heterogeneous silicon photonics sensing for autonomous cars [Invited]. Opt. Express 2019, 27, 3642–3663. [Google Scholar] [CrossRef]
- Xie, W.; Huang, J.; Komljenovic, T.; Coldren, L.; Bowers, J. Diffraction limited centimeter scale radiator: Metasurface grating antenna for phased array LiDAR. arXiv 2018, arXiv:1810.00109. [Google Scholar]
- Nagarajan, R.; Kato, M.; Pleumeekers, J.; Evans, P.; Corzine, S.; Hurtt, S.; Dentai, A.; Murthy, S.; Missey, M.; Muthiah, R.; et al. InP Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1113. [Google Scholar] [CrossRef]
- Augustin, L.M.; Santos, R.; Haan, E.; Kleijn, S.; Thijs, P.J.A.; Latkowski, S.; Zhao, D.; Yao, W.; Bolk, J.; Ambrosius, H.; et al. InP-based generic foundry platform for photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 6100210. [Google Scholar] [CrossRef]
- Poulton, C.V. Integrated LIDAR with Optical Phased Arrays in Silicon Photonics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Bian, Y.; Ren, Q.; Kang, L.; Qin, Y.; Werner, P.L.; Werner, D.H. Efficient cross-talk reduction of nanophotonic circuits enabled by fabrication friendly periodic silicon strip arrays. Sci. Rep. 2017, 7, 15817. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, Z.; Wang, H.; Liu, A.; Wang, P.; Lin, T.; Liu, X.; Lv, H. Design of a low-crosstalk half-wavelength pitch nano-structured silicon waveguide array. Opt. Lett. 2019, 44, 3266–3269. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Gatdula, R.; Abbaslou, S.; Lu, M.; Stein, A.; Lai, W.Y.; Provine, J.; Pease, F.W.; Christodoulides, D.N.; Jiang, W. High-density waveguide superlattices with low crosstalk. Nat. Commun. 2015, 6, 7027. [Google Scholar] [CrossRef] [PubMed]
- Yang, N.; Yang, H.; Hu, H.; Zhu, R.; Chen, S.; Zhang, H.; Jiang, W. Theory of high-density low-cross-talk waveguide superlattices. Photonics Res. 2016, 4, 233–239. [Google Scholar] [CrossRef]
- Kwong, D.; Hosseini, A.; Covey, J.; Xu, X.; Zhang, Y.; Chakravarty, S.; Chen, R.T. Corrugated waveguide-based optical phased array with crosstalk suppression. IEEE Photonics Technol. Lett. 2014, 26, 991–994. [Google Scholar] [CrossRef]
- Xu, J.; Cua, M.; Zhou, E.H.; Horie, Y.; Faraon, A.; Yang, C. Wide-angular-range and high-resolution beam steering by a metasurface-coupled phased array. Opt. Lett. 2018, 43, 5255–5258. [Google Scholar] [CrossRef]
- Yang, B.; Chen, H.; Yang, S.; Chen, M. An improved aperiodic OPA design based on large antenna spacing. Opt. Commun. 2020, 475, 125852. [Google Scholar] [CrossRef]
- Wang, P.; Luo, G.; Li, Y.; Wang, M.; Meng, F.; Yang, W.; Yu, H.; Zhou, X.; Zhang, Y.; Pan, J. Two-dimensional large-angle scanning optical phased array with single wavelength beam. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019; p. JTh2A.72. [Google Scholar]
- Liu, X.; Xiong, B.; Sun, C.; Hao, Z.; Wang, L.; Wang, J.; Han, Y.; Li, H.; Luo, Y. Circular optical phased array for 360° constant amplitude scanning. In Proceedings of the Tenth International Conference on Information Optics and Photonics, Beijing, China, 8–11 July 2018; SPIE: Bellingham, WA, USA, 2019; p. 109644Z. [Google Scholar]
- Zhang, F.; Zhang, D.; Pan, S. Fast and wide-range optical beam steering with ultralow side lobes by applying an optimized multi-circular optical phased array. Appl. Opt. 2018, 57, 4977–4984. [Google Scholar] [CrossRef]
- Zeng, S.; Zhang, Y.; Zhu, J.; Wu, Z.; Chen, Y.; Yu, S. 360° on chip optical beam steering based on superposition of planar spiral orbital angular momentum waves. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 23–27 June 2019. [Google Scholar]
- Hashemi, H. Monolithic optical phased arrays in silicon. In Proceedings of the 22nd Microoptics Conference (MOC), Tokyo, Japan, 19–22 November 2017. [Google Scholar]
- Fatemi, R.; Khachaturian, A.; Hajimiri, A. Scalable optical phased array with sparse 2D aperture. In Proceedings of the 2018 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 13–18 May 2018. [Google Scholar]
- Rogers, C.; Piggott, A.Y.; Thomson, D.J.; Wiser, R.F.; Opris, I.E.; Fortune, S.A.; Compston, A.J.; Gondarenko, A.; Meng, F.; Chen, X.; et al. A universal 3D imaging sensor on a silicon photonics platform. Nature 2021, 590, 256–261. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, Z.; Peng, C.; Hu, W. Phase calibration of on-chip optical phased arrays via interference technique. IEEE Photonics J. 2020, 12, 6600210. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Li, Z.; Wu, W.; Wang, G.; Sun, X.; Zhao, W.; Zhang, W. An antenna array initial condition calibration method for integrated optical phased array. arXiv 2019, arXiv:1902.06203. [Google Scholar]
- Li, L.J.; Chen, W.; Zhao, X.Y.; Sun, M.J. Fast optical phased array calibration technique for random phase modulation LiDAR. IEEE Photonics J. 2019, 11, 6900410. [Google Scholar] [CrossRef]
- Zhang, W.; Li, L.; Chen, W. A chaotic stochastic parallel gradient descent algorithm for fast phase correction of optical phased array. In Proceedings of the Eleventh International Conference on Information Optics and Photonics (CIOP), Xi’an, China, 20 December 2019; SPIE: Bellingham, WA, USA, 2019; Volume 1120956. [Google Scholar]
- Komljenovic, T.; Pintus, P. On-chip calibration and control of optical phased arrays. Opt. Express 2018, 26, 3199–3210. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Sun, J.; Yaacobi, A.; Poulton, C.V.; Watts, M.R. Design of 3D hologram emitting optical phased arrays. In Proceedings of the Integrated Photonics Research, Silicon and Nanophotonics, Boston, MA, USA, 27 June–1 July 2015. [Google Scholar]
- Clevenson, H.A.; Spector, S.J.; Benney, L.; Moebius, M.G.; Brown, J.; Hare, A.; Huang, A.; Mlynarczyk, J.; Poulton, C.V.; Hosseini, E.; et al. Incoherent light imaging using an optical phased array. Appl. Phys. Lett. 2020, 116, 031105. [Google Scholar] [CrossRef]
- Kossey, M.R.; Alt, S.; Rizk, C.; Foster, A.C. Integrated photonic arrays as a platform for infrared neural stimulation. In Proceedings of the Bio-Optics: Design and Application, San Jose, CA, USA, 2–5 April 2017. [Google Scholar]
- Sacher, W.D.; Liu, X.; Chen, F.D.; Chameh, H.M.; Almog, I.F.; Lordello, T.; Chang, M.; Naderian, A.; Fowler, T.M.; Segev, E.; et al. Beam-steering nanophotonic phased-array neural probes. In Proceedings of the 2019 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 May 2019. [Google Scholar]
- Notaros, J.; Poulton, C.V.; Raval, M.; Watts, M.R. Near-field-focusing integrated optical phased arrays. J. Lightwave Technol. 2018, 36, 5912–5920. [Google Scholar] [CrossRef]
- Notaros, J.; Poulton, C.V.; Byrd, M.J.; Raval, M.; Watts, M.R. Integrated optical phased arrays for quasi-Bessel-beam generation. Opt. Lett. 2017, 42, 3510–3513. [Google Scholar] [CrossRef]
- Sun, J.; Moresco, M.; Leake, G.; Coolbaugh, D.; Watts, M.R. Generating and identifying optical orbital angular momentum with silicon photonic circuits. Opt. Lett. 2014, 36, 5977–5980. [Google Scholar] [CrossRef]
- Li, C.; Cao, X.; Wu, K.; Li, X.; Chen, J. Lens-based integrated 2D beam-steering device with defocusing approach and broadband pulse operation for Lidar application. Opt. Express 2019, 23, 32970–32983. [Google Scholar] [CrossRef] [PubMed]
- Inoue, D.; Ichikawa, T.; Kawasaki, A.; Yamashita, T. Demonstration of a new optical scanner using silicon photonics integrated circuit. Opt. Express 2019, 27, 2499–2508. [Google Scholar] [CrossRef] [PubMed]
- Nia, B.A.; Yousefi, L.; Shahabadi, M. Integrated optical-phased array nanoantenna system using a plasmonic Rotman lens. J. Lightwave Technol. 2016, 34, 2118–2126. [Google Scholar] [CrossRef]


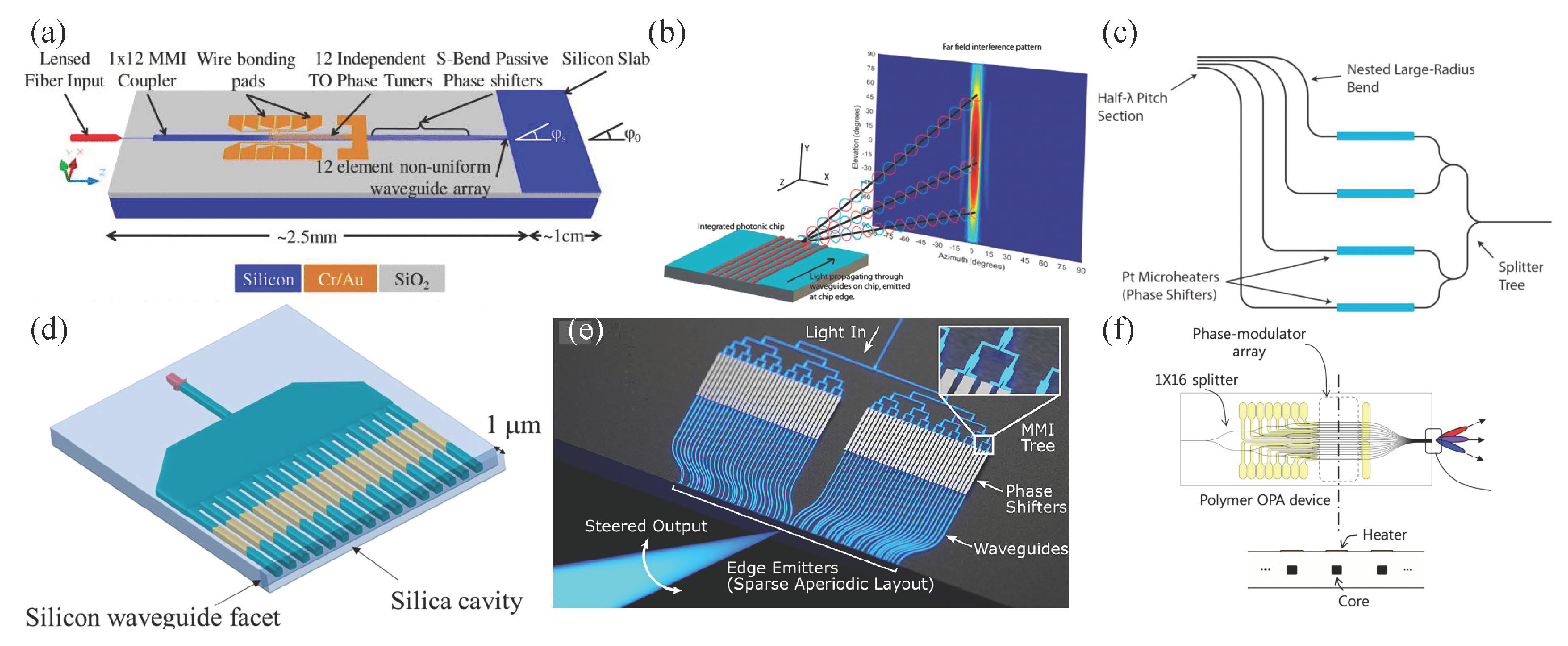
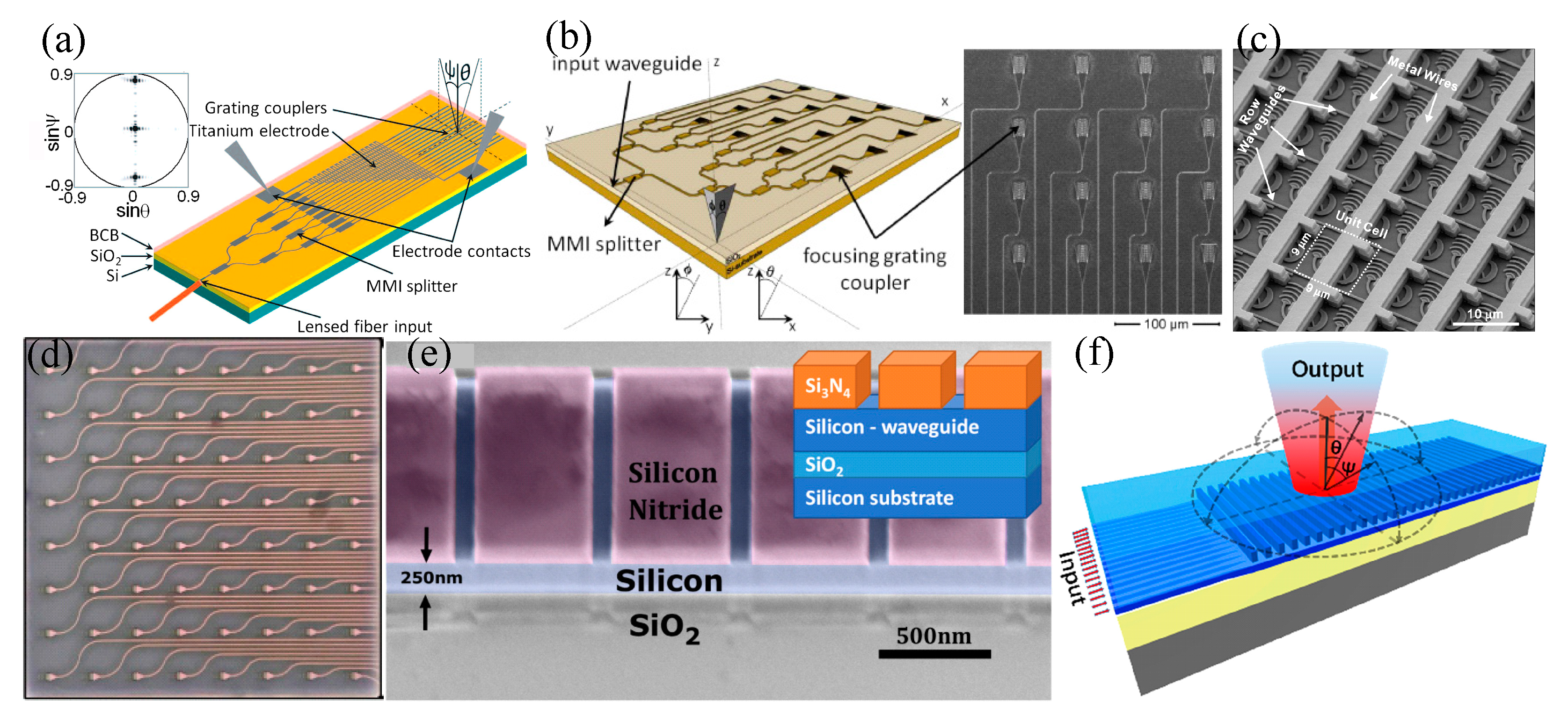
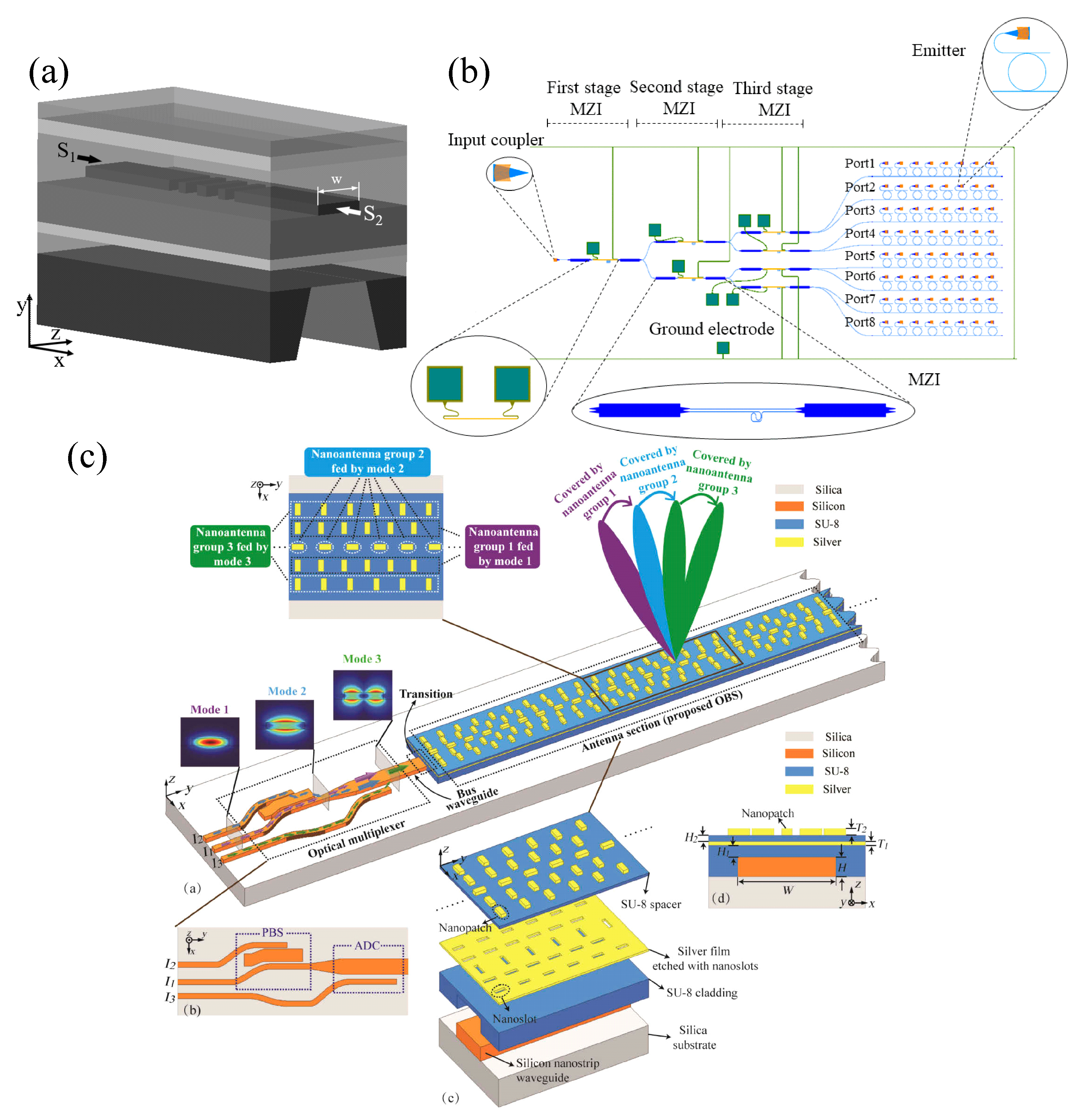
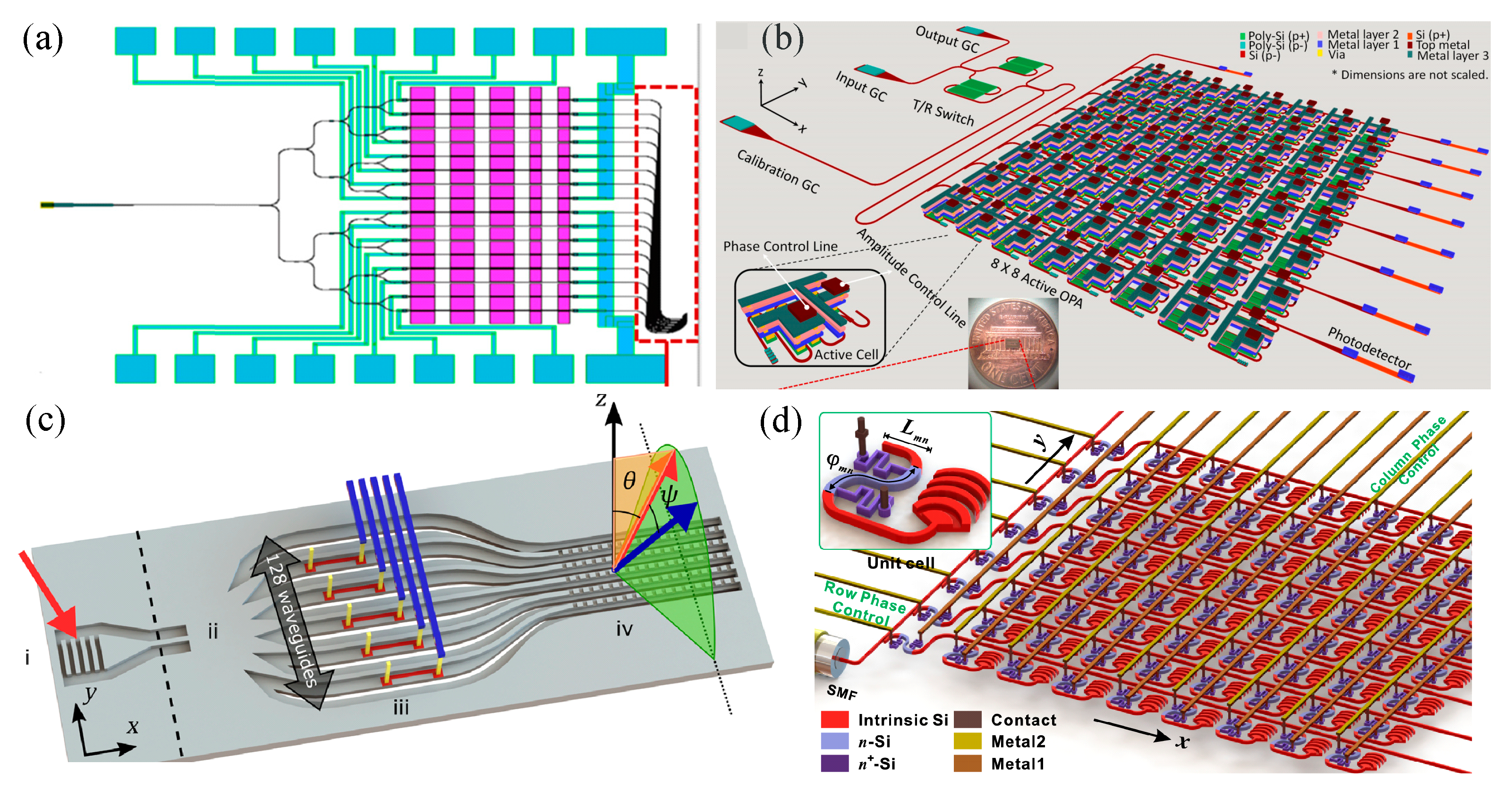
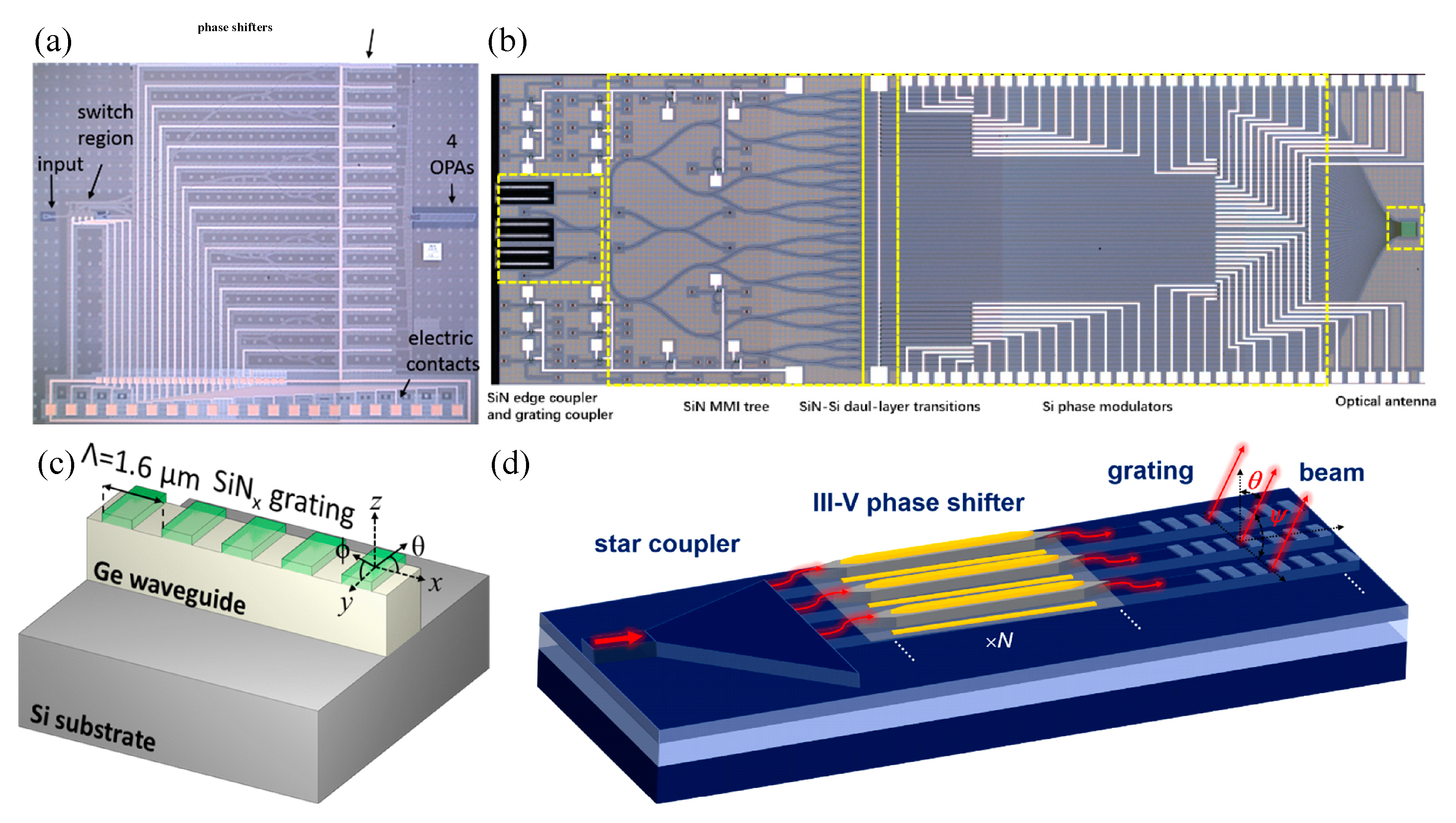
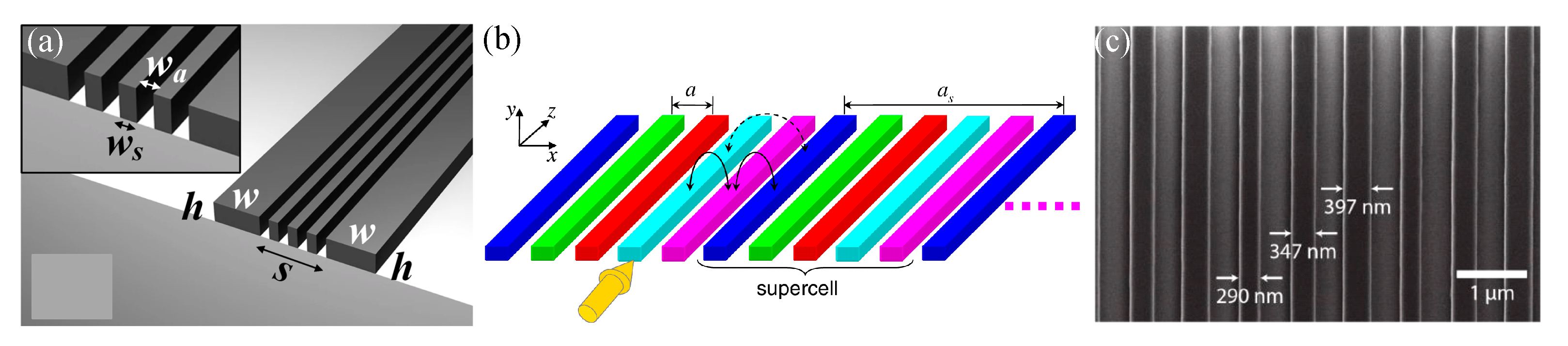
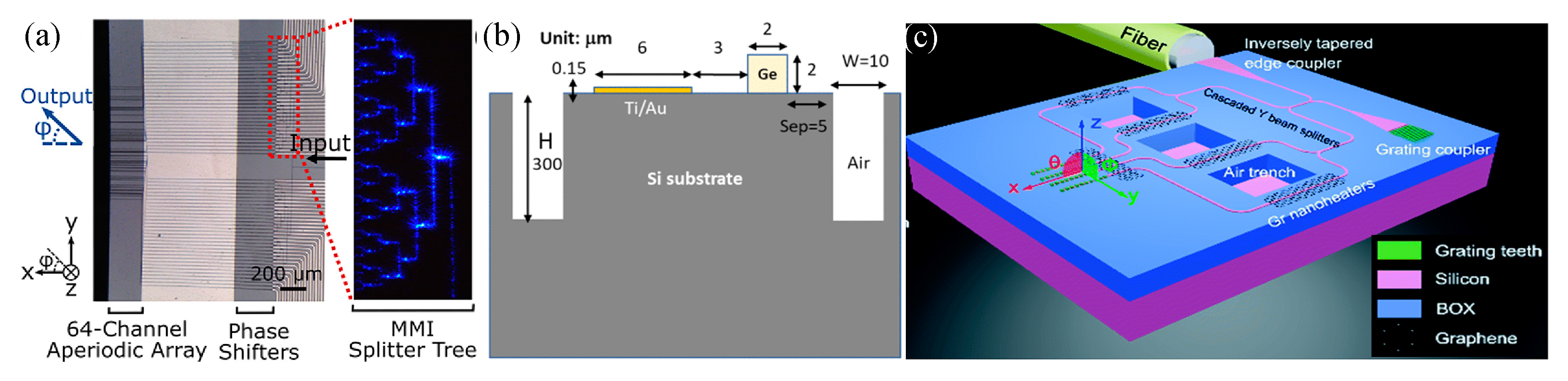
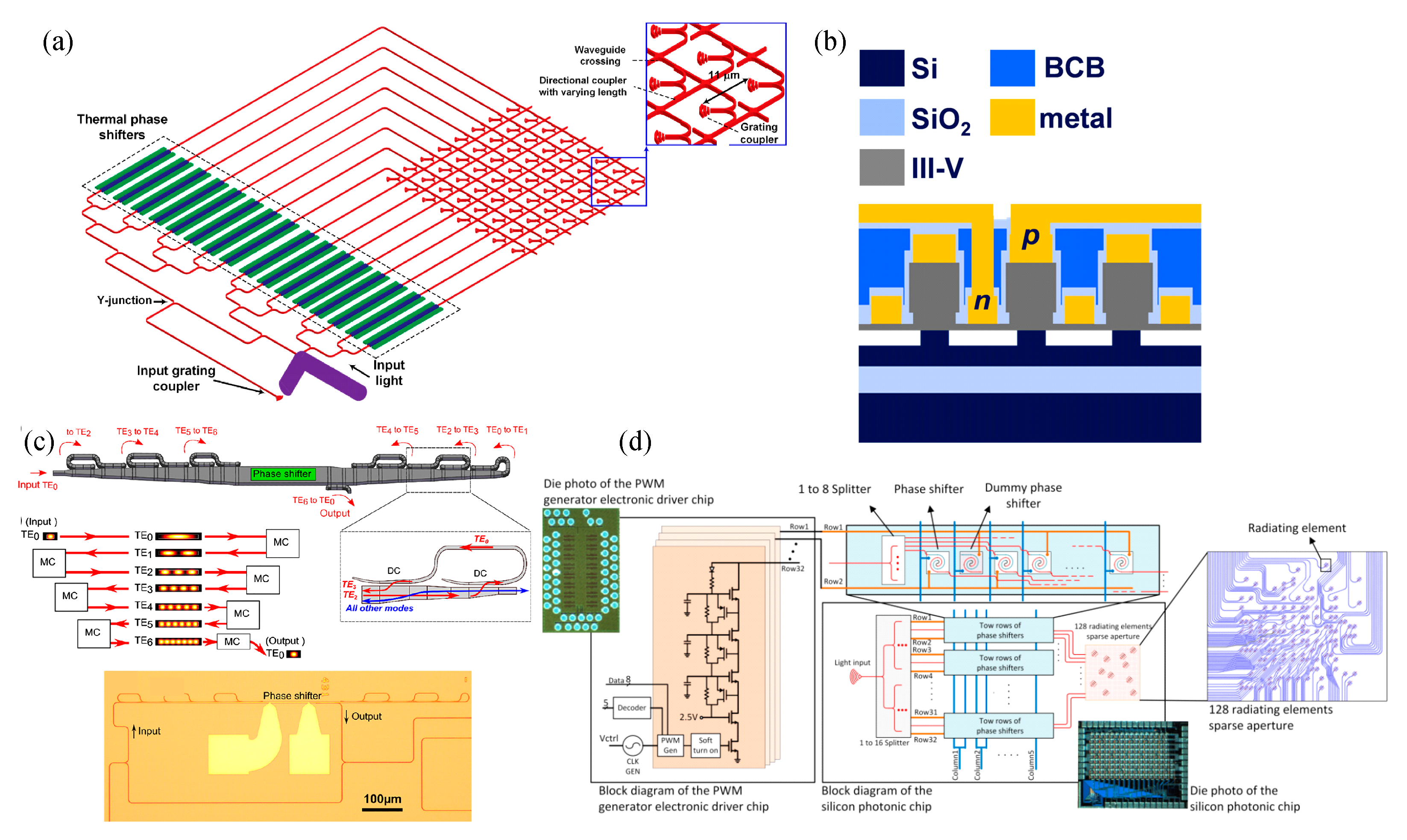
| λ, μm | FOV | Spot | Pitch, μm | Array | Size, mm2 | Material | Shifter | Power, mW/π | Speed, μs | SLL, dB | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.488 | >50° | 0.17° | >1.95 | 64 | 0.97 | Si3N4 | TO | 30 | 20 | 6.05 | [41] |
| 1.55 | 32° | N/A | >3.1 | 12 | N/A | Si | TO | 12.4 | 10 | 3 | [9] |
| 1.55 | 64° | 6.71° | 0.775 | 16 | N/A | Si | TO | N/A | N/A | 9.4 | [59] |
| 1.55 | 180° | 1.6° | 0.775 | 64 | N/A | Si | TO | N/A | N/A | 11.4 | [94] |
| 1.55 | 64° | 17° | 0.775 | 5 | N/A | Si | TO | N/A | 1000 | N/A | [61] |
| 1.55 | 164° | 0.062° | >4.14 | 128 | N/A | N/A | N/A | N/A | N/A | 14.3 | [107] |
| 1.55 | 7° | N/A | 12 | 16 | N/A | N/A | TO | 2.5 | N/A | 4.8 | [98] |
| 1.55 | 19.1° | 3.9° | 4.5 | 8 | N/A | polymer | EO | N/A | 0.5 | N/A | [97] |
| λ, μm | FOV, a° × b° | Spot, a° × b° | Pitch, μm | Array | Size, mm2 | Material | Shifter | Power, mW/π | Speed, μs | SLL, dB | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.635 | 146 | 0.06 × 0.07 | 2 | N/A | 0.5 × 0.5 | N/A | N/A | N/A | N/A | 8.7 | [65] |
| 0.905 | 3 × 17.6 | 4.3 × 0.7 | 3 | 4 × 4 | - × 0.09 | Si3N4 | TO | 87.6 | N/A | N/A | [99] |
| 1.064 | 11 × - | 1.1 | 2 | 16 | N/A | Si3N4 | TO | ~95 | ~125 | N/A | [93] |
| 1.30 | 80 × 17 | 0.14 × 0.14 | 7.25 | 128 | 1 | Si | TO | 8 | N/A | 8.9 | [12] |
| 1.55 | 2.3 × 14.1 | 2.7 × 2.4 | 2 | 16 | N/A | Si | TO | 8.2 | N/A | N/A | [7] |
| 1.55 | 20 × 14 | 1.6 × 0.6 | 3.5 | 16 | 4 × 0.2 | Si | TO | ~215 | N/A | 10 | [96] |
| 1.55 | 6 × 6 | N/A | N/A | 8 × 8 | N/A | N/A | TO | 8.5 | N/A | N/A | [10] |
| 1.55 | 10 × 6.5 | 2 × 0.2 | 5.5 | 8 | - × 0.5 | InP | EO | N/A | 0.5 | N/A | [79] |
| 1.55 | 20 × 15 | 1.2 × 0.5 | 4 | 16 | N/A | N/A | TO | 20 | N/A | >10 | [40] |
| 1.55 | 23 × 3.6 | 1 × 0.6 | 4 | 32 | N/A | Si | EO | 160 | 0.02 | 5.5 | [82] |
| 1.55 | 1.6 × 1.6 | N/A | 33 | 8 × 8 | N/A | N/A | TO | N/A | N/A | 11 | [86] |
| 1.55 | 1.5 × 1.5 | 0.5 × 0.5 | 50 | 4 × 4 | <1 | Si | EO | N/A | 0.005 | N/A | [52] |
| 1.55 | 46 | 0.02 × 0.02 | 4 | 1024 | 4 × 4 | Si3N4 | N/A | N/A | N/A | 10 | [65] |
| 1.55 | 46 × 36 | 0.85 × 0.18 | 2 | 50 | N/A | Si | TO | 13 | N/A | 8 | [17] |
| 1.55 | 6.6 | N/A | N/A | N/A | - × 1 | Si/Si3N4 | N/A | N/A | N/A | N/A | [66] |
| 1.55 | 180 | N/A | >2.3 | N/A | N/A | N/A | N/A | N/A | N/A | >13.5 | [114] |
| 1.55 | 45 | 0.03 | 2 | 1024 | 0.004 × 0.06 | Si | TO | 48 | N/A | 9 | [16] |
| 1.55 | 70 × 14 | 0.15 × 0.15 | 1.3 | 512 | N/A | N/A | TO | 2.6 | N/A | 8 | [104] |
| 1.55 | 106 × - | 6.2 × 3.8 | 0.9 | 20 | 35 × - | Si | N/A | N/A | N/A | 7 | [60] |
| 1.55 | 66 × 3.3 | N/A | 1.3 | 24 | 5 × - | Si/Si3N4 | TO | 11 | N/A | 7 | [90] |
| 1.55 | 45.6 × 20.2 | 2.4 × 2.5 | N/A | 16 | 0.08 × - | Si | N/A | N/A | N/A | 28.4 | [110] |
| 1.55 | 10 × 45.4 | 5.8 × 3.2 | 2 | 16 | 1.75 × 1.2 | Si | EO & TO | N/A, 2.3 | N/A, 0.068 | N/A | [64] |
| 1.55 | 56 × 15 | 0.04 | 1.65 | 512 | 10 | N/A | EO | <1 | <30 | 12 | [11] |
| 1.55 | - × 8.6 | N/A | N/A | N/A | 4 × - | Si/Si3N4 | N/A | N/A | N/A | N/A | [115] |
| 1.55 | 51 × 28 | 0.78 × 0.02 | 2 | 32 | 10 × - | hybrid | EO | 1.5 × 10−6 | 6.1 × 10−4 | 16 | [42] |
| 1.55 | 18.5 × 16 | 0.15 × 0.25 | 4 | 125 | 0.5 × 0.5 | N/A | TO | 20 | N/A | 7.4 | [14] |
| 1.55 | 97 × 17.1 | 2.3 × 2.8 | N/A | 32 | N/A | Si/Si3N4 | TO | N/A | N/A | N/A | [88] |
| 1.55 | 130 × - | 2.52 | 0.8 | 33 | 0.026 × 0.09 | Si | N/A | N/A | N/A | 5.2 | [116] |
| 1.50 | 7 × 7 | N/A | 11 | 8 × 8 | 1 × 0.95 | N/A | TO | N/A | N/A | N/A | [74] |
| 1.55 | 16 × 16 | 0.8 × 0.8 | 5.6 | 128 | 2.08 | Si | TO | 10.6 | N/A | 12 | [45] |
| 1.55 | 70 × 6 | 0.15 × 0.08 | 1.3 | 512 | 2 × - | Si | TO | 1.7 | 6.5 | 7.5 | [103] |
| 1.55 | 8.9 × 2.2 | 0.92 × 0.32 | 10, 40 | 8 × 8 | 7 × 3 | Si | EO | 17 | 0.05 | N/A | [44] |
| 1.55 | 97 × 17.1 | 2.3 × 2.8 | 1 | 32 | N/A | Si | TO | N/A | N/A | N/A | [117] |
| 1.55 | - × 7.4 | 0.2 × 0.6 | 4 | 32 | N/A | Si3N4 | N/A | N/A | N/A | N/A | [71] |
| 4.6 | 12.7 × 12 | 3.08 × 0.18 | 6 | 12 | 2 × - | Ge/Si3N4 | TO | ~52 | N/A | N/A | [72] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Guo, Y.; Li, C.; Zhang, H.; Zhou, X.; Zhang, L. Integrated Optical Phased Arrays for Beam Forming and Steering. Appl. Sci. 2021, 11, 4017. https://doi.org/10.3390/app11094017
Guo Y, Guo Y, Li C, Zhang H, Zhou X, Zhang L. Integrated Optical Phased Arrays for Beam Forming and Steering. Applied Sciences. 2021; 11(9):4017. https://doi.org/10.3390/app11094017
Chicago/Turabian StyleGuo, Yongjun, Yuhao Guo, Chunshu Li, Hao Zhang, Xiaoyan Zhou, and Lin Zhang. 2021. "Integrated Optical Phased Arrays for Beam Forming and Steering" Applied Sciences 11, no. 9: 4017. https://doi.org/10.3390/app11094017
APA StyleGuo, Y., Guo, Y., Li, C., Zhang, H., Zhou, X., & Zhang, L. (2021). Integrated Optical Phased Arrays for Beam Forming and Steering. Applied Sciences, 11(9), 4017. https://doi.org/10.3390/app11094017








