Novel Data Augmentation Employing Multivariate Gaussian Distribution for Neural Network-Based Blood Pressure Estimation
Abstract
1. Introduction
2. NN-Based BPE
2.1. Feature Extraction
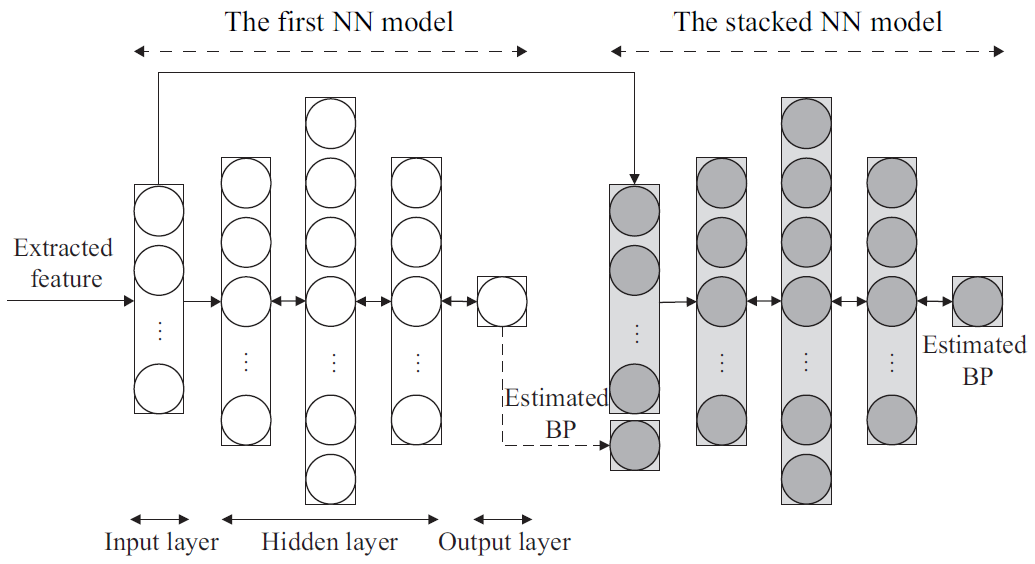
2.2. NN Training and BPE
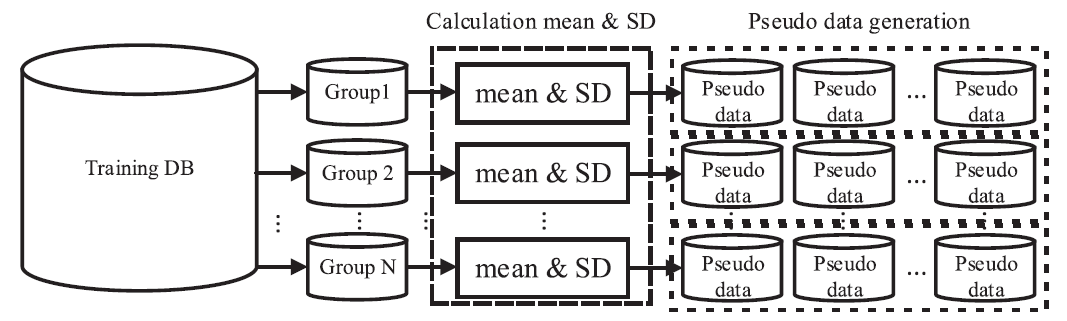
2.3. Conventional Data Augmentation Algorithm
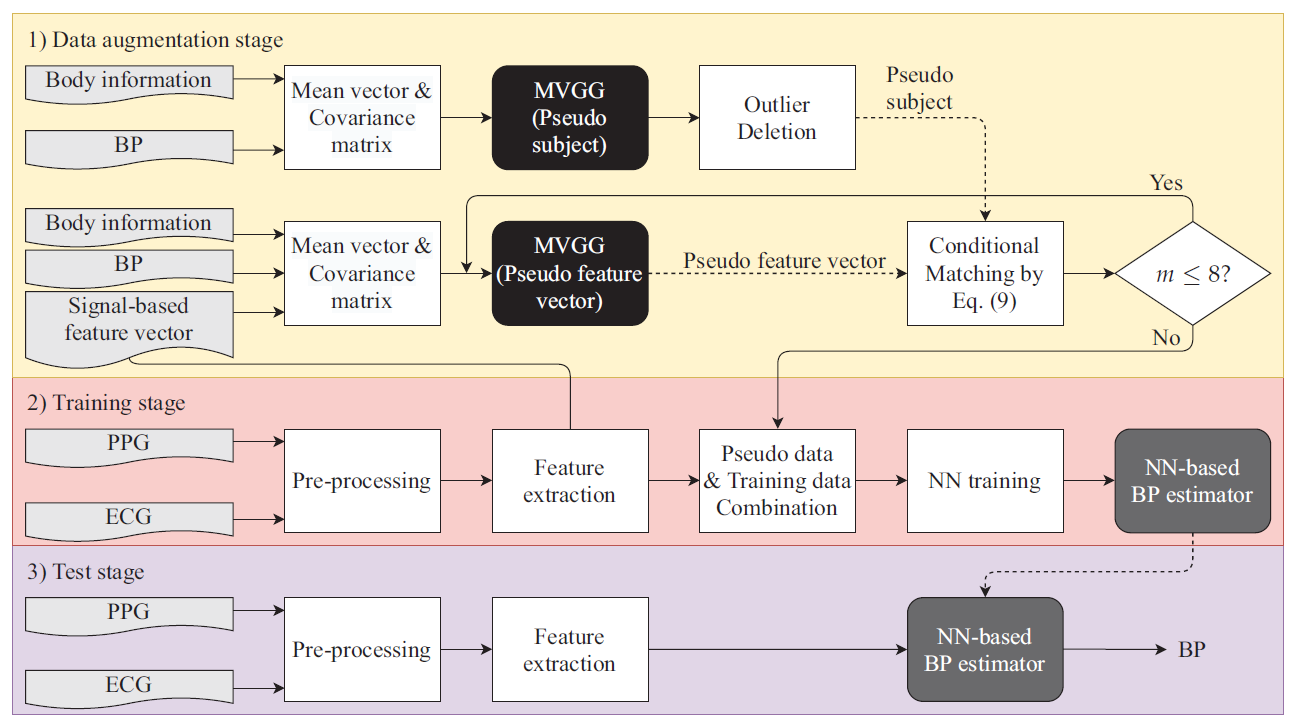
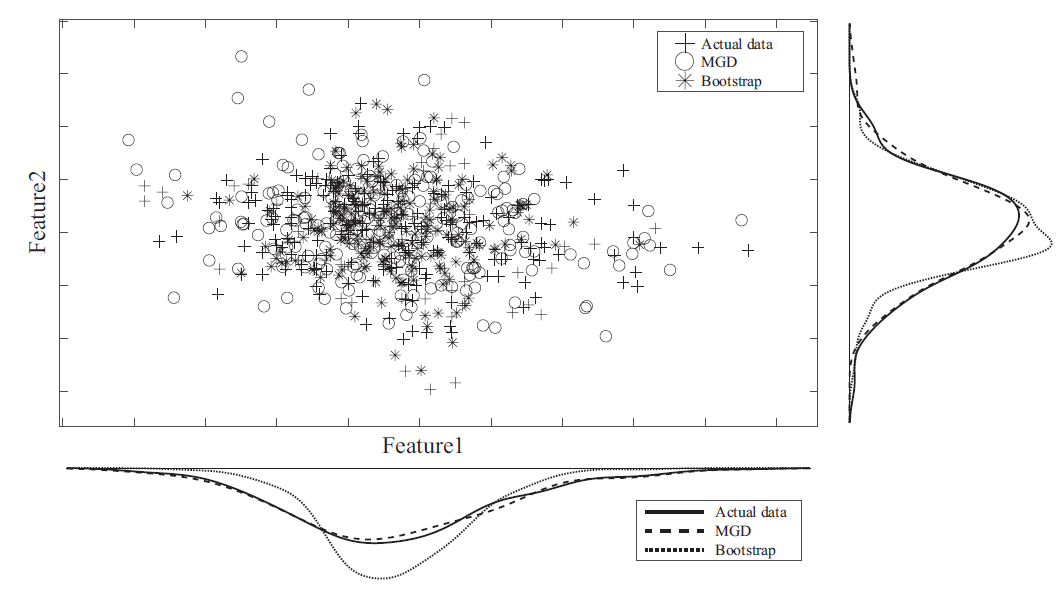
3. Method
| Algorithm 1 Matching the pseudo subject with the pseudo feature |
|
4. Results
4.1. Statistics
4.2. Data Collection Protocol and Data Sets
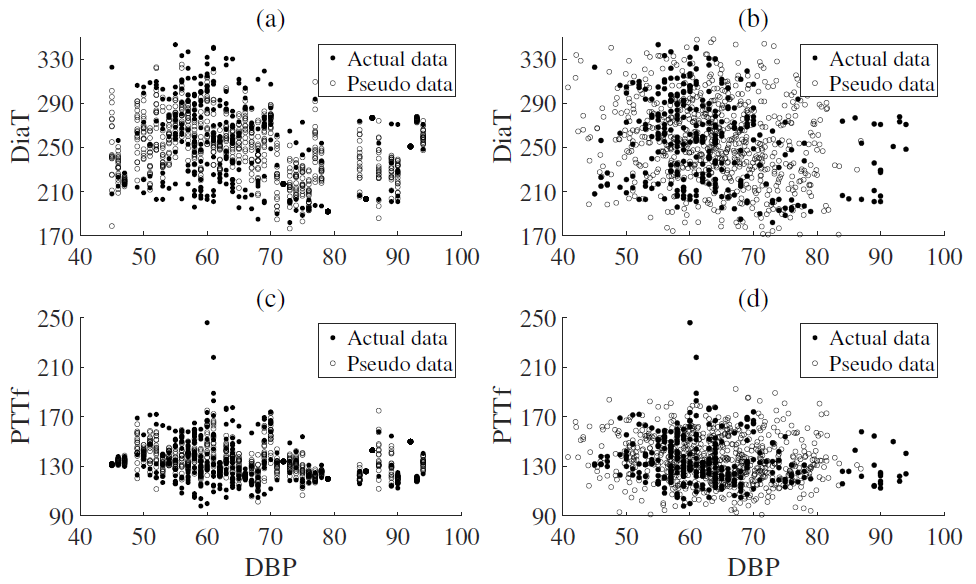
4.3. Data Augmentation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuffless blood pressure estimation algorithm for continuous health-care monitoring. IEEE Trans. Biomed. Eng. 2017, 64, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhou, W.; Xing, Y.; Zhou, X. A novel neural network model for blood pressure estimation using photoplethesmography without electrocardiogram. J. Healthc. Eng. 2018, 2018, 1006–1009. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Chang, J.-H. Oscillometric blood pressure estimation based on deep learning. IEEE Trans. Ind. Inform. 2017, 13, 461–472. [Google Scholar] [CrossRef]
- Salamon, J.; Bello, J.P. Deep convolutional neural networks and data augmentation for environmental sound classification. IEEE Signal Process. Lett. 2017, 24, 279–283. [Google Scholar] [CrossRef]
- Shen, D.; Wu, G.; Suk, H.-I. Deep learning in medical image analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef]
- Ker, J.; Wang, L.; Rao, J.; Lim, T. Deep learning applications in medical image analysis. IEEE Access. 2017, 6, 9375–9389. [Google Scholar] [CrossRef]
- Tran, T.; Pham, T.; Carneiro, G.; Palmer, L.; Reid, I. A Bayesian Data Augmentation Approach for Learning Deep Models. In Proceedings of the Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2794–2803. [Google Scholar]
- Zhang, K.; Liu, N.; Yuan, X.; Guo, X.; Gao, C.; Zhao, Z.; Ma, Z. Fine-grained age estimation in the wild with attention LSTM networks. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3140–3152. [Google Scholar] [CrossRef]
- Chang, D.; Ding, Y.; Xie, J.; Bhunia, A.K.; Li, X.; Ma, Z.; Wu, M.; Guo, J.; Song, Y.-Z. The devil is in the channels: Mutual-channel loss for fine-grained image classification. IEEE Trans. Image Process. 2020, 29, 4683–4695. [Google Scholar] [CrossRef]
- Zhang, K.; Sun, M.; Han, T.X.; Yuan, X.; Guo, L.; Liu, T. Residual networks of residual networks: Multilevel residual networks. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 1303–1314. [Google Scholar] [CrossRef]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese Neural Networks for One-Shot Image Recognition. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015. [Google Scholar]
- Ravi, S.; Larochelle, H. Optimization as A Model for Few-Shot Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Ren, M.; Triantafillou, E.; Ravi, S.; Snell, J.; Swersky, K.; Tenenbaum, J.B.; Larochelle, H.; Zemel, R.S. Meta-Learning for Semi-Supervised Few-Shot Classification. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- He, A.; Luo, C.; Tian, X.; Zeng, W. A Twofold Siamese Network for Real-Time Object Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 19–21 June 2018; pp. 4834–4843. [Google Scholar]
- Ji, Y.; Yang, Y.; Xu, X.; Shen, H.T. One-shot learning based pattern transition map for action early recognition. Signal Process. 2018, 143, 364–370. [Google Scholar] [CrossRef]
- Burrello, A.; Schindler, K.; Benini, L.; Rahimi, A. One-Shot Learning for IEEG Seizure Detection Using End-to-End Binary Operations: Local Binary Patterns with Hyperdimensional Computing. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS), Cleveland, OH, USA, 17–19 October 2018; pp. 1–4. [Google Scholar]
- Zhao, A.; Balakrishnan, G.; Durand, F.; Guttag, J.V.; Dalca, A.V. Data Augmentation Using Learned Transformations for One-Shot Medical Image Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 8543–8553. [Google Scholar]
- Lee, S.; Chang, J.-H. Deep belief networks ensemble for blood pressure estimation. IEEE Access 2017, 5, 9962–9972. [Google Scholar] [CrossRef]
- Lee, S.; Chang, J.-H. Dempster-Shafer fusion based on a deep Boltzmann machine for blood pressure estimation. Appl. Sci. 2019, 9, 1–13. [Google Scholar] [CrossRef]
- Akar, S.A.; Kara, S.; Latifoglu, F.; Bilgic, V. Spectral analysis of photoplethysmographic signals: The importance of preprocessing. Biomed. Signal Process. Control 2013, 8, 16–22. [Google Scholar] [CrossRef]
- Madhav, K.V.; Ram, M.R.; Krishna, E.H.; Komalla, N.R.; Reddy, K.A. Estimation of Respiration Rate from ECG, BP and PPG Signals Using Empirical Mode Decomposition. In Proceedings of the Instrumentation and Measurement Technology Conference, Binjiang, China, 10–12 May 2011; pp. 1–4. [Google Scholar]
- Lazaro, J.; Gil, E.; Bailon, R.; Minchole, A.; Laguna, P. Deriving respiration from photoplethysmographic pulse width. Med. Biol. Eng. Comput. 2013, 51, 233–242. [Google Scholar] [CrossRef]
- Nemati, E.; Deen, M.J.; Mondal, T. A wireless wearable ECG sensor for long-term applications. IEEE Commun. Mag. 2012, 50, 36–43. [Google Scholar] [CrossRef]
- Thomas, S.S.; Nathan, V.; Soundarapandian, K.; Shi, X.; Jafari, R. BioWatch: A noninvasive wrist-based blood pressure monitor that incorporates training techniques for posture and subject variability. IEEE J. Biomed. Health Inf. 2016, 20, 1291–1300. [Google Scholar] [CrossRef]
- McDuff, D.; Gontarek, S.; Picard, R.W. Remote detection of photoplethysmographic systolic and diastolic peaks using a digital camera. IEEE Trans. Biomed. Eng. 2014, 61, 2948–2954. [Google Scholar] [CrossRef]
- Gesche, H.; Grosskurth, D.; Kuchler, G.; Patzak, A. Continuous blood pressure measurement by using the pulse transit time: Comparison to a cuff-based method. Eur. J. Appl. Physiol. 2012, 112, 309–315. [Google Scholar] [CrossRef]
- Yoon, Y.; Cho, J.H.; Yoon, G. Non-constrained blood pressure monitoring using ECG and PPG for personal healthcare. Med. Syst. 2009, 33, 261–266. [Google Scholar] [CrossRef]
- Kumar, S.; Ayub, S. Estimation of Blood Pressure by Using Electrocardiogram (ECG) and Photoplethysmogram (PPG). In Proceedings of the International Conference on Communication Systems and Network Technologies, Dallas-Fort Worth, TX, USA, 13–15 July 2015; pp. 521–524. [Google Scholar]
- Deng, L.; Li, J.; Huang, J.-T.; Yao, K.; Yu, D.; Seide, F.; Seltzer, M.; Zweig, G.; He, X.; Williams, J.; et al. Recent Advances in Deep Learning for Speech Research at Microsoft. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 8604–8608. [Google Scholar]
- Choi, K.; Fazekas, G.; Sandler, M. Convolutional Recurrent Neural Networks for Music classification. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2392–2396. [Google Scholar]
- Lee, B.-K.; Chang, J.-H. Packet loss concealment based on deep neural networks for digital speech transmission. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 378–387. [Google Scholar] [CrossRef]
- Song, K.; Chang, J.-H. Cuff-less deep learning-based blood pressure estimation for smart wristwatches. IEEE Trans. Inst. Meas. 2020, 69, 4292–4302. [Google Scholar] [CrossRef]
- Ahrendt, P. The Multivariate Gaussian Probability Distribution; Technical University of Denmark: Kongens Lyngby, Denmark, 2005. [Google Scholar]
- IBM SPSS Statistics for Windows Version 21.0. 2012. Available online: https://www.ibm.com/ (accessed on 25 April 2021).


| No | PPG and ECG | PPG Only | ECG Only |
|---|---|---|---|
| 1 | # of RPP | ||
| 2 | TDRPP | ||
| 3 | # of VP | - | |
| 4 | TDVP | - |
| Item | BP | Baseline (without DA) | Bootstrap (5 Times) | Bootstrap (20 Times) | Proposed (50 Subjects*8) | Proposed (100 Subjects*8) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ME | SDE | r-Value | ME | SDE | r-Value | ME | SDE | r-value | ME | SDE | r-Value | ME | SDE | r-Value | ||
| 1 set | SBP | −4.5 | 10.0 | 0.37 | 0.4 | 9.5 | 0.33 | −1.4 | 10.2 | 0.30 | −1.8 | 7.2 | 0.38 | −4.6 | 7.6 | 0.41 |
| DBP | −4.4 | 8.3 | 0.42 | −2.5 | 8.7 | 0.42 | −1.2 | 8.9 | 0.18 | −3.8 | 7.8 | 0.43 | −3.2 | 7.7 | 0.46 | |
| 2 set | SBP | −1.3 | 8.4 | 0.54 | 2.0 | 10.0 | 0.52 | −2.5 | 9.9 | 0.53 | −1.8 | 8.0 | 0.57 | −1.3 | 7.8 | 0.55 |
| DBP | −0.1 | 8.2 | 0.61 | 1.3 | 9.3 | 0.50 | 2.2 | 9.2 | 0.45 | 0.4 | 7.7 | 0.67 | −0.2 | 7.9 | 0.64 | |
| 3 set | SBP | 1.4 | 7.3 | 0.43 | −0.1 | 8.2 | 0.36 | 4.5 | 7.8 | 0.46 | 1.3 | 5.2 | 0.47 | 1.3 | 5.1 | 0.51 |
| DBP | 0.0 | 6.6 | 0.46 | 4.3 | 7.4 | 0.46 | 4.7 | 7.4 | 0.43 | 0.4 | 6.3 | 0.49 | −1.6 | 6.2 | 0.48 | |
| 4 set | SBP | 1.5 | 9.7 | 0.65 | 1.5 | 10.0 | 0.65 | 0.2 | 10.7 | 0.68 | −0.7 | 8.9 | 0.72 | −1.4 | 9.1 | 0.73 |
| DBP | −3.7 | 8.1 | 0.73 | 1.3 | 8.8 | 0.66 | 0.1 | 8.9 | 0.66 | −0.3 | 7.5 | 0.77 | −0.7 | 7.7 | 0.77 | |
| 5 set | SBP | 1.9 | 8.7 | 0.50 | 4.2 | 8.8 | 0.53 | 0.8 | 8.8 | 0.49 | 1.4 | 6.6 | 0.56 | 1.6 | 6.5 | 0.57 |
| DBP | 2.0 | 7.1 | 0.44 | 3.4 | 8.1 | 0.39 | 2.9 | 8.0 | 0.42 | 1.9 | 6.6 | 0.56 | 1.0 | 6.6 | 0.54 | |
| 6 set | SBP | 2.0 | 7.8 | 0.34 | 4.9 | 7.5 | 0.33 | 4.5 | 7.5 | 0.27 | 0.0 | 4.8 | 0.51 | −0.8 | 4.6 | 0.48 |
| DBP | 3.8 | 6.5 | 0.48 | 4.5 | 7.6 | 0.32 | 2.0 | 7.7 | 0.41 | 2.0 | 4.6 | 0.70 | 1.3 | 4.6 | 0.69 | |
| mean | SBP | 0.2 | 8.7 | 0.47 | 2.2 | 9.0 | 0.45 | 1.0 | 9.2 | 0.46 | −0.3 | 6.8 | 0.54 | −0.9 | 6.8 | 0.54 |
| DBP | −0.4 | 7.5 | 0.52 | 2.1 | 8.3 | 0.46 | 1.8 | 8.4 | 0.43 | 0.1 | 6.8 | 0.60 | −0.6 | 6.8 | 0.60 | |
| CI | SBP | 2.0 | 0.8 | 0.1 | 1.5 | 0.8 | 0.1 | 2.2 | 1.0 | 0.1 | 1.1 | 1.2 | 0.1 | 1.7 | 1.3 | 0.1 |
| DBP | 2.4 | 0.6 | 0.1 | 2.0 | 0.6 | 0.1 | 1.6 | 0.6 | 0.1 | 1.6 | 0.9 | 0.1 | 1.3 | 1.0 | 0.1 | |
| Item | BP | Baseline (without DA) | Bootstrap (5 Times) | Bootstrap (20 Times) | Proposed (50 Subjects*8) | Proposed (100 Subjects*8) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ME | SDE | r-Value | ME | SDE | r-Value | ME | SDE | r-value | ME | SDE | r-Value | ME | SDE | r-Value | ||
| 1 set | SBP | −2.9 | 9.2 | 0.38 | 0.4 | 9.2 | 0.37 | −3.4 | 10.2 | 0.32 | −2.7 | 7.0 | 0.40 | −4.0 | 6.3 | 0.43 |
| DBP | −5.0 | 8.1 | 0.43 | 0.9 | 8.5 | 0.42 | −1.8 | 8.6 | 0.36 | −2.9 | 7.6 | 0.46 | −2.4 | 7.5 | 0.49 | |
| 2 set | SBP | 0.4 | 8.1 | 0.57 | 4.1 | 9.3 | 0.53 | 2.2 | 9.3 | 0.53 | 2.2 | 7.4 | 0.61 | 1.3 | 7.6 | 0.57 |
| DBP | 0.9 | 8.0 | 0.64 | −1.1 | 9.1 | 0.53 | −0.7 | 8.7 | 0.54 | 0.3 | 7.5 | 0.68 | 1.7 | 7.6 | 0.67 | |
| 3 set | SBP | 1.7 | 7.1 | 0.45 | 0.6 | 8.1 | 0.38 | 0.7 | 7.6 | 0.46 | 1.4 | 4.7 | 0.50 | 1.1 | 4.9 | 0.51 |
| DBP | 1.0 | 6.2 | 0.48 | 4.0 | 7.2 | 0.46 | 3.7 | 7.2 | 0.44 | −1.3 | 5.9 | 0.53 | 0.9 | 6.1 | 0.49 | |
| 4 set | SBP | 0.7 | 9.5 | 0.67 | 0.9 | 9.7 | 0.69 | 1.9 | 9.9 | 0.67 | −0.6 | 8.7 | 0.74 | −2.9 | 9.0 | 0.73 |
| DBP | 0.9 | 7.8 | 0.75 | 1.5 | 8.5 | 0.69 | 1.2 | 8.7 | 0.66 | 0.2 | 7.1 | 0.79 | 1.0 | 7.5 | 0.77 | |
| 5 set | SBP | 2.7 | 8.3 | 0.54 | 2.8 | 8.5 | 0.54 | 2.3 | 8.5 | 0.51 | 0.9 | 6.4 | 0.58 | −0.9 | 6.1 | 0.63 |
| DBP | 1.7 | 6.9 | 0.48 | 0.4 | 7.9 | 0.40 | 1.3 | 7.8 | 0.42 | 1.8 | 6.4 | 0.58 | 1.5 | 6.3 | 0.59 | |
| 6 set | SBP | 2.4 | 7.5 | 0.34 | 2.3 | 7.1 | 0.35 | 2.9 | 7.2 | 0.29 | 0.6 | 3.9 | 0.66 | −0.8 | 4.3 | 0.56 |
| DBP | 3.3 | 6.3 | 0.53 | 0.9 | 7.3 | 0.45 | 1.7 | 7.3 | 0.44 | 0.5 | 4.0 | 0.78 | 1.0 | 4.3 | 0.74 | |
| mean | SBP | 0.8 | 8.3 | 0.49 | 1.9 | 8.7 | 0.48 | 1.1 | 8.8 | 0.46 | 0.3 | 6.4 | 0.58 | −1.0 | 6.4 | 0.57 |
| DBP | 0.5 | 7.2 | 0.55 | 1.1 | 8.1 | 0.49 | 0.9 | 8.1 | 0.48 | −0.2 | 6.4 | 0.64 | 0.6 | 6.6 | 0.63 | |
| CI | SBP | 1.6 | 0.7 | 0.1 | 1.1 | 0.7 | 0.1 | 1.8 | 0.9 | 0.1 | 1.3 | 1.4 | 0.1 | 1.6 | 1.3 | 0.1 |
| DBP | 2.2 | 0.7 | 0.1 | 1.3 | 0.6 | 0.1 | 1.5 | 0.5 | 0.1 | 1.3 | 1.0 | 0.1 | 1.2 | 1.0 | 0.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, K.; Park, T.-J.; Chang, J.-H. Novel Data Augmentation Employing Multivariate Gaussian Distribution for Neural Network-Based Blood Pressure Estimation. Appl. Sci. 2021, 11, 3923. https://doi.org/10.3390/app11093923
Song K, Park T-J, Chang J-H. Novel Data Augmentation Employing Multivariate Gaussian Distribution for Neural Network-Based Blood Pressure Estimation. Applied Sciences. 2021; 11(9):3923. https://doi.org/10.3390/app11093923
Chicago/Turabian StyleSong, Kwangsub, Tae-Jun Park, and Joon-Hyuk Chang. 2021. "Novel Data Augmentation Employing Multivariate Gaussian Distribution for Neural Network-Based Blood Pressure Estimation" Applied Sciences 11, no. 9: 3923. https://doi.org/10.3390/app11093923
APA StyleSong, K., Park, T.-J., & Chang, J.-H. (2021). Novel Data Augmentation Employing Multivariate Gaussian Distribution for Neural Network-Based Blood Pressure Estimation. Applied Sciences, 11(9), 3923. https://doi.org/10.3390/app11093923







