Magnetic Energy Landscape of Dimolybdenum Tetraacetate on a Bulk Insulator Surface
Abstract
1. Introduction
2. Results
2.1. Magnetic States of MoMo in the Gas-Phase
2.1.1. Generalized-Gradient Approximation (GGA-PBE) Results
2.1.2. Results from Hubbard-Corrected Functionals
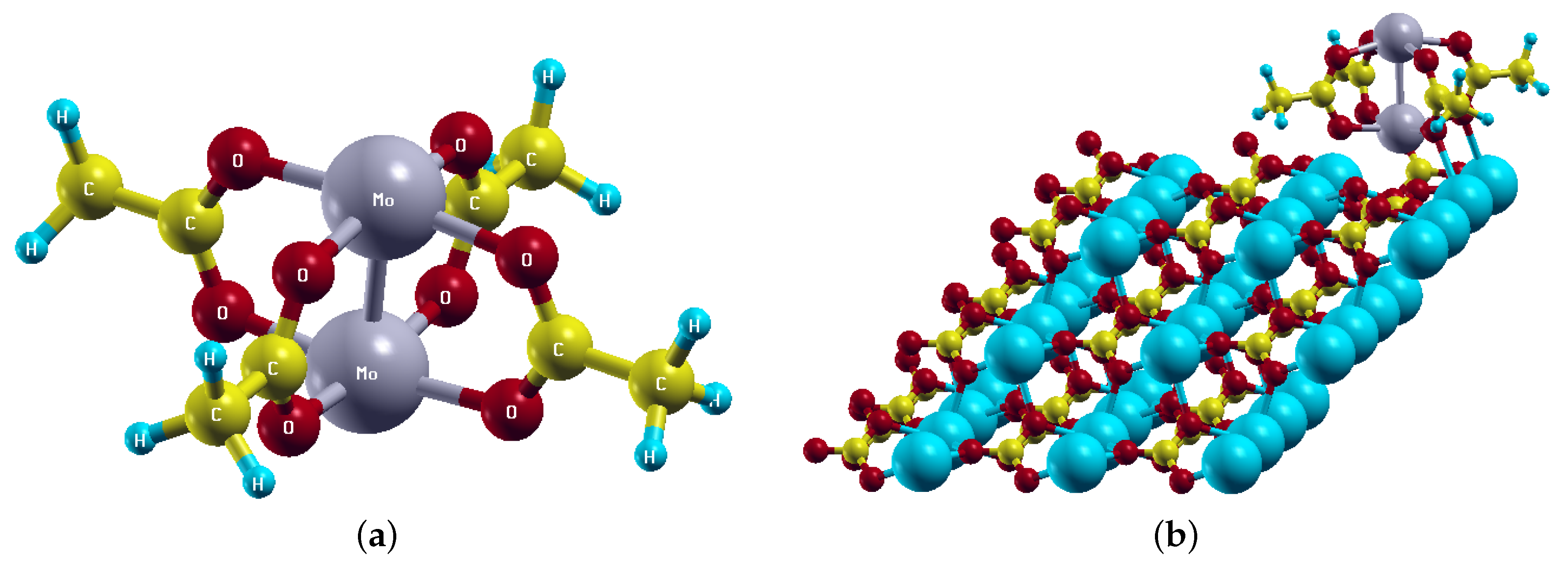
2.2. Magnetic States of MoMo Adsorbed on the Calcite (10.4) Surface
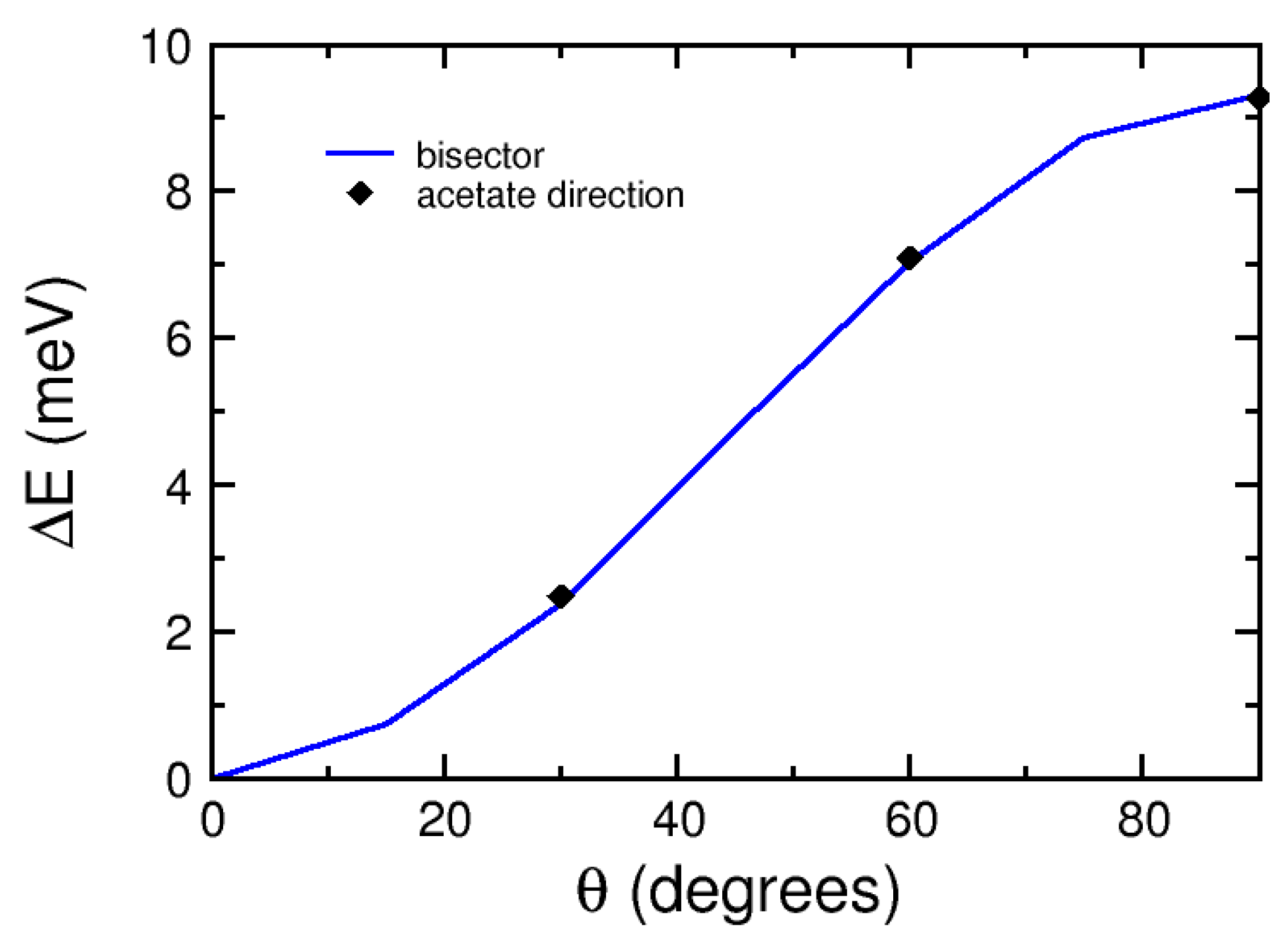
2.3. Magnetic Anisotropy Energy
3. Materials and Methods
- (1)
- For each angle , perform a non-collinear calculation on an isolated Mo-Mo dimer (the auxiliary system) without SOC, imposing (from input) the desired direction to M. Use the same Hubbard U and Mo-Mo distance as in the molecule.
- (2)
- Save the d states occupations of the two Mo atoms.
- (3)
- Perform a preliminary DFT + U + SOC calculation on the molecule, starting from the saved d states occupations, which are kept fixed for ≈10 electronic iterations.
- (4)
- From the potential achieved at the previous step, proceed with the DFT + U + SOC calculation, this time letting the occupations free to evolve and the molecule reach its self-consistent GS, at the given .
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AFiM | antiferrimagnetic |
| AFM | antiferromagnetic |
| CASSCF | Complete-active-space self-consistent field |
| DFPT | Density Functional Perturbation Theory |
| DFT | Density Functional Theory |
| EMA | easy magnetization axis |
| EVM | even-valued magnetization |
| FiM | ferrimagnetic |
| FM | ferromagnetic |
| GGA | Generalized-Gradient Approximation |
| KS | Kohn-Sham |
| MAE | Magnetic anisotropy energy |
| MoMo | dymolybdenum tetraacetate |
| Bohr magneton | |
| OVM | odd-valued magnetization |
| PBE | Perdew-Burke-Ernzerhof |
| SMM | single molecule magnet |
| SOC | spin-orbit coupling |
| TM | Transition Metal |
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141. [Google Scholar] [CrossRef]
- Christou, G.; Gatteschi, D.; Hendrickson, D.N.; Sessoli, R. Single-Molecule Magnets. MRS Bull. 2000, 25, 66–71. [Google Scholar] [CrossRef]
- Bogani, L.; Wernsdorfer, W. Molecular spintronics using single-molecule magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Ariciu, A.M.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef]
- Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef]
- Atzori, M.; Sessoli, R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019, 141, 11339–11352. [Google Scholar] [CrossRef] [PubMed]
- Holynska, M. (Ed.) Single-Molecule Magnets: Molecular Architectures and Building Blocks for Spintronics; Wiley: New York, NY, USA, 2019. [Google Scholar]
- Cornia, A.; Mannini, M. Single-Molecule Magnets on Surfaces. In Molecular Nanomagnets and Related Phenomena; Gao, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Gao, S. (Ed.) Molecular Nanomagnets and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Garlatti, E.; Allodi, G.; Bordignon, S.; Bordonali, L.; Timco, G.A.; Winpenny, R.E.P.; Lascialfari, A.; Renzi, R.D.; Carretta, S. Breaking the ring: 53Cr-NMR on the Cr8Cd molecular nanomagnet. J. Phys. Condens. Matter 2020, 32, 244003. [Google Scholar] [CrossRef]
- Herper, H.; Brena, B.; Puglia, C.; Bhandary, S.; Wende, H.; Eriksson, O.; Sanyal, B. Molecular Nanomagnets, Fundamental Understanding; Springer Nature: Singapore, 2020. [Google Scholar]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Lis, T. Preparation, structure, and magnetic properties of a dodecanuclear mixed-valence manganese carboxylate. Acta Crystallogr. Sect. B 1980, 36, 2042–2046. [Google Scholar] [CrossRef]
- Delfs, C.; Gatteschi, D.; Pardi, L.; Sessoli, R.; Wieghardt, K.; Hanke, D. Magnetic properties of an octanuclear iron(III) cation. Inorg. Chem. 1993, 32, 3099–3103. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R.; Cornia, A. Single-molecule magnets based on iron(III) oxo clusters. Chem. Commun. 2000, 725–732. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.y.; Kaizu, Y. Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Zhang, P. Lanthanide Single Molecule Magnets; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Meihaus, K.R.; Long, J.R. Actinide-based single-molecule magnets. Dalton Trans. 2015, 44, 2517–2528. [Google Scholar] [CrossRef] [PubMed]
- Freedman, D.E.; Harman, W.H.; Harris, T.D.; Long, G.J.; Chang, C.J.; Long, J.R. Slow Magnetic Relaxation in a High-Spin Iron(II) Complex. J. Am. Chem. Soc. 2010, 132, 1224–1225. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Coca, S.; Cremades, E.; Aliaga-Alcalde, N.; Ruiz, E. Mononuclear Single-Molecule Magnets: Tailoring the Magnetic Anisotropy of First-Row Transition-Metal Complexes. J. Am. Chem. Soc. 2013, 135, 7010–7018. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, J.; Pascual-Álvarez, A.; Cano, J.; Castro, I.; Julve, M.; Lloret, F.; Krzystek, J.; De Munno, G.; Armentano, D.; Wernsdorfer, W.; et al. Field-Induced Hysteresis and Quantum Tunneling of the Magnetization in a Mononuclear Manganese(III) Complex. Angew. Chem. Int. Ed. 2013, 52, 14075–14079. [Google Scholar] [CrossRef] [PubMed]
- Dey, M.; Gogoi, N. Geometry-Mediated Enhancement of Single-Ion Anisotropy: A Route to Single-Molecule Magnets with a High Blocking Temperature. Angew. Chem. Int. Ed. 2013, 52, 12780–12782. [Google Scholar] [CrossRef]
- Adelnia, F.; Arosio, P.; Mariani, M.; Orsini, F.; Radaelli, A.; Sangregorio, C.; Borsa, F.; Walsh, J.P.S.; Winpenny, R.; Timco, G.; et al. NMR Study of Spin Dynamics in V7Zn and V7Ni Molecular Rings. Appl. Magn. Reson. 2020, 51, 1277–1293. [Google Scholar] [CrossRef]
- Mariani, M.; Borsa, F.; Graf, M.J.; Sanna, S.; Filibian, M.; Orlando, T.; Sabareesh, K.P.V.; Cardona-Serra, S.; Coronado, E.; Lascialfari, A. Spin dynamics in the single-ion magnet [Er(W5O18)2]9−. Phys. Rev. B 2018, 97, 144414. [Google Scholar] [CrossRef]
- Friedman, J.R.; Sarachik, M.P.; Tejada, J.; Ziolo, R. Macroscopic Measurement of Resonant Magnetization Tunneling in High-Spin Molecules. Phys. Rev. Lett. 1996, 76, 3830–3833. [Google Scholar] [CrossRef]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef]
- Guo, F.S.; Day, B.M.; Chen, Y.C.; Tong, M.L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef]
- Jiang, J. (Ed.) Functional Phthalocyanine Molecular Materials. Structure and Bonding; Springer: Berlin/Heidelberg, Germany, 2010; Volume 135, pp. 1–44. [Google Scholar] [CrossRef]
- Malavolti, L.; Lanzilotto, V.; Ninova, S.; Poggini, L.; Cimatti, I.; Cortigiani, B.; Margheriti, L.; Chiappe, D.; Otero, E.; Sainctavit, P.; et al. Magnetic Bistability in a Submonolayer of Sublimated Fe4 Single-Molecule Magnets. Nano Lett. 2015, 15, 535–541. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Yu, A.; Higgins, D.C.; Llanos, B.G.; Chen, Z. Biologically Inspired Highly Durable Iron Phthalocyanine Catalysts for Oxygen Reduction Reaction in Polymer Electrolyte Membrane Fuel Cells. J. Am. Chem. Soc. 2010, 132, 17056–17058. [Google Scholar] [CrossRef] [PubMed]
- Delacote, G.; Fillard, J.; Marco, F. Electron injection in thin films of copper phtalocyanine. Solid State Commun. 1964, 2, 373–376. [Google Scholar] [CrossRef]
- Cheng, Z.H.; Gao, L.; Deng, Z.T.; Jiang, N.; Liu, Q.; Shi, D.X.; Du, S.X.; Guo, H.M.; Gao, H.J. Adsorption Behavior of Iron Phthalocyanine on Au(111) Surface at Submonolayer Coverage. J. Phys. Chem. C 2007, 111, 9240–9244. [Google Scholar] [CrossRef]
- Yamada, H.; Shimada, T.; Koma, A. Preparation and magnetic properties of manganese(II) phthalocyanine thin films. J. Chem. Phys. 1998, 108, 10256. [Google Scholar] [CrossRef]
- Mannini, M.; Bertani, F.; Tudisco, C.; Malavolti, L.; Poggini, L.; Misztal, K.; Menozzi, D.; Motta, A.; Otero, E.; Ohresser, P.; et al. Magnetic behaviour of TbPc2 single-molecule magnets chemically grafted on silicon surface. Nat. Commun. 2014, 5, 4582. [Google Scholar] [CrossRef]
- Ishikawa, N. Phthalocyanine-Based Magnets. In Functional Phthalocyanine Molecular Materials. Structure and Bonding; Jiang, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 135, pp. 211–228. [Google Scholar] [CrossRef]
- Li, J.; Gomez-Coca, S.; Dolinar, B.S.; Yang, L.; Yu, F.; Kong, M.; Zhang, Y.Q.; Song, Y.; Dunbar, K.R. Hexagonal Bipyramidal Dy(III) Complexes as a Structural Archetype for Single-Molecule Magnets. Inorg. Chem. 2019, 58, 2610–2617. [Google Scholar] [CrossRef]
- Gaggioli, C.A.; Gagliardi, L. Theoretical Investigation of Plutonium-Based Single-Molecule Magnets. Inorg. Chem. 2018, 57, 8098–8105. [Google Scholar] [CrossRef] [PubMed]
- Caneschi, A.; Gatteschi, D.; Totti, F. Molecular magnets and surfaces: A promising marriage. A DFT insight. Coord. Chem. Rev. 2015, 289–290, 357–378. [Google Scholar] [CrossRef]
- Brumboiu, I.E.; Totani, R.; de Simone, M.; Coreno, M.; Grazioli, C.; Lozzi, L.; Herper, H.C.; Sanyal, B.; Eriksson, O.; Puglia, C.; et al. Elucidating the 3d Electronic Configuration in Manganese Phthalocyanine. J. Phys. Chem. A 2014, 118, 927–932. [Google Scholar] [CrossRef]
- Ahlund, J.; Nilson, K.; Schiessling, J.; Kjeldgaard, L.; Berner, S.; Mårtensson, N.; Puglia, C.; Brena, B.; Nyberg, M.; Luo, Y. The electronic structure of iron phthalocyanine probed by photoelectron and x-ray absorption spectroscopies and density functional theory calculations. J. Chem. Phys. 2006, 125, 34709. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.E.; Sanyal, B.; Oppeneer, P.M. Tuning the Magnetic Interaction between Manganese Porphyrins and Ferromagnetic Co Substrate through Dedicated Control of the Adsorption. J. Phys. Chem. C 2009, 113, 14381–14383. [Google Scholar] [CrossRef]
- Atanasov, M.; Aravena, D.; Suturina, E.; Bill, E.; Maganas, D.; Neese, F. First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets. Coord. Chem. Rev. 2015, 289–290, 177–214. [Google Scholar] [CrossRef]
- Wäckerlin, C.; Donati, F.; Singha, A.; Baltic, R.; Rusponi, S.; Diller, K.; Patthey, F.; Pivetta, M.; Lan, Y.; Klyatskaya, S.; et al. Giant Hysteresis of Single-Molecule Magnets Adsorbed on a Nonmagnetic Insulator. Adv. Mater. 2016, 28, 5195–5199. [Google Scholar] [CrossRef] [PubMed]
- Annese, E.; Casolari, F.; Fujii, J.; Rossi, G. Interface magnetic coupling of Fe-phthalocyanine layers on a ferromagnetic surface. Phys. Rev. B 2013, 87, 054420. [Google Scholar] [CrossRef]
- Bartolomé, J.; Bartolomé, F.; Brookes, N.B.; Sedona, F.; Basagni, A.; Forrer, D.; Sambi, M. Reversible Fe Magnetic Moment Switching in Catalytic Oxygen Reduction Reaction of Fe-Phthalocyanine Adsorbed on Ag(110). J. Phys. Chem. C 2015, 119, 12488–12495. [Google Scholar] [CrossRef]
- Mugarza, A.; Robles, R.; Krull, C.; Korytár, R.; Lorente, N.; Gambardella, P. Electronic and magnetic properties of molecule-metal interfaces: Transition-metal phthalocyanines adsorbed on Ag(100). Phys. Rev. B 2012, 85, 155437. [Google Scholar] [CrossRef]
- Krylov, D.; Schimmel, S.; Dubrovin, V.; Liu, F.; Nguyen, T.; Spree, L.; Chen, C.; Velkos, G.; Bulbucan, C.; Westerström, R.; et al. Substrate-Independent Magnetic Bistability in Monolayers of the Single-Molecule Magnet Dy2 ScN@C80 on Metals and Insulators. Angew. Chem. Int. Ed. 2020, 59, 5756–5764. [Google Scholar] [CrossRef]
- Aeschlimann, S.; Bauer, S.V.; Vogtland, M.; Stadtmüller, B.; Aeschlimann, M.; Floris, A.; Bechstein, R.; Kühnle, A. Creating a regular array of metal-complexing molecules on an insulator surface at room temperature. Nat. Commun. 2020, 11, 6424. [Google Scholar] [CrossRef]
- Aeschlimann, S.; Lyu, L.; Stadtmüller, B.; Aeschlimann, M.; Kühnle, A. Tailoring molecular island shapes: Influence of microscopic interaction on mesostructure. Nano Res. 2020, 13, 843–852. [Google Scholar] [CrossRef]
- Richter, A.; Floris, A.; Bechstein, R.; Kantorovich, L.; Kühnle, A. On-surface synthesis on a bulk insulator surface. J. Phys. Condens. Matter 2018, 30, 133001. [Google Scholar] [CrossRef]
- Rahe, P.; Kittelmann, M.; Neff, J.L.; Nimmrich, M.; Reichling, M.; Maass, P.; Kühnle, A. Tuning Molecular Self-Assembly on Bulk Insulator Surfaces by Anchoring of the Organic Building Blocks. Adv. Mater. 2013, 25, 3948–3956. [Google Scholar] [CrossRef]
- Kittelmann, M.; P, R.; Kühnle, A. Molecular self-assembly on an insulating surface: Interplay between substrate templating and intermolecular interactions. J. Phys. Condens. Matter 2012, 24, 354007. [Google Scholar] [CrossRef] [PubMed]
- Hauke, C.M.; Bechstein, R.; Kittelmann, M.; Storz, C.; Kilbinger, A.F.M.; Rahe, P.; Kühnle, A. Controlling Molecular Self-Assembly on an Insulating Surface by Rationally Designing an Efficient Anchor Functionality That Maintains Structural Flexibility. ACS Nano 2013, 7, 5491–5498. [Google Scholar] [CrossRef]
- Bursten, B.E.; Scheider, W.F. Electronic Structure of Asymmetric Metal-Metal Multiple Bonds: The d2-d6 Complexes X4Mo-Mo(PH3)4 (X = OH, Cl). Inorg. Chem. 1989, 28, 3292. [Google Scholar] [CrossRef]
- Blaudeau, J.P.; Pitzer, R.M. Ab Initio Studies of Ligand Effects on the Metal-Metal Bond in Dimolybdenum Complexes. J. Phys. Chem. 1994, 98, 4575. [Google Scholar] [CrossRef]
- Cotton, F.A.; Mester, Z.C.; Webb, T.R. Dimolybdenum Tetraacetate. Acta Cryst. 1974, B30, 2768. [Google Scholar] [CrossRef]
- Sit, P.H.L.; Zipoli, F.; Chen, J.; Car, R.; Cohen, M.H.; Selloni, A. Oxidation State Changes and Electron Flow in Enzymatic Catalysis and Electrocatalysis through Wannier-Function Analysis. Chem. Eur. J. 2011, 17, 12136. [Google Scholar] [CrossRef]
- Sit, P.H.L.; Car, R.; Cohen, M.H.; Selloni, A. Simple, Unambiguous Theoretical Approach to Oxidation State Determination via First-Principles Calculations. Inorg. Chem. 2011, 50, 10259. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.I.; Elfimov, I.S.; Hamada, N.; Terakura, K. Charge-ordered insulating state of Fe3O4 from first-principles electronic structure calculations. Phys. Rev. B 1996, 54, 4387. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Aryasetiawan, F.; Liechtenstein, A.I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA+U method. J. Phys. Condens. Matter 1997, 9, 767. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Floris, A.; de Gironcoli, S.; Cococcioni, M. Hubbard-Corrected DFT Energy Functionals: The LDA + U Description of Correlated Systems. Int. J. Quantum Chem. 2014, 114, 14. [Google Scholar] [CrossRef]
- Campo, V.L., Jr.; Cococcioni, M. Extended DFT + U + V method with on-site and inter-site electronic interactions. J. Phys. Condens. Matter 2010, 22, 055602. [Google Scholar]
- Kulik, E.J.; Marzari, N. Systematic DFT+U study of first-row transition-metal diatomic molecules: A self-consistent approach. J. Chem. Phys. 2010, 133, 114103. [Google Scholar] [CrossRef]
- Kulik, E.J.; Marzari, N. Transition-metal dioxides: A case for the intersite term in Hubbard-model functionals. J. Chem. Phys. 2011, 134, 094103. [Google Scholar] [CrossRef]
- Kulik, E.J.; Marzari, N. Accurate potential energy surfaces with a DFT + U(R) approach. J. Chem. Phys. 2011, 135, 194105. [Google Scholar] [CrossRef]
- Scherlis, D.A.; Cococcioni, M.; Sit, H.L.; Marzari, N. Simulation of Heme Using DFT + U: A Step toward Accurate Spin-State Energetics. J. Phys. Chem. B 2007, 111, 7384. [Google Scholar] [CrossRef]
- Kulik, E.J.; Cococcioni, M.; Marzari, N. Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard U Approach. Phys. Rev. Lett. 2006, 97, 103001. [Google Scholar] [CrossRef]
- Kulik, H.J.; Marzari, N. A self-consistent Hubbard U density-functional theory approach to the addition-elimination reactions of hydrocarbons on bare FeO+. J. Chem. Phys. 2008, 129, 134314. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Marchenko, A.; Dabo, I.; Cococcioni, M. Role of electronic localization in the phosphorescence of iridium sensitizing dyes. J. Chem. Phys. 2012, 137, 154309. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA + U method. Phys. Rev. B 2005, 71, 35105–35120. [Google Scholar] [CrossRef]
- Floris, A.; de Gironcoli, S.; Gross, E.K.U.; Cococcioni, M. Vibrational properties of MnO and NiO from DFT+U-based Density Functional Perturbation Theory. Phys. Rev. B 2011, 84, 161102. [Google Scholar] [CrossRef]
- Blanchard, M.; Balan, E.; Giura, P.; Beneut, K.; Yi, H.; Morin, G.; Pinilla, C.; Lazzeri, M.; Floris, A. Infrared spectroscopic properties of goethite: Anharmonic broadening, long-range electrostatic effects and Al substitutiton. Phys. Chem. Miner. 2014, 41, 289. [Google Scholar] [CrossRef]
- Blanchard, M.; Dauphas, N.; Hu, M.Y.; Roskosz, M.; Alp, E.E.; Golden, D.C.; Sio, C.K.; Tissot, F.L.; Zhao, J.; Gao, L.; et al. Reduced partition function ratios of iron and oxygen in goethite. Geochim. Cosmochim. Acta 2015, 151, 19. [Google Scholar] [CrossRef]
- Shukla, G.; Wentzcovitch, R.M. Spin crossover in (Mg,Fe3+)(Si,Fe3+)O3 bridgmanite: Effects of disorder, iron concentration, and temperature. Phys. Earth Planet. Inter. 2016, 260, 53–61. [Google Scholar] [CrossRef]
- Shukla, G.; Cococcioni, M.; Wentzcovitch, R.M. Thermoelasticity of Fe3+- and Al-bearing bridgmanite: Effects of iron spin crossover. Geophys. Res. Lett. 2016, 43, 5661–5670. [Google Scholar] [CrossRef]
- Floris, A.; Timrov, I.; Himmetoglu, B.; Marzari, N.; de Gironcoli, S.; Cococcioni, M. Hubbard-corrected density functional perturbation theory with ultrasoft pseudopotentials. Phys. Rev. B 2020, 101, 064305. [Google Scholar] [CrossRef]
- Sun, Y.; Cococcioni, M.; Wentzcovitch, R.M. LDA + Usc calculations of phase relations in FeO. Phys. Rev. Mater. 2020, 4, 063605. [Google Scholar] [CrossRef]
- Cococcioni, M.; Marzari, N. Energetics and cathode voltages of LiMPO4 olivines (M = Fe, Mn) from extended Hubbard functionals. Phys. Rev. Mater. 2019, 3, 033801. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Katukuri, V.M.; Cococcioni, M. Origin of magnetic interactions and their influence on the structural properties of Ni2MnGa and related compounds. J. Phys. Condens. Matter 2012, 24, 185501. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Wentzcovitch, R.M.; Cococcioni, M. First-principles study of electronic and structural properties of CuO. Phys. Rev. B 2011, 84, 115108. [Google Scholar] [CrossRef]
- Hsu, H.; Blaha, P.; Cococcioni, M.; Wentzcovitch, R.M. Spin-State Crossover and Hyperfine Interactions of Ferric Iron in MgSiO3 Perovskite. Phys. Rev. Lett. 2011, 106, 118501. [Google Scholar] [CrossRef]
- Hsu, H.; Umemoto, K.; Cococcioni, M.; Wentzcovitch, R.M. First-principles study for low-spin LaCoO3 with a structurally consistent Hubbard U. Phys. Rev. B 2009, 79, 125124. [Google Scholar] [CrossRef]
- Timrov, I.; Marzari, N.; Cococcioni, M. Hubbard parameters from density-functional perturbation theory. Phys. Rev. B 2018, 98, 085127. [Google Scholar] [CrossRef]
- Timrov, I.; Marzari, N.; Cococcioni, M. Self-consistent Hubbard parameters from density-functional perturbation theory in the ultrasoft and projector-augmented wave formulations. Phys. Rev. B 2021, 103, 045141. [Google Scholar] [CrossRef]
- Timrov, I.; Aquilante, F.; Binci, L.; Cococcioni, M.; Marzari, N. Pulay forces in density-functional theory with extended Hubbard functionals: From nonorthogonalized to orthogonalized manifolds. Phys. Rev. B 2020, 102, 235159. [Google Scholar] [CrossRef]
- Bouatou, M.; Harsh, R.; Joucken, F.; Chacon, C.; Repain, V.; Bellec, A.; Girard, Y.; Rousset, S.; Sporken, R.; Gao, F.; et al. Intraconfigurational Transition due to Surface-Induced Symmetry Breaking in Noncovalently Bonded Molecules. J. Phys. Chem. Lett. 2020, 11, 9329–9335. [Google Scholar] [CrossRef] [PubMed]
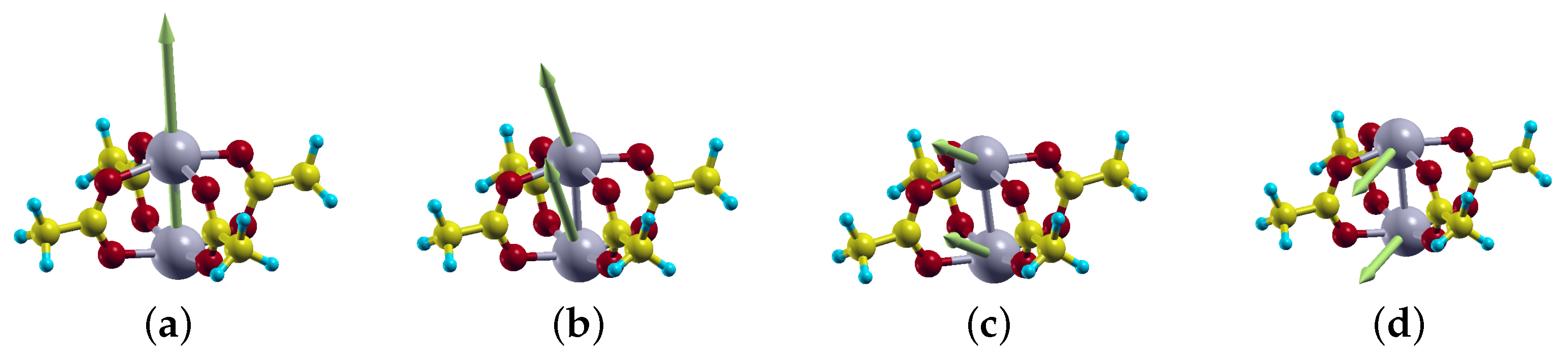
| NM | FM1 | FM2 | FM4 | FM6 | FM8 | |
|---|---|---|---|---|---|---|
| E (eV) | 0 | 0.90 | 1.43 | 3.57 | 4.08 | 5.34 |
| M () | 0 | 1 | 2 | 4 | 6 | 8 |
| d (Å) | 2.09 | 2.12 | 2.15 | 2.42 | 2.67 | 2.98 |
| n- n | 0.0 | 0.45, 0.44 | 0.88, 0.87 | 1.82, 1.81 | 2.74 | 3.51 |
| NM | AFM | FM2 | AFiM2 | FM4 | FiM4 | FM6 | FM8 | ||
|---|---|---|---|---|---|---|---|---|---|
| DFT + U | 3.84 | 3.58 | 3.54 | 4.09 | 3.61 | 3.58 | 3.60 | 3.23 | |
| 3.85 | 3.58 | 3.55 | 4.06 | 3.58 | 3.62 | 3.61 | 3.24 | ||
| DFT + U + V | 4.53 | 4.20 | 4.06 | 4.09 | 4.20 | 4.34 | 4.16 | 3.80 | |
| 4.54 | 4.20 | 4.07 | 4.17 | 4.24 | 4.23 | 4.17 | 3.81 | ||
| 0.40 | 0.07 | 0.14 | 0.01 | 0.01 | 0.07 | −0.18 | 0.18 | ||
| 1.31 | 1.20 | 1.16 | 1.16 | 1.19 | 1.27 | 1.16 | 1.08 | ||
| 1.31 | 1.20 | 1.16 | 1.19 | 1.21 | 1.22 | 1.17 | 1.08 |
| NM | AFM | FM2 | AFiM2 | FM4 | FiM4 | FM6 | FM8 | ||
|---|---|---|---|---|---|---|---|---|---|
| DFT + U | E (eV) | 2.43 | 0.0 | 1.72 | 1.51 | 1.59 | 1.78 | 1.22 | 0.99 |
| M () | 0 | 0 | 2 | 2 | 4 | 4 | 6 | 8 | |
| d (Å) | 2.09 | 2.54 | 2.14 | 2.57 | 2.70 | 2.70 | 2.66 | 2.99 | |
| n- n | 0.0 | 3.28, −3.28 | 0.94 | 3.38, −1.5 | 0.53, 3.36 | 3.36, 0.53 | 2.88 | 3.72 | |
| DFT + U + V | E (eV) | 2.45 | 0.0 | 2.05 | 1.02 | 2.65 | 1.54 | 1.26 | 0.99 |
| M () | 0 | 0 | 2 | 2 | 4 | 4 | 6 | 8 | |
| d (Å) | 2.10 | 2.58 | 2.15 | 2.57 | 2.42 | 2.72 | 2.66 | 2.98 | |
| n- n | 0.0 | 3.32, −3.32 | 0.93 | 3.32, −1.47 | 1.87, 1.93 | 3.36, 0.49 | 2.86 | 3.69 | |
| DFT + U + | E (eV) | 3.48 | 0.0 | 0.94 | 1.29 | ||||
| M () | 0 | 0 | 2 | 8 | |||||
| d (Å) | 2.12 | 2.53 | 2.51 | 2.93 | |||||
| n- n | 0.0 | 3.18, −3.20 | 3.10, −1.27 | 3.67, 3.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cococcioni, M.; Floris, A. Magnetic Energy Landscape of Dimolybdenum Tetraacetate on a Bulk Insulator Surface. Appl. Sci. 2021, 11, 3806. https://doi.org/10.3390/app11093806
Cococcioni M, Floris A. Magnetic Energy Landscape of Dimolybdenum Tetraacetate on a Bulk Insulator Surface. Applied Sciences. 2021; 11(9):3806. https://doi.org/10.3390/app11093806
Chicago/Turabian StyleCococcioni, Matteo, and Andrea Floris. 2021. "Magnetic Energy Landscape of Dimolybdenum Tetraacetate on a Bulk Insulator Surface" Applied Sciences 11, no. 9: 3806. https://doi.org/10.3390/app11093806
APA StyleCococcioni, M., & Floris, A. (2021). Magnetic Energy Landscape of Dimolybdenum Tetraacetate on a Bulk Insulator Surface. Applied Sciences, 11(9), 3806. https://doi.org/10.3390/app11093806







