Next Article in Journal
Diagnosis of Broken Rotor Bars during the Startup of Inverter-Fed Induction Motors Using the Dragon Transform and Functional ANOVA
Previous Article in Journal
Low-Calorie Beverages Made from Medicinal Plants, Flowers and Fruits: Characteristics and Liking of a Population with Overweight and Obesity
Previous Article in Special Issue
A Scheme for Controlled Cyclic Asymmetric Remote State Preparation in Noisy Environment
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 11
Issue 9
10.3390/app11093767
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Quantum Key Distribution Networks: Challenges and Future Research Issues in Security

by
Chia-Wei Tsai
1,
Chun-Wei Yang
2,
Jason Lin
3,
Yao-Chung Chang
1,* and
Ruay-Shiung Chang
4
1
Department of Computer Science and Information Engineering, National Taitung University, No. 369, University Rd., Taitung 95092, Taiwan
2
Master Program for Digital Health Innovation, College of Humanities and Sciences, China Medical University, No. 100, Sec. 1, Jingmao Rd., Beitun Dist., Taichung 406040, Taiwan
3
Department of Computer Science and Engineering, National Chung Hsing University, No. 145, Xingda Rd., South District, Taichung 40227, Taiwan
4
Department of Institute of Information and Decision Sciences, National Taipei University of Business, No.321, Sec. 1, Jinan Rd., Jhongjheng Dist., Taipei City 100025, Taiwan
*
Author to whom correspondence should be addressed.
Appl. Sci. 2021, 11(9), 3767; https://doi.org/10.3390/app11093767
Submission received: 30 March 2021 / Revised: 17 April 2021 / Accepted: 19 April 2021 / Published: 22 April 2021
(This article belongs to the Special Issue Quantum Communications and Quantum Networks)
Browse Figures
Review Reports Versions Notes

Abstract

:
A quantum key distribution (QKD) network is proposed to allow QKD protocols to be the infrastructure of the Internet for distributing unconditional security keys instead of existing public-key cryptography based on computationally complex mathematical problems. Numerous countries and research institutes have invested enormous resources to execute correlation studies on QKD networks. Thus, in this study, we surveyed existing QKD network studies and practical field experiments to summarize the research results (e.g., type and architecture of QKD networks, key generating rate, maximum communication distance, and routing protocol). Furthermore, we highlight the three challenges and future research issues in the security of QKD networks and then provide some feasible resolution strategies for these challenges.

1. Introduction

In response to the rapid development of the Internet and Internet of Things (IoT) technologies, digital applications/services have become mainstream in today’s world. This trend allows more information and data to be transmitted over the Internet. Therefore, the provision of complete cryptography mechanisms for protecting the confidentiality and integrity of data and ensuring authentication between the sender and the receiver are some of the important issues in the digital age, among which establishing secure cryptography keys through untrusted networks is a fundamental cryptography task. Although existing public-key cryptography based on computationally complex mathematical problems (e.g., RSA or Diffie Hellman key exchange protocol) can provide the session key distribution for end users/applications, the session keys distributed by these algorithms belong to theoretical computational security. That is, the computational security keys can be broken using quantum computation. To overcome this issue, some feasible solutions have been proposed, including quantum cryptography, which uses quantum mechanics to design secure communication protocols, and post-quantum cryptography, which shows that complex computational problems are secure against attacks by quantum computers to design cryptographic algorithms.
In quantum cryptography, Bennet and Brassard [1] used the properties of quantum mechanics to propose the first quantum key distribution (QKD) protocol—the BB84 protocol—which allows two end users/applications to distribute the session keys between each other. Furthermore, some studies [2,3,4] have proved that the BB84 protocol is an unconditional security protocol; that is, the session key distributed by the BB84 protocol belongs to unconditional security keys. In classical cryptography, only a one-time pad (OTP) can conform to unconditional security ciphers. Following the BB84 protocol, various QKD protocols [5,6,7,8,9,10,11,12,13,14] have been proposed. To enhance the practicality of QKD protocols under the existing quantum technologies, the semi-quantum key distribution key protocols [15,16,17] and measurement device independent (MDI) QKD key protocols [13,18,19] have also been proposed. In addition, various types of quantum communication protocol have been proposed for different applications, including quantum secure direct communication, quantum secret sharing (QSS), quantum private comparison, and quantum information splitting. However, QKD protocols cannot provide the service of key distribution as the fundamental infrastructure instead of existing public-key cryptography in the existing network environment immediately because of limitations of quantum technology (e.g., the reachable distance of qubit transmission and the accuracy of the qubit detector). Moreover, QKD protocols cannot be integrated with existing network protocols immediately because of the specificity of quantum links and network organization.
To address the aforementioned problem, the concept and framework of QKD networks have been proposed [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] to enable QKD protocols to assist the remote end users/applications in distributing security keys under the existing network environment. Previous studies [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] indicate the architectures, quantum technologies, and experimental results in the field experiments of QKD networks. Improvement methods of the routing algorithms have also been proposed [36,37,38,39,40,41] along with evaluation metrics of quantum links, in which notably the first quality of service (QoS) mechanism for QKD networks was designed in [39]. Another study [41] proposed a routing algorithm for hybrid QKD networks. A method that uses a QKD network to protect the security of power microgrids was proposed in [42,43]. In addition, for the security issue of QKD networks, [44,45] proposed feasible resolutions for avoiding the assumption that the quantum nodes must be trusted and [46] discussed how classical end users/applications can access session keys securely from QKD networks. In addition, [47] proposed an architecture of a QKD network, a quantum access network, which allows many end users/applications (up to 64 users/applications) to simultaneously distribute the security keys with a central quantum node using fiber channels. Then, [48] extended the quantum access network to the n:n framework, that is, n users could distribute security keys with n central quantum nodes simultaneously.
Although these studies discussed above obtained remarkable results within the key generating rate, communication distance, architecture of the QKD network, and routing algorithm, there are still some challenges that need to be overcome in the field of security. Therefore, this study aims to summarize the developmental trends and results of the QKD network first. Then, we highlight the challenges that need to be studied further to perfect QKD networks. For the proposed challenges, we have also provided some feasible solutions and strategies to allow researchers to devise complete solutions. The rest of this paper is organized as follows: Section 2 reviews the background of the QKD network, and Section 3 summarizes the key results in existing QKD networks. For security issues in QKD networks, we highlight the three challenges and future research issues and provide some feasible resolution strategies in Section 4. Finally, a brief conclusion is provided.

2. Background to Quantum Key Distribution (QKD) Networks

The QKD network is used to extend the range of the QKD protocol, and it consists of several static quantum nodes that have complete quantum capabilities (e.g., generating a single photon/entanglement state, storing qubits, and performing the quantum unitary operation). The quantum nodes execute the QKD protocol (e.g., the BB84 protocol) to distribute secure keys (also called local keys) between the neighboring nodes, and then, the hop-by-hop manner is adopted to assist the remote end users/applications to distribute unconditional security session keys.
The QKD network comprises quantum nodes and quantum links, and the framework of the QKD network can be divided into three layers: a communication layer, a key management layer, and a quantum layer (shown in Figure 1). The communication layer (the top layer) manages the routing tasks and provides the application interface (API) to allow the end users/applications to access the secure session keys generated by QKD protocols. The middle layer—the key management layer—is responsible for managing key generation and storage to effectively utilize the resources of quantum devices in the quantum layer. The quantum layer (the bottom layer) comprises several quantum devices and an authenticated public classical channel, and it is responsible for executing the QKD protocol for sharing local keys with neighbor nodes.
Because of limited spaces, we only focus on the quantum layer technologies to introduce quantum nodes and quantum links, and the details of classical technologies are not provided here. This study introduces the following two main components.

2.1. Quantum Node

A quantum node is equipped with quantum devices that are necessary for executing the QKD protocol, including qubit generators, qubit measurement devices, and qubit memories. The technologies and types of quantum device adopted depend on the types of QKD protocols (e.g., discrete-variable-based QKD or continuous variable-based QKD).
Quantum nodes can be categorized into three types according to the function of the quantum node: (1) the repeater node, (2) the access node, and (3) the central control node. The repeater node assists the others in transmitting packets of session keys using a suitable routing path, and the main function of the access node is to provide the API which allows end users/applications to access the session keys. In a specific QKD network (i.e., the client-server architecture), the central control node is the routing server that is responsible for controlling and managing the entire routing table of the QKD network. In addition, because the key generation rate and key service demand are dynamic, it is impossible to maintain a balance between the key supply and demand at all times. Therefore, the quantum node must require a buffer (known as the key storage) to store the local keys to enhance the tolerance of the dynamic environment in the QKD network. Protecting local keys in the key storage is an important task. Therefore, an applicable key management mechanism must be adopted to manage and protect key generation, storage, and usage within key storage.

2.2. Quantum Link

A quantum link, in which a logical connection exists between two remote QKD nodes, comprises a quantum channel and an authenticated public classical channel (shown in Figure 2). The quantum channel is used for transmitting qubits, and the public channel implemented by the classical channel and classical cryptography technologies (e.g., universal hash function [49]) is used for post-processing the exchanged information of the QKD protocol (e.g., public discussion, error-correction, and privacy amplification processes).
Two main methods can be employed to practically implement quantum channels: direct optical fibers and free line-of-sight in a point-to-point (P2P) manner. Although optical fibers can be applied and are common for transmitting qubits, installing dedicated fibers for executing QKD protocols is not practical under all situations. A free space link is sometimes convenient, although it has its drawbacks; for example, appropriate atmospheric conditions, a visible light path, an acceptable signal-to-noise ratio are required, and so on. It is worth noting that [50] proved the feasibility of transmitting the quantum and classical information over the shared optical fibers; that is, the quantum nodes can use the same optical fiber to transmit the classical and quantum information. From a deployment perspective, the technology could significantly reduce the installation costs for additional optical fiber links. In addition, different types of quantum channel correspond to different types of QKD protocol. In other words, discrete-variable-based QKD protocols are usually implemented in the fiber channel, whereas continuous variable-based QKD protocols are implemented in a free space link. The communication distance and key generation rate are the main considerations for implementing quantum links. Although the key generation rate decreases exponentially when the communication distance increases, which is known to all, improving both the performance of the communication distance and key generation rate is still an important research issue in the field of QKD networks. Generally, using fiber channels to implement a QKD network can achieve better performance in terms of both the communication distance and key generation rate than using a free space link; however, the costs (including those of an accurate single-photon detector and of establishing dedicated fibers) are still high. A previous study [51] achieved a breakthrough in the free space link using the free space link to accomplish a satellite-to-ground QKD protocol over a distance of 645 to 1200 km. In addition, Lucamarini, M. et al. [52] proposed the twin-field QKD (TF-QKD) protocol to reach 550 km communication distance using current technology under the standard optical fiber. Some studies [53,54,55,56,57] have further demonstrated the performance of the TF-QKD protocol in an experimental manner. Therefore, future mainstream technologies still need to be evaluated and observed further.

2.3. QKD Network Type

In terms of the QKD network type, we have summarized the existing practical experiments and research reports to group QKD networks into three distinct classes: (1) active optical switch networks, (2) trusted node networks, and (3) quantum repeater networks. Here, note that a practical QKD network can be implemented by the hybrid types of network rather than only one type; for example, we can adopt the active optical switch and the trusted node networks to build a QKD network. This study describes the following three types of network.

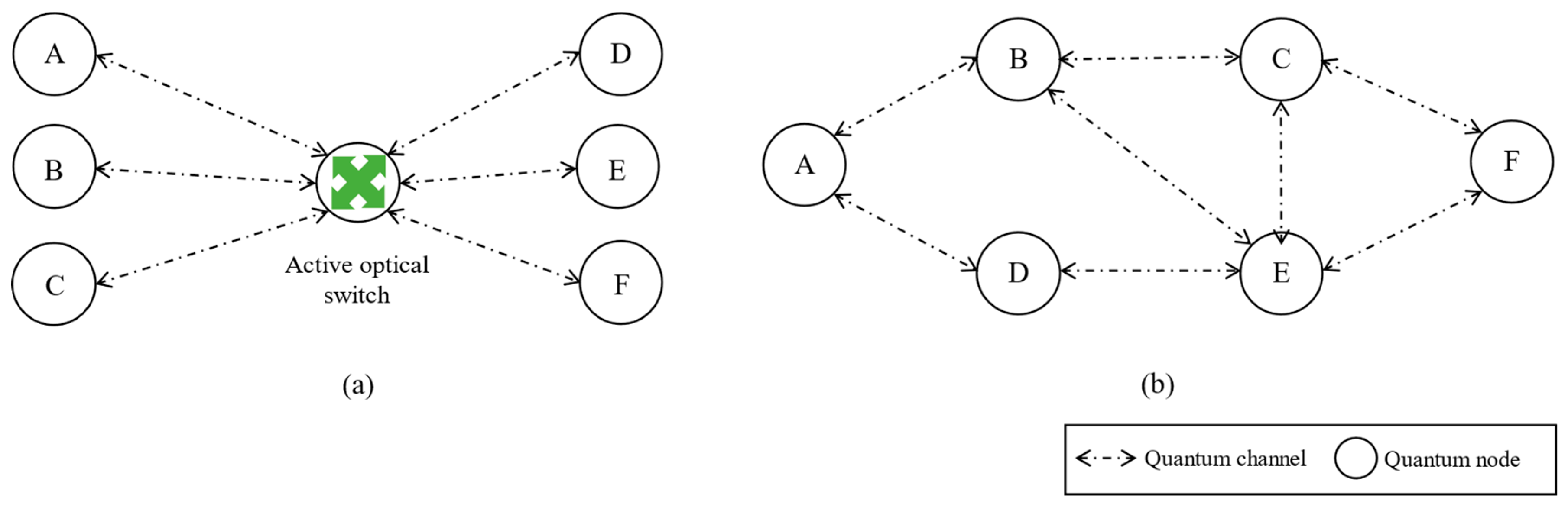
2.3.1. Active Optical Switch Network

In the active optical switch network, an active optical switch mechanism is employed to establish a direct optical P2P quantum channel between any two quantum nodes (shown in Figure 3a) [58]. Using the switching mechanism, any two quantum nodes can be employed to establish a direct connection and execute the QKD protocol without any assistance from other nodes; however, this framework has two drawbacks: (1) the communication distance of the QKD network is not extended, that is, the distance is still bounded by the maximum communication distance between any two quantum nodes, and (2) all quantum technologies applied in the network must be consistent, which may restrict the application. However, the implementation challenges of the active optical switch in the physical layer still affect the performance of qubit communication. For example, the use of active optical switch will cause additional amount of photon losses and leads to shorten the maximum distance of quantum channels [59]. Therefore, it is an important issue to develop an active optical switch with minimal loss and noise, and without disturbing the states of qubits [60,61,62].

2.3.2. Trusted Node Network

In contrast to the active optical switch network, any quantum node only establishes a quantum channel with its neighboring nodes (shown in Figure 3b), and thus, it can only generate security materials with its neighbors. Thus, the two remote nodes cannot distribute the security key using the QKD protocol directly. Therefore, if the two remote nodes want to distribute security keys, they need help from other nodes using a hop-by-hop communication strategy. For example, in Figure 3b, when node A wants to distribute the session keys with node F, it needs the help of nodes B and C. However, any node on the routing path can know the session key that the source node wants to distribute to the destination node because of the hop-by-hop communication strategy; thus, the quantum node must be assumed to be trusted (i.e., they must protect the session keys without leaking any information to attackers). Although the assumption of a quantum node is not realistic in real Internet environments, a trusted node network is still the mainstream framework in existing practical field experiments because it is not limited by communication distance or node numbers and can be made up of different QKD devices implementing different QKD technologies.

2.3.3. Quantum Repeater Network

The network topology of a quantum repeater network is similar to that of a trusted node network; however, the main difference is that the quantum node is equipped with a quantum repeater [63], which uses quantum teleportation [64,65] or entanglement swapping [66], which assists the two remote quantum nodes in transmitting single photons or sharing entanglement states. Although the quantum repeater network can provide a more complete environment than the other networks in terms of applications, the quantum repeater technology is not mature enough, and the cost of the quantum repeater is still high. Thus, a quantum repeater cannot be generally adopted in existing QKD networks.

3. Key Results of Existing QKD Networks

This section surveys existing research studies and reports to summarize the key results in existing QKD networks. To prove the practicality of QKD networks, some countries and research institutes have invested enormous resources in practical field experiments on QKD networks. BBN Technologies and Harvard and Boston Universities [20,21,22] proposed the first QKD network—the DARPA quantum network—which has 10 quantum nodes and adopts a hybrid network type (i.e., active optical switch and trusted node networks). The DARPA network adopts the BB84 protocol to generate unconditional security keys and achieved the best performance of key generating rate of 400 bps over 29 km.
Subsequently, in 2004, the European Commission’s (EC) integrated FP6 Project Secure Communication based on Quantum Cryptography (SECOQC) launched a major project—SECOQC QKD Network [23,24,25]—to define the practical applications of QKD networks and to further analyze the issues associated with QKD networks, including their security, design and architecture, communications protocols, and implementation methods. SECOQC clearly indicates that QKD networks are the infrastructure for providing key distribution and secure communication in future Internet environments. The SECOQC QKD network adopts a trusted node network framework and has six quantum nodes. In addition, six different technologies (including attenuated laser pulse, one-way weak coherent pulse, entanglement photons, and free space) are used to establish quantum links, and five different QKD protocols are adopted to distribute the local keys. The best performance in terms of the key generation rate of 3.1 kbps over 33 km was achieved by the SECOQC QKD network. The SECOQC network lays the groundwork and provides a guide for IP and routing protocols for implementing QKD networks.
The Tokyo UQCC (Updating Quantum Cryptography and Communication) QKD testbed network was launched in Japan [26,27] since 2010. It employs four access nodes and six repeater nodes to form the infrastructure of the QKD network and distribute the local keys via both the BB84 and BBM92 [5] protocols. A live demonstration of secure TV conferencing using the key distribution service of this QKD network was presented in October 2010. The best performance in terms of the key generation rate achieved by the Tokyo UQCC QKD network was 304 kpbs over 45 km.
The QKD networks have been implemented and tested on a large scale in China, and four main QKD network trials have been performed—the Beijing-Shanghai QKD network [28,29,30], the Jinan Government Private QKD Network [31,32,33], the Wuhan QKD Network [29], and the Hefei-Chaohu-Wuhu QKD Network [28,29,35]. The four QKD networks all adopted the trusted node network and the BB84 protocol to provide services of QKD networks. The numbers of quantum nodes in these QKD networks were 32, 32, 71, and 9, respectively. Notably, the Jinan government private QKD network and Wuhan QKD network use the client-server architecture to organize quantum nodes, that is, a central control node to manage the routing tables and services. The best performance in terms of key generation rate achieved among the four QKD networks was 250 kbps over 43 km by the Beijing-Shanghai QKD network. Table 1 summarizes the key results of the above-mentioned QKD networks.
In addition to improving the key generation rate and communication distance, enhancement of the routing algorithm and QoS are important and interesting research issues. The DARPA QKD network adopts the open shortest path first (OSPF) algorithm [67] to design the routing protocol. To accelerate the development process of the SECOQC QKD Network, a modified OSPFv2 protocol [67] was adopted, even though QoS cannot be supported by the OSPFv2 protocol. In another study [36], Dijkstra’s algorithm was used to design the routing protocol of the QKD network, and two performance indicators were proposed to evaluate the proposed routing protocol. Tanizawa et al. [37] also used the OSPF algorithm to design a routing protocol and evaluated its performance via simulation implemented by the AIT QKD software [68]. Yang et al. [38] proposed a routing protocol using a dynamic routing scheme that includes three components: a Hello protocol, a routing protocol, and a link state update mechanism. The Hello protocol helps quantum nodes share the network topology information, the routing protocol is used to determine the suitable routing path, and the link state update mechanism is adopted to update the routing tables. Mehic et al. [39] highlighted that the QKD network is similar to the ad hoc network in terms of the routing method, used the greedy perimeter stateless routing protocol to design the routing protocol, and then, proposed a QoS mechanism for the QKD network; a simulation was performed to evaluate the performance of the proposed routing method. Another study [40] used the local complementation technique to share P2P entanglement; the proposed routing protocol could efficiently reduce the number of measuring qubits within the quantum repeater, thus enhancing the performance of the QKD network. For the hybrid QKD network framework formed by the quantum repeater and trusted node networks, Amer et al. [41] proposed three routing protocols and evaluated the performance of the proposed routing protocol via simulations.
For security issues and assumptions of the QKD network, Tanizawa et al. [46] showed how to allow end users/applications to access the QKD network’s service securely is an open question; then, they used the OpenSSL [69] API to solve the question. However, Tanizawa et al. [46] proposed a method that decays the security level to computational security rather than unconditional security. Salvail et al. [44] used a multiple-path strategy to avoid the unrealistic assumption that the trustworthiness of a quantum node must be trusted, and proved that the QKD network can still provide key distribution services with unconditional security under t-bound situations (i.e., at most t untrusted nodes among n nodes). In addition, Tang et al. [45] proved that the MDI QKD protocol in an active optical switch network framework over 200 km is secure against untrustworthy nodes.

4. Challenges and Research Issues

Existing studies and experiments have provided fruitful results in terms of the network framework, key generation rate, communication distance, and routing protocol. However, there are still some challenges and issues that must be resolved. This study focusses on security issues (i.e., security assumptions and applications) to indicate important challenges and issues associated with QKD networks, describes these challenges and the feasible solutions and strategies for researchers to understand these challenges easily, and then, provides a basis for them to propose the appropriate solutions. The challenges are as follows:
(1)
Lacking point-to-multipoint (P2M) mechanisms in QKD networks: the key distribution service of the existing QKD network only provides point-to-point (P2P)) key distribution and lacks the P2M mechanism.
(2)
Many quantum node resources are consumed by a multiple-path strategy: although a multiple-path strategy can avoid the assumption that all quantum nodes must be trusted, many quantum node resources (e.g., the local keys that are used to help transmit the session key) are consumed to accomplish the multiple-path strategy.
(3)
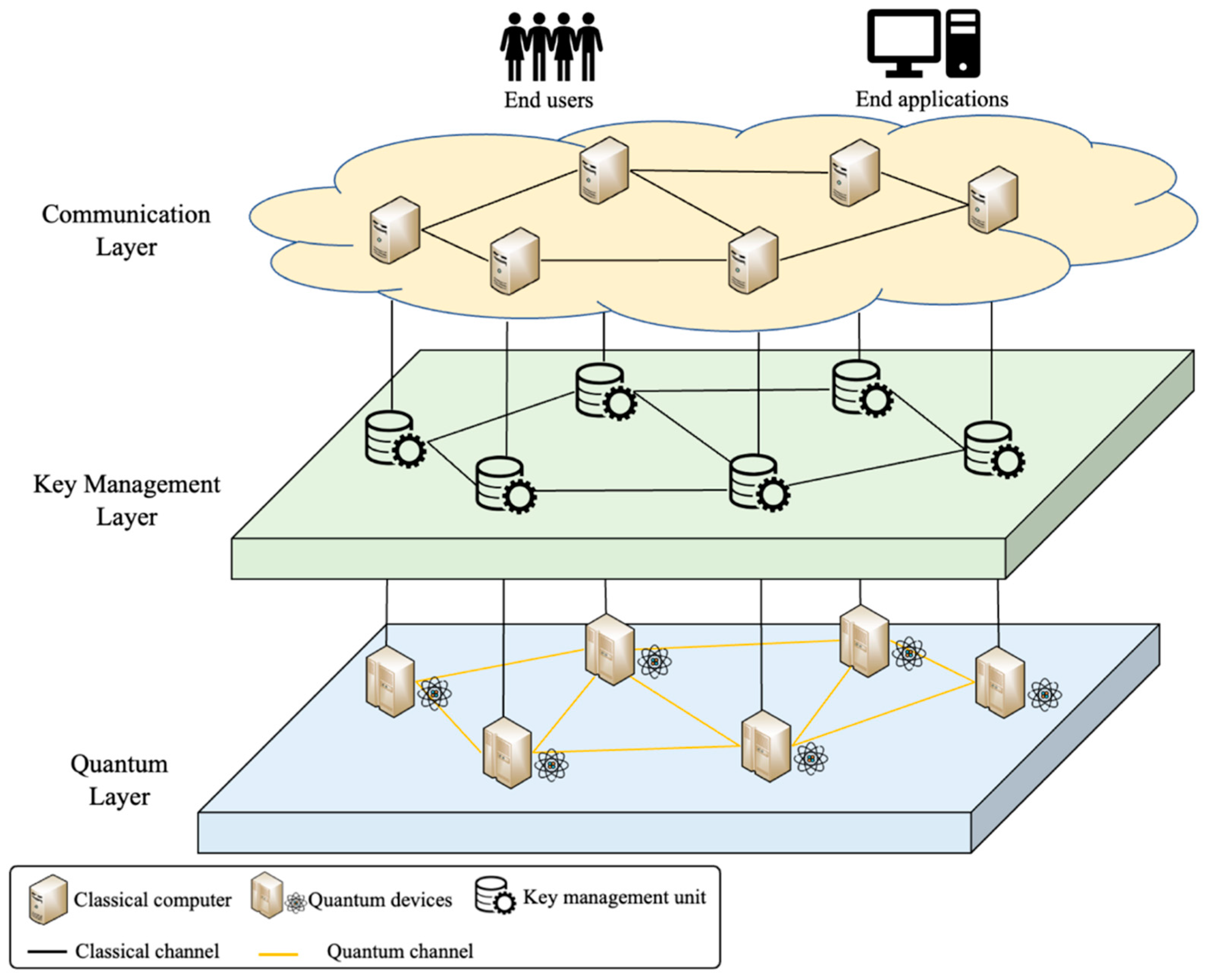
No suitable security interface between the classical end users/applications and the quantum nodes: allowing classical end users/applications to have access to the key distribution service of QKD networks securely within the quantum computing environment is an important issue.
The proposed feasible resolutions for these challenges are discussed in detail as follows.

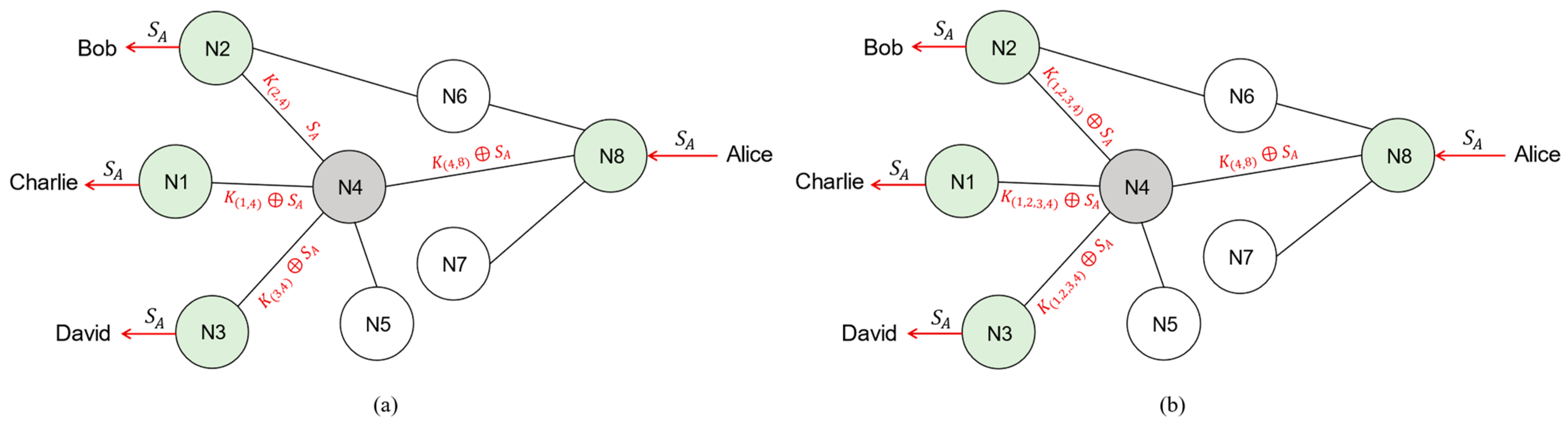
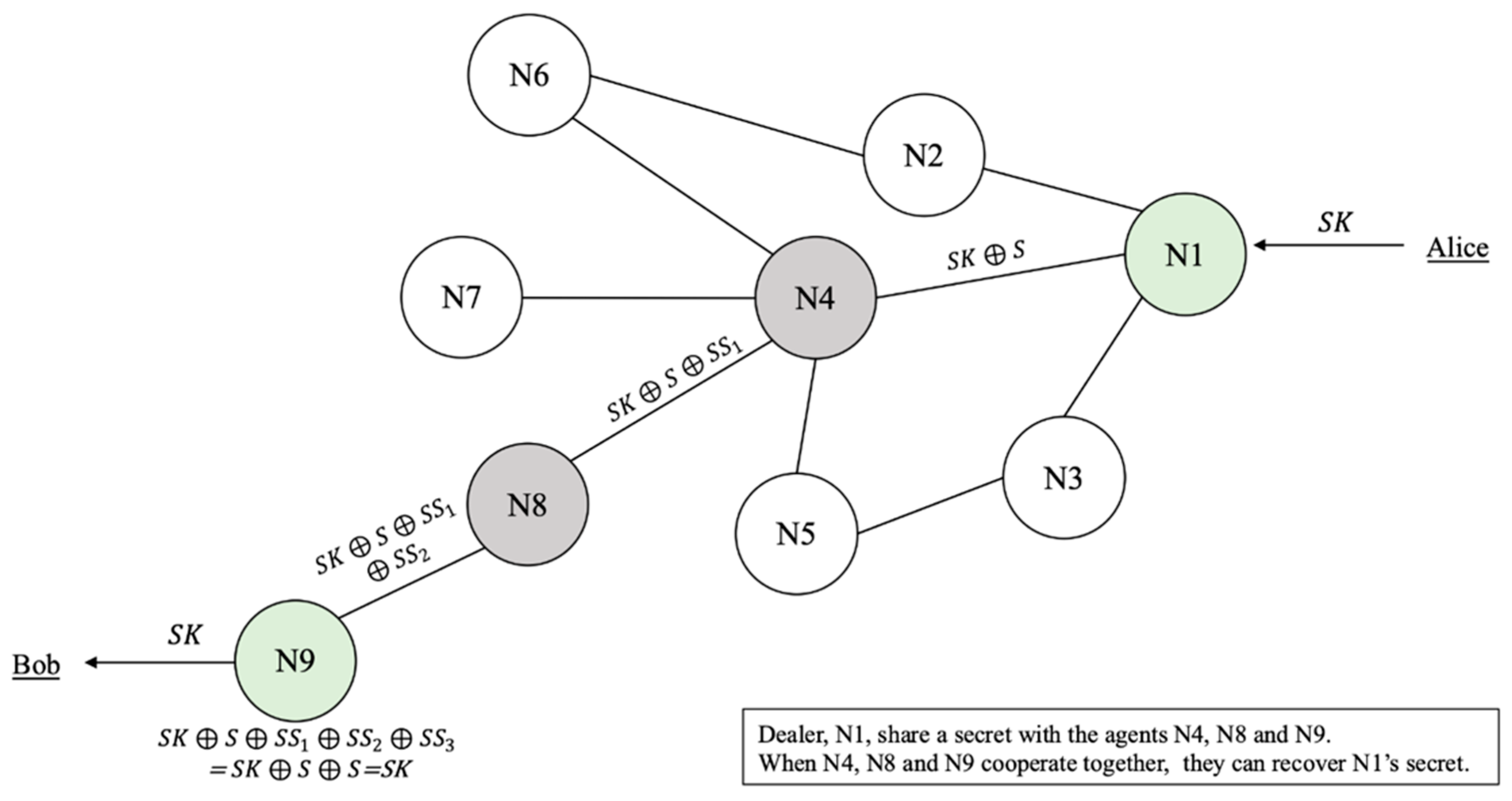
4.1. Lacking the Point-to-Multipoint (P2M) Mechanism in QKD Networks

The existing QKD networks only provide P2P key distribution services (i.e., allow two remote end users/applications to distribute the session keys). However, some information applications (e.g., broadcast) need P2M key distribution services (i.e., let one end user/application share session keys with n remote end users/applications). Although we can also use the P2P key distribution method to obtain the same results as the P2M key distribution, numerous resources of the quantum nodes must be consumed. For example, in Figure 4a, Alice wants to distribute a session key SA to Bob, Charlie, and David. Here, the quantum node N4 must consume three local keys (i.e., K(2,4), K(1,4), and K(3,4)) and perform three encryptions to perform this task. This affects the performance of QKD networks. When the load of the QKD network increases continuously, the influence tends to become serious. Reducing this burden is an important issue for enhancing the performance of QKD networks. Therefore, for this challenge, a feasible solution is to adopt the quantum conference key distribution (QCKD) protocol, which allows a multiparty to simultaneously share a conference key. For the aforementioned task, if N4 had shared a conference key with N1, N2, and N3, N4 will only consume one conference key and perform the encryption once (shown as Figure 4b); that is, a QCKD protocol is required in the QKD network. However, an efficient integration of QKD and QCKD protocols into QKD networks remains an important issue that needs to be studied further. Except for the QCKD protocols, some physical layer technologies can also be used to tackle this P2M challenge as well. For example, the time-division multiplexing (TDM) based concept will be a suitable technology. Based on the TDM-based multiuser scheme [70], Zavitsanos et al. [71] proposed an indicative P2MP technology for ultra-dense QKD networks, in which the multiple users can be served with acceptable secret key rates.

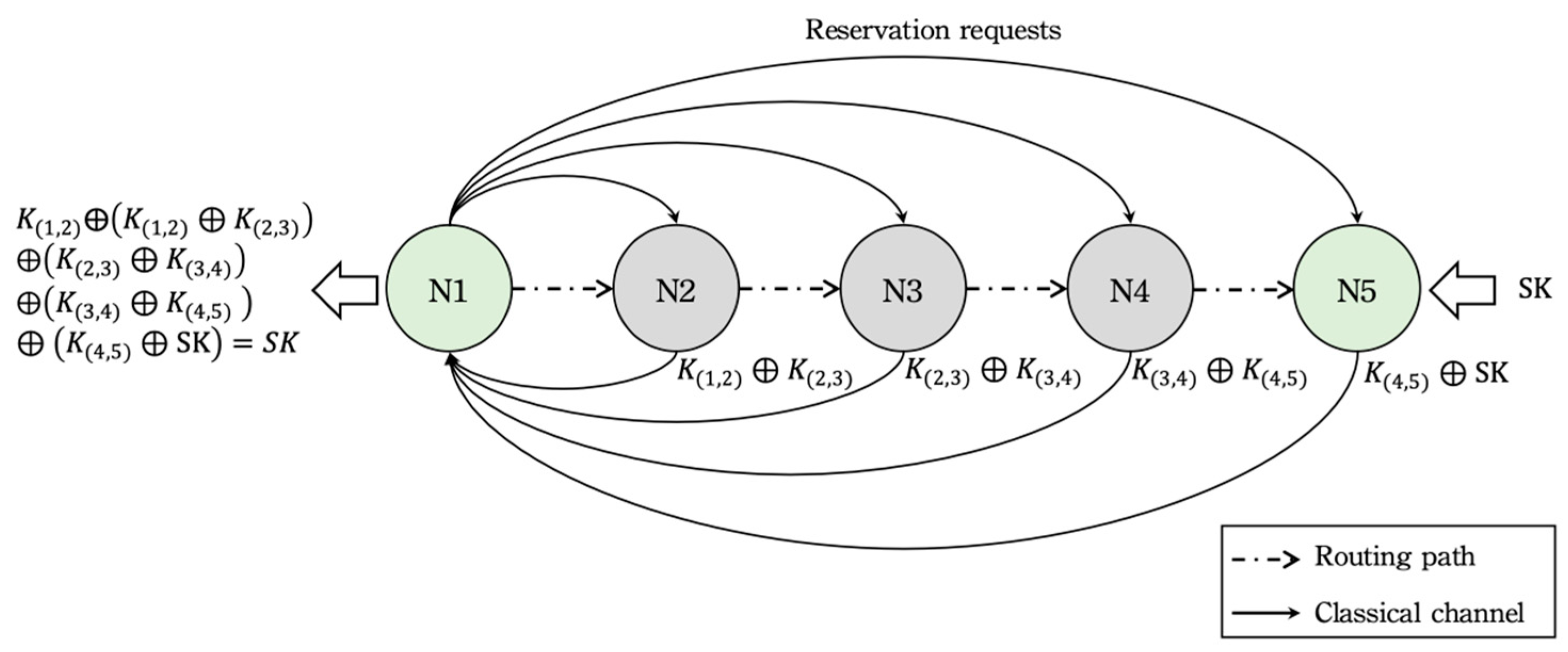
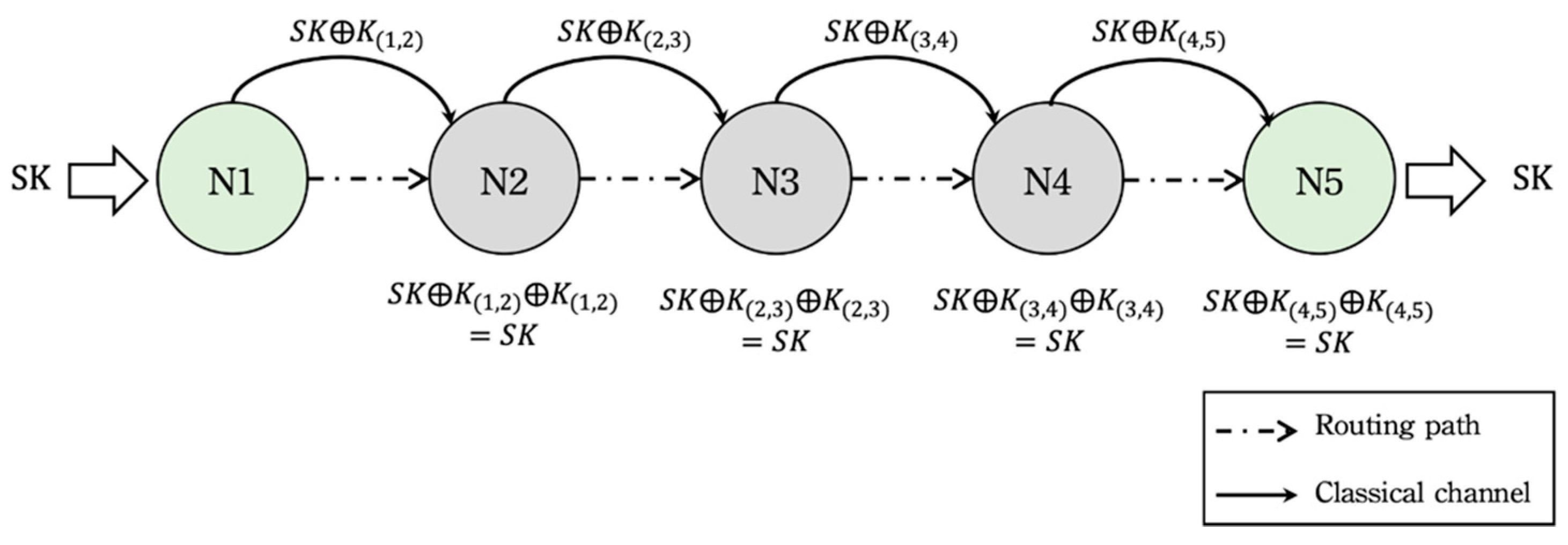
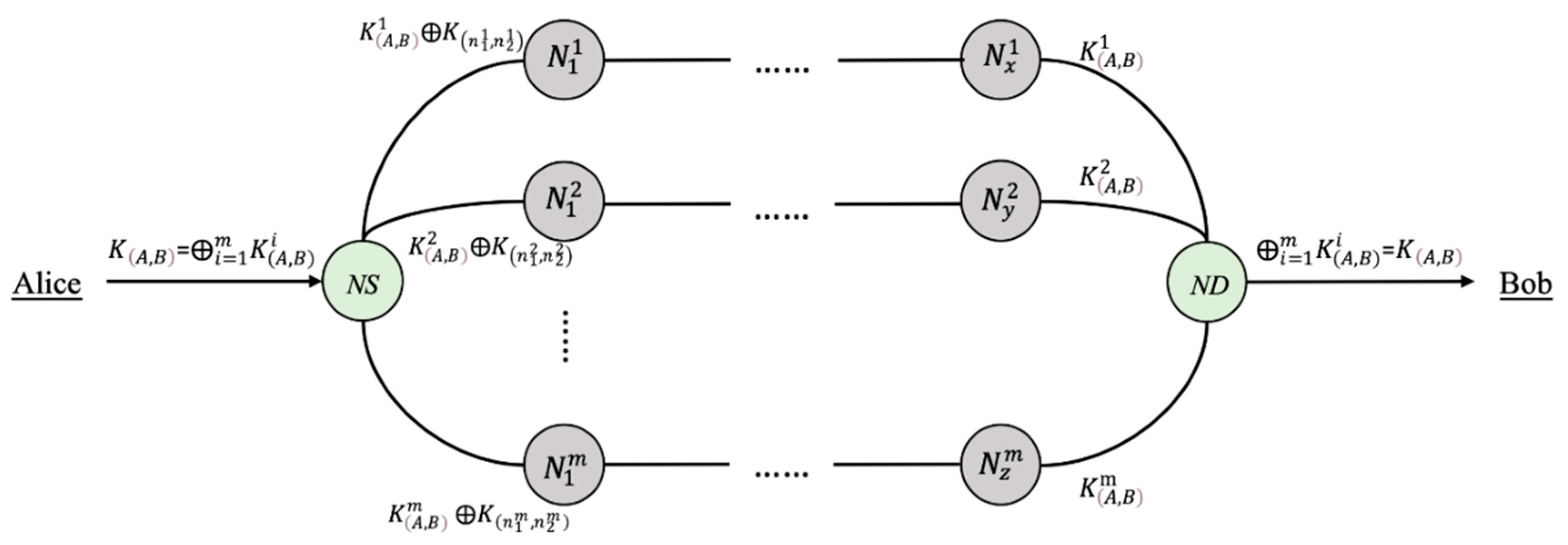
4.2. Numerous Quantum Node Resources Are Consumed by the Multiple-Path Strategy

The QKD network must use the hop-by-hop method to distribute the security session key owing to the limitation of the qubit communication distance. Any node on the routing path can know the session keys distributed from the source node to the destination node. In the DAPRA QKD network, after the routing path is decided, the source node (node N1 in Figure 5) sends reservation requests to all nodes (N2, N3, and N4 in Figure 5) in the routing path and the destination node (N5 in Figure 5). Then, these nodes use the XOR operation to encrypt the corresponding local key or session key to assist the source, and the distance nodes share the session key. By observing this session key transmission method of the DAPRA QKD network, we can determine that the session key may be leaked if the part nodes (e.g., N4 or N2) are compromised. Taking the situation in Figure 5 as an example, N4 has the local key K(4,5); thus, N4 can intercept the ciphertext K(4,5)⊕SK that is sent from N5 to N1 and then perform K(4,5)⊕K(4,5)⊕SK to obtain SK; likewise, N2 can intercept the ciphertexts K(4,5)⊕SK, K(3,4)⊕K(4,5), and K(2,3)⊕K(3,4) sent from N5, N4, and N3 to N1, respectively. It can then perform the calculation as shown in the following equation:
K(1,2)⊕(K(1,2)⊕K(2,3))⊕(K(2,3)⊕K(3,4))⊕(K(3,4)⊕K(4,5))⊕(K(4,5)⊕SK).
Because the associative properties of the XOR function, A⊕(B⊕C) = (A⊕B)⊕C and N2 owns the local keys, K(1,2) and K(2,3), in which it can extract SK.
The SECOQC QKD network adopts a similar method to transmit the session key, as shown in Figure 6. This session key transmission method allows any node in the routing path to decrypt the ciphertext of the session key, re-encrypts the session key with the local key shared between it and the next node and, then, sends fresh ciphertext to the next node. In other words, any node in the routing path can obtain the session key directly; thus, the session key will be revealed if any node among the routing path is compromised.
Although Salvail et al. [44] used the multiple-path strategy to prevent the aforementioned problem—the partial quantum nodes were compromised, and the multiple-path strategy consumed numerous resources of quantum nodes, in which the consumption of local keys was the most important because of the high cost of generating local keys. Let us take an example to explain this. Alice wants to distribute a session key to Bob with the help of the source node NS. If NS selects m paths for transmitting the session key to the destination node ND, m times the number of local keys will be used to achieve this task (also shown in Figure 7).
Therefore, reducing the consumption of the local key and avoiding the unrealistic assumption of the trustworthiness level of quantum nodes is an interesting research issue. To address this issue, we propose a feasible solution: each node in the routing path can share the secret shadow using the QSS protocol [72,73,74,75]. Only nodes in the routing path cooperate here, and the session key can be extracted; otherwise, no information regarding the session key can be revealed to anyone. Taking an example (shown in Figure 8) to explain the resolution, Alice wants to distribute a session key with Bob with the help of source node N1. All nodes in the routing path (i.e., N4, N8, and N9) share the secret shadows (i.e., SS1, SS2, and SS3) with N1, respectively, using a secure QSS protocol. After N4, N8, and N9 perform XOR operation on their secret shadows and the ciphertext sent from the previous node, the session key SK can be extracted. If N4 or N8 is compromised, the session key cannot be obtained because it cannot obtain the assistance of all agents (i.e., N4 and N9). Note that the source and destination nodes must still be trusted; however, the other nodes can be released from this unrealistic assumption. However, the routing paths within the QKD network are dynamic; thus, letting the nodes in each routing path share the secret shadows effectively is crucial for the proposed solution. This issue should be addressed in future research.

4.3. No Suitable Security Interface between the Classical End Users/Applications and Quantum Nodes

Because the construction cost of quantum nodes is still very high, it is not feasible to let each end user/application have a dedicated quantum node for accessing the service of the QKD network. Therefore, several end users/applications must share one quantum node (i.e., the access node mentioned in Section 2) in a real time environment. Therefore, the end users/applications still use the classical network to link the quantum nodes (shown in Figure 9); that is, designing a complete security mechanism for the communication between the end users/applications and the quantum nodes is an important issue. Although Tanizawa et al. [46] proposed a strategy using OpenSSL for this issue, the strategy is still not perfect within the quantum computing environment because OpenSSL is a computing-based security method.
To address this issue, we believe that post-quantum cryptography (PQC) is the optimal strategy for designing a security mechanism for the interface between the quantum node and the end users/applications. Here, PQC can be used to complete the authentication and session key transmission between the quantum and classical end user/application. After the end users/applications obtain the session keys with the quantum node using post-quantum public-key cryptography, they can use the OTP or symmetric key cryptography to communicate securely. Although using an OTP to encrypt the messages transmitted between the quantum node and the end users/applications can provide unconditional security, this method has a higher cost than using symmetric key cryptography because of the heavy demand for encryption/decryption keys. However, using symmetric key cryptography cannot provide unconditional security for the end users/application to access the session keys from the quantum node; however, the security of this method is better than that of other currently existing methods (e.g., SSL protocol) because the encryption/decryption keys are obtained from algorithms that cannot be broken by a quantum computer. We can select the suitable encryption/decryption methods depending on the practical context; that is, if the application’s security requirement is not high but the communication traffic is heavy, symmetric key cryptography will be applicable; otherwise, an OTP can be used to provide the best security protection. For demonstrating the feasibility of the integrating PQC and QDK protocol, Wang et al. [76] used an experimental approach to verify the efficiency and stability of the PQC algorithm in QKD authentication. However, the National Institute of Standards and Technology (NIST) is currently working on the new generation of quantum-resistant key encapsulation and authentication schemes, the implementation of integrating the PQC key exchange and the authentication into the standard cryptographic protocols of the classical network (e.g., SSL, TLS and so on) will need to be studied further to evaluate and optimize its performance.

5. Conclusions

The QKD network is a key infrastructure that allows end users/applications to access the key distribution service with unconditional security. To date, various countries and research institutes have invested numerous resources to execute theoretical studies and practical field experiments on QKD networks. This study surveys and summarizes the existing results of these studies and experiments and then proposes three security challenges: (1) the lack of a P2M mechanism in QKD networks, (2) many quantum node resources being consumed by the multiple-path strategy, and (3) no suitable security interface between the classical end users/applications and quantum nodes. In addition, some feasible solutions and strategies for these challenges are indicated to allow researchers to understand these challenges easily and to inspire them to propose the appropriate solutions.

Author Contributions

Conceptualization, C.-W.T. and Y.-C.C.; methodology, C.-W.T., C.-W.Y. and J.L.; investigation, C.-W.T. and Y.-C.C.; formal analysis, C.-W.T.; writing—original draft, C.-W.T. and Y.-C.C.; writing—review & editing, J.L. and R.-S.C.; project Administration, R.-S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the Ministry of Science and Technology, Taiwan, R.O.C. (Grant Nos. MOST 107-2218-E-143-002-MY2, MOST 106-2218-E-039-002-MY3 and MOST 107-2627-E-006 -001-), and China Medical University, Taiwan (Grant No. CMU109-S-01).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bennett, C.H.; Brassard, G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
  2. Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [Green Version]
  3. Gottesman, D.; Hoi-Kwong, L. Proof of security of quantum key distribution with two-way classical communications. IEEE Trans. Inf. Theory 2003, 49, 457–475. [Google Scholar] [CrossRef] [Green Version]
  4. Tsurumaru, T.; Tamaki, K. Security proof for quantum-key-distribution systems with threshold detectors. Phys. Rev. A 2008, 78, 032302. [Google Scholar] [CrossRef]
  5. Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef] [PubMed]
  6. Cerf, N.J.; Bourennane, M.; Karlsson, A.; Gisin, N. Security of Quantum Key Distribution Using d-Level Systems. Phys. Rev. Lett. 2002, 88, 127902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Long, G.; Liu, X. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 2002, 65, 032302. [Google Scholar] [CrossRef] [Green Version]
  8. Grosshans, F.; Van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238. [Google Scholar] [CrossRef] [Green Version]
  9. Hwang, W.-Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [Green Version]
  10. Lo, H.K.; Ma, X.F.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 4. [Google Scholar] [CrossRef] [Green Version]
  11. Hwang, T.; Lee, K.C.; Li, C.M. Provably secure three-party authenticated quantum key distribution protocols. IEEE Trans. Depend. Secur. 2007, 4, 71–80. [Google Scholar] [CrossRef]
  12. Li, X.H.; Deng, F.G.; Zhou, H.Y. Efficient quantum key distribution over a collective noise channel. Phys. Rev. A 2008, 78, 022321. [Google Scholar] [CrossRef] [Green Version]
  13. Lo, H.-K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Yang, C.-W. New Probabilistic Quantum Key Distribution Protocol. Int. J. Theor. Phys. 2018, 57, 3651–3657. [Google Scholar] [CrossRef]
  15. Boyer, M.; Kenigsberg, D.; Mor, T. Quantum Key Distribution with Classical Bob. Phys. Rev. Lett. 2007, 99, 140501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Boyer, M.; Gelles, R.; Kenigsberg, D.; Mor, T. Semiquantum key distribution. Phys. Rev. A 2009, 79, 032341. [Google Scholar] [CrossRef] [Green Version]
  17. Krawec, W.O. Mediated semiquantum key distribution. Phys. Rev. A 2015, 91, 032323. [Google Scholar] [CrossRef] [Green Version]
  18. Xu, F.; Qi, B.; Liao, Z.; Lo, H.-K. Long distance measurement-device-independent quantum key distribution with entangled photon sources. Appl. Phys. Lett. 2013, 103, 61101. [Google Scholar] [CrossRef] [Green Version]
  19. Liu, Y.; Chen, T.Y.; Wang, L.J.; Liang, H.; Shentu, G.L.; Wang, J.; Cui, K.; Yin, H.-L.; Liu, N.-L.; Li, L.; et al. Experimental measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2013, 111, 130502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Elliott, C.; Pearson, D.; Troxel, G. Quantum cryptography in practice. In Proceedings of the Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications (SIGCOMM’03), Karlsruhe, Germany, 25–29 August 2003; pp. 227–238. [Google Scholar]
  21. Elliott, C.; Yeh, H. DARPA Quantum Network Testbed; Technical Report; BBN Technologies Cambridge: New York, NY, USA, 2007; Available online: https://apps.dtic.mil/sti/pdfs/ADA471450.pdf (accessed on 25 March 2021).
  22. Elliott, C.; Colvin, A.; Pearson, D.; Pikalo, O.; Schlafer, J.; Yeh, H. Current status of the DARPA quantum network. In Quantum Information and Computation III; International Society for Optics and Photonics: Washington, DC, USA, 2005; Volume 5815. [Google Scholar]
  23. Kollmitzer, C.; Pivk, M. Applied Quantum Cryptography; Springer Science & Business Media: Berlin, Germany, 2010; Volume 797. [Google Scholar]
  24. Dianati, M.; Alléaume, R.; Gagnaire, M.; Shen, X. Architecture and protocols of the future European quantum key distribution network. Sec. Commun. Netw. 2008, 1, 57–74. [Google Scholar] [CrossRef]
  25. Peev, M.; Länger, T.; Lorünser, T.; Happe, A.; Maurhart, O.; Poppe, A.; Themel, T. The SECOQC quantum key distribution network in Vienna. New J. Phys. 2009, 11, 75001. [Google Scholar] [CrossRef] [Green Version]
  26. Masahide Sasaki. Tokyo QKD network and the evolution to secure photonic network. In Proceedings of the Conference on Laser Applications to Photonic Applications (CLEO’11), Baltimore, MD, USA, 1–6 May 2011; OSA: Washington, DC, USA, 2011; Volume 1. [Google Scholar]
  27. Sarkar, K.; Basavaraju, T.G.; Puttamadappa, C. Ad Hoc Mobile Wireless Networks; CRC Press: Boca Raton, FL, USA, 2008; Volume 1. [Google Scholar]
  28. Xu, F.; Chen, W.; Wang, S.; Yin, Z.; Zhang, Y.; Liu, Y.; Zhou, Z.; Zhao, Y.; Li, H.; Liu, D.; et al. Field experiment on a robust hierarchical metropolitan quantum cryptography network. Chin. Sci. Bull. 2009, 54, 2991–2997. [Google Scholar] [CrossRef] [Green Version]
  29. Han, Z.-F.; Xu, F.-X.; Chen, W.; Wang, S.; Yin, Z.-Q.; Zhang, Y.; Liu, Y.; Zhou, Z.; Li, H.-W.; Liu, D.; et al. An application-oriented hierarchical quantum cryptography net- work test bed. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 21–25 March 2010. [Google Scholar]
  30. Wang, S.; Chen, W.; Yin, Z.-Q.; Li, H.-W.; He, D.-Y.; Li, Y.-H.; Zhou, Z.; Song, X.-T.; Li, F.-Y.; Wang, D.; et al. Field and long-term demonstration of a wide area quantum key distribution network. Opt. Express 2014, 22, 21739. [Google Scholar] [CrossRef] [Green Version]
  31. European Commission. China to Launch World’s First Quantum Communication Network. 2017. Available online: https://cordis.europa.eu/article/id/122516.trending-science-china-to-launch-worlds-first-quantum-communication-network/en (accessed on 3 August 2017).
  32. ChinaDaily. Quantum Tech to Link Jinan Governments. 2017. Available online: http://www.chinadaily.com.cn/china/2017-07/11/content_30065215.htm (accessed on 11 July 2017).
  33. Travagnin, M.; Lewis, A. Quantum Key Distribution in Field Implementations. 2019. EUR 29865 EN. Available online: https://op.europa.eu/en/publicationdetail/-/publication/e93e5bf9-efc3-11e9-a32c-01aa75ed71a1/language-en (accessed on 15 October 2019).
  34. Zhao, Y. The integration of QKD and security services. In Proceedings of the ITU QIT4N Workshop, Shanghai, China, 5–7 June 2019; Available online: https://www.itu.int/en/ITU-T/Workshops-and-Seminars/2019060507/Documents/Yong (accessed on 5 June 2019).
  35. Wang, S.; Chen, W.; Yin, Z.-Q.; Zhang, Y.; Zhang, T.; Li, H.-W.; Xu, F.-X.; Zhou, Z.; Yang, Y.; Huang, D.-J.; et al. Field test of wavelength-saving quantum key distribution network. Opt. Lett. 2010, 35, 2454–2456. [Google Scholar] [CrossRef] [Green Version]
  36. Van Meter, R.; Satoh, T.; Ladd, T.D.; Munro, W.J.; Nemoto, K. Path selection for quantum repeater networks. Netw. Sci. 2013, 3, 82–95. [Google Scholar] [CrossRef] [Green Version]
  37. Tanizawa, Y.; Takahashi, R.; Dixon, A.R. A routing method designed for a Quantum Key Distribution network. In Proceedings of the 2016 Eighth International Conference on Ubiquitous and Future Networks (ICUFN), Vienna, Austria, 5–8 July 2016; pp. 208–214. [Google Scholar]
  38. Yang, C.; Zhang, H.; Su, J. The QKD network: Model and routing scheme. J. Mod. Opt. 2017, 64, 2350–2362. [Google Scholar] [CrossRef]
  39. Mehic, M.; Fazio, P.; Rass, S.; Maurhart, O.; Peev, M.; Poppe, A.; Rozhon, J.; Niemiec, M.; Voznak, M. A Novel Approach to Quality-of-Service Provisioning in Trusted Relay Quantum Key Distribution Networks. IEEE/ACM Trans. Netw. 2019, 28, 168–181. [Google Scholar] [CrossRef] [Green Version]
  40. Hahn, F.; Pappa, A.; Eisert, J. Quantum network routing and local complementation. NPJ Quantum Inf. 2019, 5, 76. [Google Scholar] [CrossRef] [Green Version]
  41. Amer, O.; Krawec, W.O.; Wang, B. Efficient Routing for Quantum Key Distribution Networks. arXiv 2020, arXiv:2005.12404. [Google Scholar]
  42. Tang, Z.; Qin, Y.; Jiang, Z.; Krawec, W.O.; Zhang, P. Quantum-Secure Networked Microgrids. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 3–6 August 2020; pp. 1–5. [Google Scholar]
  43. Tang, Z.; Zhang, P.; Krawec, W.O.; Jiang, Z. Programmable Quantum Networked Microgrids. IEEE Trans. Quantum Eng. 2020, 1, 1–13. [Google Scholar] [CrossRef]
  44. Salvail, L.; Peev, M.; Diamanti, E.; Alléaume, R.; Lütkenhaus, N.; Langer, T. Security of trusted repeater quantum key distribution networks. J. Comput. Secur. 2010, 18, 61–87. [Google Scholar] [CrossRef] [Green Version]
  45. Tang, Y.L.; Yin, H.L.; Zhao, Q.; Liu, H.; Sun, X.X.; Huang, M.Q.; Zhang, W.-J.; Chen, S.-J.; Zhang, L.; You, L.-X.; et al. Measurement-device-independent quantum key distribution over untrustful metropolitan network. Phys. Rev. X 2016, 6, 011024. [Google Scholar] [CrossRef] [Green Version]
  46. Tanizawa, Y.; Takahashi, R.; Sato, H.; Dixon, A.R.; Kawamura, S. A Secure Communication Network Infrastructure Based on Quantum Key Distribution Technology. IEICE Trans. Commun. 2016, 99, 1054–1069. [Google Scholar] [CrossRef]
  47. Fröhlich, B.; Dynes, J.F.; Lucamarini, M.; Sharpe, A.W.; Yuan, Z.; Shields, A.J. A quantum access network. Nature 2013, 501, 69–72. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  48. Cai, C.; Sun, Y.; Niu, J.; Ji, Y. A Quantum Access Network Suitable for Internetworking Optical Network Units. IEEE Access 2019, 7, 92091–92099. [Google Scholar] [CrossRef]
  49. Wegman, M.N.; Carter, J. New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 1981, 22, 265–279. [Google Scholar] [CrossRef] [Green Version]
  50. Choi, I.; Young, R.J.; Townsend, P.D. Quantum information to the home. New J. Phys. 2011, 13, 063039. [Google Scholar] [CrossRef]
  51. Liao, S.-K.; Lin, J.; Ren, J.-G.; Liu, W.-Y.; Qiang, J.; Yin, J.; Li, Y.; Shen, Q.; Zhang, L.; Liang, X.-F.; et al. Space-to-Ground Quantum Key Distribution Using a Small-Sized Payload on Tiangong-2 Space Lab. Chin. Phys. Lett. 2017, 34, 090302. [Google Scholar] [CrossRef]
  52. Lucamarini, M.; Yuan, Z.L.; Dynes, J.F.; Shields, A.J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 2018, 557, 400–403. [Google Scholar] [CrossRef]
  53. Minder, M.; Pittaluga, M.; Roberts, G.L.; Lucamarini, M.; Dynes, J.F.; Yuan, Z.L.; Shields, A.J. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nat. Photon. 2019, 13, 334. [Google Scholar] [CrossRef]
  54. Wang, S.; He, D.-Y.; Yin, Z.-Q.; Lu, F.-Y.; Cui, C.-H.; Chen, W.; Zhou, Z.; Guo, G.-C.; Han, Z.-F. Beating the Fundamental Rate-Distance Limit in a Proof-of-Principle Quantum Key Distribution System. Phys. Rev. X 2019, 9, 021046. [Google Scholar] [CrossRef] [Green Version]
  55. Liu, Y.; Yu, Z.-W.; Zhang, W.; Guan, J.-Y.; Chen, J.-P.; Zhang, C.; Hu, X.-L.; Li, H.; Jiang, C.; Lin, J.; et al. Experimental Twin-Field Quantum Key Distribution through Sending or Not Sending. Phys. Rev. Lett. 2019, 123, 100505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  56. Zhong, X.; Hu, J.; Curty, M.; Qian, L.; Lo, H.-K. Proof-of-Principle Experimental Demonstration of Twin-Field Type Quantum Key Distribution. Phys. Rev. Lett. 2019, 123, 100506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  57. Chen, J.-P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.; Hu, X.-L.; Guan, J.-Y.; Yu, Z.-W.; Xu, H.; Lin, J.; et al. Sending-or-Not-Sending with Independent Lasers: Secure Twin-Field Quantum Key Distribution over 509 km. Phys. Rev. Lett. 2020, 124, 070501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. Elliott, C. Building the quantum network. New J. Phys. 2002, 4, 46. [Google Scholar] [CrossRef]
  59. Alléaume, R.; Branciard, C.; Bouda, J.; Debuisschert, T.; Dianati, M.; Gisin, N.; Godfrey, M.; Grangier, P.; Länger, T.; Lütkenhaus, N.; et al. Using quantum key distribution for cryptographic purposes: A survey. Theor. Comput. Sci. 2014, 560, 62–81. [Google Scholar] [CrossRef]
  60. Hall, M.A.; Altepeter, J.B.; Kumar, P. Ultrafast Switching of Photonic Entanglement. Phys. Rev. Lett. 2011, 106, 053901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  61. Lu, J.; Zhou, L.; Kuang, L.-M.; Nori, F. Single-photon router: Coherent control of multichannel scattering for single photons with quantum interferences. Phys. Rev. A 2014, 89, 013805. [Google Scholar] [CrossRef] [Green Version]
  62. Lemr, K.; Bartkiewicz, K.; Černoch, A.; Soubusta, J. Resource-efficient linear-optical quantum router. Phys. Rev. A 2013, 87, 062333. [Google Scholar] [CrossRef] [Green Version]
  63. Briegel, H.J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 1998, 81, 5932–5935. [Google Scholar] [CrossRef]
  64. Bouwmeester, D.; Pan, J.-W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef] [Green Version]
  65. Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Pan, J.-W.; Bouwmeester, D.; Weinfurter, H.; Zeilinger, A. Experimental Entanglement Swapping: Entangling Photons That Never Interacted. Phys. Rev. Lett. 1998, 80, 3891. [Google Scholar] [CrossRef]
  67. RFC 2328—OSPF Version 2. RFC. The Neighborhood of Each Network Node in The Graph Depends on the Network’s Type (Point-To-Point, Broadcast, NBMA Or Point-To-Multipoint) and the Number of Routers Having an Interface to the Network. Available online: https://dl.acm.org/doi/pdf/10.17487/RFC2328 (accessed on 25 March 2021).
  68. AIT QKD R10 Software. Available online: https://github.com/axdhill/ait-qkd (accessed on 27 June 2016).
  69. OpenSSL, OpenSSL Project. Available online: onhttps://openssl.org (accessed on 25 March 2021).
  70. Townsend, P.D. Quantum cryptography on multiuser optical fibre networks. Nature 1997, 385, 47–49. [Google Scholar] [CrossRef]
  71. Zavitsanos, D.; Ntanos, A.; Giannoulis, G.; Avramopoulos, H. On the QKD Integration in Converged Fiber/Wireless Topologies for Secured, Low-Latency 5G/B5G Fronthaul. Appl. Sci. 2020, 10, 5193. [Google Scholar] [CrossRef]
  72. Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829. [Google Scholar] [CrossRef] [Green Version]
  73. Karlsson, A.; Koashi, M.; Imoto, N. Quantum entanglement for secret sharing and secret splitting. Phys. Rev. A 1999, 59, 162. [Google Scholar] [CrossRef]
  74. Bagherinezhad, S.; Karimipour, V. Quantum secret sharing based on reusable Greenberger-Horne-Zeilinger states as secure carriers. Phys. Rev. A 2003, 67, 044302. [Google Scholar] [CrossRef] [Green Version]
  75. Guo, G.-P.; Guo, G.-C. Quantum secret sharing without entanglement. Phys. Lett. A 2003, 310, 247–251. [Google Scholar] [CrossRef] [Green Version]
  76. Liu-Jun, W.; Kai-Yi, Z.; Jia-Yong, W.; Jie, C.; Yong-Hua, Y.; Shi-Biao, T.; Di, Y.; Yan-Lin, T.; Zhen, Z.; Yu, Y.; et al. Experimental Authentication of Quantum Key Distribution with Post-quantum Cryptography. arXiv 2020, arXiv:2009.04662. [Google Scholar]
Applsci 11 03767 g001 550
Figure 1. Framework of the quantum key distribution (QKD) network.
Figure 1. Framework of the quantum key distribution (QKD) network.
Applsci 11 03767 g001
Applsci 11 03767 g002 550
Figure 2. Schematic diagram of the quantum link.
Figure 2. Schematic diagram of the quantum link.
Applsci 11 03767 g002
Applsci 11 03767 g003 550
Figure 3. Active optical switch network and trusted node network, in which (a) presents the schematic diagram of active optical switch based QKD network and (b) presents the schematic diagram of a trusted QKD network.
Figure 3. Active optical switch network and trusted node network, in which (a) presents the schematic diagram of active optical switch based QKD network and (b) presents the schematic diagram of a trusted QKD network.
Applsci 11 03767 g003
Applsci 11 03767 g004 550
Figure 4. Schematic diagram of transmitting a session key, in which (a) presents the schematic diagram of transmitting session key in P2P method and (b) the schematic diagram of transmitting session key in point-to-multipoint (P2M) method.
Figure 4. Schematic diagram of transmitting a session key, in which (a) presents the schematic diagram of transmitting session key in P2P method and (b) the schematic diagram of transmitting session key in point-to-multipoint (P2M) method.
Applsci 11 03767 g004
Applsci 11 03767 g005 550
Figure 5. Session key transmission method in the DARPA QKD network.
Figure 5. Session key transmission method in the DARPA QKD network.
Applsci 11 03767 g005
Applsci 11 03767 g006 550
Figure 6. Session key transmission method in the SECOQC QKD network.
Figure 6. Session key transmission method in the SECOQC QKD network.
Applsci 11 03767 g006
Applsci 11 03767 g007 550
Figure 7. Session key transmission method using the multiple-path strategy.
Figure 7. Session key transmission method using the multiple-path strategy.
Applsci 11 03767 g007
Applsci 11 03767 g008 550
Figure 8. Session key transmission method using quantum secret sharing (QSS).
Figure 8. Session key transmission method using quantum secret sharing (QSS).
Applsci 11 03767 g008
Applsci 11 03767 g009 550
Figure 9. Security interface between the quantum node and end users/applications.
Figure 9. Security interface between the quantum node and end users/applications.
Applsci 11 03767 g009
Table
Table 1. Summary of QKD network experiments.
Table 1. Summary of QKD network experiments.
NetworkDARPASECOQCUQCCChina QKD
Project year2002–20062004–200820102014–2017
QKD Network typeActive optical switch + Trusted nodeTrusted nodeTrusted nodeTrusted node
QKD protocolBB84 protocol5 different QKD protocolsBB84 and BBM92BB84
Max. key generating rate400 bps
over 29 km		3.1 kbps
over 33 km		304 kpbs
over 45 km		250 kbps
over 43 km
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Tsai, C.-W.; Yang, C.-W.; Lin, J.; Chang, Y.-C.; Chang, R.-S. Quantum Key Distribution Networks: Challenges and Future Research Issues in Security. Appl. Sci. 2021, 11, 3767. https://doi.org/10.3390/app11093767

AMA Style

Tsai C-W, Yang C-W, Lin J, Chang Y-C, Chang R-S. Quantum Key Distribution Networks: Challenges and Future Research Issues in Security. Applied Sciences. 2021; 11(9):3767. https://doi.org/10.3390/app11093767

Chicago/Turabian Style

Tsai, Chia-Wei, Chun-Wei Yang, Jason Lin, Yao-Chung Chang, and Ruay-Shiung Chang. 2021. "Quantum Key Distribution Networks: Challenges and Future Research Issues in Security" Applied Sciences 11, no. 9: 3767. https://doi.org/10.3390/app11093767

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop