The Role of Metal Ions in the Electron Transport through Azurin-Based Junctions
Abstract
1. Introduction
2. Methods
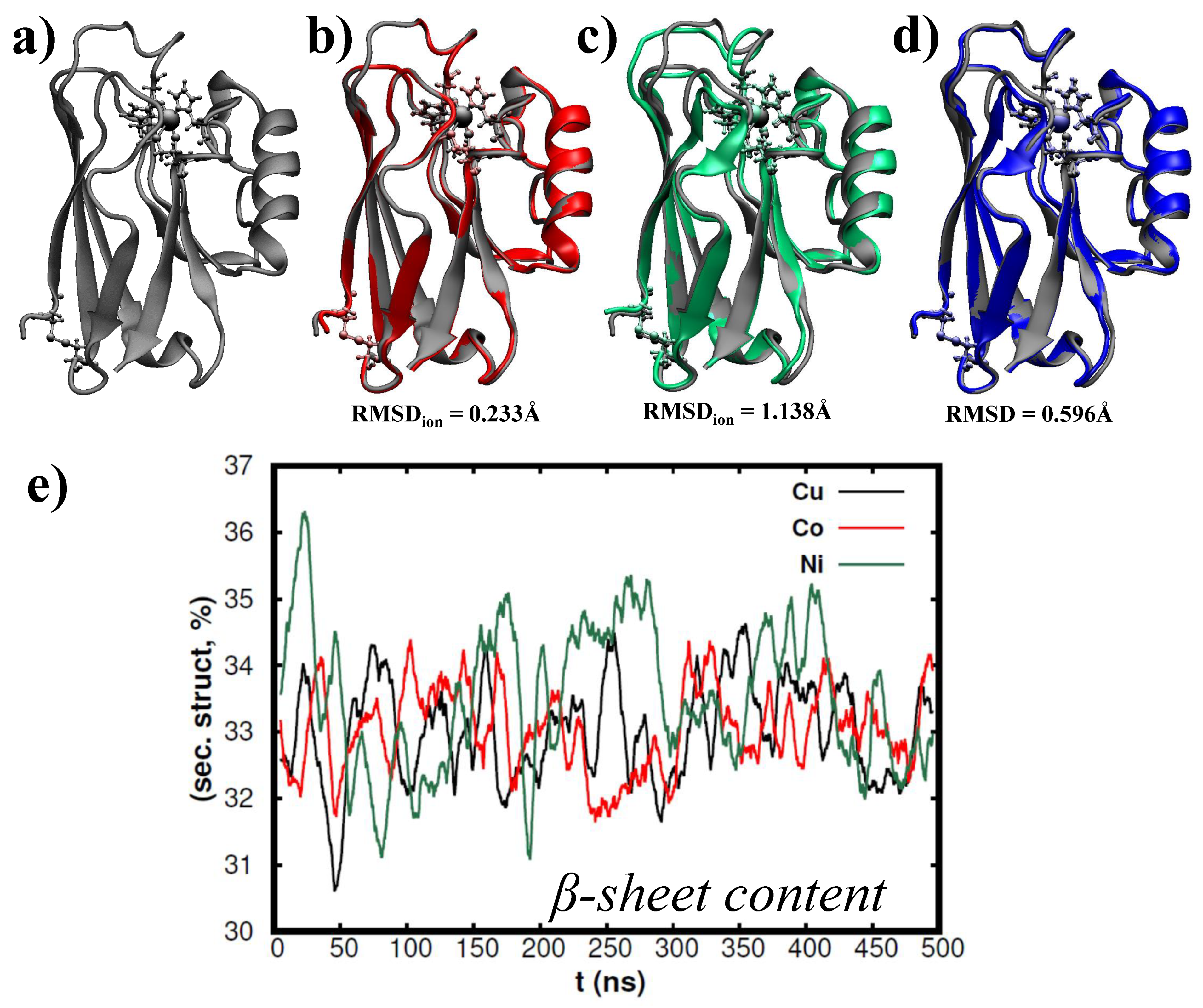
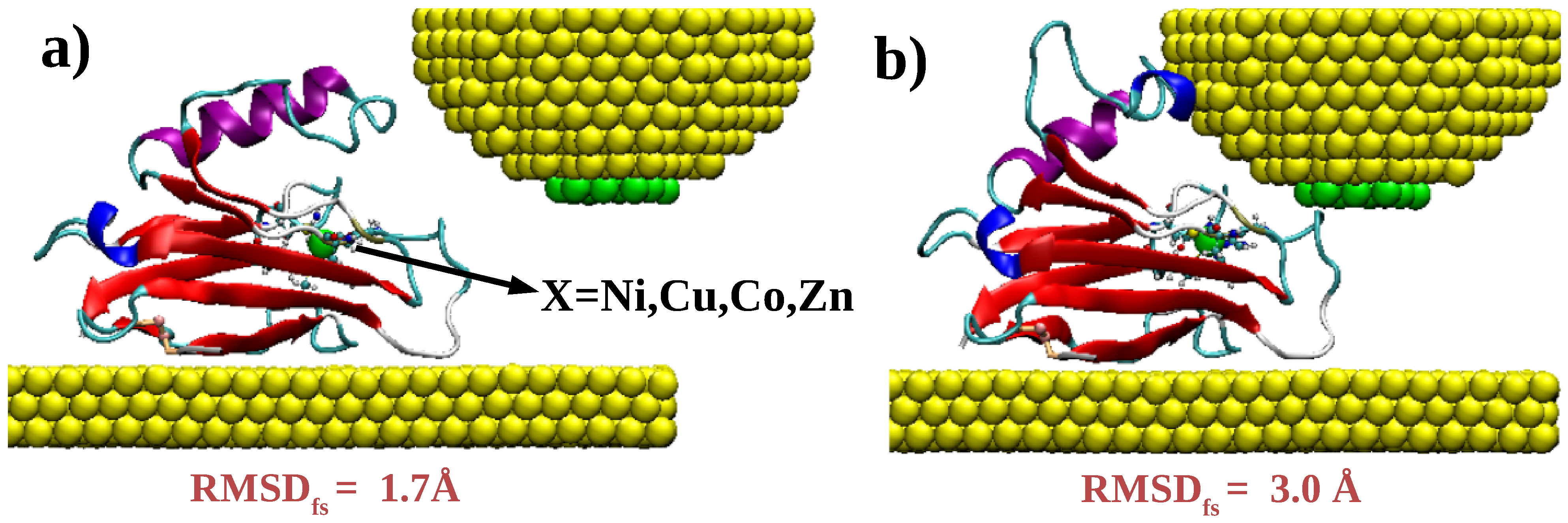
2.1. Azurin Molecular Dynamics Simulations Free Solved in Water
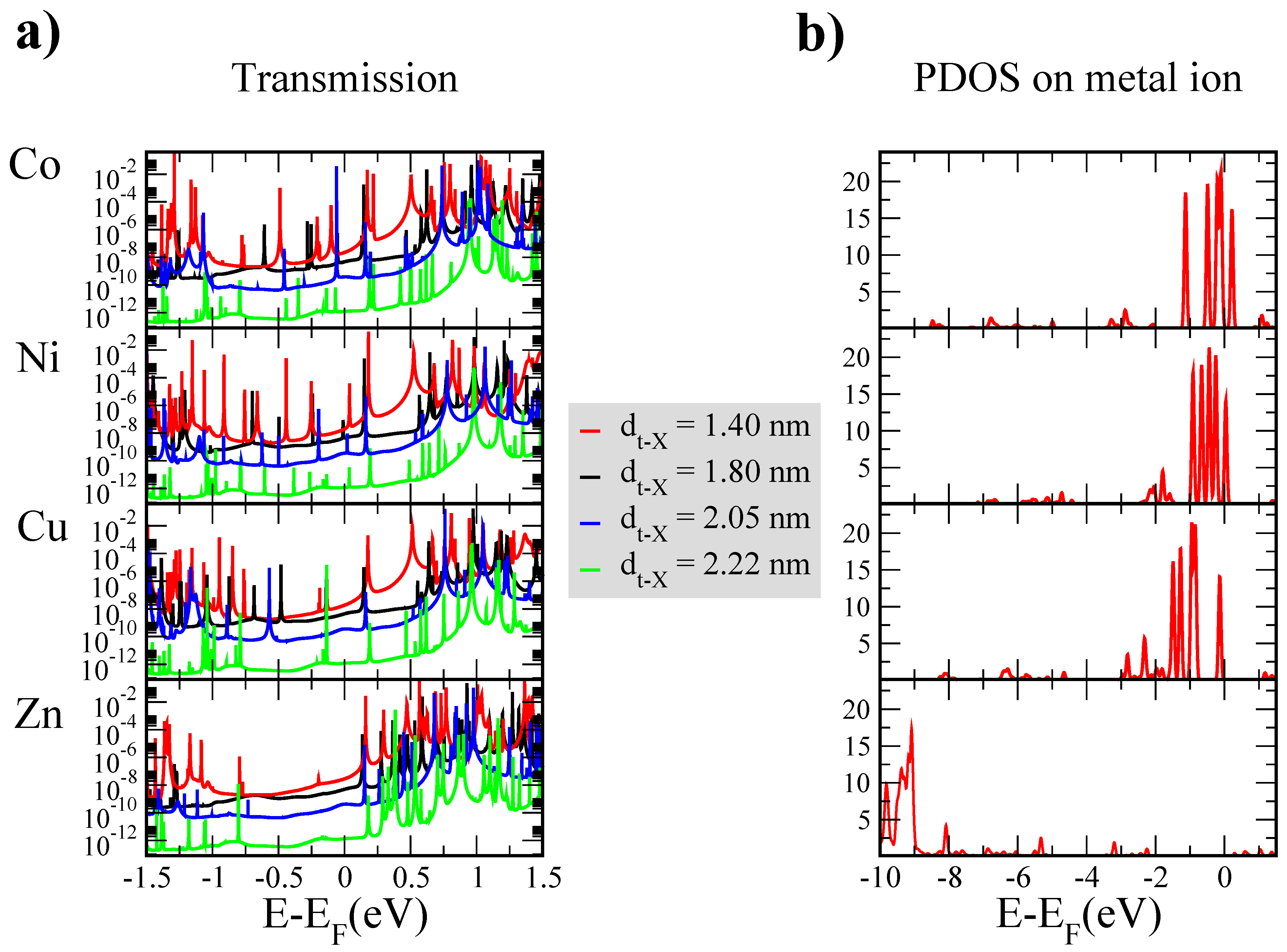
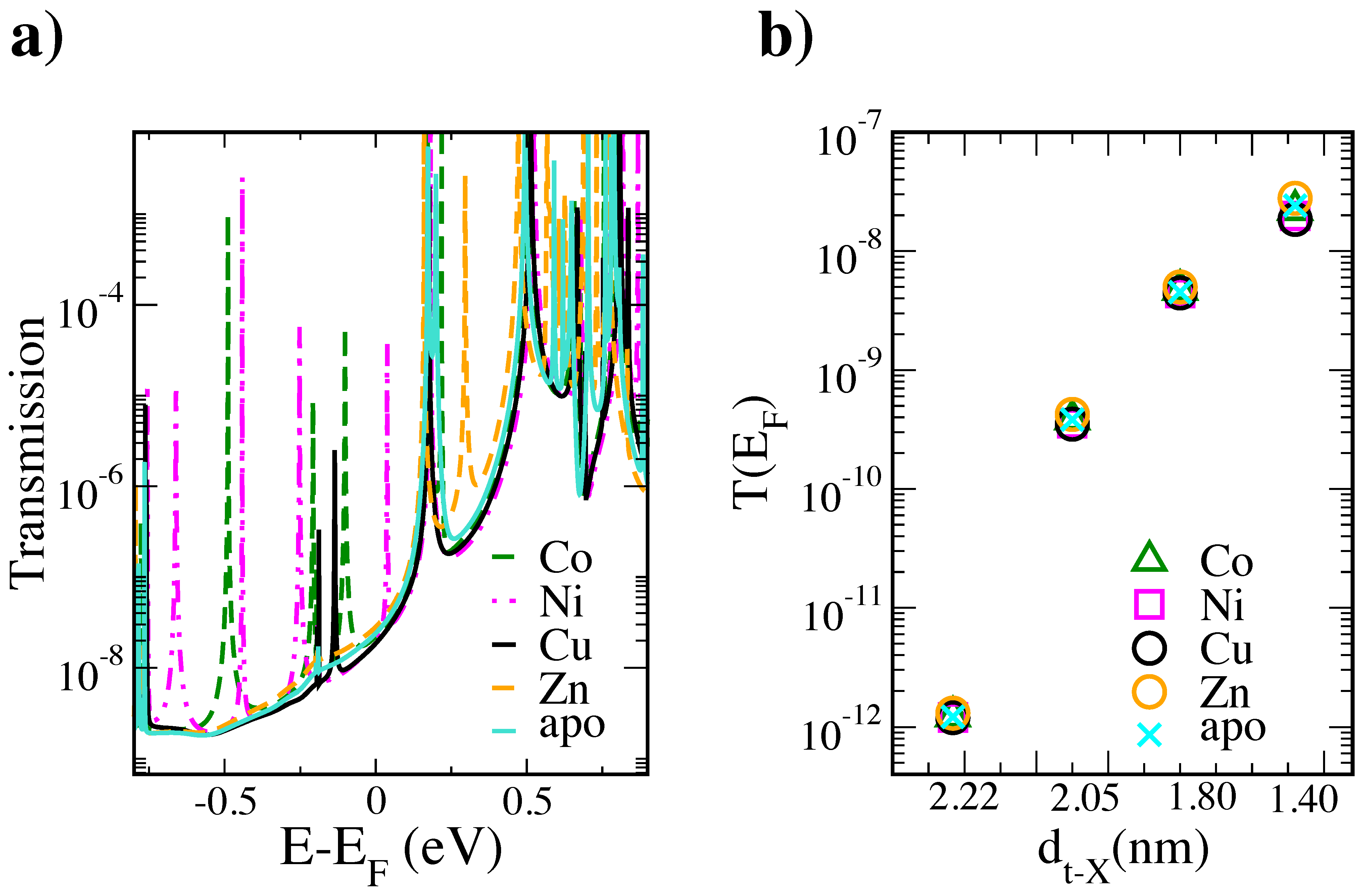
2.2. Density Functional Theory Calculations on Metal–Protein–Metal Junctions
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STM | Scanning Tunneling Microscopy |
| MD | Molecular Dynamics |
| DFT | Density Functional Theory |
| RMSD | Root-Mean-Square-Deviation |
| LUMO | Lowest Unoccupied Molecular Orbital |
| HOMO | Highest Occupied Molecular Orbital |
References
- Panda, S.S.; Katz, H.E.; Tovar, J.D. Solid-state Electrical Applications of Protein and Peptide Based Nanomaterials. Chem. Soc. Rev. 2018, 47, 3640–3658. [Google Scholar] [CrossRef]
- Chi, Q.; Farver, O.; Ulstrup, J. Long-Range Protein Electron Transfer Observed at the Single-Molecule Level: In Situ Mapping of Redox-Gated Tunneling Resonance. Proc. Natl. Acad. Sci. USA 2005, 102, 16203–16208. [Google Scholar] [CrossRef]
- Ortega, M.; Vilhena, J.G.; Zotti, L.A.; Díez-Pérez, I.; Cuevas, J.C.; Pérez, R. Tuning Structure and Dynamics of Blue Copper Azurin Junctions via Single Amino-Acid Mutations. Biomolecules 2019, 9, 611. [Google Scholar] [CrossRef]
- Bostick, C.D.; Mukhopadhyay, S.; Pecht, I.; Sheves, M.; Cahen, D.; Lederman, D. Protein Bioelectronics: A Review of what We Do and Do not Know. Rep. Prog. Phys. 2018, 81, 026601. [Google Scholar] [CrossRef] [PubMed]
- Ing, N.L.; El-Naggar, M.Y.; Hochbaum, A.I. Going the distance: Long-range conductivity in protein and peptide bioelectronic materials. J. Phys. Chem. B 2018, 122, 10403–10423. [Google Scholar] [CrossRef]
- Alessandrini, A.; Facci, P. Electron Transfer in Nanobiodevices. Eur. Polym. J. 2016, 83, 450–466. [Google Scholar] [CrossRef]
- Eleonora, A.; Reggiani, L.; Pousset, J. Proteotronics: Electronic devices based on proteins. In Sensors; Springer: New York, NY, USA, 2015; pp. 3–7. [Google Scholar]
- Fereiro, J.A.; Kayser, B.; Romero-Muñiz, C.; Vilan, A.; Dolgikh, D.A.; Chertkova, R.V.; Cuevas, J.C.; Zotti, L.A.; Pecht, I.; Sheves, M.; et al. A Solid-State Protein Junction Serves as a Bias-Induced Current Switch. Angew. Chem. Int. Ed. 2019, 58, 11852–11859. [Google Scholar] [CrossRef]
- Futera, Z.; Ide, I.; Kayser, B.; Garg, K.; Jiang, X.; van Wonderen, J.H.; Butt, J.N.; Ishii, H.; Pecht, I.; Sheves, M.; et al. Coherent Electron Transport across a 3 nm Bioelectronic Junction Made of Multi-Heme Proteins. J. Phys. Chem. Lett. 2020, 11, 9766–9774. [Google Scholar] [CrossRef]
- Ruiz, M.P.; Aragonès, A.C.; Camarero, N.; Vilhena, J.G.; Ortega, M.; Zotti, L.A.; Pérez, R.; Cuevas, J.C.; Gorostiza, P.; Díez-Pérez, I. Bioengineering a Single-Protein Junction. J. Am. Chem. Soc. 2017, 139, 15337–15346. [Google Scholar] [CrossRef]
- Fereiro, J.A.; Yu, X.; Pecht, I.; Sheves, M.; Cuevas, J.C.; Cahen, D. Tunneling Explains Efficient Electron Transport via Protein Junctions. Proc. Natl. Acad. Sci. USA 2018, 115, E4577. [Google Scholar] [CrossRef] [PubMed]
- Zotti, L.A.; Bednarz, B.; Hurtado-Gallego, J.; Cabosart, D.; Rubio-Bollinger, G.; Agrait, N.; van der Zant, H.S.J. Can One Define the Conductance of Amino Acids? Biomolecules 2019, 9, 580. [Google Scholar] [CrossRef] [PubMed]
- Zotti, L.A.; Cuevas, J.C. Electron Transport Through Homopeptides: Are They Really Good Conductors? ACS Omega 2018, 3, 3778–3785. [Google Scholar] [CrossRef] [PubMed]
- Schosser, W.M.; Zotti, L.A.; Cuevas, J.C.; Pauly, F. Doping hepta-alanine with tryptophan: A theoretical study of its effect on the electrical conductance of peptide-based single-molecule junctions. J. Chem. Phys. 2019, 150, 174705. [Google Scholar] [CrossRef] [PubMed]
- Amdursky, N.; Sepunaru, L.; Raichlin, S.; Pecht, I.; Sheves, M.; Cahen, D. Electron Transfer Proteins as Electronic Conductors: Significance of the Metal and Its Binding Site in the Blue Cu Protein, Azurin. Adv. Sci. 2015, 2, 1400026. [Google Scholar] [CrossRef]
- Liu, Z.F.; Wei, S.; Yoon, H.; Adak, O.; Ponce, I.; Jiang, Y.; Jang, W.D.; Campos, L.M.; Venkataraman, L.; Neaton, J.B. Control of Single-Molecule Junction Conductance of Porphyrins via a Transition-Metal Center. Nano Lett. 2014, 14, 5365–5370. [Google Scholar] [CrossRef]
- Mahapatro, A.K.; Ying, J.; Ren, T.; Janes, D.B. Electronic Transport through Ruthenium-Based Redox-Active Molecules in Metal-Molecule-Metal Nanogap Junctions. Nano Lett. 2008, 8, 2131–2136. [Google Scholar] [CrossRef]
- Zotti, L.A.; Leary, E.; Soriano, M.; Cuevas, J.C.; Palacios, J.J. A Molecular Platinum Cluster Junction: A Single-Molecule Switch. J. Am. Chem. Soc. 2013, 135, 2052–2055. [Google Scholar] [CrossRef]
- McLaughlin, M.P.; Retegan, M.; Bill, E.; Payne, T.M.; Shafaat, H.S.; Peña, S.; Sudhamsu, J.; Ensign, A.A.; Crane, B.R.; Neese, F.; et al. Azurin as a Protein Scaffold for a Low-coordinate Nonheme Iron Site with a Small-molecule Binding Pocket. J. Am. Chem. Soc. 2012, 134, 19746–19757. [Google Scholar] [CrossRef]
- Rajapandian, V.; Hakkim, V.; Subramanian, V. Molecular Dynamics Studies on Native, Loop-Contracted, and Metal Ion-Substituted Azurins. J. Phys. Chem. B 2010, 114, 8474–8486. [Google Scholar] [CrossRef]
- Solomon, E.I.; Szilagyi, R.K.; DeBeer George, S.; Basumallick, L. Electronic Structures of Metal Sites in Proteins and Models: Contributions to Function in Blue Copper Proteins. Chem. Rev. 2004, 104, 419. [Google Scholar] [CrossRef]
- Ron, I.; Sepunaru, L.; Itzhakov, S.; Belenkova, T.; Friedman, N.; Pecht, I.; Sheves, M.; Cahen, D. Proteins as Electronic Materials: Electron Transport through Solid-State Protein Monolayer Junctions. J. Am. Chem. Soc. 2010, 132, 4131–4140. [Google Scholar] [CrossRef]
- Sepunaru, L.; Pecht, I.; Sheves, M.; Cahen, D. Solid-State Electron Transport across Azurin: From a Temperature-Independent to a Temperature-Activated Mechanism. J. Am. Chem. Soc. 2011, 133, 2421–2423. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Lovrincic, R.; Sepunaru, L.; Li, W.; Vilan, A.; Pecht, I.; Sheves, M.; Cahen, D. Insights into Solid-State Electron Transport through Proteins from Inelastic Tunneling Spectroscopy: The Case of Azurin. ACS Nano 2015, 9, 9955–9963. [Google Scholar] [CrossRef] [PubMed]
- Fereiro, J.A.; Porat, G.; Bendikov, T.; Pecht, I.; Sheves, M.; Cahen, D. Protein Electronics: Chemical Modulation of Contacts Control Energy Level Alignment in Gold-Azurin-Gold Junctions. J. Am. Chem. Soc. 2018, 140, 13317–13326. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.S.; Pasula, R.R.; Lim, S.; Nijhuis, C.A. Long-Range Tunneling Processes across Ferritin-Based Junctions. Adv. Mater. 2016, 28, 1824–1830. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Karuppannan, S.K.; Guo, C.; Fereiro, J.A.; Bergren, A.; Mukundan, V.; Qiu, X.; Casta neda Ocampo, O.E.; Chen, X.; Chiechi, R.C.; et al. Solid-State Protein Junctions: Cross-Laboratory Study Shows Preservation of Mechanism at Varying Electronic Coupling. iScience 2020, 23, 101099. [Google Scholar] [CrossRef]
- Artés, J.M.; Díez-Pérez, I.; Gorostiza, P. Transistor-like Behavior of Single Metalloprotein Junctions. Nano Lett. 2012, 12, 2679–2684. [Google Scholar] [CrossRef]
- Artés, J.M.; López-Martínez, M.; Díez-Pérez, I.; Sanz, F.; Gorostiza, P. Conductance Switching in Single Wired Redox Proteins. Small 2014, 10, 2537–2541. [Google Scholar] [CrossRef]
- Li, W.; Sepunaru, L.; Amdursky, N.; Cohen, S.R.; Pecht, I.; Sheves, M.; Cahen, D. Temperature and Force Dependence of Nanoscale Electron Transport via the Cu Protein Azurin. ACS Nano 2012, 6, 10816–10824. [Google Scholar] [CrossRef]
- Baldacchini, C.; Bizzarri, A.R.; Cannistraro, S. Electron Transfer, Conduction and Biorecognition Properties of the Redox Metalloprotein Azurin Assembled onto Inorganic Substrates. Eur. Polym. J. 2016, 83, 407–427. [Google Scholar] [CrossRef]
- Kayser, B.; Fereiro, J.A.; Bhattacharyya, R.; Cohen, S.R.; Vilan, A.; Pecht, I.; Sheves, M.; Cahen, D. Solid-State Electron Transport via the Protein Azurin is Temperature-Independent Down to 4 K. J. Phys. Chem. Lett. 2020, 11, 144–151. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Davis, J.J.; Sansom, M.S.P.; Hung, A. Exploring the Electronic and Mechanical Properties of Protein Using Conducting Atomic Force Microscopy. J. Am. Chem. Soc. 2004, 126, 5601–5609. [Google Scholar] [CrossRef]
- Romero-Muñiz, C.; Ortega, M.; Vilhena, J.G.; Díez-Pérez, I.; Pérez, R.; Cuevas, J.C.; Zotti, L.A. Can Electron Transport through a Blue-Copper Azurin Be Coherent? An Ab Initio Study. J. Phys. Chem. C 2021, 125, 1693–1702. [Google Scholar] [CrossRef]
- Valianti, S.; Cuevas, J.C.; Skourtis, S.S. Charge-Transport Mechanisms in Azurin-Based Monolayer Junctions. J. Phys. Chem. C 2019, 123, 5907–5922. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Dutta, S.; Pecht, I.; Sheves, M.; Cahen, D. Conjugated Cofactor Enables Efficient Temperature-Independent Electronic Transport across 6 nm Long Halorhodopsin. J. Am. Chem. Soc. 2015, 137, 11226–11229. [Google Scholar] [CrossRef]
- Casta neda Ocampo, O.E.; Gordiichuk, P.; Catarci, S.; Gautier, D.A.; Herrmann, A.; Chiechi, R.C. Mechanism of Orientation-Dependent Asymmetric Charge Transport in Tunneling Junctions Comprising Photosystem I. J. Am. Chem. Soc. 2015, 137, 8419–8427. [Google Scholar] [CrossRef]
- Garg, K.; Ghosh, M.; Eliash, T.; van Wonderen, J.H.; Butt, J.N.; Shi, L.; Jiang, X.; Zdenek, F.; Blumberger, J.; Pecht, I.; et al. Direct Evidence for Heme-Assisted Solid-State Electronic Conduction in Multi-Heme c-Type Cytochromes. Chem. Sci. 2018, 9, 7304–7310. [Google Scholar] [CrossRef]
- Garg, K.; Raichlin, S.; Bendikov, T.; Pecht, I.; Sheves, M.; Cahen, D. Interface Electrostatics Dictates the Electron Transport via Bioelectronic Junctions. ACS Appl. Mater. Interfaces 2018, 10, 41599–41607. [Google Scholar] [CrossRef]
- Blaszak, J.A.; Ulrich, E.L.; Markley, J.L.; McMillin, D.R. High-resolution proton nuclear magnetic resonance studies of the nickel(II) derivative of azurin. Biochemistry 1982, 21, 6253–6258. [Google Scholar] [CrossRef]
- Czernuszewicz, R.S.; Fraczkiewicz, G.; Zareba, A.A. A Detailed Resonance Raman Spectrum of Nickel(II)-Substituted Pseudomonas aeruginosa Azurin. Inorg. Chem. 2005, 44, 5745–5752. [Google Scholar] [CrossRef]
- Jiménez, H.R.; Salgado, J.; Moratal, J.M.; Morgenstern-Badarau, I. EPR and Magnetic Susceptibility Studies of Cobalt(II)- and Nickel(II)-Substituted Azurins from Pseudomonas aeruginosa. Electronic Structure of the Active Sites. Inorg. Chem. 1996, 35, 2737–2741. [Google Scholar] [CrossRef]
- Nar, H.; Huber, R.; Messerschmidt, A.; Filippou, A.C.; Barth, M.; Jaquind, M.; van de Kamp, M.; Canters, G.W. Characterization and crystal structure of zinc azurin, a by-product of heterologous expression in Escherichia coli of Pseudomonas aeruginosa copper azurin. Eur. J. Biochem. 1992, 205, 1123–1129. [Google Scholar] [CrossRef] [PubMed]
- Bonander, N.; Vänngård, T.; Tsai, L.C.; Langer, V.; Nar, H.; Sjölin, L. The metal site of Pseudomonas aeruginosa azurin, revealed by a crystal structure determination of the co(II) derivative and co-EPR spectroscopy. Proteins Struct. Funct. Bioinf. 1997, 27, 385. [Google Scholar] [CrossRef]
- Moratal, J.M.; Romero, A.; Salgado, J.; Perales-Alarcón, A.; Jiménez, H.R. The Crystal Structure of Nickel(II)-Azurin. Eur. J. Biochem. 1995, 228, 653. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Nar, H.; Messerschmidt, A.; Huber, R.; van de Kamp, M.; Canters, G.W. Crystal Structure Analysis of Oxidized Pseudomonas Aeruginosa Azurin at pH 5.5 and pH 9.0: A pH-Induced Conformational Transition Involves a Peptide Bond Flip. J. Mol. Biol. 1991, 221, 765–772. [Google Scholar] [CrossRef]
- Gordon, J.C.; Myers, J.B.; Folta, T.; Shoja, V.; Heath, L.S.; Onufriev, A. H++: A Server for Estimating pKas and Adding Missing Hydrogens to Macromolecules. Nucleic Acids Res. 2005, 33, W368–W371. [Google Scholar] [CrossRef] [PubMed]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Simmerling, C.; Wang, J.; Duke, R.; Luo, R.; Walker, R.; Zhang, W.; Merz, K.; Roberts, B.; et al. AMBER 14; University of California: San Francisco, CA, USA, 2014; Available online: http://ambermd.org/ (accessed on 15 June 2018).
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef]
- Grand, S.L.; Götz, A.W.; Walker, R.C. SPFP: Speed without Compromise: A Mixed Precision Model for GPU Accelerated Molecular Dynamics Simulations. Comput. Phys. Commun. 2013, 184, 374–380. [Google Scholar] [CrossRef]
- Loncharich, R.J.; Brooks, B.R.; Pastor, R.W. Langevin dynamics of peptides: The frictional dependence of isomerization rates of N-acetylalanyl-N-methylamide. Biopolymers 1992, 32, 523. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally Optimized Atomic Orbitals for Large-Scale Electronic Structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical Atomic Basis Orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Romero-Mu niz, C.; Ortega, M.; Vilhena, J.G.; Díez-Pérez, I.; Cuevas, J.C.; Pérez, R.; Zotti, L.A. Ab Initio Electronic Structure Calculations of Entire Blue Copper Azurins. Phys. Chem. Chem. Phys. 2018, 20, 30392–30402. [Google Scholar] [CrossRef] [PubMed]
- Romero-Mu niz, C.; Ortega, M.; Vilhena, J.G.; Diéz-Pérez, I.; Cuevas, J.C.; Pérez, R.; Zotti, L.A. Mechanical Deformation and Electronic Structure of a Blue Copper Azurin in a Solid-State Junction. Biomolecules 2019, 9, 506. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Morrison, I.; Bylander, D.M.; Kleinman, L. Nonlocal Hermitian Norm-Conserving Vanderbilt Pseudopotential. Phys. Rev. B 1993, 47, 6728. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kerker, G.P. Efficient Iteration Scheme for Self-Consistent Pseudopotential Calculations. Phys. Rev. B 1981, 23, 3082–3084. [Google Scholar] [CrossRef]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Roe, D.R.; Cheatham, T.E. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Agam, Y.; Nandi, R.; Kaushansky, A.; Peskin, U.; Amdursky, N. The porphyrin ring rather than the metal ion dictates long-range electron transport across proteins suggesting coherence-assisted mechanism. Proc. Natl. Acad. Sci. USA 2020, 117, 32260–32266. [Google Scholar] [CrossRef] [PubMed]
- Jakobsen, S.; Kristensen, K.; Jensen, F. Electrostatic Potential of Insulin: Exploring the Limitations of Density Functional Theory and Force Field Methods. J. Chem. Theory Comput. 2013, 9, 3978–3985. [Google Scholar] [CrossRef]
- Zhao, Q.; Kulik, H.J. Where Does the Density Localize in the Solid State? divergent behavior for hybrids and DFT+ U. J. Chem. Theory Comput. 2018, 14, 670–683. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.L.; Gagliardi, L.; Truhlar, D.G. Self-Interaction Error in Density Functional Theory: An Appraisal. J. Phys. Chem. Lett. 2018, 9, 2353–2358. [Google Scholar] [CrossRef]
- Zotti, L.A.; Bürkle, M.; Pauly, F.; Lee, W.; Kim, K.; Jeong, W.; Asai, Y.; Reddy, P.; Cuevas, J.C. Heat dissipation and its relation to thermopower in single-molecule junctions. New J. Phys. 2014, 16, 015004. [Google Scholar] [CrossRef]
- Montes, E.; Vázquez, H. Role of the Binding Motifs in the Energy Level Alignment and Conductance of Amine-Gold Linked Molecular Junctions within DFT and DFT + Σ. Appl. Sci. 2021, 11, 802. [Google Scholar] [CrossRef]
- Garcia-Lastra, J.M.; Rostgaard, C.; Rubio, A.; Thygesen, K.S. Polarization-induced renormalization of molecular levels at metallic and semiconducting surfaces. Phys. Rev. B 2009, 80, 245427. [Google Scholar] [CrossRef]
- Rissner, F.; Natan, A.; Egger, D.A.; Hofmann, O.T.; Kronik, L.; Zojer, E. Dimensionality effects in the electronic structure of organic semiconductors consisting of polar repeat units. Org. Electron. 2012, 13, 3165–3176. [Google Scholar] [CrossRef] [PubMed][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero-Muñiz, C.; Ortega, M.; Vilhena, J.G.; Pérez, R.; Cuevas, J.C.; Zotti, L.A. The Role of Metal Ions in the Electron Transport through Azurin-Based Junctions. Appl. Sci. 2021, 11, 3732. https://doi.org/10.3390/app11093732
Romero-Muñiz C, Ortega M, Vilhena JG, Pérez R, Cuevas JC, Zotti LA. The Role of Metal Ions in the Electron Transport through Azurin-Based Junctions. Applied Sciences. 2021; 11(9):3732. https://doi.org/10.3390/app11093732
Chicago/Turabian StyleRomero-Muñiz, Carlos, María Ortega, Jose Guilherme Vilhena, Rubén Pérez, Juan Carlos Cuevas, and Linda A. Zotti. 2021. "The Role of Metal Ions in the Electron Transport through Azurin-Based Junctions" Applied Sciences 11, no. 9: 3732. https://doi.org/10.3390/app11093732
APA StyleRomero-Muñiz, C., Ortega, M., Vilhena, J. G., Pérez, R., Cuevas, J. C., & Zotti, L. A. (2021). The Role of Metal Ions in the Electron Transport through Azurin-Based Junctions. Applied Sciences, 11(9), 3732. https://doi.org/10.3390/app11093732







