Detecting Change between Urban Road Environments along a Route Based on Static Road Object Occurrences
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Car-Based Collection of Static Road Object Data from Various Urban Road Environments
 (“No stopping” (NS)),
(“No stopping” (NS)),  , (“Parking lot” (PL)),
, (“Parking lot” (PL)),  (“Give way” (GW)), and
(“Give way” (GW)), and  (“Max speed 30 km/h” (SL)) TSs were used herein as a priori estimates of the reference rates for the marked Poisson processes. These rates are given in Table 1 for routes within Dt and within Res areas.
(“Max speed 30 km/h” (SL)) TSs were used herein as a priori estimates of the reference rates for the marked Poisson processes. These rates are given in Table 1 for routes within Dt and within Res areas.2.2. Mathematical Models and Methods
2.2.1. Modelling TS Occurrences within a Given Urban Road Environment
2.2.2. Modelling TS Occurrences in a Neighboring Urban Road Environment
2.2.3. Modelling TS Occurrences over Two Neighboring Urban Road Environments
2.2.4. Detecting Change between Urban Road Environments and Locating the Change Point
2.2.5. Basic Properties of Functions and
3. Results
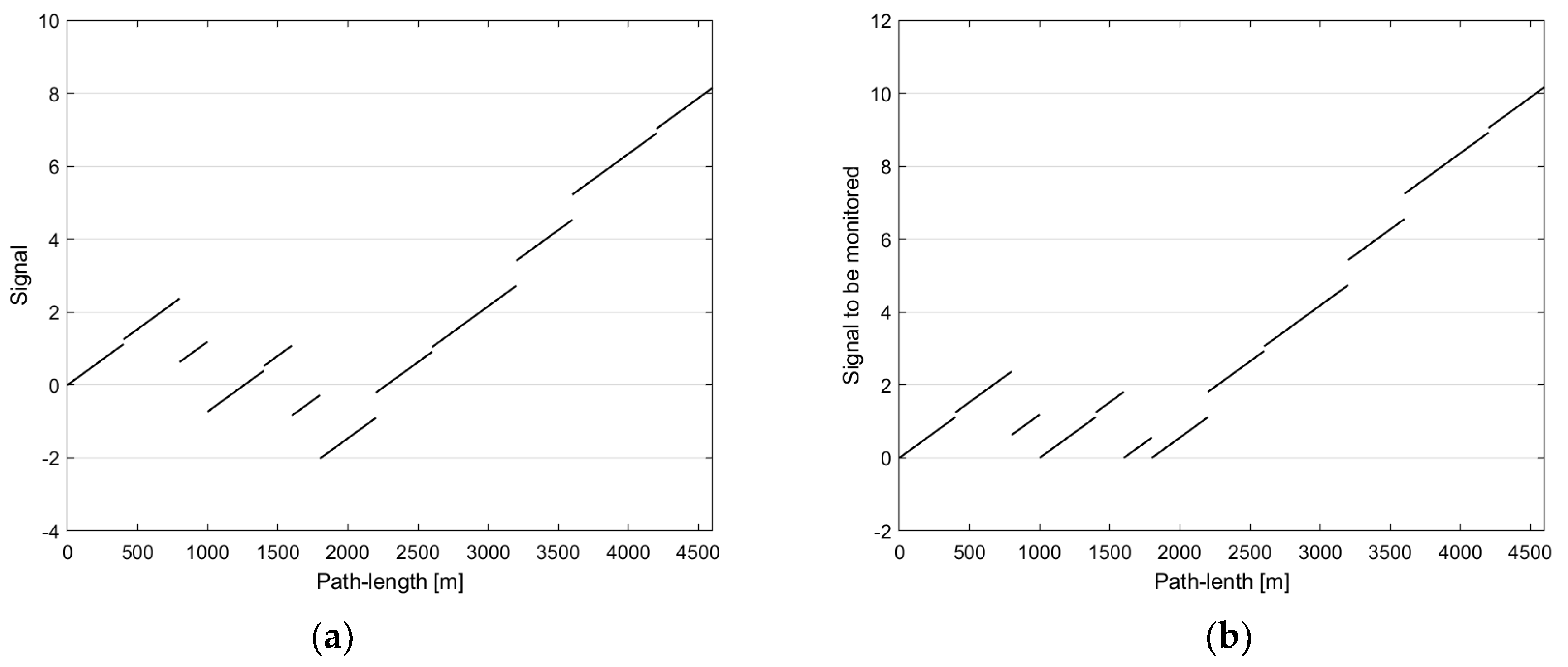
3.1. Examples
- a RET transition from a Dt to a Res area (denoted by Dt → Res), if the virtual journey is taken from the left, and
- a RET transition from a Res to a Dt area (denoted by Res → Dt), if the journey is taken from the right.
3.1.1. Example No. 1: A Dt → Res Change Detector Applied to a Homologous RET Transition
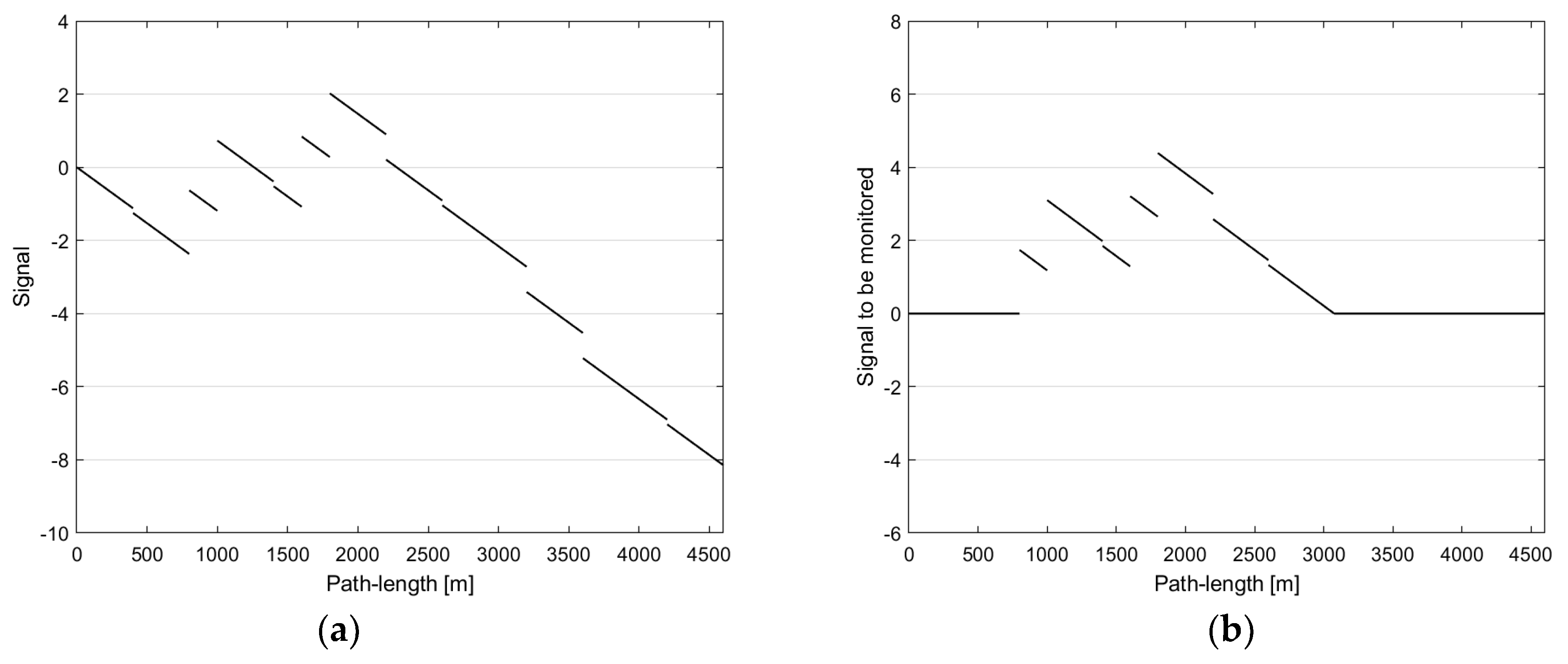
3.1.2. Example No. 2: A Res → Dt Change Detector Applied to a Homologous RET Transition
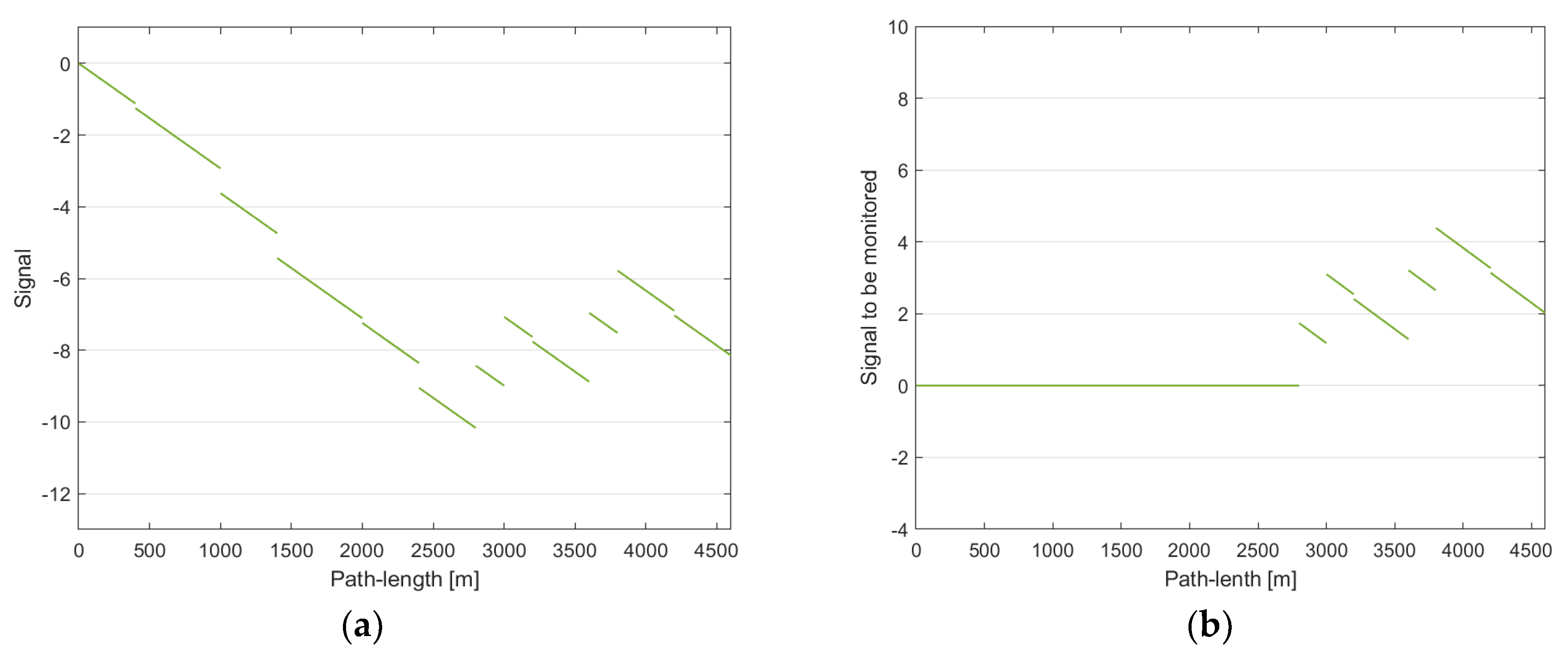
3.2. Further Examples
3.2.1. Example No. 3: A Res → Dt Change Detector Applied to a Dt → Res Transition
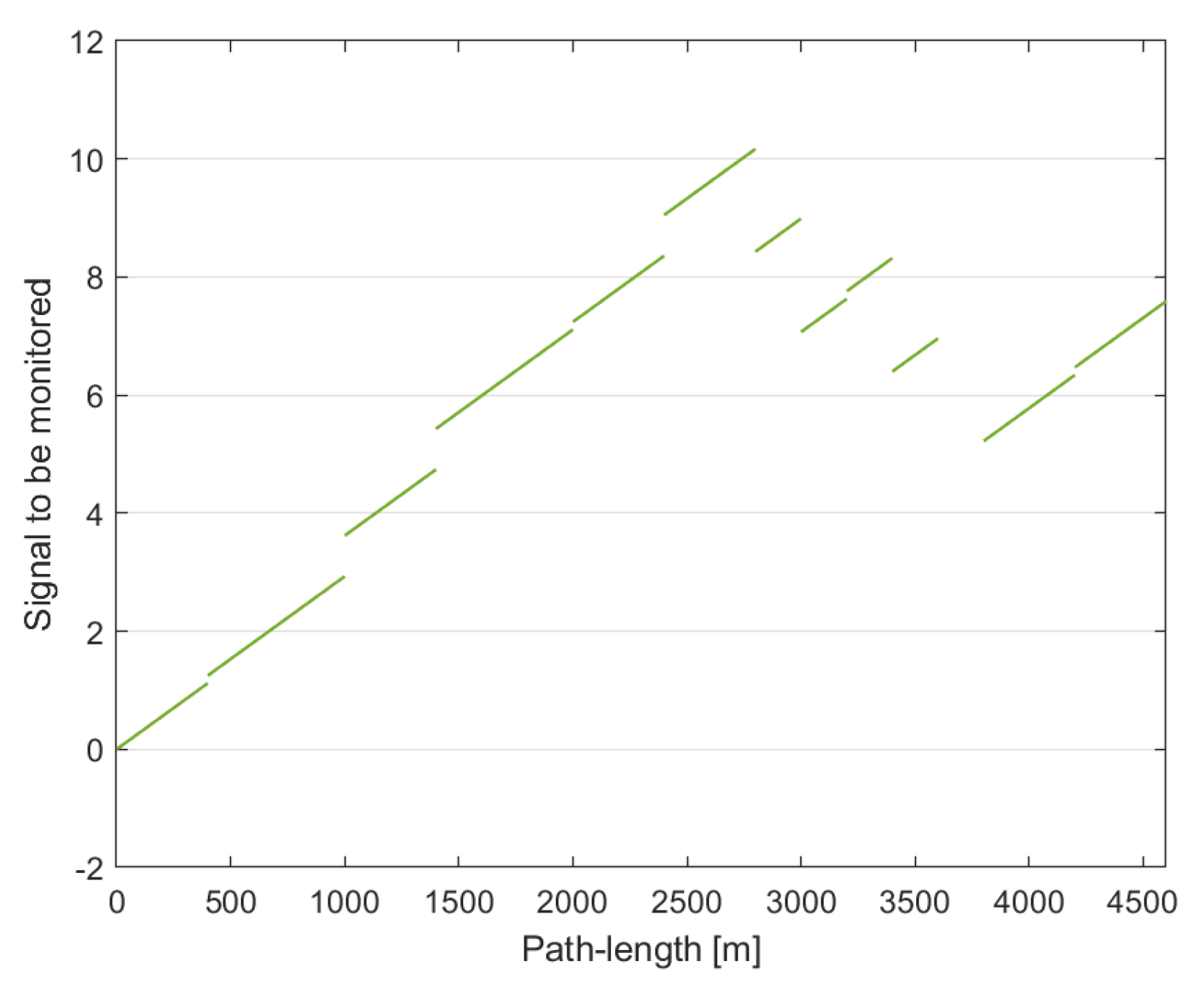
3.2.2. Example No. 4: A Dt → Res Change Detector Applied to a Res → Dt Transition
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Theeuwes, J. Self-explaining roads: Subjective categorization of road environments. In Vision in Vehicles VI; Gale, A., Brown, I.D., Taylor, S.P., Haslegrave, C.M., Eds.; Elsevier: Amsterdam, The Netherlands, 1998; pp. 279–287. [Google Scholar]
- Charlton, S.G.; Mackie, H.W.; Baas, P.H.; Hay, K.; Menezes, M.; Dixon, C. Using endemic road features to create self-explaining roads and reduce vehicle speeds. Accid. Anal. Prev. 2010, 42, 1989–1998. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, Y.; Lin, K. Quantifying the effects of visual road information on drivers’ speed choices to promote self-explaining plaining roads. Int. J. Environ. Res. Public Health 2020, 17, 2437. [Google Scholar] [CrossRef] [PubMed]
- Saha, D.; Dumbaugh, E.; Merlin, L.A. A conceptual framework to understand the role of built environment on traffic safety. J. Saf. Res. 2020, 75, 41–50. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Zhao, X.; Rong, J.; Ma, J. Experimental research on the effectiveness of speed reduction markings based on driving simulation: A case study. Accid. Anal. Prev. 2013, 60, 211–218. [Google Scholar] [CrossRef]
- Banach, M.; Długosz, R. Techniques to facilitate the use of V2I communication system as support for traffic sign recognition algorithms. In Proceedings of the 24th International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 26–29 August 2019; pp. 308–313. [Google Scholar]
- Ahangar, M.N.; Ahmed, Q.Z.; Khan, F.A.; Hafeez, M. A survey of autonomous vehicles: Enabling communication technologies and challenges. Sensors 2021, 21, 706. [Google Scholar] [CrossRef] [PubMed]
- Popescu, O.; Sha-Mohammad, S.; Abdel-Wahab, H.; Popescu, D.C.; El-Tawab, S. Automatic incident detection in intelligent transportation systems using aggregation of traffic parameters collected through V2I communications. IEEE Intell. Transp. Syst. Mag. 2017, 9, 64–75. [Google Scholar] [CrossRef]
- Sattar, F.; Karray, F.; Kamel, M.; Nassar, L.; Golestan, K. Recent advances on context-awareness and data/information fusion in ITS. Int. J. Intell. Transp. Syst. Res. 2016, 14, 1–19. [Google Scholar] [CrossRef]
- Global Navigation Satellite System (GNSS) Devices per Capita Worldwide 2019–2029. Available online: https://www.statista.com/statistics/1174568/gnss-devices-per-capita-worldwide/#statisticContainer (accessed on 21 March 2021).
- Reid, T.G.; Chan, B.; Goel, A.; Gunning, K.; Manning, B.; Martin, J.; Tarantino, P. Satellite navigation for the age of autonomy. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium, Portland, OR, USA, 20–23 April 2020; pp. 342–352. [Google Scholar]
- Schmidt, D.; Radke, K.; Camtepe, S.; Foo, E.; Ren, M. A survey and analysis of the GNSS spoofing threat and countermeasures. ACM Comput. Surv. 2016, 48, 64. [Google Scholar] [CrossRef]
- Welzel, A.; Reisdorf, P.; Wanielik, G. Improving urban vehicle localization with traffic sign recognition. In Proceedings of the 18th IEEE International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 2728–2732. [Google Scholar]
- The Traffic Safety Problem in Urban Areas. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.572.9092&rep=rep1&type=pdf (accessed on 9 December 2020).
- Wechsler, K.; Drescher, U.; Janouch, C.; Haeger, M.; Voelcker-Rehage, C.; Bock, O. Multitasking during simulated car driving: A comparison of young and older persons. Front. Psychol. 2018, 9, 910–921. [Google Scholar] [CrossRef]
- Faure, V.; Lobjois, R.; Benguigui, N. The effects of driving environment complexity and dual tasking on drivers’ mental workload and eye blink behavior. Transp. Res. Part F Traffic Psychol. Behav. 2016, 40, 78–90. [Google Scholar] [CrossRef]
- Payyanadan, R.P.; Lee, J.D.; Grepo, L.C. Challenges for older drivers in urban, suburban, and rural settings. Geriatrics 2018, 3, 14. [Google Scholar] [CrossRef]
- Tawari, A.; Sivaraman, S.; Trivedi, M.M.; Shannon, T.; Tippelhofer, M. Looking-in and looking-out vision for urban intelligent assistance: Estimation of driver attentive state and dynamic surround for safe merging and braking. In Proceedings of the IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 115–120. [Google Scholar]
- Stapel, J.; El Hassnaoui, M.; Happee, R. Measuring driver perception: Combining eye-tracking and automated road scene perception. Hum. Factors. 2020. [Google Scholar] [CrossRef]
- Tang, R.; Jiang, Z. Driver’s perception model in driving assist. In Proceedings of the IEEE 20th International Conference on Software Quality, Reliability and Security Companion, Macau, China, 11–14 December 2020; pp. 237–240. [Google Scholar]
- Rudin-Brown, C.M.; Edquist, J.; Lenne, M.G. Effects of driving experience and sensation-seeking on drivers’ adaptation to road environment complexity. Saf. Sci. 2014, 62, 121–129. [Google Scholar] [CrossRef]
- Lin, H.; Gao, J.; Zhou, Y.; Lu, G.; Ye, M.; Zhang, C.; Liu, L.; Yang, R. Semantic decomposition and reconstruction of residential scenes from LiDAR data. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, L.; Chen, Y.; Wu, Y.; Li, M. Building point detection from vehicle-borne LiDAR data based on voxel group and horizontal hollow analysis. Remote Sens. 2016, 8, 419. [Google Scholar] [CrossRef]
- Jeong, J.; Cho, Y.; Shin, Y.-S.; Roh, H.; Kim, A. Complex urban dataset with multi-level sensors from highly diverse urban environments. Int. J. Rob. Res. 2019, 38, 642–657. [Google Scholar] [CrossRef]
- Fazekas, Z.; Balázs, G.; Gerencsér, L.; Gáspár, P. Inferring the actual urban road environment from traffic sign data using a minimum description length approach. Transp. Res. Proc. 2017, 27, 516–523. [Google Scholar] [CrossRef]
- Fazekas, Z.; Balázs, G.; Gáspár, P. ANN-based classification of urban road environments from traffic sign and crossroad data. Acta Polytech. Hung. 2018, 15, 83–100. [Google Scholar]
- SAFESPOT Final Report 2010. Available online: http://www.safespot-eu.org/documents/D8.1.1_Final_Report_-_Public_v1.0.pdf (accessed on 22 March 2021).
- Map Features. Available online: https://wiki.openstreetmap.org/wiki/Map_features (accessed on 8 April 2021).
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]
- Kastner, R.; Michalke, T.; Adamy, J.; Fritsch, J.; Goerick, C. Task-based environment interpretation and system architecture for next generation ADAS. IEEE Trans. Intell. Transp. Syst. 2011, 3, 20–33. [Google Scholar] [CrossRef]
- Sindhu, O.S.S.V.; Victer, P.P. Computer vision model for traffic sign recognition and detection: A survey. In Proceedings of the International Conference on Communications and Cyber Physical Engineering, Hyderabad, India, 24–25 January 2018; pp. 679–690. [Google Scholar]
- Veronese, L.P.; Badue, C.; Cheein, F.A.; Guivant, J.; De Souza, A.F. A single sensor system for mapping in GNSS-denied environments. Cogn. Syst. Res. 2019, 56, 246–261. [Google Scholar] [CrossRef]
- Lin, C.C.; Wang, M.S. Road sign recognition with fuzzy adaptive pre-processing models. Sensors 2012, 12, 6415–6433. [Google Scholar] [CrossRef]
- Kim, T.; Park, T.-H. Extended Kalman Filter (EKF) design for vehicle position tracking using reliability function of Radar and Lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef]
- Akhlaq, M.; Sheltami, T.R.; Helgeson, B.; Shakshuki, E.M. Designing an integrated driver assistance system using image sensors. J. Intell. Manuf. 2012, 23, 2109–2132. [Google Scholar] [CrossRef]
- Belbachir, A. An embedded testbed architecture to evaluate autonomous car driving. Intell. Serv. Robot. 2017, 10, 109–119. [Google Scholar] [CrossRef]
- Manual for Streets, Department for Transport and Ministry of Housing, Communities & Local Government, UK, 29 March 2007. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/341513/pdfmanforstreets.pdf (accessed on 22 March 2021).
- Roads 2018. Available online: https://ec.europa.eu/transport/road_safety/sites/roadsafety/files/pdf/ersosynthesis2018-roads.pdf (accessed on 22 March 2021).
- Kingman, J.F.C. Poisson processes. In Encyclopedia of Biostatistics; Armitage, P., Colton, T., Eds.; Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Poor, H.V.; Hadjiliadis, O. Quickest Detection; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Tartakovsky, A.; Nikiforov, I.; Basseville, M. Sequential Analysis: Hypothesis Testing and Change Detection; Chapman and Hall/CRC: New York, NY, USA, 2014. [Google Scholar]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Hinkley, D.V. Inference about the change-point in a sequence of random variables. Biometrika 1970, 57, 1–17. [Google Scholar] [CrossRef]
- Gerencsér, L.; Prosdocimi, C. Input-output properties of the Page-Hinkley detector. Syst. Control Lett. 2011, 60, 486–491. [Google Scholar] [CrossRef]
- Rodrigues, J.; Folgado, D.; Belo, D.; Gamboa, H. SSTS: A syntactic tool for pattern search on time series. Inf. Process. Manag. 2019, 56, 61–76. [Google Scholar] [CrossRef]
| TS Type | Abbeviation | Index | Expected Number of Occurrences per km in Dt | Expected Number of Occurrences per km in Res Areas | Natural Logarithm of the Rate-Ratio | Characteristic to |
|---|---|---|---|---|---|---|
 | NS | 1 | 2.00 | 0.35 | 1.74 | Dt |
 | PL | 2 | 1.70 | 0.25 | 1.92 | Dt |
 | GW | 3 | 0.70 | 0.80 | −0.13 | Res |
 | SL | 4 | 0.20 | 0.40 | −0.69 | Res |
| Any | 4.60 | 1.80 | Dt |
| —— |  | —— |  | — |  | —— |  | — |  | — |  | —— |  | ———— |  | ——— |  | —— |  | ——— |  | —— |
| → | 1 | 2 | ||||||||||||||||||||
| → | 1 | 2 | ||||||||||||||||||||
| → | 1 | 2 | 3 | 4 | ||||||||||||||||||
| → | 1 | 2 | 3 | |||||||||||||||||||
| 2 | 1 | ← | ||||||||||||||||||||
| 2 | 1 | ← | ||||||||||||||||||||
| 4 | 3 | 2 | 1 | ← | ||||||||||||||||||
| 3 | 2 | 1 | ← |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fazekas, Z.; Gerencsér, L.; Gáspár, P. Detecting Change between Urban Road Environments along a Route Based on Static Road Object Occurrences. Appl. Sci. 2021, 11, 3666. https://doi.org/10.3390/app11083666
Fazekas Z, Gerencsér L, Gáspár P. Detecting Change between Urban Road Environments along a Route Based on Static Road Object Occurrences. Applied Sciences. 2021; 11(8):3666. https://doi.org/10.3390/app11083666
Chicago/Turabian StyleFazekas, Zoltán, László Gerencsér, and Péter Gáspár. 2021. "Detecting Change between Urban Road Environments along a Route Based on Static Road Object Occurrences" Applied Sciences 11, no. 8: 3666. https://doi.org/10.3390/app11083666
APA StyleFazekas, Z., Gerencsér, L., & Gáspár, P. (2021). Detecting Change between Urban Road Environments along a Route Based on Static Road Object Occurrences. Applied Sciences, 11(8), 3666. https://doi.org/10.3390/app11083666







