The Investigation on the Flow Distortion Effect of Header to Guarantee the Measurement Accuracy of the Ultrasonic Gas Flowmeter
Abstract
Featured Application
Abstract
1. Introduction
2. The Experiment Facilities
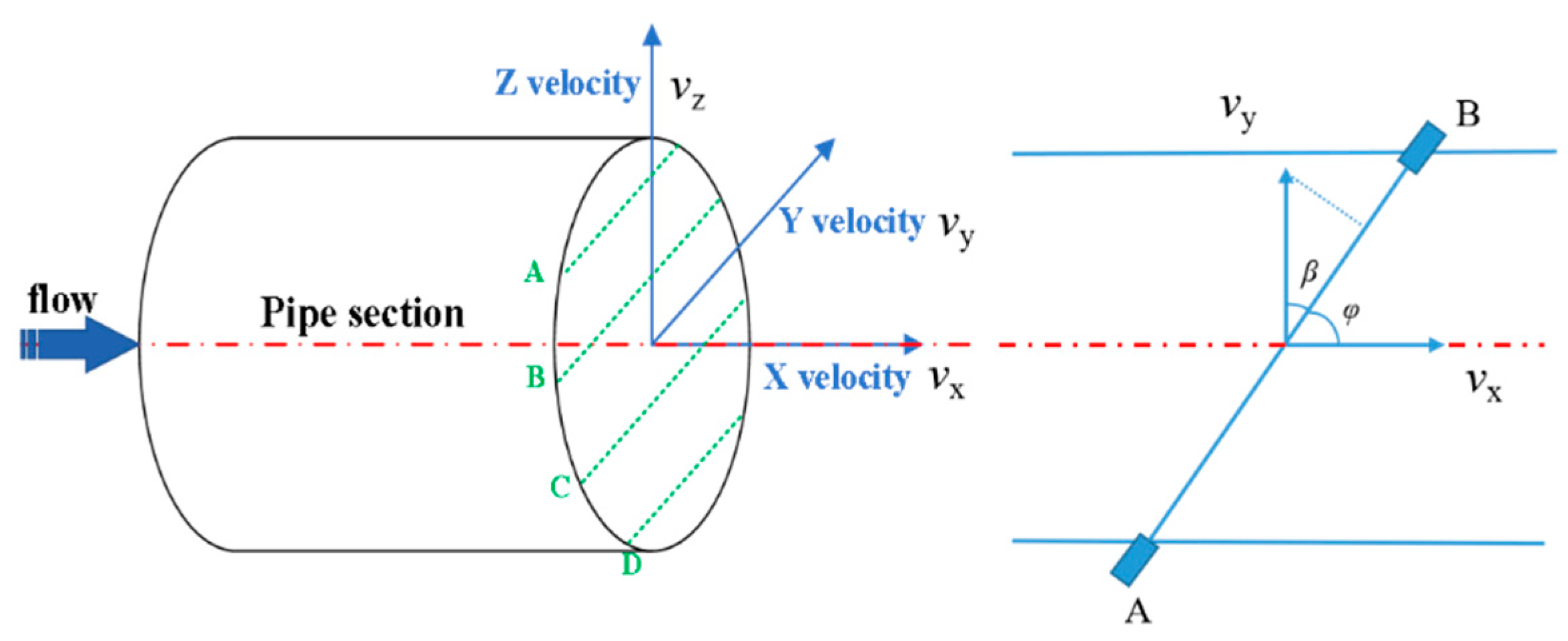
2.1. The Meter under Test
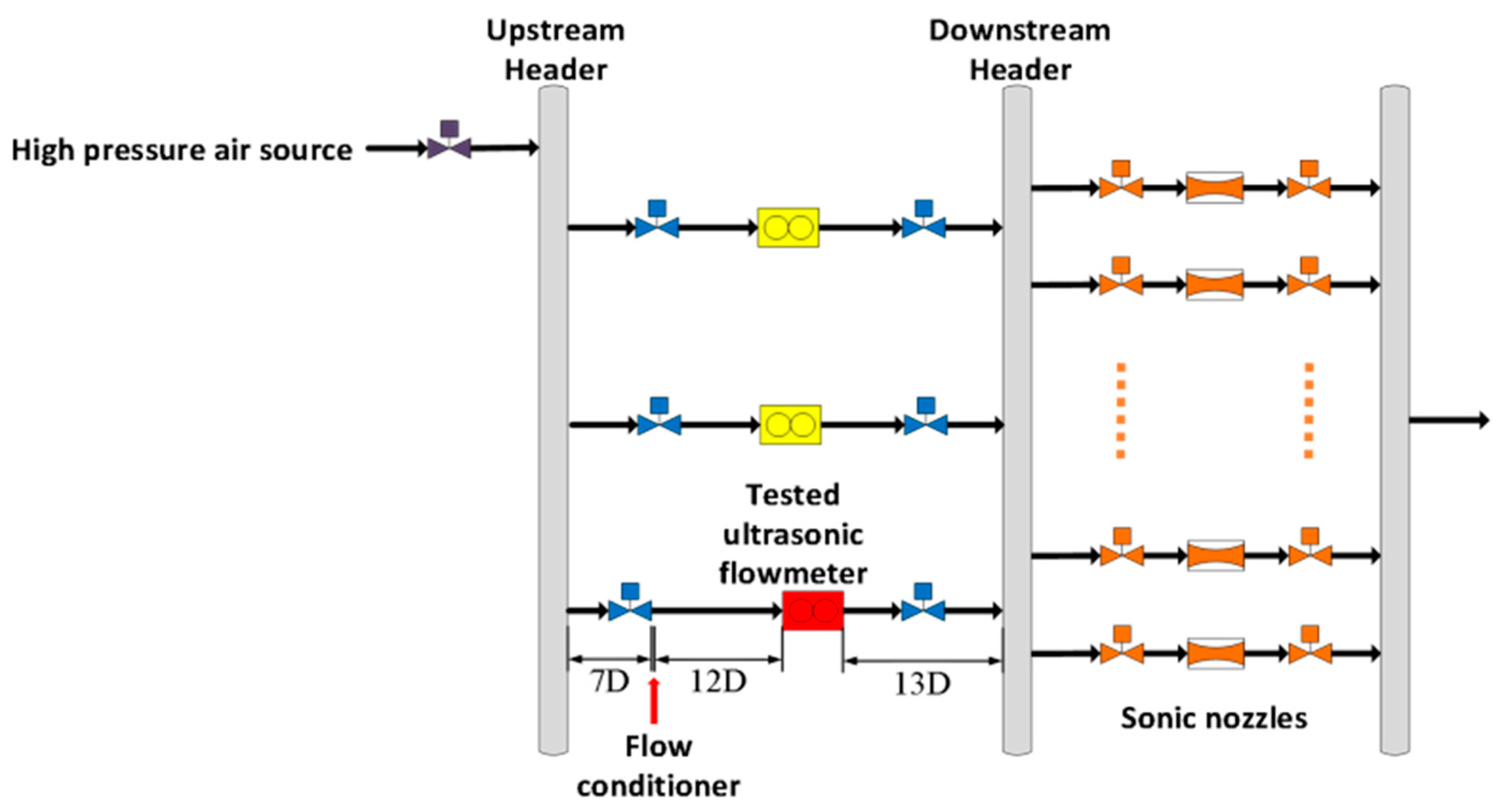
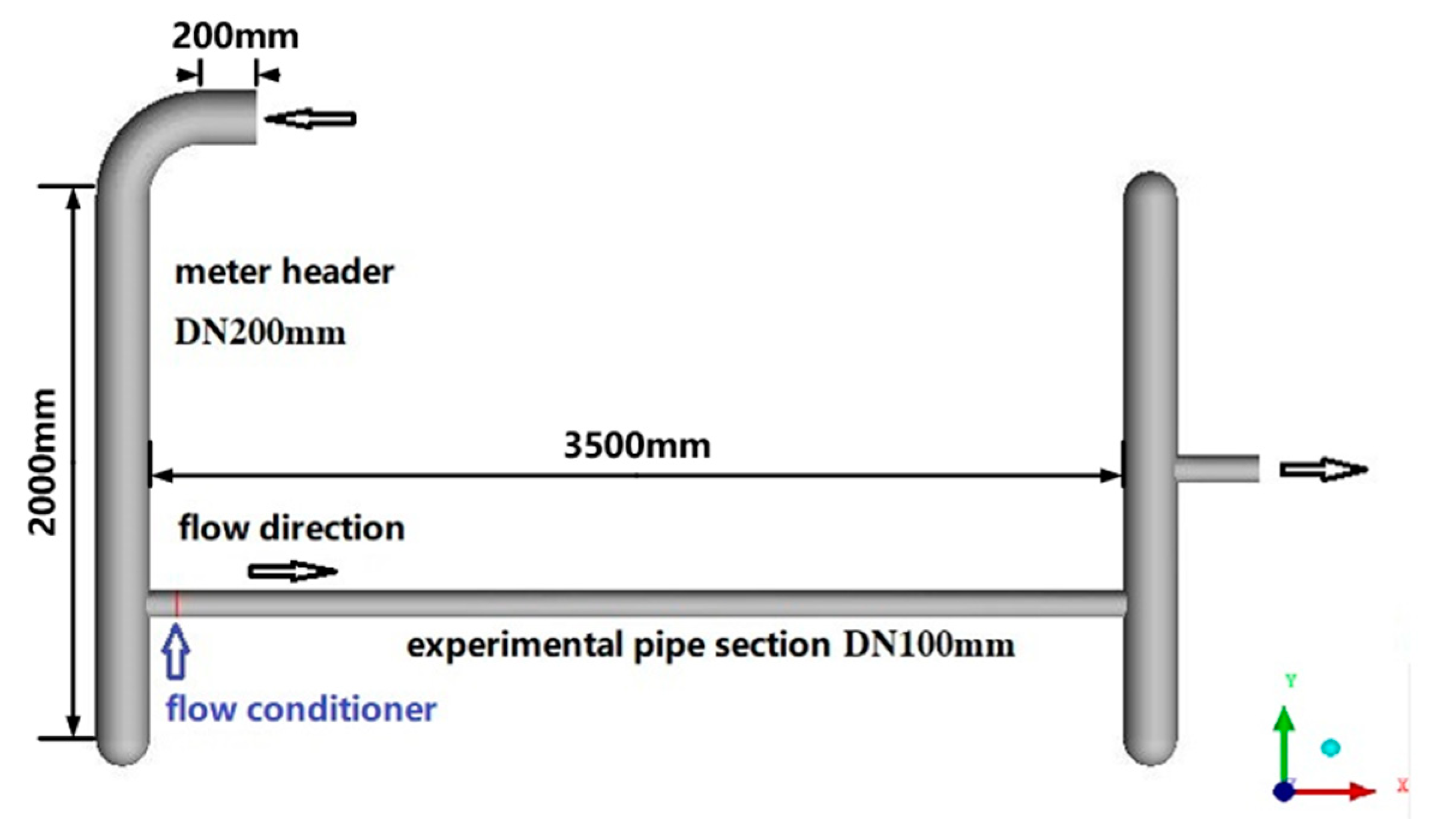
2.2. The Test Facility
- ➢
- ➢
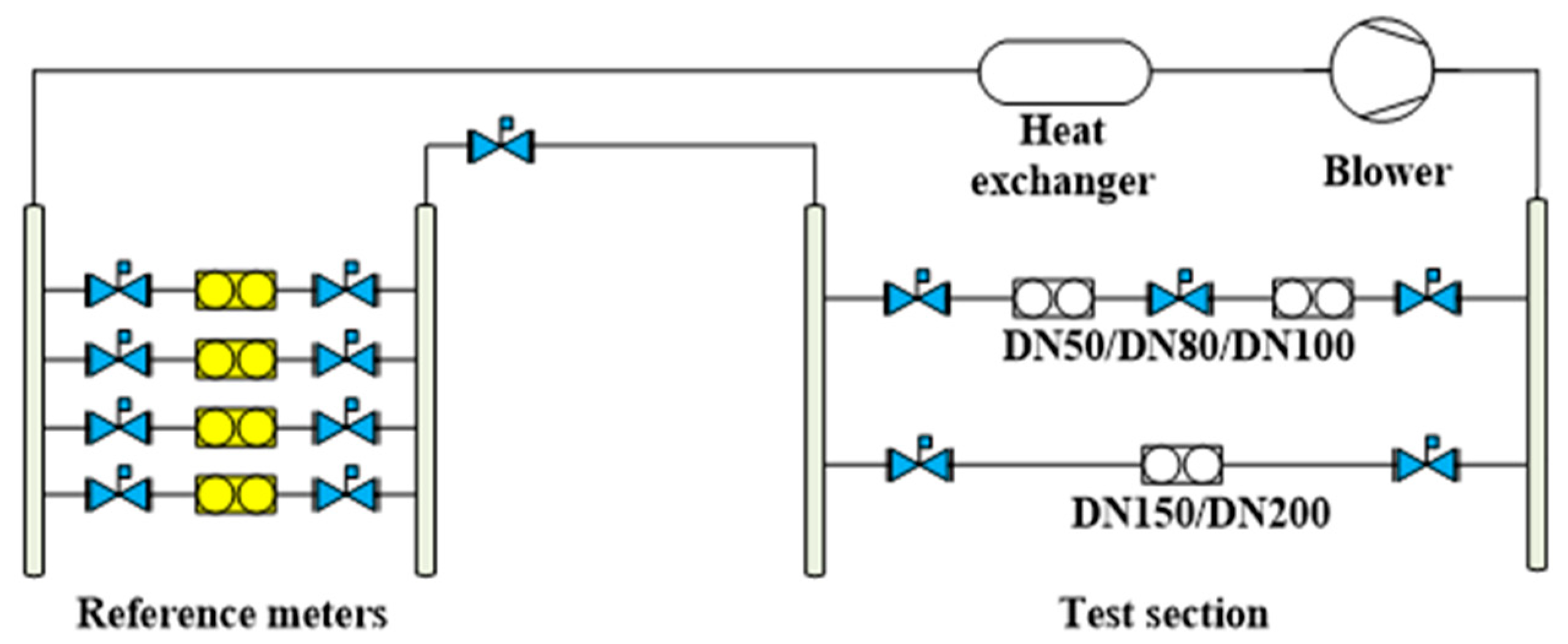
- For the close loop working standard device (CL device), there were four turbine flowmeters used as the reference meters, as shown in Figure 4. The high-pressure gas was recirculated in the standard device, which was driven by the blower and the temperature was controlled by the heat exchanger. The reference meters were traceable to the sonic nozzle secondary standard device. The maximum flowrate could be 1300 m3/h with the best measurement capabilities 0.18% (k = 2) [38].
- ➢
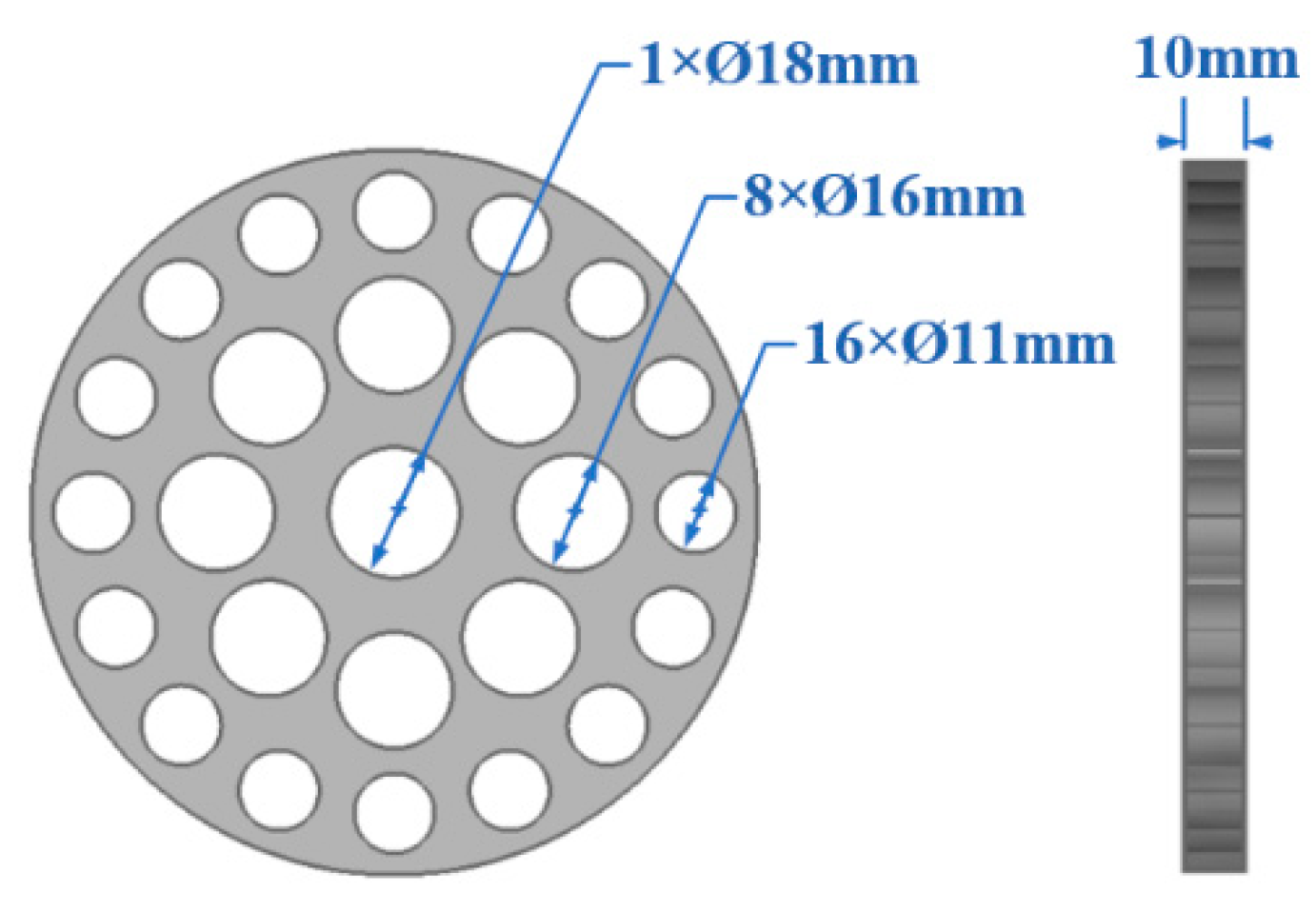
- The 36D upstream pipe length with an orifice plate flow conditioner (FC) as shown in Figure 5, which was conducted in the CL device;
- ➢
- The 19D upstream pipe length with an FC, which was conducted in the SN device;
- ➢
- The 19D upstream pipe length, which was also conducted in the SN device but without FC.
3. The Experiment Results
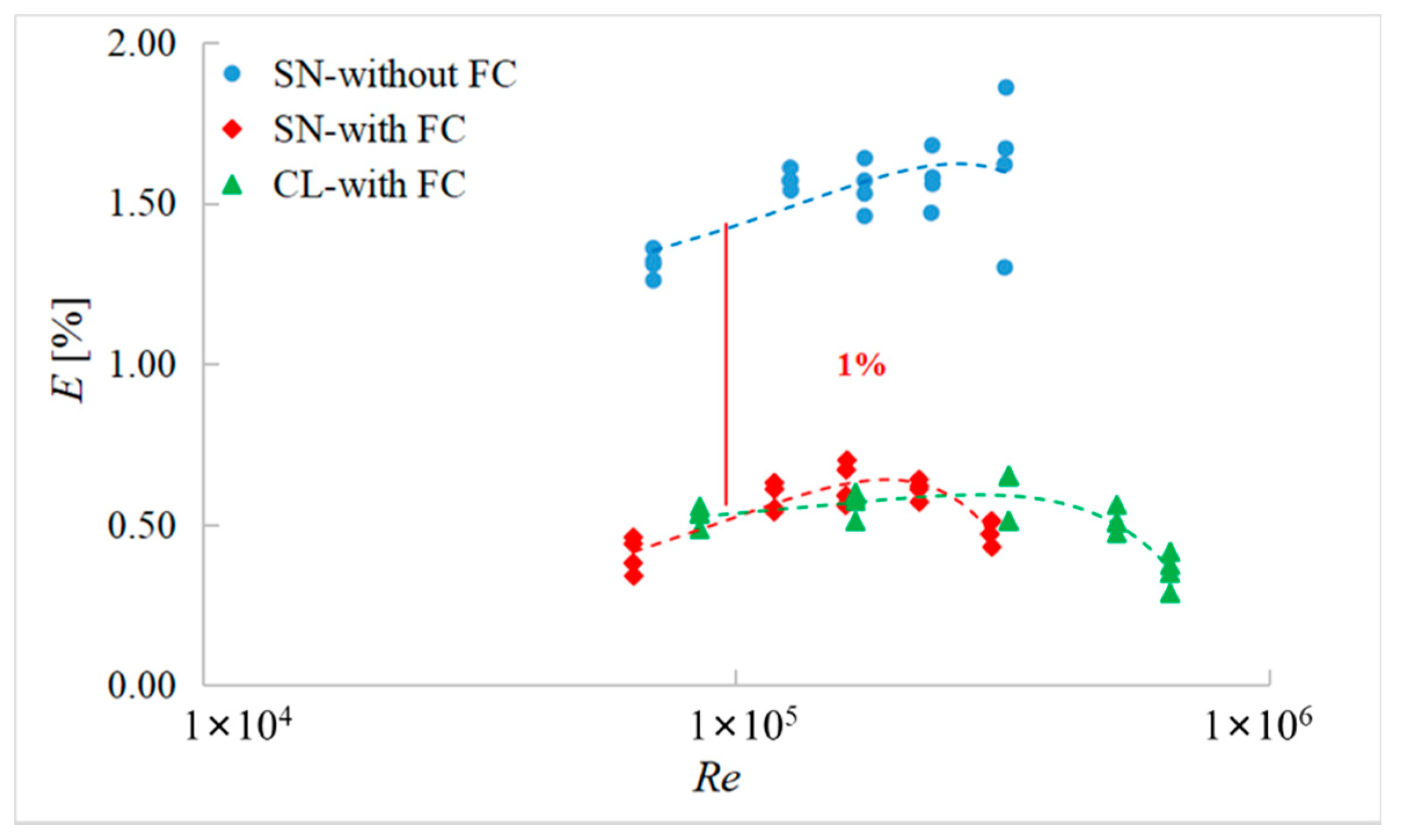
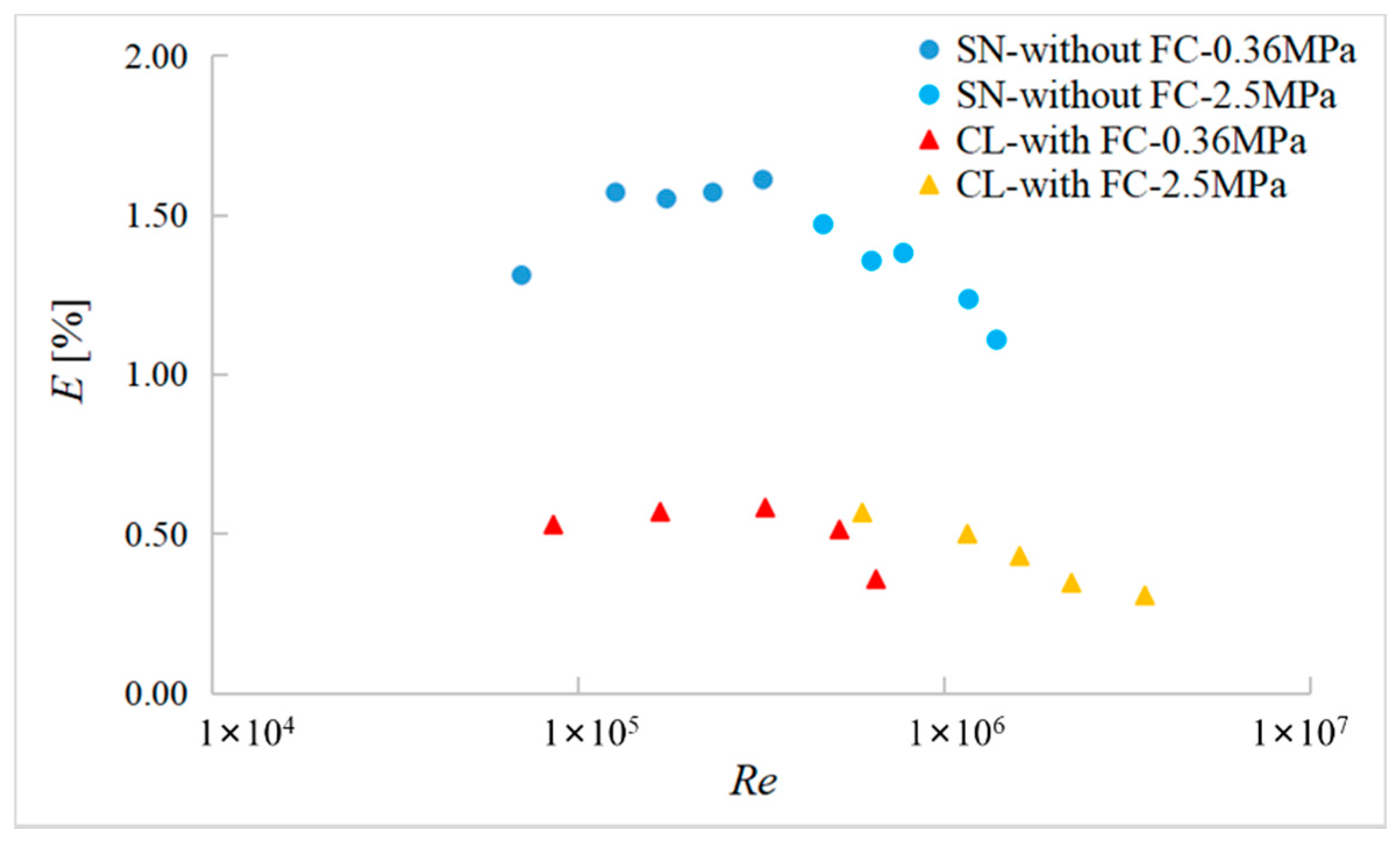
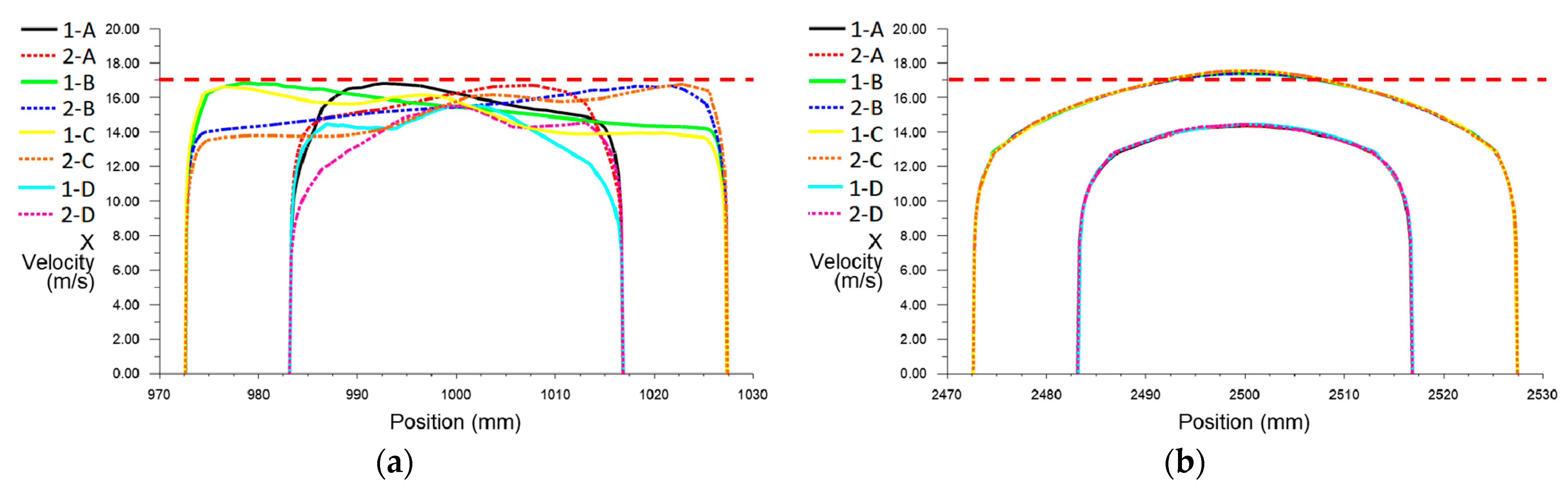
3.1. The Measurement Errors
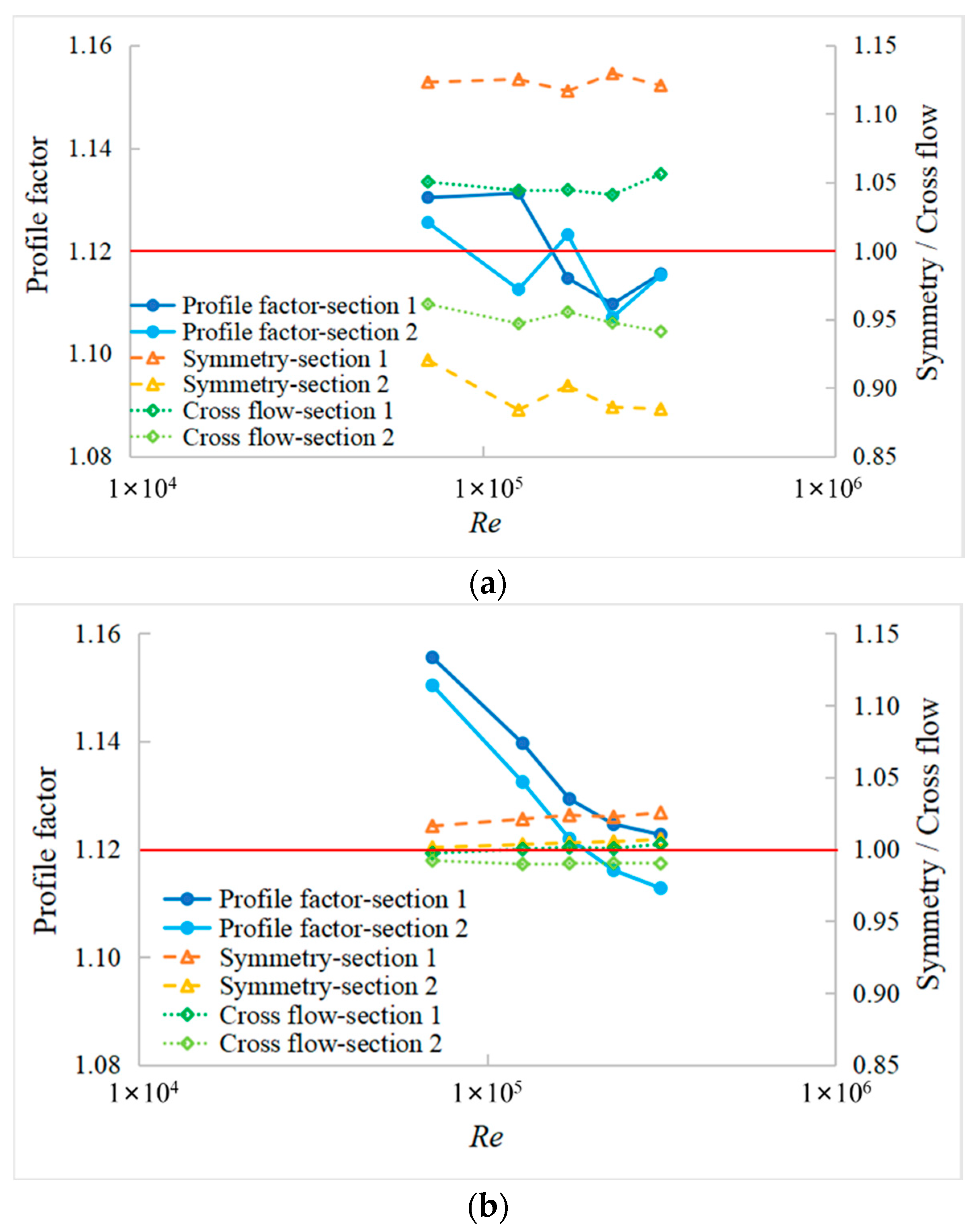
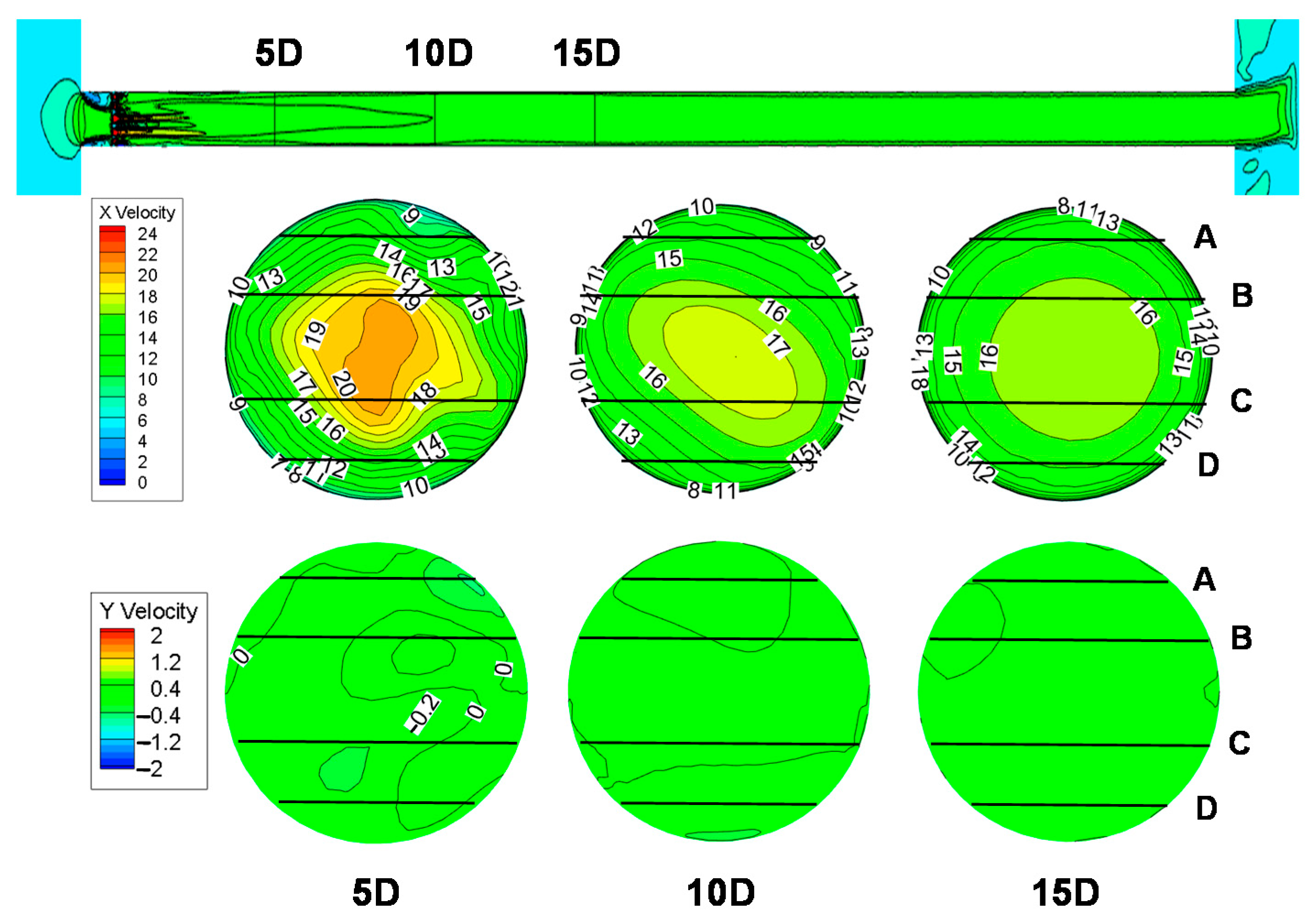
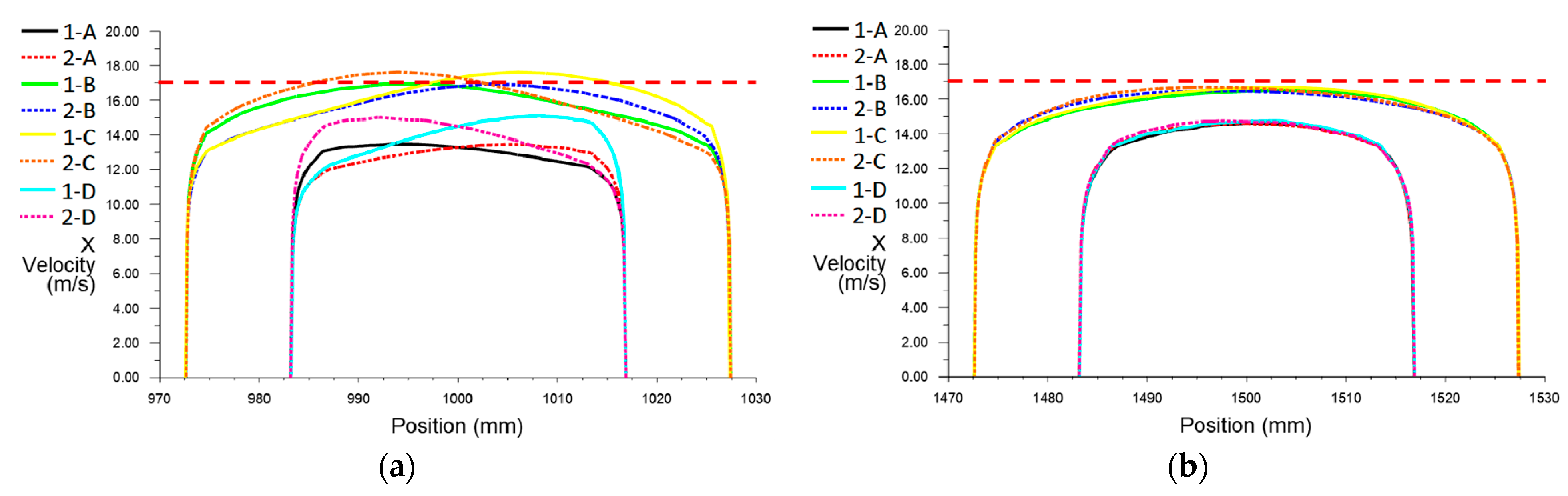
3.2. The Flow Distribution in Different Sections
- ➢
- ➢
- Symmetry: how symmetric the flow velocity was with the respect to the center of the pipe, Symmetry = (vA + vB)/(vC + vD), when it was 1 meaning a symmetric flow profile, the further away from 1 the Symmetry was, the greater the asymmetry;
- ➢
- Cross-flow: described the transversal flow or rotation, Cross-flow = (vA + vC)/(vB + vD), when it was 1 meaning no cross-flow or rotation.
4. Numerical Simulation Method
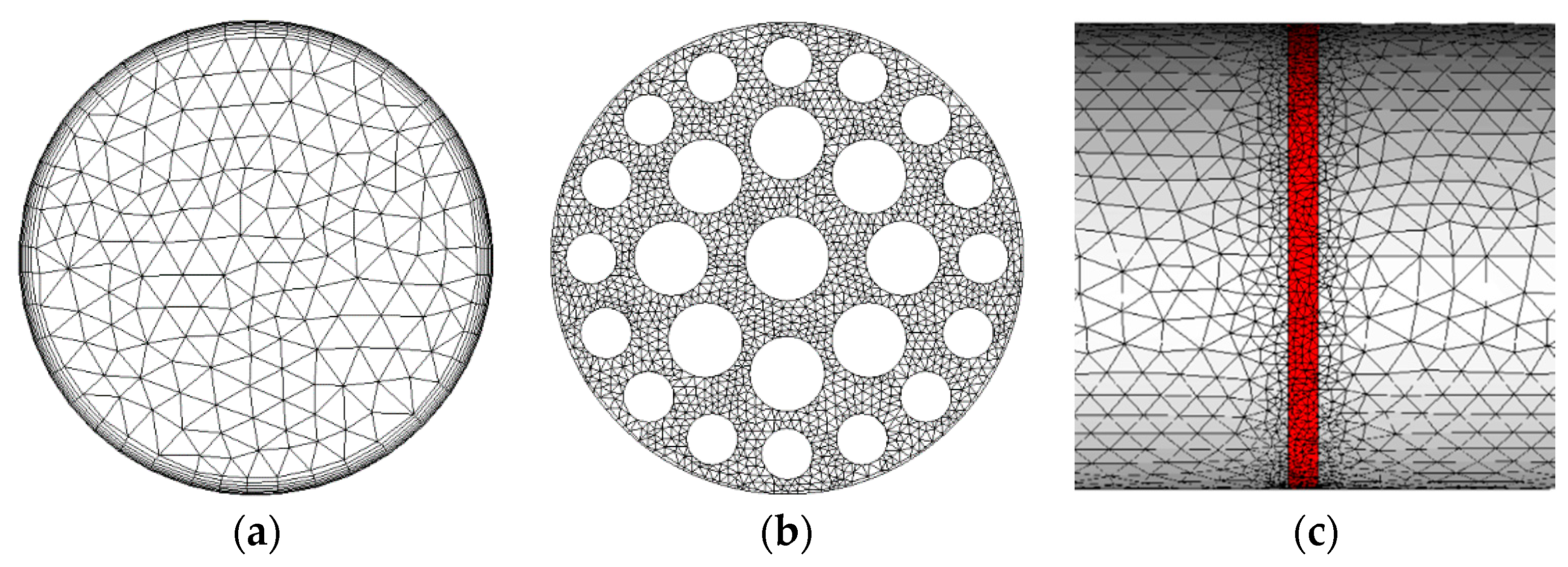
4.1. Geometric Modeling and Mesh Scheme
4.2. The Mathematical Method
- ➢
- mass conservation
- ➢
- momentum conservationwhere was the average velocity vector, , and represented the well-known turbulent or Reynolds stress tensor, due to fluctuating velocities .
4.3. Boundary Conditions
- ➢
- walls
- ➢
- inlet
- ➢
- outletwhere n was the well-known function of Reynolds number, while k and ε could be evaluated from the turbulent intensity and length scale. For the simulation of a viscous layer near the walls, simplified models were used as well as the standard wall functions, in which a velocity profile was assumed on the basis of well-known empirical relations. The equations for the turbulent flow were solved outside this layer [46].
5. Analysis of Simulation Results
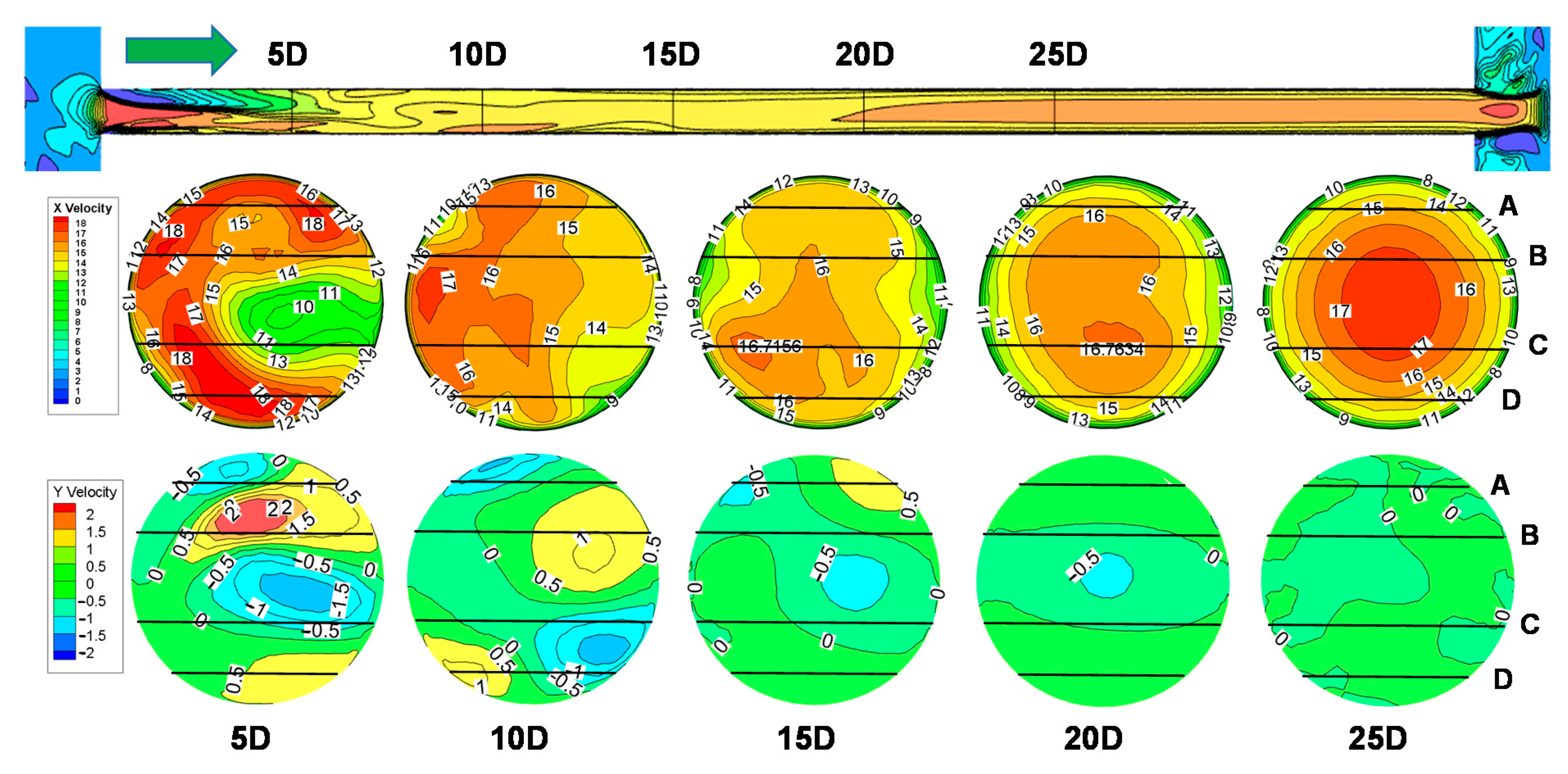
5.1. Velocity Distribution at Different Cross Sections
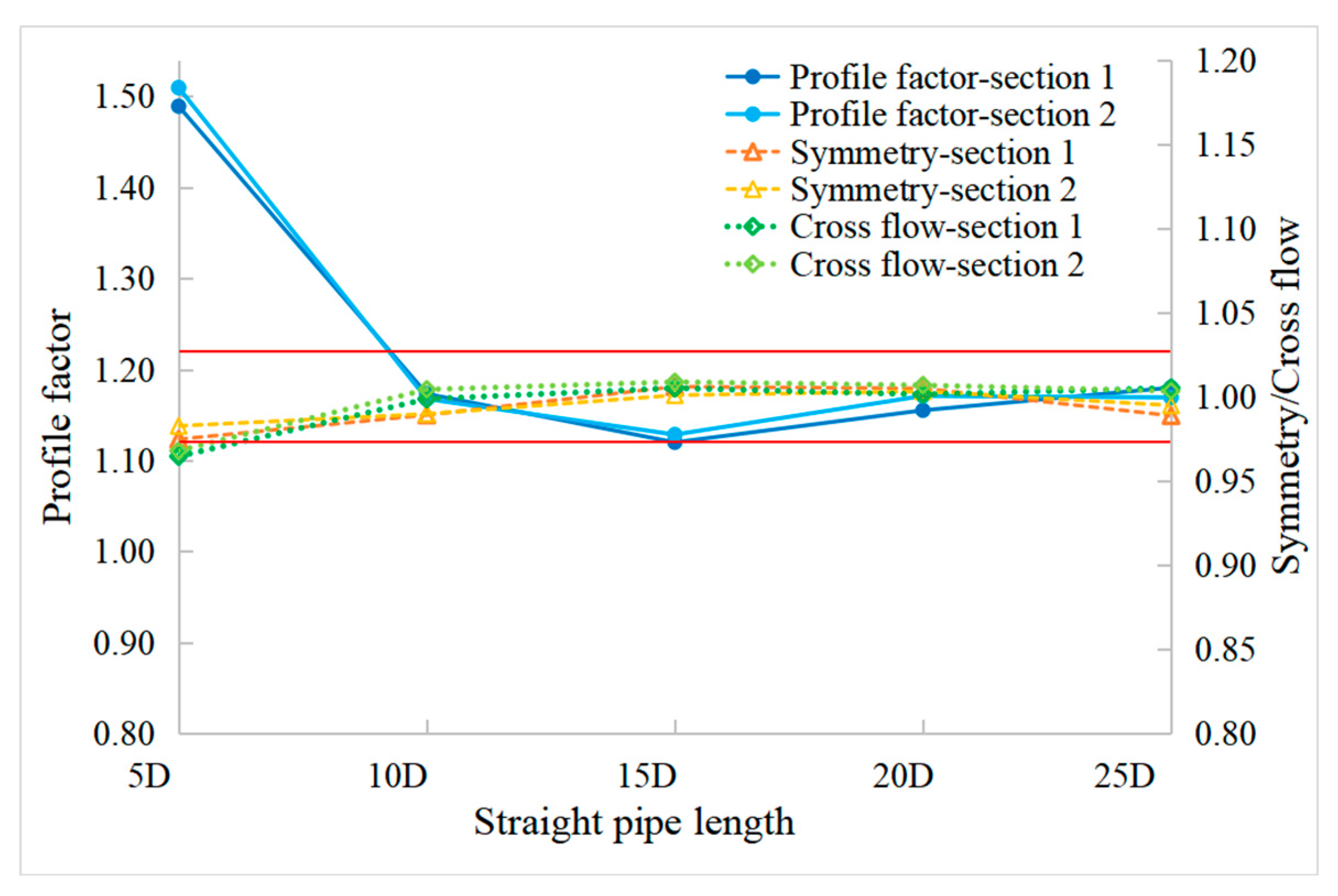
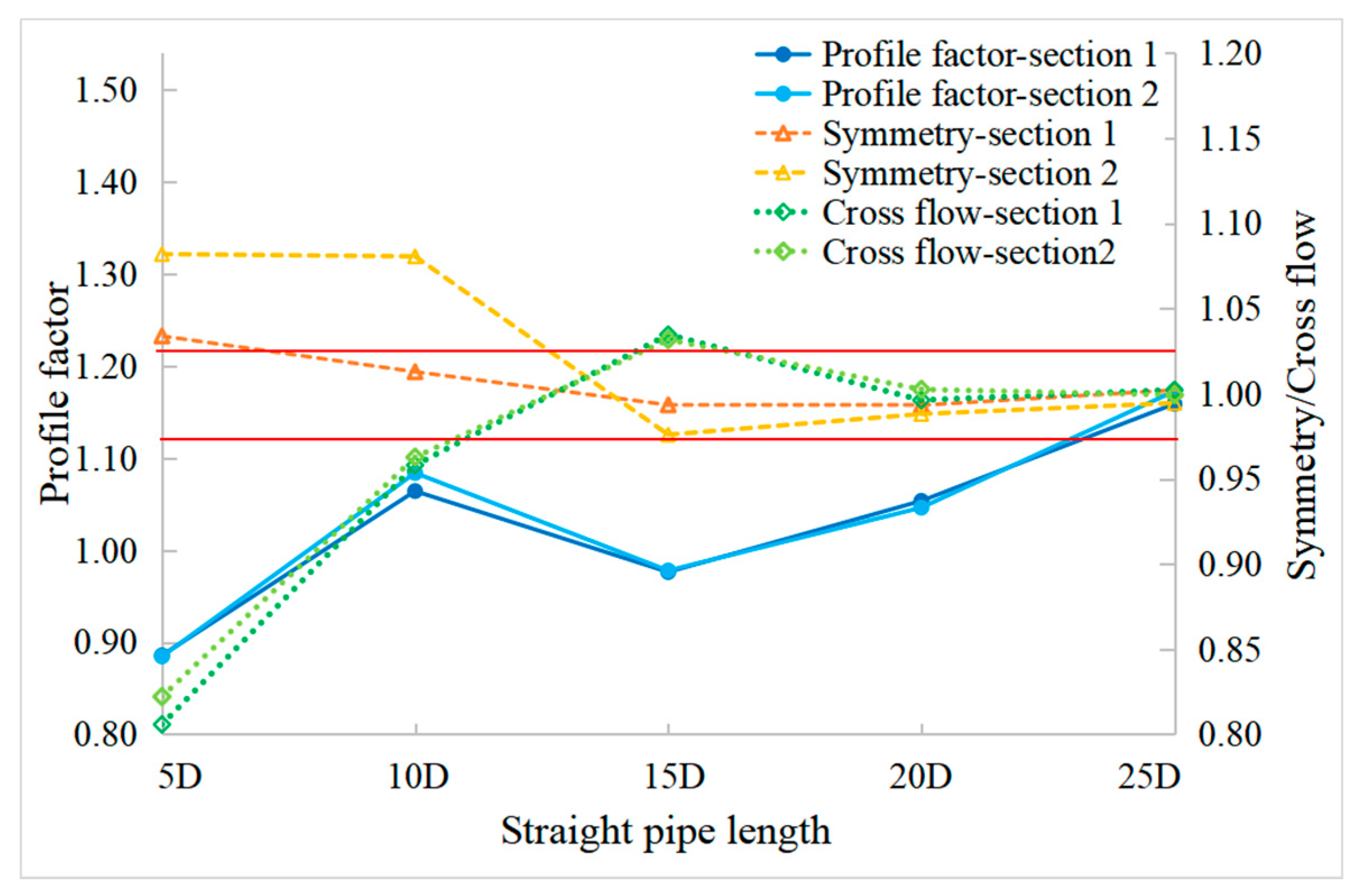
5.2. Analysis of Characteristic Parameters
6. Conclusions
- ➢
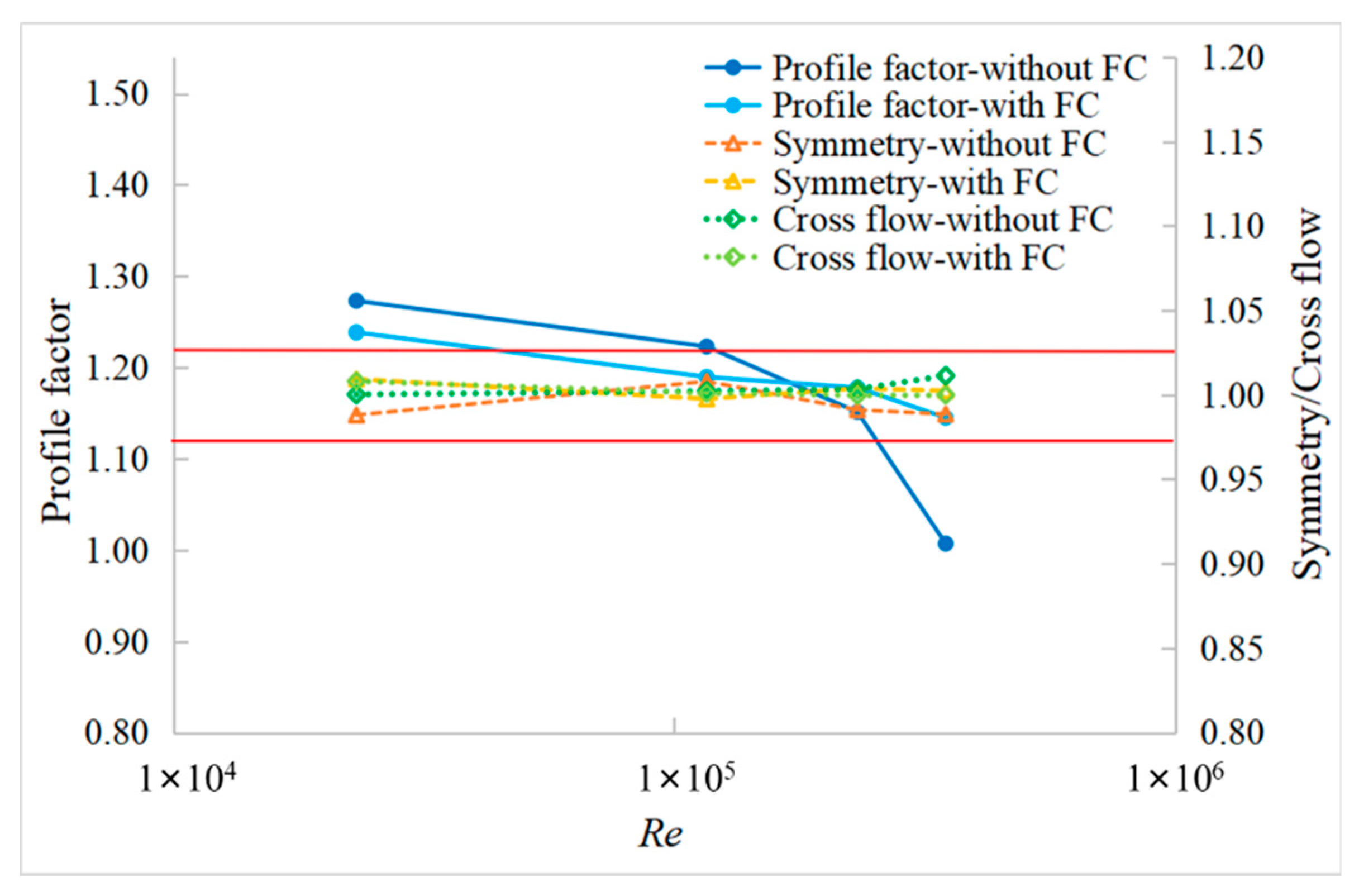
- The accurate experimental results showed that the measurement results of SN device were consistent very well with the CL device, while the measurement error of the SN device without FC was about 1% higher than the reference. The flow field distortion effect generated by the header had a significant influence on the measurement results of USM due to the nonconforming Profile factor, while the difference of Symmetry and Cross-flow could be obviously eliminated by the double-cross-section designing;
- ➢
- The simulation results showed that it was at about 25D without FC in the SN device that the velocity profile restored to a fully developed state and all characteristic parameters could meet the requirements, while it was at 10D with FC. The installation of FC could improve the accuracy of measurement results, because the FC could improve the velocity profile, and it also could effectively eliminate vortices and cross-flow.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, G.J.; Augenstein, D.R.; Cousins, T. An 8-Path Ultrasonic Master Meter for Oil Custody Transfers. In Proceedings of the XVIII IMEKO World Congress, Rio de Janeiro, Brazil, 17–22 September 2006. [Google Scholar]
- Lynnworth, L.C.; Liu, Y. Ultrasonic flowmeters: Half-century progress report, 1955–2005. Ultrasonics 2006, 44, e1371–e1378. [Google Scholar] [CrossRef] [PubMed]
- Drenthen, J.G.; Boer, G.D. The manufacturing of ultrasonic gas flow meters. Flow Meas. Instrum. 2002, 12, 89–99. [Google Scholar]
- Nabavi, M.; Siddiqui, K. A critical review on advanced velocity measurement techniques in pulsating flows. Meas. Sci. Technol. 2010, 21, 042002. [Google Scholar] [CrossRef]
- Zhou, A.G.; Ruan, J.Y.; Liu, K.; Lu, M.X. Analysis and strategy for impacts on ultrasonic flowmeters. Chin. J. Construct. Mach. 2009, 7, 469–473. [Google Scholar]
- Lin, Q.; Chen, Z.X.; Zhang, Y.Y.; Xiao, Q.; Yang, Z.Y.; Bai, X.F. Overview of ultrasonic flowmeter and numerical simulation of flow field. Tech. Superv. Petro Ind. 2018, 34, 43–47. [Google Scholar]
- Rundle, J.B. Viscoelastic crustal deformation by finite quasi-static sources. J. Geophys. Res. Solid Earth Planets 1978, 83, 5937–5945. [Google Scholar] [CrossRef]
- Mousavi, S.F.; Hashemabadi, S.H.; Jamali, J. Calculation of Geometric Flow Profile Correction Factor for Ultrasonic Flow Meter Using Semi-3D Simulation Technique. Ultrasonics 2020, 106, 106165. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.L.; Ji, T.; Wang, R.C.; Ge, X.; Tang, X.; Tang, S. Multipath ultrasonic gas flow-meter based on multiple reference waves. Ultrasonics 2017, 82, 145–152. [Google Scholar] [CrossRef]
- Lansing, J.; Herrmann, V.; Dietz, T. Investigations on an 8 path ultrasonic meter-What sensitivity ro upstream disturbance remain? In Proceedings of the 24th International North Sea Flow Measurment Workshop, St. Andrews, UK, 24–27 October 2006. [Google Scholar]
- Zhao, H.C.; Peng, L.H.; Tsuyoshi, T.; Hayashi, T.; Shimizu, K.; Yamamoto, T. ANN Based Data Integration for Multi-Path Ultrasonic Flowmeter. IEEE Sens. J. 2013, 14, 362–370. [Google Scholar] [CrossRef]
- Zheng, D.D.; Zhao, D.; Mei, J.Q. Improved numerical integration method for flowrate of ultrasonic flowmeter based on Gauss quadrature for non-ideal flow fields. Flow Meas. Instrum. 2015, 41, 28–35. [Google Scholar] [CrossRef]
- Wang, B.; Cui, Y.; Liu, W.; Luo, X. Study of Transducer Installation Effects on Ultrasonic Flow Metering Using Computational Fluid Dynamics. Adv. Mater. Res. 2013, 629, 676–681. [Google Scholar] [CrossRef]
- Chen, W.G. Analysis and Compensation Method of Non-Ideal Flow Field for Ultrasonic Gas Flowmeter. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2015. [Google Scholar]
- Heinig, D.; Wenzel, J.; Nerowski, D.A.; Dietz, T. An Innovative Approach to Increase Diagnostic Sensitivity in Ultrasonic Flow Meters. In Proceedings of the 36th North Sea Flow Measurement Workshop, Tønsberg, Norway, 22–25 October 2018. [Google Scholar]
- Hallanger, A.; Saetre, C.; Frøysa, K.E. Flow profile effects due to pipe geometry in an export gas metering station—Analysis by CFD simulations. Flow Meas. Instrum. 2018, 61, 56–65. [Google Scholar] [CrossRef]
- American Gas Association. Measurement of Gas by Multipath Ultrasonic Meters; Report No. 9; AGA: Washington, DC, USA, 1998. [Google Scholar]
- Qin, L.H.; Hu, L.; Mao, K.; Chen, W.; Fu, X. Flow profile identification with multipath transducers. Flow Meas. Instrum. 2016, 52, 148–156. [Google Scholar] [CrossRef]
- Measurement of Natural Gas Flow by Gas Ultrasonic Flow Meters; GB/T 18604-2014, ICS 75.180.30; China Standards Press: Beijing, China, 2014.
- Matiko, F.; Roman, V.; Baitsar, R. Methodology for Improving Mathematical Model of Ultrasonic Flowmeter to Study Its Error at Distorted Flow Structure. Energy Eng. Control Syst. 2015, 1, 63–70. [Google Scholar]
- Mickan, B.; Wendt, G.; Kramer, R.; Dopheide, D. Systematic investigation of flow profiles in pipes and their effects on gas meter behaviour. Measurement 1997, 22, 1–14. [Google Scholar] [CrossRef]
- Zheng, D.D.; Zhang, P.Y.; Xu, T.S. Study of acoustic transducer protrusion and recess effects on ultrasonic flowmeter measurement by numerical simulation. Flow Meas. Instrum. 2011, 22, 488–493. [Google Scholar] [CrossRef]
- Ruppel, C.; Peters, F. Effects of upstream installations on the reading of an ultrasonic flowmeter. Flow Meas. Instrum. 2004, 15, 167–177. [Google Scholar] [CrossRef]
- Leontidis, V.; Cuvier, C.; Caignaert, G.; Dupont, P.; Roussette, O.; Fammery, S.; Nivet, P.; Dazin, A. Experimental validation of an ultrasonic flowmeter for unsteady flows application. Meas. Sci. Technol. 2018, 29, 1–17. [Google Scholar] [CrossRef]
- Sætre, C.; Frøysa, K.-E.; Hallanger, A.; Chan, P. Installation effects and flow instabilities in gas metering station with multipath ultrasonic flow meters. In Proceedings of the 33rd International North Sea Flow Measurement Workshop, Tonsberg, Norwey, 20–23 October 2015. [Google Scholar]
- Zhu, W.J.; Xu, K.J.; Fang, M.; Wang, W.; She, Z.-W. Mathematical Modeling of Ultrasonic Gas Flow Meter Based on Experimental Data in Three Steps. IEEE Trans. Instrum. Meas. 2016, 65, 1726–1738. [Google Scholar] [CrossRef]
- Liu, E.B.; Tan, H.; Peng, S.B. A CFD simulation for the ultrasonic flow meter with a header. Teh. Vjesn. Tech. Gaz. 2017, 24, 1797–1801. [Google Scholar]
- Zheng, D.D.; Lv, S.H.; Mao, Y. Effect mechanism of non-ideal flow field on acoustic field in gas ultrasonic flowmeter. IET Sci. Meas. Technol. 2019, 13, 469–477. [Google Scholar] [CrossRef]
- Johnson, A.N.; Boyd, J.T.; Harman, E.; Khail, M.; Ricker, J.R.; Crowley, C.J.; Wright, J.D.; Bryant, R.; Shinder, I. Design and Capabilities of NISTs Scale-Model Smokestack Simulator (SMSS). In Proceedings of the 9th International Symposium on Fluid Flow Measurement, Arlington, VA, USA, 14–17 April 2015. [Google Scholar]
- Zhang, H.; Guo, C.W.; Lin, J. Effects of Velocity Profiles on Measuring Accuracy of Transit-Time Ultrasonic Flowmete. Appl. Sci. 2019, 9, 1648. [Google Scholar] [CrossRef]
- Zhao, H.C.; Peng, L.H.; Stephane, S.A.; Ishikawa, H. CFD Aided Investigation of Multipath Ultrasonic Gas Flow Meter Performance under Complex Flow Profile. IEEE Sens. J. 2014, 14, 897–907. [Google Scholar] [CrossRef]
- Hallanger, A.; Frøysa, K.E.; Lunde, P. CFD-simulation and installation effects for ultrasonic flow meters in pipes with bends. Int. J. Appl. Mech. Eng. 2002, 7, 33–64. [Google Scholar]
- Yao, P. Measurement Accuracy Improvement Method of Gas Ultrasonic Flowmeter in Complex Flow Field. Master’s Thesis, Zhejiang University, Hangzhou, China, 2018. [Google Scholar]
- Zhu, W.J.; Xu, K.J.; Fang, M.; Shen, Z.-W.; Tian, L. Variable ratio threshold and zero-crossing detection based signal processing method for ultrasonic gas flow meter. Measurement 2017, 103, 343–352. [Google Scholar] [CrossRef]
- ASME PTC18-2011_Hydraulic Turbines and Pump-Turbines Performance Test Codes; The American Society of Mechanical Engineers: New York, NY, USA, 2011.
- Grunert, F.; Kabra, Z. Effect of symmetric distortion of the field of fluid velocity on the readings of an ultrasonic flowmeter. Meas. Tech. 1997, 40, 445–451. [Google Scholar] [CrossRef]
- Li, C.H.; Mickan, B.; Cui, L.S. The high pressure sonic nozzle gas flow standard facility in NIM. In Proceedings of the Flomeko 2019, Lisbon, Portugal, 26–28 June 2019. [Google Scholar]
- Wang, C.; Li, C.H.; Xu, M.; Yan, W. The high pressure close loop gas flow standard facility in NIM. In Proceedings of the Flomeko 2019, Lisbon, Portugal, 26–28 June 2019. [Google Scholar]
- Hoffmann, B.H. Path Following and Collision Avoidance for an Underwater Swimming Manipulator. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
- Chun, S.; Yoon, B.R.; Lee, D.K.; Choi, H.-M. Correction of flow metering coefficients by using multi-dimensional non-linear curve fitting. J. Mech. Sci. Tech. 2012, 26, 3479–3489. [Google Scholar] [CrossRef]
- Lindsay, G. Review of NEL’s Ingernal Knowledge in the Field of Flow Meter Diagnostics; National Engineering Laboratory: East Kilbride, UK, 2019. [Google Scholar]
- Emerson Process Management; Daniel Measurement and Control, Inc. How Today’s Ultrasonic Meter Diagnostics Solve Metering Problems Technical White Paper; Daniel Measurement and Control, Inc.: Houston, TX, USA, 2010. [Google Scholar]
- Gallagher, J.E. Natural Gas Measurement Handbook; Elsevier: Amsterdam, The Netherlands, 2007; Chapter 4; pp. 79–110. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 1979; ISBN 978-3540662709. [Google Scholar]
- Erdal, A. A numerical investigation of different parameters that affect the performance of a flow conditioner. Flow Meas. Instrum. 1998, 8, 93–102. [Google Scholar] [CrossRef]
- Frattolillo, A.; Massarotti, N. Flow conditioners efficiency a comparison based on numerical approach. Flow Meas. Instrum. 2002, 13, 1–11. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1 January 1980; 214p, ISBN 9780891165224. [Google Scholar]

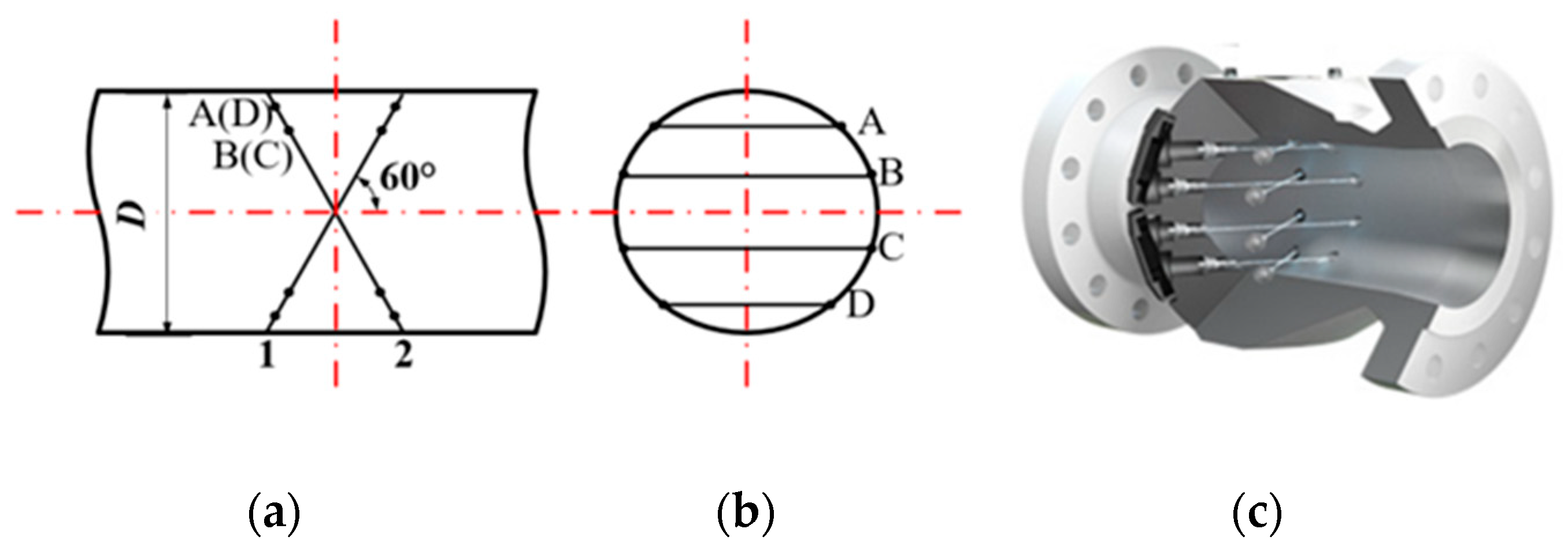


| Number of Paths | Gauss–Jacobi Positions xi = di/R | Gauss–Jacobi Weights (4 Path) wi | Velocity Weights (4/8 Path) Wi |
|---|---|---|---|
| A(1-A/2-A) | 0.8090 | 0.3693 | 0.1382/0.0691 |
| B(1-B/2-B) | 0.3090 | 0.5976 | 0.3618/0.1809 |
| C(1-C/2-C) | −0.3090 | 0.5976 | 0.3618/0.1809 |
| D(1-D/2-D) | −0.8090 | 0.3693 | 0.1382/0.0691 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Wu, J.; Li, C. The Investigation on the Flow Distortion Effect of Header to Guarantee the Measurement Accuracy of the Ultrasonic Gas Flowmeter. Appl. Sci. 2021, 11, 3656. https://doi.org/10.3390/app11083656
Chen W, Wu J, Li C. The Investigation on the Flow Distortion Effect of Header to Guarantee the Measurement Accuracy of the Ultrasonic Gas Flowmeter. Applied Sciences. 2021; 11(8):3656. https://doi.org/10.3390/app11083656
Chicago/Turabian StyleChen, Wenlin, Jianjun Wu, and Chunhui Li. 2021. "The Investigation on the Flow Distortion Effect of Header to Guarantee the Measurement Accuracy of the Ultrasonic Gas Flowmeter" Applied Sciences 11, no. 8: 3656. https://doi.org/10.3390/app11083656
APA StyleChen, W., Wu, J., & Li, C. (2021). The Investigation on the Flow Distortion Effect of Header to Guarantee the Measurement Accuracy of the Ultrasonic Gas Flowmeter. Applied Sciences, 11(8), 3656. https://doi.org/10.3390/app11083656





