Deep Neural Networks Classification via Binary Error-Detecting Output Codes
Abstract
1. Introduction
The Contribution of This Work Is the Following:
- We study the use of error-detecting linear block codes as a binary output coding (e.g., Cyclic Redundancy Check—CRC).
- We propose a novel method based on the Zadeh fuzzy logic, which enables us to train whole binary output codes at once, and to use error detection ability. We show that the proposed method achieves similar accuracy as one-hot encoding with a softmax function trained using categorical cross-entropy.
- We prove that the error detection in pattern recognition could be achieved directly by rounding the normalized network output and calculating the zero-syndrome. The result is most trustworthy from the Zadeh fuzzy logic perspective, and the truth-value can be given to the user.
- We evaluate the proposed system against other approaches to train binary codes.
- We perform further study to compare the proposed method’s performance against the one-hot encoding approach in terms of reliability and out-of-distribution accuracy.
2. Methods and Materials
2.1. Output Coding
2.2. Decision Method
- (a)
- Then the truth-value that is the winning codeword is more than one half.
- (b)
- There is only one codeword with truth-value higher than one half.
- (c)
- The winning codeword is obtained by rounding off i.e., , where .
- (a)
- Assume , and , . Because , there exists a bit that . implies , which is in contradiction with the assumption.
- (b)
- For the rounded output . According to b), is the only winning codeword. □
2.3. Dataset
2.4. Metrics
2.5. Neural Network Architectures and Training Protocol
3. Results and Discussion
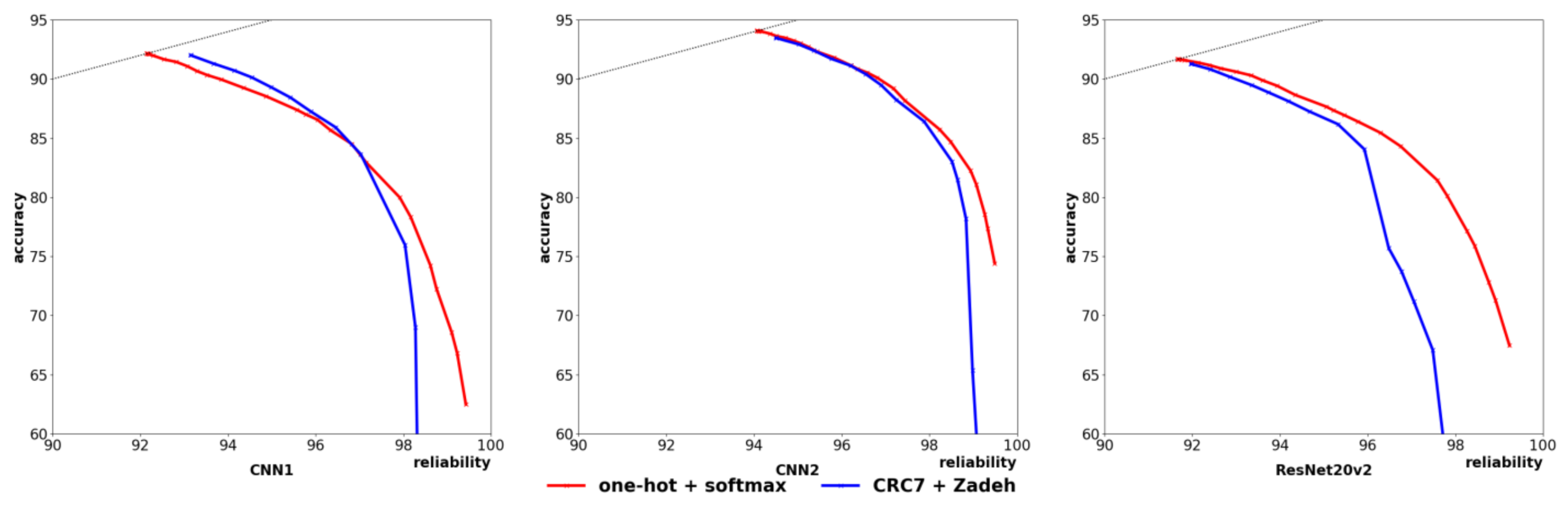
3.1. Effect of CRC Output Coding
3.2. Performance on CIFAR-10
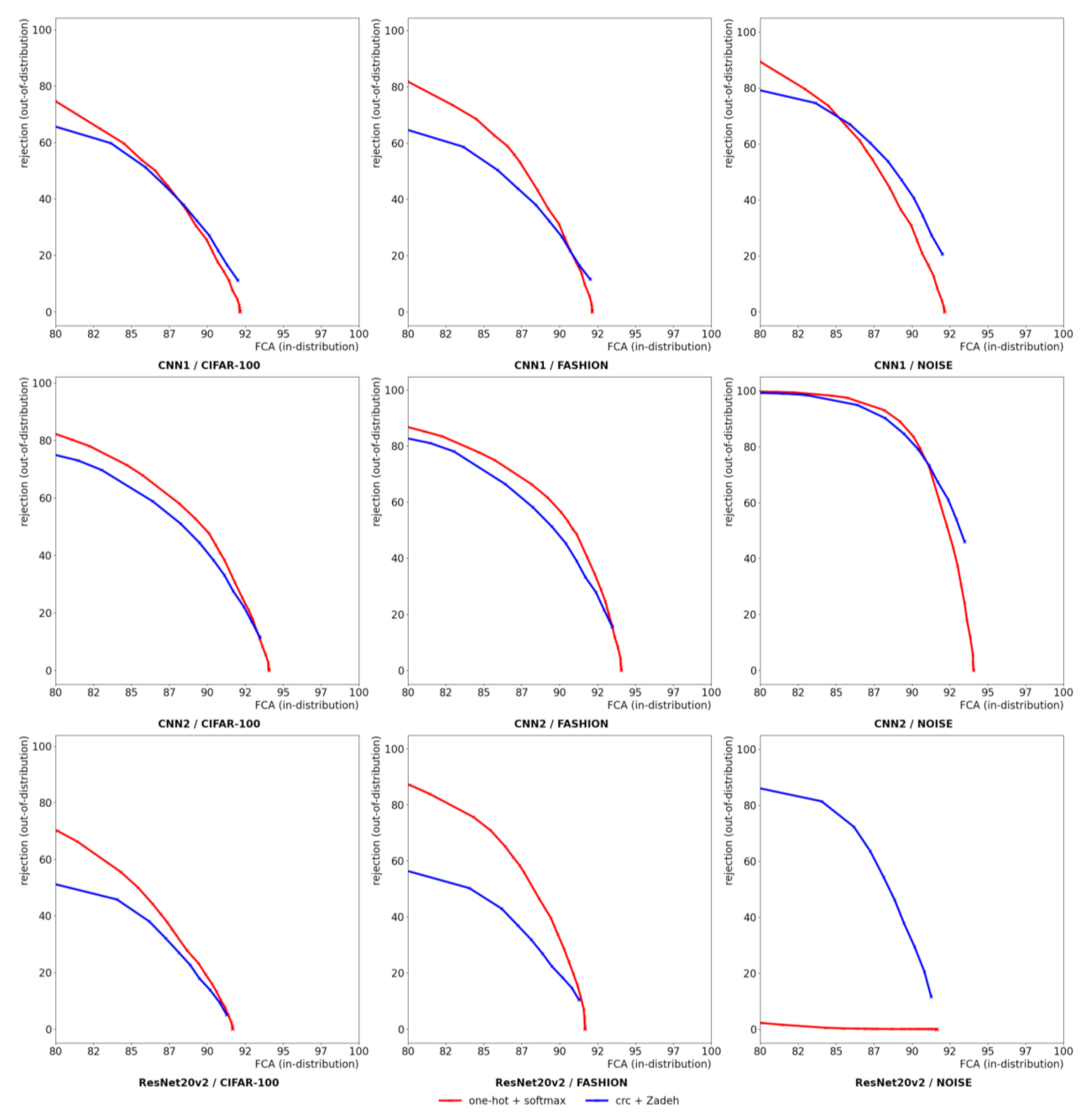
3.3. Out-of-Distribution Performance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rocha, A.; Goldenstein, S.K. Multiclass from Binary: Expanding One-Versus-All, One-Versus-One and ECOC-Based Approaches. IEEE Trans. Neural Networks Learn. Syst. 2014, 25, 289–302. [Google Scholar] [CrossRef] [PubMed]
- Aly, M. Survey on multiclass classification methods. Neural Netw. 2005, 19, 1–9. [Google Scholar]
- Anand, R.; Mehrotra, K.; Mohan, C.K.; Ranka, S. Efficient classification for multiclass problems using modular neural networks. IEEE Trans. Neural Netw. 1995, 6, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R. Classification by pairwise coupling. Ann. Stat. 1998, 26. [Google Scholar] [CrossRef]
- Friedman, J.H. Another Approach to Polychotomous Classification; Department of Statistics, Stanford University: Stanford, CA, USA, 1996. [Google Scholar]
- Platt, J.C.; Cristianini, N.; Shawe-Taylor, J. Large margin DAGs for multiclass classification. NIPS 2000, 547–553. [Google Scholar] [CrossRef]
- Šuch, O.; Barreda, S. Bayes covariant multi-class classification. Pattern Recognit. Lett. 2016, 84, 99–106. [Google Scholar] [CrossRef]
- Dietterich, T.G.; Bakiri, G. Solving Multiclass Learning Problems via Error-Correcting Output Codes. J. Artif. Intell. Res. 1995, 2, 263–286. [Google Scholar] [CrossRef]
- Pawara, P.; Okafor, E.; Groefsema, M.; He, S.; Schomaker, L.R.; Wiering, M.A. One-vs-One classification for deep neural networks. Pattern Recognit. 2020, 108, 107528. [Google Scholar] [CrossRef]
- Titsias, M.K. One-vs-each approximation to softmax for scalable estimation of probabilities. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Ithaca, NY, USA, 2016; Volume 29. [Google Scholar]
- Rodríguez, P.; Bautista, M.A.; Gonzàlez, J.; Escalera, S. Beyond one-hot encoding: Lower dimensional target embedding. Image Vis. Comput. 2018. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, H.; Suen, C.Y. Data-driven decomposition for multi-class classification. Pattern Recognit. 2008, 41, 67–76. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Soft computing, fuzzy logic and recognition technology. In IEEE World Congress on Computational Intelligence, Proceedings of the 1998 IEEE International Conference on Fuzzy Systems Proceedings, Anchorage, AK, USA, 4–9 May 1998; Cat. No.98CH36228. IEEE: New York, NY, USA, 2002. [Google Scholar]
- Blahut, R.E. Algebraic Codes for Data Transmission, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Roth, R. Introduction to Coding Theory; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Varshney, K.R.; Alemzadeh, H. On the Safety of Machine Learning: Cyber-Physical Systems, Decision Sciences, and Data Products. Big Data 2017, 5, 246–255. [Google Scholar] [CrossRef]
- Amodei, D.; Olah, C.; Steinhardt, J.; Christiano, P.; Schulman, J.; Mané, D. Concrete Problems in AI Safety. arXiv 2004, arXiv:1606.0656. [Google Scholar]
- Jiang, H.; Kim, B.; Gupta, M.; Guan, M.Y. To trust or not to trust a classifier. arXiv 2018, arXiv:1805.11783. [Google Scholar]
- Mukhoti, J.; Kulharia, V.; Sanyal, A.; Golodetz, S.; Torr, P.H.S.; Dokania, P.K. Calibrating Deep Neural Networks using Focal Loss. arXiv 2020, arXiv:2002.09437. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Nguyen, A.; Yosinski, J.; Clune, J. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 427–436. [Google Scholar]
- Hendrycks, D.; Gimpel, K. A Baseline for Detecting Misclassified Out-of-Distribution Examples. In Proceedings of the International Conference on Learning Representations 2017 (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- DeVries, T.; Taylor, G.W. Learning confidence for out-of-distribution detection in neural networks. arXiv 2018, arXiv:1802.04865. [Google Scholar]
- Grigoryan, A.; Grigoryan, M. Hadamard Transform. In Brief Notes in Advanced DSP; Apple Academic Press: Palm Bay, FL, USA, 2009; pp. 185–256. [Google Scholar]
- Yang, S.; Luo, P.; Loy, C.C.; Shum, K.W.; Tang, X. Deep representation learning with target coding. In Proceedings of the National Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Akhtar, N.; Mian, A. Threat of Adversarial Attacks on Deep Learning in Computer Vision: A Survey. IEEE Access 2018, 6, 14410–14430. [Google Scholar] [CrossRef]
- Kim, D.; Bargal, S.A.; Zhang, J.; Sclaroff, S. Multi-way Encoding for Robustness. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO, USA, 1–5 March 2020; pp. 1341–1349. [Google Scholar]
- Qin, J.; Liu, L.; Shao, L.; Shen, F.; Ni, B.; Chen, J.; Wang, Y. Zero-Shot Action Recognition with Error-Correcting Output Codes. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1042–1051. [Google Scholar]
- Wolpert, D.H.; Dietterich, T.G. Error-Correcting Output Codes: A General Method for Improving Multiclass Inductive Learning Programs. In The Mathematics of Generalization; CRC Press: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Lachaize, M.; le Hégarat-Mascle, S.; Aldea, E.; Maitrot, A.; Reynaud, R. Evidential framework for Error Correcting Output Code classification. Eng. Appl. Artif. Intell. 2018, 73, 10–21. [Google Scholar] [CrossRef]
- Li, K.-S.; Wang, H.-R.; Liu, K.-H. A novel Error-Correcting Output Codes algorithm based on genetic programming. Swarm Evol. Comput. 2019, 50. [Google Scholar] [CrossRef]
- Lian, S. Principles of Imprecise-Information Processing: A New Theoretical and Technological System; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Rudolph, L.; Hartmann, C.; Hwang, T.-Y.; Duc, N. Algebraic analog decoding of linear binary codes. IEEE Trans. Inf. Theory 1979, 25, 430–440. [Google Scholar] [CrossRef]
- von Kaenel, A.P. Fuzzy codes and distance properties. Fuzzy Sets Syst. 1982, 8, 199–204. [Google Scholar] [CrossRef]
- Tsafack, S.A.; Ndjeya, S.; Strüngmann, L.; Lele, C. Fuzzy Linear Codes. Fuzzy Inf. Eng. 2018, 10, 418–434. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms: Basic notions and properties. In Logical, Algebraic, Analytic and Probabilistic Aspects of Triangular Norms; Elsevier: Amsterdam, The Netherlands, 2005; pp. 17–60. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical Report TR-2009; University of Toronto: Toronto, ON, Canada.
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Han, X.; Kashif, R.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Krizhevsky, A.; Nair, V.; Hinton, G. CIFAR-10 and CIFAR-100 Datasets. Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 8 April 2009).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learn, San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Piscataway, NJ, USA, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 2016), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- François, C. Keras. Github Repositary. Available online: https://github.com/fchollet/keras (accessed on 5 May 2017).


| CRC1: 100,0011 | CRC2: 101,1011 | CRC3: 110,0001 | CRC4: 110,0111 | CRC5: 111,0011 |
| CRC6: 100,1001 | CRC7: 101,0111 | CRC8: 110,1101 | CRC9: 111,0101 |
| Accepted (A) | Rejected (R) | Σ | ||
|---|---|---|---|---|
| Positive (P) | Negative (N) | |||
| True (T) | TP | FN | FR | T |
| False (F) | FP | TN | TR | F |
| Σ | P | N | R | Q |
| CNN-1 | CNN-2 | |||
|---|---|---|---|---|
| Layer | Kernel Size | Kernel Stride | Feature Maps | Feature Maps |
| Conv + BN | 3 | 1 | 32 | 64 |
| Conv + BN | 3 | 1 | 32 | 64 |
| Conv + BN | 3 | 1 | 32 | 64 |
| Conv + BN | 3 | 1 | 32 | 64 |
| Conv + BN | 3 | 1 | 32 | 128 |
| MaxP | 2 | 1 | 32 | 128 |
| Dropout 0.2 | ||||
| Conv + BN | 3 | 1 | 64 | 128 |
| Conv + BN | 3 | 1 | 64 | 256 |
| MaxP | 2 | 2 | 64 | 256 |
| Dropout (0.2) | ||||
| Conv + BN | 3 | 1 | 128 | 256 |
| Conv + BN | 3 | 1 | 128 | 256 |
| MaxP | 2 | 2 | 128 | 256 |
| Dense | 1 | 1 | 10 | 10 |
| Normalization | Softmax/Sigmoid/Linear | |||
| Network | Code | Decision | Accuracy | FCA | Undetectable Error | Reliability |
|---|---|---|---|---|---|---|
| CNN1 | CRC7 | Zadeh | 92.44 | 92.01 | 6.77 | 93.15 |
| CNN1 | one-hot | Zadeh | 92.01 | 91.56 | 7.29 | 92.63 |
| CNN1 | one-hot | softmax | 92.15 | 92.15 | 7.85 | 92.15 |
| CNN1 | CRC7 | softmax | 91.85 | 91.85 | 8.15 | 91.85 |
| CNN1 | CRC7 | bit threshold | 89.56 | 89.56 | 6.8 | 92.94 |
| CNN1 | Hadamard | Euclid | 89.92 | 88.6 | 8.2 | 91.53 |
| CNN2 | CRC7 | Zadeh | 93.97 | 93.47 | 5.44 | 94.5 |
| CNN2 | one-hot | Zadeh | 93.4 | 92.66 | 5.76 | 94.14 |
| CNN2 | one-hot | softmax | 94.07 | 94.07 | 5.93 | 94.07 |
| CNN2 | CRC7 | softmax | 93.88 | 93.88 | 6.12 | 93.88 |
| ResNet20v2 | CRC7 | Zadeh | 91.56 | 91.27 | 7.97 | 91.97 |
| ResNet20v2 | one-hot | Zadeh | 84.16 | 83.28 | 14.5 | 85.17 |
| ResNet20v2 | one-hot | softmax | 91.67 | 91.67 | 8.33 | 91.67 |
| ResNet20v2 | CRC7 | softmax | 91.34 | 91.34 | 8.66 | 91.34 |
| Network | Code | Decision | MNIST | Fashion MNIST | CIFAR-100 | Noise |
|---|---|---|---|---|---|---|
| CNN1 | CRC7 | Zadeh | 10.29 | 11.59 | 11.16 | 20.6 |
| CNN1 | one-hot | softmax | 0 | 0 | 0 | 0 |
| CNN2 | CRC7 | Zadeh | 12.37 | 15.55 | 11.56 | 46.05 |
| CNN2 | one-hot | softmax | 0 | 0 | 0 | 0 |
| ResNet20v2 | CRC7 | Zadeh | 10.77 | 10.49 | 5.09 | 11.61 |
| ResNet20v2 | one-hot | softmax | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimo, M.; Lukáč, P.; Tarábek, P. Deep Neural Networks Classification via Binary Error-Detecting Output Codes. Appl. Sci. 2021, 11, 3563. https://doi.org/10.3390/app11083563
Klimo M, Lukáč P, Tarábek P. Deep Neural Networks Classification via Binary Error-Detecting Output Codes. Applied Sciences. 2021; 11(8):3563. https://doi.org/10.3390/app11083563
Chicago/Turabian StyleKlimo, Martin, Peter Lukáč, and Peter Tarábek. 2021. "Deep Neural Networks Classification via Binary Error-Detecting Output Codes" Applied Sciences 11, no. 8: 3563. https://doi.org/10.3390/app11083563
APA StyleKlimo, M., Lukáč, P., & Tarábek, P. (2021). Deep Neural Networks Classification via Binary Error-Detecting Output Codes. Applied Sciences, 11(8), 3563. https://doi.org/10.3390/app11083563







