Performance Evaluation of Stewart-Gough Flight Simulator Based on
Abstract
1. Introduction
2. Dynamic Model of Stewart-Gough Flight Simulation Platform
3. Controller Design
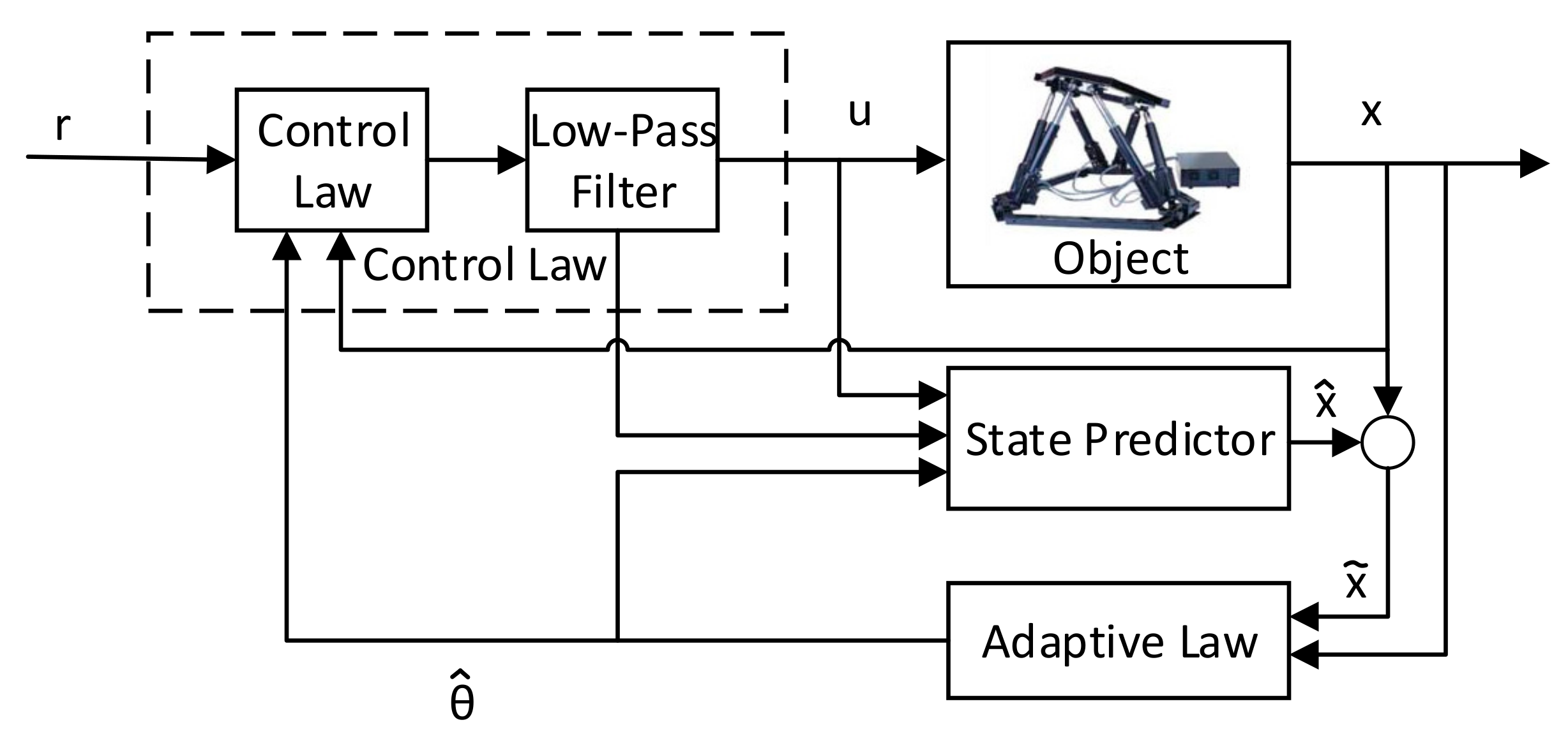
3.1. The Architecture of the MRAC Adaptive Controller
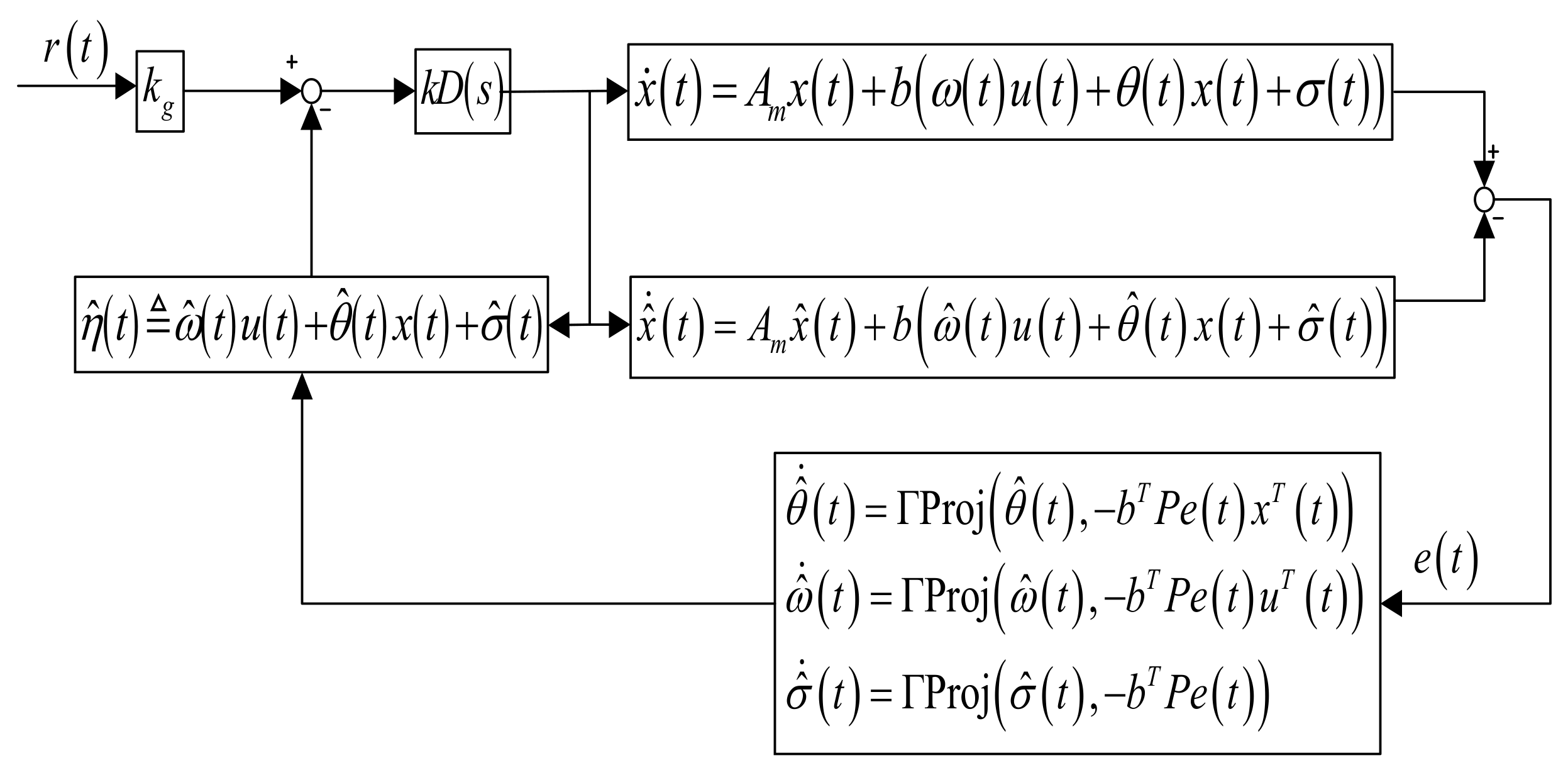
3.2. The Architecture of the Adaptive Controller
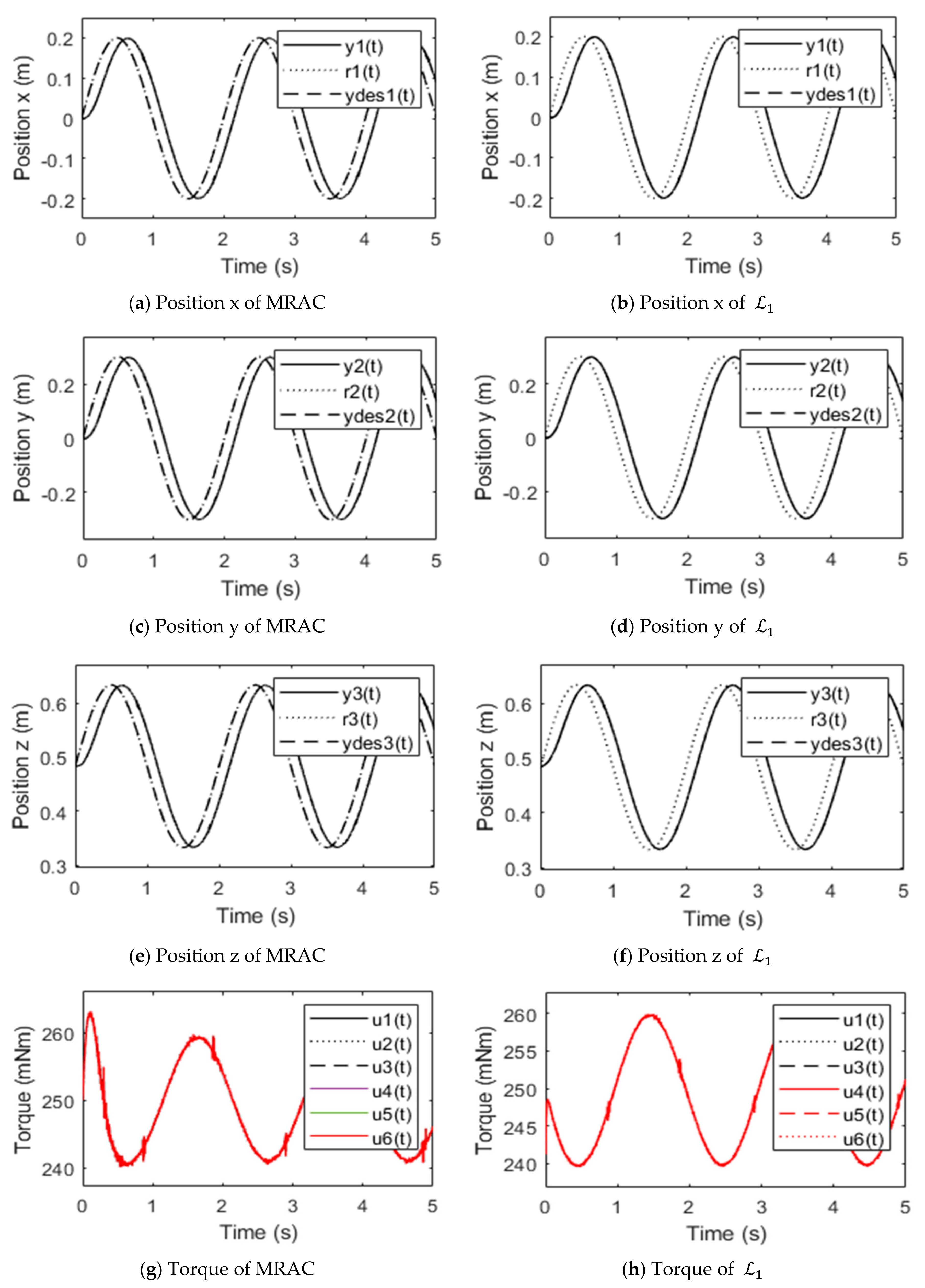
4. Experiment Verification
4.1. Plant
4.2. Path Planning
4.3. Control System
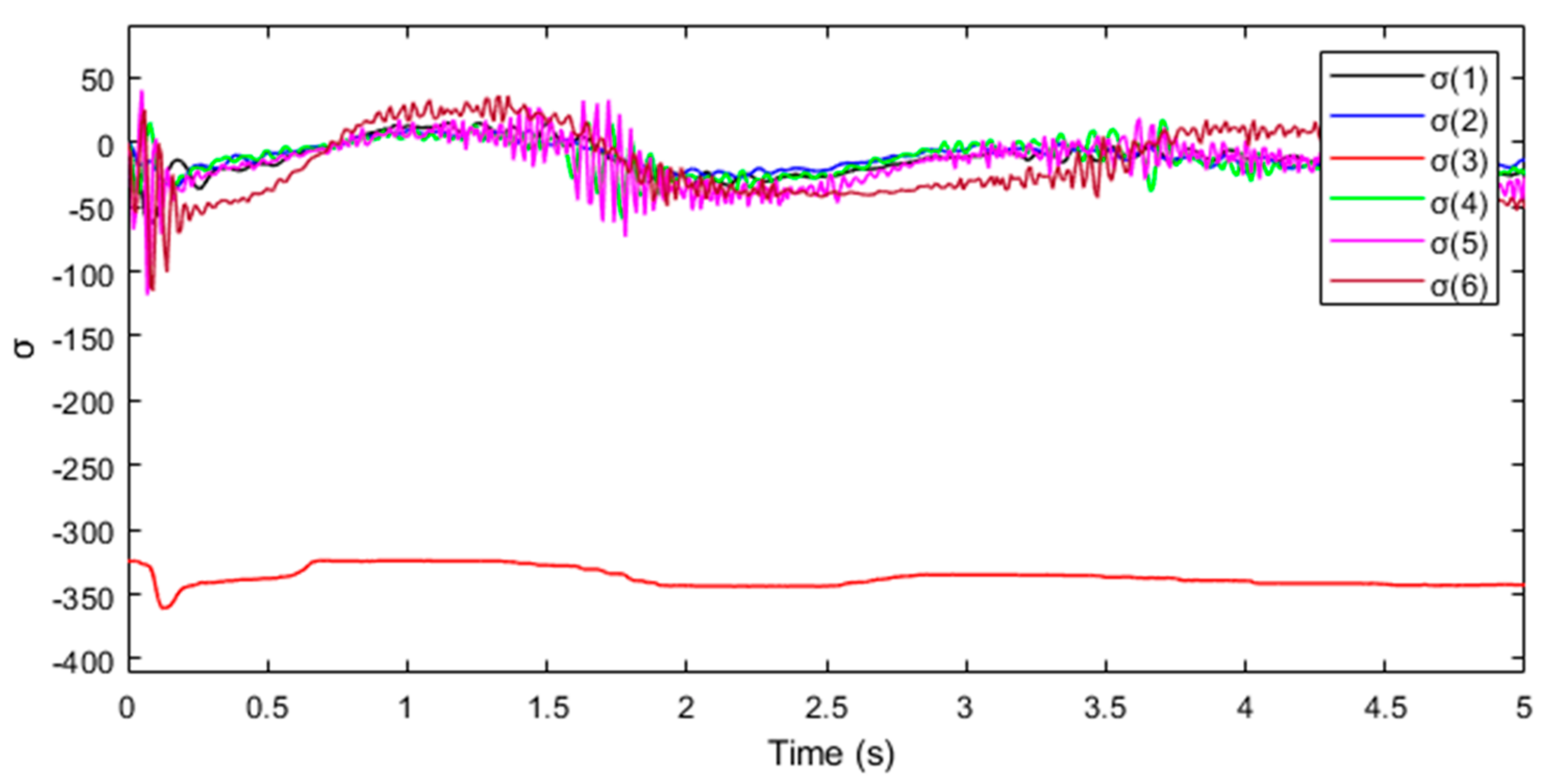
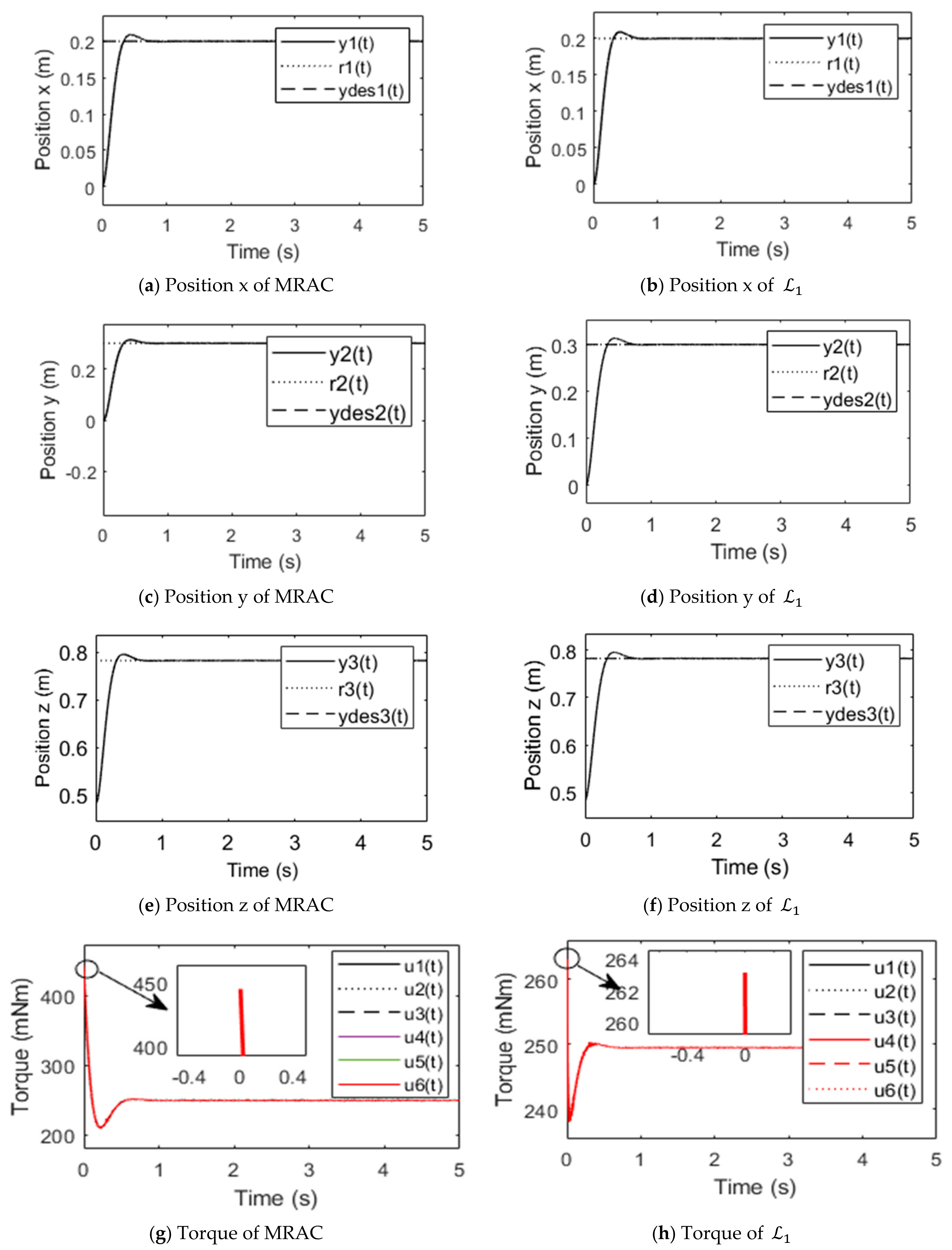
4.4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Federal Aviation Administration. Airplane Upset Recovery Training Aid; Revision 2; FAA: Washington, DC, USA, 2008. [Google Scholar]
- Boeing. Statistical Summary of Commercial Jet Airplane Accidents, Worldwide Operations 1959–2014; Boeing: Chicago, IL, USA, 2015. [Google Scholar]
- Advani, S.; Field, J. Upset prevention and recovery training in flight simulators. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Adavani, S.K.; Schroeder, J.A. Global implementation of upset prevention & recovery training. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Tsai, L.-W. Solving the Inverse Dynamics of a stewart-gough mainpulator by the principle of virtual work. J. Mech. Des. 2000, 122, 3–9. [Google Scholar] [CrossRef]
- Navvabi, H.; Markazi, A.H.D. Hybrid position/force control of Stewart Manipulator using Extended Adaptive Fuzzy Sliding Mode Controller (E-AFSMC). ISA Trans. 2019, 88, 280–295. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Q.; Zhai, Y.X.; Liu, X.F. Dynamic Characteristics Analysis of Simulator Six-DOF Platform. Appl. Mech. Mater. 2014, 651–653, 716–719. [Google Scholar] [CrossRef]
- Wu, D.S.; Gu, H.B.; Li, P. Comparative study on dynamic identification of parallel motion platform for a novel flight simulator. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO 2009), Guilin, China, 19–23 December 2009; Volumes 1–4, pp. 2232–2237. [Google Scholar]
- Yang, Y.; Zheng, S.T.; Han, J.W. Motion Drive Algorithm for Flight Simulator Based on the Stewart Platform Kinematics. Key Eng. Mater. 2011, 460–461, 642–647. [Google Scholar] [CrossRef]
- Krasnov, E.I.; Mikhaylov, V.V.; Sergeev, S.L. Development of a motion system for a training simulator based on Stewart platform. In Proceedings of the 2015 International Conference “Stability and Control Processes” in Memory of VI Zubov (SCP 2015), Saint Petersburg, Russia, 5–9 October 2015; pp. 99–101. [Google Scholar]
- Kim, H.S.; Cho, Y.M.; Lee, K.I. Robust nonlinear task space control for 6 DOF parallel manipulator. Automatica 2005, 41, 1591–1600. [Google Scholar] [CrossRef]
- Kang, J.Y.; Kim, D.H.; Lee, K.I. Robust tracking control of Stewart platform. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volumes 1–4, pp. 3014–3019. [Google Scholar]
- Yime, E.; Saltaren, R.; Diaz, J. Robust adaptive control of the Stewart-Gough robot in the task space. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 5248–5253. [Google Scholar]
- Islam, S.; Liu, P.X. Robust control for robot manipulators by using only joint position measurements. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, San Antonio, TX, USA, October 2009; pp. 4013–4018. [Google Scholar]
- Huang, C.I.; Fu, L.C. Adaptive backstepping tracking control of the Stewart platform. In Proceedings of the IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004; pp. 5228–5233. [Google Scholar]
- Pomet, J.-B.; Praly, L. Adaptive nonlinear regulation: Estimation from the Lyapunov equation. IEEE Trans. Autom. Control 1992, 37, 729–740. [Google Scholar] [CrossRef]
- Honegger, M.; Codourey, A.; Burdet, E. Adaptive control of the hexaglide, a 6 dof parallel manipulator. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; pp. 543–548. [Google Scholar]
- Wu, D.S.; Gu, H.B. Adaptive sliding control of six-DOF flight simulator motion platform. Chin. J. Aeronaut. 2007, 20, 425–433. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems. Automatica 2009, 45, 532–538. [Google Scholar] [CrossRef]
- Narendra, K.S.; Balakrishnan, J. Improving transient-response of adaptive-control systems using multiple models and switching. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; Volumes 1–4, pp. 1067–1072. [Google Scholar]
- Datta, A.; Ho, M.T. On modifying model-reference adaptive-control schemes for performance improvement. In Proceedings of the 32nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 15–17 December 1993; Volumes 1–4, pp. 1093–1094. [Google Scholar]
- Bartolini, G.; Ferrara, A. Robustness and performance of an indirect adaptive control scheme in presence of bounded disturbances. IEEE Trans. Autom. Control 1999, 44, 789–793. [Google Scholar] [CrossRef]
- Lin, X.L.; Wu, C.F.; Chen, B.S. Robust H-infinity Adaptive Fuzzy Tracking Control for MIMO Nonlinear Stochastic Poisson Jump Diffusion Systems. IEEE Trans. Cybern. 2019, 49, 3116–3130. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Li, X.M.; Yan, X.D. Inverse Kinematics Model’s Parameter Simulation for Stewart Platform Design of Driving Simulator. Lect. Notes Electr. Eng. 2018, 419, 887–898. [Google Scholar]
- Zhang, Y.P.; Ioannou, P.A. A new linear adaptive controller: Design, analysis and performance. IEEE Trans. Autom. Control 2000, 45, 883–897. [Google Scholar] [CrossRef][Green Version]
- Hovakimyan, N.; Cao, C.Y.; Kharisov, E. L1 Adaptive Control for Safety-Critical Systems Guaranteed Robustness with Fast Adaptation. IEEE Contr. Syst. Mag. 2011, 31, 54–104. [Google Scholar]
- Yime, E.; Garcia, C.; Sabater, J.M. Robot based on task-space dynamical model. IET Control Theory Appl. 2011, 5, 2111–2119. [Google Scholar] [CrossRef]
- Jafarnejadsani, H.; Sun, D.; Lee, H. Optimized L1 Adaptive Controller for Trajectory Tracking of an Indoor Quadrotor. J. Guid. Control Dyn. 2017, 40, 1415–1427. [Google Scholar] [CrossRef]
- Cao, C.Y.; Naira, H. Design and analysis of a novel L1 adaptive controller, part I: Control signal and asymptotic stability. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; Volumes 1–12, pp. 3397–3402. [Google Scholar]
- Cao, C.Y.; Hovakimyan, N. L1 adaptive controller for multi-input multi-output systems in the presence of unmatched disturbances. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; Volumes 1–12, pp. 4105–4110. [Google Scholar]
- Cao, C.; Hovakimyan, N. Design and analysis of a novel L1 adaptive controller, part II: Guaranteed transient performance. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; Volumes 1–12, pp. 3403–3408. [Google Scholar]
- Cao, C.Y.; Hovakimyan, N. Novel L1 neural network adaptive control architecture with guaranteed transient performance. IEEE Trans. Neural Netw. 2007, 18, 1160–1171. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.Y.; Hovakimyan, N. Guaranteed transient performance with L1 adaptive controller for parametric strict feedback systems. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; Volumes 1–13, pp. 2301–2306. [Google Scholar]



| Variable | Value | Units |
|---|---|---|
| 0.504 | m | |
| 0.504 | m | |
| [30,30,150,150,270,270] | deg | |
| [0,60,120,180,240,300] | deg | |
| 28.7 | kg | |
| 2.77 | kg | |
| 0.54 | kg | |
| 0.5456 | ||
| 0.305 | ||
| 1.13 | ||
| 1.13 | ||
| 2.23 | ||
| 0.21 | ||
| 0.21 | ||
| 0.001 | ||
| 0.0677 | ||
| 0.0677 | ||
| 0.000114 | ||
| [0,9.8,0] | N/kg |
| Variable | Value | Units |
|---|---|---|
| m | ||
| m | ||
| m | ||
| m | ||
| deg | ||
| 1.6 | rad/s | |
| 80 | - | |
| 150,000 | - | |
| diag[10,10,10,10,10,10] | - | |
| diag[0.7,0.7,0.7,0.7,0.7,0.7] | - | |
| - | ||
| - | ||
| - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Wu, D.; Gu, H.
Performance Evaluation of Stewart-Gough Flight Simulator Based on
Zhao J, Wu D, Gu H.
Performance Evaluation of Stewart-Gough Flight Simulator Based on
Zhao, Jiangwei, Dongsu Wu, and Hongbin Gu.
2021. "Performance Evaluation of Stewart-Gough Flight Simulator Based on
Zhao, J., Wu, D., & Gu, H.
(2021). Performance Evaluation of Stewart-Gough Flight Simulator Based on





