Total Potential Optimization Using Metaheuristic Algorithms for Solving Nonlinear Plane Strain Systems
Abstract
1. Introduction
2. Methods
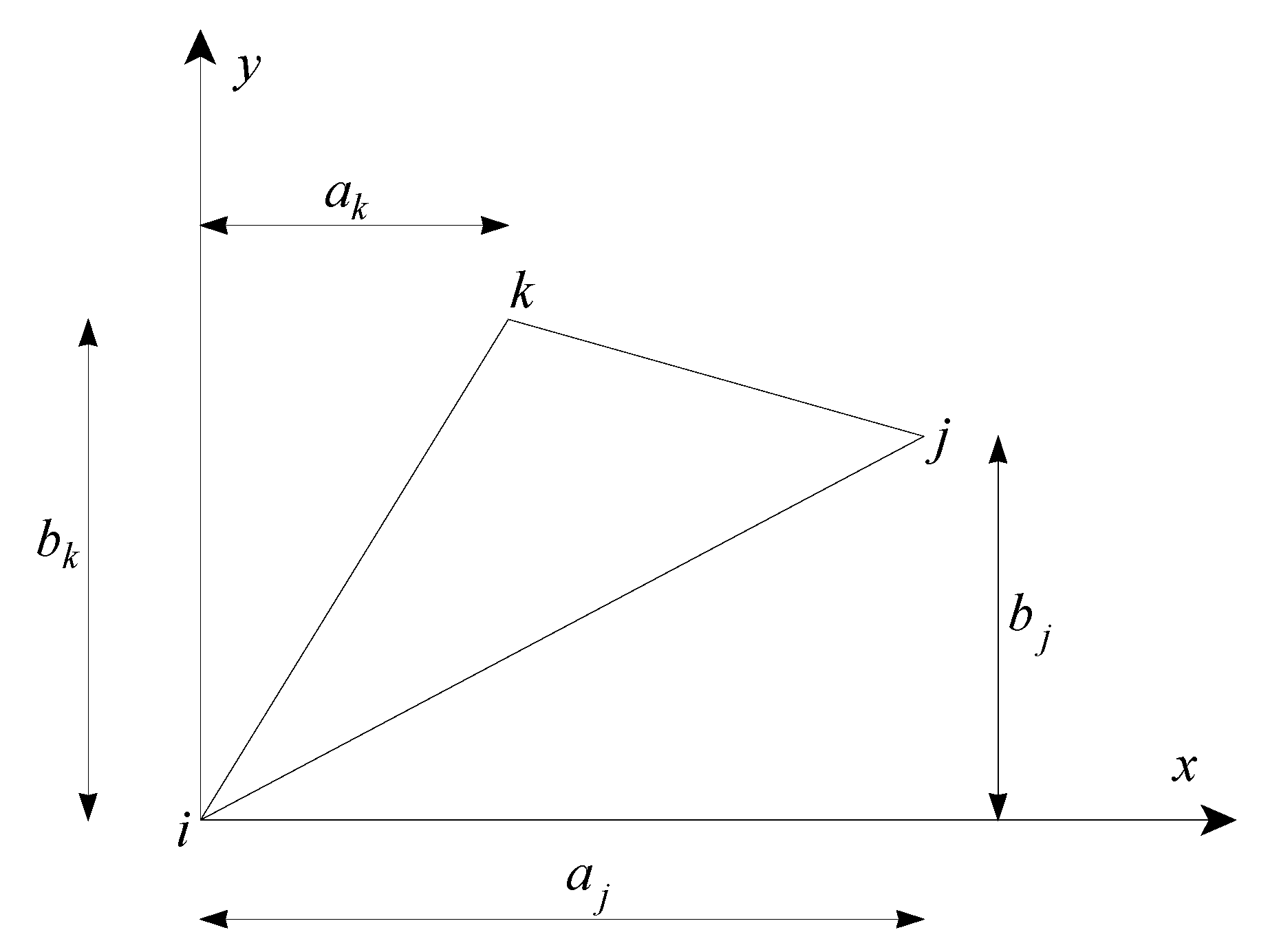
2.1. The Total Potential Energy of Plane Stress Members
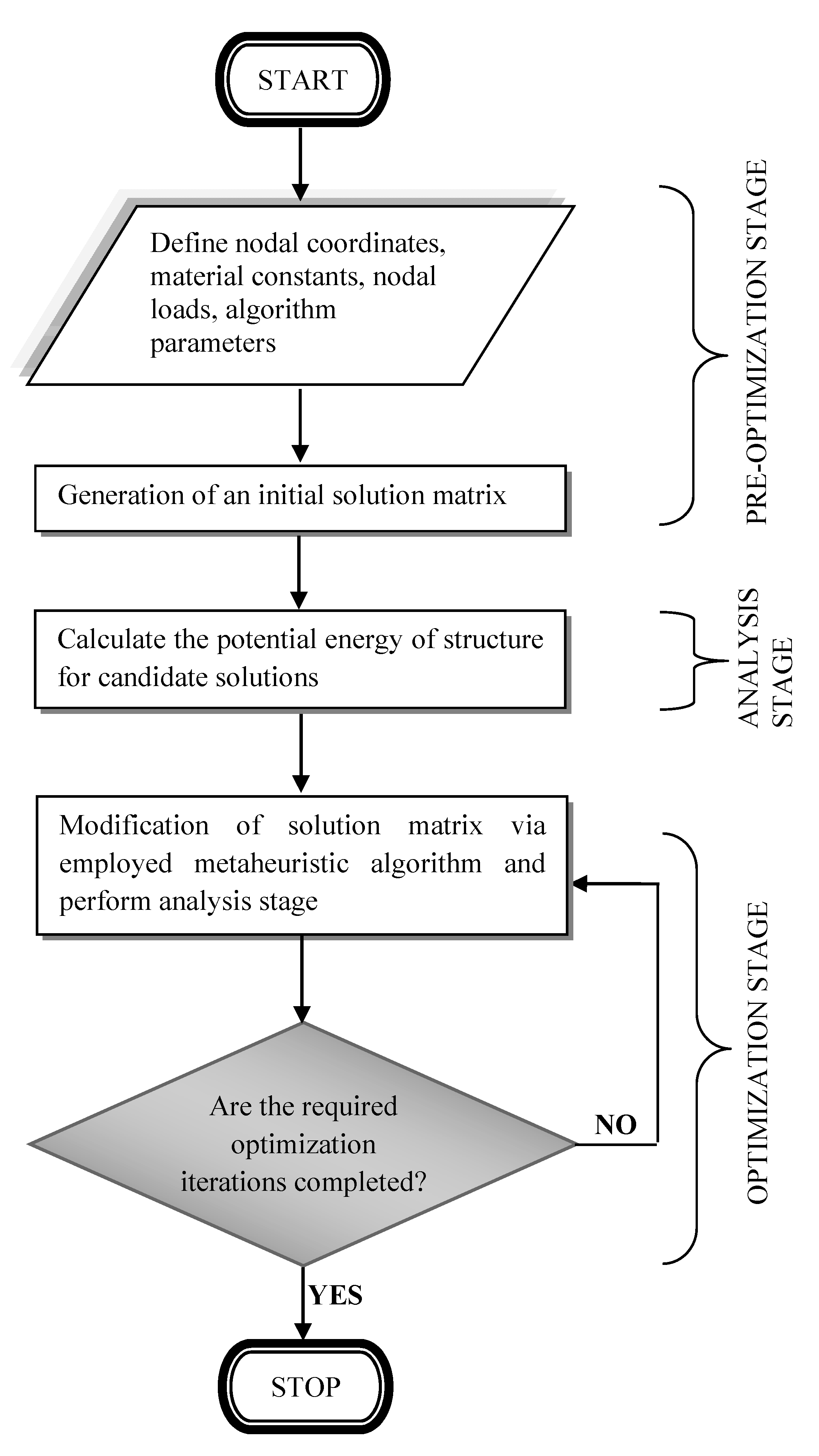
2.2. Optimization Process Via TPO/MA
2.3. Structural Models
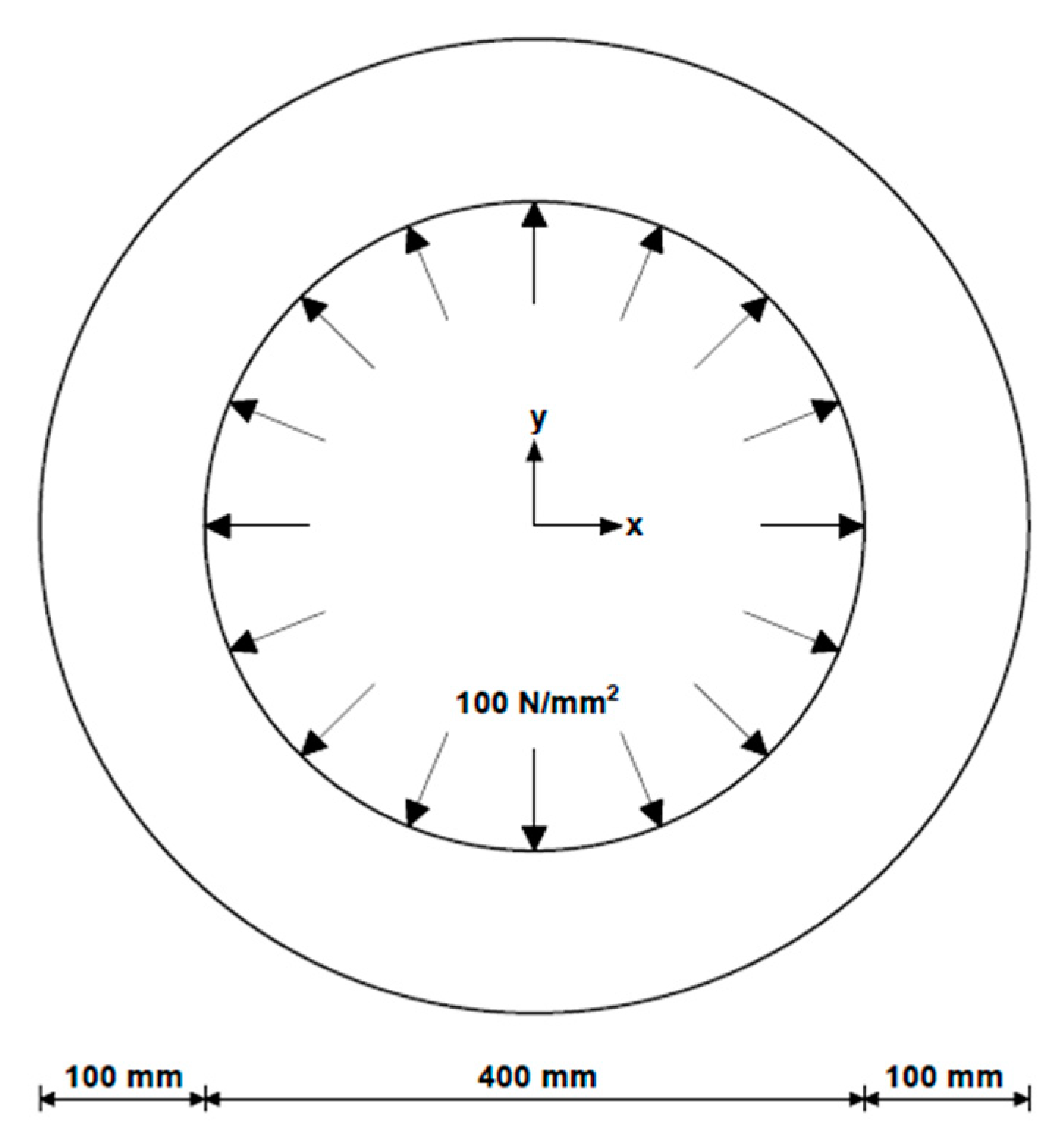
2.3.1. Structure 1: A Pipe with a Thick-Wall Subjected to Internal Pressure
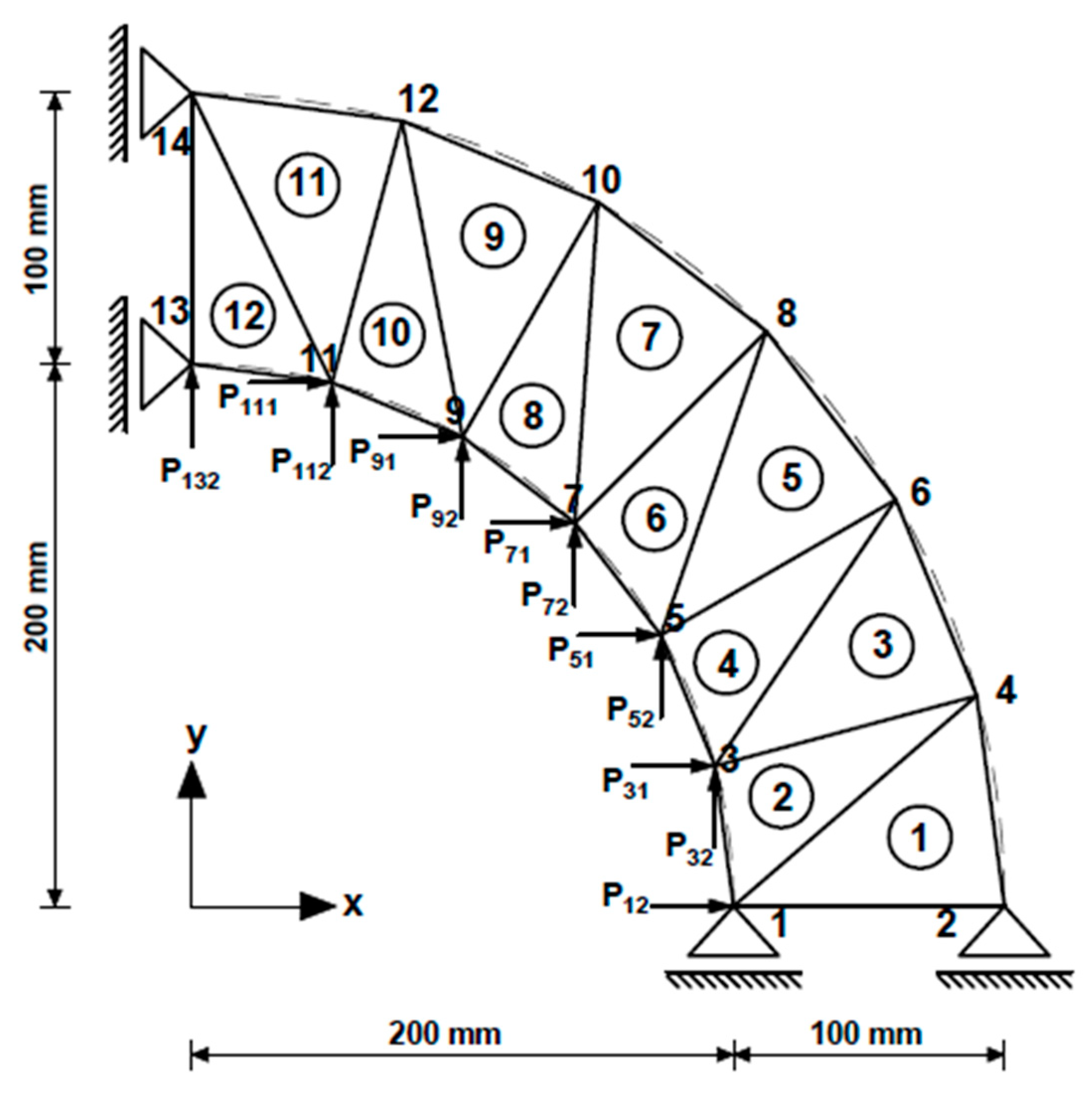
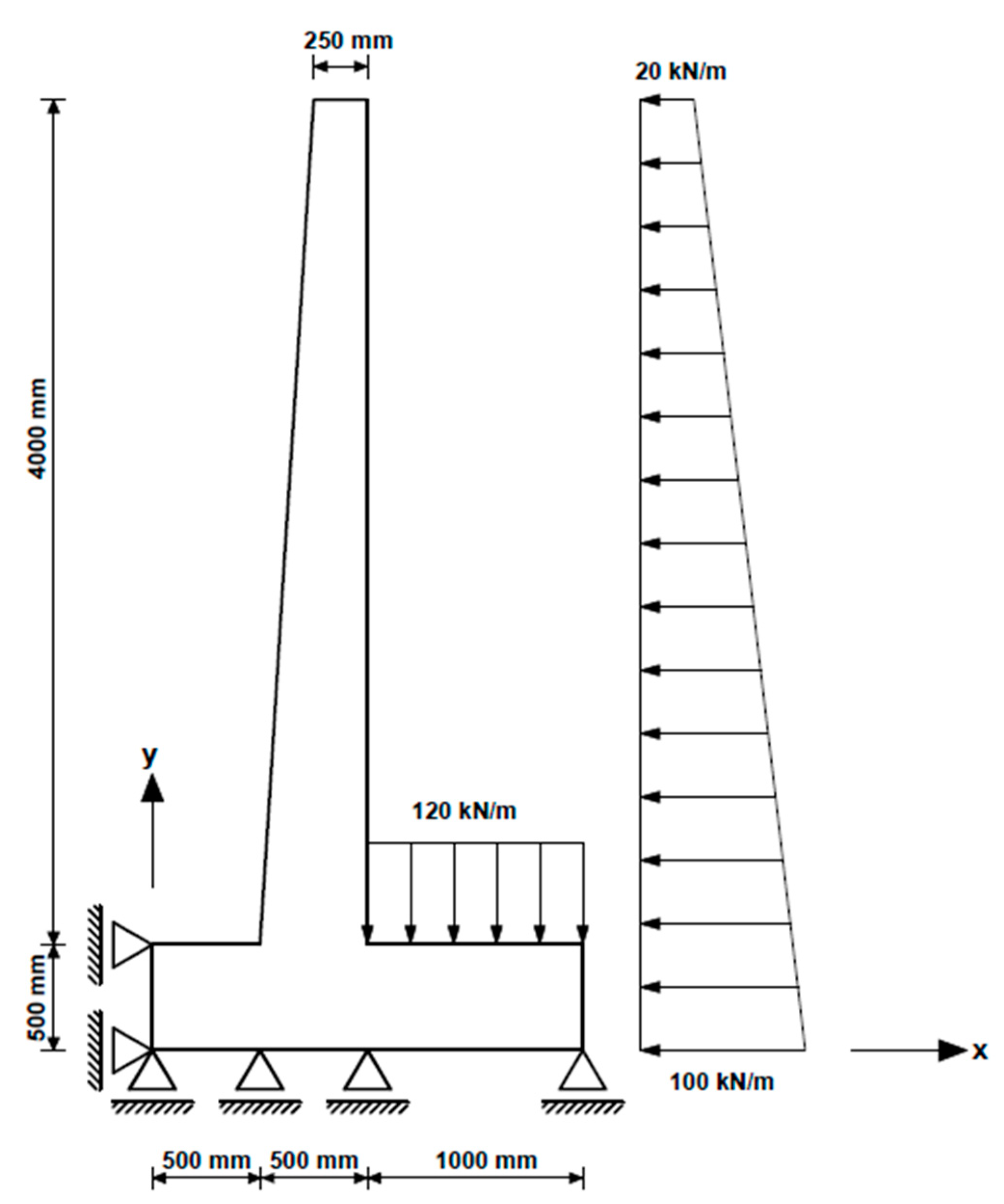
2.3.2. Structure 2: A Cantilever Retaining Wall (with 14 Members-16 Nodes)
3. Results
3.1. Structure 1
3.1.1. Linear Analysis to Evaluate Nine Employed Metaheuristics
3.1.2. Nonlinear Analysis by Employing AHS
3.1.3. Advanced Case of Structure 1 with 12 Members-14 Nodes
3.2. Structure 2
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saffari, H.; Fadaee, M.J.; Tabatabaei, R. Nonlinear Analysis of Space Trusses Using Modified Normal Flow Algorithm. J. Struct. Eng. 2008, 134, 998–1005. [Google Scholar] [CrossRef]
- Krenk, S. Non-Linear Modeling and Analysis of SOLIDS and Structures; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Greco, M.; Menin, R.; Ferreira, I.; Barros, F. Comparison between two geometrical nonlinear methods for truss analyses. Struct. Eng. Mech. 2012, 41, 735–750. [Google Scholar] [CrossRef]
- Levy, R.; Spillers, W.R. Analysis of Geometrically Nonlinear Structures; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Toklu, Y.C. Nonlinear analysis of trusses through energy minimization. Comput. Struct. 2004, 82, 1581–1589. [Google Scholar] [CrossRef]
- Toklu, Y.C.; Bekdaş, G.; Nigdeli, S.M. Analysis of under-constrained and unstable structures by the method TPO/MA. In Proceedings of the 15th International Conference of Numerical Analysis and Applied Mathematics, Thessaloniki, Greece, 25–30 September 2017. [Google Scholar]
- Kayabekir, A.E.; Bekdaş, G.; Nigdeli, S.M.; Toklu, Y.C. The Population Factor on Metaheuristic Based Analyses of Truss Structures. In Proceedings of the International Conference on Bioinspired Optimization Methods and their Applications (BIOMA 2018), Paris, France, 16–18 May 2018. [Google Scholar]
- Bekdaş, G.; Kayabekir, A.E.; Nigdeli, S.M.; Toklu, Y.C. Advanced energy-based analyses of trusses employing hybrid metaheuristics. Struct. Des. Tall Spéc. Build. 2019, 28, e1609. [Google Scholar] [CrossRef]
- Toklu, Y.C.; Uzun, F. Analysis of tensegric structures by total potential optimization using metaheuristic algorithms. J. Aerosp. Eng. 2016, 29, 04016023. [Google Scholar] [CrossRef]
- Bekdaş, G.; Kayabekir, A.E.; Nigdeli, S.M.; Toklu, Y.C. Analyses of cable nets by using energy minimization using several metaheuristic methods. In Proceedings of the International Conference on Bioinspired Optimization Methods and their Applications (BIOMA 2018), Paris, France, 16–18 May 2018. [Google Scholar]
- Nigdeli, S.M.; Bekdaş, G.; Toklu, Y.C. Total Potential Energy Minimization Using Metaheuristic algorithms for Spatial Cable Systems with increasing Second Order Effects. In Proceedings of the 12th International Congress on Mechanics (HSTAM2019), Thessaloniki, Greece, 22–25 September 2019. [Google Scholar]
- Kayabekir, A.E.; Toklu, Y.C.; Bekdaş, G.; Nigdeli, S.M.; Yücel, M.; Geem, Z.W. A Novel Hybrid Harmony Search Approach for the Analysis of Plane Stress Systems via Total Potential Optimization. Appl. Sci. 2020, 10, 2301. [Google Scholar] [CrossRef]
- Toklu, Y.C.; Kayabekir, A.E.; Bekdaş, G.; Nigdeli, S.M.; Yücel, M. Analysis of Plane-Stress Systems via Total Potential Optimization Method Considering Nonlinear Behavior. J. Struct. Eng. 2020, 146, 04020249. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution–A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department: Kayseri, Turkey, 2005; Volume 200, pp. 1–10. [Google Scholar]
- Karaboga, D.; Basturk, B. Artificial Bee Colony (ABC) Optimization Algorithm for Solving Constrained Optimization Problems. In Proceedings of the International Fuzzy Systems Association World Congress, Cancun, Mexico, 27–30 June 2007; Springer: Berlin/Heidelberg, Germany; pp. 789–798. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Yang, X.S. Flower pollination algorithm for global optimization. In Proceedings of the International Conference on Unconventional Computing and Natural Computation, Orléans, France, 3–7 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 240–249. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Topçu, A. Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi. 2015. Available online: http://mmf2.ogu.edu.tr/atopcu/ (accessed on 1 April 2019).


| TPOMA | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Пp (Nmm) | ||||||
| Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | ||
| FEM | 0.472 | 0.000 | 0.424 | 0.000 | 0.370 | 0.370 | 0.297 | 0.297 | 0.000 | 0.472 | 0.000 | 0.424 | −7611.581 |
| GA | 2.208 | 0.000 | 2.239 | 0.000 | 1.521 | 0.054 | 1.168 | 0.131 | 0.000 | −0.698 | 0.000 | −0.980 | 34,413.583 |
| DE | 0.472 | 0.000 | 0.424 | 0.000 | 0.370 | 0.370 | 0.297 | 0.297 | 0.000 | 0.472 | 0.000 | 0.424 | −7611.581 |
| PSO | 0.393 | 0.000 | 0.335 | 0.000 | 0.329 | 0.430 | 0.272 | 0.336 | 0.000 | 0.577 | 0.000 | 0.529 | −7511.990 |
| HS | 0.471 | 0.000 | 0.424 | 0.000 | 0.369 | 0.362 | 0.294 | 0.290 | 0.000 | 0.474 | 0.000 | 0.424 | −7607.300 |
| AHS | 0.472 | 0.000 | 0.424 | 0.000 | 0.370 | 0.370 | 0.297 | 0.297 | 0.000 | 0.472 | 0.000 | 0.424 | −7611.581 |
| ABC | −0.389 | 0.000 | −0.486 | 0.000 | −0.185 | 0.325 | −0.039 | 0.320 | 0.000 | 0.492 | 0.000 | 0.461 | 470.741 |
| TLBO | 0.472 | 0.000 | 0.424 | 0.000 | 0.370 | 0.370 | 0.297 | 0.297 | 0.000 | 0.472 | 0.000 | 0.424 | −7611.581 |
| FPA | 0.472 | 0.000 | 0.424 | 0.000 | 0.370 | 0.370 | 0.297 | 0.297 | 0.000 | 0.472 | 0.000 | 0.424 | −7611.581 |
| GWO | −0.656 | 0.000 | 0.037 | 0.000 | −0.400 | −2.337 | 0.816 | −2.336 | 0.000 | 0.048 | 0.000 | −0.553 | 359,953.164 |
| JA | 0.472 | 0.000 | 0.424 | 0.000 | 0.370 | 0.370 | 0.297 | 0.297 | 0.000 | 0.472 | 0.000 | 0.424 | −7611.581 |
| Best Methods | Пp (Nmm) | Mean of Пp (Nmm) | Standard Deviation of Пp (Nmm) | Best Iteration |
|---|---|---|---|---|
| DE | −7611.581 | −7611.581 | 0.000000000002 | 93,515 |
| TLBO | −7611.581 | −7611.581 | 0.000000000002 | 4882 |
| FPA | −7611.581 | −7611.581 | 0.000000000002 | 2824 |
| JA | −7611.581 | −7611.581 | 0.000000000002 | 10,698 |
| AHS | −7611.581 | −7611.581 | 0.000000000002 | 2023 |
| TPOMA (linear) | TPOMA (Nonlinear 1) | TPOMA (Nonlinear 2) | TPOMA (Nonlinear 3) | |||||
|---|---|---|---|---|---|---|---|---|
| Node | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) |
| 1 | 0.475 | 0 | 24.576 | 0 | 0.9436 | 0.0000 | 24.2151 | 0.0000 |
| 2 | 0.424 | 0 | −13.677 | 0 | 0.8473 | 0.0000 | 15.3721 | 0.0000 |
| 3 | 0.370 | 0.370 | 79.170 | 79.170 | 0.7392 | 0.7392 | 24.4123 | 24.4124 |
| 4 | 0.297 | 0.297 | 74.359 | 74.359 | 0.5936 | 0.5936 | 24.1185 | 24.1185 |
| 5 | 0 | 0.472 | 0 | 24.576 | 0.0000 | 0.9436 | 0.0000 | 24.2157 |
| 6 | 0 | 0.424 | 0 | −13.677 | 0.0000 | 0.8473 | 0.0000 | 15.3726 |
| Пp (Nmm) | −7611.581 | −7.3478558728 × 107 | −15,223.1614 | −674,376.1117 | ||||
| ν | TPOMA (Linear) | TPOMA (Nonlinear 1) | TPOMA (Nonlinear 2) | TPOMA (Nonlinear 3) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Node | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | |
| 0.27 | 1 | 0.4694 | 0.0000 | 25.6721 | 0.0000 | 0.9389 | 0.0000 | 20.1678 | 0.0000 |
| 2 | 0.4171 | 0.0000 | −14.9597 | 0.0000 | 0.8341 | 0.0000 | 10.1456 | 0.0000 | |
| 3 | 0.3696 | 0.3696 | 85.3729 | 85.3729 | 0.7392 | 0.7392 | 28.1996 | 28.1996 | |
| 4 | 0.2920 | 0.2920 | 79.8247 | 79.8247 | 0.5841 | 0.5841 | 26.3712 | 26.3712 | |
| 5 | 0.0000 | 0.4694 | 0.0000 | 25.6721 | 0.0000 | 0.9389 | 0.0000 | 20.1678 | |
| 6 | 0.0000 | 0.4171 | 0.0000 | −14.9597 | 0.0000 | 0.8341 | 0.0000 | 10.1456 | |
| Пp (Nmm) | −7593.8609 | −101,203,819.3376 | −15,187.7219 | −689,396.1522 | |||||
| 0.28 | 1 | 0.4681 | 0.0000 | 26.2344 | 0.0000 | 0.9362 | 0.0000 | 19.5071 | 0.0000 |
| 2 | 0.4136 | 0.0000 | −15.5831 | 0.0000 | 0.8273 | 0.0000 | 9.0151 | 0.0000 | |
| 3 | 0.3696 | 0.3696 | 88.4359 | 88.4359 | 0.7391 | 0.7391 | 29.2697 | 29.2697 | |
| 4 | 0.2895 | 0.2895 | 82.5355 | 82.5355 | 0.5791 | 0.5791 | 27.1497 | 27.1497 | |
| 5 | 0.0000 | 0.4681 | 0.0000 | 26.2344 | 0.0000 | 0.9362 | 0.0000 | 19.5071 | |
| 6 | 0.0000 | 0.4136 | 0.0000 | −15.5831 | 0.0000 | 0.8273 | 0.0000 | 9.0151 | |
| Пp (Nmm) | −7583.2397 | −118,167,986.0712 | −151,66.4795 | −699,183.7821 | |||||
| 0.29 | 1 | 0.4667 | 0.0000 | 26.8047 | 0.0000 | 0.9334 | 0.0000 | 19.0866 | 0.0000 |
| 2 | 0.4101 | 0.0000 | −16.1982 | 0.0000 | 0.8202 | 0.0000 | 8.1306 | 0.0000 | |
| 3 | 0.3695 | 0.3695 | 91.4805 | 91.4805 | 0.7390 | 0.7390 | 30.2294 | 30.2294 | |
| 4 | 0.2869 | 0.2869 | 85.2366 | 85.2366 | 0.5739 | 0.5739 | 27.9006 | 27.9006 | |
| 5 | 0.0000 | 0.4667 | 0.0000 | 26.8047 | 0.0000 | 0.9334 | 0.0000 | 19.0866 | |
| 6 | 0.0000 | 0.4101 | 0.0000 | −16.1982 | 0.0000 | 0.8202 | 0.0000 | 8.1306 | |
| Пp (Nmm) | −7571.4371 | −137,625,581.0665 | −15,142.8743 | −709,938.7099 | |||||
| 0.30 | 1 | 0.4652 | 0.0000 | 27.3819 | 0.0000 | 0.9304 | 0.0000 | 18.7847 | 0.0000 |
| 2 | 0.4064 | 0.0000 | −16.8072 | 0.0000 | 0.8128 | 0.0000 | 7.3561 | 0.0000 | |
| 3 | 0.3694 | 0.3694 | 94.5115 | 94.5115 | 0.7387 | 0.7387 | 31.1627 | 31.1627 | |
| 4 | 0.2843 | 0.2843 | 87.9316 | 87.9316 | 0.5686 | 0.5686 | 28.6625 | 28.6625 | |
| 5 | 0.0000 | 0.4652 | 0.0000 | 27.3819 | 0.0000 | 0.9304 | 0.0000 | 18.7847 | |
| 6 | 0.0000 | 0.4064 | 0.0000 | −16.8072 | 0.0000 | 0.8128 | 0.0000 | 7.3561 | |
| Пp (Nmm) | −7558.4473 | −159,977,948.1027 | −15,116.8946 | −721,624.5843 | |||||
| Concentrated Loads (N) | ||
|---|---|---|
| Node | x Direction | y Direction |
| 1 | P11 = 2610.5 | P12 = 171.1 |
| 3 | P31 = 5043.1 | P32 = 1351.3 |
| 5 | P51 = 4521.6 | P52 = 2610.5 |
| 7 | P71 = 3691.8 | P72 = 3691.8 |
| 9 | P91 = 2610.5 | P92 = 4521.6 |
| 11 | P111 = 1351.3 | P112 = 5043.1 |
| 13 | P113 = 171.1 | P113 = 2610.5 |
| FEM (Linear) | TPOMA (Linear) | TPOMA (Nonlinear 1) | TPOMA (Nonlinear 2) | TPOMA (Nonlinear 3) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Node | Δx (mm) | Δx (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) | Δx (mm) | Δy (mm) |
| 1 | 0.479 | 0.000 | 0.479 | 0.000 | 29.882 | 0.000 | 0.959 | 0.000 | 27.652 | 0.000 |
| 2 | 0.422 | 0.000 | 0.422 | 0.000 | −0.219 | 0.000 | 0.845 | 0.000 | 20.305 | 0.000 |
| 3 | 0.480 | 0.131 | 0.480 | 0.131 | 40.580 | 25.3407 | 0.961 | 0.261 | 28.044 | 9.018 |
| 4 | 0.404 | 0.104 | 0.404 | 0.104 | 8.190 | 18.872 | 0.807 | 0.208 | 18.110 | 6.868 |
| 5 | 0.442 | 0.254 | 0.442 | 0.254 | 59.811 | 53.252 | 0.883 | 0.508 | 28.741 | 18.130 |
| 6 | 0.368 | 0.210 | 0.368 | 0.210 | 40.500 | 48.925 | 0.736 | 0.420 | 21.545 | 16.379 |
| 7 | 0.373 | 0.373 | 0.373 | 0.373 | 86.303 | 86.303 | 0.746 | 0.746 | 24.585 | 24.585 |
| 8 | 0.294 | 0.294 | 0.294 | 0.294 | 84.501 | 84.501 | 0.588 | 0.588 | 25.376 | 25.376 |
| 9 | 0.254 | 0.442 | 0.254 | 0.442 | 53.252 | 59.811 | 0.508 | 0.883 | 18.130 | 28.741 |
| 10 | 0.210 | 0.368 | 0.210 | 0.368 | 48.925 | 40.500 | 0.420 | 0.736 | 16.379 | 21.545 |
| 11 | 0.131 | 0.480 | 0.131 | 0.480 | 25.341 | 40.580 | 0.261 | 0.961 | 9.018 | 28.044 |
| 12 | 0.104 | 0.404 | 0.104 | 0.404 | 18.872 | 8.190 | 0.208 | 0.807 | 6.868 | 18.110 |
| 13 | 0.000 | 0.479 | 0.000 | 0.479 | 0 | 29.882 | 0.000 | 0.959 | 0.000 | 27.652 |
| 14 | 0.000 | 0.422 | 0.000 | 0.422 | 0 | −0.219 | 0.000 | 0.845 | 0.000 | 20.305 |
| Пp (Nmm) | −7887.851 | −1.09356257515 × 108 | −15,775.702 | −740,764.295 | ||||||
| FEM (Linear) | TPOMA (Linear) | TPOMA (Nonlinear 1) | TPOMA (Nonlinear 2) | TPOMA (Nonlinear 3) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Node | Δx (m) | Δy (m) | Δx (m) | Δy (m) | Δx (m) | Δy (m) | Δx (m) | Δy (m) | Δx (m) | Δy (m) |
| 1 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 2 | 0.000000 | −0.000002 | 0.000000 | −0.000002 | 0.000000 | −0.176510 | 0.000000 | −0.000002 | 0.000000 | −0.002403 |
| 3 | −0.000002 | 0.000000 | −0.000002 | 0.000000 | 0.176644 | 0.000000 | −0.000002 | 0.000000 | −0.002019 | 0.000000 |
| 4 | −0.000010 | −0.000014 | −0.000010 | −0.000014 | −0.177006 | −0.177006 | −0.000010 | −0.000014 | −0.013126 | −0.012299 |
| 5 | −0.000013 | 0.000000 | −0.000013 | 0.000000 | 0.353080 | 0.000000 | −0.000013 | 0.000000 | −0.017347 | 0.000000 |
| 6 | −0.000014 | 0.000011 | −0.000014 | 0.000011 | 0.353137 | −0.176261 | −0.000014 | 0.000011 | −0.022839 | 0.014085 |
| 7 | −0.000018 | 0.000000 | −0.000018 | 0.000000 | 0.706119 | 0.000000 | −0.000018 | 0.000000 | −0.035964 | 0.000000 |
| 8 | −0.000020 | 0.000000 | −0.000020 | 0.000000 | 0.706354 | −0.177103 | −0.000020 | 0.000000 | −0.042223 | 0.005558 |
| 9 | −0.000140 | −0.000032 | −0.000141 | −0.000032 | 0.193755 | −0.531293 | −0.000140 | −0.000032 | −0.118902 | −0.024612 |
| 10 | −0.000139 | 0.000036 | −0.000140 | 0.000036 | 0.349492 | −0.528870 | −0.000138 | 0.000036 | −0.112289 | 0.035232 |
| 11 | −0.000340 | −0.000031 | −0.000342 | −0.000032 | 0.211354 | −0.884866 | −0.000339 | −0.000031 | −0.283322 | −0.027028 |
| 12 | −0.000339 | 0.000047 | −0.000341 | 0.000047 | 0.342311 | −0.881895 | −0.000338 | 0.000047 | −0.278773 | 0.042540 |
| 13 | −0.000573 | −0.000022 | −0.000576 | −0.000023 | 0.224691 | −1.237878 | −0.000571 | −0.000022 | −0.492982 | −0.024042 |
| 14 | −0.000573 | 0.000050 | −0.000576 | 0.000050 | 0.334289 | −1.235242 | −0.000571 | 0.000050 | −0.490333 | 0.045575 |
| 15 | −0.000814 | −0.000009 | −0.000818 | −0.000009 | 0.237355 | −1.590342 | −0.000811 | −0.000009 | −0.730701 | −0.015649 |
| 16 | −0.000814 | 0.000051 | −0.000818 | 0.000051 | 0.325597 | −1.588350 | −0.000811 | 0.000051 | −0.729844 | 0.042830 |
| Пp (kNm) | −0.031567 | −1,385,982.025122 | −0.031567 | −40.719902 | ||||||
| ν | TPOMA (Linear) | TPOMA (Nonlinear 1) | TPOMA (Nonlinear 2) | TPOMA (Nonlinear 3) |
|---|---|---|---|---|
| 0.15 | −0.031403525 | −654458.4484 | −0.031403525 | −39.59712014 |
| 0.16 | −0.031457332 | −771097.8575 | −0.031457332 | −39.81729795 |
| 0.17 | −0.031501216 | −900090.841 | −0.031501216 | −40.03945641 |
| 0.18 | −0.031534625 | −1044225.23 | −0.031534625 | −40.26378793 |
| 0.19 | −0.031556952 | −1205801.743 | −0.031556952 | −40.49051621 |
| 0.2 | −0.031567536 | −1385982.025 | −0.031567536 | −40.71990187 |
| 0.21 | −0.031565648 | −1586562.796 | −0.031565648 | −40.95224928 |
| 0.22 | −0.031550489 | −1812681.81 | −0.031550489 | −41.18791476 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toklu, Y.C.; Bekdaş, G.; Yücel, M.; Nigdeli, S.M.; Kayabekir, A.E.; Kim, S.; Geem, Z.W. Total Potential Optimization Using Metaheuristic Algorithms for Solving Nonlinear Plane Strain Systems. Appl. Sci. 2021, 11, 3220. https://doi.org/10.3390/app11073220
Toklu YC, Bekdaş G, Yücel M, Nigdeli SM, Kayabekir AE, Kim S, Geem ZW. Total Potential Optimization Using Metaheuristic Algorithms for Solving Nonlinear Plane Strain Systems. Applied Sciences. 2021; 11(7):3220. https://doi.org/10.3390/app11073220
Chicago/Turabian StyleToklu, Yusuf Cengiz, Gebrail Bekdaş, Melda Yücel, Sinan Melih Nigdeli, Aylin Ece Kayabekir, Sanghun Kim, and Zong Woo Geem. 2021. "Total Potential Optimization Using Metaheuristic Algorithms for Solving Nonlinear Plane Strain Systems" Applied Sciences 11, no. 7: 3220. https://doi.org/10.3390/app11073220
APA StyleToklu, Y. C., Bekdaş, G., Yücel, M., Nigdeli, S. M., Kayabekir, A. E., Kim, S., & Geem, Z. W. (2021). Total Potential Optimization Using Metaheuristic Algorithms for Solving Nonlinear Plane Strain Systems. Applied Sciences, 11(7), 3220. https://doi.org/10.3390/app11073220









