1. Introduction
The surge of high speed communication services has accelerated the demand for efficient communication techniques that have the potential to make reliable data transmissions without compromising on data rates. In this regard, space time block codes (STBCs), based on orthogonal designs, are considered one of the key techniques that have moved the capacity of wireless communication close to theoretical limits. STBCs have been used extensively such as in third generation (3G) standard and wireless local area networks (LANs) based on IEEE 802.11n. Initially, they were proposed by Tarokh et al. [
1] as a generalization of the famous Alamouti code which is a complex orthogonal design (COD) [
2]. The most attractive feature of these orthogonal designs is the provision of full diversity along with low complexity maximum-likelihood (ML) decoder. However, they achieve this attribute at the expense of code rate, that is, the ratio of the number of independent complex transmitted symbols and the number of total time slots taken to transmit a coding matrix. On the other hand, a COD with full rate and maximum diversity exists only for two single-polarized transmit antennas and maximum code rate approaches half with as the number of transmit antennas increase [
3]. To meet higher data rate demands, other designs such as complex quasi-orthogonal STBCs have also been explored that provide comparatively higher code rates but compromise on optimal decoders due to nonlinear and coupled decoding issues [
4]. To further enhance the capacity of communication systems, other combinations of diversity providing techniques are being investigated.
In [
5], orthogonally polarized transmissions through both ends of a dual-polarized antenna were modeled through quaternions and later [
6] laid the foundation of orthogonal space time polarization block codes (OSTPBCs) that utilize polarization diversity together with space and time diversity. Polarization diversity can provide nearly similar performance to spatial diversity without any measurable increase in antenna dimensions [
7]. This is achieved with the use of dual-polarized antennas, which have two antennas of orthogonal polarizations co-existing on a single antenna platform and there has been a growing interest recently [
8,
9].
Based on the combination of polarization diversity with space and time diversities, various quaternion orthogonal design (QOD) construction techniques have been proposed by Seberry et al. [
6]. The primary motivation of these designs has been their ability to provide higher code rates along with a low complexity quaternion norm-based ML decoder. To illustrate the benefit of these designs, [
6] presented an example of
order QOD and derived linear equation based decoding solution for this configuration. They argued that quaternion decoding statistics can provide decoupled decoding for any QOD. Their subsequent studies [
10,
11] used the same QOD and emphasized the similar postulate that quaternion ML norm can provide optimal decoupled decoding for any QOD construction. However, the authors corrected their decoding rule in [
12] and highlighted that the proposed decoding rule does not yield optimal decoding for all QODs, and therefore, the design of semi-optimal or optimal low complexity decoders remained an open research problem [
13]. In this regard, a recent work [
14], explored the designs for which quaternion norm-based ML decoder resulted in optimal decoding solutions. However, it is important to note that their proposed ML decoder works for a special class of STBCs.
In this paper, we investigate three famous generalized QOD construction techniques [
14] and identify two main short falls which restricts their use for large MIMO systems. Firstly, this iterative approach works only in the case when the number of transmit antennas are in powers of 2, which clearly restricts their use to other antenna configurations. Secondly, the code rate decreases very sharply for higher order designs based on these iterative techniques. Therefore, it was deem necessary to develop codes that work for any number of antenna systems besides having the main advantage of attaining decoupled decoders in the presence of quaternionic channel as was the case with iteratively generated designs [
14]. This has been done following the line of approach indicated in [
3] which gives us a class of QODs that are non-square and the code rate is bounded below by 1/2. The motivation behind this was to exploit the impact of a dual-polarized transmission channel at the receiver side in such a way that ML quaternion norm criterion simplifies to a decoupled decoding solution which reduces the decoder complexity significantly.
After obtaining a generalized ML decoder, we take one step further by exploring quasi-QODs. The proposed quasi-QOD provides a code rate of two for four transmit dual-polarized antennas. However, the quasi nature of these codes leads to a slight comprise on decoding complexity. The solutions obtained with this compromised complexity-based decoder are still better than the coupled traditional ML decoder based solutions. A detailed complexity analysis of the proposed constructions have been provided to illustrate the significance of the proposed low-complexity decoder for both pure or quasi QODs.
Briefly, we summarize the main contributions made in this paper.
We propose a new class of QODs based on Liang mechanism [
3] with stable code rate as the number of transmit antennas increases.
The class is shown as best suitable in describing point-to-point communication among dual-polarized antennas.
The proposed decoder is shown to provide linear decoding solution for all STBCs obtained from QODs.
A brief performance analysis is carried out for all obtained QODs.
Some remarks on notation are as follows—all matrices are denoted with bold letters. The real and complex numbers fields are denoted in standard form and , respectively. ℜ and ℑ represent real and imaginary parts of a complex number. denotes a quaternion field comprise of a basis of non-commuting elements , such that . The superscript , refers to quaternion conjugate and responsible for sign changes in and k. In matrices, it also includes transpose . Moreover, operators and refer to the Hermitian transpose and trace operator, respectively. Both matrices and , corresponds to quasi-orthogonal STBCs; however, the subscript Q indicates that the STBC is obtained from a QOD.
2. Quaternion Orthogonal Designs
A quaternion consists of four real numbers such that ; . As the space is isomorphic to the complex space , therefore, we obtain an equivalent representation of a quaternion . This is more useful from the point of wireless communication among dual-polarized antennas. Consequently, it makes sense to talk about space-time-polarization block codes with quaternion elements and investigate orthogonality condition in the quaternion domain.
Definition 1. A QOD comprises of quaternion variables , is defined as an matrix which can have entries from the set including possible multiplications on the left and/or right by quaternion elements and satisfies the following conditionwhere λ is a positive real number and is an identity matrix. As mentioned before that a quaternion is a combination of two complex numbers
, therefore, it is natural to think of QODs satisfying
where
and
are two complex matrices. It turned out that any two arbitrary complex matrices do not necessarily give rise to a QOD which satisfies (
1). Essentially, the authors in [
6] found the key requirements on
and
to ensure (
1), for the resulting QOD. Interestingly, the
amicable and
symmetry conditions were found to play main role for which an extensive theory was already in place and they used it to generate class of QODs. Later it was found that all proposed quaternion-based designs employed symmetric-paired complex matrices. Since the symmetry property is crucial in our study therefore we state it for a brief and self-contained exposition.
Definition 2. Two CODs and based on complex variables form a symmetric-paired design provided or is symmetric.
A relatively simple way to find such symmetric-paired designs arise from the observation that swapping of certain columns of a COD generates an equivalent COD. The resulting COD along with the original COD form a symmetric-paired design. This technique was used in [
6], for the search of viable QODs. However, it is important to note that as the dimension of COD matrix gets larger, not every permutation of columns of a COD yields a valid QOD. Therefore, only one permutation per column is allowed to generate valid QODs under this construction [
15]. Below in
Section 2.2 and
Section 2.3, we will describe other possible ways to generate QODs. For square designs, three recursive construction methods to find CODs were presented in [
3], namely Adams-Lax-Phillips, Józefiak and Wolfe constructions. It is easy to realize that all three constructions recursively generate the same class of square QODs.
According to these constructions, a recursive COD
is designed for
symbols embedded in a square matrix of order
such that
where
represents a COD of order
defined on symbols
and
. For example, for
,
. Taking this as a seed element, higher order CODs such as
and
can be constructed [
3], recursively. In the subsections, this way of COD generation is used to form different generalized QOD constructions.
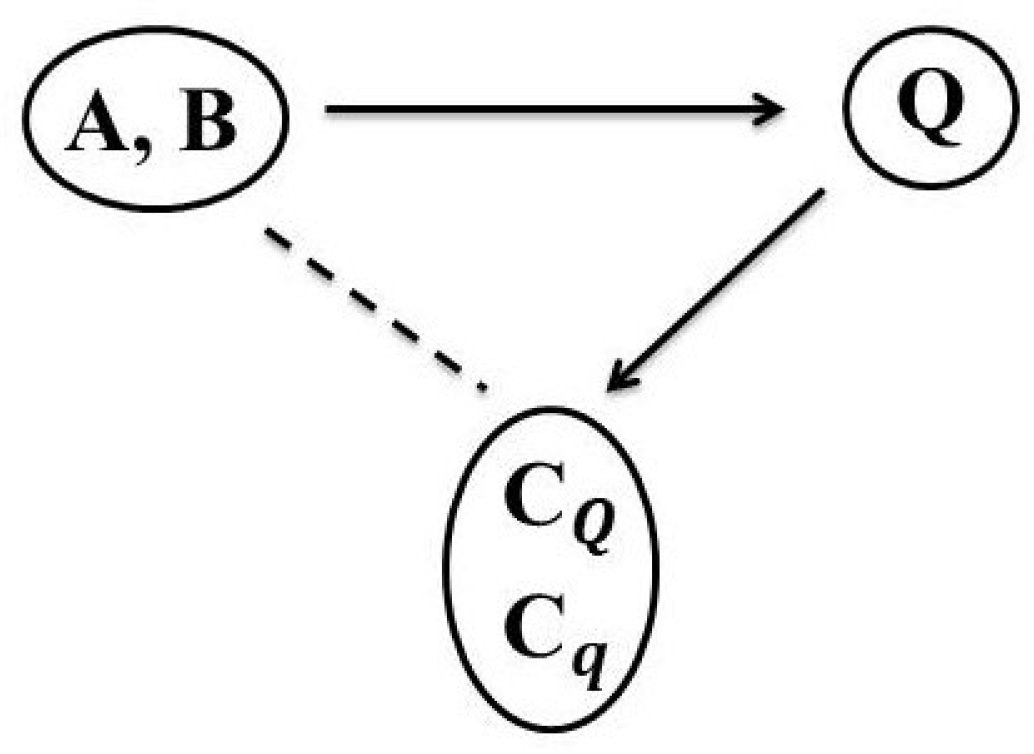
In
Figure 1, we briefly explain the basic nomenclature, which describes the main working in quaternion domain. We start with two CODs that form a symmetric-pair such that they give rise to a QOD. In earlier works, this was not directly used to describe communication among dual-polarized antennas. Rather, an STBC was constructed from a QOD and its even columns represent signals being sent through one polarization while entries in odd columns are signals transmitted through an orthogonal polarization plane. However, the simultaneous transmission through a dual-polarized antenna is being modeled by quaternions in this paper. Although, we have an enriched theory of quasi-orthogonal designs yet our main focus is to work on an approach which algorithmically identify among them, those designs that have decoders with two main characteristics, that is, linear and decoupled. In this work, we notice that the departure from the complex to quaternion domain serve this purpose. The dotted line connecting CODs
with quasi-STBCs
or
indicates a vivid difference between their working which distinguishes them in terms of code rates, decoding delays at both ends, zero vs non-zero entries, linear and decoupled decoders.
The generalized construction techniques employ (
2), which provides us the symmetric-paired square CODs that act as seeds to generate three classes of square and non-square QODs.
2.1. Symmetric-Paired Design 1: (Square QODs)
This construction technique constructs QODs
in which COD
is obtained from
through permutation of columns, where permutation operation on two columns
m and
n results in swapping the positions of these two columns with each other. For all CODs based on the permutation of CODs for a specific antenna dimension, the diversity order remains the same, therefore, without loss of generality we employ (
2) to arrive at the following result.
Theorem 1. For a given COD in (2) and its permuted version , a complex amicable and symmertic-paired design can be constructed such that the following realization,provides a QOD of dimension . The following example illustrates the construction in which we start with an Alamouti code
. Using (
2), we obtain a square matrix
of order 4. Consequently, we have a QOD.
Example 1. Using the permutation operation on , as described above and representing it with , we obtain following QOD , to be used in the configuration of 4 dual-polarized antennas This QOD transmits 3 complex symbols and in four time slots and provides a 3/4 code rate.
2.2. Symmetric-Paired Design 2: (Non-Square QODs)
The designs that do not necessarily require the use of permutation operations on columns are important for they do not limit code rates. This can be done through a relatively simple way to recursively generate QODs using a single COD and a square diagonal matrix containing an extra symbol. Therefore, these designs perform relatively better than the designs obtained from the first technique. Below we describe their generalized formulation.
Theorem 2. For a given square COD , the matrixprovides a quaternion design of order . We again start with an Alamouti code , to obtain a square COD following Wolfe construction which contains three symbols because , implies . Hence, we arrive at the following example.
Example 2. The COD along with a diagonal matrix containing an extra symbol in Equation (5) gives rise to This QOD transmits 4 complex symbols , and in eight time slots, thus provides a relatively better code rate of 1/2.
2.3. Symmetric-Paired Design 3: (Non-Square QODs)
We now come to address main issues related with quasi-CODs which promise a high data rate at the expense of coding and decoding delays besides coupled and non-linear decoding. This issue can be resolved in the quaternion domain. For example, in [
16], a quasi-COD of rate 1 was designed for four transmit antennas
using two CODs
and
, which was shown to have pair-wise decoding. We now subject these two CODs
and
to the quaternion domain which helps us reclaim decoupled and linear decoding solutions. First of all, we note that the concept used in design 2, can be generalized such that in place of a diagonal matrix which merely contains a single extra symbol, we can use a COD. It turns out that the following theorem provides us a possibility of incorporating
with
, in place of a diagonal matrix. Resultantly, we obtain another recursive construction technique which can be proved easily.
Theorem 3. For two recursively generated CODs and , a symmetric-paired design,is a QOD of dimension . It is easy to implement this technique as is shown in the subsequent example.
Example 3. To generate a QOD for 4 dual-polarized antenna, we use and to obtain two CODs of higher orders and using Wolfe construction. Consequently, Equation (8) gives rise to a QOD of rate Therefore, we have three recursive techniques to generate square and rectangular QODs from square CODs. As all of the above QODs are obtained from the recursive techniques of CODs based on famous Adams-Lax-Phillips, Józefiak and Wolfe constructions, therefore, we can use an upper bound on these to arrive at the following result.
Theorem 4. The rate , of all possible QODs in (3), (8) and (11) obtained from square CODs is given by This provides us a class of QODs, which are fully diverse [
17] and earlier these were shown to have decoupled decoders based on a semi-quaternionic channel model [
15]. In this paper we use the system model [
18] based on the characterization of pure quaternionic channel and it is shown that the above designs all have decoupled decoders and optimal decoding delays. Besides these advantages, there is one drawback as mentioned in the remark below.
Remark 1. All of the above construction techniques generate QODs for only configurations when the number of dual-polarized transmit antennas are in powers of 2, i.e, which puts a heavy toll on the code rate as sharply declines as the number of antennas increase.
Following above remark, it is essential to find quaternion designs for general configuration of dual-polarized antennas like for a –system such that and these codes have maximal coding rates. We developed such QODs in the subsequent section.
2.4. Maximal Rate QODs for General Configuration of Dual-Polarized Antennas
In Liang’s paper [
3], rectangular CODs of maximal rates are found algorithmically. The general procedure was given in the paper, however, such designs do not carry a compact form as was found in the case of (
2). As demonstrated below that our proposed procedure successfully works on the famous examples given in [
3], to generate designs for 3 and 5 dual-polarized antennas among other configurations, respectively.
Lemma 1. A maximal rate QOD for 3 dual-polarized antennas is given by Proof. We start with a rectangular COD of maximal rate
given by
and construct an equivalent COD
based on the same principle of permutation of columns such that
is symmetric which can be verified easily. Such an equivalent COD is
Consequently, we obtain a QOD for three dual-polarized antennas of rate 3/4 given by . □
To complete the discussion, we include one QOD which is suitable for 4 dual-polarized antennas and is obtained using Liang’s approach. This will be compared with the QODs based on recursive approach for the same number of antennas.
Lastly, we construct a QOD for 5 dual-polarized antennas.
Lemma 2. A maximal rate QOD for 5 dual-polarized antennas is given by Proof. The proof of this lemma is similar to the Lemma 1, however, in this case the underlying COD
is given in Equation (100) in [
3]. □
Following the same lines, it is easy to construct QODs for higher number of transmit antennas
starting with the CODs given in [
3] (Equation (101) and Appendices C and D, respectively).
4. Quaternionic Channel Model
The simultaneous transmission from both ends of a dual-polarized antenna can be regarded as a
hyper signal which consists of two complex numbers in two orthogonal polarizations. It propagates through space and received as a hyper signal by the dual-polarized antenna at the receiver end in a given time slot. This hyper signal can be represented as a quaternion [
5] which gives us a reason to develop system model in the quaternion domain. An important component of the system model is the channel which we assume to be quaternionic following the line of approach followed in [
18]. Therein, we observe that the product in the quaternion domain holds a key of consistent and viable model.
We first consider a two-input and single-output system (TISO) of dual-polarized antennas. It is necessary to emphasize the role of quaternions which is more recognizable in this case, therefore, we have
where each element in the above construction is a quaternion. Through each antenna in the above TISO system, the transmission of a pair of two complex symbols is encoded in
and another pair in
. This indicates that the above QOD exploits time and space diversities along with polarization diversity. It is worth pointing out that each quaternionic product, for example,
contains a crucial information about the nature of quaternion domain. If we decompose it for a general quaternionic product then we obtain
, where
and
. Therefore, we will obtain four complex channel gains for each antenna in a
system. Note that we have four complex channel gains between a TISO system of dual-polarized antennas. As this system is equivalent to a MIMO
system of single-polarized antennas, therefore, it may appear that it should have eight channel gains in total with two for each link. However, in our proposed model each quaternionic product results in the same number of channel gains.
Subsequently, a system model for a MIMO system of dual-polarized antennas can be constructed in the same way for such a system with
dual-polarized antennas
which transmits symbols in
–times slots, which are assumed to be points in the quadrature phase shift keying (QPSK) constellation. The channel matrix is
, where
and
. The channel is assumed to represent a flat fading channel and the path gain from
transmit dual-polarized antenna to receive dual-polarized antenna
given by a quaternion
. The complex channel gains,
and
incorporate the effects of cross polar scattering and each element of channel gain matrix is a complex Gaussian random variable (RV) with zero mean and unit variance. Moreover, the noise
, and
, such that
, represent the entries of white noise as two dimensional independent and identically distributed (i.i.d.) complex Gaussian RVs with zero mean and identical variance per dimension.
Linear and Decoupled ML Decoder
Based on the system model given in (
19), the following theorem confirms a linear decoupled solution at the receiver for all QODs constructed in
Section 2. It was previously proved for non-iterative QODs in [
18] but we now confirm its validity for all QODs obtained in
Section 2.
Theorem 6. For a given system model in (19), the ML-decoding rule assumes a linear decoupled form The main contributing factor in the above rule is , which needs to be minimized for any transmitted symbol encoded as a quaternion in a given time slot. The appearance of indicates the linearity of the decoder as well as the computational load at the receiver is reduced significantly.
As an illustration of the above result, we choose QODs given in (
4) and (
6) and demonstrate that the above ML-decoding rule is both linear and decoupled. For remaining QODs
and
in (
9), (
11), (
14), (
15) respectively, a similar decoding result can be obtained easily.
Corollary 1. The ML-decoding rule (20) for QOD given in (11), reduces to the real part ofwhere is a received quaternion vector and , and We now broaden our discussion to include designs, which have significantly higher code rates than those obtained from the approaches discussed in this paper. In order to do that we need to compromise on orthogonality in which case it is not possible to have decoupled linear decoder like (
20). It turns out that such quasi designs have other features to offer. Subsequently, we construct these quasi QODs by extending the standard approach as developed for the complex domain [
16].
6. Simulation and Results
To evaluate the performance and diversity gains, we employ QODs, that is, , corresponding to single and dual-polarized receive antenna configurations. We obtain their bit-error-rate (BER) curves against signal-to-noise (SNR) ratios. For simulations, quadrature phase shift keying is used. The receivers are aware of the channel coefficients and uniform white noise is added in each polarization. We have utilized the basic concepts of pure quaternion algebra, the matrix computations and complex domain calculations to optimize the overall system model in MATLAB.
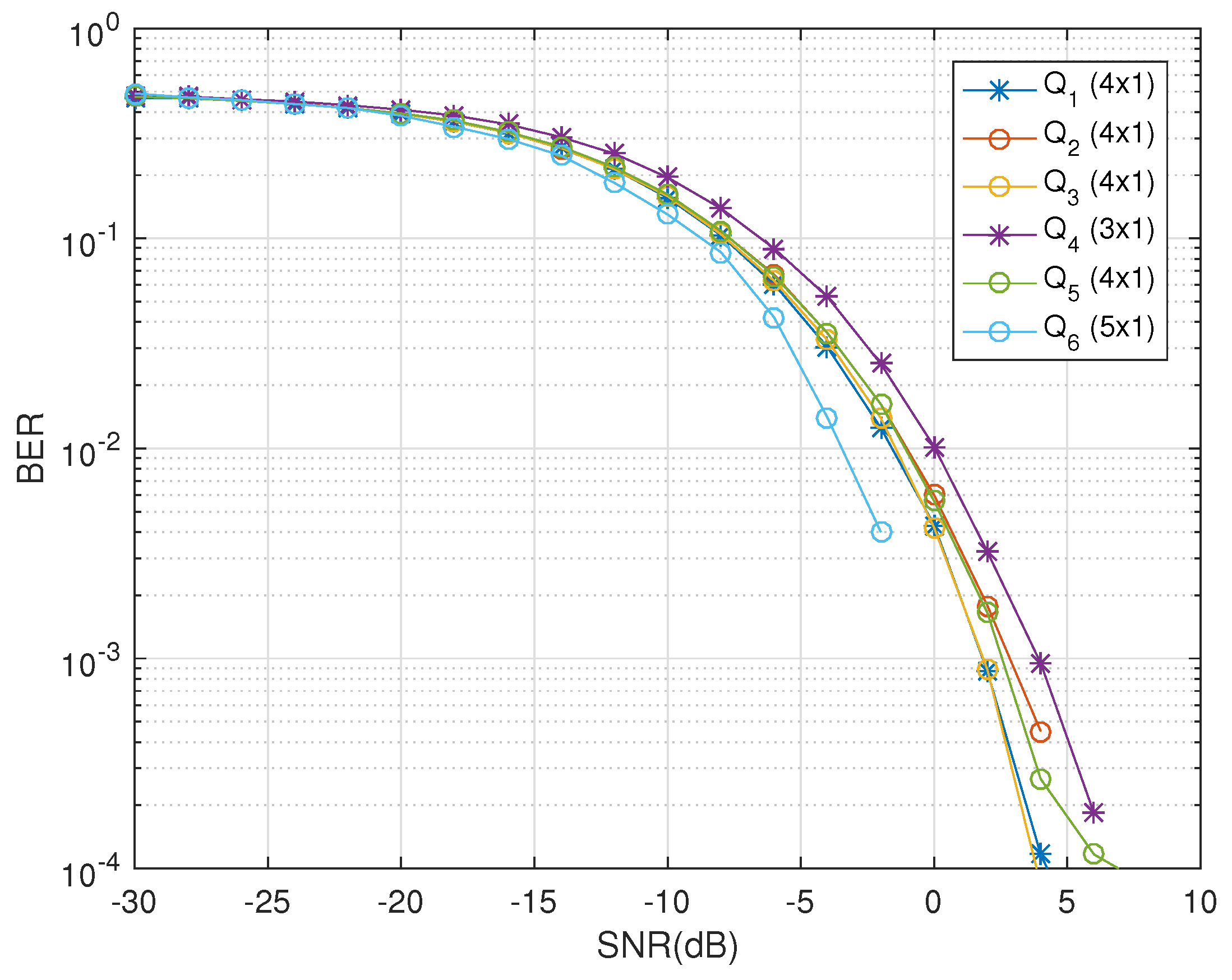
The codes constructed using the Liang based construction technique provides a lower number of complex receivers. For the codes
, in
Figure 3, it is clear that these codes have linear and decoupled decoding at the receiving end due to the use of the specific construction technique using the dual-polarized antennas and the quaternionic channel model. This has been possible due to the quaternionic channel exploiting the polarization diversity independently using the polar as well as cross-polar scattering between the dual-polarized antennas. The codes
,
and
are transmitted using four dual-polarized antennas at the transmitting end and have the code rates of
,
,
and
, respectively. These codes seem to show similar curves but they differ in their intrinsic behaviors based on the number of timeslots used and the symbols transmitted per timeslot. The codes
and
show similar performance as
, but they will experience the issue of peak-to-average power ratio (
PAPR), where switching on and off of one of the dual-polarized antenna in every timeslot is a tradeoff. Also,
shows competitive response in comparison to
by transmitting double the number of complex symbols in every timeslot, however, this has been achieved at a compromise on the increased number of timeslots used in
. Thus, it takes longer time to decode the complete code block in case of
with increased number of complex symbols when compared to
, where the receiver is able to decode the original information faster from the received code block. While, the codes
and
use three and four dual-polarized antennas in transmission which have codes rate
and
, respectively. These codes demonstrate that the proposed scheme is successful with odd number of transmit dual-polarized antennas also. Code
is a unique presentation of pure quaternion code designs that favors the utility of this approach in massive MIMO systems in future wireless communication systems. We can see that the proposed code construction technique has no restrictions on the number of transmit and receive antennas. This is demonstrated in the
Figure 3 where both even and odd number of dual-polarized antennas are used to transmit the codes.
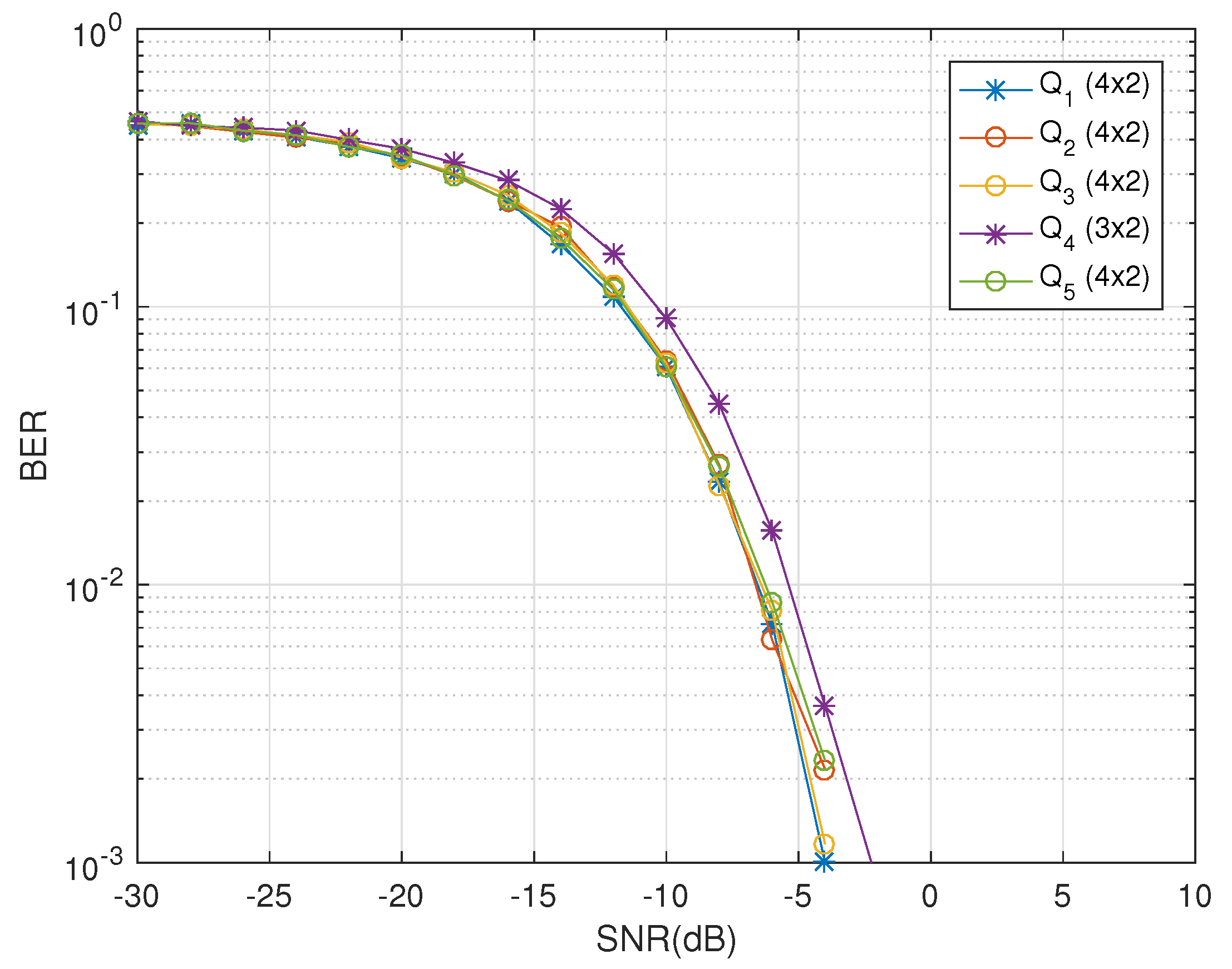
The effects of increasing the receiver diversity are visible in the
Figure 4. It clearly shows that the receiver diversity has positive impact on the diversity gains. Use of the quaternionic channel exploits the polarization diversity and promises decoupled decoder for any number of receive dual-polarized antennas. In comparison to the work done int he past, the proposed design does not compromise the code rates when the number of transmit antennas are increased. Such an increase in the code rates with higher diversity gains are the requirements of the future MIMO systems to support greater channel utilization and efficiency. The freedom of the number of receive antennas that can be utilized by the QODs during their transmission from a quaternionic channel-based system has been further emphasized in the
Figure 5. The code
shows increasing diversity gains as the number of receive dual-polarized antennas are increased at the receiving end.
The computational complexity of the proposed decoder used for the codes in the
Figure 3,
Figure 4 and
Figure 5 promises linear and decoupled decoding at the receiver. The decoder remains independent of the number of unique transmitted symbols, that is,
. This has a huge impact in simplifying the complexity of the receiver in terms of the calculations to be performed. In case of the coupled decoder, the receiver complexity remains dependent on the number of unique transmitted symbols and has an exponential relationship with it. Considering N transmit antennas and T time slots used to transmit a single block of code, the computational complexity of the coupled decoder is
. However, this reduces significantly in the case of the proposed decoder design, where the computation complexity reduces to
.
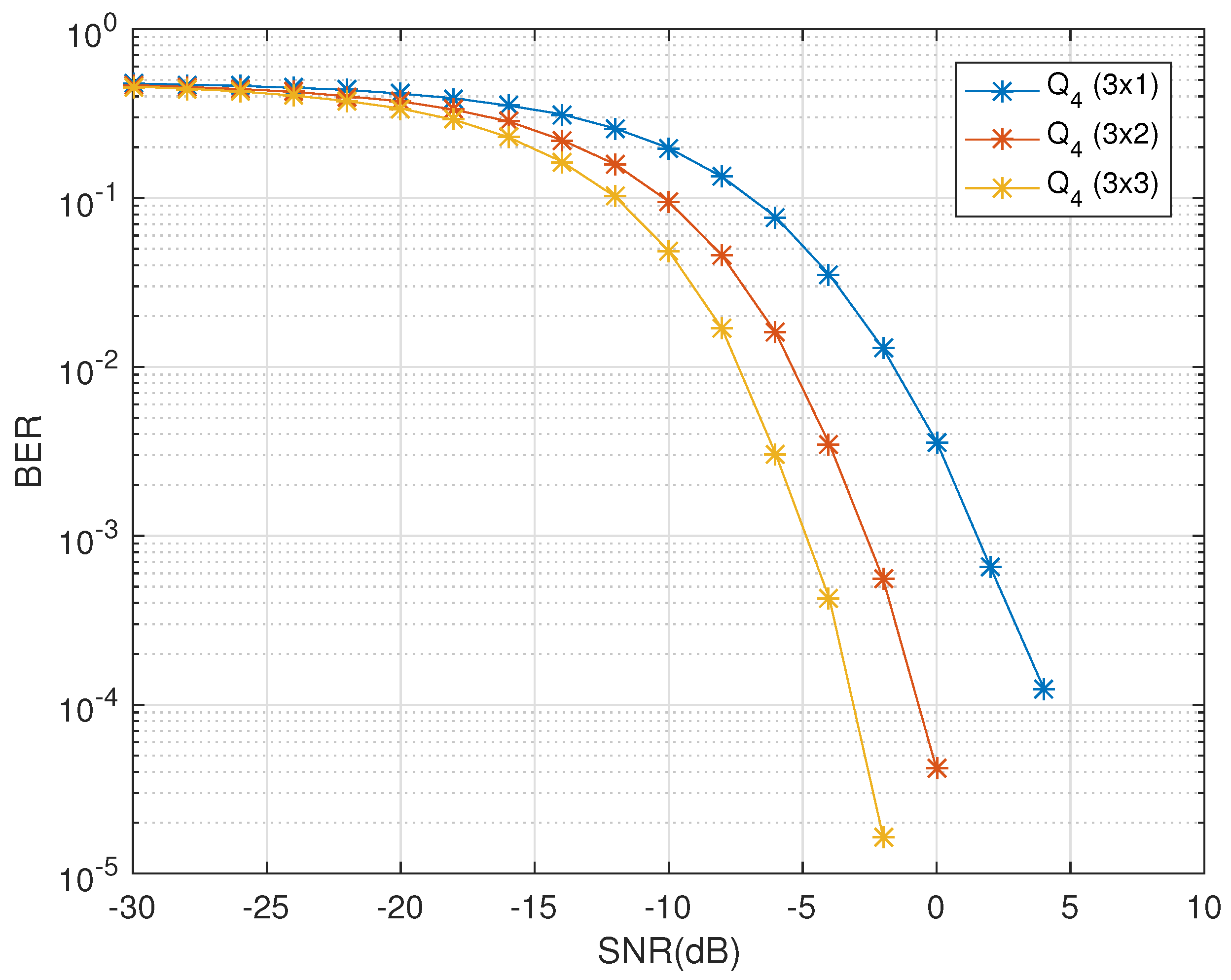
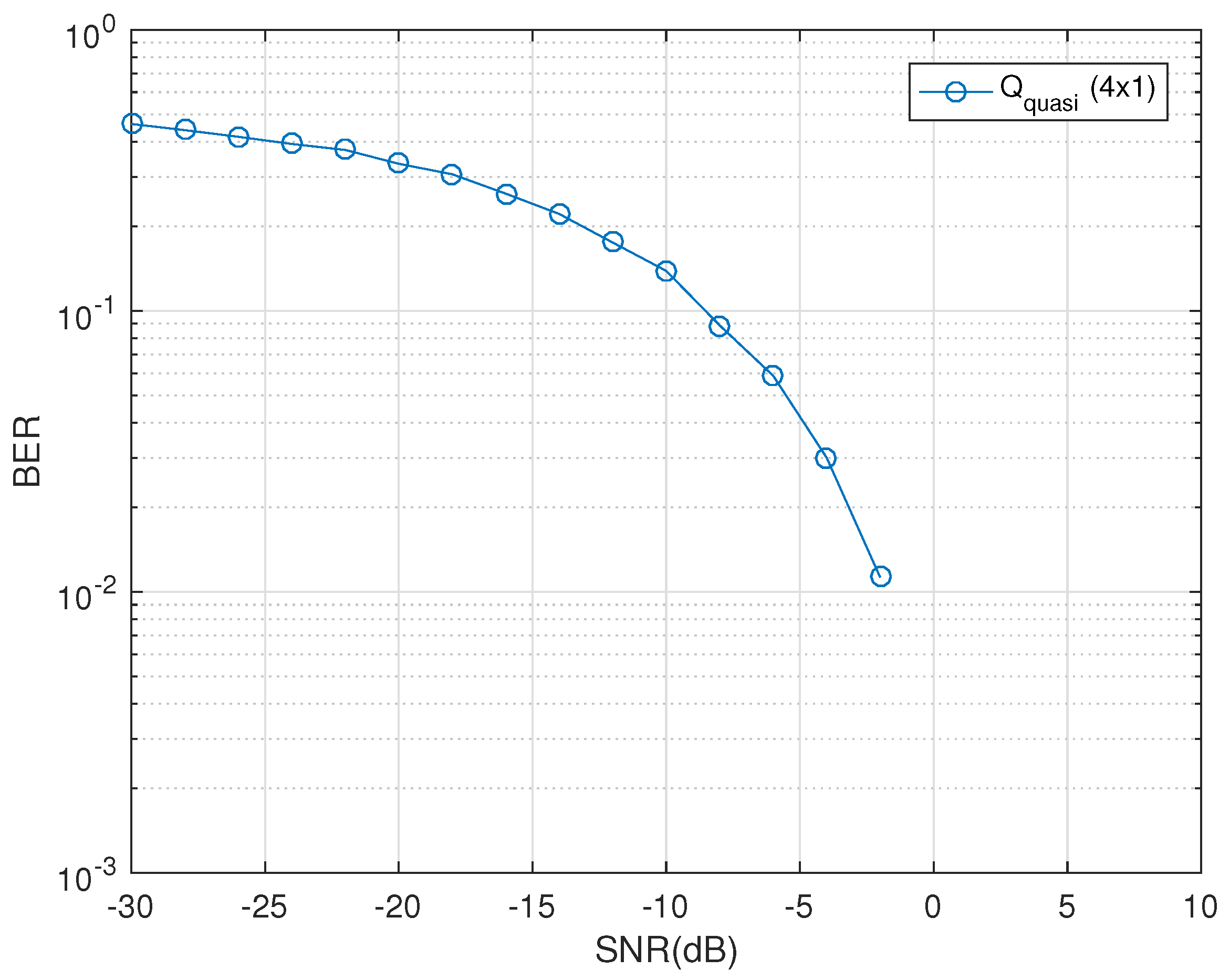
The decoupled decoding of the quasi-orthogonal codes has been a research problem as this compromises the coding rate for increased number of transmit antennas. A unique construction technique has been presented to form quasi QODs with higher code rates. For the antenna configuration of four transmit single receive dual-polarized antennas, the quasi QOD presented in (
25) has a compromised receiver complexity but promises higher gains in comparison to the coupled traditional ML-based decoder designs as is clear from the
Figure 6.