Abstract
The use of quaternion orthogonal designs (QODs) to describe point-to-point communication among dual-polarized antennas has the potential to provide higher rate orthogonal and quasi-orthogonal complex designs exploiting polarization diversity among space and time diversities. Furthermore, it is essential to have a space time block code (STBC) which offers a linear and decoupled decoder which quasi-orthogonal designs fail to attain. In this paper, we show how the realm of quaternions unexpectedly offers us a possible solution and codes obtained from quaternion designs mostly achieve both linear and decoupled decoders. This motivated us to perform an indispensable search for QODs such that the code rate is bounded below by 1/2 and does not sharply decrease as the number of transmit antennas increases. It is shown that three famous recursive techniques do not satisfy this criteria and their code rates decrease rather rapidly. Therefore, we propose another method of constructing quaternion designs suitable for any number of transmit antennas and verify that these attain linear and decoupled decoders with the system model based on quaternionic channel. It is shown that such designs outperform others in terms of transmit diversity, code rates and the optimality of the proposed decoder is validated through simulation results.
1. Introduction
The surge of high speed communication services has accelerated the demand for efficient communication techniques that have the potential to make reliable data transmissions without compromising on data rates. In this regard, space time block codes (STBCs), based on orthogonal designs, are considered one of the key techniques that have moved the capacity of wireless communication close to theoretical limits. STBCs have been used extensively such as in third generation (3G) standard and wireless local area networks (LANs) based on IEEE 802.11n. Initially, they were proposed by Tarokh et al. [1] as a generalization of the famous Alamouti code which is a complex orthogonal design (COD) [2]. The most attractive feature of these orthogonal designs is the provision of full diversity along with low complexity maximum-likelihood (ML) decoder. However, they achieve this attribute at the expense of code rate, that is, the ratio of the number of independent complex transmitted symbols and the number of total time slots taken to transmit a coding matrix. On the other hand, a COD with full rate and maximum diversity exists only for two single-polarized transmit antennas and maximum code rate approaches half with as the number of transmit antennas increase [3]. To meet higher data rate demands, other designs such as complex quasi-orthogonal STBCs have also been explored that provide comparatively higher code rates but compromise on optimal decoders due to nonlinear and coupled decoding issues [4]. To further enhance the capacity of communication systems, other combinations of diversity providing techniques are being investigated.
In [5], orthogonally polarized transmissions through both ends of a dual-polarized antenna were modeled through quaternions and later [6] laid the foundation of orthogonal space time polarization block codes (OSTPBCs) that utilize polarization diversity together with space and time diversity. Polarization diversity can provide nearly similar performance to spatial diversity without any measurable increase in antenna dimensions [7]. This is achieved with the use of dual-polarized antennas, which have two antennas of orthogonal polarizations co-existing on a single antenna platform and there has been a growing interest recently [8,9].
Based on the combination of polarization diversity with space and time diversities, various quaternion orthogonal design (QOD) construction techniques have been proposed by Seberry et al. [6]. The primary motivation of these designs has been their ability to provide higher code rates along with a low complexity quaternion norm-based ML decoder. To illustrate the benefit of these designs, [6] presented an example of order QOD and derived linear equation based decoding solution for this configuration. They argued that quaternion decoding statistics can provide decoupled decoding for any QOD. Their subsequent studies [10,11] used the same QOD and emphasized the similar postulate that quaternion ML norm can provide optimal decoupled decoding for any QOD construction. However, the authors corrected their decoding rule in [12] and highlighted that the proposed decoding rule does not yield optimal decoding for all QODs, and therefore, the design of semi-optimal or optimal low complexity decoders remained an open research problem [13]. In this regard, a recent work [14], explored the designs for which quaternion norm-based ML decoder resulted in optimal decoding solutions. However, it is important to note that their proposed ML decoder works for a special class of STBCs.
In this paper, we investigate three famous generalized QOD construction techniques [14] and identify two main short falls which restricts their use for large MIMO systems. Firstly, this iterative approach works only in the case when the number of transmit antennas are in powers of 2, which clearly restricts their use to other antenna configurations. Secondly, the code rate decreases very sharply for higher order designs based on these iterative techniques. Therefore, it was deem necessary to develop codes that work for any number of antenna systems besides having the main advantage of attaining decoupled decoders in the presence of quaternionic channel as was the case with iteratively generated designs [14]. This has been done following the line of approach indicated in [3] which gives us a class of QODs that are non-square and the code rate is bounded below by 1/2. The motivation behind this was to exploit the impact of a dual-polarized transmission channel at the receiver side in such a way that ML quaternion norm criterion simplifies to a decoupled decoding solution which reduces the decoder complexity significantly.
After obtaining a generalized ML decoder, we take one step further by exploring quasi-QODs. The proposed quasi-QOD provides a code rate of two for four transmit dual-polarized antennas. However, the quasi nature of these codes leads to a slight comprise on decoding complexity. The solutions obtained with this compromised complexity-based decoder are still better than the coupled traditional ML decoder based solutions. A detailed complexity analysis of the proposed constructions have been provided to illustrate the significance of the proposed low-complexity decoder for both pure or quasi QODs.
Briefly, we summarize the main contributions made in this paper.
- We propose a new class of QODs based on Liang mechanism [3] with stable code rate as the number of transmit antennas increases.
- The class is shown as best suitable in describing point-to-point communication among dual-polarized antennas.
- The proposed decoder is shown to provide linear decoding solution for all STBCs obtained from QODs.
- A brief performance analysis is carried out for all obtained QODs.
Some remarks on notation are as follows—all matrices are denoted with bold letters. The real and complex numbers fields are denoted in standard form and , respectively. ℜ and ℑ represent real and imaginary parts of a complex number. denotes a quaternion field comprise of a basis of non-commuting elements , such that . The superscript , refers to quaternion conjugate and responsible for sign changes in and k. In matrices, it also includes transpose . Moreover, operators and refer to the Hermitian transpose and trace operator, respectively. Both matrices and , corresponds to quasi-orthogonal STBCs; however, the subscript Q indicates that the STBC is obtained from a QOD.
2. Quaternion Orthogonal Designs
A quaternion consists of four real numbers such that ; . As the space is isomorphic to the complex space , therefore, we obtain an equivalent representation of a quaternion . This is more useful from the point of wireless communication among dual-polarized antennas. Consequently, it makes sense to talk about space-time-polarization block codes with quaternion elements and investigate orthogonality condition in the quaternion domain.
Definition 1.
A QOD comprises of quaternion variables , is defined as an matrix which can have entries from the set including possible multiplications on the left and/or right by quaternion elements and satisfies the following condition
where λ is a positive real number and is an identity matrix.
As mentioned before that a quaternion is a combination of two complex numbers , therefore, it is natural to think of QODs satisfying where and are two complex matrices. It turned out that any two arbitrary complex matrices do not necessarily give rise to a QOD which satisfies (1). Essentially, the authors in [6] found the key requirements on and to ensure (1), for the resulting QOD. Interestingly, the amicable and symmetry conditions were found to play main role for which an extensive theory was already in place and they used it to generate class of QODs. Later it was found that all proposed quaternion-based designs employed symmetric-paired complex matrices. Since the symmetry property is crucial in our study therefore we state it for a brief and self-contained exposition.
Definition 2.
Two CODs and based on complex variables form a symmetric-paired design provided or is symmetric.
A relatively simple way to find such symmetric-paired designs arise from the observation that swapping of certain columns of a COD generates an equivalent COD. The resulting COD along with the original COD form a symmetric-paired design. This technique was used in [6], for the search of viable QODs. However, it is important to note that as the dimension of COD matrix gets larger, not every permutation of columns of a COD yields a valid QOD. Therefore, only one permutation per column is allowed to generate valid QODs under this construction [15]. Below in Section 2.2 and Section 2.3, we will describe other possible ways to generate QODs. For square designs, three recursive construction methods to find CODs were presented in [3], namely Adams-Lax-Phillips, Józefiak and Wolfe constructions. It is easy to realize that all three constructions recursively generate the same class of square QODs.
According to these constructions, a recursive COD is designed for symbols embedded in a square matrix of order such that
where represents a COD of order defined on symbols and . For example, for , . Taking this as a seed element, higher order CODs such as and can be constructed [3], recursively. In the subsections, this way of COD generation is used to form different generalized QOD constructions.
In Figure 1, we briefly explain the basic nomenclature, which describes the main working in quaternion domain. We start with two CODs that form a symmetric-pair such that they give rise to a QOD. In earlier works, this was not directly used to describe communication among dual-polarized antennas. Rather, an STBC was constructed from a QOD and its even columns represent signals being sent through one polarization while entries in odd columns are signals transmitted through an orthogonal polarization plane. However, the simultaneous transmission through a dual-polarized antenna is being modeled by quaternions in this paper. Although, we have an enriched theory of quasi-orthogonal designs yet our main focus is to work on an approach which algorithmically identify among them, those designs that have decoders with two main characteristics, that is, linear and decoupled. In this work, we notice that the departure from the complex to quaternion domain serve this purpose. The dotted line connecting CODs with quasi-STBCs or indicates a vivid difference between their working which distinguishes them in terms of code rates, decoding delays at both ends, zero vs non-zero entries, linear and decoupled decoders.
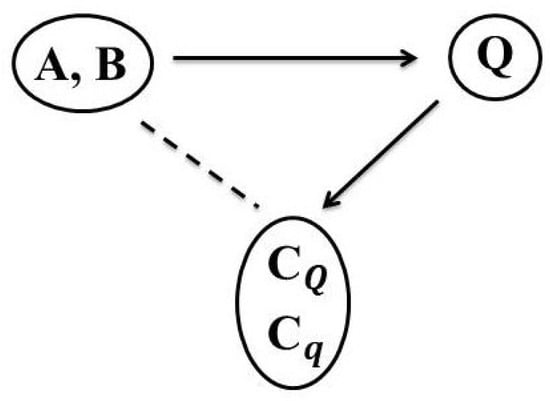
Figure 1.
Quaternionic Nomenclature: Two symmetric-paired complex orthogonal designs (CODs) and generate a quaternion orthogonal design (QOD) , which gives rise to different quasi-codes and with linear and decoupled decoders.
The generalized construction techniques employ (2), which provides us the symmetric-paired square CODs that act as seeds to generate three classes of square and non-square QODs.
2.1. Symmetric-Paired Design 1: (Square QODs)
This construction technique constructs QODs in which COD is obtained from through permutation of columns, where permutation operation on two columns m and n results in swapping the positions of these two columns with each other. For all CODs based on the permutation of CODs for a specific antenna dimension, the diversity order remains the same, therefore, without loss of generality we employ (2) to arrive at the following result.
Theorem 1.
For a given COD in (2) and its permuted version , a complex amicable and symmertic-paired design can be constructed such that the following realization,
provides a QOD of dimension .
The following example illustrates the construction in which we start with an Alamouti code . Using (2), we obtain a square matrix of order 4. Consequently, we have a QOD.
Example 1.
Using the permutation operation on , as described above and representing it with , we obtain following QOD , to be used in the configuration of 4 dual-polarized antennas
This QOD transmits 3 complex symbols and in four time slots and provides a 3/4 code rate.
2.2. Symmetric-Paired Design 2: (Non-Square QODs)
The designs that do not necessarily require the use of permutation operations on columns are important for they do not limit code rates. This can be done through a relatively simple way to recursively generate QODs using a single COD and a square diagonal matrix containing an extra symbol. Therefore, these designs perform relatively better than the designs obtained from the first technique. Below we describe their generalized formulation.
Theorem 2.
For a given square COD , the matrix
provides a quaternion design of order .
We again start with an Alamouti code , to obtain a square COD following Wolfe construction which contains three symbols because , implies . Hence, we arrive at the following example.
Example 2.
The COD along with a diagonal matrix containing an extra symbol in Equation (5) gives rise to
This QOD transmits 4 complex symbols , and in eight time slots, thus provides a relatively better code rate of 1/2.
2.3. Symmetric-Paired Design 3: (Non-Square QODs)
We now come to address main issues related with quasi-CODs which promise a high data rate at the expense of coding and decoding delays besides coupled and non-linear decoding. This issue can be resolved in the quaternion domain. For example, in [16], a quasi-COD of rate 1 was designed for four transmit antennas
using two CODs and , which was shown to have pair-wise decoding. We now subject these two CODs and to the quaternion domain which helps us reclaim decoupled and linear decoding solutions. First of all, we note that the concept used in design 2, can be generalized such that in place of a diagonal matrix which merely contains a single extra symbol, we can use a COD. It turns out that the following theorem provides us a possibility of incorporating with , in place of a diagonal matrix. Resultantly, we obtain another recursive construction technique which can be proved easily.
Theorem 3.
For two recursively generated CODs and , a symmetric-paired design,
is a QOD of dimension .
It is easy to implement this technique as is shown in the subsequent example.
Example 3.
To generate a QOD for 4 dual-polarized antenna, we use and to obtain two CODs of higher orders and using Wolfe construction. Consequently, Equation (8) gives rise to a QOD of rate
Therefore, we have three recursive techniques to generate square and rectangular QODs from square CODs. As all of the above QODs are obtained from the recursive techniques of CODs based on famous Adams-Lax-Phillips, Józefiak and Wolfe constructions, therefore, we can use an upper bound on these to arrive at the following result.
Theorem 4.
The rate , of all possible QODs in (3), (8) and (11) obtained from square CODs is given by
This provides us a class of QODs, which are fully diverse [17] and earlier these were shown to have decoupled decoders based on a semi-quaternionic channel model [15]. In this paper we use the system model [18] based on the characterization of pure quaternionic channel and it is shown that the above designs all have decoupled decoders and optimal decoding delays. Besides these advantages, there is one drawback as mentioned in the remark below.
Remark 1.
All of the above construction techniques generate QODs for only configurations when the number of dual-polarized transmit antennas are in powers of 2, i.e, which puts a heavy toll on the code rate as sharply declines as the number of antennas increase.
Following above remark, it is essential to find quaternion designs for general configuration of dual-polarized antennas like for a –system such that and these codes have maximal coding rates. We developed such QODs in the subsequent section.
2.4. Maximal Rate QODs for General Configuration of Dual-Polarized Antennas
In Liang’s paper [3], rectangular CODs of maximal rates are found algorithmically. The general procedure was given in the paper, however, such designs do not carry a compact form as was found in the case of (2). As demonstrated below that our proposed procedure successfully works on the famous examples given in [3], to generate designs for 3 and 5 dual-polarized antennas among other configurations, respectively.
Lemma 1.
A maximal rate QOD for 3 dual-polarized antennas is given by
Proof.
We start with a rectangular COD of maximal rate given by
and construct an equivalent COD based on the same principle of permutation of columns such that is symmetric which can be verified easily. Such an equivalent COD is
Consequently, we obtain a QOD for three dual-polarized antennas of rate 3/4 given by . □
To complete the discussion, we include one QOD which is suitable for 4 dual-polarized antennas and is obtained using Liang’s approach. This will be compared with the QODs based on recursive approach for the same number of antennas.
Lastly, we construct a QOD for 5 dual-polarized antennas.
Lemma 2.
A maximal rate QOD for 5 dual-polarized antennas is given by
Proof.
The proof of this lemma is similar to the Lemma 1, however, in this case the underlying COD is given in Equation (100) in [3]. □
Following the same lines, it is easy to construct QODs for higher number of transmit antennas starting with the CODs given in [3] (Equation (101) and Appendices C and D, respectively).
3. Comparative Analysis of the Construction Techniques
3.1. Code Rates
An important result, which gives us bounds on the upper limits of code rates of above QODs can be proved easily. For instance, the underlying CODs which we employ in the construction of such codes have upper bounds (Theorems 5 and 6 in [3]), therefore, result below follows immediately.
Theorem 5.
(a) For an even number of transmit dual-polarized antennas, the highest possible rate of QODs arising from rectangular CODs is bounded above by
(b) For an odd number of transmit dual-polarized antennas, the highest possible rate of QODs arising from rectangular CODs is bounded above by
Note that there is substantial difference between the code rates of QODs obtained from the above approach, denoted by , and those which are based on recursive techniques represented with . Below figure clearly describes that as the number of dual-polarized transmit antennas increases the code rate sharply declines. Quite contrary, the code rates of QODs based on Liang’s approach remain stable. In Figure 2, we compare the code rate curves from both approaches where red curve represent the code rate of QODs based on recursive methods and code rates of QODs based on Liang’s approach are depicted with green curve. Regardless of the number of transmit antennas, we can always obtain a QOD with code rate higher than or equal to 0.5, as is clear from Figure 2. So we obtain a robust approach of developing QODs based on Liang’s mechanism.
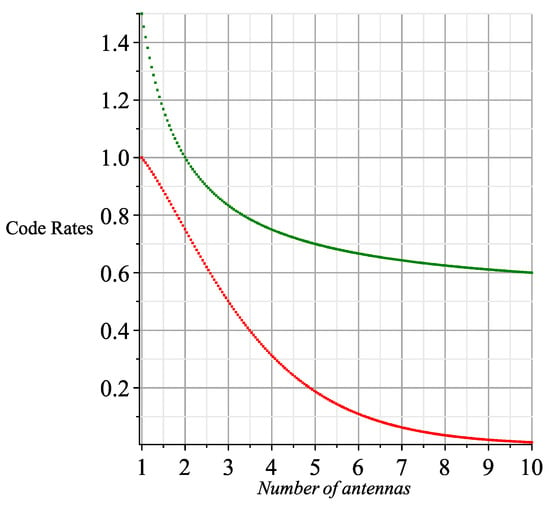
Figure 2.
The code rate of QODs based on new approach remains stable around 0.5.
3.2. Coding & Decoding Delays
In order to optimize throughput, it is essential to have codes with optimal coding delay and QODs have an advantage of it. The decoding delay, denoted here as , is an important performance measure for STBCs. Essentially, the decoding delay signifies the total number of time slots a receiver has to wait to receive a complete block of code before starting the decoding process. This implies that higher order code matrices require larger decoding delays. The performance of different STBCs schemes, that is, symmetric-paired designs 2.1, 2.2, 2.3 and Liang’s approach 2.4 are compared. We enlist values of for codes in case of and 5 dual-polarized antenna arrangements in Table 1. In the table, denotes the number of dual-polarized transmit antennas. From the table, it is seen that for 3 and 5 dual-polarized antenna systems there is no QOD obtainable from iterative techniques which we represent with ∗.

Table 1.
Decoding Delays.
4. Quaternionic Channel Model
The simultaneous transmission from both ends of a dual-polarized antenna can be regarded as a hyper signal which consists of two complex numbers in two orthogonal polarizations. It propagates through space and received as a hyper signal by the dual-polarized antenna at the receiver end in a given time slot. This hyper signal can be represented as a quaternion [5] which gives us a reason to develop system model in the quaternion domain. An important component of the system model is the channel which we assume to be quaternionic following the line of approach followed in [18]. Therein, we observe that the product in the quaternion domain holds a key of consistent and viable model.
We first consider a two-input and single-output system (TISO) of dual-polarized antennas. It is necessary to emphasize the role of quaternions which is more recognizable in this case, therefore, we have
where each element in the above construction is a quaternion. Through each antenna in the above TISO system, the transmission of a pair of two complex symbols is encoded in and another pair in . This indicates that the above QOD exploits time and space diversities along with polarization diversity. It is worth pointing out that each quaternionic product, for example, contains a crucial information about the nature of quaternion domain. If we decompose it for a general quaternionic product then we obtain , where and . Therefore, we will obtain four complex channel gains for each antenna in a system. Note that we have four complex channel gains between a TISO system of dual-polarized antennas. As this system is equivalent to a MIMO system of single-polarized antennas, therefore, it may appear that it should have eight channel gains in total with two for each link. However, in our proposed model each quaternionic product results in the same number of channel gains.
Subsequently, a system model for a MIMO system of dual-polarized antennas can be constructed in the same way for such a system with dual-polarized antennas
which transmits symbols in –times slots, which are assumed to be points in the quadrature phase shift keying (QPSK) constellation. The channel matrix is , where and . The channel is assumed to represent a flat fading channel and the path gain from transmit dual-polarized antenna to receive dual-polarized antenna given by a quaternion . The complex channel gains, and incorporate the effects of cross polar scattering and each element of channel gain matrix is a complex Gaussian random variable (RV) with zero mean and unit variance. Moreover, the noise , and , such that , represent the entries of white noise as two dimensional independent and identically distributed (i.i.d.) complex Gaussian RVs with zero mean and identical variance per dimension.
Linear and Decoupled ML Decoder
Based on the system model given in (19), the following theorem confirms a linear decoupled solution at the receiver for all QODs constructed in Section 2. It was previously proved for non-iterative QODs in [18] but we now confirm its validity for all QODs obtained in Section 2.
Theorem 6.
For a given system model in (19), the ML-decoding rule assumes a linear decoupled form
The main contributing factor in the above rule is , which needs to be minimized for any transmitted symbol encoded as a quaternion in a given time slot. The appearance of indicates the linearity of the decoder as well as the computational load at the receiver is reduced significantly.
As an illustration of the above result, we choose QODs given in (4) and (6) and demonstrate that the above ML-decoding rule is both linear and decoupled. For remaining QODs and in (9), (11), (14), (15) respectively, a similar decoding result can be obtained easily.
Corollary 1.
We now broaden our discussion to include designs, which have significantly higher code rates than those obtained from the approaches discussed in this paper. In order to do that we need to compromise on orthogonality in which case it is not possible to have decoupled linear decoder like (20). It turns out that such quasi designs have other features to offer. Subsequently, we construct these quasi QODs by extending the standard approach as developed for the complex domain [16].
5. Quasi Quaternion Orthogonal Designs
Unlike the complex domain, for two dual-polarized antennas there exists a QOD of rate 2 and was shown to attain a decoupled decoder [18]. We employ it
to construct a higher rate quasi QOD as follows. By considering an identical code matrix with different symbols
following the same line of approach as used for quasi CODs [16], we obtain a quasi QOD
Resultantly, we obtain a quasi QOD to be used in the configuration of 4 dual-polarized antennas capable of sending 8 complex symbols in four time slots yielding a code rate of 2, given by
The above code does not satisfy the main quaternion orthogonality condition as
where . However, the simulation curve for the above code is obtained in the next section.
6. Simulation and Results
To evaluate the performance and diversity gains, we employ QODs, that is, , corresponding to single and dual-polarized receive antenna configurations. We obtain their bit-error-rate (BER) curves against signal-to-noise (SNR) ratios. For simulations, quadrature phase shift keying is used. The receivers are aware of the channel coefficients and uniform white noise is added in each polarization. We have utilized the basic concepts of pure quaternion algebra, the matrix computations and complex domain calculations to optimize the overall system model in MATLAB.
The codes constructed using the Liang based construction technique provides a lower number of complex receivers. For the codes , in Figure 3, it is clear that these codes have linear and decoupled decoding at the receiving end due to the use of the specific construction technique using the dual-polarized antennas and the quaternionic channel model. This has been possible due to the quaternionic channel exploiting the polarization diversity independently using the polar as well as cross-polar scattering between the dual-polarized antennas. The codes , and are transmitted using four dual-polarized antennas at the transmitting end and have the code rates of , , and , respectively. These codes seem to show similar curves but they differ in their intrinsic behaviors based on the number of timeslots used and the symbols transmitted per timeslot. The codes and show similar performance as , but they will experience the issue of peak-to-average power ratio (PAPR), where switching on and off of one of the dual-polarized antenna in every timeslot is a tradeoff. Also, shows competitive response in comparison to by transmitting double the number of complex symbols in every timeslot, however, this has been achieved at a compromise on the increased number of timeslots used in . Thus, it takes longer time to decode the complete code block in case of with increased number of complex symbols when compared to , where the receiver is able to decode the original information faster from the received code block. While, the codes and use three and four dual-polarized antennas in transmission which have codes rate and , respectively. These codes demonstrate that the proposed scheme is successful with odd number of transmit dual-polarized antennas also. Code is a unique presentation of pure quaternion code designs that favors the utility of this approach in massive MIMO systems in future wireless communication systems. We can see that the proposed code construction technique has no restrictions on the number of transmit and receive antennas. This is demonstrated in the Figure 3 where both even and odd number of dual-polarized antennas are used to transmit the codes.
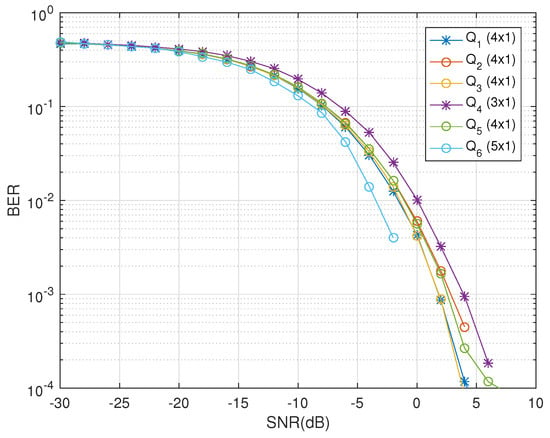
Figure 3.
BER vs. SNR performance of & for single receive dual-polarized antenna.
The effects of increasing the receiver diversity are visible in the Figure 4. It clearly shows that the receiver diversity has positive impact on the diversity gains. Use of the quaternionic channel exploits the polarization diversity and promises decoupled decoder for any number of receive dual-polarized antennas. In comparison to the work done int he past, the proposed design does not compromise the code rates when the number of transmit antennas are increased. Such an increase in the code rates with higher diversity gains are the requirements of the future MIMO systems to support greater channel utilization and efficiency. The freedom of the number of receive antennas that can be utilized by the QODs during their transmission from a quaternionic channel-based system has been further emphasized in the Figure 5. The code shows increasing diversity gains as the number of receive dual-polarized antennas are increased at the receiving end.
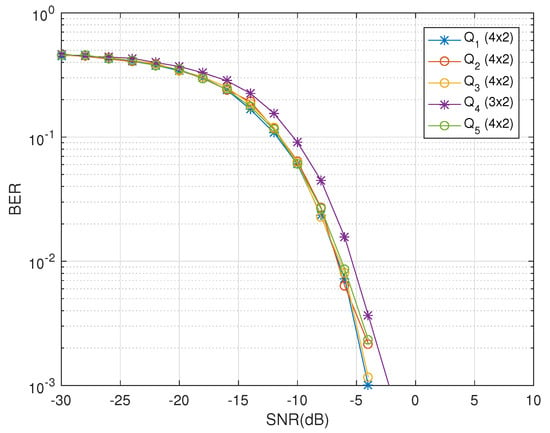
Figure 4.
BER vs. SNR performance of & for two receive dual-polarized antenna.
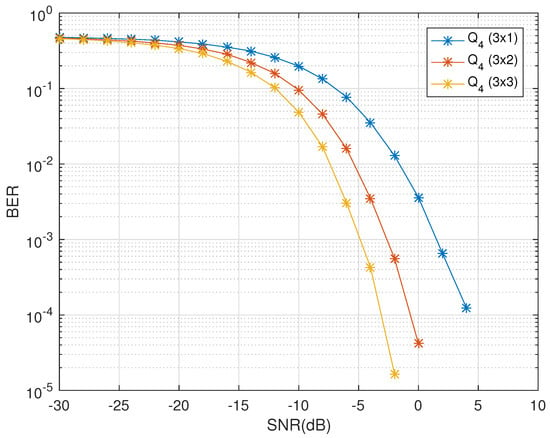
Figure 5.
BER vs. SNR performance of for one, two and three receive dual-polarized antenna.
The computational complexity of the proposed decoder used for the codes in the Figure 3, Figure 4 and Figure 5 promises linear and decoupled decoding at the receiver. The decoder remains independent of the number of unique transmitted symbols, that is, . This has a huge impact in simplifying the complexity of the receiver in terms of the calculations to be performed. In case of the coupled decoder, the receiver complexity remains dependent on the number of unique transmitted symbols and has an exponential relationship with it. Considering N transmit antennas and T time slots used to transmit a single block of code, the computational complexity of the coupled decoder is . However, this reduces significantly in the case of the proposed decoder design, where the computation complexity reduces to .
The decoupled decoding of the quasi-orthogonal codes has been a research problem as this compromises the coding rate for increased number of transmit antennas. A unique construction technique has been presented to form quasi QODs with higher code rates. For the antenna configuration of four transmit single receive dual-polarized antennas, the quasi QOD presented in (25) has a compromised receiver complexity but promises higher gains in comparison to the coupled traditional ML-based decoder designs as is clear from the Figure 6.
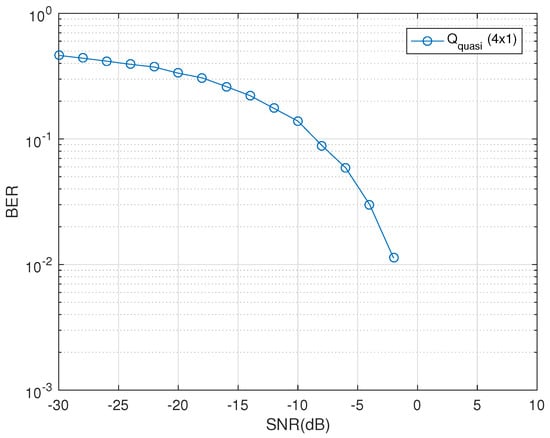
Figure 6.
BER vs. SNR performance of for one receive dual-polarized antenna.
7. Conclusions
Quaternion orthogonal designs with dual-polarized antennas have been studied to provide higher diversity gains and code rates. This paper presents the construction of QODs based on the Liang approach using the dual-polarized antennas and the quaternionic channel model. The unique method of constructing QODs provides linear and decoupled decoding at the receiving side where the computational complexity of the decoder remains independent of the number of unique transmitted symbols. Also, construction technique of quasi-QODs has been presented where the code rate is not compromised at higher number of transmit antennas. In future, these designs can be investigated for optimizing the receiver complexity further considering their suitability for future wireless communication systems.
Author Contributions
Conceptualization, S.A., S.S.Q., and S.A.H.; system modeling, S.A., methodology, S.A., S.S.Q. and S.A.H.; implementation, S.A. and S.S.Q.; writing—original draft preparation, S.A.; writing—review and editing, S.A.H. and S.S.Q.; supervision, S.A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| H | Horizontal |
| V | Vertical |
| STBC | Space Time Block Codes |
| COD | Complex orthogonal designs |
| QOD | Quaternion orthogonal designs |
| 3G | Third generation |
| 5G | Fifth generation |
| MIMO | Multiple-input multiple-output |
| SISO | Single-input single-output |
| TISO | Two-input single-output |
| LAN | Local Area Network |
| MISO | Multiple-input single-output |
| OSTPBC | Orthogonal space time polarization block code |
| QPSK | Quadrature phase shift keying |
| PAPR | Peak-to-average power ratio |
| FLOPs | Floating point operations |
| BER | Bit error rate |
| SNR | Signal-to-noise ratio |
| ML | Maximum Likelihood |
References
- Tarokh, V.; Jafarkhani, H.; Calderbank, A.R. Space-time block codes from orthogonal designs. IEEE Trans. Inf. Theory 1999, 45, 1456–1467. [Google Scholar] [CrossRef]
- Alamouti, S.M. A simple transmitter diversity scheme for wireless communications. IEEE J. Select. Areas Commun. 1998, 16, 1451–1458. [Google Scholar] [CrossRef]
- Liang, X.B. Orthogonal designs with maximal rates. IEEE Trans. Inf. Theory 2003, 49, 2468–2503. [Google Scholar] [CrossRef]
- Su, W.; Xia, X.G. Signal constellations for quasi-orthogonal space-time block codes with full diversity. IEEE Trans. Inf. Theory 2004, 50, 2331–2347. [Google Scholar] [CrossRef]
- Isaeva, O.M.; Sarytchev, V.A. Quaternion presentations polarization state. In Proceedings of the 2nd IEEE Topical Symposium of Combined Optical-Microwave Earth and Atmosphere Sensing, Atlanta, GA, USA, 3–6 April 1995; pp. 195–196. [Google Scholar]
- Seberry, J.; Finlayson, K.; Adams, S.S.; Wysocki, T.A.; Xia, T.; Wysocki, B.J. The theory of quaternion orthogonal designs. IEEE Trans. Signal Process. 2008, 56, 256–265. [Google Scholar] [CrossRef]
- Dietrich, C.B.; Dietze, K.; Nealy, J.R.; Stutzman, W.L. Spatial, polarization, and pattern diversity for wireless handheld terminals. IEEE Trans. Antennas Propagat. 2001, 49, 1271–1281. [Google Scholar] [CrossRef]
- Zafari, G.; Koca, M.; Wang, X.; Sriyananda, M.G.S. Antenna Grouping in Dual-Polarized Generalized Spatial Modulation. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–6. [Google Scholar]
- Zhang, K.; Jiang, X.; Wen, M.; Qiu, R.; Ge, H. Precoding-Aided Spatial Modulation with Dual-Polarized Antennas Over Correlated Channels. IEEE Commun. Lett. 2020, 24, 676–680. [Google Scholar] [CrossRef]
- Wysocki, B.J.; Wysocki, T.A.; Seberry, J.; Adams, S.S.; Sharif, H. A simple orthogonal space-time-polarization block code. IEEE Vehicular Tech. Conf. 2007, 754–757. [Google Scholar] [CrossRef]
- Beata, J.; Tadeusz, A.; Spence, S.; Adams, N. On an orthogonal space-time-polarization block code. J. Commun. 2009, 4, 20–25. [Google Scholar]
- Wysocki, T.A.; Wysocki, B.J.; Adams, S.S. Correction to the theory of quaternion orthogonal designs. IEEE Trans. Signal Process. 2009, 57, 3298. [Google Scholar] [CrossRef]
- Wysocki, T.; Wysocki, B.; Adams, S.S. On the issue of decoupled decoding of codes derived from quaternion orthogonal designs. In Proceedings of the 2009 3rd International Conference on Signal Processing and Communication Systems, Omaha, NE, USA, 28–30 September 2009. [Google Scholar]
- Mushtaq, E.; Ali, S.; Hassan, S.A. On low complexity ML decoder for quaternion orthogonal designs. IEEE Comm. Lett. 2017, 21, 1087–1090. [Google Scholar] [CrossRef]
- Mushtaq, E.; Ali, S.; Hassan, S.A. On Decoupled Decoding of Quasi-Orthogonal STBCs using Quaternion Algebra. IEEE Syst. J. 2019, 13, 1580–1586. [Google Scholar] [CrossRef]
- Jafarkhani, H. A quasi-orthogonal space-time block code. IEEE Trans. Commun. 2001, 49, 1–4. [Google Scholar] [CrossRef]
- Ali, S. Quaternion Orthogonal Designs with Full Diversity and Maximal Data Rates. In Proceedings of the 2020 43rd International Conference on Telecommunications and Signal Processing (TSP), Milan, Italy, 7–9 July 2020. [Google Scholar]
- Qureshi, S.S.; Ali, S.; Hassan, S.A. Optimal Polarization Diversity Gain in Dual-Polarized Antennas Using Quaternions. IEEE Signal Proc. Lett. 2018, 25, 467–471. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).