Analytical and Measured Effects of Short and Heavy Rail Cars on Railway Bridges in the USA
Abstract
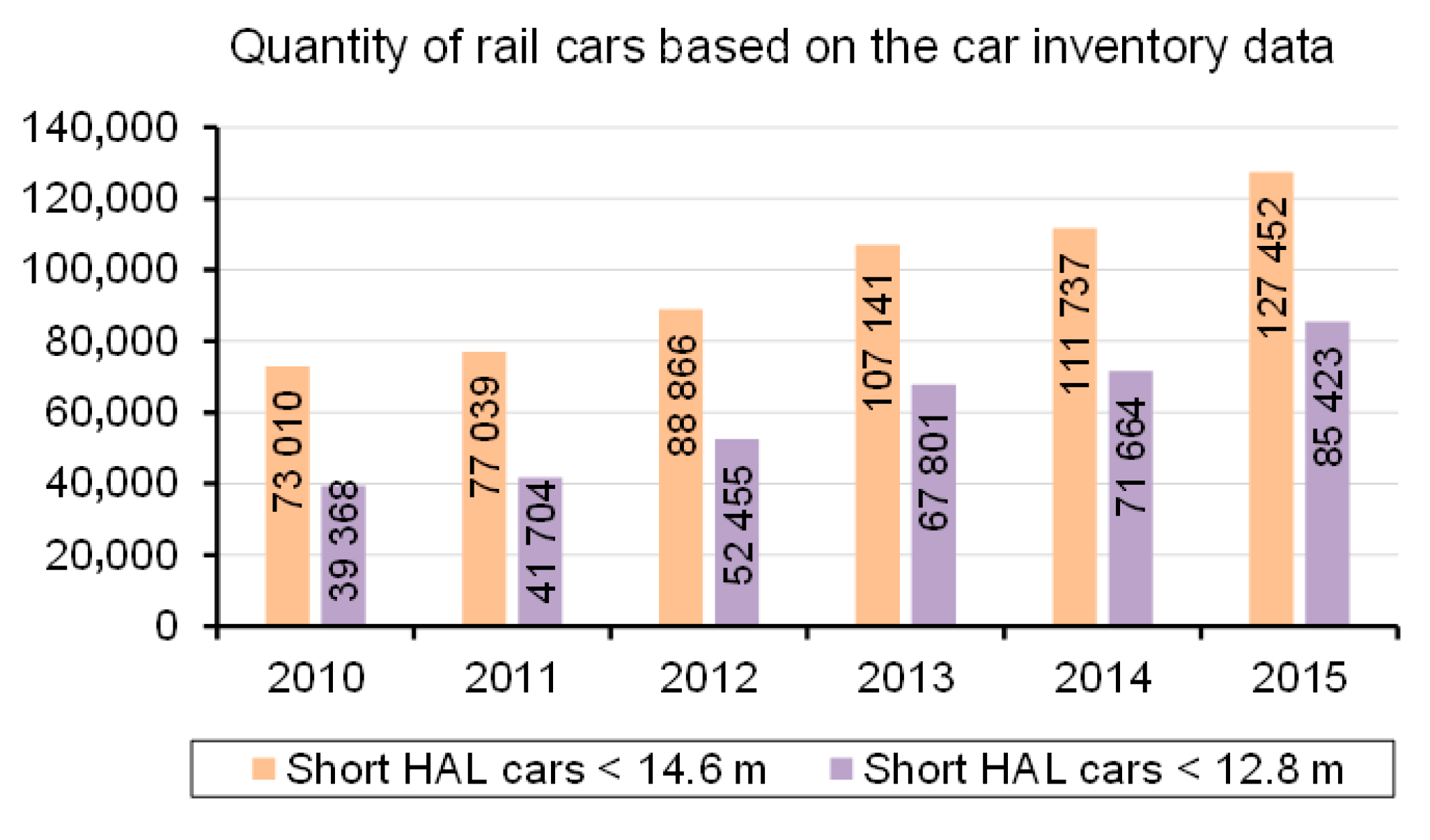
1. Introduction
2. Modeling and Analysis of a Steel Railroad Bridge
2.1. Current Design of Railroad Bridges in North America
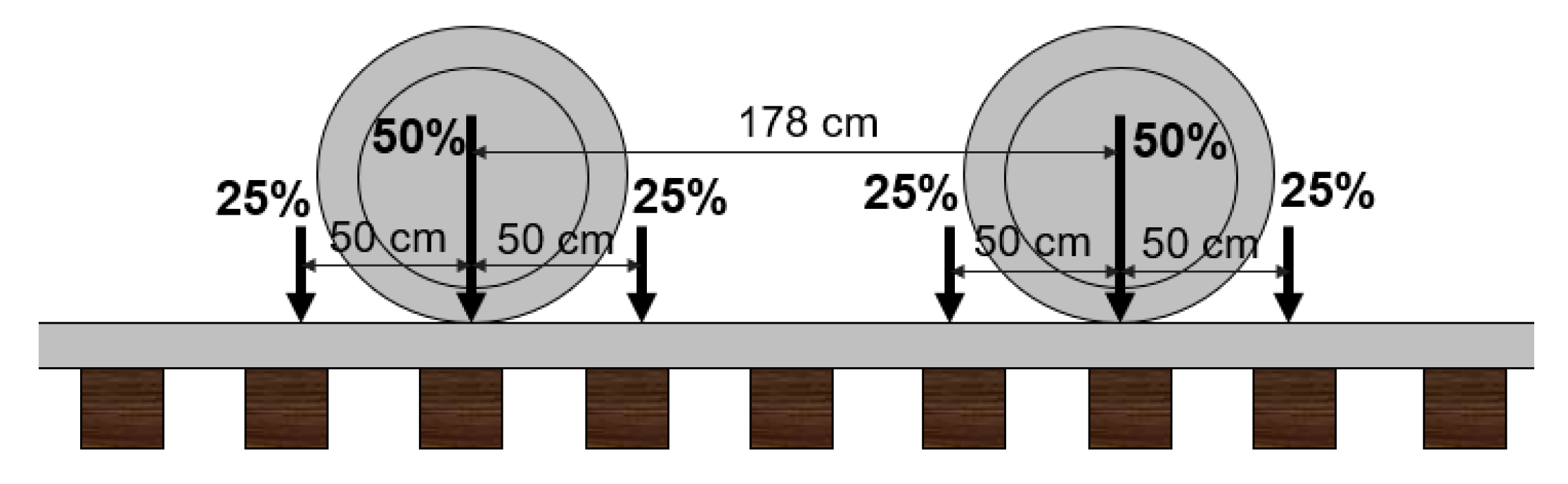
2.2. Modeling and Analysis of a Steel Railroad Bridge Using FEM Model
2.3. Description of Tested and Analyzed Bridges
3. Results of Case Studies
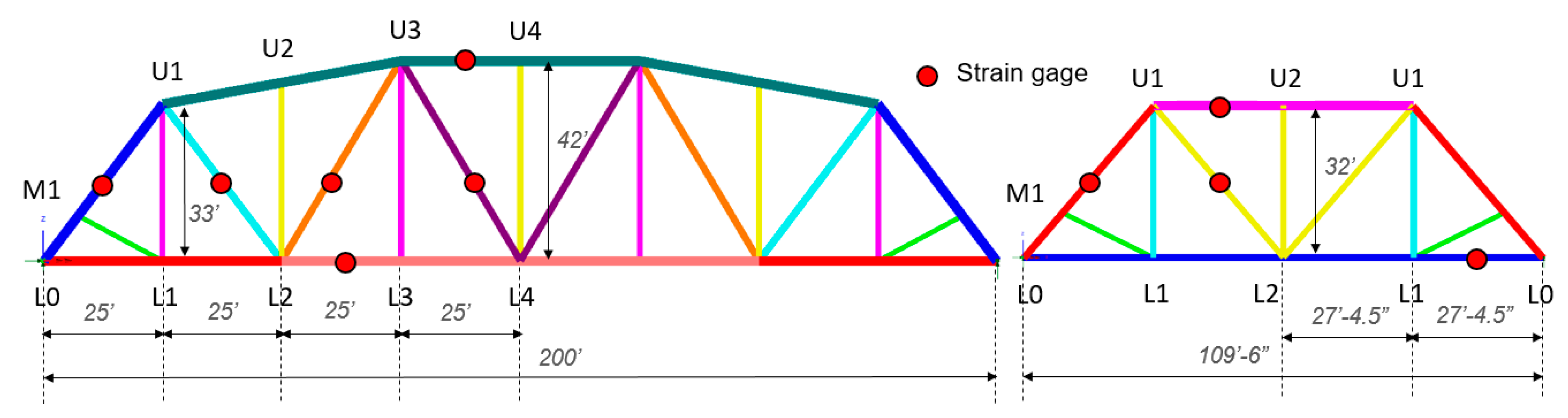
3.1. Riveted Truss Spans
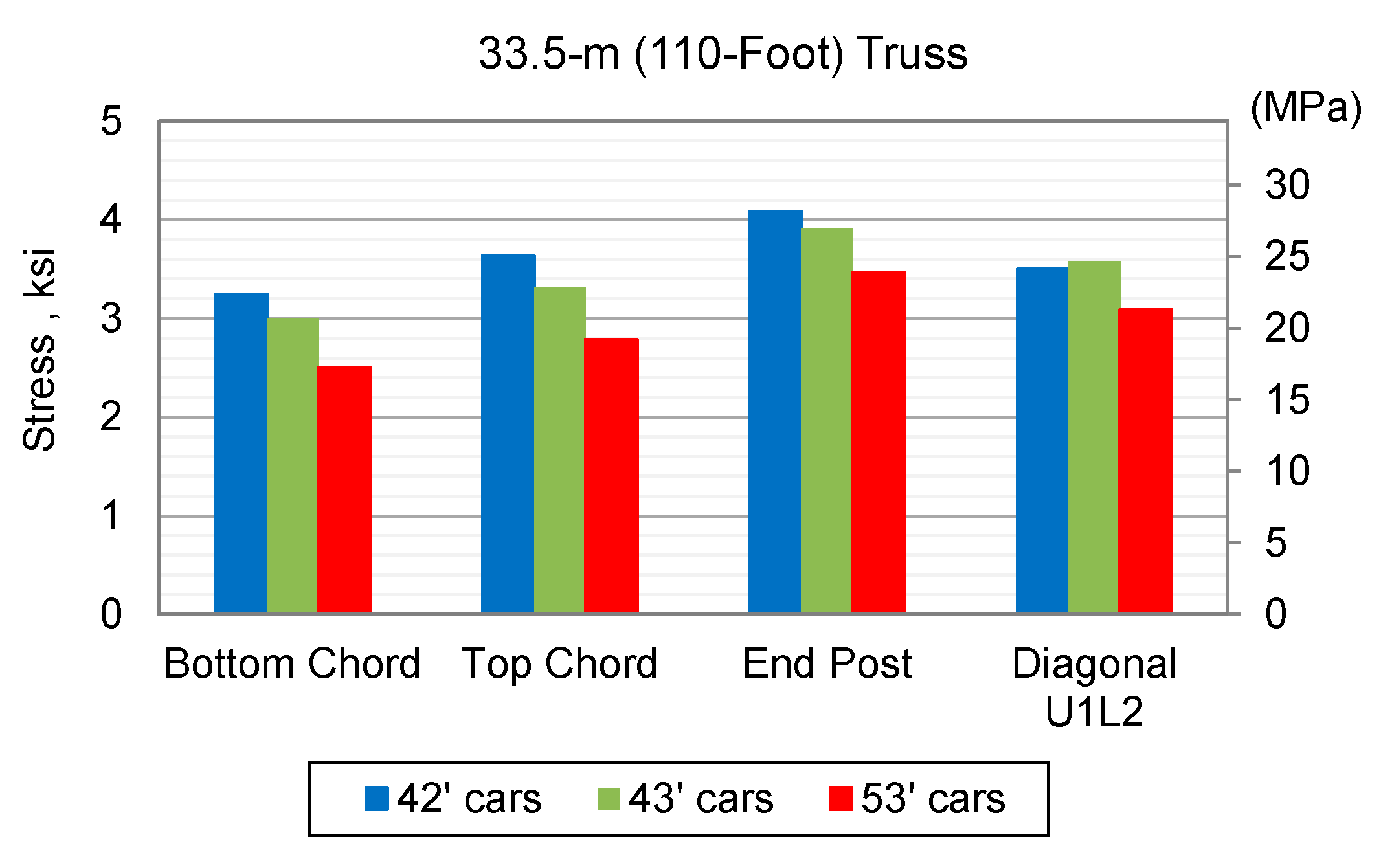
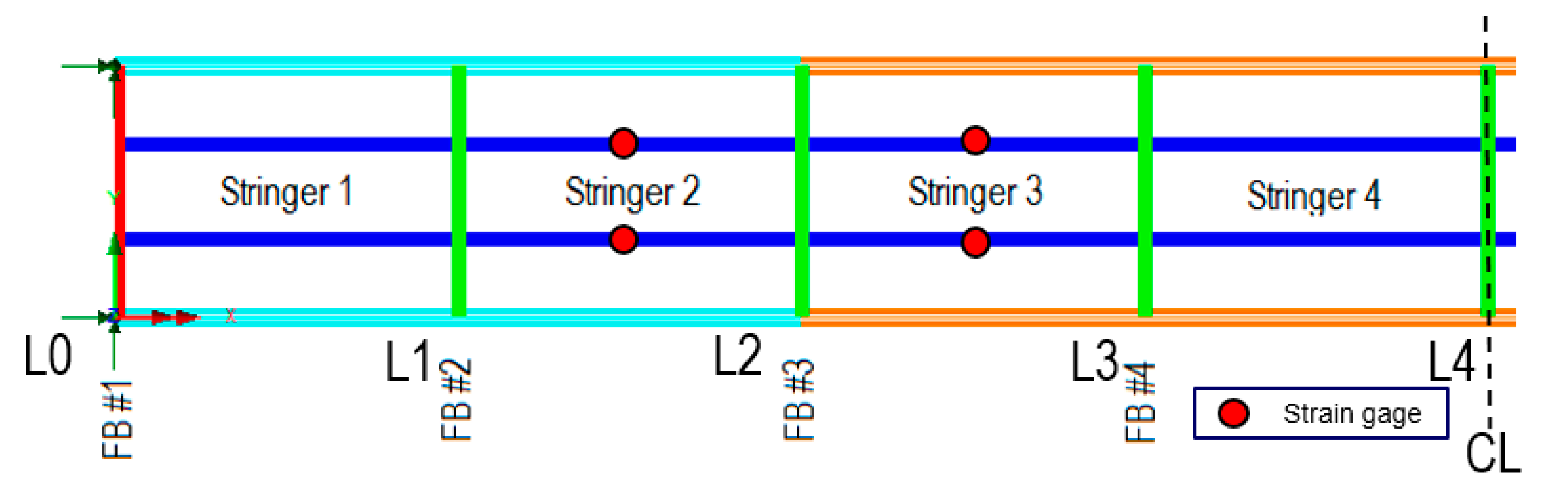
3.1.1. FEM Modeling and Analysis of Truss Bridge
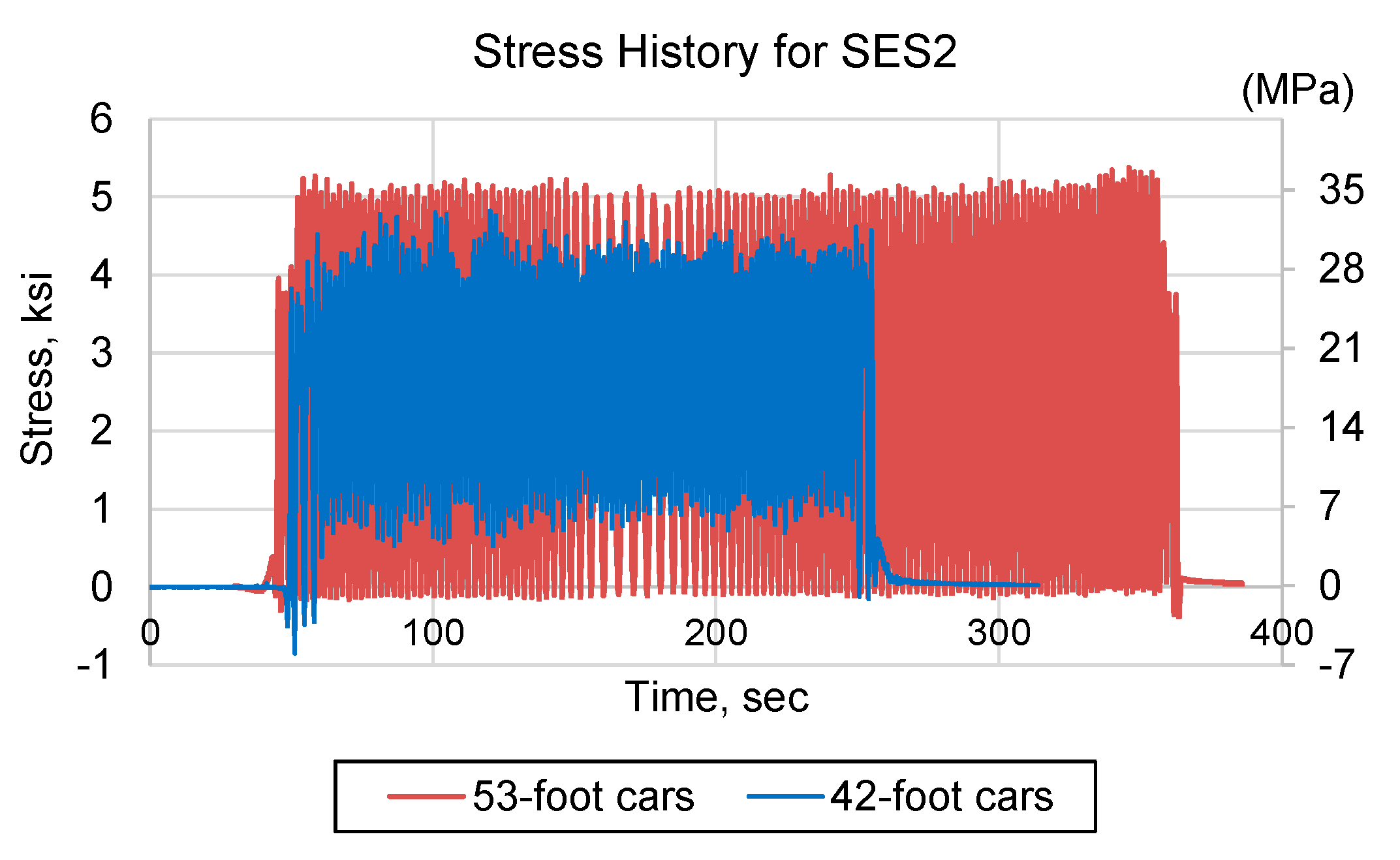
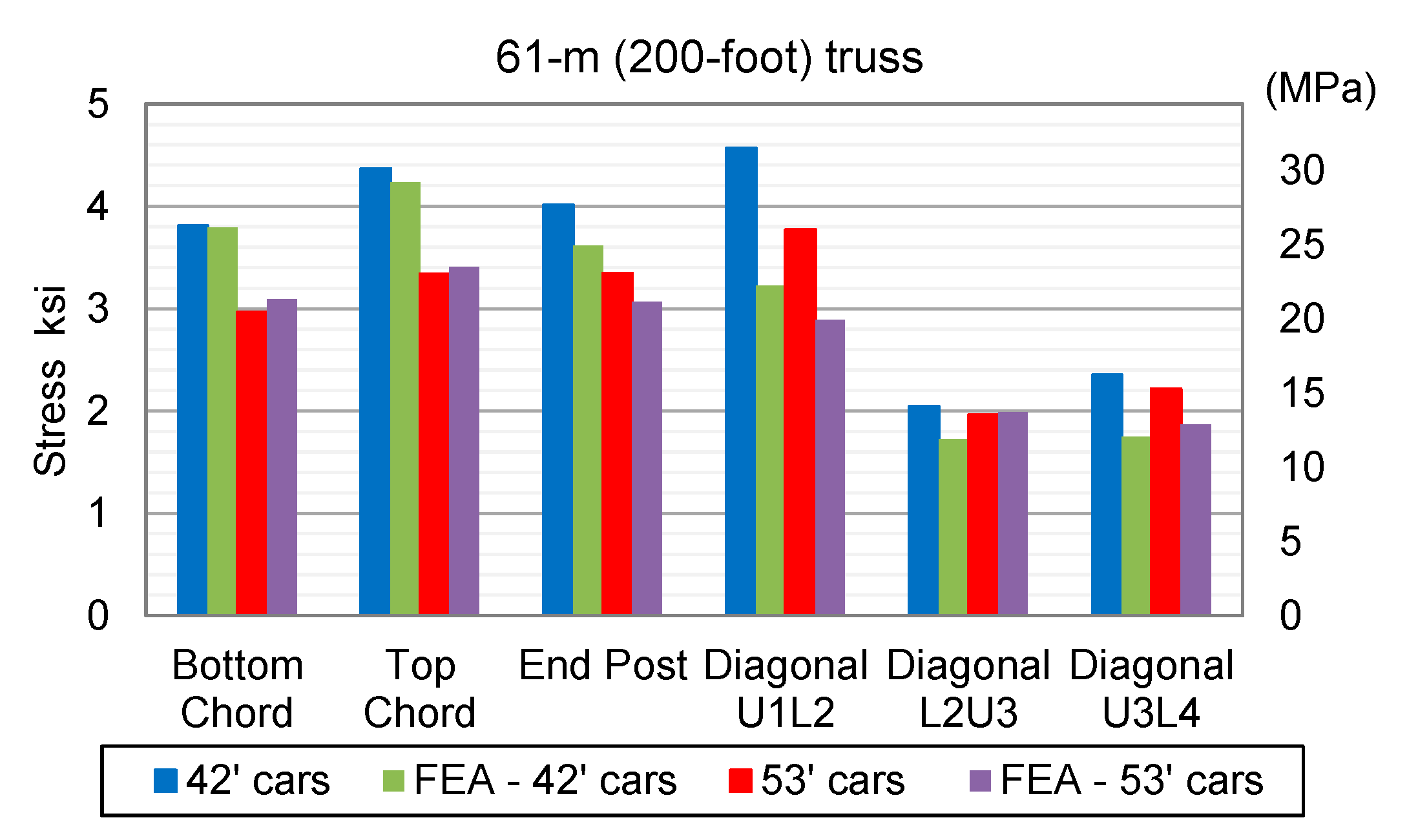
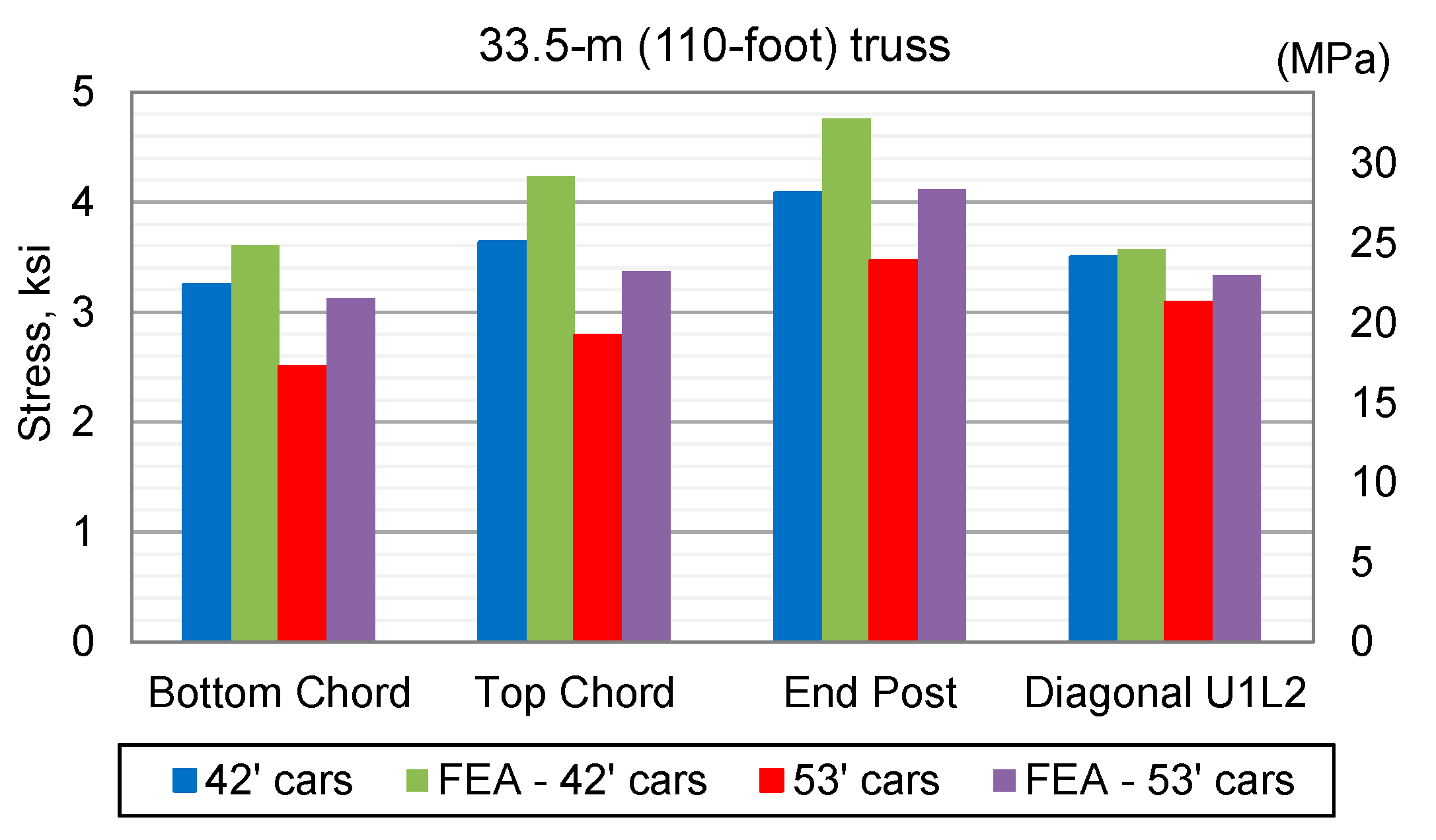
3.1.2. Results from Test of Truss Bridge
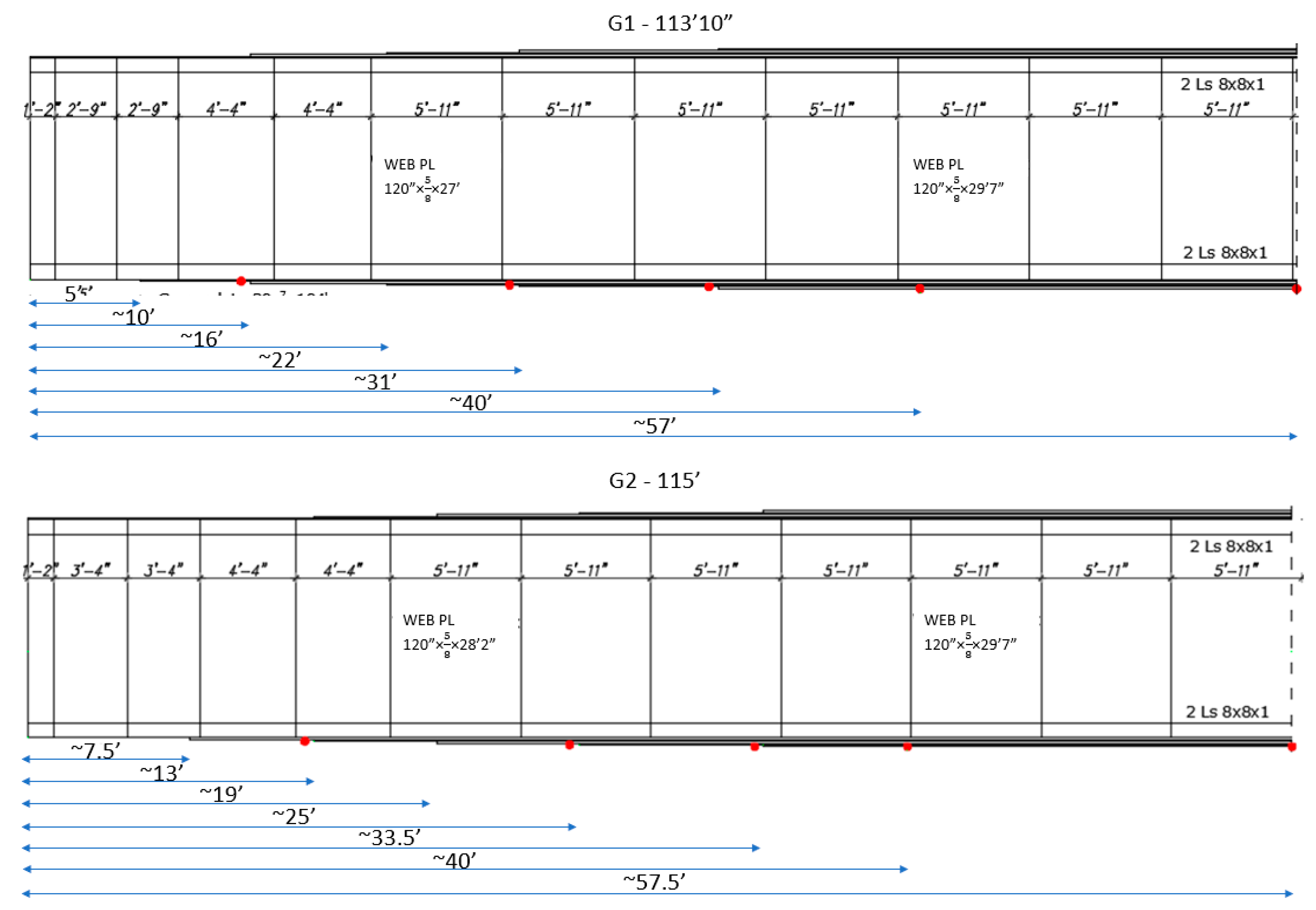
3.2. Riveted DPG Spans
3.2.1. FEM Modeling and Analysis of DPG Bridge
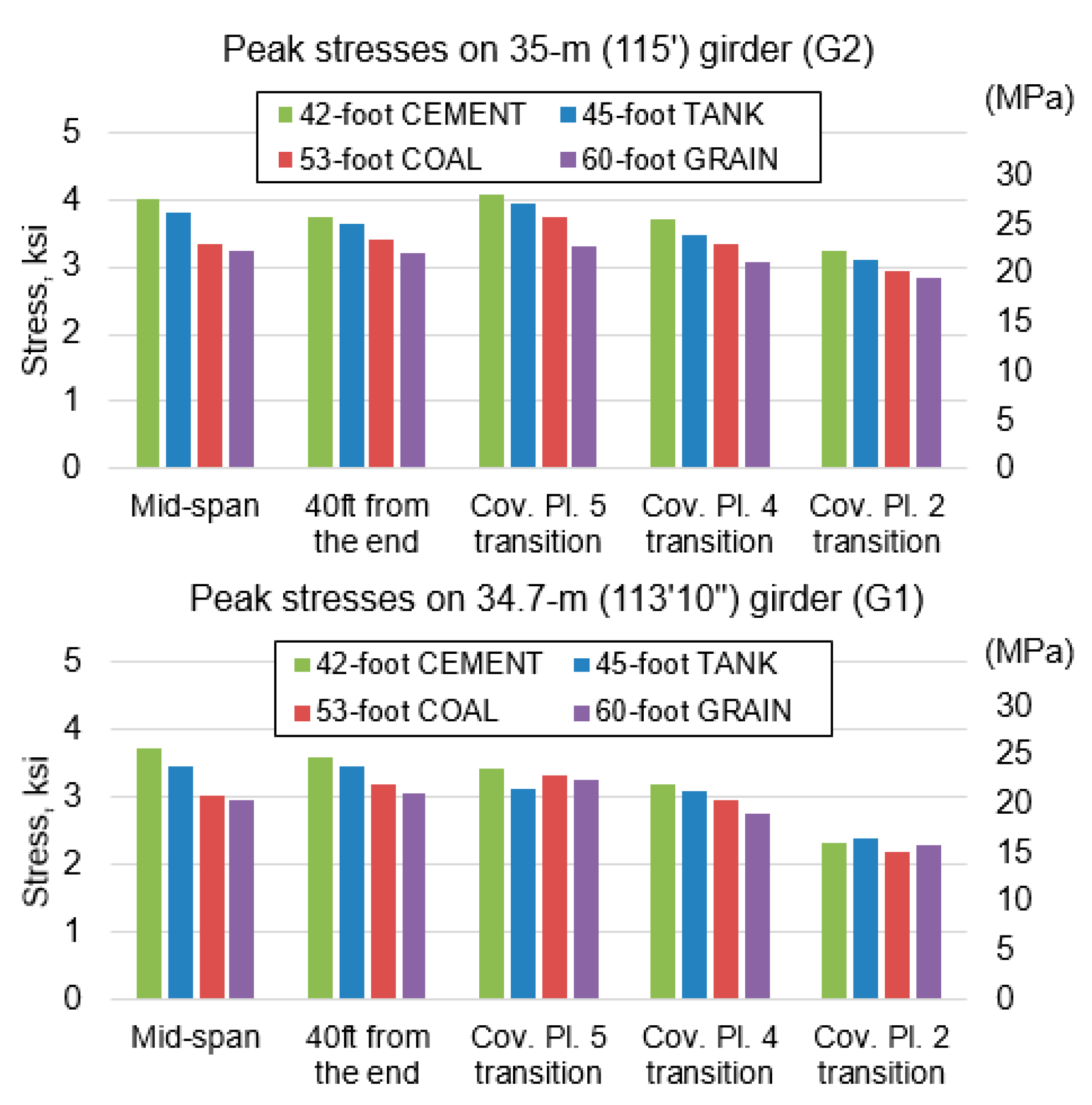
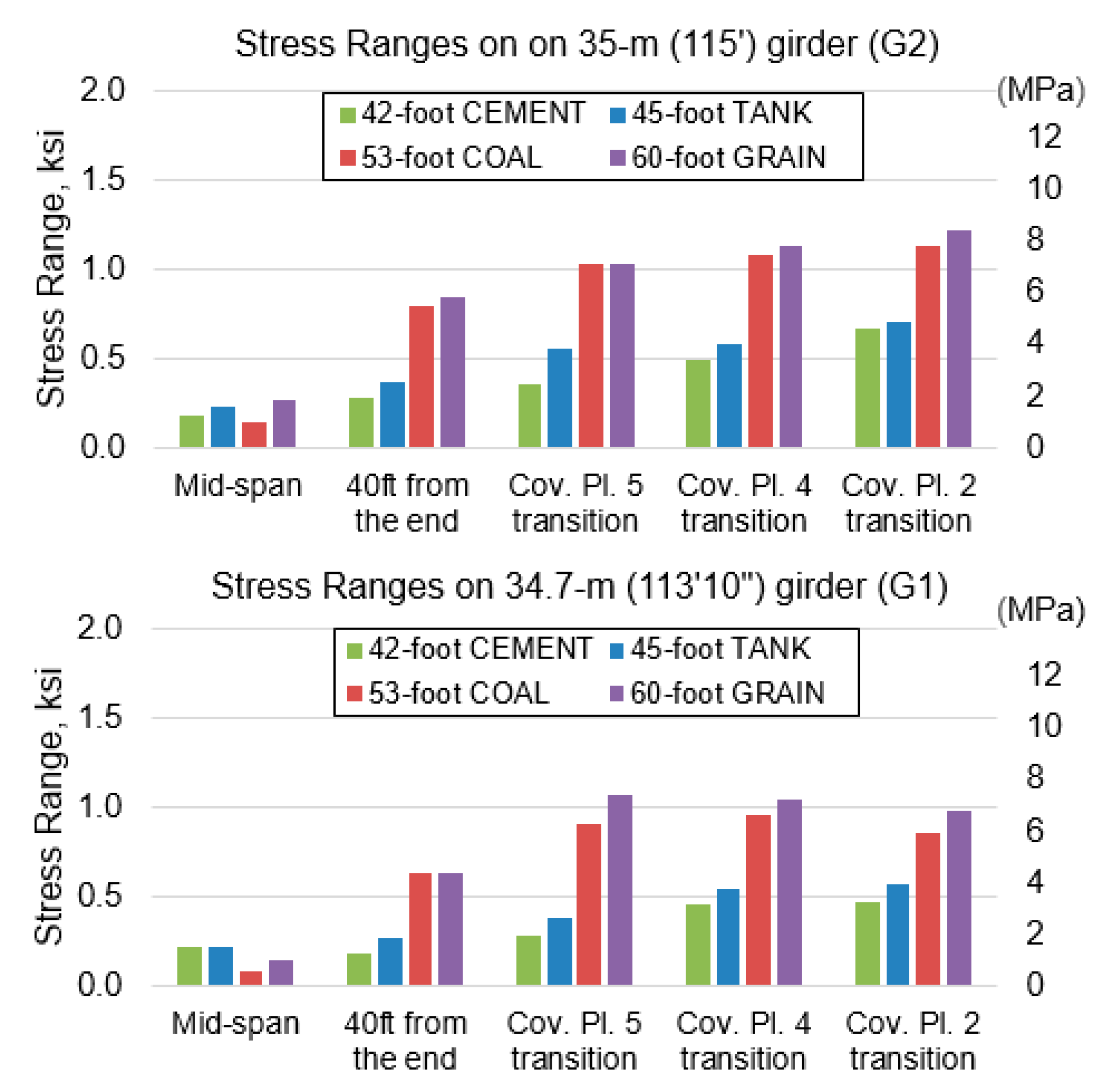
3.2.2. Results from Test of DPG Bridge
4. Discussion
5. Conclusions
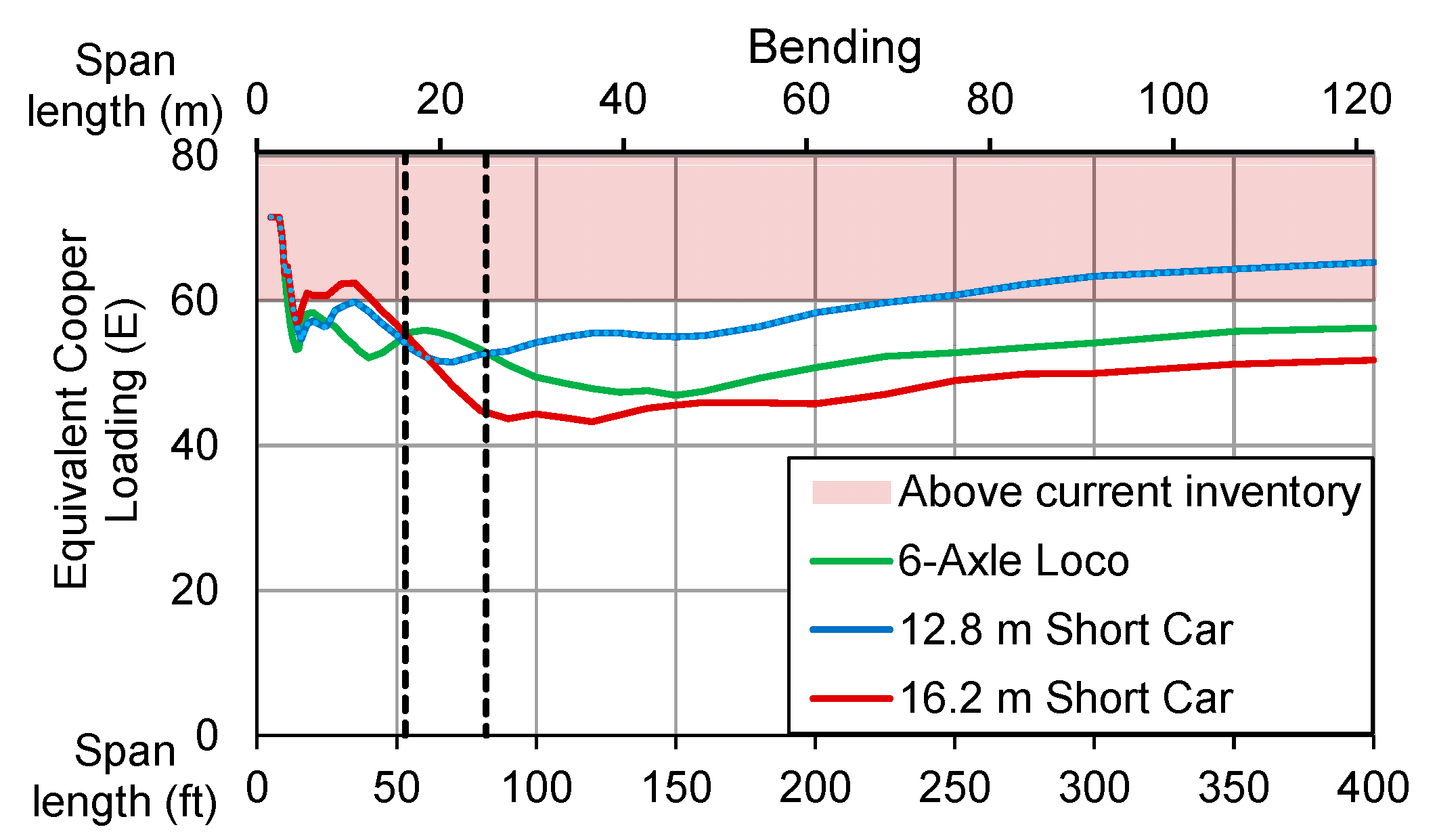
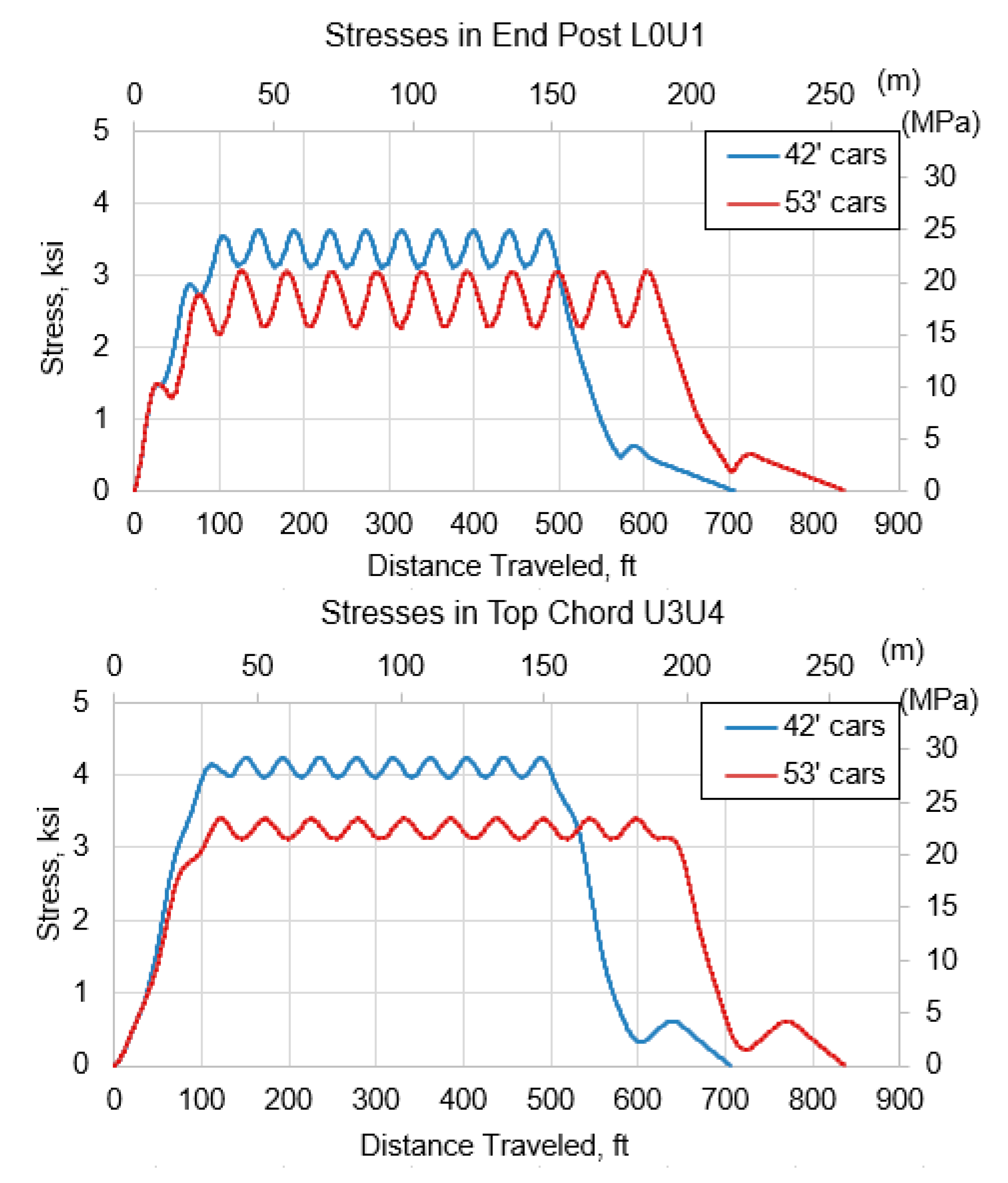
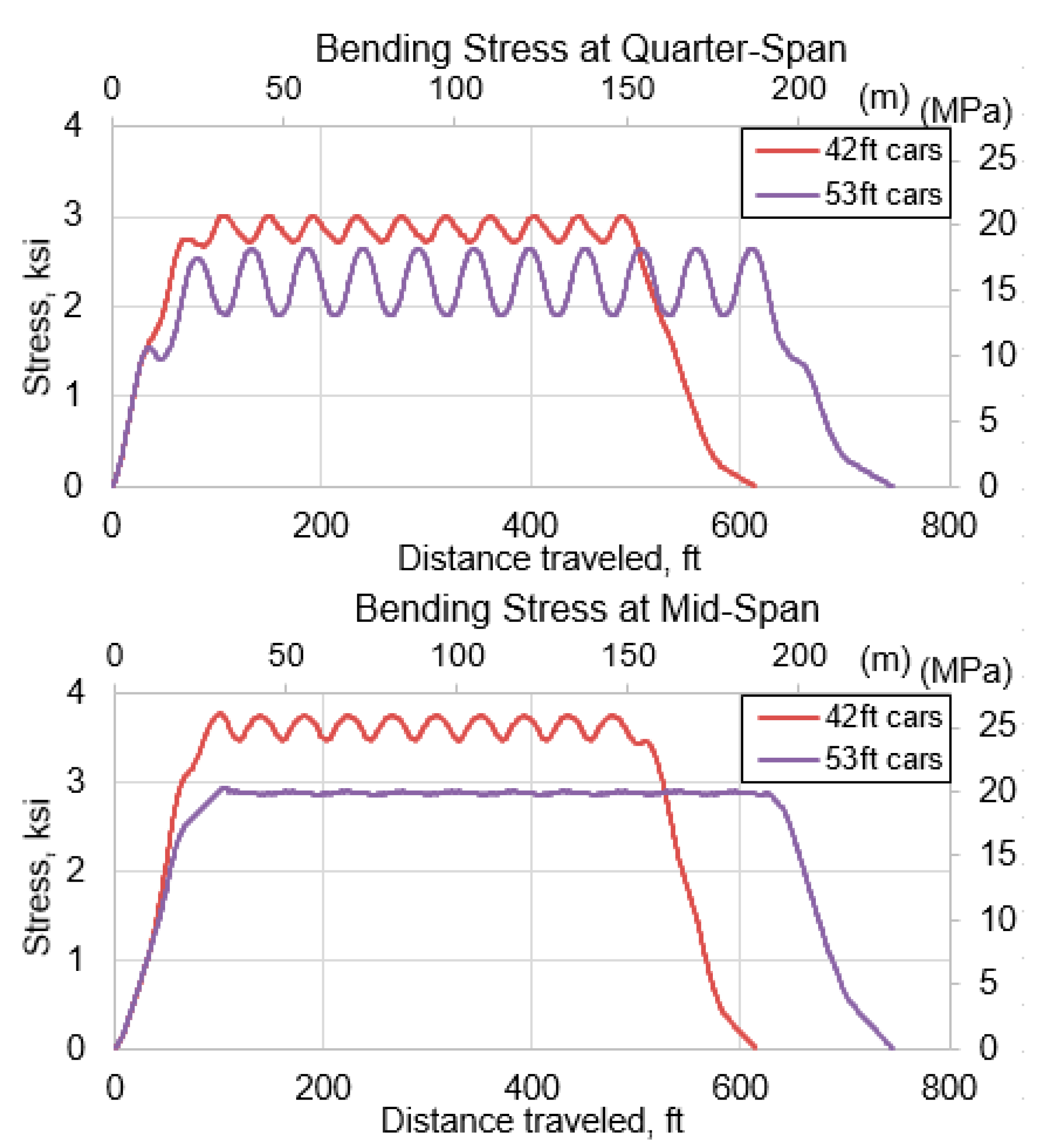
- Short railcars caused a 30% increase in stress in both the top and bottom chords of the 33.5-m (110-ft) truss span. The end post experienced a 26% stress increase due to short railcars.
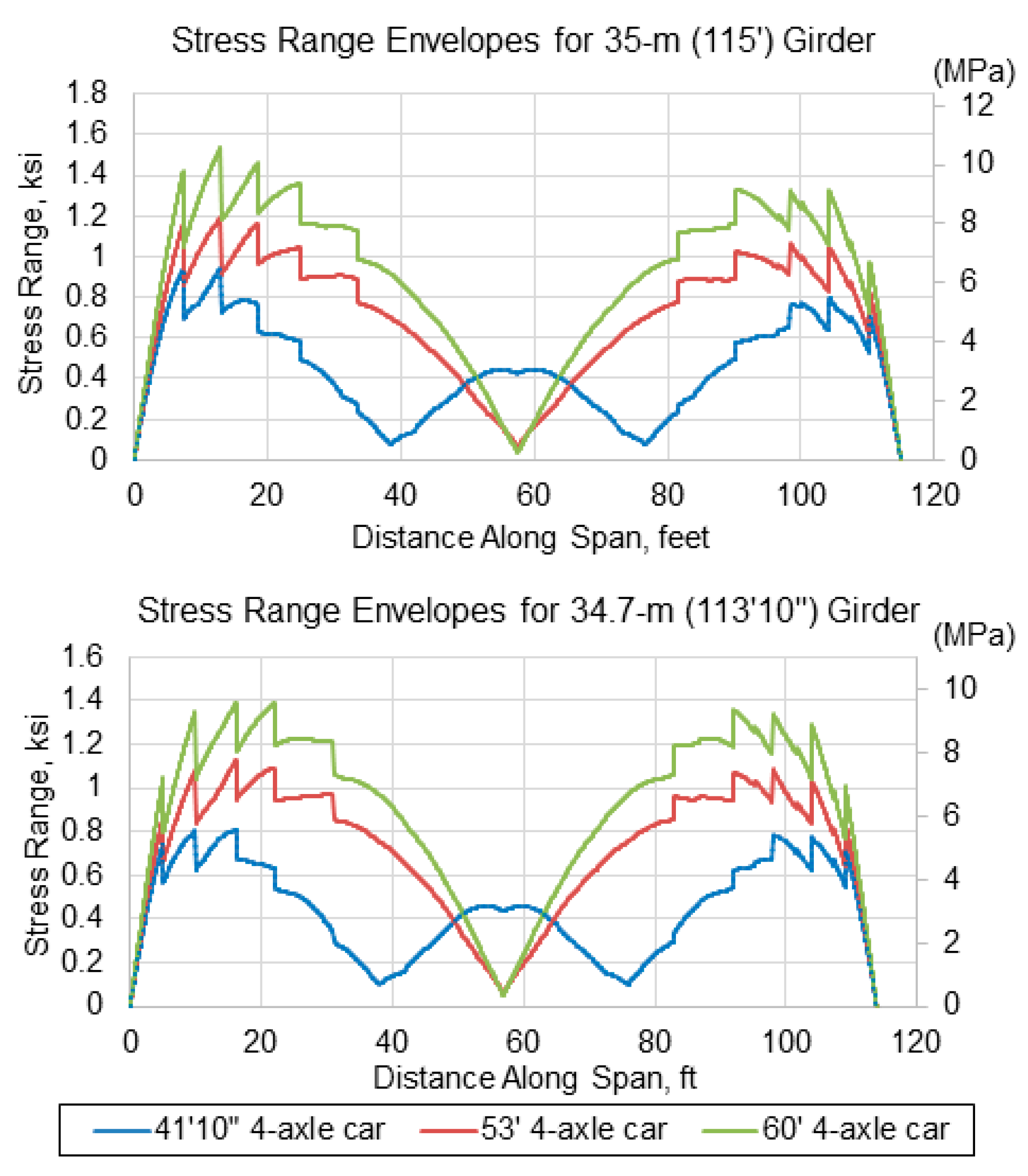
- The 12.8-m (42-ft) short railcars produced maximum live load stresses of 22 and 26% higher than 16.2-m (53-ft) common length railcars at mid-span locations of the 34.7 m (113-ft, 10-in.) girder and 35-m (115-ft) girder, respectively.
- The considered members in trusses and the location on the riveted steel DPG span govern the overall load capacity of the bridge, so shipments of multiple car blocks of short railcars should be carefully planned.
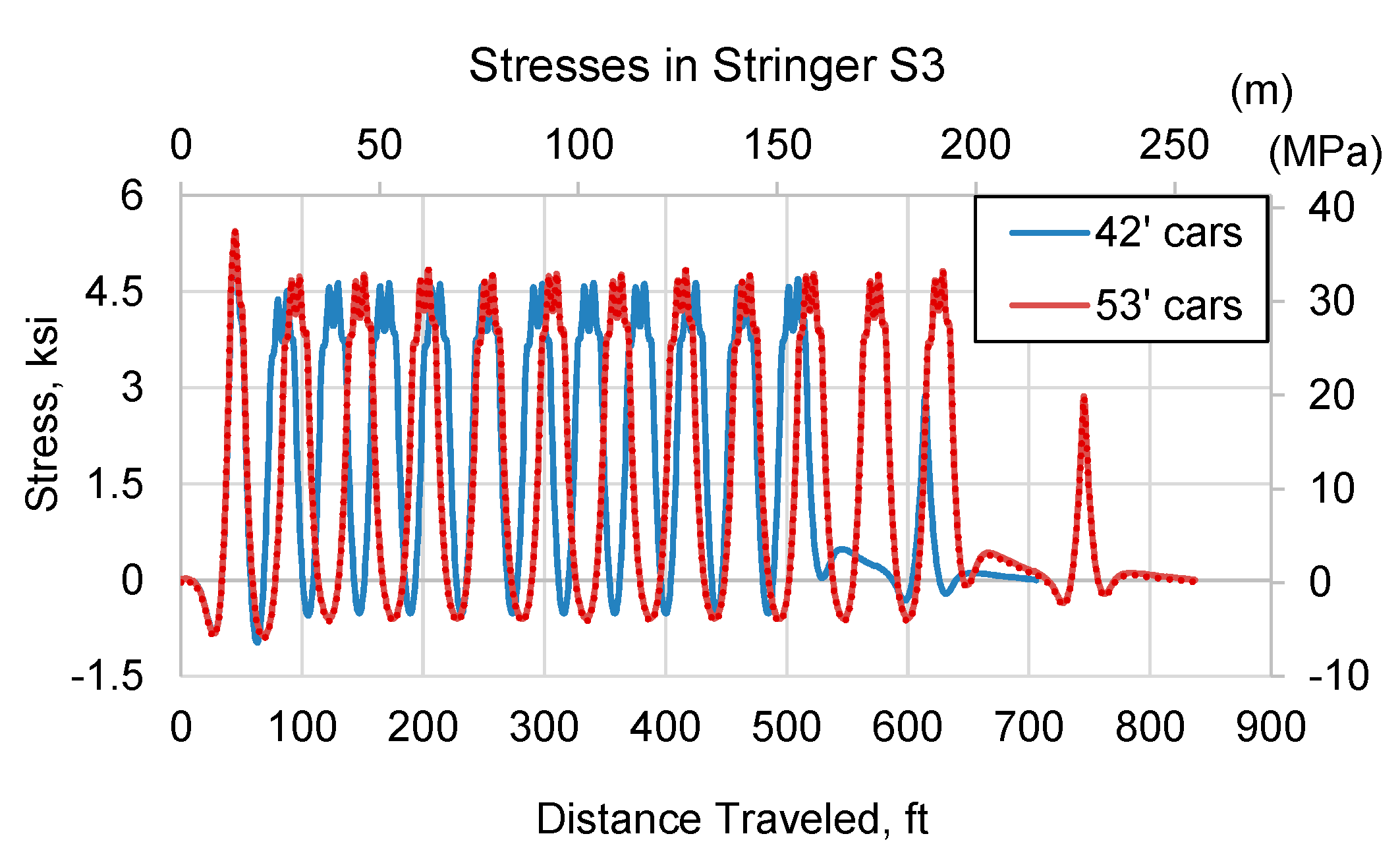
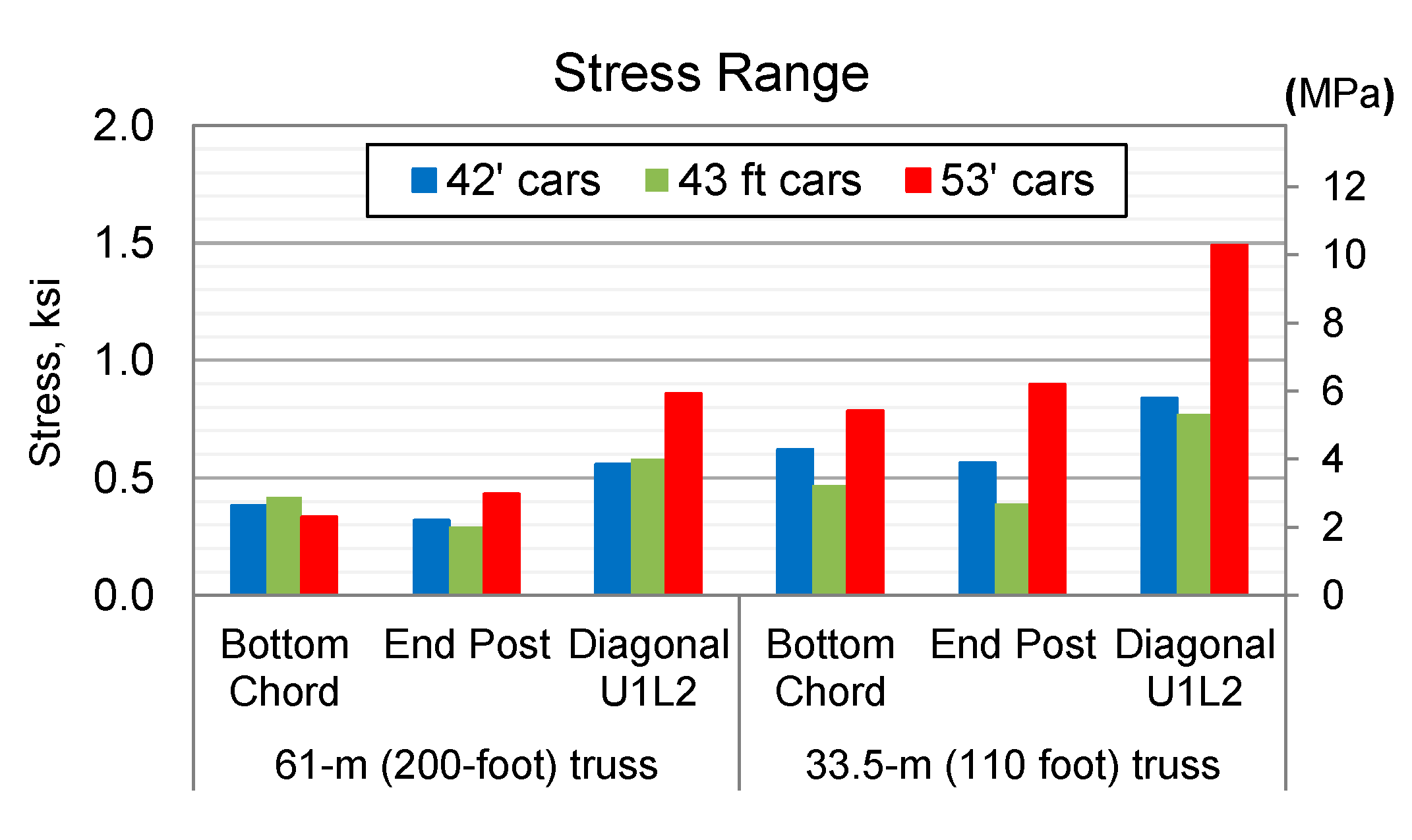
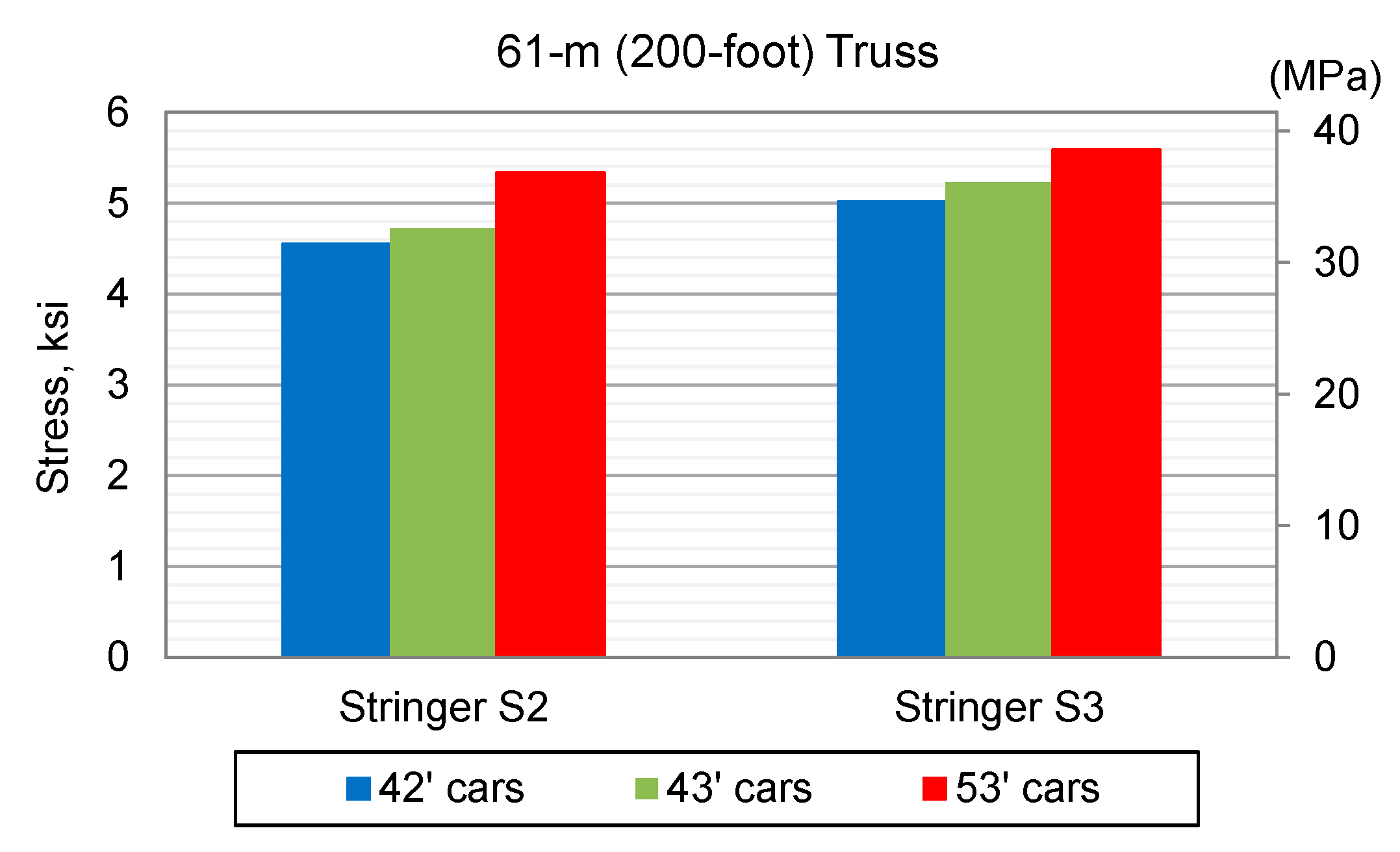
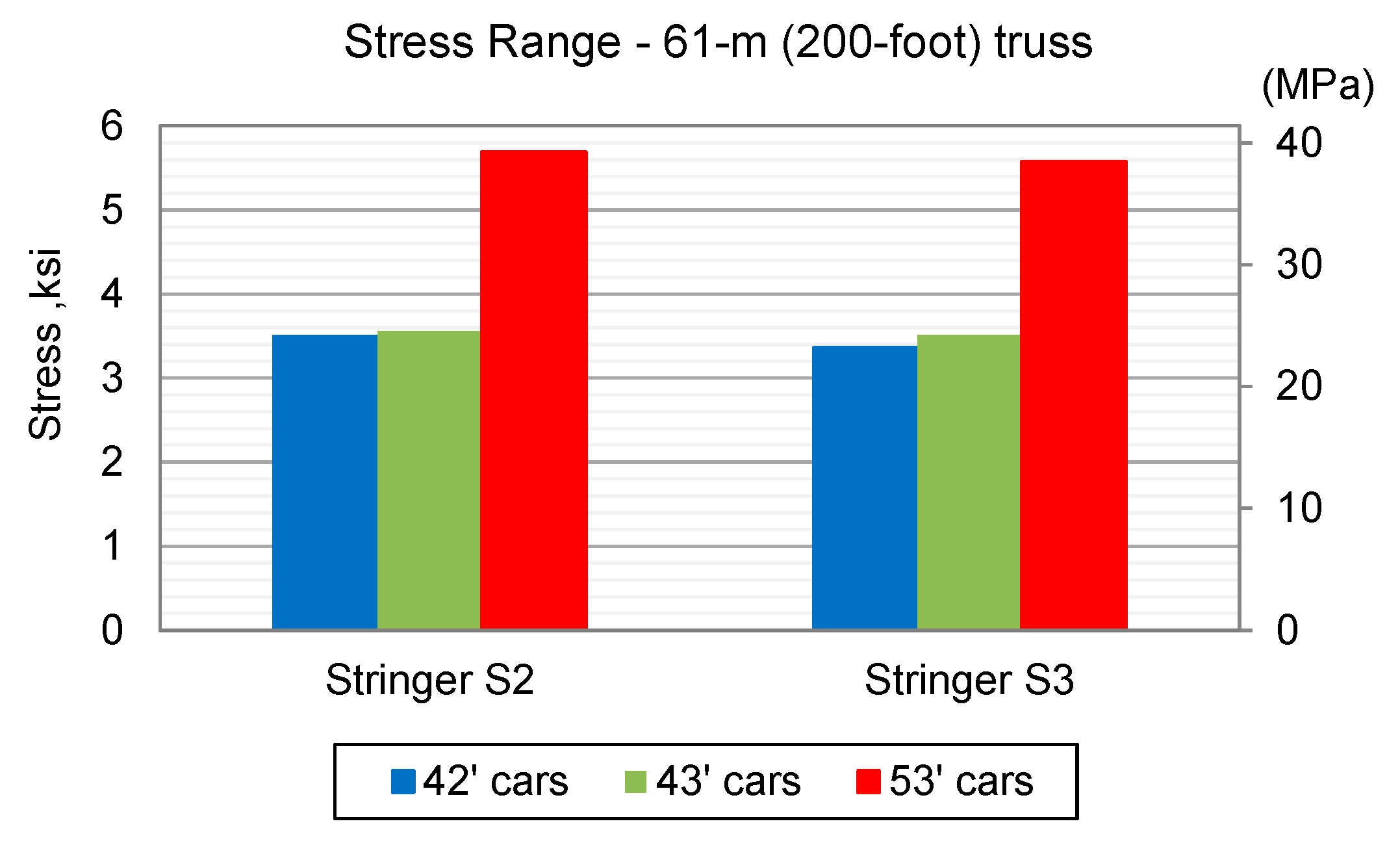
- Stringers of the 61-m (200-ft) span did not experience any increase in stresses due to short railcars. However, the stringers experienced full unloading as the train traversed, and therefore, they can be more susceptible to fatigue.
- Bridge load capacity ratings and railway operating restrictions need to consider railcar length in addition to railcar weight.
- Shorter rail cars can limit the carload capacity of a bridge due to increased load on a span.
- Longer rail cars can shorten the fatigue life of a bridge due to larger stress ranges caused by greater unloading between axles.
- The ratio of rail car length to span length is a key parameter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rakoczy, A.M.; Otter, D.E.; Basye, C. Effects of Short Cars on Bridges and Track. In Proceedings of the AREMA Conference, Orlando, FL, USA, 26–29 September 2016. [Google Scholar]
- Rakoczy, A.; Otter, D.; Dick, S. Short Heavy Axle Load Cars: Analysis of Longer Bridge Spans; Technology Digest TD-16-047; TTCI/AAR: Pueblo, CO, USA, 2016. [Google Scholar]
- Rakoczy, A.; Prough, B.; Otter, D.; Dick, S. Short Heavy Axle Load Cars: Testing of Longer Bridge Spans; Technology Digest TD-16-048; TTCI/AAR: Pueblo, CO, USA, 2016. [Google Scholar]
- Rakoczy, A.M.; Shushu, L.; Otter, D.E.; Dick, S.M. Current Loading Spectra for Evaluation of Railway Bridges; Report R-1028; AAR/TTCI: Pueblo, CO, USA, 2018. [Google Scholar]
- Cremona, C.; Eichler, B.; Johansson, B.; Larrson, T. Improved Assessment Methods for Static and Fatigue Resistance of Old Metallic Railway Bridges. J. Bridg. Eng. 2013, 18, 1164–1173. [Google Scholar] [CrossRef]
- DelGrego, M.R.; Culmo, M.P.; DeWolf, J.T. Performance Evaluation through Field Testing of Century-Old Railroad Truss Bridge. J. Bridge Eng. 2008, 13, 132–138. [Google Scholar] [CrossRef]
- Sweeney, R.A.P. Factors Derived from Tests for Fatigue Evaluation of Typical North American Steel Railway Bridges. ASCE J. Bridge Eng. 2018, 23, 04018036. [Google Scholar] [CrossRef]
- American Railway Engineering and Maintenance of Way Association (AREMA). Manual for Railway Engineering, Chapter 15; AREMA: Washington, DC, USA, 2020. [Google Scholar]
- Fryba, L. Dynamics of Railway Bridges; Thomas Telford: London, UK, 1996; ISBN 0-7277-2044-9. [Google Scholar]
- Zobel, H.; Zbiciak, A.; Oleszek, R.; Michalczyk, R.; Mossakowski, P. Numerical Identification of the Dynamic Characteristics of a Steel-Concrete Railway Bridge. Roads Bridges 2014, 13, 275–301. [Google Scholar] [CrossRef]
- Wichtowski, B. Load-Carrying Capacity of Steel Railway Bridges of the Second Half of XIX Century—Discussion. Roads Bridges 2014, 13, 261–269. [Google Scholar] [CrossRef]
- Chróścielewski, J.; Rucka, M.; Banaś, A.; Malinowski, M.; Miśkiewicz, M.; Rutkowski, R. Systemy monitorowania stanu technicznego konstrukcji na przykładzie trzech mostów. Mosty 2011, 2, 32–40. [Google Scholar]
- Malinowski, M.; Rutkowski, R. Monitorowanie w trakcie 3-letniej eksploatacji Mostu III Tysiąclenia im. Jana Pawła II w Gdańsku. Inżynieria I Budownictwo 2005, 6, 323–326. [Google Scholar]
- Leander, J. Refining the Fatigue Assessment Procedure of Existing Steel Bridges. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2009. [Google Scholar]
- Rakoczy, A.; Otter, D.; Dick, S. Testing of 115-ft. In Girder Span for Fatigue Loading and Railcar Length Effects; Technology Digest TD-17-029; TTCI/AAR: Pueblo, CO, USA, 2017. [Google Scholar]
- Bujňák, J.; Gocál, J.; Hlinka, R. Assessment of Railway Steel Bridge Structures. Procedia Eng. 2016, 156, 75–82. [Google Scholar] [CrossRef]
- LUSAS Bridge/Bridge Plus. Available online: https://www.lusas.com/products/bridge_tour_overview.html (accessed on 20 June 2014).
- Axellson, E.; Syk, A.; Ulker-Kaustell, M.; Barttini, J.M. Effect of Axle Load Spreading and Support Stiffness on the dynamic response of short span Railway Bridges. Struct. Eng. Int. 2014, 24, 457–465. [Google Scholar] [CrossRef]
- Dick, S.M.; McCabe, S.L. Fatigue Analysis of Steel Railway Girder Bridges. In Proceedings of the 2002 Conference of the American Railway Engineering & Maintenance of Way Association, AREMA, Lanham, MD, USA, 2002. [Google Scholar]
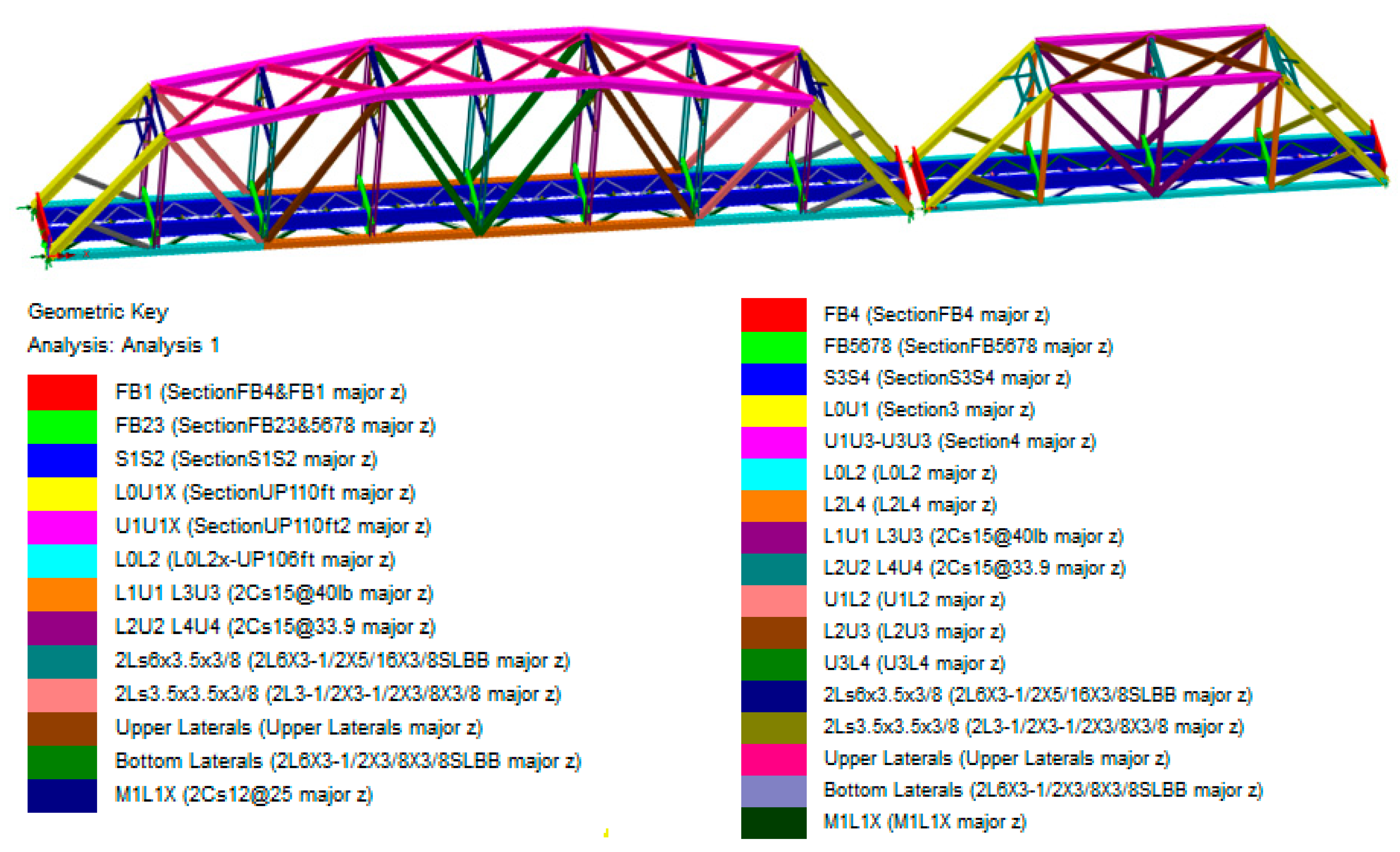




| Bottom Chords and Diagonals | Top Chords and End Posts | |
|---|---|---|
| Scheme of the cross-section |  | 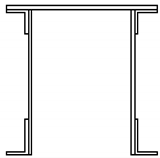 |
| 61 m truss members | Bottom Chord L0L2: 4Ls 6 × 4 × 1/2 2Pls 2 × 7/16 | Upper Chords U1U3, U3U3: 2Ls 4 × 4 × 1/2 2Ls 6 × 4 × 1/2 1 Cov. Pl 27 × 5/8 2 Web Pls 24 × 5/8 |
| Bottom Chord L2L4 4Ls 6 × 4 × 5/8 2Pls 24 × 5/8 | ||
| Diagonal U1L2: 4Ls 6 × 4× 1/2 2Pls 18 × 3/4 | Diagonal L0U1: 2Ls 4 × 4 × 5/8 2Ls 6 × 4 × 5/8 1 Cov. Pl 27 × 5/8 2 Web Pls 24 × 3/4 | |
| Diagonal L2U3: 4Ls 4 × 4 × 5/8 2Pls 18 × 1/2 | ||
| Diagonal U3L4 4Ls 4 × 4 × 3/8 2Pls 18 × 1/2 | ||
| 33.5 m truss members | Bottom Chord L0L2: 4Ls 4 × 4 × 3/8 2 Pls 18 × 3/8 | Upper Chords U1U3: 4Ls 4 × 4× 3/8 1 Cov. Pl 24 × 1/2 2 Web Pls 18 × 3/8 |
| Diagonal U1L2: 2 Cs 15@33.9 | Diagonal L0U1: 4Ls 4 × 4 × 3/8 1 Cov. Pl 24 × 1/2 2 Web Pls 18 × 1/2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakoczy, A.M.; Otter, D.E.; Dick, S.M. Analytical and Measured Effects of Short and Heavy Rail Cars on Railway Bridges in the USA. Appl. Sci. 2021, 11, 3126. https://doi.org/10.3390/app11073126
Rakoczy AM, Otter DE, Dick SM. Analytical and Measured Effects of Short and Heavy Rail Cars on Railway Bridges in the USA. Applied Sciences. 2021; 11(7):3126. https://doi.org/10.3390/app11073126
Chicago/Turabian StyleRakoczy, Anna M., Duane E. Otter, and Stephen M. Dick. 2021. "Analytical and Measured Effects of Short and Heavy Rail Cars on Railway Bridges in the USA" Applied Sciences 11, no. 7: 3126. https://doi.org/10.3390/app11073126
APA StyleRakoczy, A. M., Otter, D. E., & Dick, S. M. (2021). Analytical and Measured Effects of Short and Heavy Rail Cars on Railway Bridges in the USA. Applied Sciences, 11(7), 3126. https://doi.org/10.3390/app11073126








