Abstract
A numerical simulation study on elastic wave propagation of a phononic composite structure consisting of epoxy and tungsten carbide is presented for low-frequency elastic wave attenuation applications. The calculated dispersion curves of the epoxy/tungsten carbide composite show that the propagation of elastic waves is prohibited inside the periodic structure over a frequency range. To achieve a wide bandgap, the elastic composite structure can be optimized by changing its dimensions and arrangement, including size, number, and rotation angle of square inclusions. The simulation results show that increasing the number of inclusions and the filling fraction of the unit cell significantly broaden the phononic bandgap compared to other geometric tunings. Additionally, a nonmonotonic relationship between the bandwidth and filling fraction of the composite was found, and this relationship results from spacing among inclusions and inclusion sizes causing different effects on Bragg scatterings and localized resonances of elastic waves. Moreover, the calculated transmission spectra of the epoxy/tungsten carbide composite structure verify its low-frequency bandgap behavior.
1. Introduction
Elastic metamaterials are architecturally engineered structures that exhibit unusual properties to control the propagation of elastic waves through their structures [1,2]. Elastic metamaterials can be composed of periodically arranged phononic crystals (PnCs) that control elastic waves at a specific frequency range where the incoming wave cannot propagate—named stop bands or band gaps. The observation of the band gap results from two possible mechanisms: Bragg scattering and localized resonances of elastic waves [3]. The observation of the Bragg scattering results from the interaction of elastic waves scattered by periodic unit cells. The localized resonance is elastic waves locally oscillated around the center of the inclusion structure, mainly depending on the inclusion structure itself. Therefore, by tuning the geometry, size, arrangement, and shape of the scatterers within the soft host, it could be possible to achieve band gaps with a wider frequency range by combining these two mechanisms [4]. This is useful for a variety of applications such as noise and vibration isolation [5,6,7,8,9], energy harvesting [10,11,12,13], and acoustic and elastic filters and waveguides [14,15,16,17].
PnCs are typically designed by placing a high-stiffness material inclusion in a low-stiffness (soft) matrix [18]. Previous studies have reported that multiple bandgaps can be realized using different shapes of inclusions within a soft matrix. For example, Cheng and Shi achieved low-frequency band gaps using two- and three-component sphere inclusions [19]. Wang et al. achieved complete multiple band gaps using two-dimensional phononic crystal slabs with periodic cross-like holes [20]. Mizukami et al. achieved attenuation of broadband vibration using continuous carbon fiber-reinforced plastics with steel disks [21]. Elastic band gaps of PnCs could also be achieved by other different shapes of inclusions, such as comb-like inclusions [22], spindle shaped [23], quasi-Sierpinski carpet [24], and square/triangle shaped [25,26]. Among these studies, the geometric effect of the inclusions on the bandwidth and central frequency of the band gap are discussed by changing the size, inclusion number, and filling fraction of the unit cell. However, the effect of irregular size and locations of inclusions within a unit cell are rarely discussed but will be included in this work.
Another critical factor in determining the bandwidth and central frequencies of the bandgaps is the material properties of the inclusions and matrix used in a phononic crystal [27], which includes mass density ratio, the shear modulus ratio and Poisson’s ratios. Several studies have shown that the central frequencies of the band gap can generally be increased by increasing Poisson’s ratio of the inclusion/host material [28,29,30]. In addition, the increase in density and Young’s modulus ratios increase the bandwidth of the band gaps [31]. Recently, tungsten carbide inclusion and epoxy matrix has been used in different elastic metamaterials for broadband elastic attenuation applications owing to their high Young’s modulus ratios [32,33]. For example, Lu et al. have demonstrated that a phononic crystal composed of tungsten carbide and epoxy can achieve wider broadband phononic band gaps [34]. Li et al. achieved wide elastic bandgaps using the optimized structure of tungsten carbide spheres embraced in an epoxy matrix [35].
To realize a broad elastic bandgap in the low-frequency range, this work presents a numerical study of a periodic elastic composite composed of tungsten carbide within the epoxy host. The effects of square inclusion size within the unit cell (filling fraction), the stiffness of square inclusion, number of square inclusions, rotation angles of square inclusions, graded inclusion size, and irregular inclusion locations on their bandgap are studied systematically. A relationship between the resulting band gaps and the geometric dimensions is provided. The mechanism of the broad phononic bandgap is analyzed by solving its eigenmodes near the phononic bandgap. Two types of mechanisms, including Bragg scattering and localized resonances resulting in elastic bandgaps, are discussed. Moreover, analysis of the transmission loss also demonstrates the broad bandgap metrics of the proposed elastic metamaterials. This study is potentially beneficial as a guideline to design an elastic metamaterial with the broadband bandgap.
2. Numerical Methods
Elastic wave propagation through use of a phononic crystal was studied using a two-dimensional finite element method implemented in Solid Mechanics COMSOL modules [36]. The governing equation is given by Equation (1):
where ρ and u are the density and displacement of the elastic materials, the volumetric force fv is the force per deformed volume, and σ is the stress tensor. In this work, the proposed phononic crystals consist of high-stiffness inclusions placed in a low-stiffness matrix. The low-stiffness matrix in this study is epoxy, whereas the high-stiffness inclusions are composed of tungsten carbide [34]. The material properties are summarized in Table 1.

Table 1.
The material properties of the matrix and inclusion used in the study.
The dispersion relations describing the wave propagation behavior in a periodic phononic crystal was obtained by solving the eigenvalue problem with the periodic boundary condition. The Floquet–Bloch periodic boundary conditions were applied to the four edges of the unit cell to ensure a periodically repeating nature, as indicated by Equation (2).
where k is the periodicity vector with a length |k| = 2π/Λ, in which Λ is the period in that direction and r is the position vector. Modal analysis was performed to obtain the eigenfrequency corresponding to a given Bloch wave vector k = (kx, ky). The study was performed on a range of wave vectors covering the irreducible Brillouin zone (IBZ), which spans from Γ to X, X to M, and M to Γ, as shown in Figure 1a. The PnC is infinite and periodic in the x, y directions with a lattice constant ao = 1 m. For the elastic wave transmission simulation, the proposed epoxy/tungsten carbide composite unit cells were centered in the simulation domain with a 1 m distance away from the absorption boundary. An incident force of 1 N was applied in front of the composite structure in the propagating direction, and edges of the simulation domain were applied with the perfectly matched layers [37], which absorb all outgoing wave energy. The transmission loss as a function of frequency is given by
where P is the power derived from mechanical energy flux, and Pin and Pout are the power of the incident and transmitted elastic waves.
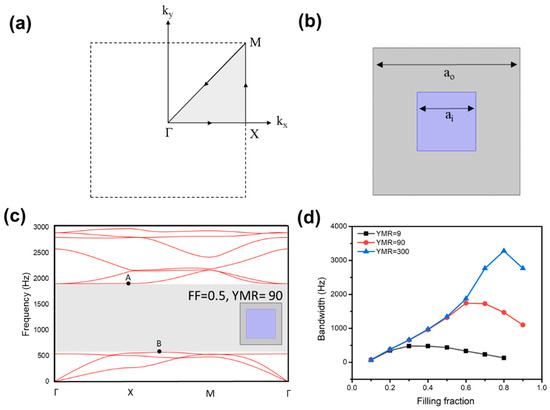
Figure 1.
(a) The irreducible Brillouin zone (IBZ) in a 2D phononic crystal. (b) The phononic crystal consisting of one-square inclusion in the soft host, where the filling fraction is controlled by varying the parameters ai and ao. (c) The dispersion curves of a phononic crystal with a square inclusion, where ao = 1 m, ai = 0.25 m, FF = 0.5, and Young’s modulus ratio (YMR) = 90. (d) For filling fraction (FF) = 0.5, variations in bandwidth with filling fraction at YMR = 9, 90, and 300, respectively.
3. Results and Discussions
3.1. Elastic Composites with Square Inclusions and Epoxy Host
- i.
- Single-square inclusion/epoxy host with different Young’s moduli.
Firstly, the unit cell composed of a single-square inclusion within a soft host was studied by varying its filling fraction (FF). The filling fraction was defined as FF = (ai)2/(ao)2, where ai is the side length of the square inclusion and ao is the unit cell length, as shown in Figure 1b. The length ao was kept constant at 1 m, and the ai was varied from 0.316 to 0.948 m, corresponding to different FFs from 0.1 to 0.9. The effect of the stiffness of the inclusion in the matrix was studied by changing its Young’s modulus ratio (YMR), defined as YMR = Ei/Eo, where Ei is Young’s modulus of the inclusion material and Eo is Young’s modulus of the host material. The material considered here for the matrix is epoxy with Eo = 4.3438 GPa, and Young’s modulus of the inclusion Ei was varied to yield YMRs of 9, 90, and 300. Figure 1c show the dispersion curves of phononic crystals with the single-square inclusion at FF = 0.5, where the shaded region represents the bandgap and points A and B are located at the maximum and minimum frequencies of the bandgap, respectively.
Figure 1d shows that in the case of YMR = 300, the bandwidth increases as the filling fraction increases, reaching a maximum of 3280 Hz at FF = 0.8, after which it starts to decrease with any further increase in FF. When YMR was 9, the elastic composite bandwidth showed a slight change with an increased filling factor value, which results from the lack of the significant contrast in the elastic stiffness of the inclusion to that of the matrix. In general, a higher YMR of the elastic composite has a broader bandgap, and its bandwidth increases and reaches a maximum point at a specific FF. Then, the bandwidth would decrease with increase in its FF. The relationship between bandwidth and filling fractions are strongly related owing to the corresponding changes in geometric dimensions in the periodic unit cell, which affects the resonance frequency of the elastic eigenmodes [26,27,28,29,30,31,32,33,34,35,36,37,38]. In Figure A1a,b of Appendix A, the lower bound frequency (LBF) and upper bound frequency (UBF) are plotted against the filling fraction of the square inclusion at YMR = 9, 90, and 300. The simulation result shows that the relationship between UBF and filling fraction followed a similar trend to that of the bandwidth in Figure 1d, which indicates that the variations in bandwidth are more dominated by UBF, and this difference between LBF and UBF would be discussed based on the eigenmode analysis in the part (iii) of Section 3.1.
- ii.
- Increasing number of square inclusions within a unit cell.
To target a wider bandgap, in the following sections, the YMR of the inclusion/matrix was fixed at 90, corresponding to the ratio of tungsten carbide to the epoxy. The phononic crystals discussed above consisted only of one inclusion in each unit cell. Here, the number of square inclusions within the unit cell was increased to four and nine to investigate the effect of the inclusion number within the unit cell on the phononic band structure. The unit cells were designed as shown in the inset of Figure 2a,b, where the filling fraction was calculated as FF = 4(ai)2/(ao)2 in the case of four-square inclusions within the unit cell and FF = 9(ai)2/(ao)2 in the case of nine-square inclusions within the unit cell. The relationship between bandgap bandwidth and their filling fractions of three different unit cells was studied by changing ai while fixing the ao at 1 m.
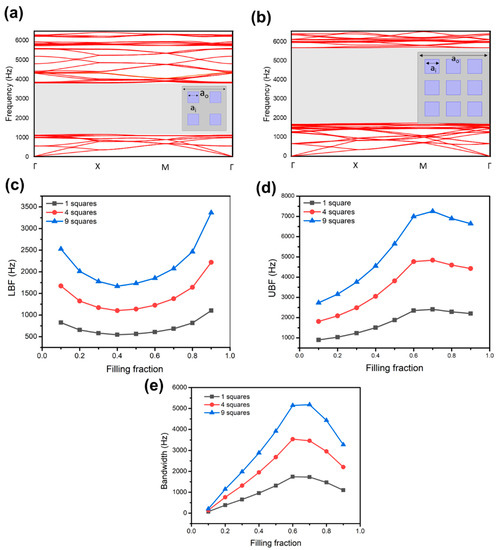
Figure 2.
(a) The dispersion curves generated for a phononic crystal with four-square inclusions with FF = 0.5. (b) The dispersion curves generated for a phononic crystal with nine-square inclusions with FF = 0.5. (c–e) lower bound frequency (LBF), upper bound frequency (UBF), and bandwidth versus filling fraction for different unit cells with one-, four-, and nine-square inclusions.
The dispersion curves of phononic crystals with the four- and nine-square inclusions are shown in Figure 2a,b, where the shaded region represents the bandgap. The simulation results show that increasing the number of inclusions not only increased the bandwidth but resulted in an upward shift in the frequency range. The bandwidth was increased from 1316 Hz for one inclusion to 2678 Hz and 3915 Hz for four and nine inclusions. Interestingly, the LBF and UBF show a nonmonotonic relationship with the filling fraction, as shown in Figure 2c,d. This relationship causes the bandwidth of the bandgap to reach a maximum at a filling faction of 0.6.
- iii.
- Eigenmode analysis.
To analyze what causes the LBF and UBF of the tungsten carbide epoxy phononic crystal to not follow the same trend with filling fractions, their deformation distributions of eigenmodes at the lowest and highest frequencies of the bandgap were calculated, as shown in Figure 3. The simulation results show that at the lower frequency near the bandgap, the localized elastic wave modes are excited and the inclusion/epoxy vibrations behave as mass-spring oscillators [39], as indicated in Figure 3b,c. The phononic crystal exhibits a bandgap at wavelengths less than gap width among inclusions and inclusion sizes [4]. The nonmonotonic shift of the LBF results from two different trend of inclusion sizes and the width among inclusions with increase in the filling fraction. Therefore, LBF has a minimal value when the filling fraction is near 0.4 for a different number of inclusions within a periodic unit cell, as shown in Figure 2c. Meanwhile, according to a previous study conducted by Cui et al. [40], local resonances mainly depend on the resonator natural frequency and total mass density ratio. Therefore, the YMR does not have a pronounced effect on the LBF, as shown in Figure A1a.
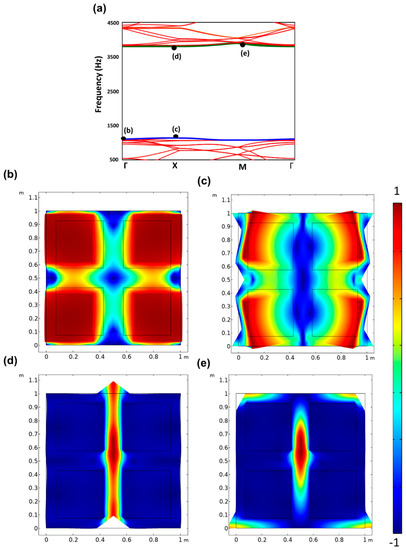
Figure 3.
(a) Dispersion relations of the phononic crystal with four-square inclusions. (b–e) Deformation distributions of eigenmodes in the phononic crystal, corresponding to four different points in the k-space near the bandgap.
At the UBF near the bandgap, elastic Bragg scattering effects were observed between the square inclusion and matrix at a higher frequency, as shown in Figure 3d,e. The Bragg scattering phenomena were induced by destructive interferences when the wavelength of the elastic wave was comparable to the periodicity of the scatterers embedded in the host elastic medium [41,42]. The first band gap was opened at wavelengths larger than the wavelength allowed by the Bragg mechanism, which is also supported by Kushwaha’s study [43]. Therefore, the observed wide broad bandgap in this study resulted from the coupling between two types of mechanisms [4]. The introduction of additional inclusions at a constant FF, as discussed in the previous section, reduced the periodicity of the inclusions, gap width among inclusions, and inclusion sizes. Thus, the reduction in these dimensions led to higher UBF and LBF, as shown in Figure 2c–e.
3.2. Effect of Rotation Angle of Square Inclusions
The effect of the orientation of the square inclusion was investigated by varying the rotation angle of the square inclusions from θ = 0°, 20°, 45°, 70° to 90° for different inclusion numbers, as shown in Figure 4a. The bandwidths of the bandgap in the phononic crystal with different inclusion numbers were plotted against the rotation angle θ for different filling fractions from 0.1 to 0.49 in Figure 4b,d. Due to the square shape of the inclusion, the simulation results show that the bandwidth versus rotation angle is symmetrical, as compared to the results between 0° to 45° and 45° to 90°. For the FF < 0.49, the bandwidth of the phononic bandgap shows a negligible change with an increase in the rotation angle of inclusions. Except when the rotation angle is 45°, the bandwidths of the bandgaps of the phononic crystal are increased owing to the reduced periodicity of square inclusions.
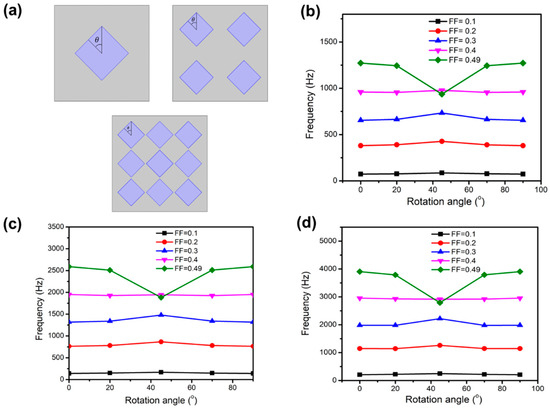
Figure 4.
(a) Phononic crystals with square inclusions rotated by an angle of θ = 45°. (b) Bandwidth versus rotation angle of composites with filling fractions of 0.1–0.5, for one- (b), four- (c), and nine-square (d) inclusions within the host.
When the FF is near 0.49, the bandwidth significantly decreases at a rotation angle of 45° due to extremely narrow gaps among inclusions. In Figure A2a,b of Appendix A, the LBF and UBF versus rotation angles of the four-square inclusion composite, for different filling fractions from 0.4 to 0.45, are presented. The simulation results show that the bandwidth of the bandgap is decreased with a decrease in the FF, mainly due to the reduction in the UBFs. The elastic vibration at the UBF is related to the Bragg scattering [43], as indicated by the eigenmode analysis in the previous section. When the spacings among square inclusions are reduced with an increasing FF, the eigenmode caused by the Bragg scattering shifts to a lower frequency (higher wavelength).
3.3. Effect of Size of Square Inclusions
The effect of using squares of different side lengths within a single unit cell was investigated. In the four-square inclusions, the inclusion sizes were controlled by the square side lengths ai1 and ai2, and the filling fraction was calculated as FF = 2(ai12 + ai22)/a0. In the case of nine squares, three square side lengths were defined as ai1, ai2, and ai3. The filling fraction was FF = 3(ai12 + ai22 + ai32)/a0. In each case, the side lengths were defined, such as ai1 < ai2 < ai3, to achieve the gradient effect, as shown in Figure 5a,b.
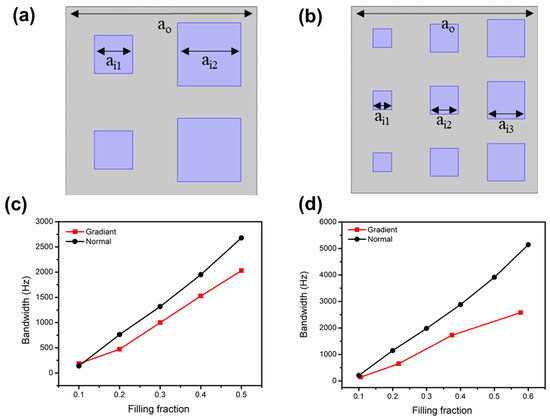
Figure 5.
(a) Phononic crystals with four-square inclusions, where their dimensions are arranged in an increasing gradient. (b) Phononic crystals with nine-square inclusions, where their dimensions are set in a growing gradient of size. (c) The bandwidth of the phononic crystals with graded square inclusions plotted against their filling fraction for four inclusions. (d) The bandwidth of the phononic crystals with graded square inclusions plotted against their filling fraction for nine inclusions.
In the case of four inclusions, phononic crystals with five different filling factions were studied, the square dimensions of which are listed in Table 2. Similarly, in the case of nine-square inclusions, phononic crystals with four different filling factions are presented in Table 3. The lower bound frequency (LBF), upper bound frequency (UBF), and bandwidth versus filling fraction are shown in Figure A3a,d. The simulation result shows that for four- and nine-square inclusions the gradient dimensions of inclusions lead to a higher LBF and a lower UBF, which indicates a narrower bandgap as compared to the equally sized inclusions, as shown in Figure 5c,d. This can be explained by the effective size of the phononic crystal with square inclusions of graded sizes. For example, when the FF = 0.3, the effective size of graded square inclusions was 0.2658 m, which is less than the effective size of normal inclusions, 0.2738. The larger bandwidth is due to the larger effective inclusion size, as indicated by the study of bandwidth versus filling fraction in Section 3.1.

Table 2.
The dimensions of the phononic crystals with 4 gradient square inclusions.

Table 3.
The dimensions of the phononic crystals with 9 gradient square inclusions.
3.4. Effect of Arrangement of Square Inclusions
In addition to the effect of number, sizing, and orientation of inclusions on the band gaps generated by the phononic crystal, the effect of the arrangement of the inclusions was investigated. A phononic crystal with four-square inclusions and a filling fraction of 0.2 is considered in this section. The location of the inclusions was varied by changing the distance r from the center of the unit cell to the center of the inclusion, as shown in Figure 6a. Figure 6b,d show that the locations of the inclusions significantly affect bandwidth of the bandgap. When the r is greater or less than the 0.3535 m, corresponding to the r in Figure 6c, the bandwidth is reduced. This study indicates that the gap width among inclusions is critical for controlling the bandwidth. A similar conclusion can be found in Section 3.1 for phononic crystals with high filling fractions.
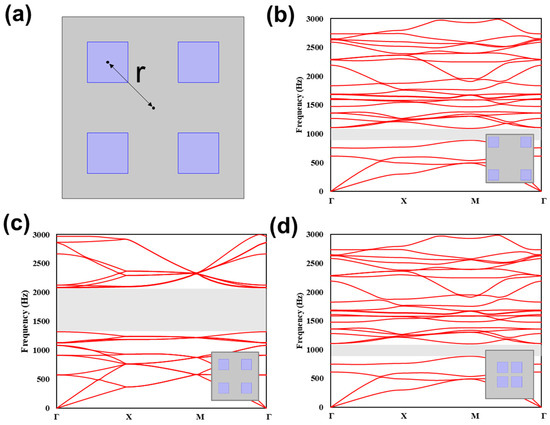
Figure 6.
(a) Phononic crystal with four-square inclusions at a filling fraction of 0.2, where the location of the inclusions were varied by changing the distance r. The dispersion curves showing the generated band gaps are plotted in the case of (b) r = 0.495, (c) r = 0.354, and (d) r = 0.212.
3.5. Transmission Loss in Elastic Metamaterial
Transmission loss analysis was performed on an elastic metamaterial with different numbers of unit cells to verify the effectiveness of the metamaterial in preventing the transmission of the elastic wave through the material within the bandgap frequencies. Figure 7a shows the transmission loss spectra with one-, three-, and five-unit cells with a filling fraction of 0.125 for each. The peak transmission loss occurred at the bandgap regions, where the metamaterial prohibits wave propagation. It was verified that increasing the number of unit cells results in higher transmission loss and more defined peaks, enabling more effective prohibition of elastic wave propagation through the material.
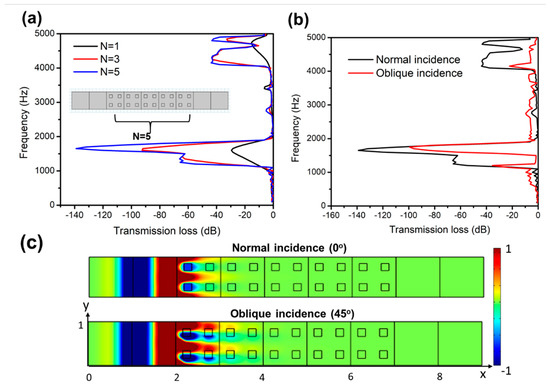
Figure 7.
(a) Transmission loss spectra of proposed elastic metamaterials with different numbers of unit cells. (b) The transmission loss spectra of the five-array elastic metamaterial under the normal and oblique (45°) incidences. (c) Deformation distributions corresponding to (b) at the frequency of 1700 Hz.
The transmission spectra were obtained for normal and oblique incidences of the incoming wave to verify the omnidirectional absorption of the metamaterial, shown in Figure 7b. It was shown that the metamaterial is more effective towards normal incident waves than oblique (45°) incident waves, where the transmission loss peak reduced from −140 to −100 dB. The corresponding deformation distributions of the metamaterials with normal and oblique incidences are at 1700 Hz, as shown in Figure 7c, where the peak transmission loss occurs. It became evident that the five-array metamaterial is active in terms of prohibiting any wave propagation through the material, resulting in zero transmittance in the specified frequency range. By tuning the geometric and material parameters within the PnC, the elastic metamaterial proposed could be utilized in a variety of passive vibration isolation applications such as in small electronic devices, sensitive lab equipment, or even in civil engineering structures. The simplicity of the design, relying solely on square inclusions, enables the ease of manufacturing of this metamaterial to be implemented in a suitable application.
4. Conclusions
The band gap generation in phononic crystals, consisting of square inclusions in the soft host, with various sizes, filling fractions, material parameters, and arrangements was investigated in this work; in general, it can be concluded that a wide bandgap of the phononic crystal can be formed by combining two mechanisms: high-frequency Bragg scattering and low-frequency local resonances. Bragg scattering results from multiple elastic wave scatterings of periodic inclusions and local resonances results from the elastic natural resonant frequencies, which is more dependent on the inclusion size and gap width among inclusions. A nonmonotonic relationship between the bandwidth and filling fraction of the composite results from different responses between geometric dimensions and these two mechanisms. Tuning of band gaps to a larger bandwidth can be followed by the following procedures:
- increasing the number of inclusions within the periodic unit cell to increase the bandwidth and cause a blue shift in the central bandgap frequency;
- increasing the filling fraction of the unit cell to increase the bandwidth, and maximum bandwidth is reached near FF = 0.6 when using a tungsten-carbide/epoxy phononic crystal;
- rotating the angle of inclusions causes a minor effect on the bandwidth of the bandgap, except when the spacing among inclusions is reduced to near or less than the vibration wavelength;
- inclusion with a graded size leads to lower bandwidth, as compared to that of equally sized inclusions in a phononic crystal;
- a narrow spacing between the inclusions drastically reduces the bandwidth and UBF, and this can be found in the study of the rotation and arrangement effect;
- simulate transmission spectra is a way to verify the near-zero transmittance of the proposed elastic metamaterials over the frequency range within the phononic bandgap.
Author Contributions
Conceptualization, D.-W.L. and A.A.; methodology, A.A., J.-Y.L., M.A.T., and F.A.; simulation, A.A.; writing—original draft preparation, J.-Y.L., Z.M., R.K.A.A.-R, V.G. and D.-W.L.; writing—review and editing, V.G., D.-W.L.; supervision and project administration M.A.T.; investigation, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be provided upon request to D.-W.L.
Acknowledgments
The authors thank the support from other members in the Advanced Materials Research Centre at Technology Innovation Institute and also thank Abu Dhabi Government’s Advanced Technology Research Council (ATRC), which oversees technology research in the emirate.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| ρ | density of the elastic material |
| u | deformation of the elastic material |
| fv | force per deformed volume |
| E | elastic modulus |
| N | Poisson’s ratio |
| ∇ | vector differential operator |
| k | periodicity k-vector; Bloch wave vector |
| Λ | spatial period in periodic directions |
| ao | length of the unit cell |
| ai | side length of the square inclusion |
| FF | filling fraction (ai)2/(ao)2 |
| YMR | Young’s modulus ratio |
| LBF | lower bound frequency |
| UBF | upper bound frequency |
| Special k points in the irreducible Brillouin zone | |
| Γ | (0, 0) |
| M | (2π/ao, 2π/ao) |
| X | (2π/ao, 0) |
Appendix A
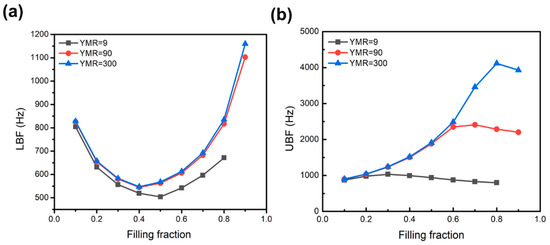
Figure A1.
(a) Lower bound frequency (LBF) and (b) upper bound frequency (UBF) of the bandgap versus the filling fraction of a single-inclusion phononic crystals with different YMRs of 9, 90, and 300.
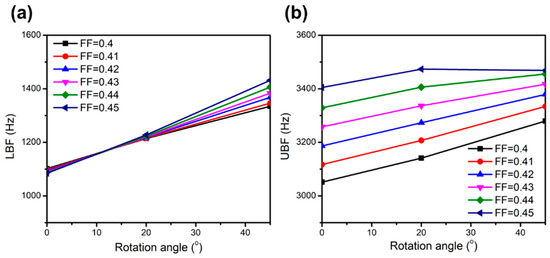
Figure A2.
(a) Lower bound frequency (LBF) and (b) upper bound frequency (UBF) of the bandgap versus rotation angle in the four-square inclusion composite with different filling fractions.
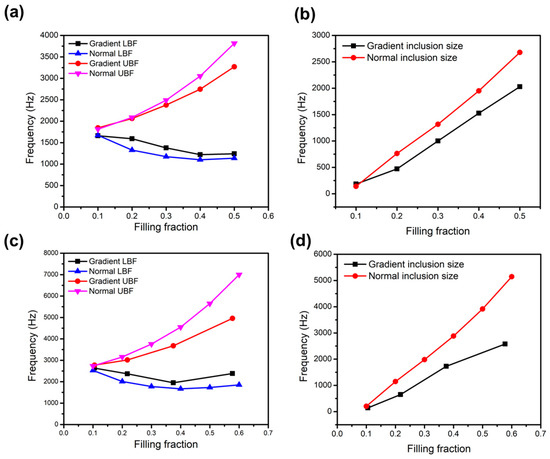
Figure A3.
LBF, UBF, and bandwidth versus filling fraction of the phononic crystals with (a,b) four inclusions and (c,d) nine inclusions.
References
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Elastic Metamaterials with Simultaneously Negative Effective Shear Modulus and Mass Density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef]
- Srivastava, A. Elastic metamaterials and dynamic homogenization: A review. Int. J. Smart Nano Mater. 2015, 6, 41–60. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, B.; Bai, Y.; Wang, L.; Rejab, M.R.M. Review of Phononic crystals and acoustic metamaterials. IOP Conf. Ser. Mater. Sci. Eng. 2020, 788, 788. [Google Scholar] [CrossRef]
- Krushynska, A.; Miniaci, M.; Bosia, F.; Pugno, N. Coupling local resonance with Bragg band gaps in single-phase mechanical metamaterials. Extreme Mech. Lett. 2017, 12, 30–36. [Google Scholar] [CrossRef]
- Yong, W.; Qibai, H.; Minggang, Z.; Zhanxin, L. A new approach of vibration isolation analysis of periodic composite structure based on phononic crystal. Int. J. Mech. Mater. Des. 2007, 3, 103–109. [Google Scholar] [CrossRef]
- Matlack, K.H.; Bauhofer, A.; Krödel, S.; Palermo, A.; Daraio, C. Composite 3D-printed metastructures for low-frequency and broadband vibration absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 8386–8390. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Hu, H.; Laude, V. Low-frequency band gap in cross-like holey phononic crystal strip. J. Phys. D Appl. Phys. 2017, 51, 045601. [Google Scholar] [CrossRef]
- Bilal, O.R.; Ballagi, D.; Daraio, C. Architected Lattices for Simultaneous Broadband Attenuation of Airborne Sound and Mechanical Vibrations in All Directions. Phys. Rev. Appl. 2018, 10, 054060. [Google Scholar] [CrossRef]
- Yin, J.; Peng, H.; Zhang, S.; Zhang, H.; Chen, B. Design of nacreous composite material for vibration isolation based on band gap manipulation. Comput. Mater. Sci. 2015, 102, 126–134. [Google Scholar] [CrossRef]
- Park, C.-S.; Shin, Y.C.; Jo, S.-H.; Yoon, H.; Choi, W.; Youn, B.D.; Kim, M. Two-dimensional octagonal phononic crystals for highly dense piezoelectric energy harvesting. Nano Energy 2019, 57, 327–337. [Google Scholar] [CrossRef]
- Gonella, S.; To, A.C.; Liu, W.K. Interplay between phononic bandgaps and piezoelectric microstructures for energy harvesting. J. Mech. Phys. Solids 2009, 57, 621–633. [Google Scholar] [CrossRef]
- Lv, H.; Tian, X.; Wang, M.Y.; Li, D. Vibration energy harvesting using a phononic crystal with point defect states. Appl. Phys. Lett. 2013, 102, 034103. [Google Scholar] [CrossRef]
- Shen, L.; Wu, J.H.; Zhang, S.; Liu, Z.; Li, J. Low-frequency vibration energy harvesting using a locally resonant phononic crystal plate with spiral beams. Mod. Phys. Lett. B 2015, 29, 1450259. [Google Scholar] [CrossRef]
- Kafesaki, M.; Sigalas, M.M.; García, N. Frequency Modulation in the Transmittivity of Wave Guides in Elastic-Wave Band-Gap Materials. Phys. Rev. Lett. 2000, 85, 4044–4047. [Google Scholar] [CrossRef]
- Khelif, A.; Djafari-Rouhani, B.; Vasseur, J.O.; Deymier, P.A. Transmission and dispersion relations of perfect and defect-containing waveguide structures in phononic band gap materials. Phys. Rev. B 2003, 68, 024302. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J.O.; Khelif, A.; Deymier, P.A. Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E 2004, 69, 046608. [Google Scholar] [CrossRef]
- Zhang, P.; To, A.C. Broadband wave filtering of bioinspired hierarchical phononic crystal. Appl. Phys. Lett. 2013, 102, 121910. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.; Hu, G. Elastic metamaterials with local resonances: An overview. Theor. Appl. Mech. Lett. 2012, 2, 041001. [Google Scholar] [CrossRef]
- Cheng, Z.; Shi, Z. Novel composite periodic structures with attenuation zones. Eng. Struct. 2013, 56, 1271–1282. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, Y.-S. Multiple wide complete bandgaps of two-dimensional phononic crystal slabs with cross-like holes. J. Sound Vib. 2013, 332, 2019–2037. [Google Scholar] [CrossRef]
- Mizukami, K.; Kawaguchi, T.; Ogi, K.; Koga, Y. Three-dimensional printing of locally resonant carbon-fiber composite metastructures for attenuation of broadband vibration. Compos. Struct. 2021, 255, 112949. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, Y.-S.; Wang, L. Two-dimensional ternary locally resonant phononic crystals with a comblike coating. J. Phys. D Appl. Phys. 2013, 47, 15502. [Google Scholar] [CrossRef]
- Wang, T.; Wang, H.; Sheng, M.-P.; Qin, Q.-H. Complete low-frequency bandgap in a two-dimensional phononic crystal with spindle-shaped inclusions. Chin. Phys. B 2016, 25, 046301. [Google Scholar] [CrossRef]
- Huang, J.; Shi, Z.; Huang, W. Multiple band gaps of phononic crystals with quasi-Sierpinski carpet unit cells. Phys. B Condens. Matter 2017, 516, 48–54. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Liang, T. Band structures in Sierpinski triangle fractal porous phononic crystals. Phys. B Condens. Matter 2016, 498, 33–42. [Google Scholar] [CrossRef]
- Goffaux, C.; Vigneron, J.P. Theoretical study of a tunable phononic band gap system. Phys. Rev. B 2001, 64, 075118. [Google Scholar] [CrossRef]
- Zhou, X.-Z.; Wang, Y.-S.; Zhang, C. Elastic band gaps of two-dimensional phononic crystals tunned by material parameters. 2009 IEEE Int. Ultrason. Symp. 2009, 1020–1023. [Google Scholar] [CrossRef]
- Hussein, M.I.; Hamza, K.; Hulbert, G.M.; Saitou, K. Optimal synthesis of 2D phononic crystals for broadband frequency isolation. Waves Random Complex Media 2007, 17, 491–510. [Google Scholar] [CrossRef]
- Li, E.; He, Z.; Wang, G.; Jong, Y. Fundamental study of mechanism of band gap in fluid and solid/fluid phononic crystals. Adv. Eng. Softw. 2018, 121, 167–177. [Google Scholar] [CrossRef]
- Su, X.-X.; Wang, Y.-F.; Wang, Y.-S. Effects of Poisson’s ratio on the band gaps and defect states in two-dimensional vacuum/solid porous phononic crystals. Ultrasonics 2012, 52, 255–265. [Google Scholar] [CrossRef]
- Huang, H.; Sun, C. Theoretical investigation of the behavior of an acoustic metamaterial with extreme Young’s modulus. J. Mech. Phys. Solids 2011, 59, 2070–2081. [Google Scholar] [CrossRef]
- Athith, D.; Sanjay, M.R.; Yashas Gowda, T.G.; Madhu, P.; Arpitha, G.R.; Yogesha, B.; Omri, M.A. Effect of tungsten carbide on mechanical and tribological properties of jute/sisal/E-glass fabrics reinforced natural rubber/epoxy composites. J. Ind. Text. 2017, 48, 713–737. [Google Scholar] [CrossRef]
- Duranteau, M.; Valier-Brasier, T.; Conoir, J.-M.; Wunenburger, R. Random acoustic metamaterial with a subwavelength dipolar resonance. J. Acoust. Soc. Am. 2016, 139, 3341–3352. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, Y.; Guest, J.K.; Srivastava, A. 3-D phononic crystals with ultra-wide band gaps. Sci. Rep. 2017, 7, srep43407. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Meng, F.; Li, Y.F.; Huang, X. Topological design of 3D phononic crystals for ultra-wide omnidirectional bandgaps. Struct. Multidiscip. Optim. 2019, 60, 2405–2415. [Google Scholar] [CrossRef]
- COMSOL Inc. COMSOL Multiphysics Reference Manual, Version 5.5; COMSOL Inc. Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 31 March 2021).
- Hastings, F.D.; Schneider, J.B.; Broschat, S.L. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation. J. Acoust. Soc. Am. 1996, 100, 3061–3069. [Google Scholar] [CrossRef]
- Krushynska, A.A.; Kouznetsova, V.V.; Geers, M.M. Towards optimal design of locally resonant acoustic metamaterials. J. Mech. Phys. Solids 2014, 71, 179–196. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, B.M.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 83049. [Google Scholar] [CrossRef]
- Cai, C.; Wang, Z.; Li, Q.; Xu, Z.; Tian, X. Pentamode metamaterials with asymmetric double-cone elements. J. Phys. D Appl. Phys. 2015, 48, 175103. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Maznev, A.A.; Laude, V. Formation of Bragg Band Gaps in Anisotropic Phononic Crystals Analyzed with the Empty Lattice Model. Crystals 2016, 6, 52. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, M.S. Stop-bands for periodic metallic rods: Sculptures that can filter the noise. Appl. Phys. Lett. 1997, 70, 3218–3220. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).