Wind Turbine Power Curve Modelling with Logistic Functions Based on Quantile Regression
Abstract
Featured Application
Abstract
1. Introduction
2. The Proposed Logistic Functions Based on Quantile Regression
2.1. Logistic Functions
2.2. Quantile Regression
2.3. Logistic Functions Based Quantile Regression
2.4. Parameter Optimization Algorithms
2.4.1. Particle Swarm Optimization
2.4.2. Whale Optimization Algorithm
2.4.3. Adam Optimization Algorithm
3. WTPC Modelling with the Proposed QRLF
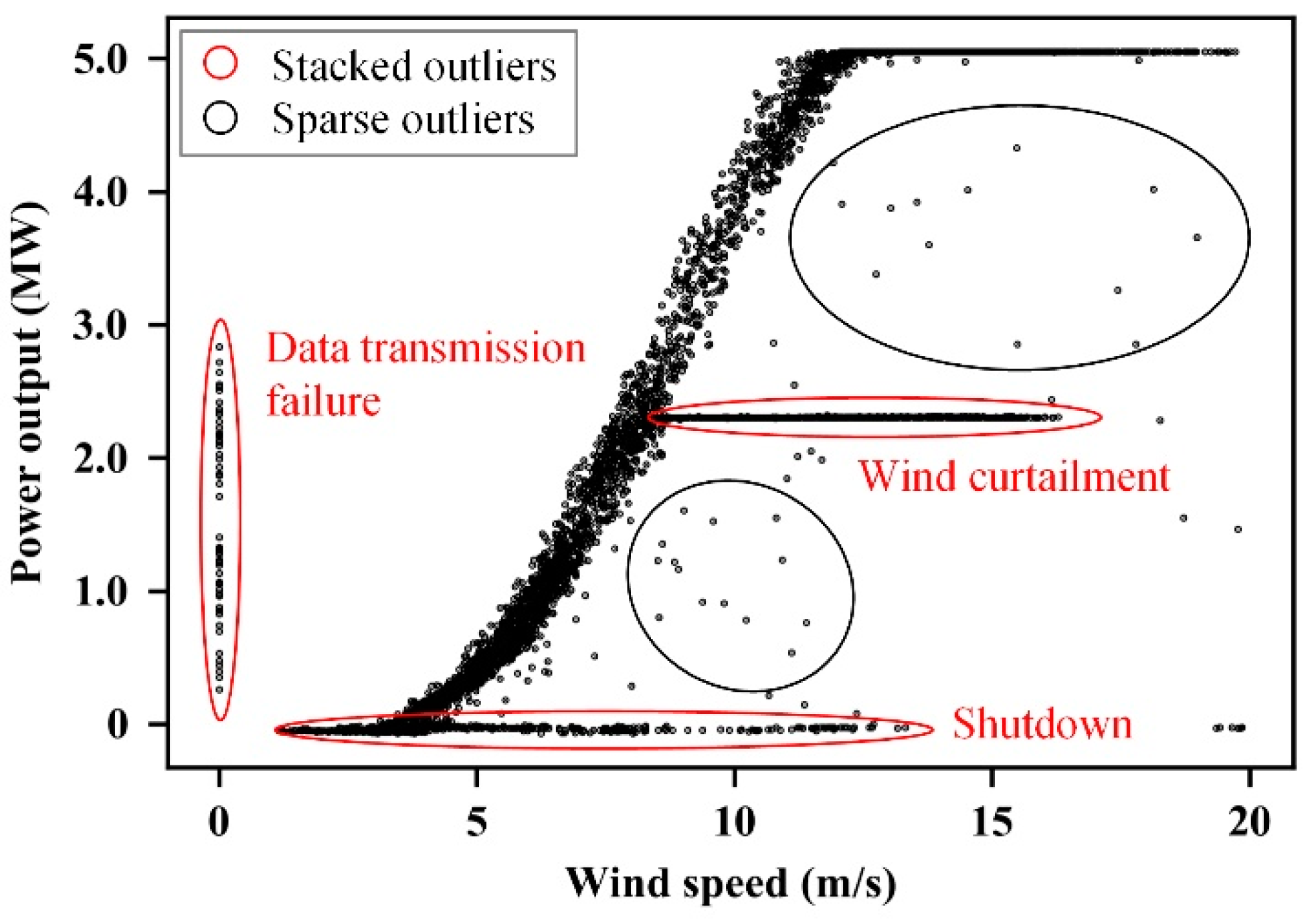
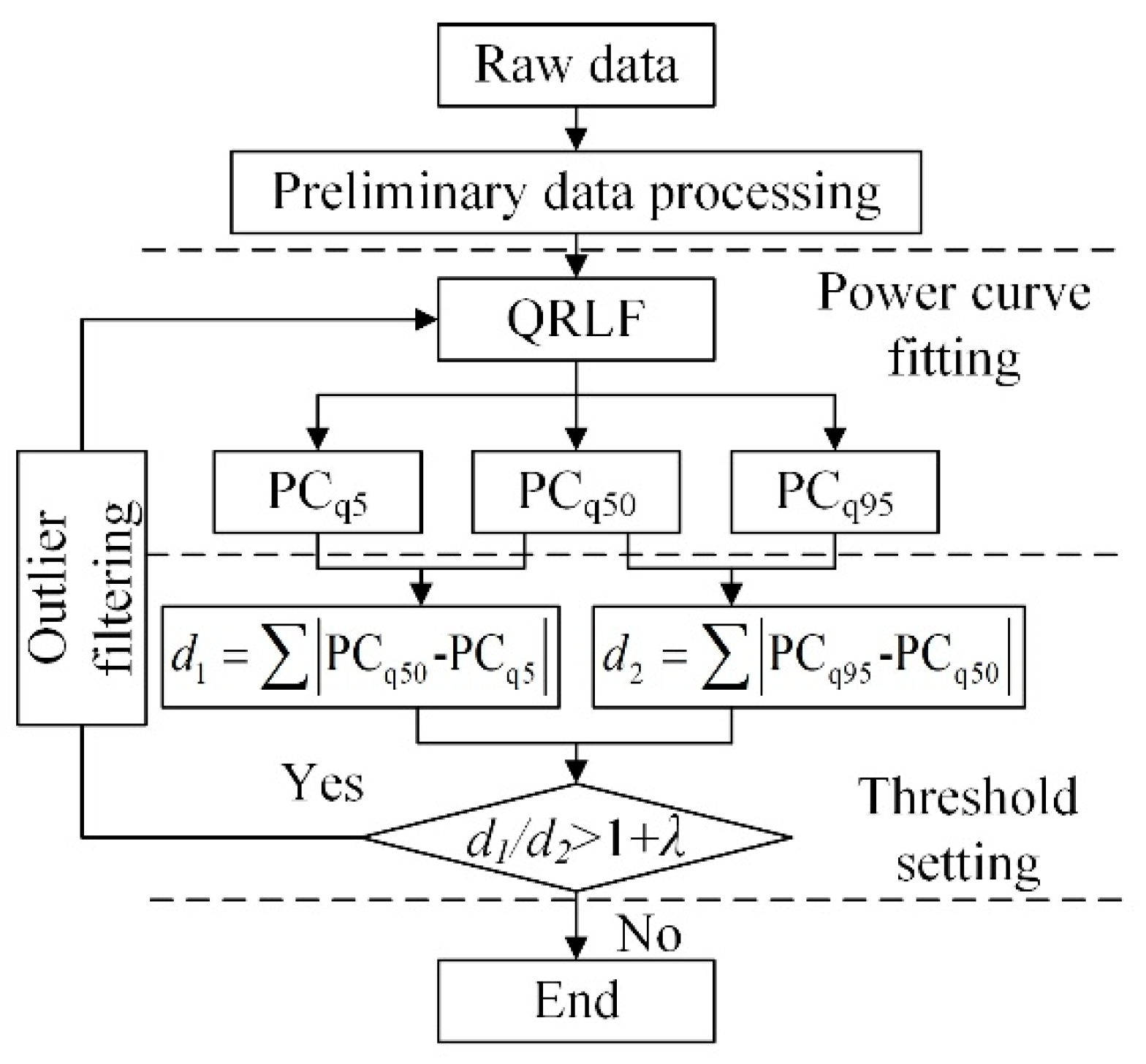
3.1. Outlier Filtering
- Preliminary data processing
- 2.
- Power curve fitting
- 3.
- Threshold setting
- 4.
- Outlier filtering
3.2. WTPC Modelling with the Proposed QRLF
4. Case Study
4.1. Data Sources
4.2. Evaluation Metrics
4.2.1. Deterministic Evaluation Metrics
4.2.2. Probabilistic Evaluation Metrics
4.3. Experimental Results
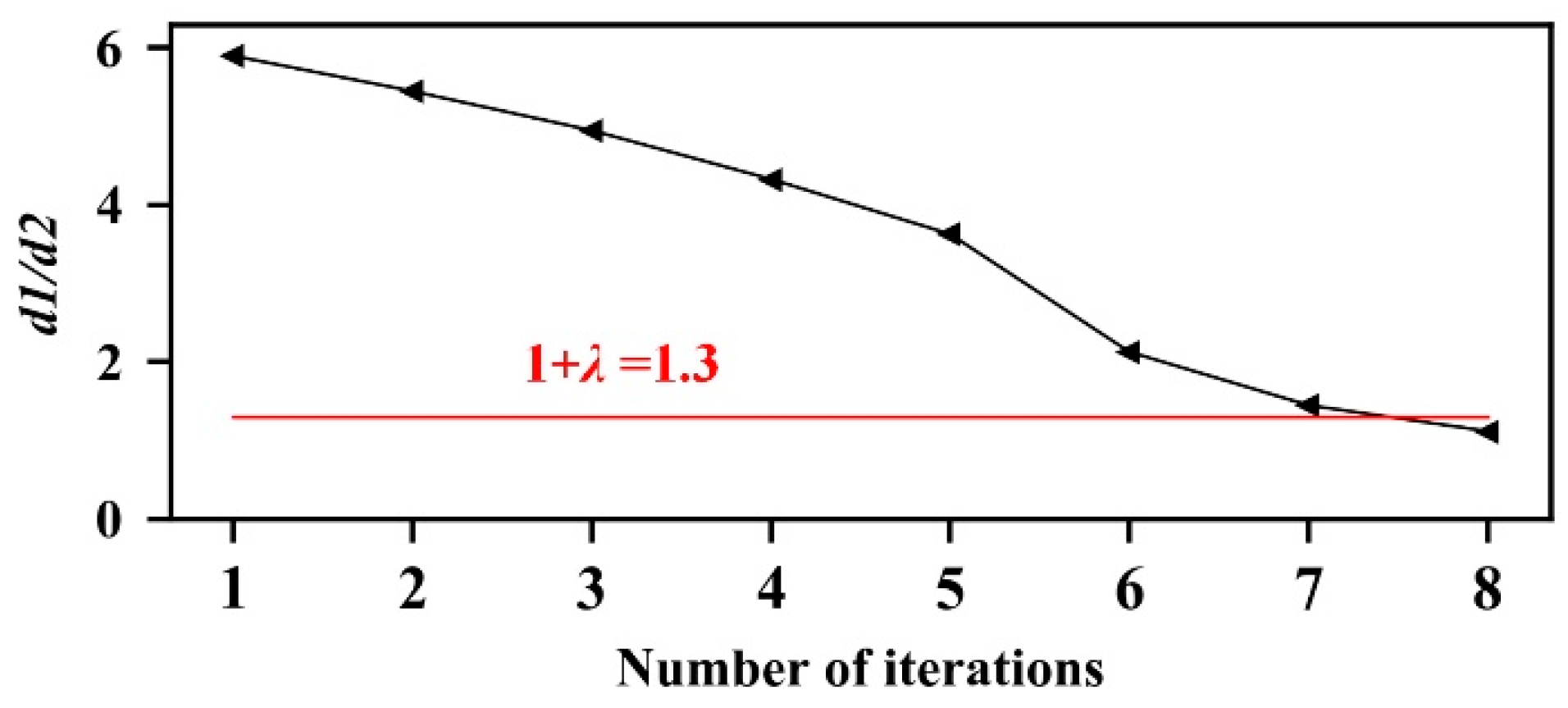
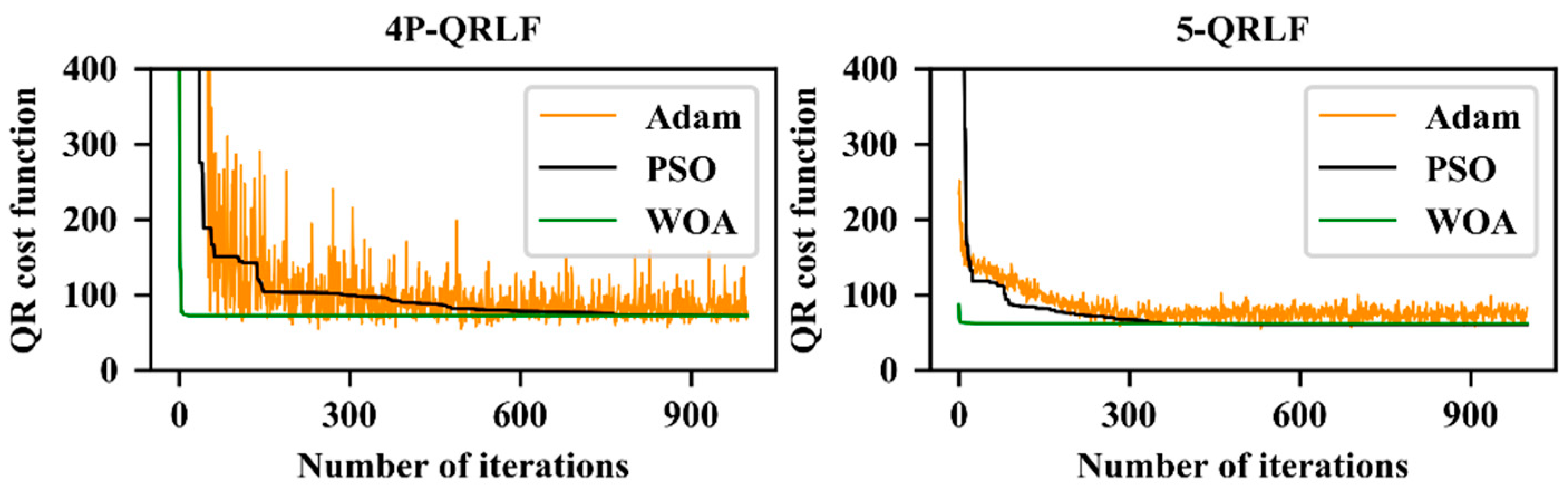
4.3.1. Results for Parameter Selection and Optimization
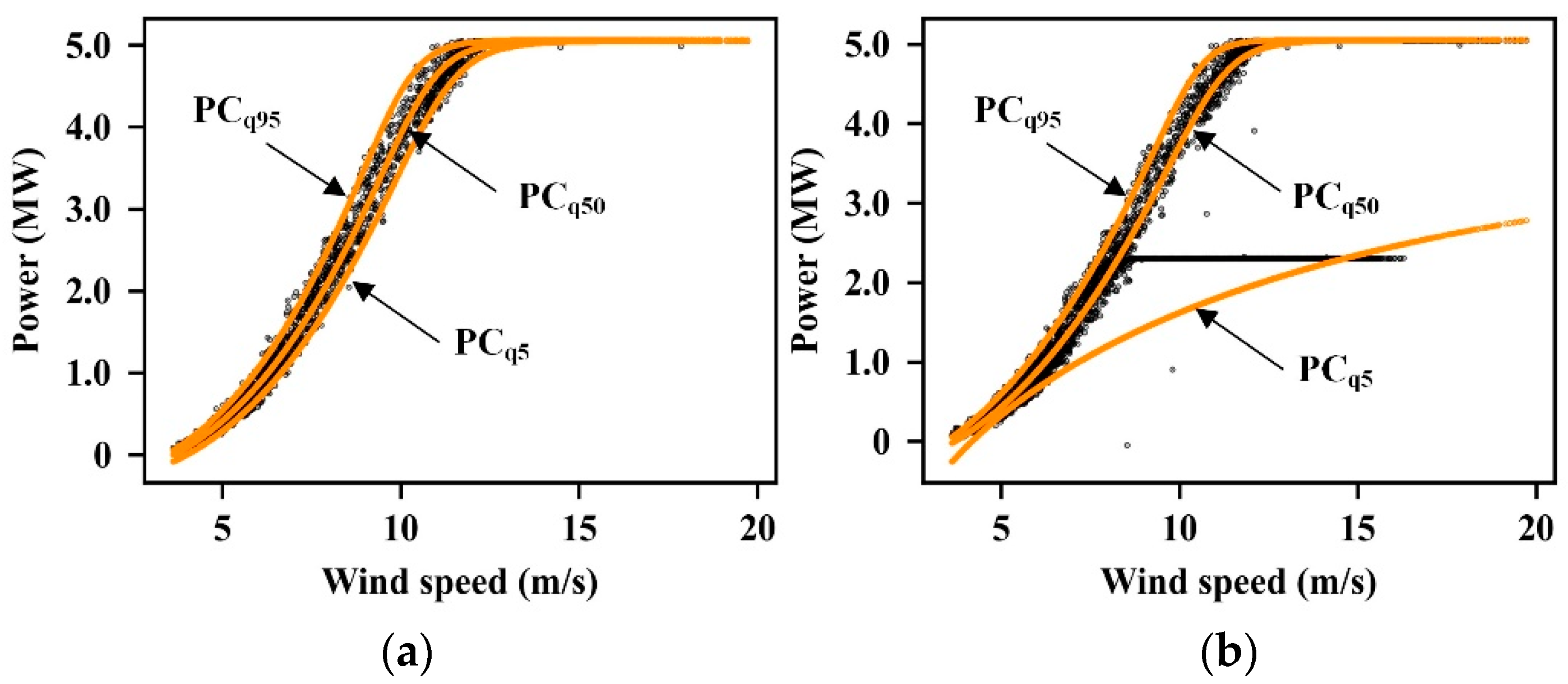
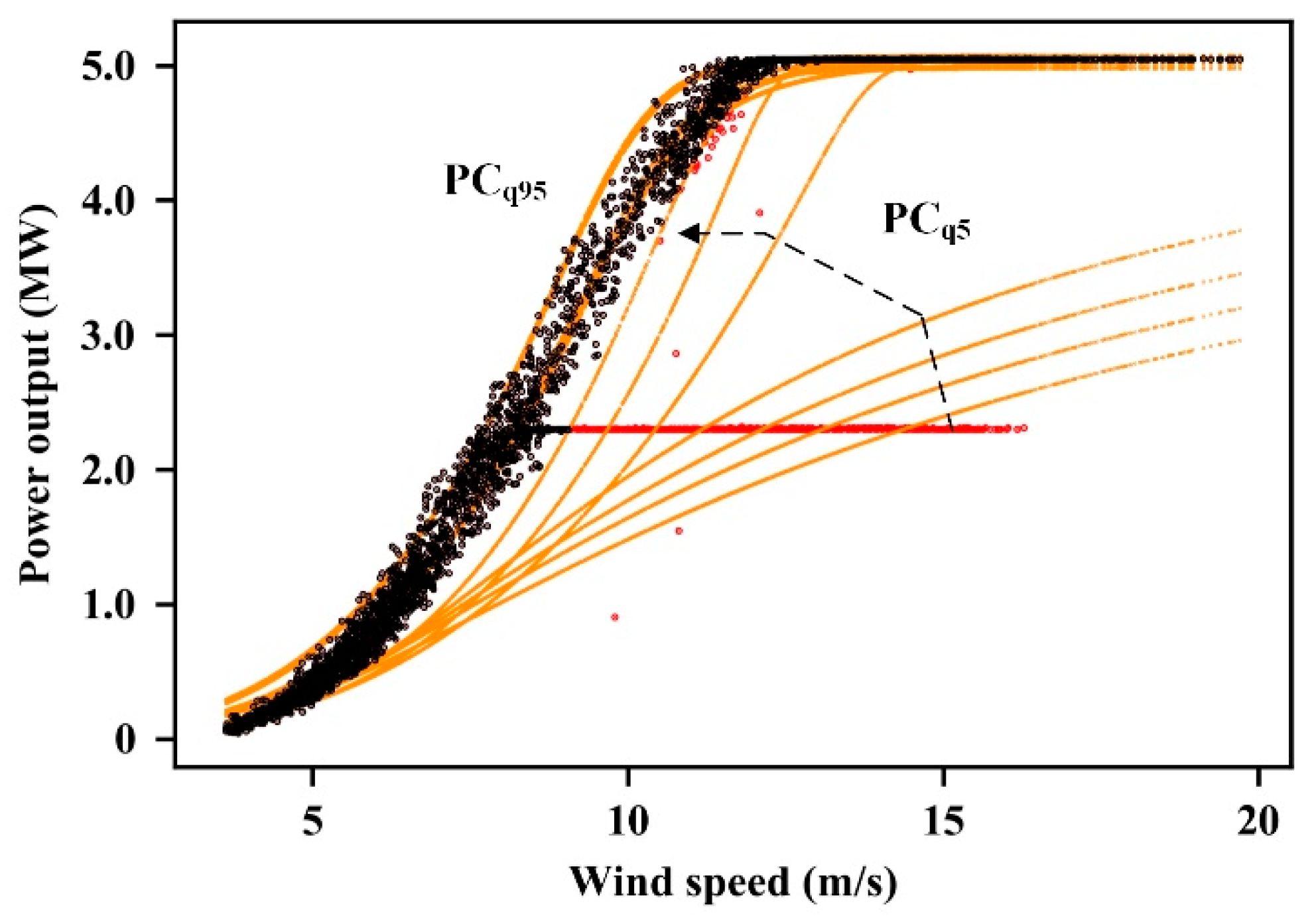
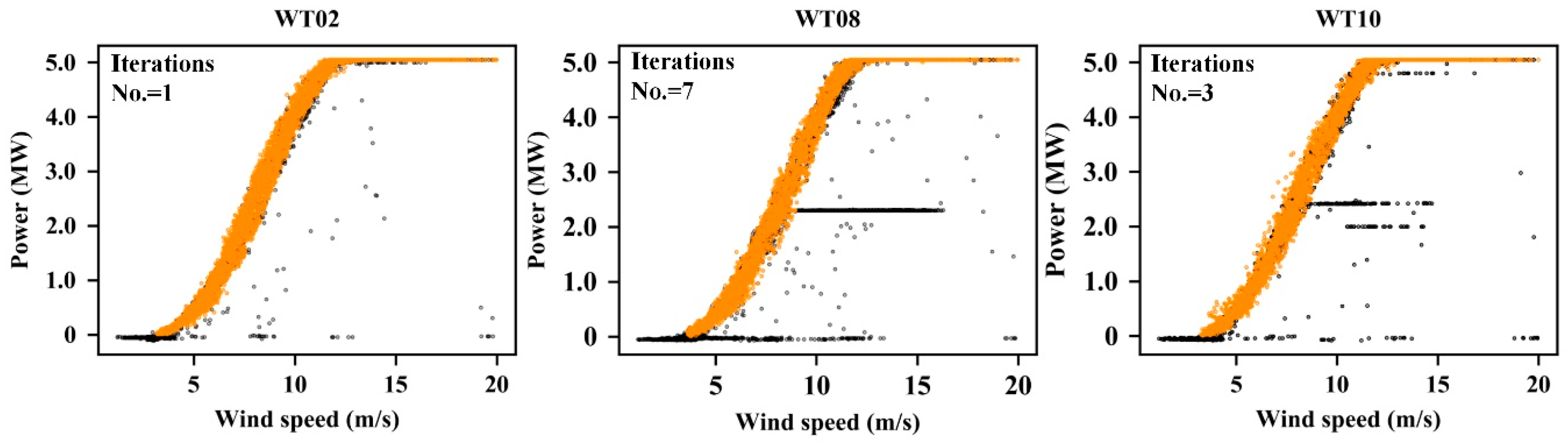
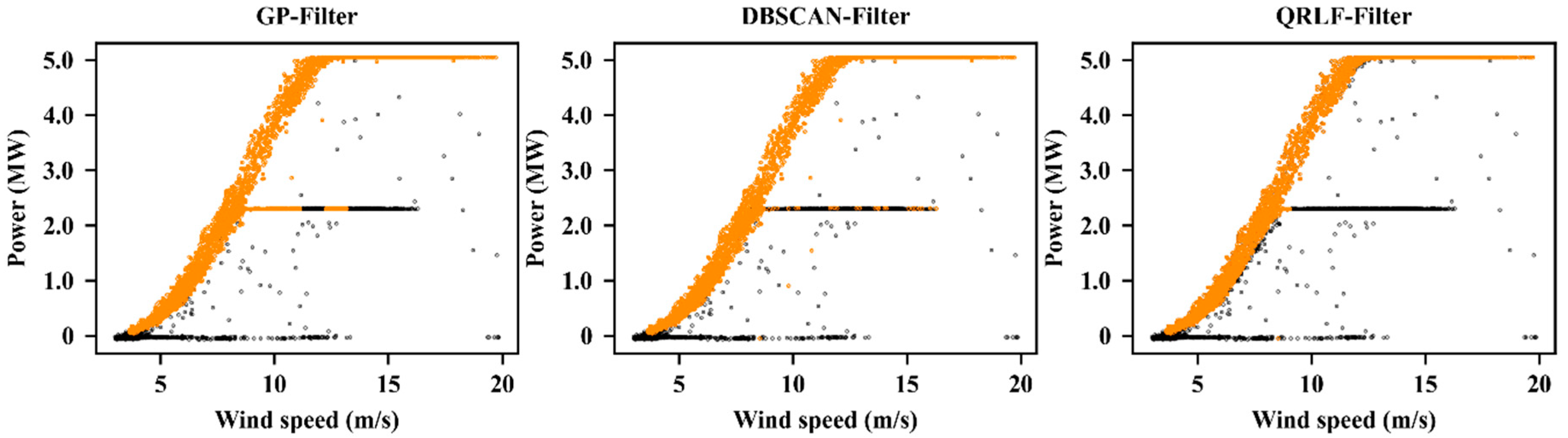
4.3.2. Results for Outlier Filtering
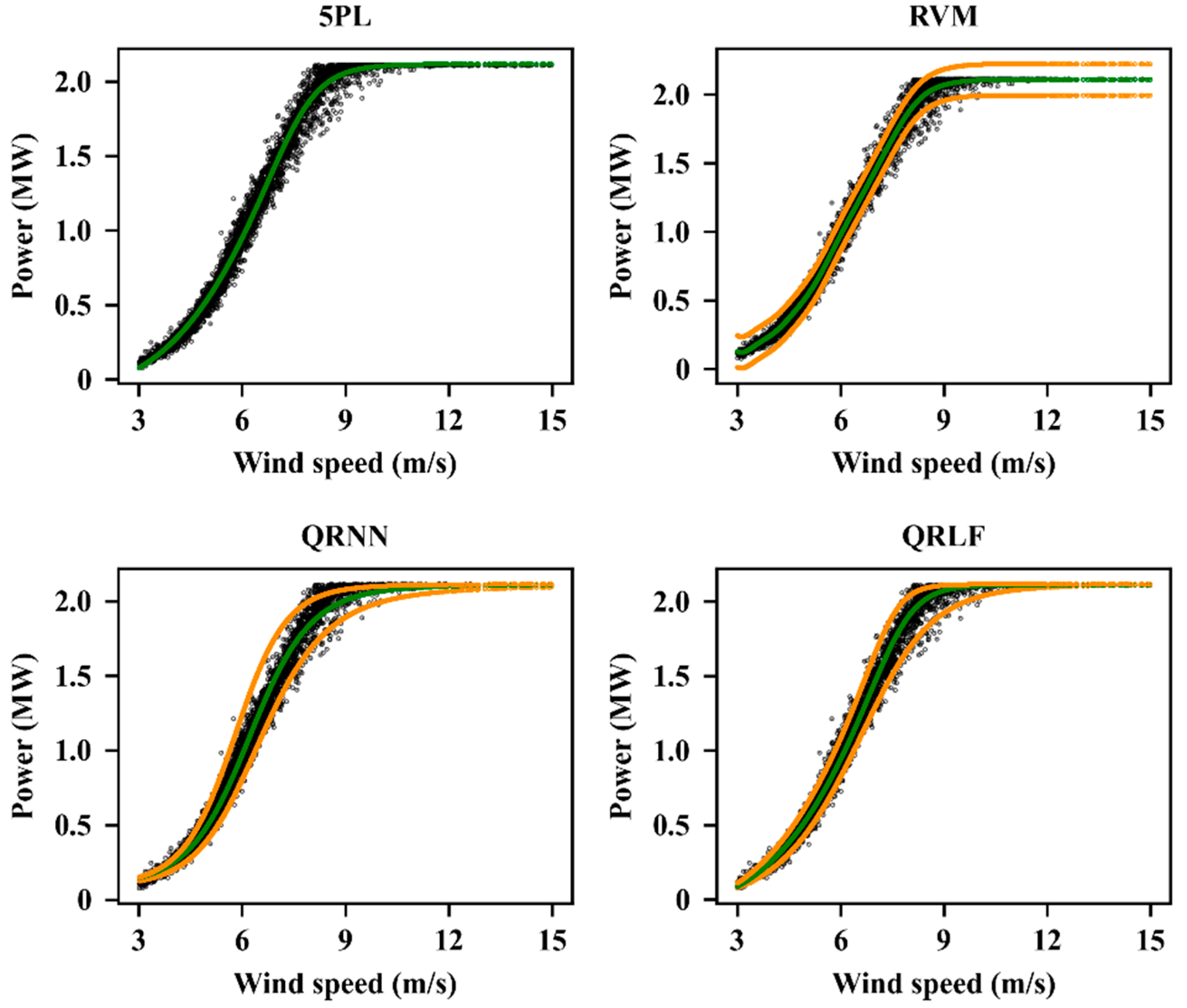
4.3.3. Results for WTPC Modelling
4.4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Neural-fuzzy Inference Systems |
| CI | Confidence interval |
| CSI | Cubic Spline Interpolation |
| GP | Gaussian process |
| KNN | K-Nearest Neighbors |
| LF | Logistic function |
| MAPE | Mean absolute percentage error |
| nPL | n-parameter logistic function |
| NRMSE | Normalized root mean square error |
| PICP | Prediction intervals coverage probability |
| PINAW | Prediction intervals normalized average width |
| PR | Polynomial Regression |
| PSO | Particle swarm optimization |
| QR | Quantile regression |
| QRLF | Quantile regression based on logistic function |
| QRNN | Quantile regression neural network |
| RVM | Relevance vector machine |
| SVM | Support Vector Machine |
| WF | Wind farm |
| WOA | Whale optimization algorithm |
| WTPC | Wind turbine power curve |
References
- Manwell, F.J.; McGowan, G.J. Wind Energy Explained, 3rd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Villanueva, D.; Feijóo, A. A review on wind turbine deterministic power curve models. Appl. Sci. 2020, 10, 4186. [Google Scholar] [CrossRef]
- Carrillo, C.; Obando Montaño, A.F.; Cidrás, J.; Díaz-Dorado, E. Review of power curve modelling for wind turbines. Renew. Sustain. Energy Rev. 2013, 21, 572–581. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Srinivasan, D.; Wang, Z. Wind power curve modeling and wind power forecasting with inconsistent data. IEEE Trans. Sustain. Energy 2019, 10, 16–25. [Google Scholar] [CrossRef]
- IET. Wind turbines Part 12–1: Power performance measurements of electricity producing wind turbines. In IEC 61400-12-1; International Electrical Comission: Geneva, Switzerland, 2005. [Google Scholar]
- Marčiukaitis, M.; Žutautaitė, I.; Martišauskas, L.; Jokšas, B.; Gecevičius, G.; Sfetsos, A. Non-linear regression model for wind turbine power curve. Renew. Energy 2017, 113, 732–741. [Google Scholar] [CrossRef]
- Teyabeen, A.A.; Akkari, F.R.; Jwaid, A.E. Power curve modelling for wind turbines. In Proceedings of the UKSim–AMSS 19th International Conference on Modelling & Simulation, Cambridge, UK, 5–7 April 2017. [Google Scholar] [CrossRef]
- Taslimi-Renani, E.; Modiri-Delshad, M.; Elias, M.F.M.; Rahim, N.A. Development of an enhanced parametric model for wind turbine power curve. Appl. Energy 2016, 177, 544–552. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A. Comparison of logistic functions for modeling wind turbine power curves. Electr. Power Syst. Res. 2018, 155, 281–288. [Google Scholar] [CrossRef]
- Seo, S.; Oh, S.; Kwak, H. Wind turbine power curve modeling using maximum likelihood estimation method. Renew. Energy 2019, 136, 1164–1169. [Google Scholar] [CrossRef]
- Lydia, M.; Selvakumar, A.I.; Kumar, S.S.; Kumar, G.E.P. Advanced algorithms for wind turbine power curve modeling. IEEE Trans. Sustain. Energy 2013, 4, 827–835. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. Models for monitoring wind farm power. Renew. Energy 2009, 34, 583–590. [Google Scholar] [CrossRef]
- Thapar, V.; Agnihotri, G.; Sethi, V.K. Critical analysis of methods for mathematical modelling of wind turbines. Renew. Energy 2011, 36, 3166–3177. [Google Scholar] [CrossRef]
- Yesilbudak, M. Implementation of novel hybrid approaches for power curve modeling of wind turbines. Energy Convers. Manag. 2018, 171, 156–169. [Google Scholar] [CrossRef]
- Manobel, B.; Sehnke, F.; Lazzús, J.A.; Salfate, I.; Felder, M.; Montecinos, S. Wind turbine power curve modeling based on Gaussian processes and artificial neural networks. Renew. Energy 2018, 125, 1015–1020. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F.; Achiche, S. Using data-mining approaches for wind turbine power curve monitoring: A comparative study. IEEE Trans. Sustain. Energy 2013, 4, 671–679. [Google Scholar] [CrossRef]
- Janssens, O.; Noppe, N.; Devriendt, C.; Walle, R.V.D.; Hoecke, S.V. Data-driven multivariate power curve modeling of offshore wind turbines. Eng. Appl. Artificial Intel. 2016, 55, 331–338. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L. Uncertainty estimation for wind energy conversion by probabilistic wind turbine power curve modelling. Appl. Energy 2019, 239, 1356–1370. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. Using Gaussian process theory for wind turbine power curve analysis with emphasis on the confidence Intervals. In Proceedings of the 6th International Conference on Clean Electrical Power (ICCEP), Santa Margherita Ligure, Italy, 27–29 June 2017. [Google Scholar] [CrossRef]
- Guo, P.; Infield, D. Wind turbine power curve modeling and monitoring with Gaussian process and SPRT. IEEE Trans. Sustain. Energy 2020, 11, 107–115. [Google Scholar] [CrossRef]
- Rogers, T.J.; Gardner, P.; Dervilis, N. Probabilistic modelling of wind turbine power curves with application of heteroscedastic Gaussian process regression. Renew. Energy 2020, 148, 1124–1136. [Google Scholar] [CrossRef]
- Virgolino, G.C.M.; Mattos, C.L.C.; Magalhães, J.A.F.; Barreto, G.A. Gaussian processes with logistic mean function for modeling wind turbine power curves. Renew. Energy 2020, 162, 458–465. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D.; Kolios, A. Gaussian process power curve models incorporating wind turbine operational variables. Energy Rep. 2020, 6, 1658–1669. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Lombardi, A.; Terzi, L. Multivariate SCADA data analysis methods for real-world wind turbine power curve monitoring. Energies 2021, 14, 1105. [Google Scholar] [CrossRef]
- Pandit, R.K.; Kolios, A. SCADA data-based support vector machine wind turbine power curve uncertainty estimation and its comparative studies. Appl. Sci. 2020, 10, 8685. [Google Scholar] [CrossRef]
- Hu, Y.; Qiao, Y.; Liu, J. Adaptive confidence boundary modeling of wind turbine power curve using SCADA data and its application. IEEE Trans. Sustain. Energy 2019, 10, 1330–1341. [Google Scholar] [CrossRef]
- Jing, B.; Qian, Z.; Wang, A.; Chen, T.; Zhang, F. Wind Turbine Power Curve Modelling Based on Hybrid Relevance Vector Machine. In Proceedings of the 4th International Symposium on Green Energy and Smart Grid, Xi’an, China, 20–22 August 2020. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, J.K.; Oh, K.Y.; Lee, J.S. Development of a novel power curve monitoring method for wind turbines and its field tests. IEEE Trans. Energy Convers. 2014, 29, 119–128. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K.F. Quantile regression. J. Econ. Perpect. 2001, 15, 143–156. [Google Scholar] [CrossRef]
- He, Y.; Zhang, W. Probability density forecasting of wind power based on multi-core parallel quantile regression neural network. Knowl. Based Syst. 2020, 209, 106431. [Google Scholar] [CrossRef]
- Pei, S.; Li, Y. Wind turbine power curve modeling with a hybrid machine learning technique. Appl. Sci. 2019, 9, 4930. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Wang, W.; Sun, H.; Ju, Y.; Tang, Y. Data-driven correction approach to refine power curve of wind farm under wind curtailment. IEEE Trans. Sustain. Energy 2018, 9, 95–105. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. SCADA-based wind turbine anomaly detection using Gaussian process models for wind turbine condition monitoring purposes. IET Renew. Power Gen. 2018, 12, 1249–1255. [Google Scholar] [CrossRef]
- Gottschalk, P.G.; Dunn, J.R. The five-parameter logistic: A characterization and comparison with the four-parameter logistic. Anal. Biochem. 2005, 343, 54–65. [Google Scholar] [CrossRef]
- He, Y.; Li, H.; Wang, S.; Yao, X. Uncertainty analysis of wind power probability density forecasting based on cubic spline interpolation and support vector quantile regression. Neurocomputing 2020, 430, 121–137. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Quan, H.; Srinivasan, D.; Khosravi, A. Uncertainty handling using neural network-based prediction intervals for electrical load forecasting. Energy 2014, 73, 916–925. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Yao, L.; Yu, X.; Lu, J.; Jiang, Z.; Feng, Z. Wind speed forecasting based on quantile regression minimal gated memory network and kernel density estimation. Energy Convers. Manag. 2019, 196, 1395–1409. [Google Scholar] [CrossRef]
| Parameter Name | Value | Attribute |
|---|---|---|
| Operation mode | 32 (Normal) | State parameters |
| Power generation | [0.01Prated, 1.05Prated] | Operation parameters |
| Wind speed | [vcut-in, vcut-out] | |
| Rotor speed | [6 r/min, 12 r/min] | |
| Pitch angle | [0°, 20°] |
| Attributes | WF1 | WF2 | WF3 |
|---|---|---|---|
| Hub height | 80 m | 84 m | 90 m |
| Rotor diameter | 108 m | 111 m | 171 m |
| Rated power | 2 MW | 2 MW | 5 MW |
| Rated wind speed | 9.5 m/s | 12 m/s | 10.9 m/s |
| Cut-in wind speed | 3 m/s | 3 m/s | 3 m/s |
| Fitting Method | Optimization Algorithm | WT02 | WT08 | WT10 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAPE | NRMSE | NC90% | MAPE | NRMSE | NCα | MAPE | NRMSE | NC90% | ||
| 4P-QRLF | PSO | 18.89% | 2.04% | 0.53 | 9.12% | 1.77% | 0.51 | 10.30% | 1.94% | 0.44 |
| WOA | 19.10% | 1.98% | 0.62 | 9.31% | 1.81% | 0.47 | 9.90% | 1.49% | 0.46 | |
| Adam | 38.50% | 2.40% | 0.72 | 22.25% | 2.37% | 0.49 | 20.99% | 2.33% | 0.57 | |
| 5P-QRLF | PSO | 12.57% | 1.52% | 0.44 | 7.42% | 1.49% | 0.39 | 7.00% | 1.37% | 0.38 |
| WOA | 9.92% | 1.92% | 0.57 | 7.31% | 1.61% | 0.43 | 8.23% | 1.56% | 0.41 | |
| Adam | 27.85% | 1.96% | 0.77 | 9.09% | 1.81% | 0.45 | 12.44% | 1.86% | 0.51 | |
| Algorithm | Control Parameters |
|---|---|
| PSO | particle number = 20; inertia weight (ω) = 0.8; acceleration constants (c1, c2) = 2 |
| WOA | search agent number (whales papulation) = 40 |
| Adam | exponential decay rates (γ1, γ2) = 0.9; learning rate = 0.0002 |
| Wind Farm | Methods | MAPE | NRMSE | PICP90% | PINAW90% | NC90% |
|---|---|---|---|---|---|---|
| WF1 (2 MW) | 5PL | 6.26% | 1.68% | N/A | N/A | N/A |
| RVM | 5.73% | 1.62% | 0.91 | 0.46 | 0.49 | |
| QRNN | 7.93% | 1.83% | 0.83 | 0.31 | 0.38 | |
| QRLF | 5.95% | 1.65% | 0.82 | 0.27 | 0.29 | |
| WF2 (2 MW) | 5PL | 11.44% | 2.21% | N/A | N/A | N/A |
| RVM | 9.12% | 2.19% | 0.90 | 0.81 | 0.89 | |
| QRNN | 15.88% | 2.34% | 0.79 | 0.43 | 0.54 | |
| QRLF | 9.28% | 2.19% | 0.91 | 0.36 | 0.39 | |
| WF3 (5 MW) | 5PL | 10.28% | 1.72% | N/A | N/A | N/A |
| RVM | 8.05% | 1.65% | 0.88 | 0.61 | 0.69 | |
| QRNN | 13.99% | 2.49% | 0.61 | 0.39 | 0.67 | |
| QRLF | 8.84% | 1.72% | 0.93 | 0.39 | 0.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, B.; Qian, Z.; Zareipour, H.; Pei, Y.; Wang, A. Wind Turbine Power Curve Modelling with Logistic Functions Based on Quantile Regression. Appl. Sci. 2021, 11, 3048. https://doi.org/10.3390/app11073048
Jing B, Qian Z, Zareipour H, Pei Y, Wang A. Wind Turbine Power Curve Modelling with Logistic Functions Based on Quantile Regression. Applied Sciences. 2021; 11(7):3048. https://doi.org/10.3390/app11073048
Chicago/Turabian StyleJing, Bo, Zheng Qian, Hamidreza Zareipour, Yan Pei, and Anqi Wang. 2021. "Wind Turbine Power Curve Modelling with Logistic Functions Based on Quantile Regression" Applied Sciences 11, no. 7: 3048. https://doi.org/10.3390/app11073048
APA StyleJing, B., Qian, Z., Zareipour, H., Pei, Y., & Wang, A. (2021). Wind Turbine Power Curve Modelling with Logistic Functions Based on Quantile Regression. Applied Sciences, 11(7), 3048. https://doi.org/10.3390/app11073048






