Intra-System Reliability Assessment of 2-Dimensional Shear Wave Elastography
Abstract
1. Introduction
2. Materials and Methods
3. Results
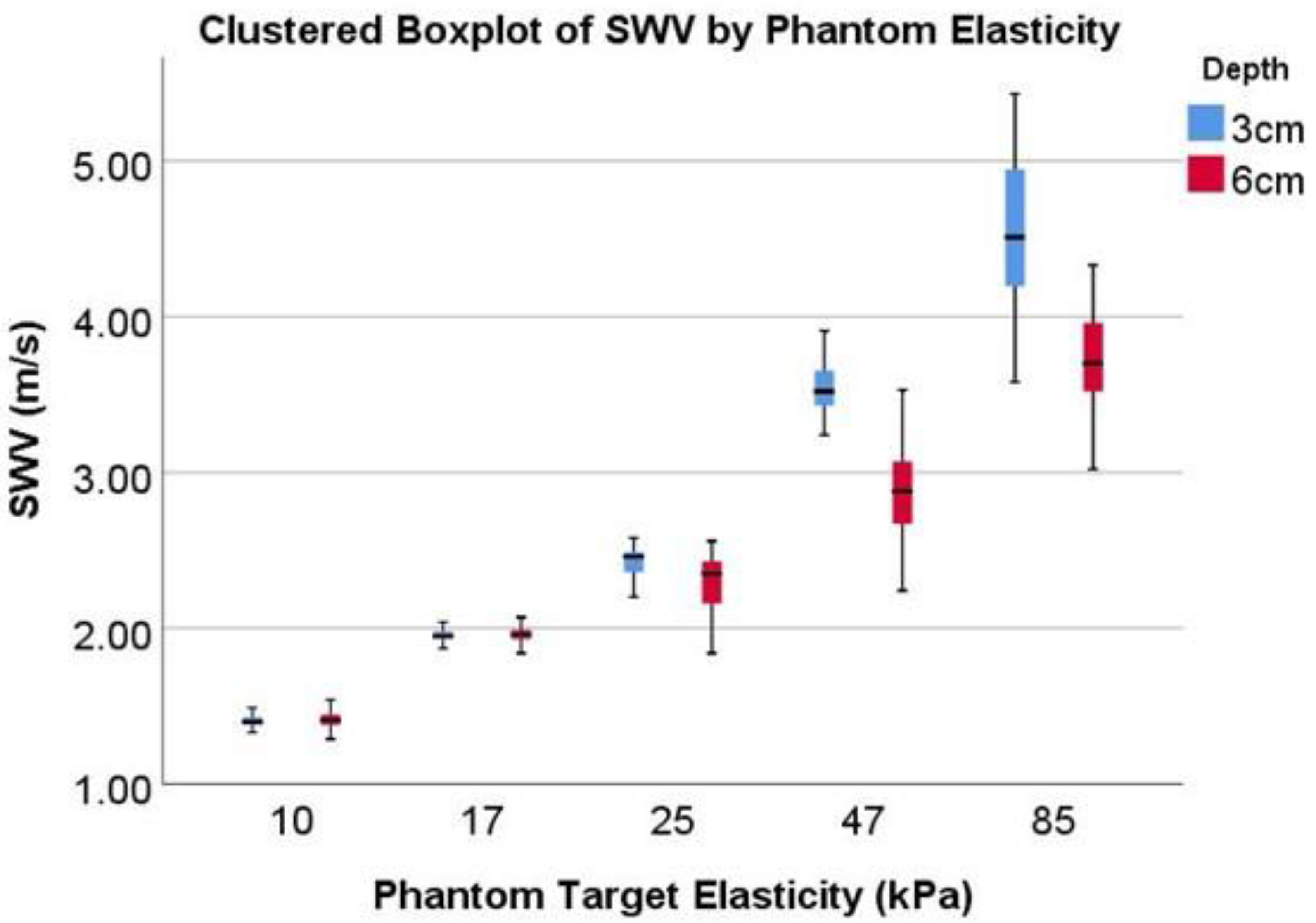
3.1. Imaging Depth
3.2. Inter-Operator Reliability
3.3. Measurement Repeatability
3.4. ROI Sampling Size
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salvatore, V.; Piscaglia, F. Ultrasound Elastography: General and Technical Overview. In Diagnostic Methods for Cirrhosis and Portal Hypertension; Berzigotti, A., Bosch, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 83–94. ISBN 978-3-319-72628-1. [Google Scholar]
- Barr, R.G.; Ferraioli, G.; Palmeri, M.L.; Goodman, Z.D.; Garcia-Tsao, G.; Rubin, J.; Garra, B.; Myers, R.P.; Wilson, S.R.; Rubens, D.; et al. Elastography assessment of liver fibrosis: Society of radiologists in ultrasound consensus conference statement. Radiology 2015, 276, 845–861. [Google Scholar] [CrossRef]
- Barr, R.G.; Nakashima, K.; Amy, D.; Cosgrove, D.; Farrokh, A.; Schafer, F.; Bamber, J.C.; Castera, L.; Choi, B.I.; Chou, Y.-H.; et al. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 2: Breast. Ultrasound Med. Biol. 2015, 41, 1148–1160. [Google Scholar] [CrossRef]
- Ferraioli, G.; Filice, C.; Castera, L.; Choi, B.I.; Sporea, I.; Wilson, S.R.; Cosgrove, D.; Dietrich, C.F.; Amy, D.; Bamber, J.C.; et al. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 3: Liver. Ultrasound Med. Biol. 2015, 41, 1161–1179. [Google Scholar] [CrossRef]
- Cosgrove, D.; Barr, R.; Bojunga, J.; Cantisani, V.; Chammas, M.C.; Dighe, M.; Vinayak, S.; Xu, J.-M.; Dietrich, C.F. WFUMB guidelines and recommendations on the clinical use of ultrasound elastography: Part 4. Thyroid. Ultrasound Med. Biol. 2017, 43, 4–26. [Google Scholar] [CrossRef]
- Sugimoto, K.; Moriyasu, F.; Oshiro, H.; Takeuchi, H.; Yoshimasu, Y.; Kasai, Y.; Itoi, T. Clinical utilization of shear wave dispersion imaging in diffuse liver disease. Ultrasonography 2020, 39, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Ohmaru, T.; Fujita, Y.; Sugitani, M.; Shimokawa, M.; Fukushima, K.; Kato, K. Placental elasticity evaluation using virtual touch tissue quantification during pregnancy. Placenta 2015, 36, 915–920. [Google Scholar] [CrossRef] [PubMed]
- Edwards, C.; Cavanagh, E.; Kumar, S.; Clifton, V.; Fontanarosa, D. The use of elastography in placental research—A literature review. Placenta 2020, 99, 78–88. [Google Scholar] [CrossRef]
- Palmeri, M.; Nightingale, K.; Fielding, S.; Rouze, N.; Deng, Y.; Lynch, T.; Chen, S.; Song, P.; Urban, M.; Xie, H.; et al. RSNA QIBA ultrasound shear wave speed phase II phantom study in viscoelastic media. In Proceedings of the 2015 IEEE International Ultrasonics Symposium (IUS), Taipei, Taiwan, 16 November 2015; Volume 3, pp. 1–4. [Google Scholar]
- Shiina, T.; Nightingale, K.R.; Palmeri, M.L.; Hall, T.J.; Bamber, J.C.; Barr, R.G.; Castera, L.; Choi, B.I.; Chou, Y.-H.; Cosgrove, D.; et al. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 1: Basic principles and terminology. Ultrasound Med. Biol. 2015, 41, 1126–1147. [Google Scholar] [CrossRef] [PubMed]
- Hudson, J.M.; Milot, L.; Parry, C.; Williams, R.; Burns, P.N. Inter- and intra-operator reliability and repeatability of shear wave elastography in the liver: A study in healthy volunteers. Ultrasound Med. Biol. 2013, 39, 950–955. [Google Scholar] [CrossRef]
- Hwang, J.; Yoon, H.M.; Jung, A.Y.; Lee, J.S.; Cho, Y.A. Comparison of 2-dimensional shear wave elastographic measurements using elastq imaging and supersonic shear imaging: Phantom study and clinical pilot study. J. Ultrasound Med. 2020, 39, 311–321. [Google Scholar] [CrossRef]
- Franchi-Abella, S.; Elie, C.; Correas, J.-M. Performances and limitations of several ultrasound-based elastography techniques: A phantom study. Ultrasound Med. Biol. 2017, 43, 2402–2415. [Google Scholar] [CrossRef] [PubMed]
- Ferraioli, G.; De Silvestri, A.; Lissandrin, R.; Maiocchi, L.; Tinelli, C.; Filice, C.; Barr, R.G. Evaluation of inter-system variability in liver stiffness measurements. Ultraschall Med. Eur. J. Ultrasound 2018, 40, 64–75. [Google Scholar] [CrossRef]
- Shin, H.J.; Kim, M.-J.; Kim, H.Y.; Roh, Y.H.; Lee, M.-J. Comparison of shear wave velocities on ultrasound elastography between different machines, transducers, and acquisition depths: A phantom study. Eur. Radiol. 2016, 26, 3361–3367. [Google Scholar] [CrossRef] [PubMed]
- Bunting, K.V.; Steeds, R.P.; Slater, L.T.; Rogers, J.K.; Gkoutos, G.V.; Kotecha, D. A Practical guide to assess the reproducibility of echocardiographic measurements. J. Am. Soc. Echocardiogr. 2019, 32, 1505–1515. [Google Scholar] [CrossRef]
- Carlsen, J.F.; Pedersen, M.R.; Ewertsen, C.; Saftoiu, A.; Lönn, L.; Rafaelsen, S.R.; Nielsen, M.B. A comparative study of strain and shear-wave elastography in an elasticity phantom. Am. J. Roentgenol. 2015, 204, W236–W242. [Google Scholar] [CrossRef]
- Hall, T.J.; Milkowski, A.; Garra, B.; Carson, P.; Palmeri, M.; Nightingale, K.; Lynch, T.; Alturki, A.; Andre, M.; Audière, S.; et al. RSNA/QIBA: Shear wave speed as a biomarker for liver fibrosis staging. In Proceedings of the 2013 IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 397–400. [Google Scholar] [CrossRef]
- Chang, S.; Kim, M.-J.; Kim, J.; Lee, M.-J. Variability of shear wave velocity using different frequencies in Acoustic Radiation Force Impulse (ARFI) elastography: A phantom and normal liver study. Ultraschall Med. Eur. J. Ultrasound 2012, 34, 260–265. [Google Scholar] [CrossRef]
- Thiele, M.; Madsen, B.S.; Procopet, B.; Hansen, J.F.; Møller, L.M.S.; Detlefsen, S.; Berzigotti, A.; Krag, A. Reliability criteria for liver stiffness measurements with real-time 2D shear wave elastography in different clinical scenarios of chronic liver disease. Ultraschall Med. Eur. J. Ultrasound 2017, 38, 648–654. [Google Scholar] [CrossRef]
- Dietrich, C.F.; Bamber, J.; Berzigotti, A.; Bota, S.; Cantisani, V.; Castera, L.; Cosgrove, D.; Ferraioli, G.; Friedrich-Rust, M.; Gilja, O.H.; et al. EFSUMB guidelines and recommendations on the clinical use of liver ultrasound elastography, update 2017 (long version). Ultraschall Med. Eur. J. Ultrasound 2017, 38, e16–e47. [Google Scholar] [CrossRef]
- Nadebaum, D.P.; Nicoll, A.J.; Sood, S.; Gorelik, A.; Gibson, R.N. Variability of liver shear wave measurements using a new ultrasound elastographic technique. J. Ultrasound Med. 2018, 37, 647–656. [Google Scholar] [CrossRef]
- Jeon, S.K.; Lee, J.M.; Joo, I.; Yoon, J.H.; Lee, D.H.; Han, J.K. Two-dimensional shear wave elastography with propagation maps for the assessment of liver fibrosis and clinically significant portal hypertension in patients with chronic liver disease: A prospective study. Acad. Radiol. 2020, 27, 798–806. [Google Scholar] [CrossRef] [PubMed]
- Elasticity, Q.A. Phantom—CIRS. Available online: https://www.cirsinc.com/products/ultrasound/zerdine-hydrogel/elasticity-qa-phantom/ (accessed on 7 January 2020).
- Cournane, S.; Fagan, A.J.; E Browne, J. Review of ultrasound elastography quality control and training test phantoms. Ultrasound 2011, 20, 16–23. [Google Scholar] [CrossRef]
- Mulabecirovic, A.; Gilja, O.; Mjelle, A.B.; Havre, R.F. In vitro quantification of tissue elasticity using three shear wave elastography platforms on liver fibrosis phantoms. Ultraschall Med. Eur. J. Ultrasound 2016, 37, E9_05. [Google Scholar] [CrossRef]
- Fernandes, D.A.; Kolios, M.C. Near-infrared absorbing nanoemulsions as nonlinear ultrasound contrast agents for cancer theranostics. J. Mol. Liq. 2019, 287, 110848. [Google Scholar] [CrossRef]
- Fernandes, D.A.; Fernandes, D.D.; Li, Y.; Wang, Y.; Zhang, Z.; Rousseau, D.; Gradinaru, C.C.; Kolios, M.C. Synthesis of stable multifunctional perfluorocarbon nanoemulsions for cancer therapy and imaging. Langmuir 2016, 32, 10870–10880. [Google Scholar] [CrossRef] [PubMed]
- Youk, J.H.; Gweon, H.M.; Son, E.J. Shear-wave elastography in breast ultrasonography: The state of the art. Ultrasonography 2017, 36, 300–309. [Google Scholar] [CrossRef] [PubMed]
- Bamber, J.; Cosgrove, D.; Dietrich, C.F.; Fromageau, J.; Bojunga, J.; Calliada, F.; Cantisani, V.; Correas, J.-M.; D’Onofrio, M.; Drakonaki, E.E.; et al. EFSUMB guidelines and recommendations on the clinical use of ultrasound elastography. Part 1: Basic principles and technology. Ultraschall Med. Eur. J. Ultrasound 2013, 34, 169–184. [Google Scholar] [CrossRef] [PubMed]
- O’Hara, S.; Zelesco, M.; Rocke, K.; Stevenson, G.; Sun, Z. Reliability Indicators for 2-Dimensional Shear Wave Elastography. J. Ultrasound Med. 2019, 38, 3065–3071. [Google Scholar] [CrossRef]
- Kwak, S.G.; Kim, J.H. Central limit theorem: The cornerstone of modern statistics. Korean J. Anesthesiol. 2017, 70, 144–156. [Google Scholar] [CrossRef]
- Ferraioli, G.; Wong, V.W.-S.; Castera, L.; Berzigotti, A.; Sporea, I.; Dietrich, C.F.; Choi, B.I.; Wilson, S.R.; Kudo, M.; Barr, R.G. Liver ultrasound elastography: An update to the world federation for ultrasound in medicine and biology guidelines and recommendations. Ultrasound Med. Biol. 2018, 44, 2419–2440. [Google Scholar] [CrossRef]
- Altman, D.G. Practical Statistics for Medical Research; Chapman & Hall/CRC: Boca Raton, FL, USA, 1999; ISBN 9780412276309. [Google Scholar]
- Fleiss, J.L. Reliability of Measurement. Des. Anal. Clin. Exp. 2011, 1–32. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Hills, M.; Fleiss, J.L. The design and analysis of clinical experiments. J. R. Stat. Soc. Ser. A (Gen.) 1987, 150, 400. [Google Scholar] [CrossRef]
- Vaz, S.; Falkmer, T.; Passmore, A.E.; Parsons, R.; Andreou, P. The case for using the repeatability coefficient when calculating test-retest reliability. PLoS ONE 2013, 8, e73990. [Google Scholar] [CrossRef]
- Huang, Z.; Zheng, J.; Zeng, J.; Wang, X.; Wu, T.; Zheng, R. Normal liver stiffness in healthy adults assessed by real-time shear wave elastography and factors that influence this method. Ultrasound Med. Biol. 2014, 40, 2549–2555. [Google Scholar] [CrossRef] [PubMed]
- Cosgrove, D.; Piscaglia, F.; Bamber, J.; Bojunga, J.; Correas, J.-M.; Gilja, O.H.; Klauser, A.S.; Sporea, I.; Calliada, F.; Cantisani, V.; et al. EFSUMB guidelines and recommendations on the clinical use of ultrasound elastography. Part 2: Clinical applications. Ultraschall Med. Eur. J. Ultrasound 2013, 34, 238–253. [Google Scholar] [CrossRef]
- Chen, S.; Urban, M.W.; Pislaru, C.; Kinnick, R.; Zheng, Y.; Yao, A.; Greenleaf, J.F. Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 55–62. [Google Scholar] [CrossRef]
- Wang, M.; Byram, B.; Palmeri, M.; Rouze, N.; Nightingale, K. On the precision of time-of-flight shear wave speed estimation in homogeneous soft solids: Initial results using a matrix array transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 758–770. [Google Scholar] [CrossRef]
- Zhao, H.; Song, P.; Urban, M.W.; Kinnick, R.R.; Yin, M.; Greenleaf, J.F.; Chen, S. Bias observed in time-of-flight shear wave speed measurements using radiation force of a focused ultrasound beam. Ultrasound Med. Biol. 2011, 37, 1884–1892. [Google Scholar] [CrossRef]
- Palmeri, M.L.; McAleavey, S.A.; Trahey, G.E.; Nightingale, K.R. Ultrasonic tracking of acoustic radiation force-induced displacements in homogeneous media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1300–1313. [Google Scholar] [CrossRef]
- Ferraioli, G.; Tinelli, C.; Zicchetti, M.; Above, E.; Poma, G.; Di Gregorio, M.; Filice, C. Reproducibility of real-time shear wave elastography in the evaluation of liver elasticity. Eur. J. Radiol. 2012, 81, 3102–3106. [Google Scholar] [CrossRef]
- Mun, H.S.; Choi, S.H.; Kook, S.H.; Choi, Y.; Jeong, W.K.; Kim, Y. Validation of intra- and interobserver reproducibility of shearwave elastography: Phantom study. Ultrasonics 2013, 53, 1039–1043. [Google Scholar] [CrossRef] [PubMed]
- Fadl, S.; Moshiri, M.; Fligner, C.L.; Katz, D.S.; Dighe, M. Placental imaging: Normal appearance with review of pathologic findings. Radiographics 2017, 37, 979–998. [Google Scholar] [CrossRef] [PubMed]
- Abramowicz, J.; Sheiner, E. Ultrasound of the placenta: A systematic approach. Part I: Imaging. Placenta 2008, 29, 225–240. [Google Scholar] [CrossRef]
- Rheinboldt, M.; DelProposto, Z. Sonography of placental abnormalities: A pictorial review. Emerg. Radiol. 2015, 22, 401–408. [Google Scholar] [CrossRef] [PubMed]
- Oudry, J.; Lynch, T.; Vappou, J.; Sandrin, L.; Miette, V. Comparison of four different techniques to evaluate the elastic properties of phantom in elastography: Is there a gold standard? Phys. Med. Biol. 2014, 59, 5775–5793. [Google Scholar] [CrossRef]
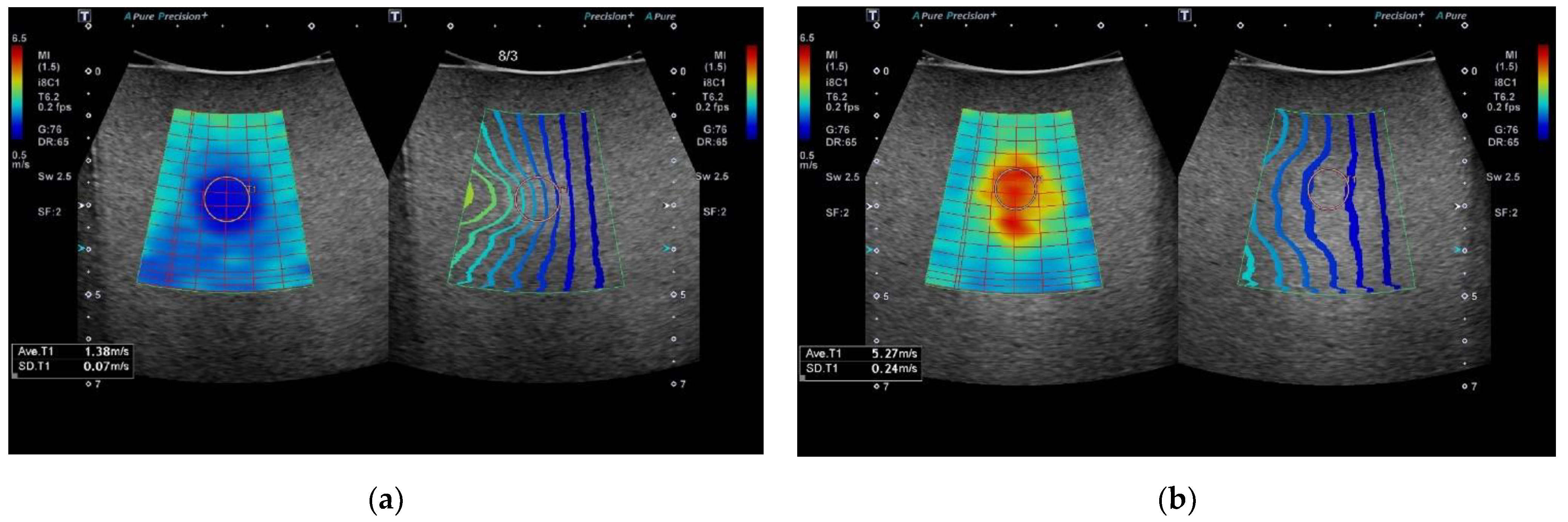
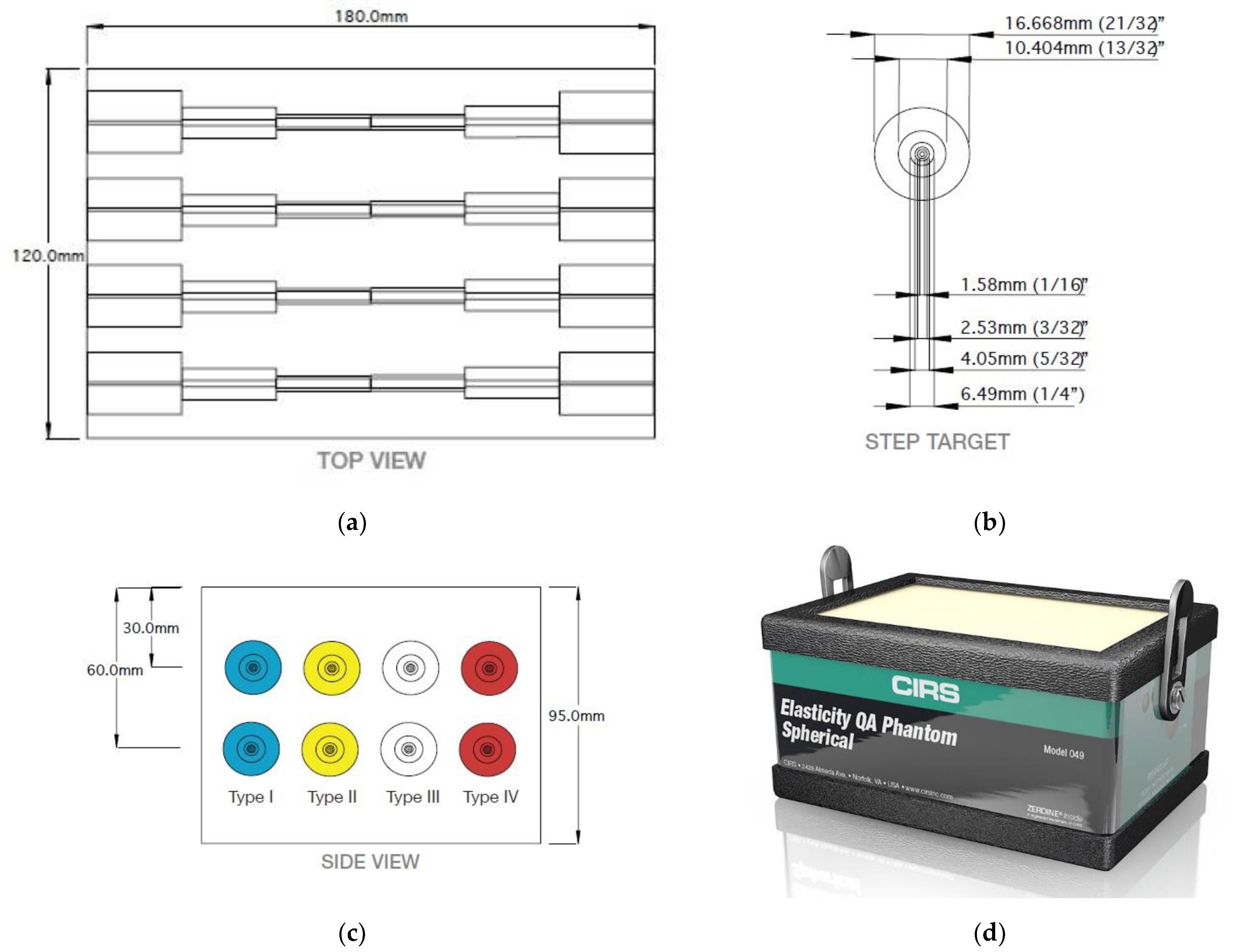
| Operator Type | ICC at 3 cm (95% CI) | ICC at 6 cm (95% CI) |
|---|---|---|
| 3 Operators | 0.976 (0.971–0.986) | 0.918(0.878–0.945) |
| 2 Operators (experienced + less experienced) | 0.978 (0.967–0.985) | 0.88 (0.823–0.919) |
| Target | Depth | Repeatability Coefficient | Coefficient of Variation |
|---|---|---|---|
| Type I (10 kPa) | 3 cm | 0.06–0.07 m/s | 1.5–1.8% |
| 6 cm | 0.21–0.24 m/s | 5.5–5.7% | |
| Type II (17 kPa) | 3 cm | 0.07–0.08 m/s | 1.3–1.4% |
| 6 cm | 0.21–0.22 m/s | 3.9–4.0% | |
| Background (25 kPa) | 3 cm | 0.31–0.55 m/s | 4.1–6.5% |
| 6 cm | 0.67–0.81 m/s | 5.5–10.4% | |
| Type III (47 kPa) | 3 cm | 0.53–0.68 m/s | 5.3–7.3% |
| 6 cm | 0.80–0.86 m/s | 9.2–11.0% | |
| Type IV (85 kPa) | 3 cm | 1.23–1.93 m/s | 10.2–15.2% |
| 6 cm | 0.82–1.13 m/s | 7.8–11.7% |
| Target | 5 mm ROI | 10 mm ROI | Significance |
|---|---|---|---|
| Type I (10 kPa) | 1.41 ± 0.04 m/s | 1.41 ± 0.04 m/s | p = 0.266 |
| Type II (17 kPa) | 1.96 ± 0.06 m/s | 1.95 ± 0.04 m/s | p = 0.396 |
| Background (25 kPa) | 2.37 ± 0.08 m/s | 2.3 ± 0.2 m/s | p = 0.105 |
| Type III (47 kPa) | 3.2 ± 0.4 m/s | 3.2 ± 0.4 m/s | p = 0.776 |
| Type IV (85 kPa) | 4.3 ± 0.5 m/s | 3.9 ± 0.6 m/s | p < 0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edwards, C.; Cavanagh, E.; Kumar, S.; Clifton, V.; Fontanarosa, D. Intra-System Reliability Assessment of 2-Dimensional Shear Wave Elastography. Appl. Sci. 2021, 11, 2992. https://doi.org/10.3390/app11072992
Edwards C, Cavanagh E, Kumar S, Clifton V, Fontanarosa D. Intra-System Reliability Assessment of 2-Dimensional Shear Wave Elastography. Applied Sciences. 2021; 11(7):2992. https://doi.org/10.3390/app11072992
Chicago/Turabian StyleEdwards, Christopher, Erika Cavanagh, Sailesh Kumar, Vicki Clifton, and Davide Fontanarosa. 2021. "Intra-System Reliability Assessment of 2-Dimensional Shear Wave Elastography" Applied Sciences 11, no. 7: 2992. https://doi.org/10.3390/app11072992
APA StyleEdwards, C., Cavanagh, E., Kumar, S., Clifton, V., & Fontanarosa, D. (2021). Intra-System Reliability Assessment of 2-Dimensional Shear Wave Elastography. Applied Sciences, 11(7), 2992. https://doi.org/10.3390/app11072992







