Low-Cost Active Anomaly Detection with Switching Latency
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions
1.3. Organization
2. System Model and Problem Formulation
2.1. System Model
2.2. Notations
3. The DMSC Policy
3.1. The DMSC Policy
| Algorithm 1: The deterministic (DMSC) policy. |
| Input: The observations y, the distributions f and g, the number of processes M, the number of anomalies L, the ratio s, the error constraint |
| Output: The set of anomalies |
| 1 Initial the sum-LLRs of the processes for ; |
| 2 Calculate the declaration threshold B according to (13); |
| 3 Calculate the statistics according to (8); |
| 4 if then |
| 5 while the number of declared processes < L do |
| 6 Probe the process with the highest sum-LLRs: ; |
| 7 Obtain an observation from the process ; |
| 8 Update based on the last observation according to (6); |
| 9 if then |
| 10 Declare the process as abnormal; |
| 11 end |
| 12 end |
| 13 Declare the L declared processes as abnormal. |
| 14 else |
| 15 while the number of declared processes < do |
| 16 Probe the process with the lowest sum-LLRs: ; |
| 17 Obtain an observation from the process ; |
| 18 Update based on the last observation according to (6); |
| 19 if then |
| 20 Declare the process as normal; |
| 21 end |
| 22 end |
| 23 Declare the remaining L processes as abnormal. |
| 24 end |
3.2. Example
3.3. Performance Analysis
3.3.1. Performance Analysis for Scenario 1
3.3.2. Performance Analysis for Scenario 2
4. Numerical Results
4.1. Scenario 1:
4.2. Scenario 2:
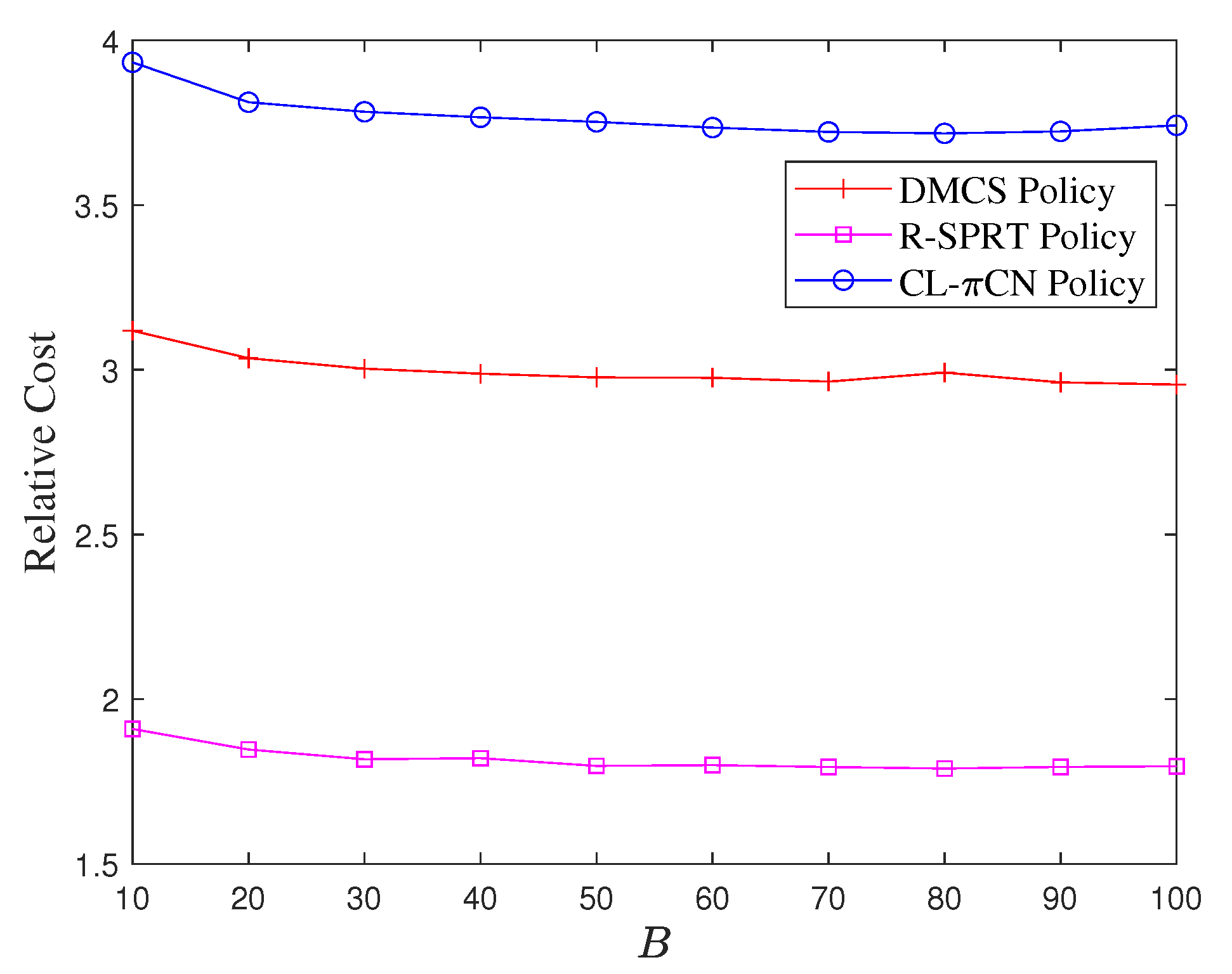
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof for Theorems
Appendix A.1. The Asymptotic Lower Bound on the Expected Cumulative Cost
Appendix A.2. The Expected Cumulative Cost of DMSC Policy
Appendix A.3. Asymptotically Optimality of DMSC Policy
Appendix A.4. Order-Optimality of DMSC Policy
References
- Wald, A. Sequential Analysis; Courier Corporation: New York, NY, USA, 2004. [Google Scholar]
- Lai, T.L. Nearly optimal sequential tests of composite hypotheses. Ann. Stat. 1988, 16, 856–886. [Google Scholar] [CrossRef]
- Pavlov, I.V. Sequential procedure of testing composite hypotheses with applications to the Kiefer–Weiss problem. Theory Probab. Its Appl. 1991, 35, 280–292. [Google Scholar] [CrossRef]
- Draglia, V.; Tartakovsky, A.G.; Veeravalli, V.V. Multihypothesis sequential probability ratio tests. I. Asymptotic optimality. IEEE Trans. Inf. Theory 1999, 45, 2448–2461. [Google Scholar] [CrossRef]
- Afshari, R.; Gildeh, B.S. Modified sequential sampling plan using fuzzy SPRT. In Proceedings of the 2017 5th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Qazvin, Iran, 7–9 March 2017; pp. 116–121. [Google Scholar]
- Zuo, J.; Ding, J.; Feng, F. Latent Leakage Fault Identification and Diagnosis Based on Multi-Source Information Fusion Method for Key Pneumatic Units in Chinese Standard Electric Multiple Units (EMU) Braking System. Appl. Sci. 2019, 9, 300. [Google Scholar] [CrossRef]
- Ainsleigh, P.L.; Luginbuhl, T.E.; Willett, P.K. A Sequential Target Existence Statistic for Joint Probabilistic Data Association. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 371–381. [Google Scholar] [CrossRef]
- Lee, D.H.; Chang, I.H.; Pham, H. Software reliability model with dependent failures and SPRT. Mathematics 2020, 8, 1366. [Google Scholar] [CrossRef]
- Chernoff, H. Sequential design of experiments. Ann. Math. Stat. 1959, 30, 755–770. [Google Scholar] [CrossRef]
- Bessler, S.A. Theory and Applications of the Sequential Design of Experiments, k-Actions and Infinitely Many Experiments. Part I. Theory; Technical report; Stanford University CA Applied Mathematics and Statistics Labs: Stanford, CA, USA, 1960. [Google Scholar]
- Naghshvar, M.; Javidi, T. Active M-ary sequential hypothesis testing. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 1623–1627. [Google Scholar]
- Naghshvar, M.; Javidi, T. Active sequential hypothesis testing. Ann. Stat. 2013, 41, 2703–2738. [Google Scholar] [CrossRef]
- Naghshvar, M.; Javidi, T. Information utility in active sequential hypothesis testing. In Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–1 October 2010; pp. 123–129. [Google Scholar]
- Naghshvar, M.; Javidi, T. Performance bounds for active sequential hypothesis testing. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; pp. 2666–2670. [Google Scholar]
- Naghshvar, M.; Javidi, T. Sequentiality and adaptivity gains in active hypothesis testing. IEEE J. Sel. Top. Signal Process. 2013, 7, 768–782. [Google Scholar] [CrossRef][Green Version]
- Cohen, K.; Zhao, Q. Active hypothesis testing for anomaly detection. IEEE Trans. Inf. Theory 2015, 61, 1432–1450. [Google Scholar] [CrossRef]
- Wang, C.; Cohen, K.; Zhao, Q. Active hypothesis testing on a tree: Anomaly detection under hierarchical observations. In Proceedings of the International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 993–997. [Google Scholar]
- Wang, C.; Cohen, K.; Zhao, Q. Information-Directed Random Walk for Rare Event Detection in Hierarchical Processes. IEEE Trans. Inf. Theory 2020, 67, 1099–1116. [Google Scholar] [CrossRef]
- Huang, B.; Cohen, K.; Zhao, Q. Active anomaly detection in heterogeneous processes. IEEE Trans. Inf. Theory 2018, 65, 2284–2301. [Google Scholar] [CrossRef]
- Hemo, B.; Gafni, T.; Cohen, K.; Zhao, Q. Searching for Anomalies Over Composite Hypotheses. IEEE Trans. Signal Process. 2020, 68, 1181–1196. [Google Scholar] [CrossRef]
- Cohen, K.; Zhao, Q.; Swami, A. Optimal index policies for anomaly localization in resource-constrained cyber systems. IEEE Trans. Signal Process. 2014, 62, 4224–4236. [Google Scholar] [CrossRef]
- Cohen, K.; Zhao, Q. Asymptotically optimal anomaly detection via sequential testing. IEEE Trans. Signal Process. 2015, 63, 2929–2941. [Google Scholar] [CrossRef]
- Gurevich, A.; Cohen, K.; Zhao, Q. Sequential anomaly detection under a nonlinear system cost. IEEE Trans. Signal Process. 2019, 67, 3689–3703. [Google Scholar] [CrossRef]
- Vaidhiyan, N.K.; Sundaresan, R. Active search with a cost for switching actions. In Proceedings of the 2015 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 1–6 February 2015; pp. 17–24. [Google Scholar]
- Chen, D.; Huang, Q.; Feng, H.; Zhao, Q.; Hu, B. Active anomaly detection with switching cost. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 5346–5350. [Google Scholar]
- Qin, F.; Chen, D.; Feng, H.; Zhao, Q.; Yang, T.; Hu, B. Active Anomaly Detection with Switching Cost. arXiv 2021, arXiv:1810.11800. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, F.; Feng, H.; Yang, T.; Hu, B. Low-Cost Active Anomaly Detection with Switching Latency. Appl. Sci. 2021, 11, 2976. https://doi.org/10.3390/app11072976
Qin F, Feng H, Yang T, Hu B. Low-Cost Active Anomaly Detection with Switching Latency. Applied Sciences. 2021; 11(7):2976. https://doi.org/10.3390/app11072976
Chicago/Turabian StyleQin, Fengfan, Hui Feng, Tao Yang, and Bo Hu. 2021. "Low-Cost Active Anomaly Detection with Switching Latency" Applied Sciences 11, no. 7: 2976. https://doi.org/10.3390/app11072976
APA StyleQin, F., Feng, H., Yang, T., & Hu, B. (2021). Low-Cost Active Anomaly Detection with Switching Latency. Applied Sciences, 11(7), 2976. https://doi.org/10.3390/app11072976







